On rheological characteristics of non-Newtonian nanofluids in the material forming process

Abstract

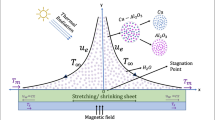
In this paper, the material forming process (such as that of the functionally graded materials) of adding nanoparticles into non-Newtonian fluids is considered. By adding nanoparticles to a non-Newtonian fluid, a new non-Newtonian fluid is created. Thus, the rheological characteristics of the original fluid matrix have been changed. This research attempts to consider the influence of the rheological characteristics combined with the Brownian diffusion, and the thermophoresis diffusion, the distribution of nano-sized particles, the heat transfer, and the pressure drop on the process of material formation. The configuration of material treatment process is an H-height horizontal parallel plate channel with laminar forced convection nanofluids-based non-Newtonian fluids flowing through. The channel is separated by three different boundary conditions: heating, cooling, and isolated, to simulate the melting, the freezing, and the flowing processes of materials in liquid form. The non-Newtonian behaviour of nanofluids is described by the power-law model. To highlight the rheological factors of power-law nanofluids which are not the same as those of the base non-Newtonian fluids, they are assumed to vary with the quantity of the added nanoparticles in the fluid matrix, that is to say, both the consistency coefficient $m$ and the power-law index $n$ are considered as functions of particle loading parameter $\phi$. Two sets of different functions of consistency coefficient $m$ and power-law index $n$ are used and compared in the later calculation. Method of finite element is adopted to solve the coupled momentum, energy and concentration equations, and conquer the difficulties arsing in the iteration of calculation. It is found that whether the rheological factors of non-Newtonian nanofluids are considered changeable or not would lead to very different results of the mass transfer. Also, as the parameter $N_{\text{T}}$ (depicting the thermophoresis diffusion) increases, both temperature and concentration profiles rise, while volume fraction of particles and temperature both fall as $N_{\text{B}}$ number (presenting the Brownian diffusion) increases. Furthermore, when two models are compared, different rheological models may possess different change rule of power-law index, but in both rheological models, the diversification of power-law index is so large that it cannot be ignored in calculation. Above all, the detailed information of velocity, temperature, and pressure drop obtained by rheological models highlights the necessity of studying the impact of rheological characteristics of non-Newtonian fluids in elaborate industrial requirements.

Appendix

Define the domain as $\varOmega \subset R^{2}$. Denote the boundary of $\varOmega$ by $\varGamma$, which is sufficiently smooth. Consider $u$ and $v$ in space ${\rm Z}$, which is defined as $H^{1} (\varOmega )$ if $n \le 1$ or $W^{1,\,n + 1} (\varOmega )$ if $n > 1$; $T$ and $\phi$ in $W$, which is defined as $W^{1,4} (\varOmega )$ if $n \le 3$ or $W^{1,\,n + 1} (\varOmega )$ if $n > 3$, and $p$ in $L^{2} (\varOmega )$ (see Shi et al. 2014). The weak formulation of the conservation equations is as follows:

$$\int_{\varOmega } {\left( {\left( {\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}} \right)v_{0} } \right){\text{d}}{\mathbf{x}} = 0} ,\forall v_{0} \in L^{2} (\varOmega )$$

(20)

$$\int_{\varOmega } {\left( {{\text{Re}}\left( {\left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right)v_{1} } \right) - \frac{{\partial v_{1} }}{\partial x}p + \frac{{\partial v_{1} }}{\partial x}\tau_{xx} + \frac{{\partial v_{1} }}{\partial y}\tau_{yx} } \right)} {\text{d}}{\mathbf{x}} + \int\limits_{\varGamma } {pv_{1} {\text{d}}s} = 0\quad \forall v_{1} \in {\rm Z}$$

(21)

$$\begin{aligned} \int_{\varOmega } {\left( {{\text{Re}}\left( {\left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right)v_{2} } \right) - \frac{{\partial v_{2} }}{\partial y}p + \frac{{\partial v_{2} }}{\partial x}\tau_{xy} + \frac{{\partial v_{2} }}{\partial y}\tau_{yy} } \right)} {\text{d}}{\mathbf{x}} \hfill \\ - \int\limits_{\varGamma } {\left( {2\left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} } \right)^{{\frac{n - 1}{2}}} \frac{\partial u}{\partial y}v_{2} {\text{d}}s} = 0,\forall v_{2} \in {\rm Z} \hfill \\ \end{aligned}$$

(22)

$$\begin{aligned} \int_{\varOmega } {\left( \begin{aligned} {\text{Re}} \cdot { \Pr }\left( {\left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right)v_{3} } \right) + \frac{{k_{\text{eff}} }}{{k_{f} }}\left( {\frac{\partial T}{\partial x}\frac{{\partial v_{3} }}{\partial x} + \frac{\partial T}{\partial y}\frac{{\partial v_{3} }}{\partial y}} \right) - \hfill \\ {\text{Re}} \cdot { \Pr }\left( {N_{\text{B}} \left( {\frac{\partial \phi }{\partial x}\frac{\partial T}{\partial x} + \frac{\partial \phi }{\partial y}\frac{\partial T}{\partial y}} \right)v_{3} + N_{\text{T}} \left( {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right)v_{3} } \right) \hfill \\ \end{aligned} \right)} {\text{d}}{\mathbf{x}} \hfill \\ + \int_{{\varGamma_{1} }} {q_{1} v_{3} {\text{d}}s} + \int_{{\varGamma_{2} }} {q_{2} v_{3} {\text{d}}s} = 0,\forall v_{3} \in {\rm Z} \hfill \\ \end{aligned}$$

(23)

$$\begin{aligned} \int_{\varOmega } {\left( {{\text{Re}} \cdot {\text{Sc}}\left( {\left( {u\frac{\partial \phi }{\partial x} + v\frac{\partial \phi }{\partial y}} \right)v_{4} } \right) + \frac{\partial \phi }{\partial x}\frac{{\partial v_{4} }}{\partial x} + \frac{\partial \phi }{\partial y}\frac{{\partial v_{4} }}{\partial y} + \frac{{N_{\text{T}} }}{{N_{\text{B}} }}\left( {\frac{\partial T}{\partial x}\frac{{\partial v_{4} }}{\partial x} + \frac{\partial T}{\partial y}\frac{{\partial v_{4} }}{\partial y}} \right)} \right)} {\text{d}}{\mathbf{x}} \hfill \\ + \int_{{\varGamma_{1} }} {\frac{{N_{\text{T}} }}{{N_{\text{B}} }}q_{1} v_{4} {\text{d}}s} + \int_{{\varGamma_{2} }} {\frac{{N_{\text{T}} }}{{N_{\text{B}} }}q_{2} v_{4} {\text{d}}s} = 0,\forall v_{4} \in {\rm Z} \hfill \\ \end{aligned}$$

(24)

In the above weak formulation, a unique item $- \int\nolimits_{\varGamma } {\left( {2\left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} } \right)^{{\frac{n - 1}{2}}} \frac{\partial u}{\partial y}v_{2} {\text{d}}s}$ has shown itself in weak formulation of the momentum conservation equations. It will only appear in the case of non-Newtonian fluids, which exhibit nonlinear viscous items.

To deal with the super-nonlinear terms $\tau_{ij}$ in equations (21–22), a specific iterative method is employed by introducing a ‘ghost’ time into the momentum equation:

$$\int_{\varOmega } {\left( {\frac{{\left( {u^{i} - u^{i - 1} } \right)}}{dt}v_{1} + {\text{Re}}\left( {\left( {u^{i - 1} \frac{{\partial u^{i - 1} }}{\partial x} + v^{i - 1} \frac{{\partial u^{i - 1} }}{\partial y}} \right)v_{1} } \right) - \frac{{\partial v_{1} }}{\partial x}p + \frac{{\partial v_{1} }}{\partial x}\tau_{xx}^{i - 1} + \frac{{\partial v_{1} }}{\partial y}\tau_{yx}^{i - 1} } \right)} {\text{d}}{\mathbf{x}} + \int\limits_{\varGamma } {pv_{1} {\text{d}}s} = 0$$

(25)

$$\begin{aligned} \int_{\varOmega } {\left( {\frac{{\left( {v^{i} - v^{i - 1} } \right)}}{{{\text{d}}t}}v_{2} + {\text{Re}}\left( {\left( {u^{i - 1} \frac{{\partial v^{i - 1} }}{\partial x} + v^{i - 1} \frac{{\partial v^{i - 1} }}{\partial y}} \right)v_{2} } \right) - \frac{{\partial v_{2} }}{\partial y}p + \frac{{\partial v_{2} }}{\partial x}\tau_{xy}^{i - 1} + \frac{{\partial v_{2} }}{\partial y}\tau_{yy}^{i - 1} } \right)} {\text{d}}{\mathbf{x}} \hfill \\ \quad \quad \quad \quad \quad \quad - \int\limits_{\varGamma } {\left( {2\left( {\frac{{\partial u^{i - 1} }}{\partial x}} \right)^{2} + 2\left( {\frac{{\partial v^{i - 1} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial u^{i - 1} }}{\partial y} + \frac{{\partial v^{i - 1} }}{\partial x}} \right)^{2} } \right)^{{\frac{n - 1}{2}}} \frac{{\partial u^{i - 1} }}{\partial y}v_{2} {\text{d}}s} = 0 \hfill \\ \end{aligned}$$

(26)

where

$$\tau_{xx}^{i - 1} = \frac{2m}{{m_{f} }}\left( {2\left( {\frac{{\partial u^{i - 1} }}{\partial x}} \right)^{2} + 2\left( {\frac{{\partial v^{i - 1} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial u^{i - 1} }}{\partial y} + \frac{{\partial v^{i - 1} }}{\partial x}} \right)^{2} } \right)^{{\frac{n - 1}{2}}} \frac{{\partial u^{i - 1} }}{\partial x}$$

$$\tau_{yx}^{i - 1} = \tau_{xy}^{i - 1} = \frac{m}{{m_{f} }}\left( {2\left( {\frac{{\partial u^{i - 1} }}{\partial x}} \right)^{2} + 2\left( {\frac{{\partial v^{i - 1} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial u^{i - 1} }}{\partial y} + \frac{{\partial v^{i - 1} }}{\partial x}} \right)^{2} } \right)^{{\frac{n - 1}{2}}} \left( {\frac{{\partial u^{i - 1} }}{\partial y} + \frac{{\partial v^{i - 1} }}{\partial x}} \right)$$

$$\tau_{yy}^{i - 1} = \frac{2m}{{m_{f} }}\left( {2\left( {\frac{{\partial u^{i - 1} }}{\partial x}} \right)^{2} + 2\left( {\frac{{\partial v^{i - 1} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial u^{i - 1} }}{\partial y} + \frac{{\partial v^{i - 1} }}{\partial x}} \right)^{2} } \right)^{{\frac{n - 1}{2}}} \frac{{\partial v^{i - 1} }}{\partial y}$$

(27)

${\text{d}}t > 0$ represents the time-step size. The superscript $i$ means data at $i \cdot {\text{d}}t$. The equation will hold even when the velocity is unchangeable once steady-state reaches. In the present research, the momentum equation is iterated 200 times to reach a steady-state.

Furthermore, the consistency coefficient $m$ and the power-law index $n$ are assumed varying as the particle loading parameter $\phi$, that is to say, following iterations should be included in the calculation:

$$m^{i} = f\left( {\phi^{i - 1} ,m_{f} } \right)$$

(28)

$$n^{i} = g(\phi^{i - 1} ,n_{f} )$$

(29)