Long-wave interface instabilities of a two-layer system under periodic excitation for thin films

Abstract

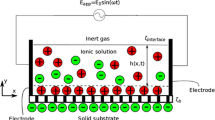
The stability of a system of two thin liquid films under AC electroosmotic flow is studied using linear stability analysis for long-wave disturbances. The system is bounded by two rigid plates which act as substrate. Boltzmann charge distribution is assumed for the two electrolyte solutions. The effect of van der Waals interactions in these thin films is incorporated in the momentum equations through the disjoining pressure. The base-state velocity profile from the present study is compared with simple experiments and other analytical results. Parametric study involving various electrochemical factors is performed and the stability behaviour is analysed using growth rate, marginal stability, critical amplitude and maximum growth rate in phase space. An increase in the disjoining pressure is found to decrease stability of the system. On the other hand, increasing the frequency of the applied electric field is found to stabilize the system. However, the dependence of the stability on parameters such as viscosity ratio, permittivity ratio, interface zeta potential and interface charge depends not only on the value of individual parameters but also on the rest of the parameters. Design of experiments (DOE) is used to observe the general trend of stability with different parameters.

Appendices

Appendix 1

The electric potential $\varPhi_{{{\text{sc}},i}}$ (i = 1, 2) due the space charge distribution can be written as follows:

$$ 0 < Y < 1: \varPhi_{{{\text{sc}},1}} = A_{1} {\text{e}}^{{\frac{Y}{{{\text{De}}_{1} }}}} + B_{1} {\text{e}}^{{ - \frac{Y}{{{\text{De}}_{1} }}}} $$

(57)

$$ 1 < Y < H_{2} : \varPhi_{{{\text{sc}},2}} = A_{2} {\text{e}}^{{\frac{Y}{{{\text{De}}_{2} }}}} + B_{2} {\text{e}}^{{ - \frac{Y}{{{\text{De}}_{2} }}}} $$

(58)

$$ A_{1} = \frac{{\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} \left( {1 + e^{{\frac{1}{{De_{1} }}}} De_{1} \bar{Q}_{I} } \right) + De_{1} \varepsilon_{R} \left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} - 2e^{{\frac{1}{{De_{1} }} + \frac{{1 + H_{2} }}{{De_{2} }}}} \left( {\text{Cosh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]\bar{\zeta }_{I} + \bar{\zeta }_{u} } \right)} \right)}}{{\left( {1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }} $$

$$ B_{1} = \frac{{e^{{\frac{1}{{De_{1} }}}} \left( {\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} \left( {e^{{\frac{1}{{De_{1} }}}} - De_{1} \bar{Q}_{I} } \right) - De_{1} \varepsilon_{R} \left( {e^{{\frac{1}{{De_{1} }}}} \left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right) - 2e^{{\frac{{1 + H_{2} }}{{De_{2} }}}} \left( {\text{Cosh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]\bar{\zeta }_{I} + \bar{\zeta }_{u} } \right)} \right)} \right)}}{{\left( {1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }} $$

$$ A_{2} = \frac{{2{\text{e}}^{{\left( {\frac{1}{{De_{1} }} + \frac{1}{{De_{2} }}} \right)}} De_{2} \left( {1 + {\text{Sinh}}\left[ {\frac{1}{{De_{1} }}} \right]De_{1} \bar{Q}_{I} - {\text{Cosh}}\left[ {\frac{1}{{De_{1} }}} \right]\bar{\zeta }_{I} } \right) - {\text{e}}^{{\frac{{H_{2} }}{{De_{2} }}}} \left( {De_{2} - De_{1} \varepsilon_{R} + {\text{e}}^{{\frac{2}{{De_{1} }}}} \left( {De_{2} + De_{1} \varepsilon_{R} } \right)} \right)\bar{\zeta }_{u} }}{{\left( {1 + {\text{e}}^{{\frac{2}{{De_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + {\text{e}}^{{\frac{2}{{De_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }} $$

$$ B_{2} = \frac{{e^{{\frac{{1 + H_{2} }}{{De_{2} }}}} \left( {2e^{{\frac{1}{{De_{1} }} + \frac{{H_{2} }}{{De_{2} }}}} De_{2} \left( {1 + \text{Sinh} \left[ {\frac{1}{{De_{1} }}} \right]De_{1} \bar{Q}_{I} - \text{Cosh} \left[ {\frac{1}{{De_{1} }}} \right]\bar{\zeta }_{I} } \right) - e^{{\frac{1}{{De_{2} }}}} \left( {De_{2} + De_{1} \varepsilon_{R} + e^{{\frac{2}{{De_{1} }}}} \left( {De_{2} - De_{1} \varepsilon_{R} } \right)} \right)\bar{\zeta }_{u} } \right)}}{{ - \left( {1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} + \left( { - 1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }} $$

Appendix 2

The set of equations with $\alpha^{0}$ order is as follows:

$$ \frac{{\partial^{4} \hat{\varPsi }_{1,0} }}{{\partial Y^{4} }} - {{Wo}}_{1}^{2} \frac{{\partial^{3} \hat{\varPsi }_{1,0} }}{{\partial \theta \partial Y^{2} }} = \sigma_{0} {{Wo}}_{1}^{2} \frac{{\partial^{2} \hat{\varPsi }_{1,0} }}{{\partial Y^{2} }} $$

(59)

$$ \frac{{\partial^{4} \hat{\varPsi }_{2,0} }}{{\partial Y^{4} }} - {{Wo}}_{2}^{2} \frac{{\partial^{3} \hat{\varPsi }_{2,0} }}{{\partial \theta \partial Y^{2} }} = \sigma_{0} {{Wo}}_{2}^{2} \frac{{\partial^{2} \hat{\varPsi }_{2,0} }}{{\partial Y^{2} }} $$

(60)

with the corresponding boundary conditions,

No slip and no penetration:

$$ \frac{{\partial \hat{\varPsi }_{1,0} }}{\partial Y}\left( {0,\theta } \right) = 0, \quad \hat{\varPsi }_{1,0} \left( {0,\theta } \right) = 0, \quad \frac{{\partial \hat{\varPsi }_{2,0} }}{\partial Y}\left( {H_{2} ,\theta } \right) = 0, \hat{\varPsi }_{2,0} \left( {H_{2} ,\theta } \right) = 0 $$

(61)

Shear stress balance:

$$ \begin{aligned} &\frac{{\partial^{2} \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \hat{H}_{0} \left( \theta \right)\frac{{\partial^{2} U_{1,b} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \hat{H}_{0} \left( \theta \right)\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial^{2} \varPhi_{1} \left( 1 \right)}}{{\partial Y^{2} }} \hfill \\ &\quad = \mu_{R} \left( {\frac{{\partial^{2} \hat{\varPsi }_{2,0} }}{{\partial Y^{2} }}\left( {1,\theta } \right) + \hat{H}_{0} \left( \theta \right)\frac{{\partial^{2} U_{2,b} \left( 1 \right)}}{{\partial Y^{2} }} + \gamma_{R,2} E_{R} \hat{H}_{0} \left( \theta \right)\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial^{2} \varPhi_{2} \left( 1 \right)}}{{\partial Y^{2} }}} \right) \hfill \\ \end{aligned} $$

(62)

Normal stress balance:

$$ \begin{aligned} &\frac{{\partial^{3} \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{{\partial Y^{3} }} - Wo_{1}^{2} \frac{{\partial^{2} \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial \theta \partial Y} - \sigma_{0} Wo_{1}^{2} \frac{{\partial \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial Y} \hfill \\ & \quad = \mu_{R} \left( {\frac{{\partial^{3} \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{{\partial Y^{3} }} - Wo_{2}^{2} \frac{{\partial^{2} \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial \theta \partial Y} - \sigma_{0} Wo_{2}^{2} \frac{{\partial \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial Y}} \right) \hfill \\ \end{aligned} $$

(63)

Continuity of normal and tangential velocity:

$$ \hat{\varPsi }_{1,0} \left( {H_{1} ,\theta } \right) = \hat{\varPsi }_{2,0} \left( {H_{1} ,\theta } \right) $$

(64)

$$ \hat{H}_{0} \left( \theta \right)\left( {\frac{{\partial U_{1,b} \left( {1,\theta } \right)}}{\partial Y} - \frac{{\partial U_{2,b} \left( {1,\theta } \right)}}{\partial Y}} \right) + \left( {\frac{{\partial \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial Y} - \frac{{\partial \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial Y}} \right) = 0 $$

(65)

Kinematic conditions:

$$ \frac{{{{Wo}}_{1}^{2} }}{{{{Re}}_{1} }}\frac{{\partial \hat{H}_{0} \left( \theta \right)}}{\partial \theta } + \sigma_{0} \frac{{{{Wo}}_{1}^{2} }}{{{{Re}}_{1} }}\hat{H}_{0} \left( \theta \right) = 0 $$

(66)

The set of equations with $\alpha^{1}$ order with $\sigma_{0} = 0$ and $\hat{H}_{0} = 1$ is as follows:

$$ \frac{{\partial^{4} \hat{\varPsi }_{1,1} }}{{\partial Y^{4} }} - {{Wo}}_{1}^{2} \frac{{\partial^{3} \hat{\varPsi }_{1,1} }}{{\partial \theta \partial Y^{2} }} - {{iRe}}_{1} U_{1,b} \frac{{\partial^{2} \hat{\varPsi }_{1,0} }}{{\partial Y^{2} }} + {{iRe}}_{1} \frac{{\partial^{2} U_{1,b} }}{{\partial Y^{2} }}\hat{\varPsi }_{1,0} = \sigma_{1} {{Wo}}_{1}^{2} \frac{{\partial^{2} \hat{\varPsi }_{1,0} }}{{\partial Y^{2} }} $$

(67)

$$ \frac{{\partial^{4} \hat{\varPsi }_{2,1} }}{{\partial Y^{4} }} - {{Wo}}_{2}^{2} \frac{{\partial^{3} \hat{\varPsi }_{2,1} }}{{\partial \theta \partial Y^{2} }} - {{iRe}}_{2} U_{2,b} \frac{{\partial^{2} \hat{\varPsi }_{2,0} }}{{\partial Y^{2} }} + {{iRe}}_{2} \frac{{\partial^{2} U_{2,b} }}{{\partial Y^{2} }}\hat{\varPsi }_{2,0} = \sigma_{1} {{Wo}}_{2}^{2} \frac{{\partial^{2} \hat{\varPsi }_{2,0} }}{{\partial Y^{2} }} $$

(68)

with the following boundary conditions:

No slip and no penetration:

$$ \frac{{\partial \hat{\varPsi }_{1,1} }}{\partial Y}\left( {0,\theta } \right) = 0, \hat{\varPsi }_{1,1} \left( {0,\theta } \right) = 0, \frac{{\partial \hat{\varPsi }_{2,1} }}{\partial Y}\left( {H_{2} ,\theta } \right) = 0, \hat{\varPsi }_{2,1} \left( {H_{2} ,\theta } \right) = 0 $$

(69)

Shear stress balance:

$$ \begin{aligned} &\frac{{\partial^{2} \hat{\varPsi }_{1,1} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \hat{H}_{1} \left( \theta \right)\frac{{\partial^{2} U_{1,b} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \hat{H}_{1} \left( \theta \right)\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial^{2} \varPhi_{1} \left( 1 \right)}}{{\partial Y^{2} }} \hfill \\ & \qquad - {\text{i}}\gamma_{R,1} E_{R} \hat{H}_{0} \left( \theta \right)\left( {\left( {\frac{{\partial \varPhi_{1} }}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right) \hfill \\ & \quad = \mu_{R} \left( {\frac{{\partial^{2} \hat{\varPsi }_{2,1} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \hat{H}_{1} \frac{{\partial^{2} U_{2,b} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \gamma_{R,2} E_{R} \hat{H}_{1} \left( \theta \right)\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial^{2} \varPhi_{2} \left( 1 \right)}}{{\partial Y^{2} }} - {\text{i}}\gamma_{R,2} E_{R} \hat{H}_{0} \left( \theta \right)\left( {\left( {\frac{{\partial \varPhi_{2} }}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{2} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right)} \right) \hfill \\ \end{aligned} $$

(70)

Normal stress balance:

$$ \begin{aligned} & \frac{{\partial^{3} \hat{\varPsi }_{1,1} \left( {1,\theta } \right)}}{{\partial Y^{3} }} - Wo_{1}^{2} \left( {\frac{{\partial^{2} \hat{\varPsi }_{1,1} \left( {1,\theta } \right)}}{\partial \theta \partial Y} + \sigma_{1} \frac{{\partial \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial Y}} \right) \hfill \\ &\qquad- iRe_{1} \left( {U_{1,b} \left( {1,\theta } \right)\frac{{\partial \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial Y} - \hat{\varPsi }_{1,0} \left( {1,\theta } \right)\frac{{\partial U_{1,b} \left( {1,\theta } \right)}}{\partial Y}} \right) \hfill \\ &\quad = i\left( {\frac{{\alpha^{2} }}{Ca} - \frac{{3A_{1} }}{{H_{1} }} - \mu_{R} \frac{{3A_{2} }}{{\left( {H_{2} - H_{1} } \right)}}} \right) \hfill \\ &\mu_{R} \left\{ {\frac{{\partial^{3} \hat{\varPsi }_{2,1} \left( {1,\theta } \right)}}{{\partial Y^{3} }} - Wo_{2}^{2} \left( {\frac{{\partial^{2} \hat{\varPsi }_{2,1} \left( {1,\theta } \right)}}{\partial \theta \partial Y} + \sigma_{1} \frac{{\partial \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial Y}} \right)} \right. \hfill \\ &\qquad -\left. { \,iRe_{2} \left( {U_{2,b} \left( {1,\theta } \right)\frac{{\partial \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial Y} - \hat{\varPsi }_{2,0} \left( {H_{1} ,\theta } \right)\frac{{\partial U_{2,b} \left( {1,\theta } \right)}}{\partial Y}} \right)} \right\} \hfill \\ \end{aligned} $$

(71)

Continuity of normal and tangential velocity:

$$ \hat{\varPsi }_{1,1} \left( {1,\theta } \right) = \hat{\varPsi }_{2,1} \left( {1,\theta } \right) $$

(72)

Kinematic conditions:

$$ \frac{{{{Wo}}_{1}^{2} }}{{{{Re}}_{1} }}\frac{{\partial \hat{H}_{1} \left( \theta \right)}}{\partial \theta } + \sigma_{1} \frac{{{{Wo}}_{1}^{2} }}{{{{Re}}_{1} }} + {\text{i}}U_{1,b} \left( {1,\theta } \right) = - {\text{i}}\hat{\varPsi }_{1,0} \left( {1,\theta } \right) $$

(73)

The kinematic condition in the first and second set of equations entails $\sigma_{0} = 0$ and $\sigma_{1} = 0$, respectively. Without loss of generality, $\hat{H}_{0} \left( \theta \right) = 1$ (Kamachi and Honji 1982). The periodic function $\hat{\varPsi }_{i,0}$ can be found by representing it as ${\text{Im}}\left( {G_{i,0} \left( Y \right){\text{e}}^{i\theta } } \right)$.

Kinematic condition corresponding to $\alpha^{2}$ order with $\sigma_{0} = 0$ and $\hat{H}_{0} = 1$:

$$ {{Wo}}_{1}^{2} \frac{{\partial \hat{H}_{2} \left( \theta \right)}}{\partial \theta } + \sigma_{2} {{Wo}}_{1}^{2} + {{iRe}}_{1} \left( {\hat{H}_{1} U_{1,b} \left( {1,\theta } \right) + \hat{\varPsi }_{1,1} \left( {1, \theta } \right)} \right) = 0 $$

(74)

Since $\hat{H}_{2} \left( \theta \right)$ must be periodic in time, $\sigma_{2}$ can be derived using only the steady part of $\hat{\varPsi }_{1,1}$. A set of time-independent equations is hence obtained from the second set (equations corresponding to $\alpha^{1}$). Since the two sets of equations are complicated owing to the number of parameters involved, they are solved by substituting the numerical values of the parameters with Mathematica’s differential equation solver package.

Considering the steady part of the above equation, expression for growth rate:

$$ \sigma_{2} = - \frac{{{{iRe}}_{1} }}{{{{Wo}}_{1}^{2} }}\left( { - H_{11} \frac{{\bar{F}_{1} \left( 1 \right)}}{{2{\text{i}}}} + H_{12} \frac{{F_{1} \left( 1 \right)}}{{2{\text{i}}}} + \hat{\varPsi }_{1,1s} \left( 1 \right)} \right) $$

(75)

$\hat{\varPsi }_{1,1s}$ is the steady part of $\hat{\varPsi }_{1,1}$. $H_{11}$ and $H_{12}$ are defined as follows:

$$ H_{11} = \frac{{{{iRe}}_{1} }}{{2{{Wo}}_{1}^{2} }}\left( {F_{1} \left( {H_{1} } \right) + G_{1,0} \left( {H_{1} } \right)} \right);H_{12} = \frac{{{{iRe}}_{1} }}{{2{{Wo}}_{1}^{2} }}\left( {\left( {\overline{{F_{1} }} \left( {H_{1} } \right) + \bar{G}_{1,0} \left( {H_{1} } \right)} \right)} \right) $$

G _1,0 (Y)is defined for $\hat{\varPsi }_{i,0} \left( {Y,\theta } \right)$ as follows:

$$ \hat{\varPsi }_{1,0} \left( {Y,\theta } \right) = {\text{Im}}\left( {G_{1,0} \left( Y \right){\text{e}}^{{{\text{i}}\theta }} } \right) $$

And $F_{1} \left( Y \right)$ is same as defined for the base state:

$$ U_{1,b} \left( {Y,\theta } \right) = {\text{Im}}\left( {F_{1} \left( Y \right){\text{e}}^{i\theta } } \right) $$

and $\bar{F}_{1} \left( Y \right)$ and $\bar{G}_{1,0} \left( Y \right)$ are the complex conjugates of $F_{1} \left( Y \right)$ and $G_{1,0} \left( Y \right)$, respectively.

Appendix 3

Table 1