Abstract
The ongoing development of microfluidic devices involves the use of highly complex fluids, even of multiphase systems. Despite the great achievements in the development of numerous applications, there is still a lack in the complete understanding of the underlying physics of the observed macroscopic effects. One prominent example is the flow through benchmark contractions where micro- and even macroscopic explanations of some of the occurring flow patterns are still missing. Here, we study the development of the flow profiles of shear thinning semi-dilute polymer solutions in microfluidic planar abrupt contraction geometries. Flow profiles along the narrow channel part are obtained by μ-PIV measurements, whereby the pressure drop along the microfluidic channel as well as the local transient viscosities downstream to the orifice are computed. A relaxation process of the flow profiles from an initially parabolic shape to the flattened steady-state flow profile is observed and traced back to the polymer relaxation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flow of complex fluids is ubiquitous to many applications of microfluidics (Stone et al. 2004). The resulting flow profiles depend on the nonlinear behavior of the medium and the channel geometry (van Steijn et al. 2007; Teh et al. 2008). While for continuous flow of complex fluids approximate solutions can predict the resulting flow profiles for standard geometries (Nguyen and Wereley 2002; Bruus 2009), much less is known on the phenomena occurring at sudden changes of channel geometry. One prominent example is the benchmark problem of entry flows into sudden contractions (Wassner et al. 1999; Alves et al. 2003; Lanzaro and Yuan 2011; Li et al. 2011; Hassell et al. 2011; Tamaddon Jahromi and Webster 2011; Sousa et al. 2011). Investigations on the entrance length of the flow of Newtonian fluids in microchannels (Ahmad and Hassan 2010) show that a steady-state flow profile is developed at a finite distance downstream to an orifice after the occurrence of small turbulences directly at the inlet. Nevertheless, with regards to non-Newtonian fluids, this situation is further complicated by the constriction geometry (Haward et al. 2010) as the extensional viscosity of the polymer dominates the fluid’s response upon channel entry. Thus, the history of polymer flow prior to channel entrance has to be taken into account (Pérez-Trejo et al. 1996). Recent studies show that the length of a constriction has even impact on the upstream flow kinematics (Rodd et al. 2010). Although detailed studies on a single-molecule level have proven to be powerful in addressing the effect of elongation on the polymer configuration (Perkins 1997; Smith 1998; Larson et al. 1999; Squires and Quake 2005; Steinhauser et al. 2012) and efforts are made in simulating and calculating the flows of complex fluids on different length scales (Feigl 1996; Doyle et al. 1998; Xue et al. 1998; Lindner et al. 2003; Kröger 2004; Lubansky et al. 2007; Castillo-Tejas et al. 2009), microscopic explanations for the observable macroscopic flow effects remain challenging. To this end, detailed studies on the flow behavior of these fluids in benchmark geometries and its relation to microscopic mechanisms are essential.
Here, we study the flow of semi-dilute polymer solutions with non-Newtonian properties in microfluidic channels. We observe that the relaxation process of the flow profiles after a planar abrupt contraction takes place on a millimeter length scale and on a 0.5–5 s timescale. The flow profile relaxation time collapses to a single curve—by normalization to the characteristic relaxation time of the fluid—and decays with increasing Weissenberg number. We monitor the relaxation process by observing changes in the flow profile of the solution from an initially parabolic shape at the entrance to the expected flattened steady-state profile further downstream. The evolution of the flow profile is reproduced for all measured solutions.
2 Materials and methods
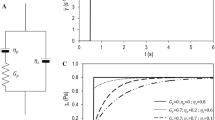
Microfluidic PDMS (Sylgard 184, World Precision Instruments) chambers with different geometries were built by the standard protocol (Duffy et al. 1998). A sketch of a geometry used for the measurements is shown in Fig. 1. For a fixed channel height of 80 μm, two constriction ratios of 7:1 (400:60 μm) and 10:1 (600:60 μm) were assembled. As the results of the two different constriction setups do not vary significantly, the reported measurements are not labeled to reflect the corresponding ratios.
The setup consists of a microfluidic channel which is mounted on a microscopy stage. Flow profiles are obtained from videos that are captured at different positions downstream of an orifice with a constriction ratio of 7:1 or 10:1. The measurement plane is in the vertical center of the channel. A schematic representation of the flow behavior of the polymer solution and configurations is depicted in the sketch
As test fluids, aqueous solutions of polyacrylamide (PAA, 5-6MDa, Sigma Aldrich), which exhibit shear thinning behavior, were used. Fluorescent microparticles (microparticles GmbH Berlin; Rhodamin B MF-Polymerpartikel, diameter 1 μm) were added to the polymer solutions as tracer particles at concentrations below 0.1 % (v/v).
The rheological properties of the solutions were determined by measurements using a rheometer with a cone-plate geometry (cone 1°0′25′′, 40 mm, AR-G2, TA-Instruments). To account for possible aging effects of the fluids, samples of the polymer solutions (including the tracer particles) used for the microfluidic measurements were concurrently measured with the rheometer. Additional measurements of the PAA solutions without tracer particles showed that the particles did not affect the rheology outcome of the experimental solutions. Random measurements of the samples that had passed the microfluidic channel confirmed that the rheological properties of the polymer solutions did not change due to the channel flow. The measurement data obtained from the rheometer are best described by an adaptation of the Carreau model: \(\eta \left( {\dot{\gamma }} \right) = \eta_{0} \left( {1 + \dot{\gamma }/\dot{\gamma }_{c} } \right)^{{\frac{1}{{m_{\text{eta}} }} - 1}}\) (Bruus 2009), where \(\dot{\gamma }\) denotes the applied shear rate, \(\eta\) the shear viscosity, \(\eta_{0}\) the zero-shear viscosity, and \(m_{\text{eta}}\) a fit parameter describing the high shear rate behavior of the viscosity. The critical shear rate \(\dot{\gamma }_{c}\) indicates the transition from the Newtonian (shear rate independent) viscosity plateau to the shear thinning region. From the critical shear rate we compute the characteristic relaxation time \(\tau_{\text{rheo}} = 1/\dot{\gamma }_{c}\) of the fluid.
To vary the characteristic relaxation times of the sample fluids, the solvent viscosity was changed by replacing water with glycerol in varying volume ratios (ranging from 0 to 50 %). The final PAA concentration was adjusted to 2 % (w/v). Unless otherwise denoted, the various sample fluids are marked with the same colors throughout the figures, and are noted in Table 1.
The measurement setup consists of a Zeiss Axiovert 100 TV microscope with a 63× long distance objective (NA 0.75, resulting in a depth of field of 6 μm) and a motorized microscopy stage (Thorlabs Max 203) on which the microfluidic channel was mounted.
A syringe pump (SP210IWZ, World Precision Instruments) was used to introduce a volume-controlled flow. The pressure at the inlet of the microfluidic channel was continually measured with a pressure transducer (Sensortechnics, 24PC02K0xxA) to ensure constant flow rates.
Videos were captured at different positions along the microfluidic channel using either a Hamamatsu Orca or an Andor Neo SCMOS camera with OpenBox (Schilling et al. 2004) or Andor Solis Software, respectively, for recording. The field of view was on the order of 100 μm × 100 μm and the measurement plane was chosen to be at the vertical center of the channel (Fig. 1). To cancel out any time-dependent measurement effects (e.g., heating of the microfluidic chamber, drift), the recording positions of the video-samples along the flow direction were not unidirectional or contiguous. The first measurement position at x = 0 mm was chosen such that the slightly round edges of the channel constriction (with a radius of ~5 μm) were just out of view.
The videos were analyzed by in-house developed Matlab scripts. The application of a brightness threshold filter to the video images reduced the depth of field to about 3 μm. To improve the measurement accuracy, a software filter for particle aggregates was also applied. A standard PIV algorithm (Williams et al. 2010) was implemented and applied to determine the flow profiles (\(v_{x} \left( y \right)\)). 1,000–3,000 image pairs were correlated for each flow profile to achieve high accuracy.
The obtained flow profiles are fitted by a power law \(v_{x} \left( y \right) = \left( {\left. a \right|y - \left. b \right|} \right)^{m + 1} + c\). Thereby a is a parameter taking into account the volume flux, c the maximum flow speed and b the experimental center of the flow profile. The measure m characterizes how much the flow profile deviates from a parabolic flow profile (where m = 1). This fit is used as it is an exact solution for the flow of power law fluids (\(\eta_{PL} \left( {\dot{\gamma }} \right) = \eta_{1} \dot{\gamma }^{{1/m_{\text{eta}} - 1}}\)) in a circular tube or infinite parallel plate geometry with \(m = m_{\text{eta}}\) (Bruus 2009). Due to the geometric boundary conditions the parameter m, obtained by fitting the fully developed flow profile of a power law fluid in rectangular geometries, varies from \(m_{\text{eta}}\) as measured by a rheometer. The correction factor is determined by numerical calculations, which show that in a rectangular geometry with the chosen aspect ratio of width to height of 0.75 we obtain \(m = - 0.24 + 1.32\;m_{\text{eta}}\).
To eliminate the artifacts due to beads sticking to the micro channel walls and roughness of the channel walls, only data points with v > ε·c and correlation values above a certain threshold were used for the power law profile fit. To evaluate the pressure drop and the transient viscosities (Figs. 3 and 4) ε was set to 0.2; for all other measurements, we set ε = 0.7 to simplify the fitting procedure. The change in the value of ε leads to only slight changes in the obtained fit parameters (±10 %).
To evaluate the relaxation of the fluid after a constriction (Fig. 1), a series of measurements of a single polymer solution at a constant flow rate was done at different positions. The resulting temporal evolution of the flow profiles was fit with the equation
where \(m_{0}\) denotes m at x = 0, \(m_{\text{end}}\) the steady-state value, and \(l_{\text{ss} }\) the decay length. The single exponential decay function was the simplest model, which fit the data best—indicating that there is one dominating relaxation process governing the response of the fluid after the contraction.
To check the flow conditions in the wider part of the channel, velocity profiles in both directions perpendicular to the flow direction were recorded far upstream of the contraction such that effects of the inlet and the orifice were negligible. The shape of the profile along the shorter axis showed the expected power law profile with the characteristic flattening, whereas the profile along the longer axis showed a pronounced “rounding”. These measured profiles were in good accordance with numerical calculations.
The Weissenberg number was varied between 10 and 1,000 by adjusting the flow speed of the syringe pump driven flow between 0.3 and 3 μl/min. \(Wi\) was calculated by \(Wi = \dot{\gamma }_{\text{eff}} \tau_{\text{rheo}}\), where \(\dot{\gamma }_{\text{eff}} = 2\frac{c}{w}\) with w the width of the narrow channel part.
Vortices upstream of the contraction were observed for the flows with Weissenberg numbers \(Wi > 100\). The Reynolds number is well below 1 for all experiments.
Data presented in Figs. 2b, 3, and 4 are obtained from the same measurement series of fluid F3 (Table 1) at \(Wi = 290\).
a Steady-shear viscosities of the polymer solutions obtained by the measurements in a cone-plate rheometer. The shear thinning behavior of the fluids is best described by a Carreau model fit. Exemplary shear rate dependence of the viscosity for three different fluids (F2, F3, F8, see Table 1), and the fit (gray line) to the obtained data of fluid F3 are shown. The arrows mark the critical shear rates \(\dot{\gamma } = 1/\tau_{\text{rheo}}\) obtained by Carreau model fits. The obtained fit parameters for fluid F3 are listed in Table 1. b Flow profiles of a non-Newtonian fluid at different positions. The flow profiles (symbols) are extracted from videos recorded at a distance x = 10 μm (black), 0.6 mm (red), 18 mm (green) downstream to the constriction for fluid F3 at Wi = 290. For better visibility, the flow profiles are normalized to their maximum flow speed and shifted along the axis of the ordinate. Each measured flow profile is fit to a power law function (lines). The obtained exponents are m = 0.94 (black), 2.3 (red), and 3.0 (green)
Dependence of the flow profile on the recording position. The fit parameter m of the power law fits to the flow profiles increases with distance of the recording position from the orifice. The development of m from m 0 directly after the orifice to the steady-state value m end at the positions further downstream can be best described by an exponential function with a decay length l ss (black line, m 0 = 1.1, m end = 2.8, l ss = 0.071 cm). Inset: dependence of the flow profiles on the Weissenberg number Wi. Squares denote m 0, circles m end. The colors correspond to the different polymer solutions with varying relaxation times τ rheo [yellow 22.5 s (F1), cyan 12.5 s (F2), green 5.8 s (F3), red 3.5 s (F4), purple 3.4 s (F5), black 2.6 s (F6), blue 1.5 s (F7), and pink 0.9 s (F8)]. The flow profiles near the orifice are parabolic (m 0 = 1) for all measured solutions at all Wi, whereas m end increases with increasing Wi
a Pressure drop along the flow direction. \({{\rm d}{p}/{\rm d}{x}}\) is calculated from the obtained flow profiles and the macro-rheological viscosity measurements. \({{\rm d}{p}/{\rm d}{x}}\) increases with increasing distance from the orifice until a final value is reached at x = 0.4 cm. b Local viscosity at different recording positions. (From red to green: recording positions x = 10 μm, 0.1 mm, 0.2 mm, 0.3 mm, 0.6 mm, and 18 mm.). The inset shows the development of the local viscosity at different y-positions (y: green 1 μm, blue 2 μm, cyan 5 μm, red 10 μm, and black 25 μm). Near the center of the flow profile (y ~ 0), the viscosity increases with increasing distance from the orifice as the polymers, initially elongated due to the orifice flow, relax to their steady state in shear flow
3 Results and discussion
The semi-dilute polymer solutions showed a pronounced shear thinning behavior, as determined by rheometer measurements (Colby et al. 2006) (Fig. 2a). Their respective characteristic relaxation times were determined to range from 0.9 to 23 s (Table 1). Flow profiles of such non-Newtonian fluids in rectangular flow chambers deviate from the flow profile expected for Newtonian fluids in similar three-dimensional geometries (Bruus 2009). While at the channel walls the shear rate is highest, the shear rate in the middle of the channel approaches zero. Thus, the shear thinning behavior of the viscosity occurs at the walls, while in the center of the channel higher viscosities dominate the flow. Consequently, the flow profile flattens in the middle of the channel (Fig. 2b).
All observed flow profiles are excellently described by a power law fit (Fig. 2b). In the limit of purely Newtonian fluids (\(\eta \left( {\dot{\gamma }} \right) = {\text{const}}\)), a parabolic flow profile is observed corresponding to \(m \approx m_{\text{eta}} = 1\). For the non-Newtonian fluid F3 (Table 1), the parameter determined by a Carreau fit of \(m_{\text{eta}} = 2.1\) should result in a power law profile in the microfluidic channel of m = 2.6. Indeed, in good agreement an exponent of m = 2.8 ± 0.1 was observed in steady-state conditions in the microfluidic channels (Fig. 3).
Once the fluid is forced into an orifice flow, the flow profile changes significantly. To quantify the development of the flow after the orifice, the fit exponent m at different measurement positions x along the narrow channel is plotted (Fig. 3). The fit of the velocity profile directly at the entrance of the narrow channel part at x = 0 mm yields m = 1. This corresponds to a parabolic flow profile. For 0 mm < x < 2 mm, the fit exponent shows a steep growth followed by a flattening until x = 4 mm, where it reaches a value of m = 2.8. The growth in the exponent m stems from a flattening in the center and simultaneous broadening of the flow profiles at the respective positions. This change in the flow profile is the dominating effect due to polymer relaxation. The volume constraint along the flow direction of the fluid causes a variation of the maximum flow speed of at most 15 %, which is also observed in the measurements. The steady-state value of m extracted from the flow measurements corresponds to the value found using cone-plate shear rheometry, and is unchanged from x = 4 mm until the last measurement position at x = 20 mm. This relaxation behavior is replicated for all fluids studied.
At the orifice—the first measurement position—a parabolic shape is found for all \(Wi = 10 \ldots 1,000\) (Fig. 3 inset), indicating a constant local viscosity along the axis perpendicular to the flow direction. The effect of shear thinning on the steady-state flow profiles increases with increasing \(Wi\) from m = 2 to 4 (Fig. 3 inset). The reason is that the steady-state flow profile contains all shear rates from zero (at the center of the channel) to the respective shear rates at the walls. As the viscosity measurement shows a Newtonian plateau at low shear rates, the flow profile should still fit a parabola (m = 1) within a region near the center of the channel in contrast to the assumption of a power law velocity profile with m > 1. With increasing flow speed, the shear rates increase and therefore the region in which the profile follows a parabola diminishes. This enhances the quality of the power law fit, since the fit is less influenced by the Newtonian viscosity plateau—the determinant of the flow profile center in steady state. Therefore, \(m_{\text{end}}\) increases with increasing \(Wi\).
The analysis of the shape of the flow profile allows for the calculation of the local pressure drop and hence an estimation of the local and transient viscosities at each measurement position. The calculation is based on the assumption that the contributions of elastic effects to the stress tensor are small compared to the viscous effects. This is justified, as the velocity components perpendicular (\(v_{y}\) and \(v_{z}\)) to the flow direction (\(v_{x}\)) are negligible and are not observable by the PIV. Thus, the pressure drop is constant along the axes perpendicular to the flow direction at each measurement position x. The pressure drop can be calculated by assuming that the fluid elements near the walls are already in their steady state. This assumption can be justified by the flow conditions at the walls: the effective shear rate is always chosen such that \(Wi > 1\), thus, the shear flow dominates the polymer relaxation. Polymers near the wall experience the highest shear rate and thus reach their steady-state configuration faster (Takahashi et al. 1987). In addition, the flow speed near the channel wall is the lowest. Thus, at a given distance from the orifice polymers near the walls have enough time to relax to their steady-state configuration. This can be directly seen by computing the ratio of the corresponding time scales \(k(x) = t_{\text{flow}} \dot{\gamma }_{w} = \left( {x + \frac{d}{2}} \right)\frac{{2(m + 1)\beta^{m} }}{{w(1 - \beta^{m + 1} )}}\), where \(t_{\text{flow}}\) denotes the time a fluid element has travelled in the flow, β = y/w the fractional distance from the center of the channel, \(\dot{\gamma }_{w}\) the corresponding shear rate and d the width of the recording area of a single video. For the given geometry layout and near the channel walls, we compute k ≫ 1 for all measurement positions. Thus, the polymers at the walls have travelled much longer in the fluid than the characteristic timescale of the flow (\(1/\dot{\gamma }_{w}\)). This further supports the notion that the polymers at the walls have reached their steady-state configuration by the first measurement position at x = 0 mm. From the law of conservation of momentum, it follows that
with p denoting the pressure.
In Fig. 4a, the pressure drop is plotted at different positions along the narrow channel. The pressure drop is lowest near the orifice. It increases from \(1 \times 10^{6} \frac{\text{Pa}}{\text{m}}\) at the orifice to about \(5 \times 10^{6} \frac{\text{Pa}}{\text{m}}\) with a decay length of ca. 1 mm. The steady state is reached at a distance of 4 mm from the orifice.
The calculated pressure drop is in good accordance with the overall pressure drop measured by a pressure transducer. This is expected, as the narrow microfluidic channel contributes most to the overall pressure drop between the pressure transducer and the outlet of the microfluidic channel at ambient pressure.
Now the local transient viscosities \(\eta^{ + }\) perpendicular to the flow direction (Fig. 4b) can be computed at each measurement position from the pressure drop using
To prevent the calculation of infeasible outcomes near the center of the channel, where the shear rates fall to zero, the transient viscosities are limited to the corresponding steady-state viscosity values determined by the rheometer measurement.
It can be seen that directly at the orifice (x ~10 μm) the viscosity is dramatically lower than for the measurement positions further downstream. Moreover, as this profile shows a nearly parabolic shape (m ~1), the local viscosity perpendicular to the flow direction is almost constant. With increasing distance from the orifice, the shear thinning behavior, which manifests in the sharp dependence of the viscosity on the position perpendicular to the flow direction, becomes more pronounced. Near the middle of the channel—at y = 1 μm—a sharp increase in the viscosity is observed, with maximal viscosity attained at x ~ 4 mm (Fig. 4b inset). From there on, the local viscosity profile along the flow direction remains unchanged and the steady state is reached. Near the channel walls, the local viscosity shows a slight decrease. As the shear rates near the center of the channel decrease, observed by a flattening of the flow profiles, the shear rates near the channel walls increase to maintain the volume flux. Since the local viscosity at the channel walls is always in its steady state described by the Carreau model, the viscosity decreases moderately with an increasing distance from the orifice.
To better quantify the development of the flow profiles, the parameter m(x) is fitted with an exponential function (Fig. 3) and the obtained decay lengths \(l_{\text{ss}}\) are plotted in Fig. 5 (inset) as a function of the dimensionless Weissenberg number \(Wi\). The colors correspond to different test fluids with varying relaxation times (Table 1). The decay length increases up to a factor of 7 for all measured solutions with increasing \(Wi\) (Fig. 5 inset). Already for moderate \(Wi\) of about 1–10, the decay length \(l_{\text{ss}}\) is in the range of 0.3–1 mm; for high \(Wi = 100 \ldots 1,000\), \(l_{\text{ss}}\) reaches up to 2 mm. Thus, the relaxation process plays an important role on a length scale that is much larger than the smallest channel dimension (10–100 μm). This is contrary to the common steady-state conditions in microfluidic devices where only the smallest dimensions of the channel must be considered.
Normalized flow profile relaxation time τ norm versus Wi. The longest measured relaxation time equals the characteristic relaxation time of the fluid (τ norm = 1). τ norm collapses on a single curve for all measured solutions at all Wi, and decreases with increasing Wi. The black line denotes a power law fit \(\tau_{\text{norm}} = k_{1} Wi^{{k_{2} }}\) with k 1 = 3.58 and k 2 = − 0.53. Inset: entrance length l ss versus Wi. Lines through power law fits for individual polymer solutions serve as a guide to the eye
To relate the observed relaxation process to the physical mechanism, we compute the decay time \(\tau_{\text{channel}}\) from the decay length \(l_{\text{ss}}\) by considering the maximal flow velocity at y = 0. Fig. 5 shows the normalized relaxation times of the flow profiles \(\tau_{\text{norm}} = \tau_{\text{channel}} /\tau_{\text{rheo}}\) in the microfluidic channel at various dimensionless Weissenberg numbers \(Wi\), at varying flow speeds and for fluids with different characteristic relaxation times. This results in a collapse of \(\tau_{\text{norm}}\) to a single curve, which decays with increasing \(Wi\). For moderate \(Wi \sim 10\), the measured relaxation time in the microfluidic channel equals the characteristic relaxation time of the polymer solutions (\(\tau_{\text{norm}} = 1\)). With increasing flow speed, the relaxation time of the flow profile in the microfluidic channel is drastically decreased to about \(0.04\tau_{\text{rheo}}\) at \(Wi = 1,000\).
4 Conclusion
While the flow of Newtonian fluids in microfluidic setups always obeys parabolic flow profiles, the non-Newtonian behavior of polymer solutions introduces a history dependence, which needs to be taken into account. Shear thinning fluids in channel flows show a flattened flow profile, which is best described by a power law, whereby varying flow geometries complicate matters further. Here, we present the effect of an extensional flow geometry, where we observed a parabolic flow profile of a semi-dilute polymer solution directly after an orifice, and that appears to be independent of the flow rate. The subsequent relaxation process is flow rate dependent, yet can be renormalized by the characteristic relaxation time of the fluid.
The parabolic shape of the flow profiles measured directly after the orifice can be explained by considering the flow conditions directly upstream of the orifice. The extensional flow caused by the orifice leads to an extension of the polymers. Consequently, the resistance of the polymers to the extensional flow increases and results in an adjustment of the extensional flow to minimize the dissipated energy. Finally, all polymers along the axis perpendicular to the flow direction are equally extended. As all polymers along this axis have similar average configurations, they affect the same resistance to the flow. Thus, a parabolic flow profile is observed. Above a certain extensional rate, which is mandatory to start the extension of the polymers from their equilibrium conformation, this outcome is independent of the flow rate (Perkins 1997; Smith 1998; Larson et al. 1999). The relaxation of the initially stretched polymers in shear flow after the contraction causes an increase in their hydrodynamic diameter and consequently an increase in the dissipation of energy (Colby et al. 2006). Therefore, the local viscosities along the flow direction increase until the polymers reach their steady-state conformation.
For moderate \(Wi \sim 10\), the time that the fluid needs to reach its steady-state flow profile equals the characteristic relaxation time. At such low \(Wi\), the shear rate in the center of the channel (−6 μm < y < 6 μm) is lower than the critical shear rate. Therefore, the polymers relax to their equilibrium conformation within their characteristic relaxation time \(\tau_{\text{rheo}}\).
With increasing \(Wi\), the relaxation time of the flow profile decreases. The reason is that at high \(Wi\), the region around the center of the flow profile, where the local shear rate is smaller than \(1/\tau_{\text{rheo}}\), diminishes and thus only marginally affects the overall flow profile. Consequently, the flow profile is determined by the relaxation of the polymers at high shear rates \(\dot{\gamma } > 1/\tau_{\text{rheo}}\). In this regime, polymers that are exposed to higher shear rates reach their steady state faster, since with higher shear rates only modes of the polymers with short relaxation times can relax (Colby et al. 2006). Consequently, the steady state of the polymer configuration is further away from the initially stretched state for polymers exposed to low shear rates than for polymers exposed to higher shear rates. Therefore, this relaxation is observable for the longest time near the symmetry axes of the channel (y ~ 0) where it causes a flattening of the flow profile and the relaxation time of the complete flow profile decreases with increasing \(Wi\).
The detailed insights of the flow profile relaxation of polymer solutions may pave the way for a broader development of complex microfluidic devices. Generally, the physical phenomena presented in this work play a role in all flows of complex fluids in microfluidic channels with extensional flow geometries. In particular, fluids in which anisotropies can be induced by such geometries may show the relaxation process examined here. Many of the commonly used fluids, such as emulsions and suspensions containing large biomolecules, industrial polymers or other non-spherical particles, will show the presented effects. The long relaxation times may turn out to be important for bio-analytical assays. There may also be ways of harnessing such local viscosity differences in chemical reactions in emerging lab-on-a-chip applications.
References
Ahmad T, Hassan I (2010) Experimental analysis of microchannel entrance length characteristics using microparticle image velocimetry. J Fluids Eng 132(4):041102. doi:10.1115/1.4001292
Alves MA, Oliveira PJ, Pinho FT (2003) Benchmark solutions for the flow of Oldroyd-B and PTT fluids in planar contractions. J Nonnewton Fluid Mech 110(1):45–75. doi:10.1016/s0377-0257(02)00191-x
Bruus H (2009) Theoretical microfluidics. Oxford master series in physics, Oxford Univ Press
Castillo-Tejas J, Rojas-Morales A, López-Medina F, Alvarado JFJ, Luna-Bárcenas G, Bautista F, Manero O (2009) Flow of linear molecules through a 4:1:4 contraction–expansion using non-equilibrium molecular dynamics: extensional rheology and pressure drop. J Nonnewton Fluid Mech 161(1–3):48–59. doi:10.1016/j.jnnfm.2009.04.005
Colby RH, Boris DC, Krause WE, Dou S (2006) Shear thinning of unentangled flexible polymer liquids. Rheol Acta 46(5):569–575. doi:10.1007/s00397-006-0142-y
Doyle PS, Shaqfeh ESG, McKinley GH, Spiegelberg SH (1998) Relaxation of dilute polymer solutions following extensional flow. J Nonnewton Fluid Mech 76(1–3):79–110. doi:10.1016/s0377-0257(97)00113-4
Duffy DC, McDonald JC, Schueller OJ, Whitesides GM (1998) Rapid prototyping of microfluidic systems in poly(dimethylsiloxane). Anal Chem 70(23):4974–4984. doi:10.1021/ac980656z
Feigl K (1996) A numerical study of the flow of a low-density-polyethylene melt in a planar contraction and comparison to experiments. J Rheol 40(1):21. doi:10.1122/1.550736
Hassell DG, Lord TD, Scelsi L, Klein DH, Auhl D, Harlen OG, McLeish TCB, Mackley MR (2011) The effect of boundary curvature on the stress response of linear and branched polyethylenes in a contraction–expansion flow. Rheol Acta 50(7–8):675–689. doi:10.1007/s00397-011-0551-4
Haward SJ, Li Z, Lighter D, Thomas B, Odell JA, Yuan X-F (2010) Flow of dilute to semi-dilute polystyrene solutions through a benchmark 8:1 planar abrupt micro-contraction. J Nonnewton Fluid Mech 165(23–24):1654–1669. doi:10.1016/j.jnnfm.2010.09.002
Kröger M (2004) Simple models for complex nonequilibrium fluids. Phys Rep 390(6):453–551. doi:10.1016/j.physrep.2003.10.014
Lanzaro A, Yuan X-F (2011) Effects of contraction ratio on non-linear dynamics of semi-dilute, highly polydisperse PAAm solutions in microfluidics. J Nonnewton Fluid Mech 166(17–18):1064–1075. doi:10.1016/j.jnnfm.2011.06.004
Larson RG, Hu H, Smith DE, Chu S (1999) Brownian dynamics simulations of a DNA molecule in an extensional flow field. J Rheol 43(2):267. doi:10.1122/1.550991
Li Z, Yuan X-F, Haward SJ, Odell JA, Yeates S (2011) Non-linear dynamics of semi-dilute polydisperse polymer solutions in microfluidics: a study of a benchmark flow problem. J Nonnewton Fluid Mech 166(16):951–963. doi:10.1016/j.jnnfm.2011.04.010
Lindner A, Vermant J, Bonn D (2003) How to obtain the elongational viscosity of dilute polymer solutions? Physica A 319:125–133. doi:10.1016/s0378-4371(02)01452-8
Lubansky AS, Boger DV, Servais C, Burbidge AS, Cooper-White JJ (2007) An approximate solution to flow through a contraction for high Trouton ratio fluids. J Nonnewton Fluid Mech 144(2–3):87–97. doi:10.1016/j.jnnfm.2007.04.002
Nguyen NT, Wereley ST (2002) Fundamentals and applications of microfluidics. Artech House Publishers, London
Pérez-Trejo L, Méndez-Sánchez AF, Pérez-González J, Vargas L (1996) Influence of polymer conformation on the entrance length in capillary flow. Rheol Acta 35(2):194–201. doi:10.1007/bf00396046
Perkins TT (1997) Single polymer dynamics in an elongational flow. Science 276(5321):2016–2021. doi:10.1126/science.276.5321.2016
Rodd LE, Lee D, Ahn KH, Cooper-White JJ (2010) The importance of downstream events in microfluidic viscoelastic entry flows: consequences of increasing the constriction length. J Nonnewton Fluid Mech 165(19–20):1189–1203. doi:10.1016/j.jnnfm.2010.06.003
Schilling Jr, Sackmann E, Bausch AR (2004) Digital imaging processing for biophysical applications. Rev Sci Instrum 75(9):2822. doi:10.1063/1.1783598
Smith DE (1998) Response of flexible polymers to a sudden elongational flow. Science 281(5381):1335–1340. doi:10.1126/science.281.5381.1335
Sousa PC, Coelho PM, Oliveira MSN, Alves MA (2011) Effect of the contraction ratio upon viscoelastic fluid flow in three-dimensional square–square contractions. Chem Eng Sci 66(5):998–1009. doi:10.1016/j.ces.2010.12.011
Squires T, Quake S (2005) Microfluidics: fluid physics at the nanoliter scale. Rev Mod Phys 77(3):977–1026. doi:10.1103/RevModPhys.77.977
Steinhauser D, Köster S, Pfohl T (2012) Mobility gradient induces cross-streamline migration of semiflexible polymers. ACS Macro Lett 1(5):541–545. doi:10.1021/mz3000539
Stone HA, Stroock AD, Ajdari A (2004) Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu Rev Fluid Mech 36:381–411. doi:10.1146/annurev.fluid.36.050802.122124
Takahashi Y, Isono Y, Noda I, Nagasawa M (1987) Stress relaxation in linear polymer solutions after stepwise decrease of shear rate. Macromolecules 20(1):153–156. doi:10.1021/ma00167a026
Tamaddon Jahromi HR, Webster MF (2011) Transient behaviour of branched polymer melts through planar abrupt and rounded contractions using pom–pom models. Mech Time-Depend Mater 15(2):181–211. doi:10.1007/s11043-010-9130-9
Teh SY, Lin R, Hung LH, Lee AP (2008) Droplet microfluidics. Lab Chip 8(2):198–220. doi:10.1039/b715524g
van Steijn V, Kreutzer MT, Kleijn CR (2007) mu-PIV study of the formation of segmented flow in microfluidic T-junctions. Chem Eng Sci 62(24):7505–7514. doi:10.1016/j.ces.2007.08.068
Wassner E, Schmidt M, Münstedt H (1999) Entry flow of a low-density-polyethylene melt into a slit die: an experimental study by laser-Doppler velocimetry. J Rheol 43(6):1339. doi:10.1122/1.551050
Williams SJ, Park C, Wereley ST (2010) Advances and applications on microfluidic velocimetry techniques. Microfluid Nanofluid 8(6):709–726. doi:10.1007/s10404-010-0588-1
Xue SC, Phan-Thien N, Tanner RI (1998) Three dimensional numerical simulations of viscoelastic flows through planar contractions. J Nonnewton Fluid Mech 74(1–3):195–245. doi:10.1016/s0377-0257(97)00072-4
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Kleβinger, U.A., Wunderlich, B.K. & Bausch, A.R. Transient flow behavior of complex fluids in microfluidic channels. Microfluid Nanofluid 15, 533–540 (2013). https://doi.org/10.1007/s10404-013-1171-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10404-013-1171-3