Quantification of the performance of chaotic micromixers on the basis of finite time Lyapunov exponents

Abstract

Chaotic micromixers such as the staggered herringbone mixer developed by Stroock et al. allow efficient mixing of fluids even at low Reynolds number by repeated stretching and folding of the fluid interfaces. The ability of the fluid to mix well depends on the rate at which “chaotic advection” occurs in the mixer. An optimization of mixer geometries is a non-trivial task which is often performed by time consuming and expensive trial and error experiments. In this paper an algorithm is presented that applies the concept of finite-time Lyapunov exponents to obtain a quantitative measure of the chaotic advection of the flow and hence the performance of micromixers. By performing lattice Boltzmann simulations of the flow inside a mixer geometry, introducing massless and non-interacting tracer particles and following their trajectories the finite time Lyapunov exponents can be calculated. The applicability of the method is demonstrated by a comparison of the improved geometrical structure of the staggered herringbone mixer with available literature data.

1 Introduction

Microfluidic devices have found applications in various scientific and industrial processes. A typical example is their integration as important components of chemical and biological sensors (Burns et al. 1996). A micromixer is a microfluidic device used for effective mixing of different fluid constituents. It can be used to efficiently mix, for example a variety of bio-reactants such as bacteria cells, large DNA molecules, enzymes and proteins in portable integrated microsystems with minimum energy consumption. It is also used in mixing of solutions in chemical reactions (Watts 2003), sequencing of nucleic acids or drug solution dilution. Hence, the design of practical and efficient micromixers is a major research topic in microfluidics (Kim et al. 2004; Whitesides 2001), especially in the development of micro total analysis systems. Over the years, various methods of efficient mixing have been developed and many of those have been successfully applied in industry (Hessel et al. 2005).

The small length scales of the micromixers has a negative impact on mixing as it results in laminar flows inside the channels. In this flow regime, mixing is influenced mainly by the process of molecular inter-diffusion (Aref 1990). Experiments with channels with complex surface topology including grooved walls have revealed that microscale mixing is enhanced by “chaotic advection”, a process which was first reviewed by Aref (1984). He describes how mixing is still possible even at low Reynolds number by repeated stretching and folding of fluid elements (Ottino et al. 1994). If properly applied, this mechanism causes the interfacial area between the fluids to increase exponentially, which can then lead to an enhanced intermaterial transport, hence mixing. A comprehensive mathematical description of the exponential growth of interfacial surfaces can be found in the book by Ottino (1989). Mixers, which utilize the principle of “chaotic advection”, were designed in the following years (Kim 2007). However, it is important to note that the term “chaotic” is used strictly in a Lagrangian sense (Amon et al. 1996).

Depending on the working principle, micromixers can be categorized into two important types: if energy from an external source is used to drive the mixing process, then they are termed as “active mixer”. These external energy sources can be acoustic bubble-induced vibrations, periodic variation of the flow rate, piezoelectric vibrating membranes, valves, etc. The external sources are often moving components such as micropumps and they require advanced fabrication steps (Zhang et al. 2007). The second category of micromixers is based on restructuring the flow profile using static but sophisticated mixer geometries. These are termed as “passive mixer”. Passive micromixers have the advantage of simple fabrication, easy operation and no elements which can generate heat. The absence of heating is an important factor for applications to biological studies where temperature is a sensitive parameter. The mixing length and mixing time are defined as the distance and time span the fluid constituents have to flow inside the mixer in order to obtain a homogeneous mixture. An effective micromixer should reduce the mixing length and mixing time substantially in order to achieve rapid mixing. A common practice to design passive micromixers is to create alternating thin fluid lamellae. These result in an interfacial area that increases with the number of lamellae rendering the diffusion process more effective and hence allowing fast mixing (Bessoth et al. 1999). There are many examples of bi-lamellation (Gobby et al. 2001; Mingquiang 2000) and multi-lamellation (Hessel et al. 2005) in the literature on micromixers. However, the drawback of such devices is that the number of lamellae is generally limited due to the negative impact on the applied pressure drop caused by the required microstructures inside the channel. Other examples of passive micromixers include the twisted pipe mixer (Liu et al. 2000), the superfocus micromixer, where several jets are made to collide at the focal point of the jets and the three-dimensional serpentine model (Hessel et al. 2005).

The recently developed so-called “chaotic micromixer” has gained substantial interest in the literature since it overcomes some of the drawbacks of conventional mixers based on muti-lamellation. Such a device consists of microstructured objects such as “herringbones” (see Fig. 1). The staggered herringbone mixer (SHM) was introduced as one of the first experimental implementations of chaotic micromixers in 2002 by Stroock et al. (2002). The half cycles of the SHM consist of grooves with two arms which are asymmetric and unequal in length. These arms are inclined at an angle of 45° to the wall and 90° against each other, while the pattern interchanges every half cycle of the herringbone. The peculiar arrangement of the herringbone structure enhances the mixing process by “chaotic advection” where the interfacial area between the fluids grows exponentially in time—an important advantage over mixers using the concept of multi-lamellation. The SHM was used by several authors for studies related to mixing and analysis of mixing quality. To characterize the mixing quality of the SHM, Aubin et al. (2003) implemented particle tracking techniques using the variance of tracer dispersion (Li 2005). Li and Chen report on an optimization of the SHM using the standard deviation of particle concentrations. As in the current paper, they used the lattice Boltzmann (LB) method to model the flow field. Further, the SHM was used by Kirtland et al. (2006) to study the mass transfer to reactive boundaries from three-dimensional micro-channels.

Fig. 1

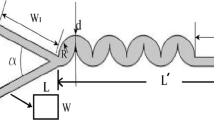
A typical example of a SHM geometry as it is used for the simulations. The dimensions of this channel are $32\times64\times D/\Updelta x$ lattice units, where D depends on the distance between the grooves d and the number of grooves per half cycle n. H height of the channel and w horizontal length of the long arm. We define the height fraction as $\alpha= h/H,$ the width fraction as $\beta=w/W,$ and the distance fraction as γ = d/D. The wall at x = 32 is not shown in the figure, in order to view the inside of the channel

For the development of micromixers it is important to have reliable tools at hand to quantify their performance. Efficiency and mixing quality have been studied by various methods in the past. These include the analysis of the probability density function of the flow profiles, studying the stretching of the flow field, the Poincaré section analysis, or the intensity of segregation as introduced by Danckwerts (1952). In this paper, an alternative numerical procedure is presented which is tailored for the optimization of chaotic micromixers. It is based on LB simulations to describe the flow inside complex mixer geometries together with a measurement of finite time Lyapunov exponents (FTLE) as obtained from trajectories of massless tracer particles immersed in the flow. The LB method can easily handle flows in complex geometries, which makes this method convenient for flows in advanced microstructures such as the micromixers the current paper focuses on. The Lyapunov exponent provides a quantitative measure of long-term average growth rates of small initial flow perturbations and thus allows a quantification of the efficiency of chaotic advection (Ziehmann et al. 2000; Lapeyre 2002). Since the systems of interest are finite and simulations are limited to a finite time span, the proposed method utilizes Wolf’s method to calculate the FTLE (Bessoth et al. 1999). While LB simulations of flows in micromixers and FTLE computations to quantify the degree of chaotic advection have been reported in the literature before, their combination for three-dimensional performance quantification of realistic chaotic micromixers has to our knowledge not been published before. The numerical scheme has the potential to assist an experimental optimization since geometrical parameters or fluid properties can easily be changed without requiring a new experiment. To demonstrate its applicability, the scheme is applied to evaluate the parameters of the staggered herringbone mixer that lead to improved performance.

In the following sections the lattice Boltzmann method which is applied to simulate the fluid flow and the Wolf’s algorithm from which the FTLE are obtained are described. Finally, the numerical results and conclusions are given.

2 Simulation method

The lattice Boltzmann method is used to describe the fluid flow. The LB method is a simplified approach to solve the Boltzmann equation in discrete space, time and with a limited set of discrete velocities (Succi 2001). The Boltzmann equation, given as

$$ \partial_{t} f + \vec{c} \cdot \nabla f = \Upomega(f), $$

(1)

represents the evolution of the velocity distribution function $f(\vec{r},\vec{c},t)$ by molecular transport and binary intermolecular collisions. $f(\vec{r},\vec{c},t)$ represents the distribution of velocities in continuous position and velocity space, $\vec{r}$ and $\vec{c},$ respectively. In the LB approach the position $\vec{x}$ at which $f(\vec{x},\vec{c}_{k},t)$ is defined is restricted to a discrete set of points on a regular lattice with lattice constant $\Updelta x,$ implying that space is discretized. The velocity is restricted to a set of velocities $\vec{c}_{k}$ implying that velocity is discretized along specific directions. $\Updelta t$ denotes the discrete time step. The model we adopt is a D3Q19 model which is a three-dimensional model with 19 different velocity directions, $k=0,1,\ldots,18$ (Qian et al. 1992). The right hand side of the above equation represents the collision operator which is simplified to the linear Bhatnagar–Gross–Krook (BGK) (1954) form. In a discretized form the BGK operator is written as

$$ \Upomega_{k} = \omega( f_{k}^{\rm eq} (\vec{x},t) - f_{k} (\vec{x},t)). $$

(2)

Here, ω is the reciprocal of the relaxation time of the system controlling the relaxation towards the Maxwell-Boltzmann equilibrium distribution $f_{k}^{\rm eq} (\vec{x},t).$ By considering small velocities and constant temperature, a third order Taylor expansion of the above equilibrium distribution function can be written as

$$ \begin{aligned} f_{k}^{{\rm eq}} (\vec{x},t) &= \zeta_{k} \frac{\rho}{{\rho}_{\circ}} \left(1 + \frac{ \vec{c}_{k} \cdot \vec{u}^{{\rm eq}} }{ {c_{{\rm s}}}^{2}} + \frac{ ( \vec{c}_{k} \cdot \vec{u}^{{\rm eq}} )^{2}}{2 {c_{{{\rm s}}}}^{4}} - \frac{ \vec{u}^{{\rm eq}} \cdot \vec{u}^{{\rm eq}} }{2 {c_{{\rm s}}}^{2}}\right.\\ &\quad\left.+ \frac{( \vec{c}_{k} \cdot \vec{u}^{{\rm eq}} )^{3}}{6 {c_{{\rm s}}}^{6}} - \frac{ ( \vec{c}_{k} \cdot \vec{u}^{{\rm eq}} )( \vec{u}^{{\rm eq}} \cdot \vec{u}^{{\rm eq}} )} {2 {c_{{\rm s}}}^{4}} \right), \end{aligned} $$

(3)

where f ^eq _k denotes the equilibrium distribution function corresponding to the velocity vector $\vec{c}_{k}, \zeta_{k}$ are the lattice weights, ρ is the density, ${{\rho}_{\circ}}$ a reference density, and ${c_{\rm s}} = (1/\sqrt{3}) \Updelta x / \Updelta t$ is the speed of sound. $\vec{u}^{\rm eq}$ is the equilibrium velocity of the fluid, which is shifted from the mean velocity by an amount $\vec{g} / \omega$ under the influence of a constant acceleration $\vec{g}.$ The evolution of the LB process takes place in two steps: the collision step where the velocities are redistributed along the directions of the lattice and the propagation step by which they are displaced along these directions. These discrete LB steps are implemented by the equation

$$ f_{k} (\vec{x} + \Updelta t \vec{c}_{k}, t + \Updelta t) - f_{k} (\vec{x},t) = -\omega \Updelta t ( f_{k}^{\rm eq} (\vec{x},t) - f_{k} (\vec{x},t) ), $$

(4)

which gives the dynamic evolution of the distribution function and is referred to as a discretized Boltzmann kinetic equation. The macroscopic fluid density is given by

$$ \rho (\vec{x},t) = {\rho}_{\circ} \sum_{k} f_{k} (\vec{x},t) $$

(5)

and the macroscopic fluid velocity in the presence of external forcing is given by Narváez et al. (2010)

$$ \vec{u} (\vec{x},t) = \frac{{\rho}_{\circ}} {\rho(\vec{x},t)} \sum_{k} f_{k} (\vec{x},t) \vec{c}_{k} - \frac{\Updelta t}{2}\vec{g}. $$

(6)

It can be shown by a Chapman-Enskog expansion that the macroscopic fields $\vec{u}$ and ρ from the above equations fulfill the Navier Stokes equation in the low Mach number limit and for isothermal systems (Succi 2001). In order to simulate a fluid flow through microchannels, periodic boundary conditions are implemented along the z direction (see Fig. 1) and no-slip bounce back boundary conditions are imposed at the channel walls. The experimental setup of Stroock et al. consists of a number of repeated cycles (~15) consisting of two asymmetric half cycles each. By simulating one full cycle only and applying periodic boundary conditions we can reduce the required computational effort substantially. If the system is in steady state, we do not expect any substantial differences in the flow field in different cycles. Therefore, this approach is valid. If, however, the experimental system would not be periodic, such a simplification would not be allowed and the full geometry would have to be simulated.

We simulate a fluid which is hydrodynamically similar to water, flowing inside a SHM with a cross section of 96 μm × 192 μm The length of the channel is 1,536 μm but can be varied in order to always accommodate a full cycle of the herringbone structure. For computational efficiency we have chosen a lattice resolution of Δx = 3 μm resulting in a fixed cross section of $32 \Updelta x \times 64 \Updelta x$ and system lengths of the order of 512Δx. Such a relatively low resolution is sufficient to properly resolve the flow field as can be observed from Fig. 2, where the velocity field perpendicular to the flow is shown at positions within different half cycles (a, b). Figure 2c shows the profile in flow direction. While the first two subfigures nicely demonstrate the swirling motion of the flow, the third one depicts how the flow penetrates between the grooves and stays mostly unaffected close to the upper boundary of the channel. Previously, we have shown that a well-resolved velocity field with less than 4% error as compared to the analytical solution can be obtained even for a resolution of 6–8 lattice nodes in the case of a three-dimensional rectangular Poiseuille flow (Narváez et al. 2010). We further demonstrated that flow over random rough surfaces can be well resolved even if the smallest obstacles are only described by 2–4 lattice units (Kunert 2007; Kunert et al. 2010). In the LB method, the kinematic viscosity is related to the discrete time step through the expression $\nu = {c_{{\rm s}}}^{2} ( 1 / \omega - \Updelta t / 2 ).$ Since ${\omega \Updelta t}$ is chosen to be 1 to minimize artifacts due to the mid-grid bounce back boundary conditions and the simulated fluid has the kinematic viscosity of water, $\nu = 10\sp{{-6}}\,\hbox{m}^{2} \,\hbox{s}^{-1},$ this implies for the current choice of $\Updelta x$ that $\Updelta t = 1.5 \times 10\sp{{-6}}\,\hbox{s}$ and ${c_{{\rm s}}} = 1.15\,\hbox{m\, s}^{-1}.$ When the magnitude of $\vec{g}$ is $1.2\times 10\sp{{-3}}\, \hbox{m\,s}^{-2}$ along the z direction, the average steady state velocity of the system is $u\approx 6.0\times 10\sp{{-3}}\,\hbox{m\,s}^{-1}$ which corresponds to a subsonic flow. The Reynolds number $\hbox{Re} = u L / \nu$ of the flow is ${\approx} 1.3,$ where $L = \sqrt{ H^{2} + W^{2}}$ is the characteristic length of the channel. One set of simulations is obtained for $\vec{g}$ being $0.4\times 10\sp{{-3}} \,\hbox{m\,s}^{-2}$ which corresponds to $\hbox{Re} \approx 0.4.$

Fig. 2

The velocity field perpendicular to the flow direction at z = 30 and z = 460 is shown in a and b, respectively. The figures depict the circulating motion of the flow which is triggered by the asymmetry of the herringbone shaped surface structures. c The velocity field in flow direction at y = 21. Due to the choice of β = 0.66 this value corresponds to a position close to the tips of the herringbones in case of the first half cycle and to a case in the center of the long arm in the case of the second half cycle. As can be observed the velocity vectors point strongly downwards within the first half of the channel, but mostly upwards in the second half

When the flow simulation has reached its steady state, P = 1,000 massless and non-interacting tracer particles are introduced at fluid nodes in the z = 0 plane and then their velocities are integrated at each time step. To calculate the FTLE from particle trajectories a group of five particles forms four pairs, with every fifth particle placed at the center and the remaining ones being placed at the four nearest off-diagonal neighboring LB lattice sites. The particle at the center traces a fiducial orbit. With this arrangement we are able to follow 800 particle pairs using only 1,000 particles.

The trajectories are obtained by integrating the vector equation of motion

$$ \frac{\hbox{d} \vec{R}_{j}}{\hbox{d}t} = \vec{u} (\vec{R}_{j}), \quad j=1,\ldots,P, $$

(7)

where $\vec{R}_{j}$ denotes the position vector of an individual tracer particle. The velocity $\vec{u} (\vec{R}_{j})$ is obtained from the discrete LB velocity field through a trilinear interpolation scheme.

“Chaotic” systems, in general, have the important feature that two nearby trajectories diverge exponentially in time. The rate at which these trajectories diverge can be related to the ability of the flow field to create conditions for chaotic mixing. The Lyapunov exponent is a possible measure of the performance of a micromixer as it is related to the rate of stretching of the fluid elements. It is defined by

$$ \lambda_{\infty} = \lim_{t\to\infty} \frac{1}{t} \ln\frac{{\mathcal{D}} (t)}{{\mathcal{D}} (0)}, $$

(8)

where $\mathcal{D} (t)$ is the distance between two trajectories at time t which evolve from an initial separation $\mathcal{D} (0).$ $\lambda_{\infty}$ gives the value of the Lyapunov exponent as t tends to infinity. Due to the finite size of any microfluidic system it is not possible to implement this definition in a simulation code to study the performance of a micromixer Also, when two trajectories separate from each other, this definition does not allow to understand the ongoing stretching and folding dynamics of the flow. A quantitative measure of the mixer performance based on the Lyapunov exponent can be obtained using the FTLE instead of the previous expression (Ruiquiang 2007; Tang 1996). The FTLE takes the dynamical process more completely into account and provides a numerically implementable scheme for quantification of the performance of mixers. The FTLE is defined as (Lee et al. 2007)

$$ \lambda_{{\rm FTLE}} = \frac{1}{\delta t} \ln\frac{{\mathcal{D}} (t+\delta t)}{ {\mathcal{D}} (t) }, $$

(9)

where t is any particular instant of time and $\delta t$ is a finite time after which the FTLE is measured. The same process is repeated over N times, where N is a large number denoting the number of times the FTLE is evaluated from trajectories of particle pairs. Amon et al. (1996) named the FTLE as finite time Lagrangian Lyapunov exponent. The convergence of the average FTLE to the Lyapunov exponent for large N is discussed in the paper by Tang and Boozer (1996),

$$ \lim_{N \to \infty} \langle\lambda_{{\rm FTLE}}\rangle_{N} = \lambda_{\infty}. $$

(10)

Wolf et al. (1985) suggested a method to calculate the FTLE from a set of experimental data which is well applicable to our simulations (Bessoth et al. 1999). The key idea of the method is to monitor the distance between particles forming a pair and to renormalize it by moving back one of the two particles towards the other one in case they have separated more than a given threshold distance. The FTLE is then computed from the sum of individual Lyapunov exponents measured between replacements. The method has been verified on systems with known Lyapunov spectra and exact results have been achieved. Following Wolf’s approach, we implement the following equation to quantify the mixer performance on the basis of the average FTLE as

$$ \langle\lambda\rangle_{N} = \frac{1}{N} \sum_{i=0}^{N-1} \frac{1}{\tau_{i}}\ln\frac{{\mathcal{D}} (t_{i}+ \tau_{i})}{ {\mathcal{D}} (t_{i})}, $$

(11)

where t _i is the ith time when a FTLE is evaluated, $\mathcal{D} (t_{i} + \tau_{i})$ and $\mathcal{D} (t_{i})$ are the distance between particle pairs at time step $t_{i}+\tau_{i}$ and t _i , respectively. $\tau_{i}$ is the number of time steps which a pair of particles take until the next replacement and its magnitude could be different for each measure. N is the total number of replacements made until time t when $\langle\lambda \rangle_{N}$ is evaluated. If $\langle\lambda\rangle_{N}$ has a positive and non-zero value the particles separate from each other at an exponential rate. These particle pairs are initially very close to each other and evolve in time. If the separation between the pair is greater than a maximum distance, the distance between the particles is re-adjusted to the initial distance $\mathcal{D} (t_{0}).$ For the implementation of the scheme, for every particle pair one of the trajectories is chosen as the fiducial path, while the position of the other particle is replaced if the distance becomes larger than the threshold value. This is schematically represented in Fig. 3. The choice of the maximum distance is based on a variation of it together with a comparison of the obtained FTLE: if it is chosen too large, many tracer particles hit the channel walls and do not separate any further resulting in a too low value of the FTLE. If it is chosen too small, the tracers do not have a sufficient amount of time to separate sufficiently so that an exponential increase of the distance cannot be detected. The chosen value H/2 has been found to be a good compromise between the two extreme cases. In order to avoid errors due to orientation, one of the particles of a pair is placed along the line of separation. In case a replacement point cannot be found due to a wall node present at the location, a nearby fluid node is selected as the replacement point. If even such points cannot be found since all surrounding nodes are surface nodes, the replacement is postponed until a suitable replacement is possible.

Fig. 3

A schematic representation of Wolf’s method. $\mathcal{D} (t_i)$ is the distance between a particle pair at an arbitrary time t _i . If the distance is greater than a maximum distance then one of the particles is replaced near to the other particle along the line of separation

The following section presents how FTLE can be utilized for an optimization strategy for chaotic micromixers. As an example, the influence of different parameters which directly affect the performance of the SHM is evaluated. These are the ratio of the height of the grooves to the height of the channel α, the ratio of the horizontal length of the long arm to the channel width β, the ratio of distance between the grooves to the length of the channel γ and the number of grooves per half cycle n. The width of the grooves is kept fixed at 24 μm for all simulations. Figure 1 provides a pictorial representation of these parameters.

3 Results and discussion

The performance of the SHM is studied by varying four geometrical parameters. While keeping all other parameters fixed (γ = 0.089, α = 0.2, n = 10), the width fraction ($\beta=w/W$) is varied within the range of 0.5 and 0.82 and the distance fraction ($\gamma=d/D$) from 0.04 to 0.11. Then, the number of grooves per half cycle (n) is varied from 2 to 10 and the height fraction ($\alpha=h/H$) from 0.125 to 0.343. The optimization of the SHM as presented here is meant to demonstrate the feasibility of the algorithm only since several optimization studies of the SHM are already available in the literature. Therefore, our optimization is reduced to a limited variation of the four-dimensional parameter space. This surely leads to a local optimum of the geometrical parameters, but it is not assured that the global optimum has been found. However, as shown below, our parameters correspond to the optimal ones found by other groups suggesting that our local optimum coincides with the global optimum.

Figure 4 depicts simulated $\langle\lambda\rangle_{N}(t)$ for different width fractions β = 0.66, 0.71, and 0.82. The Reynolds number is kept fixed at Re = 1.3 and $\langle\lambda\rangle_{N}(t)$ is obtained from tracing the trajectories of 1,000 particles. From Fig. 4 it can be observed that in each case $\langle\lambda\rangle_{N}$ fluctuates before finally converging to a particular value after ~6.0 × 10⁵ time steps. All further simulations are run until the FTLE have thoroughly converged. The effect of the geometry can be measured by comparing the average of the converged FTLE which is denoted by $\lambda.$ The error bars in Figs. 5, 6, 7, and 8 are given by the standard deviation of the data from the point where it has converged.

Fig. 4

The average FTLE for 1,000 particles is shown versus the time steps for Re = 1.3. After 6.0 × 10⁵ time steps, $\langle\lambda\rangle_{N}$ is converged and the average of this converged value is denoted by λ. The value of λ depends on the width fraction β as it is further investigated below

Fig. 5

The variation of the maximum averaged finite time Lyapunov exponent λ with different width fraction β, for two different Reynolds numbers. The data indicate that the maximum λ can be obtained for a width fraction of β = 2/3. Error bars are given by the standard deviation of the mean value of $\langle\lambda\rangle_N.$

When one of the parameters is varied it is taken care that the other parameters remain unchanged, because we are interested in the dependence of the individual parameters on the performance of the SHM. Figure 5 shows the variance of λ and as such the performance of the SHM with respect to the parameter β for two different Reynolds numbers, Re = 0.4 and 1.3. Larger values are difficult to obtain due to the limits of the LB method or would include a substantial increase in computing time. Due to the symmetry of the mixer geometry, only values for β ≥ 0.5 are shown. The datasets peak at β = 2/3 which implies that the degree of chaotic advection is maximized for this particular value of the width fraction β. According to the units chosen above this corresponds to w = 130 μm. The curves for the different Reynolds numbers depict that changing the driving force of the fluid does influence the absolute value of λ, but has no influence on the general shape of the curve. Similar studies of the Re dependence for other geometrical parameters and various different driving forces confirm this behavior. Our findings are consistent with the original experimental work of Stroock et al. (2002) as well as two-dimensional numerical optimizations by Stroock and McGraw (2004). The latter study how the so-called heterogeneity factor $I =\frac{\sqrt{\langle(C-\langle C \rangle)^{2}\rangle}} {\langle C \rangle}$ of a dye concentration C varies with the number of cycles in the mixer. In both publications it is found that β = 2/3 generates a maximum swirling motion of the fluid.

For the next set of simulations β is fixed at the optimized value of 2/3 and the distance fraction γ is varied from 0.04 to 0.11. Since it is observed from the previous results that the optimal value is independent of the Reynolds number, the following simulations are performed at a constant Re = 1.3. The average value of converged FTLE for different distance fractions is shown in Fig. 6. It can be observed that after a moderate increase of λ with γ, the curve has a sharp peak at γ = 0.07, which corresponds to a value of d = 105 μm for the current choice of Δx. Afterwards, λ decreases in a similar fashion as for small γ, but still at higher absolute values. A possible explanation is as follows: when the grooves are very close to each other, they create “dead spaces”, i.e. regions in the micro-channel where the fluid gets trapped and cannot move freely. With increasing the distance between the grooves, the transverse component of the velocity increases, hence “chaotic advection” is enhanced resulting a large value for λ. On the other hand, if the distance between grooves is too large, the mixer behaves like a plain channel without any chaotic advection component. The maximum in Fig. 6 is then given by the optimal interplay of these two effects.

Fig. 6

The variation of λ versus the distance fraction γ for Re = 1.3 and β = 2/3. The FTLE rises with the increase of γ until it reaches a distinct peak. After that the data show a decrease, indicating that the optimized performance of the micromixer is at a groove distance γ = 0.07. Error bars are given by the standard deviation from the mean

After having optimized the values for β and γ, the number of grooves per half-cycle n is varied from 2 to 10. It can be understood from Fig. 7 that a variation of n has the largest impact on the performance of the mixer as compared to β or γ. For the current setup, by variation of n it is possible to change the value of λ by a factor of 2.3 as compared to 1.2 for β and 1.3 for γ. Figure 7 clearly shows that a staggered herringbone mixer with n = 5 performs best. The existence of a maximum performance in dependence on the number of grooves can be explained by the fact that interplay between advection in flow direction and the swirling motion needs to be optimized for a well performing mixer. If the number of grooves is too small, the flow field is not sufficiently rotated when flowing through a half cycle. The change of direction of the swirling motion at the beginning of the following half cycle does not result in a relevant distortion of the trajectories then. If the number of grooves is too large, however, the fluid might perform one or more full rotations and come back to its original position before entering the next half cycle. An optimized value for n therefore depends on the ratio of optimum rotation to the frequency at which the distortions at the end of a half cycle occur. Similar to the work presented in the current paper, Li and Chen (2005) performed LB simulations and used tracers to follow the flow field. They, however, quantify mixing by computing the standard deviation of the local tracer concentration and conclude that SHM with n = 5 or n = 6 perform best. Even though this result is in agreement with our finding, the FTLE analysis clearly shows that the channel with n = 5 performs better than the one with n = 6.

Fig. 7

The variation of λ with the number of grooves per half cycle (n) is shown. It can be observed that the SHM with n = 5 performs best. Error bars are given by the standard deviation from the mean

The final parameter to be varied is the ratio of the half depth of the grooves to the height of the channel α. Figure 8 shows the average value of the converged Lyapunov exponents for different α between 0.125 and 0.343. After a strong increase of λ(α), the data show a maximum at α = 0.25. For the units chosen above this corresponds to a groove depth of 24 μm. For larger α the value of λ decreases again. Our result is similar to the original experimental analysis of Stroock et al. (2002). Again, an argument can be found for the existence of an optimal value for the ratio between groove depth and system height: if the grooves are too shallow, they are not able to generate the swirling motion required for chaotic advection. On the contrary, if the grooves are too deep the flow is not able to fully penetrate the grooves. Further, the volume between grooves and top surface becomes so small that the swirling motion cannot develop anymore.

Fig. 8

The variation of the average converged FTLE with the height fraction (α). The data indicate that the maximum FTLE can be obtained for α = 0.25. Error bars are given by the standard deviation from the mean

In this section, we have demonstrated that a numerical scheme based on the LB method for the flow in complex mixer geometries together with Wolf’s method to calculate FTLE from trajectories of passive tracers are a powerful tool for the quantification of chaotic mixing. Without loosing generality, a limited optimization study was performed for the particular example of the SHM. The optimal parameters α = 0.25, β = 2/3, γ = 0.07 and n = 5 have been found which is in good agreement with known experimental and numerical literature data.

4 Conclusion

Mixing at the microscale can be efficient if a large interface between fluids is provided. This can be obtained by passive chaotic micromixers utilizing repeated stretching and folding of the fluid interfaces. The performance of such mixers depends on the rate at which “chaotic advection” of the fluid takes place. For the development of efficient chaotic micromixers it is mandatory to understand the underlying transport processes as well as their dependence on the geometric structure of the microfluidic device. In this paper, we have demonstrated an efficient numerical scheme which allows the quantification of the performance of a micromixer. The scheme is based on a LB solver to describe the time-dependent flow field in complex mixer geometries combined with Wolf’s method to compute FTLE from passive tracer trajectories. We have demonstrated the applicability of the quantification method by applying it to find an optimal geometrical configuration of the SHM, but the scheme should be generally applicable to any chaotic mixer. By performing a systematic variation of the relevant geometrical parameters we obtained a set of optimal values which is consistent with literature data published by others. However, those data were obtained from experiments or numerical simulations not taking the chaotic nature of the tracer trajectories into account. The method presented here, however, allows a quantification and optimization of the mixing performance by investigation of the underlying flow profiles. Further work could include the optimization of other chaotic micromixer geometries and the introduction of multiple fluids to the problem. For the latter, the lattice Boltzmann method offers a number of possibilities to simulate multicomponent flows and is thus a well-suited candidate.