Comprehensive model of electrokinetic flow and migration in microchannels with conductivity gradients

Abstract

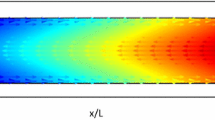
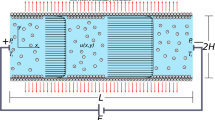
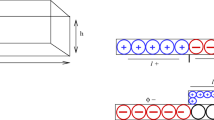
A comprehensive model of electrokinetic flow and transport of electrolytes in microchannels with conductivity gradients is developed. The electrical potential is modeled by a combination of an electrostatic and an electrodynamic approach. The fluid dynamics are described by the Navier–Stokes equations, extended by an electrical force term. The chemistry of the system is represented by source terms in the mass transport equations, derived from an equilibrium approach. Moreover, the interaction between ionic species concentration and physicochemical properties of the microchannel substrate (i.e. zeta-potential) is taken into consideration by an empirical approach. Approximate analytical solutions for all variables are found which are valid within the electrical double layer. By using the method of matched asymptotic expansions, these solutions provide boundary conditions for the numerical simulation of the bulk liquid. The models are implemented in a Finite-Element-Code. As an example, simulations of an electrophoretic injection/separation process in a micro-electrophoresis device are performed. The results of the simulations show the strong coupling between the involved physicochemical phenomena. Simulations with a constant and a concentration-depend zeta-potential clarify the importance of a proper modeling of the physicochemical substrate characteristics.

Appendix

One result of the present article is that under certain conditions migration does not influence the concentration field of an electrolyte, which was first proposed by Kohlrausch (1897). Let us consider a channel filled with a liquid containing the positively and negatively charged species A⁺ and B⁻, respectively. The electrolytes in the left part (index l) of the channel have the concentration $c_{{\rm A^+,l}}, c_{{\rm B^-,l}} ,$ whereas the electrolytes $(c_{{\rm A^+},r}, c_{{\rm B}^-,r})$ in the right part are diluted with the factor n.

The migration of an electrolyte species can also be interpreted as a partial current density

$$ \vec{j_i} = -F z_i \lambda_i c_i \nabla \varphi_a. $$

(37)

The overall current density is the sum of the partial current densities, that is also expressed by Ohm’s law, i.e.

$$ \vec{j} = -F \sum_i z_i \lambda_i c_i \nabla \varphi_a = \sigma \nabla \varphi_a. $$

(38)

Hence, the electrical potential gradient can be expressed as

$$ \nabla \varphi_a = {\frac{\vec{j}}{\sigma}}. $$

(39)

Relation (39) is inserted into the species transport equation 26. If the electrophoretic mobility is constant and charge conversation $\nabla \cdot \vec{j}=0$ is accounted for, we obtain

$$ {\frac{\partial c_j}{\partial t}} = - \nabla \cdot (c_j \vec{v}) + \nabla \cdot (D_j \nabla c_j) - \vec{j} \lambda_j \nabla \cdot \left ({\frac{c_j }{\sigma}} \right)+r_j. $$

(40)

When we neglect the concentration gradient between the undiluted and diluted liquid, the ratio of the concentrations (conductivities) within the left channel part to the concentrations (conductivities) within the right channel part corresponds everywhere to n, i.e.

$$ {\frac{c_{A^+,l}}{c_{A^+,r}}} = {\frac{c_{B^-,l}}{c_{B^-,r}}} ={\frac{c_{j,l}}{c_{j,r}}} = {\frac{\sigma_l}{\sigma_r}} = n. $$

(41)

Consequently, the ratio of species concentration to the conductivity is constant at a fixed location too, we have

$$ {\frac{c_{j,l}}{\sigma_l}} = {\frac{c_{j,r}}{\sigma_r}} = {\rm const}. $$

(42)

Inserting this statement in Eq. 40 reveals that the migration term vanishes and the concentration field is influenced by convection and diffusion only. Referring to Sect. 4.1, the shown derivation explains that for every buffer electrolyte species the same qualitative concentration field is found.