1 Introduction

Measuring financial integration between the “new” EU member states and the Eurozone ranks high on the agenda of policymakers and researchers. To begin, both theory and empirical findings suggest that financial integration contributes to a more efficient capital allocation, which, in turn, fosters economic growth (see Levine et al. 2000). Several studies find that financial integration in the “old” EU member countries resulting from the introduction of the euro is beneficial for economic development and growth (see e.g., Guiso et al. 2004). In addition, the extent to which financial markets in the “new” EU member states are integrated with the Eurozone countries is an important factor in the recent debate on the appropriate time to adopt the euro in these countries (see Brada et al. 2005; Kutan and Yigit 2005). Although the benefits from giving up monetary autonomy and adopting a single currency are considered to be proportional to the degree of financial integration already achieved, the financial integration itself can be promoted by the elimination of currency risks following the expansion of the Eurozone. Finally, financial integration has an important implication for international investors and portfolio managers. More integrated financial markets offer greater opportunities for agents to diversify portfolios and share idiosyncratic risks across countries (Baele et al. 2004). However, the more integrated financial markets can also lead to spill-overs of negative systematic shocks originating in the “old” EU countries to the “new” EU member states.

Despite the importance of financial integration for monetary convergence and economic development in the “new” EU member states, only few studies provide a quantitative account of the degree and development of financial integration in these countries. Most of the existing studies focus on various aspects of financial integration in the most developed “new” EU member states, including the Czech Republic, Hungary, and Poland, for which the information on various financial indicators is more readily available, although some recent studies cover more countries and financial markets. A popular approach for studying financial integration is based on the so-called β-convergence and σ-convergence measures borrowed from the economic growth literature (see Baele et al. (2004) for an application of this methodology to “old” EU members and Babetskii et al. (2007) for a recent application to the “new” EU member states). The β-convergence detects catching-up tendencies across countries, while σ-convergence identifies the state of the convergence for a particular period in time. Both measures are based on the law of one price, which disregards the presence of market frictions and transaction costs.

Another widely used technique employed in the financial integration literature is based on the co-movement of interest rates across countries. The workhorse methodology in this type of empirical work is cointegration analysis (see MacDonald (2001) and Voronkova (2004) for a recent application of this methodology to “new” EU member states). However, similarly to the previous measures, a simple linear cointegration methodology is too restrictive since it does not take into account the impact of transaction costs and market frictions that restrict the adjustment of interest rates towards long run equilibrium (Balke and Fomby 1997). In addition, a direct application of cointegration methods in the context of “new” EU member countries, most of which evolved through the transformation process from a planned to a market economy during the 1990s, is problematic as during the transformation period relationships are changing (Brada et al. 2005).

Given the wide variety of empirical strategies employed for studying financial integration in the “new” EU member states, it is not surprising that the evidence coming from these studies is controversial (a more extensive discussion is provided in the next section). In this paper, we address the issue of financial market integration in the “new” EU member states using the threshold cointegration methodology. This methodology has been developed recently to take the possibility of discontinuous adjustment to the long-run equilibrium due to market frictions into account and thereby overcome some of the disadvantages of the standard cointegration approach (Balke and Fomby 1997; Hansen and Seo 2002). Threshold vector error-correction models (TVECM) have not been integrated into standard software packages thus far, which explains why their application is limited. The only study we are aware of that applies the TVECM methodology for studying financial integration in the “old” EU member countries is Poghosyan and De Haan (2007). To our best knowledge, the present paper is the first attempt to apply the threshold cointegration methodology for studying financial integration in the “new” EU member countries.

Our conjecture is that various market frictions, including different types of legal and economic barriers and situations of asymmetric information, result in transaction costs that hamper arbitrage across financial markets in different countries. These market frictions can be subdivided into two broad categories: frictions due to legal and administrative issues, such as differences in tax regimes and regulatory rules, and frictions due to technical issues, such as the absence of harmonized market conventions on security settlement procedures, business days and other operational prerequisites for efficient financial market functioning (Baele et al. 2004). In both cases, domestic and foreign investors are treated unequally, which imposes additional transaction costs for cross-border arbitrage and hampers financial integration. The pre-accession reforms in the “new” EU countries aimed at harmonization of national market conventions should eventually result in a diminishing role of market frictions and in establishing more integrated financial markets (Thimann 2002).

In order to test our hypothesis, we evaluate the transaction costs related to the mentioned frictions explicitly from the data. For this reason, we employ threshold cointegration analysis on interest rate data for the “new” EU members and corresponding Eurozone rate. The TVECM model is applied to fixed, seven-year samples, using a moving window approach, enabling us to take into account structural changes that took place in these countries during their economic transformation from a planned to a market-based economic system. For each window, a transaction costs parameter (labeled as “transaction costs band”) is estimated and its significance evaluated. By plotting the transaction costs parameter over time and taking into account its significance, we provide a measure of the financial integration dynamics for each country under research.

Our estimation results suggest that financial markets in “new” EU members gradually became more financially integrated with “old” EU members. However, the degree of integration differs across financial segments: money markets appear to be the most integrated ones due to lower transaction costs, while loan markets display the lowest degree of integration. In addition, significant differences exist across financial segments within “new” member states.

The remainder of the paper is organized as follows. Section 2 discusses the relevant literature on the topic. Section 3 describes our methodological approach. Data and estimation results are presented in Section 4, and the last section concludes.

2 Measuring financial integration

2.1 Background and literature review

There is no single measure which would capture all aspects of financial integration. Baele et al. (2004) consider financial markets to be integrated if all potential market participants with the same relevant characteristics face similar rules in dealing with financial instruments, have equal access to the mentioned financial instruments, and are treated equally when active in the market. The authors divide existing measures of financial integration into three broad categories: (a) price-based; (b) news-based; and (c) quantity-based measures. The first set of measures is based on the interest parity relationship, which is a representation of the no-arbitrage condition (law of one price) in financial markets. The second set of measures makes use of the asset pricing theory and distinguishes between common (systematic) and local (idiosyncratic) risks. The markets are considered to be fully integrated when only the common risk factors (often proxied by yields in the benchmark country) determine the equilibrium returns. Finally, the third group of measures accounts for quantitative characteristics of cross-border investment activities in the form of capital flows, listings, M&A, and other relevant indicators.

Most of the existing studies on EU financial integration have focused exclusively on financial integration in the “old” EU member states (see among others Baele et al. 2004; Hartmann et al. 2003; Hardouvelis et al. 2006; Poghosyan and De Haan 2007). This literature documents that European countries have become more financially integrated over time, and that the degree of integration has accelerated following the launch of the single currency in 1999. However, the current level of financial integration differs across different financial segments. In particular, some financial markets still exhibit various frictions preventing full integration.

The evidence on financial integration in the “new” EU member states is far less exhaustive. The existing studies on financial integration in the “new” EU members can be subdivided into descriptive studies and quantitative empirical applications. The descriptive studies focus on various aspects of legal and institutional adjustments, which took place in the “new” EU member countries to adjust their financial markets to the European standards (Thimann 2002 contains a collection of such studies). A common finding in this literature is that increasing harmonization of the regulatory framework and integration of underlying financial infrastructures has bolstered the general convergence tendencies in the “new” member states.

The quantitative studies make a use of standard measures of financial integration and apply them to different financial market segments in the “new” EU member states, usually using Germany as a benchmark country. Among those studies, Crespo-Cuaresma and Wojcik (2004), Herrmann and Jochem (2003), and Holtemöller (2005) analyze integration of money markets. A common finding in these studies is that money markets in the “new” member countries show an increasing degree of integration with the Euro area. However, in most of these countries the discrepancies from the interest parity condition are not completely eliminated yet due to transaction costs caused by the low level of liquidity and underdeveloped financial markets, which diminish the possibilities of arbitrage.Footnote 1

Reininger and Walko (2005) and Kim et al. (2006) study government bond market integration between three major “new” member countries (the Czech Republic, Hungary, and Poland) and a subset of “old” EU member states. They show that integration between the “new” EU members and the Euro area has evolved through different phases: the bull period 2000–2003 characterized by a sharp spread contraction, the bear period 2003–2004 of spread widening, and the second bull period 2004–2005. The level of integration has grown at varying pace across different countries, reflecting differences in regulatory and legal barriers to integration.

A number of recent papers studied integration of equity markets in the “new” member states using different methodologies. MacDonald (2001), Gilmore and McManus (2002), Voronkova (2004) and Syriopoulos (2006, 2007) apply linear cointegration methods. Syriopoulos (2006) and Moroe and Wang (2007) employ a GARCH methodology, while Babetskii et al. (2007) make use of the β– and σ–convergence indicators. Cappiello et al. (2006) use a “comovement box” methodology based on the conditional correlations of different time-varying quantiles of the returns.Footnote 2 The common conclusion coming from these studies is that equity markets are becoming more integrated over time, which is reflected in statistically significant long-run relationships between stock indices (cointegration) and decreasing time varying volatility of stock returns in more recent periods.Footnote 3 However, the speed and degree of integration greatly varies across countries, and the studies provide contradictory conclusions in this regard. For example, Voronkova (2004) argues that there was a break in the cointegrating relationship between countries in the late 1990s, while Syriopoulos (2007) concludes that long-run relationships between “new” member countries estimated for two sub-samples, separated by the introduction of the euro, did not change. Furthermore, while Syriopoulos (2006) finds persistent volatility effects in equity markets of the “new” member states, Moroe and Wang (2007) conclude that volatility effects have diminished over time. The conflicting results coming from different studies can be explained by different sample periods and different methodologies applied in those studies.

2.2 Interest parity condition and financial integration: why may transaction costs play an important role?

The theoretical background for analyzing financial integration employed in most of the previous studies is the no-arbitrage condition in international financial markets (law of one price). Analytically, the no-arbitrage condition can be expressed in the form of the covered interest parity (CIP) condition (see Sarno and Taylor 2002 for a textbook exposition):

$$\label{Eq: CIP} i_t - i_t^* = f_t - s_t, $$
(1)

where f t is the logarithm of the forward exchange rate at time t for delivery at time t + 1, s t is the logarithm of the spot exchange rate, and i t and \(i_t^*\) are domestic and foreign interest rates, respectively. The CIP states that when the domestic interest rate is higher than the foreign interest rate, the domestic currency is expected to depreciate by an amount approximately equal to the interest rate differential. It assumes that investors cover risks related to exchange rate uncertainty by purchasing forward contracts in the foreign exchange market. The forward exchange rate f t can be further decomposed into an expected exchange rate (E t [s t + 1]) and a risk premium (RP t ) required by risk averse investors: f t  = E t [s t + 1] + RP t . The presence of the risk premium combined with the assumption of rational expectations (s t + 1 = E t [s t + 1] + ε t + 1) leads to the uncovered interest parity condition:

$$\label{Eq: UIP} i_t - i_t^* = \big[s_{t+1}-s_t\big]-\varepsilon_{t+1} + RP_t, $$
(2)

where ε t + 1 is the rational expectations forecast error at time t + 1, RP t is a time-varying foreign exchange risk premium, and E t (.) is the mathematical expectation operator conditional on information at time t. Expression (2) suggests that the stochastic properties of the interest rate differential are related to the stochastic properties of its linear components on the right-hand side of the equation: the exchange rate change, the rational expectations error, and the risk premium. A number of empirical studies document that the exchange rate follows a martingale process, which implies stationarity of exchange rate changes (see e.g., Meese and Rogoff 1983). The rational expectations error term is also stationary by definition. Finally, there is no theoretical justification to predict stochastic trending behavior of the currency risk premium. Empirically, there is substantial support for the stationarity of the time-varying risk premium (Fama 1984). In sum, there is a good reason to expect that the interest differential is a stationary process, and cross country interest rates in levels are cointegrated. Many studies on financial integration in the “new” EU member countries have adopted this relationship as background for their empirical investigations (see MacDonald 2001 and Voronkova 2004, among others).

However, the major assumption behind the interest parity condition is the absence of market frictions and instantaneous arbitrage across countries when the parity is violated. In the presence of transaction costs and market frictions, which is a more realistic assumption, the adjustment to the parity condition will depend on the relative size of the deviation with respect to the degree of transaction costs.Footnote 4 The presence of market frictions and transaction costs creating impediments for financial integration between the “new” and “old” EU member countries has been widely documented in previous literature. For instance, Herrmann and Jochem (2003) show that cross-border money market transactions in the Czech Republic, Hungary, Poland and Slovakia were hampered by regulations on capital outflows imposed by authorities in the initial period of transition, which has resulted in persistent deviations from the interest parity condition in the money market. After dismantling of restrictions on short-term capital movements in late 1990s, the discrepancies from the interest parity condition have been reduced significantly, reflecting elimination of transaction costs due to capital regulation.Footnote 5 Similarly, Syriopoulos (2007) show that information costs of investors trading in stock markets of Central and Eastern European countries are higher than EU average due to stricter listing requirements and regulatory rules. This explains relatively lower liquidity of stock markets and higher transaction costs for trading and investment, which limit international portfolio allocation in these countries and their integration to international financial markets. Still another important factor limiting financial integration across countries is differential tax treatment of domestic and foreign investors (Baele et al. 2004). Hence, harmonization of tax legislation in preparations for the EU accession has substantially reduced transaction costs for cross-border investments in the “new” EU member countries and fostered the financial integration process (Thimann 2002).

The discussion above suggests that the size of the transaction costs depends on the level of financial integration across countries. Therefore, evaluating the degree of transaction costs from the data and analyzing their dynamics over time should provide information on the extent to which financial markets have become more integrated in the “new” EU member countries.

2.3 Financial integration and discontinuous adjustment

In the standard cointegration framework, adjustment to the long-run equilibrium is linearly dependent on the magnitude of the deviation. However, in practice we observe different types of market frictions related to barriers to trade, asymmetric information, and transaction costs necessary for making arbitrage across spatially differentiated financial markets. These frictions introduce a non-linear adjustment to the long-run equilibrium (Balke and Fomby 1997). The idea is that market imperfections result in a “transaction costs band” around the long-run equilibrium path, within which there is no incentive for arbitraging. Therefore, deviations from the long-run equilibrium should be large enough to move outside of the transaction costs band and induce arbitrage across markets.

A popular approach, which is designed to account for transaction costs in the adjustment to the long-run equilibrium is the threshold cointegration methodology. This approach was pioneered by Balke and Fomby (1997) and generalized to the multiple equations setting by Hansen and Seo (2002). The appealing feature of the threshold cointegration approach is that it allows to explicitly estimate the unobservable transaction costs band and test for its significance.

The invention of the threshold cointegration methodology has inspired a stream of empirical studies on market integration in different fields of economics. Some applications can be found in the finance literature because such markets are believed to clear quickly. Siklos and Granger (1997) apply regime-sensitive cointegration methodology to U.S. and Canadian financial markets and report the presence of cointegration only beyond some threshold. Balke and Wohar (1998) study the integration of U.S. and UK financial markets. They find that the equilibrium relationship between two interest rate series is more persistent within the transaction costs band, while outside the band deviations from dis-equilibrium tend to be smoothed out faster. Similarly, Peel and Taylor (2002) apply the threshold cointegration methodology for the U.S. and UK data in the late 1920s, reporting strong evidence in favor of a transaction costs band in the covered interest parity relationship. Deviations from the long-run equilibrium become significantly mean reverting outside the neutral band, but within the band they exhibit moderately persistent behavior. More recently, Holmes and Maghrebi (2006) test for asymmetries in the adjustment mechanism towards a real interest parity relationship in major industrialized countries. The authors find that the speed of adjustment tends to be higher with respect to increasing rather than decreasing deviations from the long-run equilibrium. They attribute this discontinuous adjustment to asymmetric monetary policy responses documented in some of the industrialized countries. Finally, Poghosyan and De Haan (2007) apply the TVECM methodology for analyzing the degree and dynamics of financial integration in the “old” EU member countries. They report evidence in support of discontinuous adjustment due to market frictions. For some country pairs and financial market segments these frictions show declining dynamics, suggesting increased financial integration over time.

3 Methodology

Similar to Poghosyan and De Haan (2007), we use a multivariate extension of the threshold cointegration methodology developed in Balke and Fomby (1997) to study financial integration in the “new” EU members.

In our empirical investigation, we adopt a threshold cointegration specification suggested by Hansen and Seo (2002):

$$ \begin{array}{lll}\label{Eq: TVECM} \Delta Y_t &=& \left(\mu_1+\sum_{j=1}^{k} \Gamma_{1j} \Delta Y_{t-j}+\Pi_1 ECT_{t-1}\right) I(|ECT_{t-1}| \le \gamma) \\ & &+\, \left(\mu_2+\sum_{j=1}^{k} \Gamma_{2j} \Delta Y_{t-j}+\Pi_2 ECT_{t-1}\right) I(|ECT_{t-1}| > \gamma) + \epsilon_t, \end{array} $$
(3)

where \(Y_t=\big(r^{{\kern.6pt}i}, r^j\big)'\) is a vector of nominal interest rates for countries i and j, respectively, I(.) is an indicator function depending on the size of the deviation from the long-run equilibrium in the previous period (ECT t − 1) relative to the threshold parameter (γ); μ 1 and μ 2 are 2×1 vectors of intercepts; Γ1j and Γ2j are 2×2 matrices of constant parameters representing short-run responses; and Π1 and Π2 are 2×2 diagonal matrices representing speed of adjustment to the long-run equilibrium in the first and second regime, respectively. k is the number of lags and ε t are i.i.d. Gaussian disturbances. This specification assumes that adjustment towards equilibrium is regime-dependent and is conditioned upon the relative size of the dis-equilibrium and the threshold parameter. In particular, the speed of adjustment parameters Π are assumed to have lower values in the non-adjustment regime (regime 1) and potentially could be even insignificant. Figure 1 provides a visual illustration of the discontinuous adjustment mechanism. The horizontal axis plots deviations from the long-run equilibrium between interest rates in the “new” and “old” EU member countries (the error-correction term, ECT) and vertical axis plots interest rate adjustment in the “new” EU member country. The linear error-correction model predicts that the size of the interest rate adjustment in the “new” EU member country is a linear function of the error-correction term (continuous adjustment). Unlike the linear model, the threshold error-correction model predicts that the linear adjustment takes place only in the second regime, in which the deviation from the long-run equilibrium exceeds the threshold γ in absolute terms. If the deviations from the long-run equilibrium are relatively low (the first regime), then interest rates in the “new” EU member country do not adjust, implying persistent disequilibrium. The larger is the size of the threshold γ, the greater is the extent to which the persistent disequilibrium can exist, implying a lower degree of financial integration. Therefore, we interpret the size of the threshold parameter γ as a measure of financial integration.

Fig. 1
figure 1

Visual representation of the TVECM model

Full size image

The algorithm for the threshold vector error-correction model (TVECM) estimation involves procedure in three steps. The first step consists of testing for stationarity and cointegration using ADF and Johansen (1991) tests, respectively. In the second step, the series that are integrated of order one are used in a standard linear error-correction model. In the final step, the TVECM is estimated for the cointegrated series using the maximum likelihood procedure described in Hansen and Seo (2002). For this purpose, the threshold parameter γ is determined using the following selection criterion:Footnote 6

$$\label{Eq: GAMMA} \xi (\hat{\gamma}) = min \biggl(log \biggl| \frac{1}{n} \sum_{t=1}^n \hat{\varepsilon}_t(\gamma) \hat{\varepsilon}_t(\gamma)' \biggr| \biggr). $$
(4)

Once the value of γ that minimizes Eq. 4 is chosen, an additional restriction is imposed to which each regime should contain at least a pre-specified fraction of the total sample (π 0) on this grid search procedure:Footnote 7

$$\label{Eq: PI} \pi_0 \leq P(|ECT_{t-1}| \leq \gamma) \leq 1-\pi_0. $$
(5)

The statistical significance of the threshold parameter γ (the nuisance parameter) contains elements of non-standard inference. Therefore, the p-values are calculated using the SupLM test and the bootstrapping techniques proposed by Hansen and Seo (2002).

Applying a rolling window approach enables us to observe the evolution of the transaction costs bands over time. Intuitively, the more integrated the markets are, the smaller the transaction costs band should be, taking other parameters as constant. Therefore, we interpret the decreasing dynamics of transaction costs band as evidence in favor of the gradual integration of financial markets in the “new” EU member states.

4 Data and estimation results

We employ interest rate series from different segments of the financial markets in Germany (the benchmark country) and eight “new” EU members: the Czech Republic, Estonia, Hungary, Lithuania, Latvia, Poland, Slovenia, and Slovakia.Footnote 8 Our dataset runs from 1994 to 2006 and includes a monthly series on T-bill, interbank, deposit, and loan rates (see Table 1). The interest rate series are comparable across countries and are obtained from the IMF’s International Financial Statistics and Eurostat databases.Footnote 9

Table 1 Data description
Full size table

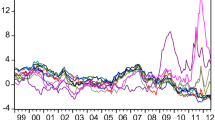
The dynamics of interest rates are present in Fig. 2. Over our sample period, interest rates in the “new” EU member countries have converged to the German rates in all financial segments. To investigate whether the adjustment contains elements of regime-dependence, we undertake the following steps.

Fig. 2
figure 2

Interest rates. Source: International Financial Statistics (IMF) and Eurostat

Full size image

To begin, we test the interest rate series for stationarity using the Augmented Dickey-Fuller (ADF) and the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) tests (see Table 2). The ADF test results suggest that practically all series are I(1), since the null hypothesis of no stationarity is (is not) rejected for series in levels (first differences). We cross-check these results using the the KPSS test, which is based on the null hypothesis of stationarity. With very few exceptions, the KPSS test results support this finding. Therefore, in the next step, we proceed by testing whether the series are cointegrated.

Table 2 Unit root test results
Full size table

We perform Johansen (1988, 1991) cointegration rank tests on a pair of corresponding interest rate series in the “new” EU member states and Germany. In our error correction specification, we allow for a deterministic trend in the data generating a process of interest rate series since omission of the deterministic trend may produce test statistics that are biased toward rejection of the cointegration relationship (Zhou 2003). In addition, following Brada et al. (2005), we test for cointegration using fixed rolling samples with 84 observations (7 years). The rolling window approach is more robust to the possibility of structural breaks in the data (especially in the early transition period) than is the total sample estimation approach (Brada et al. 2005; Holtemöller 2005). In addition, it allows us to measure the dynamics of convergence in interest rates over time.

Johansen’s test is based on the following vector autoregressive (VAR) system:

$$\label{Eq: Johansen} \Delta X_t = \sum_{j=1}^{k-1} \Gamma_j \Delta X_{t-j} + \Pi X_{t-1} + c_0 + \varepsilon_t, $$
(6)

where X t is a vector of n variables, c 0 is a constant term, and ε t is a vector of Gaussian errors with mean zero and the variance-covariance matrix Σ. Inclusion of c 0 allows a linear time trend to be present in the data generating process of X t . The cointegration hypotheses involve properties of the matrix Π. If the rank of Π is r, where r ≤ n − 1, then r is called the cointegration rank, and Π can be decomposed into two n ×r matrices, α and β, such that Π = αβ′. The economic interpretation of the components of matrix Π is as follows: β consists of r linear cointegrating vectors, while α represents r vector error correction parameters. Cointegration tests are carried out using Johansen (1991)’s maximum eigenvalue (λ max ) tests with critical values provided in Osterwald-Lenum (1992). Since our estimations are applied to a set of country pairs, our null-hypothesis is r = 0 cointegrating relationships (no cointegration) against r = 1 relationship (cointegration).

The results of cointegration tests are presented in Table 3. It is remarkable that when the total sample is used in the Johansen test, the hypothesis of no cointegration in each financial segment cannot be rejected for most of the countries. The exceptions are Slovenia and some Baltic states. In addition, in some cases when the hypothesis of no cointegration is rejected for the whole sample, it cannot be rejected for quite a large number of sub-samples (e.g. T-bill rates in the Czech Republic). This finding reflects structural changes in the “new” EU members’ financial markets during their transformation from a centrally-planned to a market-oriented economy (Voronkova 2004; Holtemöller 2005). Unfortunately, given the short sample period at hand, it is difficult to test for the existence of the long-term relationship among financial market instruments with a higher degree of reliability. Therefore, our results on the number of cointegration relationships should be interpreted with caution.

Table 3 Cointegration test results
Full size table

For the sub-samples where cointegration was established, we investigate whether the adjustment towards the long-run equilibrium is regime-dependent and is affected by the relative size of the deviation with respect to the threshold. For this purpose, we estimate the TVECM Eq. 3 and test for the significance of the threshold parameter γ (using a 10% confidence interval) for each of the sub-samples with cointegration. Unfortunately for the threshold models, we cannot test for the autocorrelation in residuals using the standard asymptotic theory (Lukkonen et al. 1988). Given the low number of observations available in each rolling sub-sample, in our estimations, we uniformly set the number of lags to 1.Footnote 10

Table 4 contains a summary of the threshold cointegration estimations for each of the countries and financial sub-samples. The estimation results suggest that the interbank market appears to be the most integrated as the average number of sub-samples for which cointegration was established (51) is the highest for this segment. In addition, the average share of significant thresholds in the total number of estimated thresholds (25%) is the second lowest for the interbank market, followed by the T-bills market (21%). This finding suggests that there is less support for discontinuous adjustment in money markets, which can be attributed to relatively low transaction costs in this particular market segment. By the same reasoning, the loan market is the least integrated segment—it is described by the lowest number of sub-samples for which cointegration was established (18) and the highest share of sub-samples for which significant thresholds were obtained (41%). This ranking of financial segments in terms of degree of integration obtained with thresholds cointegration methodology echoes the results by Baele et al. (2004) for the “old” EU member states.

Table 4 Summary of threshold estimation results
Full size table

Cross-country comparison reveals significant differences in the degree of financial integration across “new” members. Latvia is leading in terms of the number of sub-samples for which cointegration was established: It has the highest scores in all market segments, except for the loans market, in which the highest score is recorded for Slovenia. However, in terms of the share of the significant thresholds the results are mixed. Slovenia shows the lowest degree of discontinuous adjustment in the deposit markets, Latvia in the interbank market, Slovakia in the loans market, and Hungary in the T-bills market. Such a diverse outcome suggests that substantial differences exist with respect to the transaction costs and market frictions across financial segments within a particular country.

To obtain a dynamic picture of transaction costs, we present the rolling window estimation results in Figs. 3, 4, 5, 6, 7, 8, 9 and 10. The interpretation of the figures is as follows: solid lines indicate estimated threshold parameter for a given rolling sub-sample and bars indicate that the thresholds are significant. On the horizontal axis, we report the end of the sub-sample for which the estimations were performed. The Figures reveal a decreasing magnitude of the thresholds in most of the countries and financial segments, which implies that, on average, financial markets have become more integrated over time. In addition, we can see that for many of the countries, we were able to establish a cointegrating relationship for most recent sub-samples. This suggests that the stochastic properties of financial returns became more similar over time, implying a strengthening of financial linkages with Germany. Thus, based on a conceptually new measure, we find support for the increasing degree of financial integration between “new” and “old” EU member states.

Fig. 3
figure 3

Czech Republic. The figures represent dynamics of transaction costs in financial markets proxied by the threshold parameters obtained from the TVECM. The solid lines indicate estimated threshold parameters and bars denote those estimates that are significant. The end of the sub-sample for which the estimations were performed is reported on the horizontal axis

Full size image
Fig. 4
figure 4

Latvia. The figures represent dynamics of transaction costs in financial markets proxied by the threshold parameters obtained from the TVECM. The solid lines indicate estimated threshold parameters and bars denote those estimates that are significant. The end of the sub-sample for which the estimations were performed is reported on the horizontal axis

Full size image
Fig. 5
figure 5

Hungary. The figures represent dynamics of transaction costs in financial markets proxied by the threshold parameters obtained from the TVECM. The solid lines indicate estimated threshold parameters and bars denote those estimates that are significant. The end of the sub-sample for which the estimations were performed is reported on the horizontal axis

Full size image
Fig. 6
figure 6

Poland. The figures represent dynamics of transaction costs in financial markets proxied by the threshold parameters obtained from the TVECM. The solid lines indicate estimated threshold parameters and bars denote those estimates that are significant. The end of the sub-sample for which the estimations were performed is reported on the horizontal axis

Full size image
Fig. 7
figure 7

Slovenia. The figures represent dynamics of transaction costs in financial markets proxied by the threshold parameters obtained from the TVECM. The solid lines indicate estimated threshold parameters and bars denote those estimates that are significant. The end of the sub-sample for which the estimations were performed is reported on the horizontal axis

Full size image
Fig. 8
figure 8

Estonia. The figures represent dynamics of transaction costs in financial markets proxied by the threshold parameters obtained from the TVECM. The solid lines indicate estimated threshold parameters and bars denote those estimates that are significant. The end of the sub-sample for which the estimations were performed is reported on the horizontal axis

Full size image
Fig. 9
figure 9

Slovakia. The figures represent dynamics of transaction costs in financial markets proxied by the threshold parameters obtained from the TVECM. The solid lines indicate estimated threshold parameters and bars denote those estimates that are significant. The end of the sub-sample for which the estimations were performed is reported on the horizontal axis

Full size image
Fig. 10
figure 10

Lithuania. The figures represent dynamics of transaction costs in financial markets proxied by the threshold parameters obtained from the TVECM. The solid lines indicate estimated threshold parameters and bars denote those estimates that are significant. The end of the sub-sample for which the estimations were performed is reported on the horizontal axis

Full size image

5 Conclusion

In this paper, we study the dynamics of financial integration in the “new” EU member states using a new measure accounting for the possibility of transaction costs and other market frictions. We apply a threshold vector error correction model with fixed rolling windows on a set of interest rate series from different financial segments. This methodology is more general than those applied in previous studies as it is based on a more realistic assumption of the existence of various transaction costs, such as controls on short-term capital movements, differences in tax systems, and legal restrictions. Furthermore, it allows us to test for the presence of regime-dependent adjustment to the long-run equilibrium.

Our main finding is that financial linkages between “new” and “old” EU member states (benchmarked by Germany) have strengthened over time. This finding is valid for each of the four financial segments (T-bill, interbank, deposit, and loan rates) under consideration, although the findings vary across countries and segments. Probably the most important factors driving the acceleration of financial integration are related to the policy measures undertaken by the “new” member states in order to meet European financial standards, including the liberalization of capital accounts, legal, and institutional reforms. All these measures resulted in a reduction of market frictions and transaction costs.

The degree of financial integration exhibits variation across financial segments. Our estimation results suggest that money markets are the most integrated ones, followed by T-bill and deposit markets. Loans markets exhibit the lowest degree of integration. These differences are related to the transaction costs necessary to make arbitrage across countries, which differ from market to market. However, our results on the existence of a long-term relationship between financial market instruments should be interpreted with caution, since these results are based on a relatively small sample of observations.

The increasing degree of financial integration has important practical implications for the “new” member states. Increased financial integration implies that the benefits from adopting the euro will increase over time. Financial linkages are anticipated to strengthen even further with the introduction of the euro due to the elimination of transaction costs necessary for hedging against risks related to unexpected currency fluctuations.