Introduction

Mixed mountain forests of Norway spruce (Picea abies (L.) Karst.), silver fir (Abies alba Mill.) and European beech (Fagus sylvatica L.) cover more than 10 million hectares in Europe (Hilmers et al. 2020a), and more than 200 thousand hectares only in Romania. These temperate forests are considered more resilient and productive than pure forests (Griess et al. 2012; Pretzsch et al. 2013, 2021) and they are expected to have an essential role in mitigating climate change impacts (Vacek et al. 2021). Future forest adaptation strategies would also rely on the conversion of pure to mixed stands (Hilmers et al. 2020b; Reventlow et al. 2021) making reliable tree and stand growth future projections indispensable for a holistic and sustainable management of these forests. Mixed mountain forests dimensional arrangements usually assemble uneven-aged forests, which have higher stability and productivity over time than even-aged forests (O’Hara 1998; Dănescu et al. 2016; Bauhus et al. 2017; Vacek et al. 2021), but their high structural complexity is hindering growth assessment. Since most of the growth models developed worldwide have been designed for even-aged stands with intense management and short rotation periods, classic growth models such as normal yield tables are inapplicable for such forests due to mixed stands overyielding production (Pretzsch and Schütze 2009). On the other hand, mixed forest yield tables were found hardly applicable in forestry practice (Hasenauer 2006). In addition, recent studies (Bosela et al. 2018; Pretzsch et al. 2020) demonstrate that the above-mentioned species’ growth has increased in the last three centuries and their increment was found to vary significantly with climate and altitude, making growth prediction even more difficult for forest planners and policy makers.

These difficulties have been overcome in other parts of the world by developing individual tree growth models which are able to provide accurate estimates in complex stands with mixed species composition (Newnham and Smith 1964; Wykoff et al. 1982; Monserud et al. 1997; Pretzsch et al. 2002; Hasenauer et al. 2006). However, the data sets available for developing growth models usually come from national forest inventories (Wykoff 1990; Monserud and Sterba 1996; Vospernik 2021), which are not specifically designed for the development of growth models (García 2006), and therefore tend to fit better the most frequent stand structure, namely the even-aged forest structure.

Diameter increment is one of the most important sub-models within individual tree growth models. Many studies have chosen to develop basal area increment (\({i}_{g}\)) models instead of \({i}_{d}\) models (Jevšenak and Skudnik 2021; Ozdemir 2021; Vospernik 2021) due to the high dbh–\({i}_{g}\) correlation compared to the correlation between dbh and \({i}_{d}\). Nevertheless, West (1980) showed that the accuracy of the prediction is the same regardless of which of the two variables is used as the dependent variable, yet Russell et al. (2011) results underline that when the model error terms are incorporated in growth simulations, \({i}_{d}\) equations project future growth in the long term more accurately than \({i}_{g}\) equations.

Diameter growth dynamics is inherently different in uneven-aged stands compared with even-aged stands. Hynynen et al. (2019) found that the growth rates registered in Finnish spruce uneven-aged stands were 20% lower than in even-aged stands. The mean annual increment recorded in black spruce—Picea mariana (Mill.) Britton, Sterns & Poggenburg—uneven-aged stands achieved only 30% of the even-aged stands observed growth (Rossi et al. 2009). Trees in uneven-aged stands maintain steady growth rates for a far longer period reaching the asymptote much later than the ones growing in even-aged stands (von Guttenberg 1915; Assmann 1970; Pretzsch et al. 2020). Therefore, there is a big difference in the growth dynamics between the two types of structure, making different models highly necessary to accurately estimate stand growth and carbon sink projections for each of them, especially for old grown protected forests.

Diameter increment has been historically associated with various theoretical growth functions (TGF) with high biological interpretability (Zeide 1993; Vanclay 1994; Kiviste et al. 2002; Weiskittel et al. 2011; Burkhart and Tomé 2012) as a function of tree or stand age. Since stand or tree age data are hardly available or even inexistent in national forest inventories, empirical growth functions (EGF) are more frequently applied than theoretical functions for predicting the \({i}_{d}\) (Vanclay 1994; Weiskittel et al. 2011).

Most of the EGF predict tree \({i}_{d}\) as a function of its size, competition and site factors, and have a similar sigmoid shape as TGF, but without a clear interpretation of the parameters’ relation with the biological process described by the response variable. In order to use the TGF, Tomé et al. (2006) proposed a method for developing age-independent growth functions based on the algebraic difference approach (ADA) (Bailey and Clutter 1974). Age-independent growth functions are developed by first solving the TGF for age equal with t and later reformulating the growth function for age as follows: t + proj, where proj is the projection length in years. This method produces a family of curves if one of the functions’ parameters is expressed as a function of the site variables. However, invariant tree level dbh yield projections are obtained only if the parameters are expressed as a function of variables that do not change with time.

Site index is the most commonly used variable to rewrite one of the algebraic difference equations’ parameters and obtain a family of curves; however, the applicability of site index curves is rather limited in uneven-aged stands. A phytocentric indicator used for assessing site productivity in uneven-aged stands is a growth index (GI) based on the trees’ past growth (Vanclay 1989, 1992; Trasobares et al. 2004). However, past tree growth data are rare, making this method hardly useful if there are not enough past tree growth observations for a certain site. A mixed effects modelling (MEM) framework is particularly handy in such situations as it allows model calibration for new stands even when a small number of observations are available (Calama and Montero 2005; Mehtätalo et al. 2015). The use of a mixed effects model could increase the applicability of this method in evaluating site productivity in forest practice.

Mixed effects models, frequently employed for modelling hierarchical autocorrelated data, have also been previously used to develop \({i}_{d}\) models, allowing random components’ estimation for each hierarchical level (Uzoh and Oliver 2008; Subedi and Sharma 2011; Huy et al. 2021). Therefore, mixed effects age-independent EGF models can be helpful in obtaining reliable increment predictions for complex structures such as uneven-aged mixed forest stands.

With the purpose of building \({i}_{d}\) models that are suitable for the main species in uneven-aged mixed forests using different types of data, this research employs inventory data from a permanent sampling network and increment core data sampled from trees around the mean tree of the stand to build two types of age-independent \({i}_{d}\) models based on EGF and TGF.

The main objectives of this study are to (i) develop a \({i}_{d}\) model for the main species (spruce, fir and beech) growing in (Romanian mountain) mixed uneven-aged stands, (ii) estimate mixed-stands productivity using an age-independent site quality index based on the tree past growth by using a mixed effect modelling framework and determine the best calibration strategy (iii) develop an \({i}_{d}\) model for spruce based on increment cores data using theoretical growth functions reformulated as age-independent difference equations that can accurately predict \({i}_{d}\) dynamics at a tree and stand level.

Materials and methods

Study area

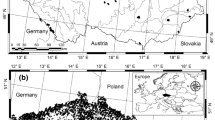
The study area (Ciceu et al. 2020) is located in the south-western Carpathians, within the oldest of the 14 national parks established in Romania, the Retezat National Park (RNP), legally constituted in 1935. Covering approximately 2800 ha of the 38,138 ha occupied by the park, the study area stretches over protected and strictly protected areas, such as the virgin forests of Gemenele Scientific Research, administrated by the Romanian Academy. The study area is characterized by a rough landscape dominated by moderate to steep slopes and altitudes ranging between 650 and 2509 m a.s.l. The geological materials of Retezat mountains, and the study area within it, are Danubian metamorphic rocks dominated by slightly metamorphosed crystalline schists. Annual precipitations vary between 900–1400 mm at lower altitudes and 1600–1800 mm at higher altitudes, while the annual average temperatures are 6 °C at lower altitudes and -2 °C at altitudes above 2000 m. Forests cover over 45% of the park, spruce, beech and fir being the predominant woody species. The diameter distribution of the stands can be associated with a negative exponential function (Ciceu et al. 2021). More details on the geographical location and characteristics of the study can also be found in Ciceu et al. (2020) and Fig. 1.

Fig. 1
figure 1

From top to bottom, altitude, slope and aspect of the study area within the limits of the Retezat National Park

Full size image

The forest stands in which the measurements were done benefit from strict measures of protection. Most of them have an important role for land and soil protection being located on slopes with an inclination of more than 35°. A small proportion of them are also classified as forests with a high scientific interest for protecting the genetic resources (genofund). Intensive forest management is strictly forbidden in these stands.

Data collection

A permanent sampling network was installed in 2015 and remeasured in 2020 in the RNP (Fig. 1). The sampling grid (400 m × 400 m) includes a total number of 178 permanent sampling plots (PSP), out of which 115 were measured in both inventories. Each PSP has two circular sub-sampling plots (SSP) placed 60 m apart from each other. The SSP area varies according to the tree dbh size within the SSP. The SSP area is 200 m2 when the maximum dbh is lower than 28 cm and 500 m2 otherwise.

The variables measured for all trees above 8 cm dbh are: tree circumference, tree height, tree height to the crown base, tree polar coordinates, i.e. distance and azimuth from the plot centre, and plot centre geographical coordinates. Only tree circumference was used in this study; it was measured in both inventories with a tape band to the nearest mm. The trees measured were tagged in order to prevent tree misidentification during field surveys. A total of 6341 trees were identified and measured in both inventories; 5556 of them were classified as alive. The total observations used to develop the individual tree \({i}_{d}\) model for the three main species of the study area are 3182 spruce trees, 727 beech trees and 454 fir trees (Fig. 2).

Fig. 2
figure 2

Spruce 1-year tree core increments and spruce, beech and fir 5-year \({i}_{d}\) derived from tree circumference observations

Full size image

Together with the measurements above, an additional data set of 719 tree increment cores extracted from spruce, beech and fir was built during the 2020 inventory. The cores were extracted from 5 to 10 representative trees (dbh close to the SSP mean dbh) in the immediate vicinity of each SSP. Given spruce abundance in the study area, 465 of the increment cores were taken from spruce trees, ensuring enough sample size to cover a wide range of site conditions. The sample cores were glued on wooden slides, ground and polished on a sanding machine using paper with varying grit, cleaned with compressed air and scanned at a 1600 dpi true resolution. The tree ring width was measured with a precision of 0.01 mm using CooRecorder software (Elektronik 2010). Each increment core (Fig. 2) was then checked for missing rings and dating error using dplR package (Bunn 2008, 2010). Individual series were cross-validated with the mean series of the trees sampled from the same SSP. A \({i}_{d}\) series was obtained for each tree core using the measured tree ring widths.

In order to estimate the influence of the physiographic variables on tree \({i}_{d}\), the elevation (m), slope (%) and aspect (radians) were derived from 30 m × 30 m resolution SRTM (Farr et al. 2007) digital elevation models for each SSP (Fig. 1).

Data analysis and modelling approach

For modelling the \({i}_{d}\) based on available data, two types of models have been considered. The first model (EGF) predicts spruce, beech and fir 5-year tree \({i}_{d}\) based on EGF as a function size, competition and site variables using the inventory data. The second one (TGF) is based on a TGF reformulated as age-independent difference equation that predicts spruce tree \({i}_{d}\) from increment cores.

Diameter increment model based on empirical growth function (EGF-model)

The base EGF used to develop the age-independent model was written as a mixed effects model with two random effects associated with the intercept and the explanatory variable \(ln\left(dbh\right)\) (Eq. 1).

$$\mathit{ln}\left({{i}_{{d}_{5}}}_{ij}\right)={a}_{1}+{a}_{2}{dbh}_{ij}^{2}+{a}_{3}\mathit{ln}\left({dbh}_{ij}\right)+{b}_{j}^{(1)}+{b}_{j}^{(2)}\mathit{ln}\left({dbh}_{ij}\right)+{\epsilon }_{ij}$$
(1)

where \(ln\)—is the natural logarithm, \({{i}_{{d}_{5}}}_{ij}\)—5-year \({i}_{d}\) registered by tree i in plot j (cm), \( {a}_{1},{a}_{2},{a}_{3}\)—fixed regression coefficients, \( {dbh}_{ij}\)—dbh at breast height (cm), \({\epsilon }_{ij}\)—is the residual error with mean zero and unknown variance \({\sigma }^{2}\), \({b}_{j}^{(1)}{b}_{j}^{(2)}\)—are the normally distributed random effects with mean zero and unknown unrestricted variance covariance matrix.

Although the inventory data has two levels of hierarchy (trees inside the SSP and SSP inside the PSP), the higher proportion of variance was explained when we used SSP as a single level of grouping than when applying the nested design of SSP inside of PSP.

A logarithmic transformation of the response variable was used to remove the heteroscedasticity associated with the residuals. In order to back-transform model predictions to their original units, several methods of bias correction have been tested, including the Finney approximation (Finney 1941), the Baskerville method (Baskerville 1972) and the empirical ratio method proposed by Snowdon (Snowdon 1991).

The explanatory variables used to develop the base model were restricted to distance-independent variables, although distances between pair of trees were also available. The reason behind this decision was to enable model application to common inventories which usually do not measure the distance between trees.

EGF model generalization

The size component of the model, being represented by the dbh and its various transformations, can be generalized by introducing biological and environmental variables to cover a wider range of site conditions (Bronisz and Mehtätalo 2020; Ciceu et al., 2020). The competition (i.e. biological) component included the quadratic mean dbh (Dg; Eq. 2), basal area per hectare (G; Eq. 3), basal area of larger trees (BAL; Eq. 4), number of trees per hectare (N; Eq. 5) and the ratio between trees' dbh and SSP Dg (RD; Eq. 6). Aspect (ASP), altitude (ALT) and slope (SL) were considered site component variables.

$${Dg}_{j}=\sqrt{\sum_{\mathrm{i}=1}^{n}\frac{{dbh}_{ij}^{2}}{n}}$$
(2)
$${G}_{j}=\frac{10000}{{S}_{j}}\left({\sum }_{i=1}^{n}\frac{\pi }{4}{dbh}_{ij}^{2}\right)$$
(3)
$${BAL}_{ij}= \frac{10000}{{S}_{j}}\sum_{i=1}^{n} \frac{\pi }{4}{dbh}_{gj}^{2}$$
(4)
$${N}_{j}=\frac{10000}{{S}_{j}}\left({\sum }_{i=1}^{n}{n}_{i}\right)$$
(5)
$${RD}_{ij}=\frac{{d}_{ij}}{{Dg}_{j}}$$
(6)

where \({Dg}_{j}\)—is the quadratic mean diameter of the SSP j (cm), \({G}_{j}\)—the basal area per hectare of SSP j (m2/ha), \({BAL}_{ij}\)—the basal area of trees larger than the tree i in SSP \(j\) (m2/ha) where \(\frac{\pi }{4}{dbh}_{gj}^{2}\) are all trees larger than subject tree i in SSP j, \({N}_{j}\)—is the number of trees per hectare in SSP j, \({RD}_{ij}\)—is the ratio between the dbh of tree i in SSP j (dbhij) and the quadratic mean diameter of SSP j (\({Dg}_{j}\)), \(n\)—is the number of trees in each SPP, and \({S}_{j}\)—is the SSP j area.

EGF calibration

One of the most important advantages mixed effects models bring is their ability to predict random parameters and obtain a localized (calibrated) curve for a new plot (Lappi 1986; Lappi and Bailey 1988; Mehtätalo and Lappi 2020). Random parameter prediction is justified and will provide more accurate results than using only fixed parameters even if only a small number of observations of the dependent variable are available. The best linear unbiased predictor (BLUP) for the random effects can be calculated for a new plot using past increments observations and the following expression (Calama and Montero 2005; Eq. 7):

$$\widehat{b}={\widehat{D}{\widehat{Z}}^{T}\left(\widehat{R}+\widehat{Z}\widehat{D}{\widehat{Z}}^{T}\right)}^{-1}\left(\widehat{y}-y\right)$$
(7)

where \(\widehat{b}\)—is the vector of BLUPs for the random components, for the plot grouping level, \( \widehat{D}\)—is the block diagonal matrix whose dimension is given by the number of random effects to be predicted, \( \widehat{Z}\)—is the design matrix for the random components specific to the additional observations, \( \widehat{R}\)—is the estimated matrix for the residual variance, \( y\)—are observed values of the predicted variable, \( \widehat{y}\)—are predicted values using only the fixed parts of the model (population parameters).

Knowing that past increment observations for a new plot are rare, we tested which is the best calibration strategy following Ciceu et al. (2020). For that purpose, we used up to nine trees with various sizes to establish from what trees one should sample in order to obtain the best localized curve.

We selected only the SSPs with more than 9 trees. The trees within these plots were divided into a calibration data set and a testing data set. The nine trees in the calibration set were grouped into 3 dbh categories (small trees, medium trees with dbh around SSP Dgj and large trees) with 3 trees each. The trees were selected iteratively from 1 to 9 and in combinations from 1 to 9 in order to estimate plot random parameters. A total of 511 different combinations of tree sizes and number of trees were used as a sampling strategy. Later, the trees in the testing data sets were used to predict \({i}_{d}\) in two different ways by using only the fixed part of the generalized mixed model as well as by using the random effects computed from the calibration data sets together with the fixed part of the generalized mixed model.

Diameter increment model based on theoretical growth function (TGF-model)

The second model, the \({i}_{d}\) theoretical model (TFG), was developed with spruce increment tree core data. The first step involved determining the best age-independent equation to model the \({i}_{d}\) for spruce. Three widely used dbh growth equations (Zeide 1993) were considered for building the model: Lundqvist–Korf (L-K), Chapman–Richards (C-R) and Hossfeld (H). These equations were reformulated as age-independent difference equations using the method proposed by Tomé et al. (2006) (Table 1; Eqs. 8–10).

Table 1 Growth model equations in its original, age-dependent form and reformulated as age-independent difference equations by using different free parameters
Full size table

Within the age-dependent base equations where Y—is the dbh, A—is the asymptote diameter of the function, k—is the growth rate related parameter, t—is the age of the tree, m—is the shape parameter, and a, b—are the Hossfeld parameters. In the age-independent equations, \({Y}_{i}\) and \({Y}_{i+proj}\)—are the dbh of the mean trees at age i and i + proj; proj —is the projection length in years; and A, k, m, a, b, c—are parameters to be estimated.

The models were fitted using nonlinear mixed effects and two nested levels of hierarchy were specified: SSPs and trees within it. Different stationary autocorrelation structures were specified, e.g. the AR (1) and ARMA (1,1), in order to account for the temporal autocorrelation of the increments of each tree core.

The potential heteroscedasticity of the age-independent TGF model was explored and controlled by fitting the model with the power type function (Eq. 11).

$$var\left({e}_{ij}\right)={\sigma }^{2}{{dbh}_{ij}}^{2\delta }$$
(11)

where \({e}_{ij}\) is \(\widehat{y}-y\), while the \({\sigma }^{2}\) and \(\delta\) are the estimated scale and shape parameters of the power-type function.

TGF generalization by growth index (GI)

Knowing that the site conditions play a major role in trees’ growth rates, a phytocentric past \({i}_{d}\) productivity index was developed (Vanclay 1992; Trasobares et al. 2004; Dănescu et al. 2017). Using the 2020 inventory data of the permanent sampling network from the past 5 years, \({i}_{d}\) was predicted as a function of the size and competition variables. The model was fitted using mixed effects to enable model calibration as described above. Once the model components were obtained, the GI was calculated using the following expressions (Eqs. 12–13):

$${\rm GI}_{1}=\frac{1}{n}\sum_{i}^{n}\frac{{i}_{{d}_{5}}}{{\widehat{i}}_{{d}_{5}}}$$
(12)
$${GI}_{2}={b}_{i}^{(2)}$$
(13)

where \({\rm GI}_{i}\)—growth index 1 or 2, \( {i}_{{d}_{5}}\)—observed 5 years past \({i}_{d}, {\widehat{i}}_{{d}_{5}}\)—predicted 5 years past \({i}_{d}, n\)—number of trees in the SSP, \( { b}_{i}^{(i)}\)—random parameter associated with the model developed.

The GI computed for each SSP that gave the best results in fitting the increment core data was further included in the TGF, rewriting the “free” parameter of the equation as a function of GI. The same calibration procedure as described above was employed in order to determine which is the best calibration strategy to obtain the random parameters and predict a GI for a new plot.

Model evaluation and validation

The following statistics (Eqs. 14–16) were used to evaluate and validate the models:

$$\mathrm{Root\; Mean\; \,Squared\; \,Error }(RMSE) =\sqrt{\sum_{i=1}^{n}\frac{({{y}_{i}-{\widehat{y}}_{i})}^{2}}{n-p}}$$
(14)
$$\mathrm{Mean\;Error }(ME)=\sum_{i=1}^{n}\left(\frac{{y}_{i}-{\widehat{y}}_{i}}{n-p}\right)$$
(15)
$$\mathrm{Akaike \,\, Information \,\, Criterion }(AIC)= -2logL+p \cdot df$$
(16)

where \({y}_{i}\)—the ith observed value of the dependent variable, \(\widehat{y}\)—the ith predicted value, \( n\)—number of observations, \( p\)—number of parameters used, \(logL\)—loglikelihood of the model, \( df\)—degrees of freedom of the model.

As there was no other independent data set to validate the EGF, a cross-validation method was used by iteratively removing one SSP to obtain model parameters and predict the \({i}_{d}\) for the SSP removed. The final parameters were obtained by fitting the model to the entire data set.

The TGF was evaluated using the inventory data set. Knowing that the model predicts the dbh under bark, the equation developed by Giurgiu et al. (2004) was used to subtract the double bark thickness from the total dbh measure in 2015 and 2020 ensuring data comparability. The Giurgiu et al. (2004) double bark thickness equation (Eq. 17) is:

$${{c}_{i}= a}_{0}+{{a}_{1}{dbh}_{i}+ a}_{2}{dbh}_{i}^{2}+e$$
(17)

where \({c}_{i}\)—is double bark thickness in cm of tree i, \({dbh}_{i}\)—is tree diameter at breast height in cm, e is the error term of the model \({a}_{0}\) = 0.278, \({a}_{1}=\) 0.0398 and \({a}_{2}\) = -0.000156 are species-specific coefficients.

The basal area (Gj) and the basal area increment for each SSP were later computed and compared based on the observed and predicted tree values.

All analyses were performed using R statistical software (R Core Team 2020), the models’ parameters were obtained using the lme and nlme functions of the nlme package (Pinheiro et al. 2018), the residuals were analysed using the function mywhiskers in the R-package lmfor (Mehtatalo 2019), dplyr package (Wickham et al. 2019) was used to manipulate the data, while the packages tmap (Tennekes 2018) and ggplot2 (Wickham 2016) were used to obtain the graphs.

Results

EGF model

Having considered different transformations of the independent variable, the final model that showed a desirable residual behaviour was given by Eq. 18. The explanatory variables included in the model have a biological interpretation of the \({i}_{d}\) process and represent the three main components that are usually used to explain the \({i}_{d}\) variability: size, competition and site. The parameters of the explanatory variables dbh, BAL and G were forced to be negative and all parameters were significant at 0.05 level, while both random parameters were found significant at 0.0001 level. The shape of the growth curve is unimodal with a positive skew, typical to the tree \({i}_{d}\) process (Fig. 3).

Fig. 3
figure 3

EGF model fit for spruce after back-transformation. In each graph within Fig. 3, the values used to obtain the curves were kept constant except the dbh and the values of the variable the graph was built for. The values kept constant represent the mean values found in the permanent sampling network: Alt = 1472, BAL = 38, ASP = 3, G = 58, Slope = 49, RD = 1. For example, for the graph “Alt (m)” the values used to obtain the curves were the ones mentioned above except for the values of the mean altitude. The altitude variable iteratively took the following values 800, 1200, 1400 and 1600 (m)

Full size image
$$\mathrm{ln}\left({{{i}_{d}}_{5}}_{ij}\right)\;=\;{a}_{1}+{a}_{2}{{dbh}^{2}}_{ij}+{a}_{3}ln\left(dbh\right)+{a}_{4}\left(\frac{{BAL}_{ij}}{{G}_{ij}}\right)+{a}_{5}{RD}_{ij}+{a}_{6}\mathrm{ln}({G}_{ij})+{a}_{7}{Alt}_{ij}+{a}_{8}\left[{Slope}_{ij}\cdot cos\left({ASP}_{ij}\right)\right]+{a}_{9}\left[{Slope}_{ij}\cdot sin\left({ASP}_{ij}\right)\right]+{b}_{j}^{\left(1\right)}+{b}_{j}^{\left(2\right)}ln\left({d}_{ij}\right)+{\epsilon }_{ij}$$
(18)

where \({{{i}_{d}}_{5}}_{ij}\) is the 5-year dbh increment for tree i in SSP j, dbh and dbh2 are the dbh and squared dbh in cm, BAL is the basal area of the larger trees than the tree i from SSP j (m2 ha−1), G is the basal area of the stand (m2 ha−1), RD is the ratio between tree i dbh and SSP j Dg, Alt is the altitude in m, Slope is the slope in percentage, ASP is the aspect in radians, \({b}_{j}^{\left(1\right)}{b}_{j}^{\left(2\right)}\) are normally distributed random effects with mean zero and unrestricted variance–covariance matrix.

According to the model fitted for spruce, the maximum \({i}_{d}\) is around 40 cm. When the tree dbh exceeds 140 cm the model will produce \({i}_{d}\) close to 0 regardless of the tree size, competition or site characteristics. The other species—beech and fir, showed similar behaviour. The maximum \({i}_{d}\) of beech and fir was predicted to be around 50 cm.

Although BAL and Slope estimated values are small, they are significant for spruce and beech species. For fir only, the dbh and G explained the dbh variability (Table 2).

Table 2 Parameter estimates (bold) and standard errors (italics-in parenthesis) for the age-independent EGF model
Full size table

The most robust bias-correction method has proved to be the empirical ratio proposed by Snowdon (1991) calculated with the following expression:

$${c}^{*}=\frac{\sum y}{\sum exp\left(\widehat{y}\right)}$$
(19)

where \({c}^{*}\) is the correction factor, \(y\) is the observed variable (in our case 5-year dbh increment), and \(\widehat{y}\) is the fixed prediction using Eq. 18.

The correction factor (\({c}^{*}\)) varies between 1.29 and 1.4, the value of the RMSE statistics is close to 1 cm for all three species (Table 3), while the ME value reveals that the models are practically unbiased.

Table 3 Variance components and fit statistics of the \({i}_{d}\) models: standard deviation of the random parameters—sd, correlation between the random parameters—corr, residual variance—\({\sigma }^{2}\), the correction factor—c*—calculated with Eq. 19. In italics, the fit statistics when the model was fitted using only the random intercept
Full size table

The graphical analysis of the residues showed that log-linearizing the model removes the heteroscedasticity. Furthermore, mean residual values are 0 or very close to 0 for all dbh classes and there is no trend of residues over the entire range of observed dbh (Fig. 4) and \({i}_{d}\) predicted values (Fig. 5).

Fig. 4
figure 4

EGF residuals as a function of the observed dbh, grouped in 10 quantiles. For each group, the mean standard deviations and standard error of the mean residual errors were calculated. The black lines represent the standard deviations of the mean (mean \(\pm\) 1.96 sd), the red ones represent the standard error of the mean for a 95% confidence interval, and the dots represent the mean residual errors

Full size image
Fig. 5
figure 5

EGF residuals as a function of the \({i}_{d}\) predicted values, grouped in 15 quantiles. For each group, the mean standard deviations and standard error of the mean residual errors were calculated. The black lines represent the standard deviations of the mean (mean \(\pm\) 1.96 sd), the red ones represent the standard error of the mean for a 95% confidence interval, and the dots represent the mean residual errors

Full size image

The results obtained using the fixed parameters of the model are close to those obtained using both sets of parameters; however, the amplitude of the residual errors using the fixed and random parameters is reduced, thus increasing the accuracy of the model.

EGF validation

The cross-validation method applied is similar to the leave one out refitting and prediction method (Allen 1971). The low standard deviation (sd) values obtained show that the model is robust. The mean RMSE is close to 1 cm, while the mean ME is close to 0.1 cm. Using both fixed and random parameters parameters provided much higher accuracy than using only fixed parameters. For example, the RMSE, using fixed + random, parameters decreased by 17.6% for spruce, 21% for beech and 10% for fir compared with the RMSE using only fixed effects (Table 4).

Table 4 Fit statistics and sensitivity analysis of the c* factor, obtained by the mixed model and the fixed part of the model prediction using the leave one out cross-validation method
Full size table

Using this method of validation, a sensitivity analysis was also conducted in order to determine what is the influence of the extreme observations on c* value. Again, the small values of the sd indicate that the bias correction factors obtained are fit for the study area.

EGF mixed effects calibration

The accuracy of the random parameters’ prediction is influenced by the number of trees used for calibration and their sizes. This information is relevant to forestry practitioners in order to achieve the desired results. Out of the 511 combinations used to calibrate the random effects, the best calibration strategy for each species is presented in Fig. 6.

Fig. 6
figure 6

taken from each dbh category (min, mean, max) is indicated over the bars. The y-axis indicates the total number of trees sampled and the x-axis indicates the mean RMSE

Mean RMSE of the predicted \({i}_{d}\) using EGF fixed effects parameters and the calibrated random effects obtained by sampling n trees with different dbh (min, mean, max underline that the sampling was done around trees with a dbh close to the thinnest trees, mean or largest trees of the SSP). The number of trees

Full size image

The results of the calibration optimization strategy show that any prediction of the random effect, even with one single observation, improves model prediction accuracy. For all three species, the results obtained show that sampling 3 trees around the minimum, the maximum and the mean diameter is a good compromise between the necessary sampling effort and the accuracy achieved.

Growth index

Using a similar model to the one formulated above (Eq. 18), but without including the site variables, equation no. 20 was formulated in order to predict the 5-year past \({i}_{d}\) using the inventory data obtained in 2020. The equation includes the dimensional and competition components so that the residual deviations from the prediction made with this function were used to calculate a productivity index for each SSP and species.

$$\mathit{ln}\left({{{i}_{d}}_{5}}_{ij}\right)={a}_{1}+{a}_{2}{{d}^{2}}_{ij}+{a}_{3}ln\left(d\right)+{a}_{4}\left(\frac{{BAL}_{ij}}{{G}_{ij}}\right)+{a}_{5}{RD}_{ij}+{a}_{6}ln({G}_{ij})+{b}_{j}^{\left(1\right)}+{b}_{j}^{\left(2\right)}ln\left({d}_{ij}\right)+{\epsilon }_{ij}$$
(20)

Most of the parameters presented in Table 5 are significant at the 0.05 level for two species: spruce and beech. Few explanatory variables have significant effect on fir growth: only the dbh and G are found to explain last 5-year \({i}_{d}\). RD is nonsignificant for the three species after reformulating the model as Eq. 20.

Table 5 Parameter estimates (bold) and standard errors (italics-in parenthesis) for the 5-year past \({i}_{d}\) model
Full size table

The variance components presented in Table 6 are necessary to predict random parameters. The values are similar to the ones obtained for the EGF which suggests that the same optimized calibration strategy as the one obtained above can also be applied to this model.

Table 6 Variance components and fit statistics of the past 5-year past \({i}_{d}\) increment model
Full size table

Using Eq. 20, the past 5-year \({i}_{d}\) was predicted for each tree and a growth index for each species and SSP (GI1) was computed using Eq. 12. The second index, GI2, was equalled to the value of the random parameter \({b}_{j}^{(2)}\), being the one that had the strongest correlation with the dbh growth series. The two growth indexes were scaled (Eq. 21) in five classes based on the Romanian yield class tradition so that class 1 represents the most productive class and class 5 the least productive.

$${\rm GI}=1+3.99\left(\frac{{\rm GI}_{E}-\mathrm{max}\left({\rm GI}_{E}\right)}{\mathrm{min}\left({\rm GI}_{E}\right)-\mathrm{max}\left({\rm GI}_{E}\right)}\right)$$
(21)

where GI is the growth index scaled and \({\rm GI}_{E}\) is the estimate growth index.

TGF model

The three age-independent TGF had a similar fitting when using spruce 1-year increment data from tree ring core records (Table 7). However, only the Lundqvist–Korf (L-K) and the Chapman–Richards (C-R) models were further developed to include the growth index because of the undesired trend of the residuals of the Hossfeld (H) model.

Table 7 Fit statistics for the age-independent TGF
Full size table

Since the value obtained for the Asymptote (A) when fitting the model was illogical (900 cm), a fixed value of 150 was set for this parameter. This value represents the maximum dbh recorded in the RSI for this species and was considered plausible as an asymptotic dbh value in the study area.

In the next step, the k parameter of the C-R (Eq. 22) and L-K (Eq. 23) age-independent equations was expressed as a linear function of GI.

$${Y}_{i+proj}=150{\left\{1-\mathrm{exp}\left(-\left({b}_{0}+{b}_{1}GI\right)proj\right)\left[1-{\left(\frac{{Y}_{i}}{150}\right)}^{1-m}\right]\right\}}^{\frac{1}{1-m}}$$
(22)
$${Y}_{i+proj}=150exp\left\{-({c}_{0}+{c}_{1}GI)\frac{1}{{\left[{\left(\frac{-({c}_{0}+{c}_{1}GI)}{ln\left({Y}_{i}/150\right)}\right)}^\frac{1}{m}+proj\right]}^{m}}\right\}$$
(23)

where \({b}_{0}, { b}_{1}, {c}_{0},{ c}_{1}, m\)—are parameters to be estimated, \(GI\)—is the growth index; \({Y}_{i}\) and \({Y}_{i+proj}\) are the dbhs of the mean trees at ages i and i + proj; proj is the projection length in years.

Heteroscedasticity was detected by graphical analysis of residuals and controlled by fitting the model with the power type function. The autocorrelation between the measurements of the same tree was also specified in the model. The ARMA (1,1) type autocorrelation structure gave the best results for both LK and RC models.

The LK model has an undesired trend of residuals that overestimates the \({i}_{d}\) of small trees and underestimates the growth of large trees (Fig. 7). Therefore, the analyses were continued using only the C-R model.

Fig. 7
figure 7

Residuals of TGF models with the respect of the predicted values, grouped in 10 quantiles. For each group, black lines represent the standard deviations of the mean (mean \(\pm\) 1.96 sd), the red ones represent the standard error of the mean for 95% confidence interval, and the dots represent the mean residual errors

Full size image

By introducing the growth index, GI, as an independent variable the model gave better results than by using the basic equation (Table 8). The growth index based on the last 5-year \({i}_{d}\), GI1, attained better results than the growth index computed based on the \({b}_{j}^{(2)}\) random effect parameter, GI2. GI1 improved the RMSE of the model by 6.4% and reduced the systematic error (ME) by 31.8%.

Table 8 Fit statistics for the Chapman–Richards TGF with the growth index
Full size table

All the coefficients obtained significant p values with α ≤ 0.0001, showing that the introduction of the growth index led to the improvement of the model (Table 9).

Table 9 Parameter estimates (bold) and standard errors (italics-in parenthesis) for TGF model
Full size table

Spruce annual increment ranges from 0.4 ≤ x ≤ 0.8 cm for small trees (≤ 1 cm) to 0 ≤ x ≤ 0.1 in large trees, bigger than 120 cm dbh, according to the age-independent TGF. For trees growing on sites with GI = 1 \({i}_{d}\) showed an approximately double rate than trees growing on the poorest sites (GI = 5) all over the range of tree dbh explored (Fig. 8).

Fig. 8
figure 8

Spruce annual dbh increment (\({i}_{d}\)) curves for tree growth index classes 1–5

Full size image

EGF and TGF validation

For each spruce tree, the \({i}_{d}\) was predicted using the two models developed (EGF model and TGF model). The basal area of the measured spruce species in each SSP was cumulated and compared with the predicted basal area (Fig. 9).

Fig. 9
figure 9

Basal area prediction at a plot level using the two developed models for spruce species where G and \({i}_{G}\) is the basal area and the basal area increment

Full size image

For the TGF model, when predicting the individual tree diameter, the value of RMSE is 1.105 cm and the value of ME (overall bias) is -0.094 cm, while for the EGF model the values of RMSE and ME statistics are 1.042 cm and 1.156777e-16 cm, respectively. Figure 9 also shows the higher variance for plots with large BA and the undesired downward trend (\({i}_{G}\)) caused by the higher systematic error (ME) in the case of the TGF model. In the case of predicting the increase in basal area for each SSP, the RMSE and ME statistics for the TGF model are 0.043 m2 and 0.011 m2, respectively, while the EGF model errors are RMSE = 0.047 m2 and ME = -0.003 m2.

Discussion

The purpose of this research work was to build age-independent \({i}_{d}\) models for the main species in the Retezat National Park uneven-aged mixed forest. A permanent sampling network has been developed for this purpose and two types of data regarding the dbh growth were collected in order to build the models. Forest inventories deliver a large number of observations describing trees growing in numerous environmental conditions and various inter and intra-specific competition. While most tree \({i}_{d}\) models for uneven-aged stands are developed based on the forest inventories permanent sampling plots data (Wykoff 1990; Monserud and Sterba 1996; Long et al. 2021; Oboite and Comeau 2021; Vospernik 2021), we demonstrated that \({i}_{d}\) models can also be based on increment cores data.

Results demonstrate a similar output between the two model types (EGF and TGF) developed for spruce. The models can be used in different circumstances and depending on the data available.

EGF model

The empirical sigmoid equation used to develop the EGF has been also successfully applied in previous studies for modelling both \({i}_{d}\) (Wykoff 1990; Uzoh and Oliver 2008; Hamidi et al. 2021) and tree height increment (Uzoh 2001). The explanatory variables included in the model are easy to measure, common to basic forest inventories, have a strong biological interpretation so they can be grouped into different ecological components according to their characteristics and have been widely used to explain tree growth (Biging and Dobbertin 1995; Pommerening 2002; Maleki et al. 2020). The size and competition components used to explain growth variability were computed based on the dbh values which is the most common measurement in forest inventory. The dbh proved to be one of the most important predictors of \({i}_{d}\) (Adame et al. 2008; Uzoh and Oliver 2008; Hamidi et al. 2021; Long et al. 2021; Oboite and Comeau 2021). The dbh value can be simultaneously classified as a measure of past competition experienced and an indicator of potential increment in the following period. The inclusion of the dbh at the second power helps the model to produce smaller increment for large dbhs thus emulating the biological dynamics of \({i}_{d}\) process.

The competition component was introduced at both the tree and the stand levels. BAL is an index of asymmetric unilateral competition, which means that the growth of small trees is affected by large trees while large trees growth is not affected by small trees presence (Biging and Dobbertin 1995; Contreras et al. 2011). This variable is an indicator of competition for light and it is especially selected in modelling trees’ growth in irregular complex forests such as uneven-aged forests (Weiskittel et al. 2011). Contrary to BAL, the G variable is considered a symmetrical bilateral competition index, because trees growth is affected by G values regardless of their size. The negative value of the parameter associated with this index leads to a decrease in tree growth in stands with a large G/ha, and to an increase in growth when G/ha value is low. The ratio between BAL and the G ensured the inclusion of the competition process in the growth function. The negative value of the parameter associated with this variable reduces the tree growth when BAL ≅ G and will intensify the growth when BAL < G. RD is a measure of the tree’s hierarchical position in the stand (Burkhart and Tomé, 2012). This variable is particularly important in stands with multiple forest canopy layers (Daniels 1976). This parameter within our model stimulates the growth of trees that are larger than the mean tree and reduces the growth of trees smaller than the mean tree.

Site biogeoclimatic variables were introduced into the model as part of the environmental component using the transformation proposed by Stage (1976). We found altitude, slope and aspect to have a major effect in spruce and beech \({i}_{d}\) rates. Similar findings were reported by Pretzsch et al. (2020) for spruce, beech and fir. However, their research shows that only beech and fir growth rates are significantly affected by a change in altitude, while spruce shows a change in growth with de Martone indices variation. Since de Martone is computed based on precipitation and temperature values, it is commonly considered a proxy for altitude (Vospernik 2021).

Monserud and Sterba (1996) and Andreassen and Tomter (2003) reported, in agreement with our results, more intense growth for spruce and beech in lower altitudes, while Pretzsch et al. (2020) found beech decreasing growth rates. These differences are likely the result of the altitudinal range covered by each study: our study area reaches the tree line, while Pretzsch et al.’s (2020) apparently does not.

For spruce and beech, most of the variables used proved to be significant; however, the fir competition component is represented only by G, likely due to the low number of spruce trees in each SSP, though this particular behaviour might also be influenced by its ecophysiology, being a species that tolerates shade (Kneeshaw et al. 2006)—a characteristic that ensures growth under closed canopies like those of old-grown forests.

The correction of the logarithmic transformation was performed using the empirical ratio method proposed by Snowdon (1991), since it provided the best results. This was also encountered in the development of biomass equations for Scots pine and spruce in Finland (Repola 2009) and that of individual tree dbh growth model for rebollo oak in northwest Spain (Adame et al. 2008).

Mixed effect calibration

Mixed effects models’ calibration can provide a significant increase in accuracy. This benefit has been demonstrated in many studies (Lappi 1991; Calama and Montero 2005; Ciceu et al. 2020) as well as in this one. Our results show the capacity of a single measurement to improve the accuracy of the model prediction. The calibration strategy, which can be different for each species and response variable, is very important because it can considerably affect the accuracy of the predictions made (Bronisz and Mehtätalo 2020). Moreover, the stand structure could also be a factor that determines which is the optimal calibration strategy. Calama and Montero (2005) and Adame et al. (2008) found that sampling 2–3 trees regardless of their size is considerably increasing the individual-tree dbh growth model accuracy for stone pine (Pinus pinea L.) and rebollo oak (Q. pyrenaica), while for beech in Slovakia Sharma et al. (2019) found that sampling randomly 4 trees could be considered the best calibration strategy. Both studies have tested a 3 or 4 randomly selected trees as a calibration strategy. The results obtained in this paper are similar to those obtained above; however, the number of strategies tested in our study is much higher with both the number of trees and their sizes varying. We found that regardless of species sampling, 3 trees around the minimum mean and maximum dbh of the stand can be considered the best calibration strategy.

Growth index

Although site index curves based on height-dbh relationship have been previously developed for uneven-aged stands, they are rarely introduced in dbh growth models (Shongming Huang and Titus 1993; Duan et al. 2018). Past GI are preferred for explaining \({i}_{d}\) and for site productivity assessment in structurally complex stands. GI was firstly developed for rain forests species (Vanclay 1989), for Pinus brutia stands in north-east Greece (Palahí et al. 2008) or Pinus halepensis in Catalonia, north-east Spain (Trasobares et al. 2004). In all cases GI was developed for uneven-aged or multilayered stands and was considered a substitute for the site index. Later, Dănescu et al. (2017) found that the \({i}_{d}\) could be better predicted using the growth index compared to the site index as a predictor in dominated by fir and/or spruce stands located in south-western Germany. However, none of these studies report what is the necessary sample size of past growth observations one has to determine for accurately computing GI. Furthermore, these studies do not consider model calibration by a mixed effects framework. We believe that this index could be more easily applied in forestry practice using random effects calibration. Through our study, we found that the same calibration strategy as the one described above can be employed for calibrating the past growth dbh model in order to obtain the GI for a new stand.

TGF model

In order to build tree growth models for the mean tree for a particular or for all dbh classes, the increment cores in even-aged stands must be taken from trees that cover the entire dbh distribution (van Laar and Akça 2007). Conversely, most of the trees in uneven-aged stands have a similar course through the social structure of the stand. Young trees in the understory are strongly suppressed, thus registering low growth rates, the ones that survive make their way to the middle storey, where their growth intensifies, and wait their turn to reach the overstorey, where predominant, dominant and co-dominant trees grow (Assmann 1970). Therefore, extracting increment cores from trees around the mean tree of the stand ensures that all the growth phases are equally represented.

The three growth equations tested here (Lundqvist–Korf—L-K, Chapman–Richards—C-R and Hossfeld—H) are widely used in modelling tree growth. In Romania, Giurgiu and Drăghiciu (2004) compared the C-R and L-K equations in the process of building yield tables for 29 species. They eventually chose L-K, though still recognising a good performance of the C-R function. We additionally chose H as an alternative function. However, C-R, and then L-K, performed better fitting for \({i}_{d}\) data. Similar to our results, Tomé et al. (2006) found that C-R performed better than L-K for \({i}_{d}\) of dominant trees in sparse cork oak (Quercus suber L.) stands while L-K performed better than C-R when modelling dominant height growth of Eucalyptus globulus plantations.

The algebraic difference approach used in modelling the \({i}_{d}\) involves rewriting one of the parameters as a function of site variables. Contrary to Amaro et al. (1998), who selected m as the free parameter for the generalized model, the k parameter of the C-R function, being strongly related with the growth rate of the function, was found to be the parameter most strongly related to site quality. Initially, we tested the correlation of all three parameters with the GI and we found k to be the most correlated one.

In order to produce invariant length projections of dbh growth, the growth index was assumed to be invariant with time as it is assumed for site index (Dănescu et al. 2017). Other stand variables could be easily derived from the nearby SSP and introduced in the model. Stand volume, for example, could have been used as another invariant variable since in uneven-aged balanced stands the stand volume is more or less constant over time (Garet et al. 2009). The same hypothesis was made by Gea-Izquierdo et al. (2008), who considered stand density invariant over time for Quercus ilex in Iberian open oak woodlands. Nevertheless, due to the short inventory period we could not test this assumption and we used only the GI to obtain a family of \({i}_{d}\) curves.

The TGF model has the advantage of projecting future dbh yield (Tomé et al. 2006) instead of \({i}_{d}\). Furthermore, models based on TGF were found to perform better outside of the limits of the data used for its construction having adequate properties for extrapolation (Vanclay 1994; Tomé et al. 2006). However, there are no studies that show the EGF inferiority to TGF if the former is developed in a biologically interpretable structure.

Conclusion

This study focuses on mountain old grown uneven-aged mixed forests and reveals the main drivers of \({i}_{d}\) for spruce, beech and fir. A mixed effect modelling framework and the algebraic difference approach were used to build two \({i}_{d}\) models for mixed uneven-aged stands based on empirical and theoretical growth functions. In the first model, \({i}_{d}\) is predicted as a function of size, competition and site variables, while the second model predicts the mean \({i}_{d}\) for each dbh class based on a past growth index. Mixed effects calibration can be easily employed to calibrate and improve the model prediction for the \({i}_{d}\) model and the GI model by sampling three trees around the minimum mean and maximum dbh values. Both models produce reliable predictions of dbh growth and therefore can be a useful tool for assessing mountain forest growth dynamics.