Introduction

Severe storm events cause damage to humans and property and substantial economic losses on large-scale levels (Berlemann 2016). With regard to forests, severe storm events have the potential to cause substantial quantities of timber from thrown or dead trees (van Lierop et al. 2015). This has a negative effect on forest functions (Thorn et al. 2017). For example timber stocks of the affected stands are reduced, and by this, the importance of forests as a carbon sink is diminished. Sustainable forest management practices aiming at the continuous supply with timber are also threatened in the long term. Increasing numbers of extreme weather events due to climate change (McCarthy et al. 2001) cause substantial forest stock losses and surplus harvesting quantities (Bolte et al. 2009). This can negatively affect the function of forests as a carbon sink (Lindroth et al. 2009). An excessive timber supply after severe and large-scale storm events, can cause timber markets to react with increasing price falls. In such cases, timber storage plays an important role for forest enterprises to mitigate economic losses by such supply-driven timber price falls (Kinnucan 2016).

There is a wealth of literature related to climate change-induced extreme weather events as well as numerous publications dealing with impacts of natural disturbances on forests, such as Thorn et al. (2017) as well as related adaption strategies, such as Yousefpour et al. (2017). However, literature exploring the recurring phenomenon of timber storage in the context of natural disturbances is scarce. In this context, to the best of our knowledge only Zimmermann et al. (2018) have analyzed the determinants for timber storage accumulation after severe storm events in Germany.

Nevertheless, the identification of controls for forest enterprises’ timber storage behavior is essential for two reasons. Time-specific information on the continuance of timber from thrown or dead trees is important to assess the economic impacts of storm events on forestry and to generate improvement strategies toward storm-related forest management practices as proposed by Riguelle et al. (2017). Moreover, detailed information on the temporal progression of timber storage after severe storm events helps to improve national and international timber accounting schemes (Jochem et al. 2015), such as the Greenhouse Gas Emission Reporting System for the National Inventory Report (NIR), the Economic Accounts for Forestry (EAF) or the European Forest Accounting (EFA).

One reason for the divergent behavior of forest enterprises with regard to timber storage could lie in technical suitability of long-term storage of affected tree species. The coniferous tree species groups Norway spruce (Picea abies L. Karst) and Scots pine (Pinus sylvestris L.) are suitable for multi-year wet storage. The non-coniferous tree species groups European beech (Fagus sylvatica L.) and oak (Quercus spec.) are recommended to be stored for a maximum duration of less than 1 year, as wood quality deteriorates significantly within that time period (Odenthal-Kahabka 2004). Regarding wet storage of pine, Hapla (1992) suggests a maximum storage duration of 5 years. For spruce, Odenthal-Kahabka (2004) suggests a maximum wet storage duration of 3 years.

Another factor, which potentially affects forest enterprises’ timber storage behavior, is the timber price reaction after a specific storm event (Rosenkranz et al. 2018). Generally, stronger price falls are connected to higher timber quantities from natural disturbances (Kinnucan 2016). In contrast, the affected forest enterprises may be confronted with higher up front logging expenses. The forest enterprises might be forced to sell higher quantities of their stored timber at an earlier stage after the storm event to maintain corporate liquidity.

Different ownership groups might show significant differences regarding their timber storage behavior. Countervailing measures by the state and municipal forest enterprises to support the private forest enterprises have already been found in conjunction with extreme storm events in terms of increased timber storage accumulation activities (Odenthal-Kahabka 2004; Zimmermann et al. 2018). In accordance, such countervailing measures by the public forest enterprises could result in prolonged storage durations as well as longer residence times of timber in storage.

A further factor which could influence forest enterprises’ timber storage behavior is the market power effect of forest enterprises. Larger forest enterprises might be able to sell their stored timber earlier due to a stronger market position. Therefore, larger forest enterprises should show shorter residence times of timber in storage.

Forest enterprises’ internal production cost structures might have an influence on distributions of timber storage outflows. Forest enterprises with high relative fixed costs for their production capacities in terms of permanent staff costs might need to maintain their timber production at higher levels after a storm event compared to those with low relative fixed costs. Consequently, the related forest enterprises might distribute outflows from timber storage over an extended period of time as compared to others.

The availability of data in the context of severe storm events is crucial to assess the impact of such factors on timber storage.

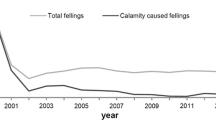
So far, the typical residence times of timber in storage and, thus, the timescales on which storage management has an impact on the market have not yet been explored. However, when comparing storm-related storage in- and outflows of a large forestry database (German Forest Accountancy Data Network (FADN)), outflows from timber storage show a diverging distribution in terms of delayed and longer lasting time sequences (see Fig. 1).

Fig. 1
figure 1

Exemplary annual means of timber storage accumulation (TSA) and timber storage outflows (TSO) based on German FADN data

Full size image

In the past, in environmental systems the concept of “residence times” was often used to characterize the average carbon-related residence in a specific system. These include, e.g., forests (Prescott et al. 1989); bamboo stands (Isagi 1994); soils (Post et al. 1982) or native and cultivated ecosystems as a whole (Buyanovsky et al. 1987). These approaches describe mean carbon residence times based on observed or simulated long- or short-term carbon balances with continuous in- and outflows into and out of the system (growth and degradation of biomass). To prevent the degradation of wood quality, calamity-caused fellings are harvested and taken into timber storage within a year of the storm event (Odenthal-Kahabka 2004). Severe storm events cause single pulses of large felling quantities in timber storage inventories (Zimmermann et al. 2018). We thus utilize an approach for systems characterized by a single input pulse and continuous output signals originating from chemical sciences: residence time distributions of chemical reactors as described by Danckwerts (1953) and also Levenspiel (1972). The Gamma distribution is a commonly used distribution to quantify residence time dynamics in environmental systems such as wetlands (e.g., Kadlec 1994) and groundwater aquifers (e.g., Maloszewski and Zuber 1982; Gilmore et al. 2016) or carbon storage in ecosystems (e.g., Belshe et al. 2019; Oberle et al. 2019).

Since forest enterprises’ storage management decisions show noticeable deviations in terms of the empirical normalized distributions of timber storage outflows (see exemplary cases in Fig. 2), it is our goal to detect and to characterize the related controls.

Fig. 2
figure 2

Visualization of differing empirical normalized distributions of timber storage outflows of selected forest enterprises for spruce related to storm events from the storm year to the 5th year after the storm based on FADN data

Full size image

Our methodological approach is to characterize the empirical frequency distribution of the hectare normalized TSO by the 1st and 2nd moment of their probability density function. The 1st moment τ translates into the expected residence time, and the 2nd moment σ2 translates into the variance around τ. Since the Gamma distribution is the typical function for duration time analysis, we expect it to suit empirical normalized distributions of timber storage outflows.

Our research goal is to explore and characterize the determining groups for different shapes of the distribution functions of timber storage outflows. Therefore, τ and σ2 are analyzed by means of regression analysis.

Based on the identified control variables from the regression analysis, we reanalyze the database by grouping the data sets and determine their mean timber storage outflow distributions after the storm events as well as associated expected residence times and their variances. We apply the resulting parameters with the continuous gamma distribution to simulate TSO residence time distributions.

The related research question is formulated as follows: “Which variables determine the temporal course of timber storage outflows?”

We formulate the following research hypothesis based on the previously deduced indications from the current state of knowledge and our described rationale: Forest enterprises’ management decisions regarding the release of timber from storage in the years following severe storm events are affected by tree species group, timber price reaction, forest worker capacities per hectare, type of ownership and areal size class.

For the purpose of a detailed and temporally higher resolved (sub-annual timescale) analysis of storm event-related timber storage management, the application of established mathematical distribution functions offers the possibility to predict continuous storage outflows over the complete relevant time span.

Methods

Database

The FADN is a valuable time series to analyze forest enterprises’ decision-making processes (Wildberg and Möhring 2019). With respect to our research goal, we find the FADN to be a suitable source of data. The FADN is coordinated by the German Federal Ministry of Food and Agriculture (BMEL). Forest enterprises’ operational data are available from 1991 ongoing till to date (Lohner et al. 2016). This allows us to include the two storm events, Lothar (1999) and Kyrill (2007), in our analyses. The two storms are classified to be among the severest wind storms since the beginning of regulated forestry in Germany (Hillmann 2007). The data set contains a section in which forest enterprises’ annual timber storage accumulation as well as timber storage outflow is surveyed. Furthermore, the questionnaire contains economic, institutional and species-related variables which are suitable for testing with regard to their explanatory contribution toward the residence time of timber stocks in storage. The sample is restricted to forest enterprises with a total production area of at least 200 ha. The sample size lies at about 350 state, municipal and private forest enterprises annually. As the FADN, due to its underlying sampling procedure, is classified as a judgment sample, a sample weight, which is provided in the FADN database, is used to balance occurring representability deviations, as described in Zimmermann et al. (2018).

With regard to storm event impacts, the signal isolation of storm-related changes in timber storages is our first step before the actual data analysis is carried out. In accordance with Zimmermann et al. (2018), who used the same approach to estimate storm-related timber storage accumulation (TSA), we apply a baseline correction on the original data to reduce uninformative short-term fluctuations as far as possible and thus isolate the storm-related values from the regular timber storage outflows as follows:

$$\alpha \left( t \right) = \frac{1}{5}\mathop \sum \limits_{t = - 5}^{t = - 1} x\left( t \right),$$
(1)

Here t is the year of a storm event and x stands for the annual timber storage outflow values. Applying Eq. (1) we firstly generate a baseline value (α) by calculating an average timber storage outflow value based on the 5 years before the respective SE.

$${\text{TSO}}\left( t \right) = \left\{ {\begin{array}{*{20}l} {x\left( t \right) - \alpha \left( t \right),} \hfill & { {\text{if}}\;x\left( t \right) - \alpha \left( t \right) \ge 0} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(2)

Applying Eq. (2) we subtract the previously generated baseline value from the actual outflow values of the years of the storm and the five following years. The resulting annual values (TSO (t)) represent each of the storm years’ as well as the five poststorm years’ outflow values from timber storage. Each annual TSO value cannot turn negative by means of the baseline correction. The α, x and TSO are measured in m3.

To approximate the timber price reactions (TPR) of the storm-affected regions, we employ the state forestry departments’ annual timber price data (ZMP 2002, 2008). Based on the timber prices from the year before the storm event and the storm year we calculate timber price delta values (PDS). We correct these delta values from other price trends by subtracting the corresponding timber price (PDN) delta values of non-storm-affected regions, respectively, non-storm-affected federal states:

$${\text{TPR}} = (\overline{\text{PDS}}_{ t} - \overline{\text{PDS}}_{t - 1} ) - (\overline{\text{PNS}}_{ t} - \overline{\text{PNS}}_{t - 1} ),$$
(3)

where \(\overline{\text{PDS}}\) is the mean of the timber prices in storm-affected federal states and \(\overline{\text{PNS}}\) is the mean of the timber prices in non-storm-affected federal states. TPR at the spatial scale of federal states is extracted as €/m3.

Statistical moments of empirical observations

The following supplemental information about distribution properties (Jawitz 2004) holds for arbitrary distributions and not only for our developed duration model.

The residence time distribution RT (t) of timber stock in storage can be described by normalizing observed annual timber storage outflows (TSO (t)) with the sum of storm event-related TSO over all observation years:

$${\text{RT}}\left( t \right) = \frac{{{\text{TSO}}\left( t \right)}}{{\mathop \smallint \nolimits_{0}^{\infty } {\text{TSO}}\left( t \right){\text{d}}t}} .$$
(4)

The integral of all observed TSO (t) should approximately equal timber storage accumulation (TSA), as described in Zimmermann et al. (2018) in the year of the storm event. Based on observed TSO (t), RT (t) now describes the distribution of probabilities of each annual fraction of TSA to be released from timber storages over the observation period with the unit 1/year and thus

$$\mathop \smallint \limits_{0}^{\infty } {\text{RT}}\left( t \right){\text{d}}t = 1.$$
(5)

Using statistical moment analysis, the mean residence time of timber stock in storage (τ) can be determined by

$$\tau = \mathop \smallint \limits_{0}^{\infty } t{\text{RT}}\left( t \right){\text{d}}t$$
(6)

and the temporal variance (σ2) by

$$\sigma^{2} = \mathop \smallint \limits_{0}^{\infty } \left( {t - \tau } \right)^{2} {\text{RT}}\left( t \right){\text{d}}t.$$
(7)

Selection of independent variables

Following our research hypothesis, we test the independent variables species group (SG), timber price reaction (TPR), forest worker capacity (FWC), type of ownership (OT), areal size class (ASC) and storm event (SE) regarding their explanatory contribution toward the residence time of timber in storage.

We test the variable species group (SG) due to differences in storm affectedness, monetary value as well as suitability for long-term storage. Because of the indicated longer storage capability we expect a longer mean residence time for pine compared to spruce. As perennial timber storage is only relevant for coniferous species groups, related analyses are limited to the relevant species groups (SGs) spruce and pine based on dummy variable coding.

We use the variable timber price reaction (TPR) to test for strategical sales decisions from storage in order to minimize financial losses by sales at low timber prices. One possible result could be a negative correlation with τ. At higher price falls, forest enterprises might be under a higher economic pressure due to accumulated harvesting expenses. Reversely, a positive correlation with σ2 is expected due to the ambition of forest enterprises to sell remaining stored timber as late as possible in order to minimize financial losses.

We test the variable forest worker capacity (FWC) as a measure for forest enterprises’ fixed production cost structure. Based on forest enterprises’ full-time equivalents of employed forest workers, we create a continuous variable expressing the relative density of employed forest workers in forest enterprises. Here we divide full-time equivalents of employed forest workers by the total production area. We expect a positive correlation between FWC and τ. Forest enterprises with high fixed costs in terms of employed forest workers might maintain their timber production at higher levels after a storm event compared to such with low relative fixed costs. Related forest enterprises might extend the dispersion period of stored timber.

The variable type of ownership (OT) is used to test for a countervailing behavior of state and municipal forest enterprises toward private forest enterprises. We expect public forest enterprises to hold back stored timber quantities for an extended period to alleviate timber markets.

We use areal size class (ASC) as a variable to test for differences in timber storage residence times based on market power effects between forest enterprises. Accordingly, we expect larger forest enterprises to show shorter residence times of timber in storage. We add three ASC categories to the data set to test for the presence of market power effects. Depending on the species group-specific production areas, we test the areal size class (ASC) categories ASC1 (\(0\;{\text{ha}} < x < 200\;{\text{ha}}\)), ASC2 (\(200\;{\text{ha}} \le x < 500\;{\text{ha}}\)) and ASC3 (\(x \ge 500\;{\text{ha}}\)).

We employ the variable storm event (SE) to test for general effects between the underlying SEs regarding timber storage residence times in our data set. Related significances could be a sign for, e.g., different storage regimes possibly related to the chronological incidence of the storm events or differences in the availability of storage locations in the affected regions.

To generate the effective sample, a spatial selection of storm-affected regions is carried out on the federal states’ level. Furthermore, a sufficient representation of all categories of the analyzed variables is mandatory for the selection of regions. In this regard, we could solely identify considerable TSO signals in correlation with the extremely severe storm events Lothar (2000) and Kyrill (2007) (for the used variables see Table 1).

Table 1 Variable abbreviations and explanations
Full size table

Weighted multiple linear regression analysis

We characterize RT (t) of each forest enterprise, SE and SG in the FADN based on the parameters τ and σ2, as described in detail above. Accordingly, we conduct two separate multiple linear regression analyses for the parameters τ and σ2.

Here, τ is explained by species group (SG), timber price reaction (TPR), forest worker capacities (FWC), type of ownership (OT), areal size class (ASC) and storm event (SE) as independent variables. The resulting estimation function of the multiple linear regression analysis regarding τ is:

$$\tau = {\text{SG}}\beta_{1} + {\text{TPR}}\beta_{2} + {\text{FWC}}\beta_{3} + {\text{OT}}\beta_{4} + {\text{ASC}}\beta_{5} + {\text{SE}}\beta_{6} + \varepsilon ,$$
(8)

where β is the coefficient and ε is the error term.

So, τ expresses the mean residence time of storm event related timber in storage. The parameter value can be interpreted in relation to the respective storm event (t = 0). Consequently, estimates of τ represent the elapsed time after the respective storm event in years.

To avoid model-over-specification, we eliminate insignificant variables from our final model in a backward selection procedure.

The parameter σ2 is explained by species group (SG), timber price reaction (TPR), forest worker capacities (FWC), type of ownership (OT), areal size class (ASC) and storm event (SE) as independent variables. The resulting estimation function of the multiple linear regression analysis is:

$$\sigma^{2} = {\text{SG}}\beta_{1} + {\text{TPR}}\beta_{2} + {\text{FWC}}\beta_{3} + {\text{OT}}\beta_{4} + {\text{ASC}}\beta_{5} + {\text{SE}}\beta_{6} + \varepsilon ,$$
(9)

where β is the coefficient and ε is the error term.

We eliminate insignificant variables ASC and SE in a backward selection procedure from our final model to avoid model-over-specification.

The enterprises have different forest areas. According to Backhaus et al. (2016), cases involving larger sampling areas contribute more heavily to the regression function than cases involving smaller sampling areas. Consequently, we use the underlying sampling areas to weight the cases of the sample. Furthermore, we integrate the FADNs’ sample expansion factor into the weight variable in a multiplicative way to achieve the highest possible representability of the sample. The resulting weight scales the case’s contribution to the loss function by \(w^{ - 1/2}\) (JMP 2017; SAS Institute 2016). The loss function is the sum of squared deviations of the observations from the model, in our case of standard least squares estimation in a linear model. The weight variable has an impact on estimates and standard errors. However, it does not affect the degrees of freedom used in the hypothesis tests.

Concerning the performed multiple regression analyses, we consider whether the requirements regarding heteroscedasticity, autocorrelation and multicollinearity are met in the applied analyses. As recommended by Gujarati (2003), we examine heteroscedasticity by a visual inspection of the distribution of residuals over the predictions. We test autocorrelation with Durbin–Watson statistic. Finally a test on multicollinearity is performed using the variance inflation factor (VIF), as recommended by Neter et al. (1985).

Continuous simulation of timber stock residence time distributions

Jawitz (2004) gives a detailed overview how the parameterization of continuous univariate distributions can be facilitated for the simulation of probability density functions of environmental processes by using the statistical moments of each distribution. One of the recommended distributions is the probability density function of the Gamma distribution

$$p\left( x \right) = \frac{{\beta^{b} x^{b - 1} e^{ - px} }}{\varGamma \left( b \right)},$$
(10)

which is implemented in this form (Eq. 10) in many data analysis and spreadsheet software packages (e.g., Microsoft Excel). While Γ(b) describes the Gamma function, the shape parameter b and the scale parameter p can be related to the statistical moments of the probability density function. To allow the continuous description (simulation) of the empirical residence time distribution RT (t) the statistical moments τ and σ2 of the observed distribution can be used to parameterize the probability distribution function of a given continuous univariate distribution (e.g., Maloszewski and Zuber 1982). The parameters of the probability density function of the Gamma distribution are related to the mean of the distribution (equals τ) and its variance (equals σ2) as follows:

$$\tau = \frac{b}{p}$$
(11)
$$\sigma^{2} = \frac{b}{{p^{2} }}.$$
(12)

We use mean τ and σ2 obtained by the multiple linear regression analysis to characterize typical residence time distributions with regard to the different explaining variables and to parameterize the probability distribution function of the Gamma function.

We scale estimated continuous RT (t) to observed TSO (t) by using the group-specific mean sums of TSO (t) over the observation period to evaluate modeling results of τ and σ2 with observed TSO. Subsequently we compare the group-specific scaled cumulative RT (t) to cumulative observations of group-related annual mean sums of TSO (t).

Results

After the selection of storm-affected regions, timber stock outflow data from 111 forest enterprises can be analyzed. We find clear differences within the data set: Over all data sets the mean residence time τ is 2.48 years, which varies between 0.64 years and as a maximum 4.59 years, combined with variances σ2 in mean larger than 1 year2. The related minimum and maximum values of τ and σ2 illustrate the big range captured by the FADN data set. The strongest price fall in the data set lies at TPR 29.34 €/m3 and the weakest price fall at TPR − 5.43 €/m3. The forest enterprises contained in the FADN represent a considerable range of employed forest workers per hectare which starts at FWC = 0 and goes up to FWC = .91 with a mean of one worker/10 ha (an overview on the descriptive statistics is given in Table 2).

Table 2 Statistical moment analysis of continuous variables τ, σ2, TPR and FWC
Full size table

Storm-induced timber price reactions

For the species group spruce in Baden-Wuerttemberg a strong price reaction can be found in conjunction with the storm event Lothar (1999) (see Fig. 3 based on ZMP 2002, 2008). We find a price fall of 25.8 €/m3 from the year before the storm (− 1) to the storm year (0) after the correction from price trends as explained in methods section. In the subsequent years, a recovery and approximation of the price for spruce in Baden-Wuerttemberg to timber prices of the non-affected regions can be found.

Fig. 3
figure 3

Selected federal states’ timber prices for spruce from 1996 to 2016 based on ZMP (2002, 2008) and HMI-Marktbilanz Forst und Holz (2013, 2018)

Full size image

Only weak differences in price reactions between the affected (e.g., Rhineland-Palatine, North Rhine-Westphalia) and the non-affected federal states (e.g., Baden-Wuerttemberg) can be observed related to the storm event Kyrill (2007). One major reason for the weak price reactions after Kyrill is seen in the high demand for timber at that time (Jochem et al. 2015) causing relatively stable timber prices.

Weighted multiple linear regression analysis

Concerning the requirements of the performed multiple regression analyses, we cannot identify suspicious signs of a non-random distribution of the residuals. No related results show indications of autocorrelation (see Tables 2, 3). Regarding multicollinearity, all related results are considerably below the cutoff of 10, so no suspicious signs of multicollinearity occur.

Table 3 Best fit results of the weighted multiple regression analysis on the TSO distribution parameter τ
Full size table

To identify the determinants for the residence times of the coniferous timber stocks in storage succeeding severe storm events, we analyze the empirical TSO-based parameters τ and σ2 of the resulting RT (t)s as dependent variables in two separate linear multiple regression analyses, as explained in methods section.

We find that the explanatory variables SE, SG, OT, TPR and the constant show a significant correlation with τ at a 99% confidence interval or at a 95% confidence interval, respectively (compare coefficient results in Table 3). The estimated constant expresses the culmination of timber storage outflows under the nominal variables’ setting SE1, SG pine and OT state forest. The related coefficient estimate lies at 1.98, expressing that almost two years after the storm event the mean residence time of TSO can be observed.

Looking at the variable type of ownership (OT), the private forest enterprises show the shortest interval between the storm event and the mean residence time of TSO. These are followed by the state and the municipal forest enterprises. The distance between the private and the state forest enterprises lies at .46 and between the state and the municipal forest enterprises at .18.

Regarding the variable storm event (SE), Lothar (SE1) shows a remarkably shorter mean residence time compared to Kyrill (SE2). The distance between the coefficients lies at .38.

Considering the analyzed species groups (SGs) spruce and pine, we find a shorter mean residence time for spruce compared to pine. The distance between the coefficients for spruce and pine lies at .18.

The variable timber price reaction (TPR) shows a significant negative correlation with a coefficient estimate of − .03. Accordingly, the mean residence time of timber in storage shortens at .03 years at a price decrease of each Euro.

We cannot identify significant differences between the tested categories with regard to the analyzed variable areal size class (ASC). This result indicates that forest enterprises’ behavior in terms of the mean residence time of timber in storage does not vary significantly between the different size classes. Reversely, our results do not support a relation between storage disposals of forest enterprises and market power effects. Due to the avoidance of model-over-specification, we eliminate the variable ASC in a backward-elimination procedure from our model.

Because of a relatively high remaining unexplained variation, the related statistical model shows a relatively low explanatory power (see R2 in Table 3), but the residual analyses revealed no systematic trends, so we can assume that the remaining variability is purely random and does not contain any necessary information. The model validity is thus not compromised by the relatively high remaining variability.

The parameter σ2 was estimated with a weighted multiple linear regression analysis under the nominal variables’ setting SG pine and OT state forest (compare coefficient results in Table 4). The resulting mean estimate lies at σ2 = 1.41 which translates into an average stretch of TSO (RT (t), respectively) of almost one and a half years.

Table 4 Best fit results of the weighted multiple regression analysis regarding the TSO distribution parameter σ2
Full size table

Looking at the different ownership categories (OT), the shortest and most accentuated outflow period can be found for the private forest enterprises, followed by the state and the municipal forest enterprises. The distance between the private and the state forest enterprises lies at .41 years and between the state and the municipal forest enterprises at .38 years.

Considering the variable employed forest worker capacities (FWC), we find a significant positive correlation with σ2. The coefficient value lies at .51, which can be translated into an additional storage stretch of half of a year for each additional forest worker per hectare.

The variable species group (SG) shows a significantly higher σ2 for spruce compared to pine with a coefficient difference of .32.

Furthermore, we find a significant positive correlation of timber price reaction (TPR) with σ2. The coefficient value of .03 can be interpreted as follows: at an additional price fall of 1€, the dispersion period from storage prolongs at .03 years. This result is in line with the relevance of timber price reactions for timber storage. It indicates a substantial influence of the timber price reaction on the TSO distribution. While stronger price falls induce shorter mean residence times due to increased initial cash flow-oriented economic pressure, they lead to a wider stretch of the TSO distribution due to a longer continuance of the remaining stored timber.

Regarding the variables storm event (SE) and areal size class (ASC), we cannot find a significant correlation with σ2 in the underlying data. This indicates that neither the considered storm events nor the considered areal size classes vary significantly in terms of the dispersion duration of timber from storage. Due to the avoidance of model-over-specification, we eliminate the insignificant variables SE and ASC in a backward-elimination procedure from our statistical model.

A relatively high remaining unexplained variation between the individual cases leads to a rather low explanatory power of the resulting statistical model (see R2 in Table 4).

Continuous simulation of timber stock residence time distributions

In order to transform our results into a continuous distribution, we first generate mean expressions of the significant variables categories. Subsequently, we generate the related mean τ and mean σ2 values and utilize them to parameterize the probability density function of the Gamma distribution as described in Chapter 2.5. As suggested by Hill and Lewicki (2006), we estimate least squares means (LS means) based on our linear regression model to account for the influence of all used factors of the model. Resulting curves represent probability density functions of mean RT (t) related to the time since the storm event (see Fig. 4). Considering the variable storm event (SE), SE1 shows a smaller τ compared to SE2. Regarding the analyzed species groups (SGs), spruce shows a smaller τ but a higher σ2 value, which is expressed in a lower peak and a larger spread. Regarding the types of ownership, the private forest enterprises show the smallest τ and σ2 values. This can be translated into the earliest culmination and the shortest storage duration followed by the state and the municipal forest enterprises. To simulate the impact of the continuous variable timber price reactions (TPR) on the curvature of TSO, we first take the empirical quartiles directly from the data. Then we calculate τ and σ2 of the lower and the upper quartile from the empirical data. As a result, a shorter mean residence time can be observed for high price reactions (lower quartile), while low price reactions (upper quartile) are related to later outflows from timber storage. Regarding the continuous variable fixed cost effects in terms of the employed forest worker capacities per hectare (FWC), we principally apply the same visualizing procedure as applied for TPR. However, we use the lower and the upper 10% quantile to visualize the influence of the variable expression on the residence time of timber in storage. As a result, we find the main difference is a higher σ2 value for the forest enterprises with a greater relative stock of employed forest workers upper 10% quantile).

Fig. 4
figure 4

Continuous residence time distributions of TSO for the variables a storm event, b species group, c type of ownership, d timber price reaction and e forest worker capacity

Full size image

To validate these results and to visualize the categories’ differing storage levels, we scale the continuous probability density distributions with the corresponding empirical TSO mean sums and generate cumulated TSO progressions (see Fig. 5). Considering the analyzed storm events (SEs), we find higher total storage after Lothar (SE1) compared to Kyrill (SE2), possibly related to the stronger price falls and the higher damage rates per hectare after Lothar as compared to Kyrill.

Fig. 5
figure 5

Cumulative distributions of simulated and observed TSO values after the storm event of the variables a storm event, b species group, c type of ownership, d timber price reaction, e forest worker capacity

Full size image

Regarding the considered species groups (SGs), we find a higher storage level for spruce compared to pine, substantiating the outstanding affectedness of spruce in terms of storm-related timber quantities and the central quantitative role of spruce regarding timber storage.

Scaling the probability distributions of the forest enterprises’ ownership categories (OT) emphasizes the prominent role of the state forest enterprises in terms of leveling timber storage quantities. Furthermore, it reveals that despite the longer storage retention of the municipal forest enterprises mean TSO levels between the municipal and the private forest enterprises are on a similar level.

Looking at the variable timber price reaction (TPR), it becomes evident that the cases with stronger timber price falls (1st quartile) are related to a higher TSO level compared to the cases with less pronounced timber price falls (4th quartile).

With regard to the employed forest worker capacities per hectare (FWC), besides the mentioned correlation regarding the dispersion period, we find a higher storage level for the forest enterprises with higher numbers of forest workers (90–100%-Quantile).

Besides the scaled and accumulated continuous residence times of timber in storage, we plot the annual mean TSO values related to the variables categories. In comparison with these empirical mean values, we find a good representability of our continuous Gamma distributions (see Fig. 5).

Discussion

Our results fundamentally support the relevance of timber storage for forest enterprises in the context of surplus harvesting quantities after severe storm events, as stated by Kinnucan (2016). Forest enterprises store significant quantities of timber or carbon, respectively, over an extended period of time. They create a temporary pool, which should be taken into consideration for national timber accounting duties as proposed by Jochem et al. (2015).

Regarding mean timber stock storage residence times and associated variances we find statistically significant coefficients among the variables tree species group (SG), timber price reaction (TPR), forest worker capacity (FWC,) type of ownership (OT) and storm event (SE) which supports our research hypothesis. Conversely, the variable areal size class (ASC) does not show any significance among its categories in the conducted regression analyses which does not support our research hypothesis.

Concerning the variable SG, spruce shows a shorter residence time and a longer dispersion period regarding its TSO distribution compared to pine. This can be explained by the higher monetary value and storm-related timber quantities of spruce. Also, the better suitability for longer-term storage for pine compared to spruce as found by Hapla (1992) and Odenthal-Kahabka (2004) supports this result. According to the increased exposure of the coniferous species toward storms but also toward biotic damages such as bark beetle calamities, we recommend a stronger focus on timber storage management for regions with high incidence of spruce and pine.

Concerning the variable OT, our results confirm our assumption in terms of public forest enterprises showing a delayed and prolonged TSO course compared to private forest enterprises as stated by Odenthal-Kahabka (2004). Also Zimmermann et al. (2018) noted an intensified timber storage accumulation of public forest enterprises compared to private forest enterprises. Conversely, shifts in framework conditions such as the privatization of public forest enterprises could potentially lead to changes in the proportions of timber storage across other independent variables.

In line with the findings of Kinnucan (2016), our results regarding the variable TPR show a correlation with the residence time of timber stocks in storage. The regression results show a significant negative correlation between the timber price reactions (TPR) and the TSO-based τ. We refer this to an increased cost pressure and the need to monetarize the stored timber at an earlier stage after the storm event. Reversely, we find a significant positive correlation between the timber price reactions (TPR) and the TSO-based σ2. We refer this to forest enterprises’ economic incentive to increase the duration of storage with increasing timber price falls. Regarding timber price data, we observe a relatively high variability between different federal states and years due to the complexity and the interrelation of timber markets and timber prices. Therefore, uncertainties regarding the causal relation between price changes and storm events cannot be neglected. Furthermore, timber prices were not available on the individual enterprises’ level. Accordingly, they might not represent the individual basis for storage-related decision-making. Another reason could lie in the global financial crisis, which took place in the years after 2007. During that time the demand for timber was at a low point mainly due to a crisis in the construction sector. Accordingly, timber prices declined which might have been an incentive for forest enterprises not to sell their stored timber.

Regarding forest enterprises’ fixed internal production costs, the regression results indicate that our hypothesis can be partially confirmed. As expected, we find a significant positive correlation between relative forest worker capacities (FWC) and σ2 in our results. This result can be traced back to higher fixed costs and less flexibility for the related forest enterprises in terms of cutting back their harvesting volumes. Fixed costs for harvesting capacities in terms of the employed forest workers per hectare lead to an extended period and a less accentuated peak of timber storage outflows. It should be noted that forest enterprises have substantially increased the degree of contracting since the considered storm events to reduce their fixed costs (Wippel et al. 2015). Consequently, timber storage residence times might change in succession of future storm events due to the changes in forest enterprises’ fixed cost structure.

With regard to the variable SE, we find that SE1 shows a significantly shorter mean residence time compared to SE2. One central reason could lie in the global financial crisis which had its peak in 2008, as during this time the demand for timber and consequently timber prices went down significantly. Accordingly, forest enterprises kept their stored timber in storage during that low price phase (Jochem et al. 2015), which led to a longer mean residence time after SE2

With regard to the relatively low explanatory power (see R2 in Tables 2, 3) of the regression models related to τ and σ2 as dependent variables, we cannot exclude further unobserved determinants for the course of TSO. One reason for the relatively low R2 values in the performed multiple regression analyses could lie in the used regional timber price data (TPR). As these generalized prices might not represent the individual forest enterprises’ timber prices, the related management decisions regarding storage continuation might deviate individually. Furthermore, timber storage capacities could be subject to change. As environmental protection is gaining importance, approval procedures for long-term sites for wet storage might have aggravated and thus storage behavior might have changed.

The database used includes solely the two severe storm events Lothar and Kyrill. Due to the high complexity of the timber storage phenomenon succeeding severe storm events, the statistical robustness of our statistical models in terms of predictions is limited.

With regard to the underlying data of our analyses, the FADN as a judgment-based sample is vulnerable toward bias (Toscani 2016; Toscani and Sekot 2018). Conversely, collecting a random sample causes a great additional effort and is, therefore, rejected in the FADN context. Hence, the German Forest Accountancy Data Network (FADN) is the most appropriate source of data for our purpose. Despite controversy with regard to the robustness of estimations related to weighting, e.g., Carroll and Ruppert (1988), we assert that resulting estimates are most possibly accurate and could otherwise be severely biased. According to the representability analysis by Zimmermann et al. (2018), the conducted sample weighting measures are appropriate to correct for sampling-based bias of the FADN.

We assume that our effective sample is sufficient for the conducted analysis. The data set used contains the data of approximately 350 forest enterprises from 1991 until 2015. Nevertheless, a spatial selection of storm-affected regions with a sufficient representation of all categories of the analyzed variables is carried out which remarkably reduces our effective sample.

The applied baseline approach for generating the analyzed TSO values could be subject to uncertainties, as it does not account for long-term trends regarding TSO continuation. Nevertheless, upon visual inspection, no such trends could be identified in the underlying sample.

Looking at the correlation between forest enterprises’ TSO and TSA, we notified in methods section that the integral of all observed TSO (t) should approximately equal TSA in the year of the storm event. The slope of the according regression line lies at .93 with an R2 of .91 meaning that based on the regression results 93% of the accumulated timber storage quantities (TSA) can be found as outflows from timber storage (TSO) in the empirical data. This relation is plausible, as the missing share of 7% can be interpreted either as loss rate due to quality deterioration or as estimation error of the applied baseline procedure.

With regard to the used lag order 5, we tested the appearance of timber in storage in the used data set by visual inspection of the annual mean storage quantities. We could not find any remarkable signs of timber in storage later than 5 years after the storm events. Also, timber should not be stored longer than 5 years (Odenthal-Kahabka 2004). Additionally, comparing the magnitudes of total (6 year) TSO with storm-TSA we found that the mean storage outflow of the five storm-antecedent years as a baseline value results in clear agreement of both measures (R2, slope significance). Nevertheless, we did not perform a sensitivity analysis of the lag order toward the regression results.

Another concern we want to address is that under the chosen approach, possible interaction effects between the chosen storm-affected regions in terms of German federal states and neighboring regions were neglected. However, keeping the federal states’ boundaries for our analysis has the advantages of a comparability with other sources regarding representability concerns and the spatial congruence of the variable timber price reaction (TPR) which also relates to the federal states’ level. Therefore, we suggest that such interaction effects should be analyzed by further research. The FADN does not provide data for forest enterprises with a productive forest area below 200 hectares. However, because small-scale forest enterprises represent a substantial group, it would be of great interest to test this group of forest enterprises via existing small-scale FADNs in relation to the existing data. Additionally, we are not able to exclude a possible influence of assortment- and quality-related issues regarding their influence on long-term timber storage, which could be another topic for further research.

In line with the recommendations of Riguelle et al. (2017), we believe that developing appropriate storage strategies can be crucial for the mitigation of economic pressure for European forestry after severe storm events. We assert that our quantitative results can be an integral component for such strategic storage planning. For example, we are able to derive the related species group-specific timber storage residence times based on the defined shares of outflows from the total stored timber quantities, as e.g., 50% in Fig. 6. We can show group-specific differences in storage management after specific time intervals (compare e.g., years 1 and 4 for pine and spruce in Fig. 6). After the extrapolation with related timber quantities, the time-specific demand as well as the costs for storage facilities could be derived and distributed fairly among stakeholders of the forest-based sector.

Fig. 6
figure 6

Percentage residence time of timber in storage for the species groups spruce and pine

Full size image

Conclusions

Concluding from our results we want to point out that individual controls should be taken into account for the estimation of timber stock residence times in storage, as they support timber accounting accuracy, especially under the European forestry framework conditions. Due to the complexity of the analyzed timber storage phenomenon, we want to stress that the related statistical models could profit from the integration of further empirically based data regarding their reliability for predictions. Further existing European FADN databases in Austria, Denmark, Finland, Germany, Norway, Sweden, Switzerland and the UK could be employed to enhance the robustness of related estimations.

The development of specific timber storage strategies in the context of biotic drivers such as bark beetle calamities succeeding severe phases of drought could also play an important role for forest enterprises as substantial quantities of timber may arise through such threats. Our methodological approach based on the residence time concept could be suitable to develop appropriate strategies for the logistical challenges related to bark beetle-infested timber. Due to their empirical foundation, the methodological approach used and missing supplementary studies, we believe that our results are of interest for scientists, policy makers and market participants related to the timber and forest sector in the context of climate change and related forest damages.