Skip to main content
SpringerLink
Log in

Nonlinear Bifurcation and Post-buckling Analysis of Cylindrical Composite Stiffened Laminates Based on Weak Form Quadrature Element Method

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

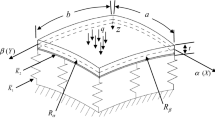
This paper presents a weak form quadrature element formulation in the analysis of nonlinear bifurcation and post-buckling of cylindrical composite stiffened laminates subjected to transverse loads. A total Lagrangian updating scheme is used in combination with arc-length method, and the branch-switching method is adopted to identify the whole post-buckling procedure of the laminates. The formulation of the shell model and beam model are based on the basic concept of Ahmad. The coincidence of discrete nodes and integration points in quadrature element endows it with compactness and conciseness in the nonlinear buckling analysis of the cylindrical stiffened laminates. Several numerical examples are firstly presented to verify the effectiveness and accuracy of present formulation. Parametric studies on the effects of the height-to-breadth ratio, lamination schemes, positions, distribution, number of the stiffeners on the bifurcation and post-buckling behavior are performed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Data Availability

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Sinha G, Mukhopadhyay M. Static and dynamic analysis of stiffened shells–a review. Proc Indian Natl Sci Acad. 1995;61(3&4):195–219.

    Google Scholar 

  2. Bedair OK. A contribution to the stability of stiffened plates under uniform compression. Comput Struct. 1998;66(5):535–70.

    Article  MATH  Google Scholar 

  3. Prusty B. Static, dynamic, buckling and failure analysis of composite stiffened shell structures: a finite element approach. [Ph.D. thesis]. Kharagpur, India: Indian Institute of Technology; 2001.

  4. Bisagni C, Vescovini R. Analytical formulation for local buckling and postbuckling analysis of stiffened laminated panels. Thin-Walled Struct. 2009;47(3):318–34.

    Article  MATH  Google Scholar 

  5. Stamatelos D, Labeas G, Tserpes K. Analytical calculation of local buckling and post-buckling behavior of isotropic and orthotropic stiffened panels. Thin Wall Struct. 2011;49(3):422–30.

    Article  Google Scholar 

  6. Sun L, Harik IE. Buckling of stiffened antisymmetric laminated plates. J Eng Mech. 2013;139(8):1110–23.

    Article  Google Scholar 

  7. Möcker T, Reimerdes HG. Postbuckling simulation of curved stiffened composite panels by the use of strip elements. Compos Struct. 2006;73(2):237–43.

    Article  Google Scholar 

  8. Rikards R, Chate A, Ozolinsh O. Analysis for buckling and vibrations of composite stiffened shells and plates. Compos Struct. 2001;51(4):361–70.

    Article  Google Scholar 

  9. Chen NZ, Soares CG. Progressive failure analysis for prediction of post-buckling compressive strength of laminated composite plates and stiffened panels. J Reinf Plast Compos. 2007;26(10):1021–42.

    Article  Google Scholar 

  10. Shi SS, Sun Z, Ren MF, Chen HR, Hu XZ. Buckling response of advanced grid stiffened carbon-fiber composite cylindrical shells with reinforced cutouts. Composit Part B-Eng. 2013;44:26–33.

    Article  Google Scholar 

  11. Eugenio R. Effects of nonlinear strain components on the buckling response of stiffened shear-deformable composite plates. Compos Part B-Eng. 2015;69:31–43.

    Article  Google Scholar 

  12. Yuanming X, Yan T, Manqing L, Bajracharya S. A new effective smeared stiffener method for global buckling analysis of grid stiffened composite panels. Compos Struct. 2016;158:83–91.

    Article  Google Scholar 

  13. Maciej T, Ryszard B, Michal K. Nonlinear buckling and post-buckling response of stiffened FGM plates in thermal environments. Compos Part B-Eng. 2017;109:238–47.

    Article  Google Scholar 

  14. Wardle BL, Lagace PA, Tudela MA. Buckling response of transversely loaded composites shells, part 2: numerical analysis. AIAA J. 2004;42(7):1465–73.

    Article  Google Scholar 

  15. Wardle BL. Solution to the incorrect benchmark shell-buckling problem. AIAA J. 2008;46(2):381–7.

    Article  Google Scholar 

  16. Zhou Y, Ilinca S, Thomas E, Michael S. Nonlinear elastic buckling and postbuckling analysis of cylindrical panels. Finite Elem Anal Des. 2015;96:41–50.

    Article  MathSciNet  Google Scholar 

  17. Zhong H, Yu T. Flexural vibration analysis of an eccentric annular Mindlin plate. Arch Appl Mech. 2007;77(4):185–95.

    Article  MATH  Google Scholar 

  18. Zhong H, Gao M. Quadrature element analysis of planar frameworks. Arch Appl Mech. 2010;80(12):1391–405.

    Article  MATH  Google Scholar 

  19. Zhong H, Zhang R, Yu H. Buckling analysis of planar frameworks using the quadrature element method. Int J Struct Stabil Dyn. 2011;11(2):363–78.

    Article  MathSciNet  MATH  Google Scholar 

  20. He R, Zhong H. Large deflection elasto-plastic analysis of frames using the weak-form quadrature element method. Finite Elem Anal Des. 2012;50:125–33.

    Article  Google Scholar 

  21. Xiao H, Zhong H. Nonlinear quadrature element analysis of planar frames based on geometrically exact beam theory. Int J Non-Linear Mech. 2012;47(5):481–8.

    Article  MathSciNet  Google Scholar 

  22. Zhang R, Zhong H. Weak form quadrature element analysis of planar slender beams based on geometrically exact beam theory. Arch Appl Mech. 2013;83(9):1309–25.

    Article  MATH  Google Scholar 

  23. Zhang R, Zhong H. Weak form quadrature element analysis of geometrically exact shells. Int J Non-Linear Mech. 2015;71:63–71.

    Article  Google Scholar 

  24. Ahmad S. Analysis of thick and thin shell structures by curved finite elements. Int J Numer Meth Eng. 1970;2(3):419–51.

    Article  Google Scholar 

  25. Patera T. A spectral element method for fluid dynamics: laminar flow in channel expansion. J Comput Phys. 1984;54:468–88.

    Article  MATH  Google Scholar 

  26. Wagner W, Wriggers P. Simple method for the calculation of postcritical branches. Eng Comput. 1988;5(2):103–9.

    Article  Google Scholar 

  27. Wriggers P, Simo J. General procedure for the direct computation of turning and bifurcation points. Int J Numer Meth Eng. 1990;30(1):155–76.

    Article  MATH  Google Scholar 

  28. Ahmad S. Analysis of thick and thin shell structures by curved finite elements. Int J Numer Meth Eng. 1970;2:419–51.

    Article  Google Scholar 

  29. Sze KY, Liu XH, Lo SH. Popular benchmark problems for geometric nonlinear analysis of shell. Finite Elements Anal Design. 2003;40:1551–69.

    Article  Google Scholar 

  30. Adnan I, Francois F. Stress resultant geometrically nonlinear shell theory with drilling rotations-Par II. Computational aspects. Comput Method Appl Mech Eng. 1994;118:285–308.

    Article  MATH  Google Scholar 

  31. Bellman RE, Casti J. Differential quadrature and long-term integration. J Math Anal Appl. 1971;34(2):235–8.

    Article  MathSciNet  MATH  Google Scholar 

  32. Quan JR, Chang CT. New insights in solving distributed system equations by the quadrature method I: analysis. Comput Chem Eng. 1989;13:779–88.

    Article  Google Scholar 

  33. Striz AG, Chen WL, Bert CW. Static analysis of structures by the quadrature element method (QEM). Int J Solids Struct. 1994;31(20):2807–18.

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The work described in the paper was supported by the National Natural Science Foundation of China (Nos. 12202148, 12172136), the Natural Science Foundation of Guangdong Province (No. 2021A1515010279), the National Science Fund for Distinguished Young Scholar (No. 11925203), and the Science and Technology Project of Guangzhou (No. 202102020656).

Author information

Authors and Affiliations

  1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou, Guangdong, China

    Xiang Ou, Xiaohu Yao & Run Zhang

Authors
  1. Xiang Ou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaohu Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Run Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

XO proposed a weak form quadrature element formulation in the analysis of nonlinear bifurcation and post-buckling of cylindrical composite stiffened laminates subjected to transverse loads. XO also performed parametric studies on the effects of the height-to-breadth ratio, lamination schemes, positions, number of the stiffeners, and the lamination sequences of the cylindrical composite shell and stiffeners, boundary conditions on the bifurcation and post-buckling behavior. XY conceived of the study and participated in its design and coordination and helped to draft the manuscript. RZ participated in the design of the study. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Xiaohu Yao.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Consent for Publication

Written informed consent was obtained from the patient for publication of this case report and any accompanying images. A copy of the written consent is available for review by the Editor-in-Chief of this journal.

Ethical Approval

Written informed consent for publication of this paper was obtained from the South China University of Technology and all authors.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ou, X., Yao, X. & Zhang, R. Nonlinear Bifurcation and Post-buckling Analysis of Cylindrical Composite Stiffened Laminates Based on Weak Form Quadrature Element Method. Acta Mech. Solida Sin. 36, 817–836 (2023). https://doi.org/10.1007/s10338-023-00424-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-023-00424-w

Keywords

Search

Navigation