Wave Propagation in Viscoelastic Functionally Graded Nanoplates: Comparison of the Integral and Differential Nonlocal Models

Abstract

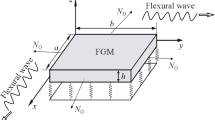
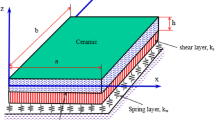
As one of the popular non-classical continuum theories in functionally graded material (FGM) nanostructures, the modified nonlocal theory (MNT) has been applied in various mechanical problems. However, due to the difficult solution process, the original integral formulation of MNT (IMNT) is transformed into a differential formulation of MNT (DMNT), which results in an inevitable approximation error. To clarify the consistency and difference between two formulations, the Lamb wave characteristics in viscoelastic FGM nanoplates are investigated. Two mathematical models are established based on the IMNT and DMNT, and solved by the proposed displacement-based and strain-based Legendre polynomial series approaches (LPSAs), respectively. Comparisons with the available data verify the validates of the presented LPSAs. Numerical examples indicate that the results from the DMNT and IMNT are significantly different at high frequencies. Several important differences are discovered. For example, the escape frequency only appears in the results from DMNT, but not in IMNT. In addition to comparing with classical structures, more attention should be paid to the attenuation characteristics of nonlocal nanostructures.

Appendices

Appendix A

Letting t = (2z−h)/h, and defining

$$ \begin{gathered} u\left[ {\alpha ,\beta ,\gamma } \right] \hfill \\\quad = \frac{1}{{2\lambda h^{\alpha } }}\int_{ - 1}^{1} {\left( {2z - h} \right)^{\alpha } Q_{n} (z)\frac{{{\text{d}}^{\gamma } }}{{{\text{d}}z^{\gamma } }}\int_{ - 1}^{1} {{\text{e}}^{{ - \frac{{\left| {v - z} \right|}}{\lambda }}} \frac{{{\text{d}}^{\beta } }}{{{\text{d}}v^{\beta } }}Q_{m} (v){\text{d}}v} {\text{d}}z} \hfill \\v\left[ {\alpha ,\beta } \right] = \frac{1}{{h^{\alpha } }}\int_{ - 1}^{1} {\left( {2z - h} \right)^{\alpha } Q_{n} (z)\frac{{{\text{d}}^{\beta } }}{{{\text{d}}z^{\beta } }}Q_{m} (z){\text{d}}z} \hfill \\w\left[ {\alpha ,\beta ,\gamma } \right] \hfill\\\qquad = \frac{1}{{2\lambda h^{\alpha } }}\int_{ - 1}^{1} {\left( {2z - h} \right)^{\alpha } Q_{n} (z)\frac{{{\text{d}}^{\gamma } }}{{{\text{d}}z^{\gamma } }} \int_{ - 1}^{1} {{\text{e}}^{{ - \frac{{\left| {v - z} \right|}}{\lambda }}} \frac{{{\text{d}}^{\beta } }}{{{\text{d}}v^{\beta } }}Q_{m} (v){\text{d}}v} \frac{{{\text{d}}\pi \left( z \right)}}{{{\text{d}}z}}{\text{d}}z} \hfill \\\end{gathered} $$

where n and m are from 0 to N. The detailed expressions for A, B and D in Eq. (18) are given here.

$$ \begin{gathered} A_{11}^{n,m} = - C_{11}^{\left( j \right)} u\left[ {j,0,0} \right] \hfill \\ B_{12}^{n,m} = {\text{i}}C_{13}^{\left( j \right)} u\left[ {j,1,0} \right] + {\text{i}}2jC_{55}^{\left( j \right)} u\left[ {j - 1,0,0} \right]/h\hfill \\ \qquad + {\text{i}}C_{55}^{\left( j \right)} u\left[ {j,0,1} \right] + {\text{i}}C_{55}^{\left( j \right)} w\left[ {j,0,0} \right] \hfill \\ D_{11}^{n,m} = 2jC_{55}^{\left( j \right)} u\left[ {j - 1,1,0} \right]/h + C_{55}^{\left( j \right)} u\left[ {j,1,1} \right]\hfill \\ \qquad + C_{55}^{\left( j \right)} w\left[ {j,1,0} \right] + \omega^{2} \rho^{\left( j \right)} v\left[ {j,0} \right] \hfill \\ A_{22}^{n,m} = - C_{55}^{\left( j \right)} u[j,0,0] \hfill \\ B_{21}^{n,m} = {\text{i}}C_{55}^{\left( j \right)} u[j,1,0] + {\text{i}}2jC_{13}^{\left( j \right)} u[j - 1,0,0]/h\hfill \\ \qquad + {\text{i}}C_{13}^{\left( j \right)} u[j,0,1] + {\text{i}}C_{13}^{\left( j \right)} w[j,0,0] \hfill \\ D_{22}^{n,m} = 2jC_{33}^{\left( j \right)} u[j - 1,1,0]/h + C_{33}^{\left( j \right)} u[j,1,1]\hfill \\ \qquad + C_{33}^{\left( j \right)} w[j,1,0] + \omega^{2} \rho^{\left( j \right)} v[j,0] \hfill \\ \end{gathered} $$

Appendix B

Refining

$$ \begin{aligned} & u\left[ {\alpha ,\beta } \right] = \left( \frac{1}{h} \right)^{\alpha } \int_{ - 1}^{1} {\left( {2z - h} \right)^{\alpha } Q_{n} (z)\frac{{{\text{d}}^{\beta } }}{{{\text{d}}z^{\beta } }}Q_{m} (z){\text{d}}z} \\& v\left[ {\alpha ,\beta ,\gamma } \right] = \left( \frac{1}{h} \right)^{\alpha } \int_{ - 1}^{1} {\left( {2z - h} \right)^{\alpha } Q_{n} (z)\frac{{{\text{d}}^{\beta } }}{{{\text{d}}z^{\beta } }}Q_{m} (z)\frac{{{\text{d}}^{\gamma } \pi \left( z \right)}}{{{\text{d}}z^{\gamma } }}{\text{d}}z}\end{aligned} $$

where n and m are from 0 to N. The detailed expressions for G, E and F in Eq. (28) are given here.

$$ \begin{gathered} G_{11}^{nm} = \omega^{2} \lambda^{2} \rho^{\left( p \right)} u\left[ {p,0} \right] - C_{11}^{\left( j \right)} u\left[ {j,0} \right] \hfill \\ G_{12}^{nm} = - C_{13}^{\left( j \right)} u\left[ {j,0} \right] \hfill \\ E_{13}^{nm} = 2{\text{i}}C_{55}^{\left( j \right)} \left( {2ju\left[ {j - 1,0} \right]/h + u\left[ {j,1} \right] + v\left[ {j,0,1} \right]} \right) \hfill \\ F_{11}^{nm} = \omega^{2} \rho^{\left( p \right)} u\left[ {p,0} \right] - \omega^{2} \rho^{\left( p \right)} \lambda^{2} u\left[ {p,2} \right] \hfill \\ G_{22}^{nm} = \omega^{2} \lambda^{2} \rho^{{\left( {2p} \right)}} u[2p,0] \hfill \\ E_{23}^{nm} = 2{\text{i}}\rho^{\left( p \right)} C_{55}^{\left( j \right)} (2ju[j + p - 1,0]/h + u[j + p,1] \hfill \\ \qquad + v[j + p,0,1] - 2pu[j + p - 1,0]/h) \hfill \\ \end{gathered} $$

$$ F_{21}^{nm} = C_{13}^{(j)} \rho^{(p)}\left[ \begin{gathered} ({4j( {j - 1} ) - 4jp} )u[j + p - 2,0]/h^{2}\hfill \\ \qquad + u[j + p,2] + 2v[j + p,1,1] + v[j + p,0,2] \hfill \\ \qquad + ( {4j - 2p} )( u[j + p - 1,1] \hfill \\ \qquad + v[j +p - 1,0,1])/h \hfill \\ \end{gathered} \right] $$

$$ \begin{gathered} F_{22}^{nm} = C_{33}^{(j)} \rho^{(p)}\Big[( {4j( {j - 1} ) - 4jp} )u[j + p - 2,0]/h^{2}\hfill \\\qquad + ( {4j - 2p} )({u[j + p - 1,1] + v[j + p - 1,0,1]} )/h \Big] \hfill \\\qquad + C_{33}^{( j )} \rho^{( p )} ( {u[j + p,2] + 2v[j + p,1,1] +v[j + p,0,2]} )\hfill \\\qquad + \omega^{2} \rho^{{( {2p} )}} u[2p,0] - \omega^{2}\rho^{{( {2p})}} \lambda^{2} u[2p,2]\hfill \\\end{gathered} $$

$$ \begin{gathered} G_{33}^{nm} = 2\omega^{2} \lambda^{2} \rho^{{\left( {2p} \right)}} u[2p,0] - 2\rho^{\left( p \right)} C_{55}^{\left( j \right)} u[j + p,0] \hfill \\E_{31}^{nm} = {\text{i}}\rho^{\left( p \right)} \Big(\left( {C_{11}^{\left( j \right)} + C_{13}^{\left( j \right)} } \right)\left( {2ju[j + p - 1,0]/h + u[j + p,1]} \right)\hfill \\\qquad \quad - 2pC_{11}^{\left( j \right)} u[j + p - 1,0]/h + C_{13}^{\left( j \right)} v[j + p,0,1] \Big) \hfill \\E_{32}^{nm} = {\text{i}}\rho^{\left( p \right)} \Big[\left( {C_{13}^{\left( j \right)} + C_{33}^{\left( j \right)} } \right) (2ju[j + p - 1,0]/h+ u[j + p,1])\hfill \\\qquad \quad - 2pC_{13}^{\left( j \right)} u[j + p - 1,0]/h + C_{33}^{\left( j \right)} v[j + p,0,1] \Big] \hfill \\F_{33}^{nm} = C_{55}^{\left( j \right)} \rho^{\left( p \right)} \Big[\left( {8j\left( {j - 1} \right) - 8jp} \right)u[j + p - 2,0]/h^{2} \hfill \\\qquad \quad + \left( {8j - 4p} \right)\left( {u[j + p - 1,1] + v[j + p - 1,0,1]} \right)/h\Big] \hfill \\\qquad \quad + 4v[j + p,1,1] + 2v[j + p,0,2] + 2u[j + p,2] \hfill \\\qquad \quad + \omega^{2} \rho^{{\left( {2p} \right)}} u[2p,0]-\omega^{2}\lambda^{2} \rho^{{\left( {2p} \right)}} u[2p,2] \hfill \\\end{gathered} $$