1 Introduction

Phononic crystals (PnCs), as a periodic composite structure [1], can block the propagation of elastic or acoustic waves in a specific frequency range [2]. The forbidden band characteristics have a wide range of applications in vibration and noise reduction [3,4,5,6,7], as well as acoustic filters [8, 9] and sensors [10]. Active adjustment of the band gap is one of the most important issues for PnCs.

In recent years, to realize the active adjustment of the elastic wave band gap, some intelligent materials have been employed to design PnCs. Hou et al. studied the band structure of two-dimensional piezoelectric PnCs by using the plane-wave-expansion (PWE) method. They found that the piezoelectric effect can expand the band gap width with the large filling fraction [11]. Bou Matar et al. [12] studied the effect of an external magnetic field on the effective elastic constant of magnetostrictive materials to reveal the magnetic field regulation characteristics of the band gap of two-dimensional magnetostrictive PnCs. Zhang et al. conducted a series of studies on the band gap characteristics of magnetostrictive PnCs based on the nonlinear magnetic-mechanical-thermal coupled constitutive law of magnetostrictive materials [13,14,15]. Gu and Jin [16] studied the changes in band gaps and defect bands of point defects of two-dimensional infinite magnetostrictive PnCs under the magnetic field and pre-stress.

With the development of soft materials, more and more new intelligent soft materials have attracted extensive attention. Due to high reversibility and controllability, soft materials such as magnetorheological (MR) material, electrorheological (ER) material, and silicone rubber have been used to make high-performance PnC structures [17,18,19,20,21,22,23,24,25,26]. For example, Yeh [17] studied the band gap characteristics of two-dimensional ER PnCs and found that the applied electric field can adjust the width and position of the band gap. Xu et al. [18] adjusted the shear wave band gap characteristics of MR elastomer PnCs by the external magnetic field. Zhang and Gao [19] studied the elastic wave propagation of PnCs with MR and ER inclusions and revealed the combined regulation of magnetic field and electric field on the band gap. In these previous studies [17,18,19], the band gap was usually affected by modulus, and the effect of large deformation on the band gap was scarcely considered. Bertoldi and Boyce [24] investigated the large deformation characteristics of hyperelastic soft PnCs and found that the change of geometric configuration of soft PnCs with holes induced by the compressive load can result in a rich band gap characteristic [25]. Babaee et al. [26] designed a helical array structure using silicone rubber materials and controlled the open and close frequencies of the acoustic band gap via an axial stretch. As mentioned above, all these studies [24,25,26] focused on the effect of geometric deformation caused by mechanical loads on the tunability of band gap.

In comparison with conventional mechanical loading to control deformation, magnetic field regulation can exhibit a series of advantages, such as contactless, fast response, and high control precision. In addition, the fabrication of magnetic materials is relatively simple. Therefore, designing new magnetically sensitive intelligent soft PnCs and using the magnetic field to control geometric deformation and band gap is very attractive.

Hard-magnetic soft materials (HmSMs) are a new type of magnetically sensitive intelligent soft materials proposed in recent years [27,28,29,30,31,32]. Under a uniform magnetic field, HmSMs are subjected to magnetic torque and thus achieve fast, complex, and programmable 3D shape changes [33, 34]. Chen et al. developed 2D and 3D models of HmSM beams under the applied magnetic fields by theoretical methods to predict the deformation response [35, 36] quantitatively, and discussed the effect of the volume fraction of magnetic particles on the mechanical properties of HmSM beam [37]. Zhao et al. [38] proposed a nonlinear theoretical framework of finite deformation for magnetic-elastic coupling of HmSMs and developed a nonlinear finite element program for the finite deformation of HmSMs based on the ABAQUS/Standard finite element software. Their study provided a theoretical basis for the further design and study of the multi-field coupling behavior of HmSM structures with complex shape changes. Sun et al. [39] investigated the deformation of the magnetorheological thin film sound-absorbing material fabricated by NdFeB particles and discussed the adjustment effect on the peak sound absorption frequency under magnetic field. Montgomery et al. [40] designed a magneto-mechanical metamaterial with asymmetric joints using HmSMs. The metamaterial structure has significantly different shapes to regulate its acoustic characteristics by the external magnetic fields. The emergence of HmSMs has provided an effective strategy for designing new shape-programmable acoustic metamaterials and the regulation of low-frequency band gaps, leading to potential applications in the fields of acoustic lenses, acoustic stealth, acoustic imaging, and energy harvesting.

Although HmSMs have already obtained much attention, there is still a lack of study on hard-magnetic soft material phononic crystals (HmSM-PnCs). A few studies on this topic only focused on the numerical simulation and planar models, without systematically investigating the wave propagation and band gap characteristics of HmSM-PnCs with different encoding modes. In this work, a programmable finite element model for HmSM-PnCs is established, and the effects of magnetic field, magnetic anisotropy encoding mode and geometric size (structure thickness and porosity) on band gap characteristics are investigated. The paper is organized as follows: In Sect. 2 the test samples of HmSMs were made and some useful parameters were measured through experiments. In Sect. 3, some theoretical formulae on the deformation of HmSMs and wave motion are presented. In Sect. 4, a finite element analysis of the band gap of HmSM-PnCs is given. In Sect. 5, some numerical results and discussions on the band gap characteristics are provided. And some conclusions are briefly summarized in Sect. 6.

2 Material Characterization

The HmSMs were fabricated using PDMS (Sylgard 184, DowCorning, USA) with a weight ratio of base to curing agent being 10:1. Next, NdFeB powder with a weight fraction of 75 wt% was added to the mixture before curing. Finally, fumed silica nanoparticles (5 wt%) with an average size of 15 nm were added to the mixture before curing to increase the ink viscosity to achieve desired printability. The shear moduli of the fabricated HmSMs were measured by using a universal material testing machine with a self-made dual-lap shear test fixture [41], as shown in Fig. 1a. The test samples were obtained from a previously self-assembled 3D printer [23]. The dimension of the printed specimen is 25 mm × 20 mm × 4 mm (see Fig. 1b). The shear stress–strain curve is presented in Fig. 2a, in which the obtained shear modulus is 535 kPa. The magnetization of the HmSMs was measured by the vibrating-sample magnetometer (VSM). The magnetic hysteresis loop was obtained, as shown in Fig. 2b, indicating the magnetization of the magnetic materials to be 243 kA/m.

Fig. 1
figure 1

The dual-lap shear test fixture and HmSM sample: a the dual-lap shear test fixture with an HmSM specimen; b a pictorial view of an HmSM sample obtained by 3D printing

Full size image
Fig. 2
figure 2

The shear stress–strain curve and magnetic hysteresis loop of HmSMs: a the shear stress–strain curve of HmSMs; b magnetic hysteresis loop of HmSMs measured by a vibrating-sample magnetometer (VSM)

Full size image

3 Basic Theoretical Formulae for HmSM-PnCs

3.1 Large Deformation of HmSMs

In the reference configuration, the static equilibrium equation for large deformation can be written as [42]

$$ {\text{Div}}{\kern 1pt} {\kern 1pt} {\varvec{P}}{ + }{\kern 1pt} {\kern 1pt} {\varvec{f}}_{{{0}}} = 0 $$
(1)

where Div is the divergence operator in the reference configuration, \({\varvec{P}}\) denotes the first Piola–Kirchoff (PK) stress tensor, and \({\varvec{f}}_{{{0}}}\) is the body force vector. For hyperelastic materials, the relationship between the first PK stress tensor and the deformation gradient can be expressed as

$$ {\varvec{P}} = \frac{\partial W}{{\partial {\varvec{F}}}} $$
(2)

where \(W\) is the strain energy density function of the material, and F is the deformation gradient, which is defined as \({\varvec{F}} = \frac{{\partial {\varvec{x}}}}{{\partial {\varvec{X}}}}\), with \({\varvec{X}}\) and \({\varvec{x}}\) respectively the points in the reference and current configurations, satisfying \({\varvec{x}} = {\varvec{\chi}}({\varvec{X}},t)\).The neo-Hookean hyperelastic model is used to describe the material properties of HmSMs, and the total strain energy density function can be expressed as [38]

$$ W{\kern 1pt} {\kern 1pt} { = }{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{G}{{2}}(J^{{ - \frac{3}{2}}} {\varvec{I}}_{{{\text1}}} - 3) + \frac{K}{{2}}(J - 1)^{2} - \frac{1}{{\mu_{0} }}{\varvec{FB}}_{{\varvec{r}}} \cdot {\varvec{B}} $$
(3)

where G is the shear modulus, K is the bulk modulus, \(J{\text{ = det(}}{\varvec{F}}{)}\) is the , \({\varvec{I}}_{{{{1}}}} {\text{ = tr(}}{\varvec{F}}^{{\text{{T}}}} {\varvec{F}}{)}\), \({\varvec{B}}\) denotes the applied magnetic field vector, \({\varvec{B}}_{{\varvec{r}}}\) is the residual magnetic flux density vector of the material in the reference configuration, and \(\mu_{0}\) is the vacuum permeability. Substituting Eq. (3) into Eq. (2), the constitutive law of HmSMs can be obtained

$$ {\varvec{P}} = GJ^{{ - \frac{3}{2}}} \left({\varvec{F}} - \frac{{{\varvec{I}}_{{{\text{1}}}} }}{3}{\varvec{F}}^{{ - {\text{T}}}} \right) + KJ(J - 1){\varvec{F}}^{{{ -{\text{T}}}}} - \frac{1}{{\mu_{0} }}{\varvec{B}} \otimes {\varvec{B}}_{{\varvec{r}}} $$
(4)

where operation \(\otimes\) is the dyadic product.

In the current study, the body force is not taken into account, so the equilibrium equation reduces to

$$ {\text{Div}}{\kern 1pt} {\kern 1pt} {\varvec{P}} = 0 $$
(5)

3.2 Elastic Wave Propagation of Deformed Bodies

For a wave motion problem, the configuration of the elastomer after static deformation requires superimposing an increment displacement \(\dot{\user2{x}}({\varvec{X}},t)\) on the static deformation \({\varvec{x}}{\mathbf{ = }}{\varvec{\chi}}{\mathbf{(}}{\varvec{X}}{\mathbf{)}}\). The incremental form of governing equation for the reference configuration is expressed as

$$ {\text{Div}}{\kern 1pt} {\kern 1pt} \dot{\user2{P}} - \rho_{0} \frac{{{\text{D}}^{{2}} \dot{\user2{x}}}}{{{\text{D}}t^{{2}} }} = 0 $$
(6)

where \({\text{D/D}}t\) is the material time derivative, \(\dot{\user2{x}}\) is the incremental displacement, \(\rho_{0}\) is the initial material density, and \(\dot{\user2{P}}\) denotes the increment of the first PK stress tensor, the linear approximation of which can be expressed as

$$ \dot{\user2{P}} = {\varvec{A}}:\dot{\user2{F}} $$
(7)

where \(\dot{\user2{F}}\) is the increment of deformation gradient, and \({\varvec{A}}\) is a fourth-order elasticity tensor defined as

$$ A_{\alpha i\beta j} = \frac{{\partial^{2} W}}{{\partial F_{i\alpha } \partial F_{j\beta } }} $$
(8)

The incremental form of governing equation for the current configuration is expressed as

$$ {\text{div}}{\kern 1pt} {\kern 1pt} \dot{\user2{P}}_{{{0}}} - \rho \frac{{\partial^{2} {\varvec{u}}}}{{\partial t^{{2}} }} = 0 $$
(9)

where \(\rho { = }J^{ - 1} \rho_{0}\) is the material density in the current configuration, \({\varvec{u}}({\varvec{x}},t) = \dot{\user2{x}}\) is the incremental displacement, and \(({\text{grad}}{\kern 1pt} {\kern 1pt} {\varvec{u}}) = \dot{\user2{F}}\user2{F}^{{{\mathbf{ - 1}}}}\).

The linear incremental constitutive law can be written as

$$ \dot{\user2{P}}_{{{0}}} = {\varvec{A}}_{{{\kern 1pt} {{0}}}} :{\text{grad}}{\kern 1pt} {\kern 1pt} {\varvec{u}} $$
(10)

where the components of the fourth-order tensor \({\varvec{A}}_{{{\kern 1pt} {{0}}}}\) can be expressed as

$$ A_{0piqj} = J^{ - 1} F_{p\alpha } F_{q\beta } A_{\alpha i\beta j} $$
(11)

When elastic wave propagation is considered, the displacement increment can be defined as

$$ {\varvec{u}}({\varvec{{x}}},t) = \overline{\user2{u}}({\varvec{x}}){\kern 1pt} {\kern 1pt} {\text{e}}^{{ - {\text{i}}\omega t}} $$
(12)

where \(\overline{\user2{u}}{\mathbf{(}}{\varvec{x}}{\mathbf{)}}\) denotes the amplitude of the incremental displacement, and \(\omega\) is the angular frequency. The stress increment can be defined as

$$ \dot{\user2{P}}_{{{0}}} {\mathbf{ = }}\overline{\user2{P}}_{{{0}}} ({\varvec{x}}){\kern 1pt} {\text{e}}^{{ - {\text{i}}\omega t}} $$
(13)

where \(\overline{\user2{P}}_{{{0}}} {\mathbf{(}}{\varvec{x}}{\mathbf{)}}\) denotes the amplitude of the stress increment. Substituting Eq. (12) and Eq. (13) into Eq. (9), the frequency domain governing equation can be expressed as

$$ {\text{div}}{\kern 1pt} {\kern 1pt} \overline{\user2{P}}_{{{0}}} + \rho \omega^{{2}} \overline{\user2{u}} = 0 $$
(14)

According to the Bloch–Floquet theorem, periodic boundary conditions apply to the unit cell

$$ {\varvec{u}}{\mathbf{(}}{\varvec{r}}{\mathbf{ + }}{\varvec{a}}{\mathbf{)}} = {\text{e}}^{{{\text{i}}{\varvec{ka}}}} {\varvec{u}}{\mathbf{(}}{\varvec{r}}{\mathbf{)}} $$
(15)

where \({\varvec{r}}\) is the position vector, \({\varvec{a}}\) is the lattice vector, and \({\varvec{k}}\) is the wave vector. Combining Eq. (14) and Eq. (15) gives the dispersion relation. The effect of viscoelasticity on the low-frequency band gaps of phononic crystals is not significant, which is, therefore, not taken into account in this study.

4 Finite Element Model

Firstly, the deformation of HmSM structure shown in Fig. 3a is numerically simulated based on the finite element software ABAQUS/Standard. The material parameters used in the simulation are taken from the experiments: shear modulus G = 535 kPa, bulk modulus K = 1000 G, density \(\rho_{0}\) = 2345 kg/m3, and magnetic moment density M = 243 kA/m (see material characterization). The square structure with a hole is shown in Fig. 3a, of which L = 8 mm, b = 4 mm and h = 0.2 mm. The red arrow indicates the direction of the magnetic moment. The magnetic anisotropy of the unit cell can be encoded by finite element analysis. The four boundaries (the blue lines) and corner points (the red points) of the unit cell are shown in Fig. 3b. To meet the compatibility of overall geometry and consistency of the dimensions of the periodic structure, the boundaries need to satisfy only the movement along the z-direction, i.e., \(U_{x} = 0\) and \(U_{y} = 0\) at boundaries. A completely fixed condition is applied at the four corner points. The grid cell type is chosen as C3D8IH, and the number of grid cells is 11040. The user-element subroutine (UEL) uses the force-magnetic coupling program proposed by Zhao et al. [33, 38] for large deformation calculations. The deformed configuration can be exported by ABAQUS/Standard software, and the specific wave characteristics and band gap characteristics can be calculated in COMSOL Multiphysics software.

Fig. 3
figure 3

Geometry of the HmSM unit cell: a magnetic anisotropy encoding of the unit cell; b boundaries and corner points

Full size image

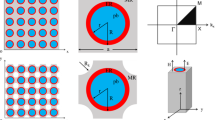
Figure 4 shows the unit cell, supercell structure of the HmSM-PnCs, and the first irreducible Brillouin zone. Due to the periodicity of the PnC structure, only the band gap characteristics of a unit cell are considered.

Fig. 4
figure 4

Geometry of HmSMs-PnCs and the first irreducible Brillouin zone of the lattice: a the unit cell diagram; b the \(5 \times 5\) lattice diagram; c the first irreducible Brillouin zone of the lattice

Full size image

A free tetrahedral mesh with 9636 mesh cells is used to calculate the band gap of HmSM-PnCs by scanning along the path \({\rm M}{ - }\Gamma { - }{\rm X}{ - }{\rm M}\) in the first irreducible Brillouin zone. The wave vector \({\varvec{k}} = k_{x} {\varvec{i}} + k_{y} {\varvec{j}}\) is set, and the Bloch–Floquet periodic boundary conditions given in Eq. (15) are applied to the unit cell structure in the x-direction and the y-direction.

The transmission spectrum is an important index to reflect the band gap structure of PnCs. A finite structure composed of 24 unit cells in the x-direction can be obtained by the finite element model, and the Bloch–Floquet period boundary conditions are applied in the y-direction. A perfectly matched layer (PML) is used on both sides of the structure to absorb elastic wave perturbations without generating reflections. Meanwhile, the displacement excitation \(w_{0}\) is applied to the left side of the finite structure, and then the boundary integral is applied to the right side displacement amplitude of the finite structure. The response \(w_{a}\) can be obtained by dividing the displacement amplitude integral by the side length, and then the transmission spectrum of the periodic structure can be obtained by the following formula:

$$ T = 20 \times {\text{log}}\left(\frac{{w_{a} }}{{w_{0} }}\right) $$
(16)

5 Numerical Results

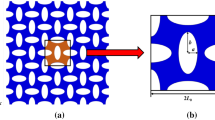
In order to verify the proposed finite element model, we calculated the band structures of 2D hyperelastic soft PnCs with longitudinal and transverse elliptical holes based on the neo-Hookean hyperelastic model as shown in Fig. 5a. It can be seen that our results are consistent with the results in [43], which indicates that our model is reliable and effective. The numerical results for magnetically controlled deformation are plotted in Fig. 5b, in which the deformation characteristics of a hard-magnetic soft beam under the applied magnetic field are presented. Compared with the numerical results and experimental data in [38], the model we used to calculate the deformation of HmSMs is correct and effective.

Fig. 5
figure 5

Numerical calculation method validation: a band gap structure for a porosity of 50% with a long-to-short axis ratio of 3; b large deformation of hard-magnetic soft beam under the applied magnetic field

Full size image

5.1 Effect of Magnetic Anisotropy Encoding Mode on Band Structure of HmSM-PnCs

We calculated the deformation mode of HmSM-PnCs with three magnetic anisotropy encoding modes, as shown in Fig. 6a–c. Meanwhile, the applied magnetic field direction is assumed to be along the normal direction of the plate plane. Figure 6d shows the driven deformation under positive–negative magnetic fields. It can be seen that the structure deformation patterns are significantly different under different magnetic anisotropy encoding modes, and the positive and negative magnetic fields have opposite deformation patterns. Figure 6e shows the boundary midline displacement curves along the z-direction of three different encoding structures under the excitation of positive magnetic field. Encoding mode I has one curve wave peak in the middle and the maximum wave peak displacement among the three encoding structures. Encoding modes II and III have two and three curve wave peaks, respectively. It can be seen that the displacement \(U_{z}\) increases with the increase of magnetic field as shown in Fig. 6f.

Fig. 6
figure 6

Magnetic anisotropy encoding mode and the driven deformation under positive–negative magnetic fields: a encoding mode I; b encoding mode II; c encoding mode III; d the driven deformation under positive–negative magnetic fields; e the boundary midline displacements along the z-direction of three different encoding structures under the positive magnetic field; f the boundary midline displacements in the \(z\)-direction of encoding structure I under different positive magnetic fields

Full size image

5.1.1 Encoding Mode I

Figure 7 shows the band structure of HmSM-PnCs with encoding mode I under different magnetic fields. It can be seen that no band gap occurs in the absence of external magnetic fields (see Fig. 7a). However, when the applied magnetic field is 30 mT, as shown in Fig. 7b, a band gap appears between the 5th and the 6th bands (the red region), and the frequency range is 275–297 Hz. When the magnetic field increases from 30 to 100 mT and then to 250 mT, it is noticed that the width of the band gap increases remarkably (as shown in Fig. 7c and Fig. 7d), the location of band gap changes from 275–297 Hz to 237–394 Hz and then to 185–354 Hz, respectively. These results indicate that the magnetic field can effectively tune the band gap by changing the geometric configuration.

Fig. 7
figure 7

The band structures with encoding mode I under different magnetic fields: a B = 0 mT; b B = 30 mT; c B = 100 mT; d B = 250 mT

Full size image

Figure 8 shows variation of the start and stop frequencies and the band gap width with magnetic field for encoding structure I. The magnetic field not only affects the start and stop frequencies of the band gap but also affects the band gap width of HmSM-PnCs. Figure 8a shows that the start frequency of the band gap decreases with the increase of magnetic field, while the stop frequency first increases and then decreases. The stop frequency reaches the maximum value at B = 90 mT, which is 397 Hz. Figure 8b shows the variation of band gap width with magnetic field. It can be seen that with the increase of magnetic field, the width of band gap increases initially and gradually tends to a constant value. In other words, in a low field region (< 90mT), the band gap width is sensitive to the magnetic field; while in a large field region (> 90mT), the band gap width is almost magnetic field-independent.

Fig. 8
figure 8

Variation of start (black line) and stop (red line) frequencies and band gap width under different magnetic fields: a variation of start and stop frequencies with magnetic field; b variation of band gap width with magnetic field

Full size image

5.1.2 Encoding Mode II

Figure 9 shows the band structure of HmSM-PnCs with encoding mode II. Similar to the case of mode I, only one band gap appears within 556–566 Hz when the magnetic field arrives at 80 mT (denoted as band gap I). As the magnetic field increases from 80 to 150 mT, a new band gap from 220–240 Hz appears between the 5th and the 6th bands (denoted as band gap II). Moreover, the width of band gap I increases significantly from 10 to 74 Hz. With a further increase of the magnetic field, a new band gap from 673–678 Hz appears between the 10th and the 11th bands(denoted as band gap III)at B = 200 mT, as shown in Fig. 9c. When the magnetic field reaches 250 mT, band gaps II and III are significantly widened, while band gap I is slightly narrowed.

Fig. 9
figure 9

The band structures with encoding mode II under different magnetic fields: a B = 80 mT; b B = 150 mT; c B = 200 mT d B = 250 mT

Full size image

Figure 10 shows variation of the start and stop frequencies and the band gap width with magnetic field for the unit cell with encoding mode II. In contrast to the unit cell with encoding mode I, the mode II structure has a larger number of band gaps during the increase of magnetic field, and the critical magnetic field value for band gap opening is larger. It is noteworthy that only the width of band gap I (9th-10th bands) shows a non-monotonic change with magnetic field, while those of the other two band gaps increase continuously. This is mainly because the start frequency is almost a constant, whereas the stop frequency of band gap I first increases and then decreases.

Fig. 10
figure 10

Variation of start and stop frequencies and band gap width with magnetic field for magnetic anisotropy encoding mode II: a variation of start and stop frequencies with magnetic field; b variation of band gap width with magnetic field

Full size image

5.1.3 Encoding Mode III

In this sub-section, the band gap characteristics of HmSM-PnCs with magnetic anisotropy encoding mode III (as shown in Fig. 6c) are calculated. Figure 11 shows the band structure varying with magnetic fields. It can be seen that for this encoding mode structure, the magnetic field corresponding to the first band gap generation is higher than those of other encoding mode structures, and the center frequency of the first band gap is higher. Another important phenomenon is that more band gaps appear in the range of 0–250 mT of the magnetic field.

Fig. 11
figure 11

The band structures with encoding mode III under different magnetic fields: a B = 130 mT; b B = 150 mT; c B = 200 mT; d B = 250 mT

Full size image

Figure 12 shows the effect of magnetic field on the band structure with magnetic anisotropy encoding mode III. It can be found that the magnetic field has a significant effect on the band structure. There are six band gaps generated in 0–250 mT. It is noteworthy that different from other band gaps, the fourth band gap (27th-28th bands) only appears in a specific magnetic field range, which opens at 130 mT, and closes at 190 mT.

Fig. 12
figure 12

Variation of start and stop frequencies with magnetic field for magnetic anisotropy encoding mode III

Full size image

In a word, when the magnetic field ranges from 0–250 mT, the maximum number of band gaps for the magnetic anisotropic encoding mode I, II, and III structures are 1, 3, and 6, respectively. The magnetic anisotropic encoding mode I structure has the lowest critical magnetic field value, which is about 30 mT. The critical magnetic field values for the magnetic anisotropic encoding mode II and III structures are 80 mT and 130 mT, respectively. The magnetic anisotropy encoding mode actually determines the critical magnetic field and the number of band gaps.

5.2 Effects of Thickness and Porosity on the Band Structure of HmSM-PnCs

Next, the effect of thickness on the band structure of HmSM-PnCs is investigated. The band structures of magnetic anisotropy encoding mode I with different thicknesses at B = 100 mT are plotted in Fig. 13. As can be seen, the band gap between the 5th and the 6th bands moves to higher frequency with the increase of thickness, which shows a stepped shape with the band gap width first being widened, and then gradually narrowed. When the thickness is h = 0.5 mm, the band gap disappears completely. This result shows that the thickness plays an essential role in the position and width of the band gaps.

Fig. 13
figure 13

The band structures with different thicknesses under the magnetic field B = 100 mT: a h = 0.1 mm; b h = 0.2 mm; c h = 0.3 mm; d h = 0.4 mm; e h = 0.45 mm; f h = 0.5 mm

Full size image

Figure 14 shows the start and stop frequencies of the band gap varying with thickness under different magnetic fields. It can be seen that with the increase of the thickness, the stop frequency first increases and then gradually tends to be constant, while the start frequency increases continuously. Therefore, the band gap can be tuned by changing the thickness of the structure. It is also found that for a given magnetic field, there exists a critical thickness. When the thickness of structures exceeds the critical value, the band gap will disappear. In addition, the external magnetic field can increase the critical thickness. That is to say, applying a magnetic field may allow one to obtain an available band gap in a thicker structure.

Fig. 14
figure 14

Variation of start and stop frequencies with thickness under different magnetic fields

Full size image

Finally, the effect of porosity on the band gap structure is studied. Here we define porosity as \(\Phi {\kern 1pt} {\kern 1pt} { = }{\kern 1pt} {\kern 1pt} \frac{b}{L}\) (h = 0.2 mm). Figure 15a shows that the porosity affects the start and stop frequencies of band gap structure. With increasing the porosity from \(\Phi {\kern 1pt} {\kern 1pt} { = }{\kern 1pt} {\kern 1pt} 0.125\) (b = 1 mm, L = 8 mm) to \(\Phi {\kern 1pt} {\kern 1pt} { = }{\kern 1pt} {\kern 1pt} 0.875\) (b = 7 mm, L = 8 mm), the band gap width changes significantly. When \(\Phi {\kern 1pt} {\kern 1pt} { = }{\kern 1pt} {\kern 1pt} 0.5\) (b = 4 mm, L = 8 mm), the band gap width arrives at the maximum value, as shown in Fig. 15b.

Fig. 15
figure 15

Variation of start and stop frequencies and band gap width with porosity: a variation of start and stop frequencies with porosity; b variation of band gap width with porosity

Full size image

6 Conclusion

In this paper, we studied programmable HmSM-PnCs with three different magnetic anisotropy encoding modes and investigated the band gap tunability of programmable HmSM-PnCs under the applied magnetic field through finite element simulation. The main conclusions are as follows:

  1. (1)

    The applied magnetic field is very effective in adjusting the band gap by changing the configuration of HmSM-PnCs. The applied magnetic field can tune the generation and closure of the band gap, and a larger band gap width can be obtained by changing the magnetic field.

  2. (2)

    The geometric size also plays an important role in the band gap of HmSM-PnCs. Increasing the thickness of the structure can increase the start and stop frequencies of the band gap. The band gap width changes significantly with the increase of porosity, and there is a maximum band gap width when porosity \(\Phi {\kern 1pt} {\kern 1pt} { = }{\kern 1pt} {\kern 1pt} 0.5\).

  3. (3)

    The magnetic anisotropy encoding mode significantly affects the number of band gaps and the critical magnetic field value for the appearance of the band gap. The more complex is the magnetic anisotropy encoding mode, the larger is the number of band gaps during the entire loading process of magnetic field.

This study and the relevant results may provide a theoretical reference for designing and developing new shape-programmable acoustic metamaterials and low-frequency intelligent phononic crystals to promote environmental noise reduction.