1 Introduction

Solid–liquid composites (SLCs) are composites with liquid components incorporated into a solid matrix to develop thermal/electronic/mechanical properties. They have been widely applied to such fields as smart electronics and soft robotics. For example, when liquid metals are dispersed into solid phases, electronics and machines with capabilities of stretching, bending, and even cutting can be created [1, 2]. In addition, SLCs exhibit unexpected properties whereby the liquid droplets can increase energy dissipation near the tip of the crack [3]. The novel static physical properties of SLCs as well as their dynamic behaviors, such as resistance to damage and impact, are also critical to developing reliable and durable applications. For example, robotics working for search, rescue, and exploration of dangerous, unstable sites urgently need the properties of damage resistance [4]. However, most research has focused on improving the impact resistance of SLCs by combining with high tough soft matrix [1] or shear-thickening liquid [5], while the role of interaction between the basic compositions of SLCs, i.e., liquid phase and solid matrix, on the impact resistance has not been well studied. Therefore, it is necessary to study the dynamic impact behavior of SLCs from the view of the interaction between the liquid phase and solid matrix.

SLCs usually have high impact resistance through the shear-thickening properties of the liquid phase [6,7,8] and flow interactions with the solid phase [9,10,11]. Porous [12] or fabric materials [13] containing shear-thickening fluids have remarkable impact resistance owing to the prominent increase in the strength of the shear-thickening fluid at high strain rates. Similarly, composites containing electro-rheological (ER) and/or magneto-rheological (MR) fluids tend to have excellent energy dissipation at high loading rates under electronic and/or magnetic fields [14, 15]. SLCs containing these functional liquids have high impact resistance only in special loading environments, i.e., at high loading rates, which significantly limits their application. SLCs containing simple liquids can also have high energy dissipation. Navid et al. [3] added micron-sized liquid metal (LM) droplets to a soft elastomer, and found that the fracture energy of this solid–liquid composite drastically increased by up to 50 times because the deformed liquid metal droplets deflected and blunted cracks, leading to high energy dissipation. Xu et al. [16] enhanced the energy dissipation of porous materials by adding a liquid phase to hydrophobic nanoporous materials that could cyclically absorb and release energies. Zhang et al. [11] used molecular dynamics simulations to analyze the competition between the infiltration by the liquid and the buckling deformation of the cell wall in these liquid-containing nanoporous materials to understand their mechanism of energy dissipation. Although the energy adsorption of SLCs that contain functional fluids and fluid infiltration has been examined, the impact resistance of SLCs containing simple liquids, a common form of SLCs used in cutting-edge fields, has not been studied.

This work focused on the influence of liquid properties on the impact resistance of SLCs containing simple fluid inclusions. SLCs containing liquid inclusions with different viscosities were fabricated and used to conduct dynamic split-Hopkinson pressure bar (SHPB) tests under multiple strain rates (\(\dot{\varepsilon }\approx 100\,\hbox {s}^{-1}\sim 800\,\hbox {s}^{-1}\)). The influences of the viscosity and volume fraction of the liquid inclusions on the extent of energy dissipation of the SLCs were then analyzed. The results showed that the energy dissipation was dominated by viscosity in the strain rates ranging from 100 to \(400\,\hbox {s}^{-1}\), and by the volume fraction in the strain rates ranging from 500 to \(800\,\hbox {s}^{-1}\). The process of fracture of the SLCs was also recorded to identify the mechanism of their enhanced energy dissipation.

2 Experimental Tests

2.1 Fabrication of SLCs

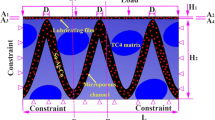
The SLCs tested in this paper are fabricated through the self-built microfluidics 3D printer [17] with commercial photosensitive resin (CLEAR PLGPCL04, Formlabs) as matrix and silicone oil (DOW XIAMETER PMX-200) as liquid inclusions. In the microfluidic chip fixed at the printed head, silicon oil and resin are injected independently at controlled flow rates into the inlet channels and meet at the needle tip of the flow-focusing configuration. Silicon oil is then sheared into droplets by the continuous immiscible resin at the needle tip, and mixed with the resin as a printable ink. Then, the ink is printed and cured into cylindrical samples with a diameter of 12 mm and length of 12 mm. Fabrication details can be found in our previous work with line precision of \(500\,\upmu \hbox {m}\) [17]. The liquid inclusions inside the SLCs are in size of about \(200\,\upmu \hbox {m}\), and are uniformly dispersed in the solid matrix without being connected. Three types of SLCs with silicon oil viscosities of 50 cst, 100 cst, and 350 cst are studied, which are named as 50 cst SLC, 100 cst SLC, and 350 cst SLC, respectively. The volume fraction of the liquid inclusions in the tested SLCs ranges from 10 to 40%.

Fig. 1
figure 1

The printed specimen and the SEM images of the fracture surface: a, b pristine resin; c, d SLC. The SLC specimen in (c) contains 40% liquid inclusions. The closed pores in (d) indicate the locations of liquid inclusions without connections

Full size image

2.2 Dynamic Impact System

The dynamic properties and impact resistance of the SLCs were tested through an air gun-driven SHPB containing a loading device, bar components, and a data recording system. The illustration and principle of the SHPB are shown in Fig. 2. The bar components consisted of a striker bar, an incident bar, and a transmission bar, all of which were made of aluminum with an elastic modulus of 72 GPa and strength of 450 MPa, and each had a diameter of 14 mm. The striker bar was launched by the sudden release of compressed air in the pressure chamber in the loading device. The launched striker bar was then accelerated until it impacted the end of the incident bar and applied an impact stress wave on it [18]. The strain rate of the applied stress wave was controlled by changing pressure within the chamber over a range of \(\dot{\varepsilon }\approx 100\,\hbox {s}^{-1}\sim 800\,\hbox {s}^{-1}\). A copper sheet was located between the incident bar and the striker bar as a pulse shaper to obtain a half-sine stress wave, whose thickness affects the overlapping ranges between the waveforms in the incident and transmitted bars, as illustrated in Fig. 3. The SLC specimen was sandwiched between the incident bar and the transmission bar, and was aligned with the loading axis. When the stress wave reaches the interface between the specimen and incident bar, part of it will be reflected back, and part of it will be transmitted through the specimen and pass through the transmission bar. Strain gauges with a resistance of 120 \(\Omega \) were arranged at the incident and transmission bars to record the propagation of the strain wave. An opposite-bridge connection mode was used to avoid the wave oscillation, as shown in Fig. 2. The stress equilibrium assumption for the SHPB requires the equivalence between stress waves at the ends of the specimen, i.e., the equivalence between the transmitted stress wave and the superposition of the incident stress wave and reflected stress wave.

A highspeed CMOS camera (Phantom V2512) with an image resolution of \(512 \times 352\ \hbox {pixels}\), frame speed of 110,000 fps, and exposure time of \(9\,\upmu \hbox {s}\) was used to capture the evolution of cracks in the tested SLCs induced by dynamic loading.

Fig. 2
figure 2

Schematics of SHPB experimental tests

Full size image
Fig. 3
figure 3

Waveforms recorded by strain gauges in the incident bar and transmitted bar, which are shaped by a copper sheet with a thickness of 1 mm and 1.5 mm under \(P_{\mathrm{gas}}=0.028\,\hbox {MPa}\), respectively

Full size image

2.3 Quantitative Characterization of Energy Dissipation

The SHPB test is based on two basic assumptions: (1) the stress wave propagation in the bar is one-dimensional; (2) the length of the specimen is much smaller than the stress wave wavelength. Thus, the stress in the specimen is uniform along its length after the stress wave propagates back and forth several times in the specimen. Figure 4 illustrates the propagation of the strain wave during the SHPB tests. When the incident strain wave was transmitted to the I–I interface between the incident bar and the SLC specimen, part of the wave was reflected and the remainder was transmitted into the SLC specimen. At the II–II interface between the SLC specimen and the transmission bar, the strain wave was transmitted into the transmission bar. The incident strain wave (\(\varepsilon _{\mathrm{I}}\)) and the reflected strain wave (\(\varepsilon _{\mathrm{R}}\)) were recorded by the strain gauge at the incident bar, while the transmission strain wave (\(\varepsilon _{\mathrm{T}}\)) was recorded by the strain gauge at the transmission bar.

Fig. 4
figure 4

The principle of the SHPB experimental tests

Full size image

Based on the assumption of 1D stress waves, uniform stress in the bar, and the stress equilibrium of the specimen [19], the basic equations for the SHPB test are as follows:

$$\begin{aligned} {F}_{1}= & {} {EA}(\varepsilon _{I} +\varepsilon _{R}) \end{aligned}$$
(1)
$$\begin{aligned} F_{2}= & {} EA \varepsilon _{T} \end{aligned}$$
(2)
$$\begin{aligned} \sigma _{\mathrm{s}}= & {} \frac{F_{1} +F_{2} }{2A_{0}} =\frac{EA}{2A_{0}}(\varepsilon _{\mathrm{I}} +\varepsilon _{\mathrm{R}} +\varepsilon _{\mathrm{T}}) \end{aligned}$$
(3)
$$\begin{aligned} \varepsilon _{\mathrm{S}}= & {} \frac{u_{1} -u_{2} }{l_{0}} =\frac{\hbox {c}}{l_{0}}\int _0^t {(\varepsilon _{I} -\varepsilon _{R} -\varepsilon _{T})\hbox {d}t} \end{aligned}$$
(4)

where E is elastic modulus; c is the velocity of the longitudinal wave; A is the cross-sectional area of the compressive bars; A is the cross-sectional area of the SLC specimens; l is the initial length of the SLC specimens; \(\varepsilon _{\mathrm{I}}\), \(\varepsilon _{\mathrm{R}}\), and \(\varepsilon _{\mathrm{T}}\) are the measured incident, reflected, and transmitted strain waves, respectively;\( F_{1}\) and \(F_{2}\) represent contact forces at I–I and II–II interfaces, respectively; and \(u_{1}\) and \(u_{2}\) are the displacements produced by \(\varepsilon _{I}\) and \(\varepsilon _{\mathrm{T}}\), respectively. \(W_{\mathrm{I}}\), \(W_{\mathrm{R}}\), and \(W_{\mathrm{T}}\) represent the incident, reflected, and transmitted strain energies, respectively, and are calculated as

$$\begin{aligned} W_{\mathrm{I}} (t)= & {} EAc\int _0^T \varepsilon _{\mathrm{I}}^{2} (t)\text{ d }t \end{aligned}$$
(5)
$$\begin{aligned} W_{\mathrm{R}} (t)= & {} EAc\int _0^T \varepsilon _{\mathrm{R}}^{2} (t)\text{ d }t \end{aligned}$$
(6)
$$\begin{aligned} W_{\mathrm{T}} (t)= & {} EAc\int _0^T \varepsilon _{\mathrm{T}}^{2} (t)\text{ d }t \end{aligned}$$
(7)

Based on the law of energy conservation, the cumulative dissipated energy \(W_{\mathrm{S}}\) is obtained as

$$\begin{aligned} W_{\mathrm{S}} (t)=W_{\mathrm{I}} (t)-W_{\mathrm{R}} (t)-W_{\mathrm{T}} (t) \end{aligned}$$
(8)

The rate of energy dissipation \(\gamma \) of the specimens is

$$\begin{aligned} \gamma =\frac{W_{\mathrm{S}} (t)}{W_{\mathrm{I}} (t)}\times 100\% \end{aligned}$$
(9)

3 Results and Analyses

3.1 Analysis of Stress Equilibrium and Energy Dissipation

Figure 5 shows the histories of stresses on both sides of the specimen under the applied gas pressures of 0.032 MPa for pristine resin and 50 cst SLCs and 0.035 MPa for 100 cst SLCs and 350 cst SLCs, respectively. The values of dynamic compressive stress \(\sigma _{\mathrm{c}}\) measured by the strain gauges at both sides of the specimen were identical, and the dynamic stress balance proved the validity of the SHPB test in this work [19].

Fig. 5
figure 5

The dynamic compressive stress \(\sigma _{\mathrm{c}}\) at both sides of the specimen. The solid lines represent stress in the incident bar as \(E(\varepsilon _{\mathrm{I}}+\varepsilon _{\mathrm{R}})\). The dashed lines involve stress in the transmission bar as \(E\varepsilon _{\mathrm{T}}\). The SLC specimens contained 30% liquid inclusions

Full size image

Figure 6 shows the stress–time curves of the SLC specimens and the pristine resin specimen under dynamic loading. The liquid inclusions in the SLC specimens had a volume fraction of 30%. The larger slope of the stress–time curve in the initial stage showed that the pristine resin specimen responded more quickly to the dynamic loading than the SLC specimens. The introduction of liquid inclusions had little effect on the peak dynamic stress of the specimen, as the peak stresses in the stress–time curve were almost the same for the pristine resin specimen and the SLC specimens. However, the SLC specimens had a longer response time, i.e., enhanced the deformation, in contrast with the pristine resin specimens. This is because higher liquid viscosity can enhance the viscous dissipation of stress wave propagating inside the SLCs and trapping inside the liquid inclusion, and eventually enlarge the duration time of dynamic response of SLCs.

Fig. 6
figure 6

The dynamic stress–time curves of the SLC specimens and the pristine resin specimen. The liquid inclusions in the SLC specimens had a volume fraction of 30%. The gas pressure was 0.03 MPa

Full size image

The above results clearly showed that the properties of liquid inclusions played an important role in the impact resistance of the SLCs. To better understand the underlying mechanism of energy dissipation of the SLCs under impact loading, the SHPB test was carried out under a low gas pressure (i.e., strain rate in the range of \(\dot{\varepsilon }\approx 100\,\hbox {s}^{-1}\sim 400\,\hbox {s}^{-1}\)), at which the specimen deformed without fracture; and under a high gas pressure (i.e., strain rate in the range of \(\dot{\varepsilon }\approx 500\,s^{-1}\sim 800\,\hbox {s}^{-1}\)), at which the specimen deformed and fractured, respectively.

3.2 Energy-Dissipated Mechanism of SLCs

3.2.1 Energy Dissipation at Strain Rates Ranging from 100 to \(400\,\mathrm{s}^{-1}\)

In this set of experiments, we set the applied rates of impact loading over a range of 100–400 \(\hbox {s}^{-1}\) at five gas pressures (0.020 MPa, 0.022 MPa, 0.025 MPa, 0.028 MPa, and 0.030 MPa). The SLCs underwent elastic deformation without damage under these loads. Figure 7 plots the rate of energy dissipation \(\gamma \) as a function of the applied gas pressure. It showed that SLCs containing 350 cst and 100 cst liquid inclusions exhibited a higher rate of energy dissipation at all tested gas pressure than the pristine resin. However, SLCs with 50 cst of liquid inclusions had a higher rate of energy dissipation than the pristine resin only at small gas pressures (\(\le 0.023\ \hbox {MPa}\)). Furthermore, the rate of energy dissipation was dependent on the loading rate, and increased with the gas pressure for both the pristine resin and the SLCs. Compared with the pristine resin, the addition of liquid inclusions with low viscosity (50 cst) reduced the sensitivity of the rate of energy dissipation to the loading rate, whereas the addition of liquid inclusions with medium and high viscosities (100 cst and 350 cst) increased this sensitivity.

Fig. 7
figure 7

Energy dissipation versus gas pressure \(P_{\mathrm{gas}}\) for SLCs with liquid inclusions of different viscosities, and the pristine resin. The volume fraction of the liquid inclusions in the SLCs was 30 %

Full size image

Table 1 shows the energy dissipation of the SLCs versus the volume fraction and viscosity of the liquid inclusions. Energy dissipation increased with the volume fraction and viscosity of the liquid inclusions, possibly owing to the viscous damping of the deformed liquid inclusions. Table 1 shows the growth factor of energy dissipation \(\gamma _{\mathrm{SLC}}/\gamma _{\mathrm{pristine}}\) of the SLCs as a function of the coefficients of viscosity. \(\gamma _{\mathrm{SLC}}\) and \(\gamma _{\mathrm{pristine}}\) are the energy dissipations of the SLCs and the pristine resin, respectively. The growth factor of the SLCs was dependent on the strain rate, and increased with the applied gas pressure, possibly owing to the higher damping of the deformed inclusions caused by the higher loading rate. The 350 cst SLCs had a growth factor twice as large as that of the 100 cst SLCs and three times as much as that of the 50 cst SLCs at all volume fractions. The SLCs with high volume fractions of liquid inclusions had high growth factors. The dependence of the growth factor on the volume fractions was significantly enhanced by increasing the viscosity of the liquid inclusions. Therefore, the latter played a leading role in the energy dissipation of SLCs at lower rates of strain-induced loads. SLCs containing more viscous liquid inclusions are thus more suitable for applications at low impact rates.

Table 1 Growth factor of energy dissipation \(\gamma _{\mathrm{SLC}}/ \gamma _{\mathrm{pristine}}\) of SLCs at strain rates ranging from 100 to \(400\,\hbox {s}^{-1}\)
Full size table

3.2.2 Energy Dissipation at Strain Rates Ranging from 500 to \(800\,\mathrm{s}^{-1}\)

Liquid inclusions in composites can help redistribute the cracks in them [20]. Thus, SLCs exhibited excellent impact resistance to higher strain rates induced by loading. To study the energy dissipation of SLCs under loading with higher strain rates, we set the applied impact load at four high gas pressures (0.032 MPa, 0.035 MPa, 0.038 MPa, and 0.040 MPa). The SLCs underwent damage, fracture, and eventually broke down.

Figure 8 shows the compressive strength (the peak stress point on the curve of dynamic stress) of 50 cst SLCs as a function of the volume fraction under different gas pressures. SLCs containing less viscous liquid inclusions recorded a rapid increase in dynamic compressive strength as the volume fraction increased from 10 to 20%, and then were in a stable zone as the applied higher gas pressure increased. The obvious platform period results from the high loading rates, which damage the SLCs with high volume fraction (30% and 40%) and low stiffness quickly. The quick damage of SLCs makes the stress wave unable to enter the liquid inclusions and be dissipated through the viscosity of the liquid, which eventually cannot consume more incident energy. Considering the stiffness of the SLCs, there may be an optimal volume fraction in response to a high rate of impact.

Fig. 8
figure 8

The compressive strength of 50 cst SLCs under the strain rates ranging from 500 to \(800\,\hbox {s}^{-1}\)

Full size image
Fig. 9
figure 9

Results of rate dependence of the energy dissipation of SLCs at the strain rates ranging from 500 to \(800\,\hbox {s}^{-1}\)

Full size image
Fig. 10
figure 10

The fracture process of 350 cst SLCs and pristine resin materials under dynamic loading (gas pressure of 0.04 MPa): a SLCs with 20% liquid inclusions; b SLCs with 30% liquid inclusions; c pristine resin

Full size image

Figure 9 shows the growth factor of the energy dissipation \(\gamma _{\mathrm{SLC}}/\gamma _{\mathrm{pristine}}\) of the SLCs at a high gas pressure (\(0.032\sim 0.04\ \hbox {MPa}\)). The growth factor was related to the viscosity and volume fraction of the liquid inclusion. Although SLCs with highly viscous liquid inclusions had high growth factors, the dependence of the growth factor on the volume fraction of the liquid inclusions was nonmonotonic. The maximum growth factor for all specimens was observed at a volume fraction of 20% when the loading gas pressure was higher than 0.035 MPa (green and red points). When the loading gas pressure was less than 0.035 MPa, the maximum growth factor was observed at a volume fraction of 30% and gas pressure of 0.035 MPa (purple points). The maximum growth factor was observed at a volume fraction of 40% when the gas pressure was 0.032 MPa (black points). Thus, the volume fraction of liquid inclusions in SLCs played a dominant role in energy dissipation at high loading rates. SLCs with a volume fraction of 20% are better for use in applications at such a range of impact rates.

3.3 Fracturing Modes of SLCs at Strain Rates Ranging from 500 to \(800\,\hbox {s}^{-1}\)

We used a high-speed camera to capture the entire process of fracture process of the SLCs under high dynamic loads to determine how the liquid inclusion affected the evolution of cracks during the damage and fracture processes. Figure 10 shows the process of fracture and modes of distribution of cracks in 350 cst SLCs and the pristine material at a gas pressure of 0.04 MPa. In Fig. 10a, the SLCs containing 20% liquid inclusions showed fragmented zones (yellow zone) with a large number of microcracks (red lines). The SLCs containing 30% liquid inclusions appeared to have gone through a relatively moderate fracture process, with fewer microcracks and smaller crush zones as shown in Fig. 10b. In comparison, the pristine resin material had one long tensile crack. The process of energy dissipation in composites could be viewed as the initiation, propagation, and coalescence of cracks activated during impact loadings. Thus, the SLCs with a large number of microcracks consumed more energy in case of dynamic loading than the pristine resin with only one tensile crack. In addition, the SLCs containing 20% liquid inclusions had higher energy dissipation than those containing 30% liquid inclusions.

4 Conclusion

This study examined the impact resistance of solid–liquid composites (SLCs), and revealed the influences of the viscosity and volume fraction of liquid inclusions on the energy dissipation in SLCs at lower and higher strain rates. The work here can help regulate the energy-absorbing properties of SLCs with functional inclusions of different viscosities and volume fractions to meet the requirements of protection under different strain rates of loading. The main results can be summarized as follows:

  1. (1)

    At the strain rates ranging from 100 to \(400\,\hbox {s}^{-1}\), the addition of 100 cst and 350 cst liquid inclusions enhanced the energy dissipation of SLCs to be higher than that of the pristine resin material. The dependence of the growth factor of energy dissipation of the SLCs on the volume fraction of the liquid inclusion increased monotonically, and was significantly enhanced by increasing the viscosity of the liquid inclusions. The 350 cst SLCs showed a rate of increase in energy dissipation that was nearly two and three times as high as those of the 100 cst SLCs and 50 cst SLCs, respectively. More viscous SLCs are more suitable for the case of low rate loading.

  2. (2)

    At the strain rates ranging from 500 to \(800\,\hbox {s}^{-1}\), the 100 cst and 350 cst SLCs had higher energy dissipation than the pristine resin material. The dependence of energy dissipation on the volume fraction of liquid inclusions of different viscosities was nonmonotonic. The maximum rate of energy dissipation for all SLCs occurred at a volume fraction of 20% when the loading gas pressure was higher than 0.035 MPa. The rate of energy dissipation of 350 cst SLCs was 3.5 times that of the pristine resin. The SLCs with a volume fraction of 20% are thus more suitable for use in the case of a high rate of impact.

  3. (3)

    By using a highspeed camera, it showed that more microcracks appeared in SLCs than in the pristine resin material under loads. This was because of the crack deflection induced by the deformed liquid inclusion, which enhanced the energy dissipation of SLCs.

Although the influence of liquid inclusions on the rate of energy dissipation of SLCs is experimentally studied here, there is still a lack of theoretical models, which is an interesting issue and will be investigated in our future work.