1 Introduction

Phononic crystals have received a great deal of attention since nearly two decades ago [1,2,3]. As periodic artificial materials and structures, phononic crystals are characterized by the regulation and control of their elastic properties, including elastic constants [4, 5], moduli and mass densities [6, 7], etc. Moreover, elastic waves cannot propagate at some frequency ranges because of the band gaps [8,9,10].

Recently, elastic wave metamaterials have been widely applied to the acoustic fields, e.g., sound radiation [11, 12], nonreciprocal wave propagation [13], acoustic clock [14,15,16] and sound transmission [17, 18]. Comparing with the novel materials, one of the significant properties of the elastic wave metamaterials is the negative dynamic effective material parameter in some frequency regions [19,20,21]. The ability to control the dynamic effective parameters with these metamaterials has attracted considerable attention [20, 22].

Huang and Sun [19] studied an acoustic metamaterial model with effective mass density and Young’s modulus. They found that the elastic wave propagation displayed a peculiar elastic wave motion in the region of double negative characteristics. After that the active elastic metamaterials with negative capacitance piezoelectric shunting was presented [22]. A similar research showed the influences of lateral local resonators on the transverse wave propagation in a metamaterial [23]. Some numerical calculations and experiments of the elastic metamaterials have been performed to show two stop bands at higher and lower frequency ranges with local resonators [24, 25].

The problem of sound transmission is of great concern in many related acoustic metamaterial fields [26,27,28,29]. Similar to the beam with local resonators [30], for elastic wave metamaterials with a two-dimensional case, an equivalent single layer plate was applied [17]. The sound transmission through a double-panel lined with poroelastic material in the core was studied, and the results showed the influence of external mean flow on the sound transmission loss (STL) [31]. The sound wave propagation with fluid flow was presented, and the acoustic wave traveling in a fluid could result in a steady flow called acoustic streaming [32]. The influence of mean flow of the external surrounding fluid on the STL has drawn close attention [17, 33]. It was also demonstrated that a higher STL could be generated if the Mach number became larger when the external mean flow was applied on the outer side of a cylindrical shell [34].

It is generally acknowledged that the active and passive feedback controls can modulate the vibration and elastic wave propagation by changing the control actions [35,36,37,38,39]. Chen et al. [40] studied an adaptive metamaterial beam with hybrid shunting circuits. They proposed a negative capacitance, and this mechanical mechanism can produce high- and low-pass filtering capabilities. Airoldi and Ruzzene [41] designed a one-dimensional tunable acoustic metamaterial using an elastic beam bonded by a periodic array of piezoelectric patches. It was illustrated that the equivalent mechanical impedance can be tuned without changing elastic structures. Owning the abilities to receive external information and make timely response, the active feedback control action has superior characteristics and engineering applications [38].

In our recent work [42], the STL was derived by the virtual work principle and wave function truncation with two infinite equations. However, the effective mass density and STL of that metamaterial were discussed separately with the control action. The effective medium method was not applied to show the STL properties, and the external mean flow was not taken into account. The present research considers the effective density to describe its STL and extends to show the sound transmission for the metamaterial. The dynamic equivalent method is developed to the periodic structure immersed in the external mean flow. Furthermore, we also present the influences of structural damping, Mach number and incident angle on the STL, and show the STL comparison between the virtual work principle in our previous investigation [42] and the dynamic equivalent result in this work.

2 STL of the Equivalent Single-Layer Plate Model with External Mean Flow

2.1 Problem Statement

Fig. 1
figure 1

Equivalent single plate of the elastic wave metamaterial subjected to incident sound pressure wave with external mean flow: a the perspective view; b the front view; c the vertical view; d the unit cell of the single plate with local resonators attached to the active feedback control systems

Full size image

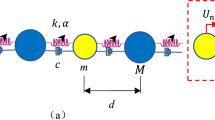
A Cartesian coordinate system (x, y, z) is used, in which its x-axis and y-axis locate on the lower surface of the plate and the positive direction of the z-axis is upward. Figure 1a gives the equivalent single plate model of the elastic wave metamaterial. The displacement, thickness, density, structural damping, Young’s modulus and Poisson’s ratio of this plate are w, h, \(\rho \), \(\eta \), E and \(\nu \), respectively.

In the incident field, the influences of the external mean flow on the sound transmission through the elastic wave metamaterial is discussed. In Fig. 1a, a harmonic plane pressure with elevation angle \(\varphi _{1}\) and azimuth angle \(\beta \) is incident from the upper surface. The fluid and structure coupling is considered, in which the external mean flow combines with fluid properties as the density \(\rho _{1}\) and sound speed \(c_{1}\). And the lower surface is emerged in the stationary fluid with the mass density \(\rho _{2}\) and sound speed \(c_{2}\). The incident pressure wave \(p_{{inc}}\) will result in a pressure disturbance in the surrounding medium which leads to a reflected sound pressure \(p_{{ref}}\) in the incident field and a transmitted sound pressure \(p_{{tr}}\) in the transmitted field. The elevation angles of the transmission wave are \(\varphi _{2}\) and \(\beta \) shown in Fig. 1b and c.

Figure 1d illustrates a unit cell of the elastic wave metamaterial from the perspective view, which is used to calculate the dynamic effective mass density [42]. The upper and lower plates are connected by two four-link mechanisms, in which two lateral local resonators with the mass constant \(m_{2}\) are connected by the spring \(k_{2}\). The horizontal distance, lateral distance and displacements of the upper and lower four-link mechanisms are L, D, \(v_{1}\) and \(v_{2}\), respectively. A vertical local resonator with the mass constant \(m_{1}\) is attached to both four-link mechanisms by the spring \(k_{1}\). The displacements of the upper and lower lateral local resonators are \(u_{2}^{(1)} \) and \(u_{2}^{(2)} \), respectively, and \(u_{1}\) is the displacement of the vertical resonator. In this research, the active feedback control system is attached to the vertical local resonator, which is used to tune the elastic wave properties [38, 42]. \(G_{1}\) and \(G_{2}\) are the acceleration and displacement feedback constants of the automatic control system with the Laplace variation s.

2.2 Basic Equations and Derivations of STL

As shown in Fig. 1a, an external mean flow with moving velocity V is parallel to the boundary of the upper surface of the equivalent single plate in the incident field. The sound pressure in the moving fluid should satisfy the convection equation with the following expression [43,44,45,46]:

$$\begin{aligned} \left( \frac{\partial }{\partial t}+V\cdot \nabla \right) ^{2}[p_{inc}(x,y,z;t)+p_{ref} (x,y,z;t)] =c_{1}^{2} \nabla ^{2}[p_{inc}(x,y,z;t)+p_{ref}(x,y,z;t)] \end{aligned}$$
(1)

where \(\nabla ^{2}\) is the Laplace operator; \(\nabla \) is the gradient; \(p_{inc}(x\), y, z; t) and \(p_{ref}(x\), y, z; t) are incident and reflected pressures, respectively.

The incident pressure on the upper surface of the equivalent single plate and the corresponding reflected sound pressure can be expressed as:

$$\begin{aligned}&p_{inc} (x,y,z;t)=P_{inc} \mathrm{e}^{-\mathrm{i}(k_{1x} x+k_{1y}y-k_{1z} z-\omega t)} \end{aligned}$$
(2a)
$$\begin{aligned}&p_{ref} (x,y,z,t)=P_{ref} \mathrm{e}^{-\mathrm{i}(k_{1x} x+k_{1y} y+k_{1z} z-\omega t)} \end{aligned}$$
(2b)

where \(P_{inc}\) and \(P_{ref}\) are the pressure amplitudes of the incident and reflected sound waves, respectively, and

$$\begin{aligned} k_{1x} =k_{1} \cos \varphi _{1} \sin \beta , \quad k_{1y} =k_{1} \cos \varphi _{1} \cos \beta , \quad k_{1z} =k_{1} \sin \varphi _{1} \end{aligned}$$
(3a--c)

The external mean flow moves along the y-direction and Eq. (1) can be simplified as [33]

$$\begin{aligned} \left( \frac{\partial }{\partial t}+V\cdot \frac{\partial }{\partial y}\right) ^{2}[p_{inc}(x,y,z;t)+p_{ref}(x,y,z;t)] =c_{1}^{2} \nabla ^{2}[p_{inc} (x,y,z;t)+p_{ref} (x,y,z;t)] \end{aligned}$$
(4)

Substituting Eqs. (2a), (2b) and (3) into Eq. (4), we obtain

$$\begin{aligned} k_{1} =\frac{\omega }{c_{1} (1+M\cos \varphi _{1} \cos \beta )} \end{aligned}$$
(5)

where \(M=V/c_{1}\) is the Mach number of the external mean flow. For the steady fluid (i.e., \(M=0\)), Eq. (5) will be reduced to \(k_{\mathrm{1}}=\omega /c_{1}\).

The pressure can transmit through the equivalent single plate, and its expression is

$$\begin{aligned} p_{tr} (x,y,z;t)=P_{tr} \mathrm{e}^{-\mathrm{i}(k_{2x} x+k_{2y} y-k_{2z}z-\omega t)} \end{aligned}$$
(6)

Moreover, the wave numbers of the transmitted wave are

$$\begin{aligned} k_{2x} =k_{2} \cos \varphi _{2} \sin \beta , \quad k_{2y} =k_{2} \cos \varphi _{2} \cos \beta \end{aligned}$$
(7a, b)
$$\begin{aligned} k_{2z} =k_{2} \sin \varphi _{2}, \quad k_{2} =\omega /c_{2} \end{aligned}$$
(8a, b)

where \(\varphi _{2}\) is the refracted angle of the transmitted waves, and \(c_{2}\) represents the sound speed in the fluid for the lower plate surface.

Correspondingly, the displacement of the equivalent single plate with amplitude W can be given by the following form:

$$\begin{aligned} w(x,y;t)=W\mathrm{e}^{-\mathrm{i}(k_{mx} x+k_{my} y-\omega t)} \end{aligned}$$
(9)

The wavenumbers of Eq. (9) are

$$\begin{aligned} k_{mx} =k_{m} \sin \beta , \quad k_{my} =k_{m} \cos \beta , \quad k_{m} =\frac{\omega }{c_{m} } \end{aligned}$$
(10a--c)

where \(c_{m}\) is the transverse wave velocity of the equivalent single plate.

The governing equation for the equivalent single plate is

$$\begin{aligned} D\nabla ^{4}w(x,y;t)-\rho _{eff} h\frac{\partial ^{2}w(x,y;\,t)}{\partial t^{2}} =p_{inc}(x,y,z;\,t)+p_{ref} (x,y,z;\,t)-p_{tr} (x,y,z;\,t) \end{aligned}$$
(11)

where \(D=\textit{Eh}^{3}(1+\hbox {i}\eta )/[12(1-\nu ^{2})]\); \(\rho _{eff}\) is the effective mass density of this model and its expression with the detailed derivation process can be found in [42].

Based on the boundary conditions, the wavelengths of the acoustic wave in the fluid and the bending wave in the plate should be consistent, resulting in

$$\begin{aligned} k_{1x} =k_{2x} =k_{mx} , \quad k_{1y} =k_{2y} =k_{my} \end{aligned}$$
(12a, b)

Substituting Eqs. (3), (5), (7), (8) and (10) into Eq. (12), the refracted angle in the transmitted field can be obtained as

$$\begin{aligned} \varphi _{2} =\arccos \left( {\frac{c_{2} \cos \varphi _{1} }{c_{1} (1+M\cos \varphi _{1} \cos \beta )}} \right) \end{aligned}$$
(13)

Here, the material properties on the upper and lower plates are the same, and the acoustic velocities along the upper and lower surfaces of the equivalent single plate are the same, i.e., \(c_{1}=c_{2}\); but the incident elevation and refracted angles are not equal, i.e., \(\varphi _{1}\ne \varphi _{2}\). According to Eq. (13), we can find that the refracted angle of transmitted wave deviates from the incident wave because of the external mean fluid.

Considering the fluid and structure coupling at the interface, the displacement continuity conditions at the upper and lower surfaces can be given as [17, 33]:

$$\begin{aligned} \frac{\partial [p_{inc}(x,y,z;t)+p_{ref} (x,y,z;t)]}{\partial z}\bigg |_{z=0}&=-\rho _{1} \left( \frac{\partial }{\partial t}+V\frac{\partial }{\partial y}\right) ^{2}w(x,y;t) \end{aligned}$$
(14a)
$$\begin{aligned} \frac{\partial [p_{tr} (x,y,z;t)]}{\partial z}\bigg |_{z=0}&=-\rho _{2} \frac{\partial ^{2}w(x,y;t)}{\partial t^{2}} \end{aligned}$$
(14b)

Substituting Eqs. (2), (6) and (9) into Eqs. (14a) and (14b), we can obtain the transmitted and reflected waves by the incident wave and the displacement of the plate as

$$\begin{aligned} P_{inc} -P_{ref}&=-\frac{\mathrm{i}\rho _{1} c_{1} \omega }{\sin \varphi _{1} (1+M\cos \varphi _{1} \cos \beta )}W \end{aligned}$$
(15a)
$$\begin{aligned} P_{tr}&=-\frac{\mathrm{i}\rho _{2} c_{2} \omega }{\sin \varphi _{2} }W \end{aligned}$$
(15b)

Then, Eq. (15a) can be rewritten as

$$\begin{aligned} P_{inc} -P_{ref} =\frac{\rho _{1} c_{1} \sin \varphi _{2} }{\rho _{2} c_{2} \sin \varphi _{1} (1+M\cos \varphi _{1} \cos \beta )}P_{tr} \end{aligned}$$
(16)

Based on Eqs. (11), (15b) and (16), the displacement of the equivalent single plate can be given as

$$\begin{aligned} W=\frac{2P_{inc} }{\chi (\omega ,\varphi _{1,} \beta )} \end{aligned}$$
(17)

where

$$\begin{aligned} \chi (\omega ,\varphi _{1} ,\beta )=Dk_{1}^{4}\cos ^{4}\varphi _{1} -\rho _{eff} h\omega ^{2} -\frac{\hbox {i}\omega \rho _{1} c_{1} }{\sin \varphi _{1} (1+M\cos \varphi _{1} \cos \beta )} -\frac{\hbox {i}\omega \rho _{2} c_{2} }{\sin \varphi _{2}} \end{aligned}$$
(18)

The sound power transmission coefficient is

$$\begin{aligned} \tau =\left| \frac{P_{inc}}{P_{tr}}\right| ^{2} \end{aligned}$$
(19)

Then, we can derive that

$$\begin{aligned} \tau =\left| -\frac{2\hbox {i}\omega \rho _{2} c_{2}}{\sin \varphi _{2} \chi (\omega , \varphi _{1}, \beta )}\right| ^{2} \end{aligned}$$
(20)

Finally, the STL can be expressed as the decibel (dB) scale [17, 18, 33, 47] and

$$\begin{aligned} \mathrm{STL}=10\mathrm{log}_{10} \left( \frac{1}{\tau }\right) \end{aligned}$$
(21)

3 Results and Discussion

3.1 Numerical Results and Discussions of the Effective Mass Density

Table 1 Parameters of the elastic wave metamaterial
Full size table

Material parameters of the equivalent single plate and the surrounding air fluid for the incident and transmitted fields are shown in Table 1. In our previous paper [42], the calculation for the effective mass density with \(L/D=1.8\) was presented. In this section, its numerical results with \(L/D= 0.5\) for the unit cell are proposed in Fig. 2. We can find that there are two modes in the elastic wave metamaterial for the double-plate model. Figure 2a and b show the dynamic effective mass densities for the in-phase and anti-phase modes, respectively. In Fig. 2a, the curve of the normalized effective mass density can be divided into three frequency regions. From 0 to 225 Hz, the first region is related to the local resonators including the vertical and lateral ones. The second frequency region locates between 225 and 378 Hz, in which the curve has a wide oscillating range and shows two regions for the negative effective mass density: one from 235.8 to 238.6 Hz and the other from 339.6 to 378 Hz. The third frequency region exceeds 378 Hz, in which the normalized effective mass density \(\rho _{{ eff}}/\rho \) gradually approaches 1.0. Comparing with the first frequency region, we can observe that the mass density \(\rho _{m}\) is close to \(1.35\rho \).

Fig. 2
figure 2

Dynamic effective mass density of the elastic wave metamaterial: a in-phase mode; b anti-phase mode

Full size image

Similarly, as shown in Fig. 2b, the curve can be divided into two parts for the whole frequency region. The first is from 0 to 260 Hz, in which the curve also oscillates obviously. There are two frequency regions that can generate negative values of effective density: one from 0 to 160.9 Hz and the other from 256.1 to 257.3 Hz. In the region where the frequency is higher than 260 Hz, the normalized effective density is positive and extends to 1.0.

Fig. 3
figure 3

Comparison of STLs with different mass densities: a in-phase mode; b anti-phase mode

Full size image

3.2 The STL for the Equivalent Single Plate

The effective mass density of the elastic wave metamaterial has important influences on sound transmission properties. Figure 3 illustrates the STL with three different mass densities as \(\rho \), \(\rho _{m}\) and \(\rho _{{ eff}}\). We set the incident angles being \(\varphi _{1}=\pi /6\) and \(\beta =\pi /4\). In Fig. 3a, it can be seen that the STL of the single-layer plate \(\rho _{m}\) for the in-phase mode is almost the same as that of the equivalent single plate, in which the frequency range locates from 10Hz to 225Hz. In the same frequency region, the STL of the single-layer plate with \(\rho \) is about 2–3 dB lower than the equivalent single plate model. When the frequency exceeds 1000 Hz in Fig. 3a and b, both STLs for the single plates with densities \(\rho _{{ eff}}\) and \(\rho \) agree very well. Because of the local resonance, the STL of the equivalent single plate model shows peaks and dips at some frequency regions in which the effective mass density has negative values.

Fig. 4
figure 4

Influence of the positive acceleration feedback control on the STL: a in-phase mode; b anti-phase mode

Full size image

Figure 4a and b show the influence of positive acceleration feedback control on the STL. In Fig. 4a, three different groups of positive acceleration are compared by \(G_{1}=0\), \(0.5m_{1}\) and \(1.0m_{1}\). It can be found that the second frequency region corresponding to the effective mass density decreases with the increase in \(G_{1}\). The second peak for \(G_{1}=1.0m_{1}\) is higher than the other two cases. Figure 4b is the STL of an equivalent single plate for the anti-phase mode. It shows that the positive acceleration feedback has no effects on this mode. According to the previous results [42], both positive and negative actions for the acceleration or displacement feedback controls make no difference on the effective mass density. Then, we will contribute our attention on the in-phase mode for the STL in the later discussions.

Comparing with Fig. 4a, the sound transmission responses remain unchanged when the frequency is above 1000 Hz in Fig. 5. The fluctuation region of frequency becomes wider with the negative value of \(G_{1}\) increasing. When \(G_{1}=-0.7m_{1}\), the first peak and dip of the STL decrease but the second peak reaches the maximum among these three curves. It is worth noting that the two frequency peaks turn to the left as the positive acceleration feedback control increases; but for the negative acceleration feedback control, they both move to the right.

Fig. 5
figure 5

STL with different negative acceleration feedback control actions for the in-phase mode

Full size image

Figures 6 and 7 present the STL with different positive and negative displacement feedback control actions for the in-phase mode of the equivalent single plate. We can find that before 700 Hz, these three curves oscillate obviously. Comparing with Figs. 6 and 7, it can be seen that no matter \(G_{2}\) is positive or negative, the behavior of the STL for the in-phase mode is similar to that for the anti-phase mode. It is necessary to mention that when \(G_{2}=-1.0k_{1}\), the STL shows different trends before the first peak appears. The second dip disappears for the case of \(G_{2}=-2.0k_{1}\). With the analysis for the positive and negative displacement feedback control actions on the STL, similar properties for the effective mass density can also be found.

Fig. 6
figure 6

STL with different positive displacement feedback control actions for the in-phase mode

Full size image
Fig. 7
figure 7

STL with different negative displacement feedback control actions for the in-phase mode

Full size image

From the comparisons of Figs. 4a, 5, 6 and 7, we can find that both positive and negative feedback controls for the in-phase mode can change the three frequency regions, especially for the second region corresponding to the local resonance. The fluctuation scope for the STL changes significantly, which indicates an important research area. This characteristic can also turn the properties of the sound transmission effectively. Moreover, it can show that the active feedback control action is worthy of the acoustic-structure coupling.

Fig. 8
figure 8

Effects of structural damping on the STL plotted with the elevation angle \(\varphi _{1}=\pi /6\), azimuth angle \(\beta =\pi /4\) and Mach number \(M=0\): a in-phase mode; b anti-phase mode

Full size image

The coincident frequency is a special index for sound transmission, which appears when the wavenumber of the acoustic exciting flexural wave is equal to that of the free vibration for the plate. Once the coincidence occurs, the structure is easier to be excited by the acoustic wave, which results in the efficient transmission of sound energy from one side to another. In the presence of external mean flow, the coincident frequency can be given by the effective medium method as

(22)

Based on the analysis above, the effective mass density of the elastic wave metamaterial only has obvious changes in the lower frequency region. Then, we can rewrite the coincident frequency as [17, 48]

$$\begin{aligned} f_{\text {co}} \approx \frac{c_{2}^{2} }{2\pi \cos ^{2}(\varphi _{2})}\sqrt{\frac{\rho h}{D}} \end{aligned}$$
(23)

From Eq. (23), it can be seen that the coincident frequency is related to the refracted angle which can be affected by the plate and the transmitted fluid field. We can obtain the coincident frequency of the equivalent plate with the parameters in Table 1 and \(f_{\text {co}}=5300\ \hbox {Hz}\).

As an important factor, the structural damping plays an indispensable role on engineering practice, which also has impacts on the dynamic responses of structural acoustics. As shown in Fig. 8a and b, the STL corresponding to the coincident frequency increases obviously with the structural damping being larger. There is little change at other frequencies for the in-phase and anti-phase modes.

From Eqs. (18) and (20), the STL is derived by the incident angles which include the elevation and the azimuth ones. Figure 9 illustrates the variations of the STL through the equivalent plate with different incident angles. We consider the influences of elevation angles with \(\beta =\pi /4\) and \(M=0\). Both the in-phase and anti-phase modes have similar trends at the same frequency region. Before 8000 Hz, it can be found that the STL increases and its coincident frequency moves to the higher frequency region with the elevation angle increasing.

In this study, the external mean flow is considered, and we give the effects of different Mach numbers being from 0 to 0.8 in Fig. 10. The STL can be divided by the peaks and dips into three parts for the in-phase mode and two parts for the anti-phase mode. It can be seen that the third frequency region for the in-phase mode is different from the other two cases. Once the frequency region is below 8000 Hz for both modes, the STL increases with the increase in Mach number. For the region between the first peak and the second dip for the in-phase mode, the external mean flow almost has no influence on the STL except for the frequency region with a negative density. And the effect of Mach number on the STL can be helpful for the design of elastic wave metamaterials in practical application.

Figure 11 gives the effects of the incident azimuth angle being from 0 to \(\pi /3\) with \(M=0.4\) and \(\varphi _{1}=\pi /6\). We can see that the STL decreases with the increase in the azimuth angle, which gives an opposite result by changing the elevation angle. The frequency of the third dip corresponding to the coincident frequency shifts to a lower frequency region as the azimuth angle increases. It means that the resonance of the equivalent single-layer plate with a large incident azimuth angle occurs more easily. If the Mach number \(M=0\), the STL nearly has no change as the azimuth angle increases. It is illustrated that the STL can be affected by the azimuth angle with different Mach numbers. Hence, the azimuth angle is a significant parameter for the sound transmission with the external mean flow.

Fig. 9
figure 9

Effects of elevation angle on the STL with the structural damping \(\eta =0.05\), Mach number \(M=0\) and azimuth angle \(\beta =\pi /4\): a in-phase mode; b anti-phase mode

Full size image
Fig. 10
figure 10

Effects of Mach number on the STL with the structure damping \(\eta =0.05\), elevation angle \(\varphi _{1}=\pi /6\) and azimuth angle \(\beta =\pi /4\): a in-phase mode; b anti-phase mode

Full size image

In this research, the elastic wave metamaterial is modeled as an equivalent single plate using the effective mass density method. The STL can be calculated by the principle of virtual work in [42] and a single plate in this work with the above method. With the same parameters, Fig. 12 shows the comparison between the STLs of the elastic wave metamaterial with double-plate model and an equivalent single-plate model by the two approaches. For the region from 10 Hz to 230 Hz, the behavior of the STL for the double-plate model is almost the same as that for the equivalent single-layer plate model. And the result for the elastic wave metamaterial is almost 10 dB higher than the equivalent single-layer plate model. For the region above 378 Hz, the difference of the STL between two curves gradually become larger with the increase of frequency. It is observed that the curves fluctuate obviously at the region which corresponds to the second frequency region of the effective mass density. Furthermore, the peaks and dips appear at the frequencies for the negative density. In other regions, both curves have sudden drops at the coincident frequency \(f_{\text {co}}=5300\ \hbox {Hz}\).

Fig. 11
figure 11

Effects of azimuth angle on the STL with the structure damping \(\eta =0.05\), Mach number \(M =0.4\) and elevation angle \(\varphi _{1}=\pi /6\): a in-phase mode; b anti-phase mode

Full size image

Figure 13 shows the comparison between a pure single-layer plate model and a double-plate model (without local resonators and four-link mechanisms) in [42]. By comparison with Fig. 12, we can find that the curves of equivalent and pure single-plate models have similar trends. The pure double-plate model and the elastic wave metamaterial oscillate clearly in the second frequency region but not obviously in other regions. We can also find that the results in Figs. 12 and 13 distinguish between the two acoustic propagation paths (i.e., double-plate models with and without local resonators and four-link mechanisms) for sound transmission.

Fig. 12
figure 12

Comparisons of the STLs between the equivalent single-plate model and the elastic wave metamaterial

Full size image
Fig. 13
figure 13

Comparisons of the STLs between pure single-plate model and double-plate model (without local resonators and four-link mechanisms)

Full size image

4 Conclusions

This work investigates the elastic wave metamaterial with the double-plate model and active feedback control systems immersed in the external mean fluid. The derivation of the STL for the metamaterial with effective mass density is presented, which is based on the dynamic effective medium theory. The results are compared between a double-plate model using the virtual work principle and a pure single-layer plate by the dynamic equivalent method. Numerical calculations of sound transmission are performed to discuss the influences of both the acceleration and displacement feedback controls. It is found that in the region of the negative effective mass density generating, the STL curve oscillates obviously. There are two frequency regions showing the negative effective mass density for the in-phase and anti-phase modes. Both the effective density and the STL can be changed by the positive and negative feedback control actions for the in-phase mode. The positive and negative acceleration feedback controls have opposite influences on the STL for the equivalent single plate. Moreover, as the Mach number and incident elevation angle increase, the STL becomes larger nearly before 8000 Hz and the coincident frequency moves to the higher frequency region; but with the increase in azimuth angle, the STL decreases with a small scope and the coincident frequency behaves in the opposite direction.