Skip to main content

Advertisement

SpringerLink
Log in

Minimum Control Energy of Spatial Beam with Assumed Attitude Adjustment Target

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

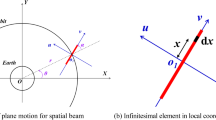
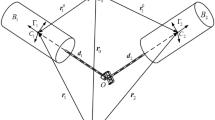
Abstract

The dynamic analysis on the ultra-large spatial structure can be simplified drastically by ignoring the flexibility and damping of the structure. However, these simplifications will result in the erroneous estimate on the dynamic behaviors of the ultra-large spatial structure. Taking the spatial beam as an example, the minimum control energy defined by the difference between the initial total energy and the final total energy in the assumed stable attitude state of the beam is investigated by the structure-preserving method proposed in our previous studies in two cases: the spatial beam considering the flexibility as well as the damping effect, and the spatial beam ignoring both the flexibility and the damping effect. In the numerical experiments, the assumed simulation interval of three months is evaluated on whether or not it is long enough for the spatial flexible damping beam to arrive at the assumed stable attitude state. And then, taking the initial attitude angle and the initial attitude angle velocity as the independent variables, respectively, the minimum control energies of the mentioned two cases are investigated in detail. From the numerical results, the following conclusions can be obtained. With the fixed initial attitude angle velocity, the minimum control energy of the spatial flexible damping beam is higher than that of the spatial rigid beam when the initial attitude angle is close to or far away from the stable attitude state. With the fixed initial attitude angle, ignoring the flexibility and the damping effect will underestimate the minimum control energy of the spatial beam.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Glaser PE. Power from the sun: its future. Science. 1968;162:857–61.

    Article  Google Scholar 

  2. NASA, Final Proceedings of the Solar Power Satellite Program Review, DoE/NASA Conference 800491, 1980.

  3. Mankins J. SPS-ALPHA: The First Practical Solar Power Satellite via Arbitrarily Large Phased Array, NASA NIAC Phase 1 Project, 2012.

  4. Yin TT, Deng ZC, Hu WP, Wang XD. Dynamic modeling and simulation of deploying process for space solar power satellite receiver. Appl Math Mech—Engl Edit. 2018;39:261–74.

    Article  MathSciNet  Google Scholar 

  5. Yang Y, Zhang YQ, Duan BY, Wang DX, Li X. A novel design project for space solar power station (SSPS-OMEGA). Acta Astronaut. 2016;121:51–8.

    Article  Google Scholar 

  6. Pao LY. Minimum-time control characteristics of flexible structures. J Guid Control Dyn. 1996;19:123–9.

    Article  Google Scholar 

  7. Liu XD, Xin X, Li Z, Chen Z, Sheng YZ. Near minimum-time feedback attitude control with multiple saturation constraints for agile satellites. Chin J Aeronaut. 2016;29:722–37.

    Article  Google Scholar 

  8. Zhu JM, Trelat E, Cerf M. Minimum time control of the rocket attitude reorientation associated with orbit dynamics. SIAM J Control Optim. 2016;54:391–422.

    Article  MathSciNet  Google Scholar 

  9. Eldad O, Lightsey EG, Claudel C. Minimum-time attitude control of deformable solar sails with model uncertainty. J Spacecr Rockets. 2017;54:863–70.

    Article  Google Scholar 

  10. da Silva MRC, Zaretzky CL. Nonlinear dynamics of a flexible beam in a central gravitational field I. Equations of motion. Int J Solids Struct. 1993;30:2287–99.

    Article  Google Scholar 

  11. da Silva MRC, Zaretzky CL. Nonlinear dynamics of a flexible beam in a central gravitational field II. Nonlinear motions in circular orbit. Int J Solids Struct. 1993;30:2301–16.

    Article  Google Scholar 

  12. Chen ZQ, Agar TJA. Geometric nonlinear analysis of flexible spatial beam structures. Comput Struct. 1993;49:1083–94.

    Article  Google Scholar 

  13. Quadrelli B, Atluri S. Analysis of flexible multibody systems with spatial beams using mixed variational principles. Int J Numer Methods Eng. 1998;42:1071–90.

    Article  MathSciNet  Google Scholar 

  14. Yang H, Hong JZ, Yu ZY. Dynamics modelling of a flexible hub-beam system with a tip mass. J Sound Vib. 2003;266:759–74.

    Article  Google Scholar 

  15. Cai GP, Lim CW. Dynamics studies of a flexible hub-beam system with significant damping effect. J Sound Vib. 2008;318:1–17.

    Article  Google Scholar 

  16. Zhang ZG, Qi ZH, Wu ZG, Fang HQ. A spatial Euler–Bernoulli beam element for rigid-flexible coupling dynamic analysis of flexible structures. Shock Vib. 2015;. https://doi.org/10.1155/2015/208127.

    Article  Google Scholar 

  17. Yin TT, Deng ZC, Hu WP, Li QJ, Cao SS. Dynamic modelling and simulation of orbit and attitude coupling problems for structure combined of spatial rigid rods and spring. Chin J Theor Appl Mech. 2018;50:87–98.

    Google Scholar 

  18. Hu WP, Li QJ, Jiang XH, Deng ZC. Coupling dynamic behaviors of spatial flexible beam with weak damping. Int J Numer Methods Eng. 2017;111:660–75.

    Article  MathSciNet  Google Scholar 

  19. Hu WP, Deng ZC. Non-sphere perturbation on dynamic behaviors of spatial flexible damping beam. Acta Astronaut. 2018;152:196–200.

    Article  Google Scholar 

  20. Hu WP, Deng ZC, Yin TT. Almost structure-preserving analysis for weakly linear damping nonlinear Schrödinger equation with periodic perturbation. Commun Nonlinear Sci Numer Simul. 2017;42:298–312.

    Article  MathSciNet  Google Scholar 

  21. Hu WP, Song MZ, Deng ZC, Yin TT, Wei BQ. Axial dynamic buckling analysis of embedded single-walled carbon nanotube by complex structure-preserving method. Appl Math Model. 2017;52:15–27.

    Article  MathSciNet  Google Scholar 

  22. Hu WP, Deng ZC, Wang B, Ouyang HJ. Chaos in an embedded single-walled carbon nanotube. Nonlinear Dyn. 2013;72:389–98.

    Article  MathSciNet  Google Scholar 

  23. Hu WP, Deng ZC, Han SM, Zhang WR. Generalized multi-symplectic integrators for a class of Hamiltonian nonlinear wave PDEs. J Comput Phys. 2013;235:394–406.

    Article  MathSciNet  Google Scholar 

  24. Hu WP, Song MZ, Deng ZC. Energy dissipation/transfer and stable attitude of spatial on-orbit tethered system. J Sound Vib. 2018;412:58–73.

    Article  Google Scholar 

  25. Hu WP, Song MZ, Deng ZC, Zou HL, Wei BQ. Chaotic region of elastically restrained single-walled carbon nanotube. Chaos. 2017;27:023118.

    Article  MathSciNet  Google Scholar 

  26. Hu WP, Deng ZC. Chaos in embedded fluid-conveying single-walled carbon nanotube under transverse harmonic load series. Nonlinear Dyn. 2015;79:325–33.

    Article  Google Scholar 

  27. Song G, Agrawal BN. Vibration suppression of flexible spacecraft during attitude control. Acta Astronaut. 2001;49:73–83.

    Article  Google Scholar 

Download references

Acknowledgements

The research is supported by the National Natural Science Foundation of China (11672241, 11972284, 11432010), Fund for Distinguished Young Scholars of Shaanxi Province (2019JC-29), Fund of the Youth Innovation Team of Shaanxi Universities, the Seed Foundation of Qian Xuesen Laboratory of Space Technology, and the Open Foundation of State Key Laboratory of Structural Analysis of Industrial Equipment (GZ1605).

Author information

Authors and Affiliations

  1. School of Civil Engineering and Architecture, Xi’an University of Technology, Xi’an, 710048, China

    Weipeng Hu

  2. State Key Laboratory of Eco-Hydraulics in Northwest Arid Region of China, Xi’an University of Technology, Xi’an, 710048, China

    Weipeng Hu

  3. Department of Aeronautical Machinery Engineering of Army Aviation Institute, Beijing, 101123, China

    Lingjun Yu

  4. School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi’an, 710072, China

    Zichen Deng

Authors
  1. Weipeng Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lingjun Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zichen Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weipeng Hu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hu, W., Yu, L. & Deng, Z. Minimum Control Energy of Spatial Beam with Assumed Attitude Adjustment Target. Acta Mech. Solida Sin. 33, 51–60 (2020). https://doi.org/10.1007/s10338-019-00132-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-019-00132-4

Keywords

Search

Navigation