Nonlinear Vibration Analyses of Cylindrical Shells Composed of Hyperelastic Materials

Abstract

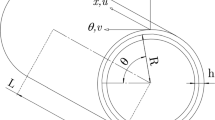
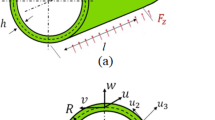
The nonlinear vibration problem is studied for a thin-walled rubber cylindrical shell composed of the classical incompressible Mooney–Rivlin material and subjected to a radial harmonic excitation. With the Kirchhoff–Love hypothesis, Donnell’s nonlinear shallow shell theory, hyperelastic constitutive relation, Lagrange equations and small strain hypothesis, a system of nonlinear differential equations describing the large-deflection vibration of the shell is derived. First, the natural frequencies of radial, circumferential and axial vibrations are studied. Then, based on the bifurcation diagrams and the Poincaré sections, the nonlinear behaviors describing the radial vibration of the shell are illustrated. Examining the influences of structural and material parameters on radial vibration of the shell shows that the vibration modes are highly sensitive to the thickness–radius ratio when the ratio is less than a certain critical value. Moreover, in terms of the results of multimodal expansion, it is found that the response of the shell to radial motion is more regular than that without considering the coupling between modes, while there are more phenomena for the uncoupled case.

Appendixes

Elements of the mass matrix:

$$\begin{aligned} {{\varvec{M}}}= & {} \left[ {{\begin{array}{lll} {M_{11} }&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad {M_{99} } \\ \end{array} }} \right] \nonumber \\ M_{11}= & {} M_{44} =\frac{\pi \rho lRh}{2}, M_{22} =M_{33} =M_{55} =M_{66} =\pi \rho lRh, M_{77} =\frac{\pi \rho h^{3}}{24lR}\left( {n^{2}l^{2}+\pi ^{2}R^{2}} \right) +\frac{\pi \rho lRh}{2},\nonumber \\ M_{88}= & {} \frac{\pi \rho hR}{12l}\left( {12l^{2}+\pi ^{2}h^{2}} \right) , M_{99} =\frac{\pi \rho hR}{4l}\left( {4l^{2}+3\pi ^{2}h^{2}} \right) \end{aligned}$$

(A1)

Elements of the linear stiffness matrix:

$$\begin{aligned} {{\varvec{K}}}= & {} \left[ {{\begin{array}{lll} {K_{11} }&{}\quad \cdots &{}\quad {K_{19} } \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ {K_{91} }&{}\quad \cdots &{}\quad {K_{99} } \\ \end{array} }} \right] \nonumber \\ K_{11}= & {} \frac{\pi n^{2}lh}{2R}\left( {\mu _1 -4\mu _2 } \right) +\frac{2\pi ^{3}Rh}{l}\left( {\mu _1 -\mu _2 } \right) , K_{14} =K_{41} =-\pi ^{2}nh\left( {\mu _1 -\mu _2 } \right) -\frac{\pi ^{2}nh}{2}\left( {\mu _1 -4\mu _2 } \right) ,\nonumber \\ K_{17}= & {} K_{71} =-\pi ^{2}h\left( {\mu _1 -\mu _2 } \right) , K_{12} =K_{13} =K_{15} =K_{16} =K_{18} =K_{19} =0,\nonumber \\ K_{22}= & {} \frac{4\pi ^{3}Rh}{l}\left( {\mu _1 -\mu _2 } \right) , K_{28} =K_{82} =-2\pi ^{2}h\left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{21}= & {} K_{23} =K_{24} =K_{25} =K_{26} =K_{27} =K_{29} =0, K_{33} =\frac{36\pi ^{3}Rh}{l}\left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{39}= & {} K_{93} =-6\pi ^{2}h\left( {\mu _1 -\mu _2 } \right) , K_{31} =K_{32} =K_{34} =K_{35} =K_{36} =K_{37} =K_{38} =0,\nonumber \\ K_{44}= & {} \frac{2\pi n^{2}lh}{R}\left( {\mu _1 -\mu _2 } \right) +\frac{\pi ^{3}Rh}{l}\left( {\mu _1 -4\mu _2 } \right) , K_{47} =K_{74} =\frac{2\pi nlh}{R}\left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{42}= & {} K_{43} =K_{45} =K_{46} =K_{48} =K_{49} =0, K_{55} =\frac{\pi ^{3}Rh}{l}\left( {\mu _1 -4\mu _2 } \right) ,\nonumber \\ K_{51}= & {} K_{52} =K_{53} =K_{54} =K_{56} =K_{57} =K_{58} =K_{59} =0, K_{66} =\frac{9\pi ^{3}Rh}{l}\left( {\mu _1 -4\mu _2 } \right) ,\nonumber \\ K_{61}= & {} K_{62} =K_{63} =K_{64} =K_{65} =K_{67} =K_{68} =K_{69} =0,\nonumber \\ K_{77}= & {} \left( {\frac{2\pi lh}{R}+\frac{\pi n^{4}lh^{3}}{6R^{3}}+\frac{\pi ^{5}Rh^{3}}{6l^{3}}+\frac{\pi ^{3}n^{2}h^{3}}{6lR}} \right) \left( {\mu _1 -\mu _2 } \right) +\frac{\pi ^{3}n^{2}h^{3}}{6lR}\left( {\mu _1 -4\mu _2 } \right) ,\nonumber \\ K_{72}= & {} K_{73} =K_{75} =K_{76} =K_{78} =K_{79} =0, K_{88} =\left( {\frac{4\pi lh}{R}+\frac{\pi ^{5}Rh^{3}}{3l^{3}}} \right) \left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{81}= & {} K_{83} =K_{84} =K_{85} =K_{86} =K_{87} =0, K_{99} =\left( {\frac{4\pi lh}{R}+\frac{27\pi ^{5}Rh^{3}}{l^{3}}} \right) \left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{91}= & {} K_{92} =K_{94} =K_{95} =K_{96} =K_{97} =K_{98} =0. \end{aligned}$$

(A2)