Skip to main content
SpringerLink
Log in

Investigation on the Anisotropic Transformation Surfaces of Super-Elastic NiTi Shape Memory Alloys Under Multiaxial Cyclic Loading Conditions

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

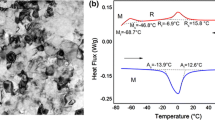
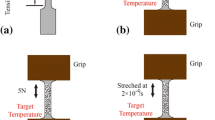
Abstract

The cyclic transformation behaviors of polycrystalline super-elastic NiTi shape memory alloys (SMAs) under multiaxial loading paths with different angles between axial and torsional loading orientations were experimentally investigated. The experimental results showed that the start stresses of forward and reverse transformations decreased with the increase in the number of cycles and exhibit obvious anisotropic evolutions. The start stresses of forward and reverse transformations in the tensile and torsional directions did not satisfy the von Mises criterion. The shape of transformation surface during the forward and reverse transformations evolved with the increase in the number of cycles. Then, new cyclic anisotropic transformation surfaces were established by introducing an anisotropic tensor into the von Mises equivalent stress based on a typical transformation criterion related to \(J_2 \) and \(J_3 \). Moreover, the evolution equations of material parameters used in the proposed transformation surfaces were established to describe the subsequent evolutions of transformation surfaces. Finally, the start stresses of forward and reverse transformations predicted using the proposed transformation surfaces were compared with the experimental results. It shows that the proposed transformation surfaces can reasonably describe the start stresses of forward and reverse transformations, which are helpful for establishing a three-dimensional cyclic constitutive model to describe the cyclic transformation behaviors of super-elastic NiTi SMAs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Orgéas L, Favier D. Stress-induced martensitic transformation of a NiTi alloy in isothermal shear, tension and compression. Acta Mater. 1998;46(15):5579–91.

    Article  Google Scholar 

  2. Liu Y, Xie Z, Humbeeck JV, Delaey L. Asymmetry of stress–strain curves under tension and compression for NiTi shape memory alloys. Acta Mater. 1998;46(12):4325–38.

    Article  Google Scholar 

  3. Sun QP, Li ZQ. Phase transformation in superelastic NiTi polycrystalline micro-tubes under tension and torsion-from localization to homogeneous deformation. Int J Solids Struct. 2002;39(13):3797–809.

    Article  Google Scholar 

  4. Miyazaki S, Otsuka K, Suzuki Y. Transformation pseudoelasticity and deformation behavior in a Ti-50.6at%Ni alloy. Scr Metall. 1981;15(3):287–92.

    Article  Google Scholar 

  5. Lagoudas DC, Bo Z. Thermomechanical modeling of polycrystalline SMAs under cyclic loading, part II: material characterization and experimental results for a stable transformation cycle. Int J Eng Sci. 1999;37(9):1141–73.

    Article  Google Scholar 

  6. Sehitoglu H, Anderson R, Karaman I, Gall K, Chumlyakov Y. Cyclic deformation behavior of single crystal NiTi. Mater Sci Eng A. 2001;314(1):67–74.

    Article  Google Scholar 

  7. Gall K, Maier HJ. Cyclic deformation mechanisms in precipitated NiTi shape memory alloys. Acta Mater. 2002;50(18):4643–57.

    Article  Google Scholar 

  8. Wang X, Xu B, Yue Z. Phase transformation behavior of pseudoelastic NiTi shape memory alloys under large strain. J Alloys Compd. 2008;463(1):417–22.

    Article  Google Scholar 

  9. Song D, Kang G, Kan Q, Yu C, Zhang C. Non-proportional multiaxial transformation ratchetting of super-elastic NiTi shape memory alloy: experimental observations. Mech Mater. 2014;70(1):94–105.

    Article  Google Scholar 

  10. Lim TJ, Mcdowell DL. Mechanical behavior of an Ni–Ti shape memory alloy under axial-torsional proportional and nonproportional loading. J Eng Mater Technol. 1999;121(1):9–18.

    Article  Google Scholar 

  11. Liu Y, Xie Z, Humbeeck JV. Cyclic deformation of NiTi shape memory alloys. Mater Sci Eng A. 1999;273–275(3):673–8.

    Article  Google Scholar 

  12. Iadicola MA, Shaw JA. The effect of uniaxial cyclic deformation on the evolution of phase transformation fronts in pseudoelastic NiTi wire. J Intell Mater Syst Struct. 2002;13(2):143–55.

    Article  Google Scholar 

  13. Auricchio F, Marfia S, Sacco E. Modelling of SMA materials: training and two way memory effects. Comput Struct. 2003;81(24):2301–17.

    Article  Google Scholar 

  14. Auricchio F, Reali A, Stefanelli U. A three-dimensional model describing stress-induced solid phase transformation with permanent inelasticity. Mech Adv Mater Struct. 2007;14(1):43–55.

    Article  Google Scholar 

  15. Hartl DJ, Chatzigeorgiou G, Lagoudas DC. Three-dimensional modeling and numerical analysis of rate-dependent irrecoverable deformation in shape memory alloys. Int J Plast. 2010;26(10):1485–507.

    Article  Google Scholar 

  16. Lagoudas D, Hartl D, Chemisky Y, Machado L, Popov P. Constitutive model for the numerical analysis of phase transformation in polycrystalline shape memory alloys. Int J Plast. 2012;32–33(2):155–83.

    Article  Google Scholar 

  17. Lagoudas DC, Entchev PB. Modeling of transformation-induced plasticity and its effect on the behavior of porous shape memory alloys. Part I: constitutive model for fully dense SMAs. Mech Mater. 2004;36(9):865–92.

    Article  Google Scholar 

  18. Zaki W, Moumni Z. A 3D model of the cyclic thermomechanical behavior of shape memory alloys. J Mech Phys Solids. 2007;55(11):2427–54.

    Article  Google Scholar 

  19. Zhang X, Yan X, Xie H, Sun R. Modeling evolutions of plastic strain, maximum transformation strain and transformation temperatures in SMA under superelastic cycling. Comput Mater Sci. 2014;81(2):113–22.

    Google Scholar 

  20. Kan Q, Kang G. Constitutive model for uniaxial transformation ratchetting of super-elastic NiTi shape memory alloy at room temperature. Int J Plast. 2010;26(3):441–65.

    Article  MathSciNet  Google Scholar 

  21. Saint-Sulpice L, Chirani SA, Calloch S. A 3D super-elastic model for shape memory alloys taking into account progressive strain under cyclic loadings. Mech Mater. 2009;41(1):12–26.

    Article  Google Scholar 

  22. Yu C, Kang G, Kan Q. A physical mechanism based constitutive model for temperature-dependent transformation ratchetting of NiTi shape memory alloy: one-dimensional model. Mech Mater. 2014;78(78):1–10.

    Google Scholar 

  23. James RD, Hane KF. Martensitic transformations and shape-memory materials. Acta Mater. 2000;48(1):197–222.

    Article  Google Scholar 

  24. Wang J, Moumni Z, Zhang W, Xu Y, Zaki W. A 3D finite-strain-based constitutive model for shape memory alloys accounting for thermomechanical coupling and martensite reorientation. Smart Mater Struct. 2017;26(6):065006 (065015pp).

    Article  Google Scholar 

  25. Wang J, Moumni Z, Zhang W. A thermomechanically coupled finite-strain constitutive model for cyclic pseudoelasticity of polycrystalline shape memory alloys. Int J Plast. 2017;97:174–221.

    Article  Google Scholar 

  26. Zhang X, Huang D, Yan X, Zhou X. Modeling functional fatigue of SMA using a more accurate subdivision of martensite volume fractions. Mech Mater. 2016;96:12–29.

    Article  Google Scholar 

  27. Yu C, Kang G, Kan Q, Zhu Y. Rate-dependent cyclic deformation of super-elastic NiTi shape memory alloy: thermo-mechanical coupled and physical mechanism-based constitutive model. Int J Plast. 2015;72:60–90.

    Article  Google Scholar 

  28. Zaki W. An approach to modeling tensile-compressive asymmetry for martensitic shape memory alloys. Smart Mater Struct. 2010;19(2):328–35.

    Article  Google Scholar 

  29. Zaki W, Moumni Z, Morin C. Modeling tensile-compressive asymmetry for superelastic shape memory alloys. Mech Adv Mater Struct. 2011;18(7):559–64.

    Article  Google Scholar 

  30. Auricchio F, Petrini L. A three-dimensional model describing stress-temperature induced solid phase transformations: solution algorithm and boundary value problems. Int J Numer Meth Eng. 2004;61(6):807–36.

    Article  MathSciNet  Google Scholar 

  31. Bouvet C, Calloch S, Lexcellent C. Mechanical behavior of a Cu–Al–Be shape memory alloy under multiaxial proportional and nonproportional loadings. J Eng Mater Technol. 2002;124(2):112–24.

    Article  Google Scholar 

  32. Bouvet C, Calloch S, Lexcellent C. A phenomenological model for pseudoelasticity of shape memory alloys under multiaxial proportional and nonproportional loadings. Eur J Mech A Solids. 2004;23(1):37–61.

    Article  MathSciNet  Google Scholar 

  33. Saleeb AF, Kumar A, Ii SAP, Dhakal B. The cyclic and evolutionary response to approach the attraction loops under stress controlled isothermal conditions for a multi-mechanism based multi-axial SMA model. Mech Mater. 2013;63(1):21–47.

    Article  Google Scholar 

Download references

Acknowledgements

Financial supports by the National Natural Science Foundation of China (11572265; 11532010), the Excellent Youth Found of Sichuan Province (2017JQ0019), the Open Project of Traction Power State Key Laboratory (TPL1606) and the Exploration Project of Traction Power State Key Laboratory (2017TPL_T04) are acknowledged.

Author information

Authors and Affiliations

  1. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu, 610031, China

    Bo Qiu, Qianhua Kan & Guozheng Kang

  2. Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu, 610031, China

    Qianhua Kan, Tianxing Zhao, Xi Xie & Guozheng Kang

Authors
  1. Bo Qiu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qianhua Kan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tianxing Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xi Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Guozheng Kang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qianhua Kan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qiu, B., Kan, Q., Zhao, T. et al. Investigation on the Anisotropic Transformation Surfaces of Super-Elastic NiTi Shape Memory Alloys Under Multiaxial Cyclic Loading Conditions. Acta Mech. Solida Sin. 31, 744–757 (2018). https://doi.org/10.1007/s10338-018-0034-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-018-0034-6

Keywords

Search

Navigation