Abstract
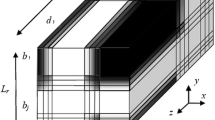
The aim of this paper is to apply the asymptotic homogenization method to determining analytically and numerically the transversely isotropic viscoelastic relaxation moduli of the equivalent particle for the intercalated multi-layer stack of intercalated type nanoplastics. A two-phase multilayered material containing n layers is considered. The matrix is assumed to be an isotropic viscoelastic standard linear body and the reinforcement is assumed to be an isotropic elastic body. Final explicit analytical formulae for the effective elastic moduli of the multilayered material are derived first; and then the correspondence principle is employed to obtain the homogenized relaxation moduli of the equivalent intercalated particle. A numerical example is given. Final explicit analytical formulae in the time domain derived here make it convenient to estimate the influence of all the particle parameters of micro-structural details on the effective properties of the equivalent intercalated particle. The results of this paper can also be applied to multi-layer composites.
Similar content being viewed by others
References
Usuki, A., Kojima, Y., Kawasumi, M., Okada, A., Fukushima, Y., Kurauchi, T. and Kamigaito, O., Synthesis of nylon 6-clay hybrid. Journal of Materials Research, 1993, 8(5): 1179–1184.
Kojima, Y., Usuki, A., Kawasumi, M., Okada, A., Fukushima, Y., Kurauchi, T. and Kamigaito, O., Mechanical properties of nylon 6-clay hybrid. Journal of Materials Research, 1993, 8(5): 1185–1189.
Suprakas Sinha Ra and Masami Okamoto, Polymer/layered silicate nanocomposites: a review from preparation to processing. Progress in Polymer Science, 2003, 28: 1539–1641.
Jyi-Jiin Luo and Isaac M. Daniel. Characterization and modeling of mechanical behavior of polymer/clay nanocomposites. Composites Science and Technology, 2003, 63: 1607–1616.
Daniel F. Sias, Branca F. Oliveira, Samir Maghous and Guillermo J. Creus, Application of homogenization theory to composite materials. Jornadas Sul-Americanas de Engenharia Estrutural, 2002: 1–6.
Liu Wenhui and Zhang Chunyuan, Application of asymptotic homogenization theory to viscoelastic multilayered composites. Natural Science Journal of Xiangtan University, 2003, 25: 91–97.
Marcin Kamiński, Sensitivity analysis of homogenized characteristics for some elastic composites. Computer Methods in Applied Mechanics and Engineering, 2003, 192: 1973–2005.
Maghous, S. and Creus, G.J., Periodic homogenization in thermo-viscoelasticity: case of multilayered media with ageing. International Journal of Solids and Structures, 2003, 40: 851–870.
Shutian Liu, Kezhang Chen and Xinan Feng, Prediction of layered materials. International Journal of Solids and Structure, 2004, 41: 3675–3688.
Zhang Chunyuan, Viscoelastic Fracture Mechanics. Beijing: Science Press, 2006.
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (Grant Nos.10672138 and 10372087).
Rights and permissions
About this article
Cite this article
Zhang, W., Zhang, P., Deng, X. et al. Prediction of the viscoelastic properties of the equivalent particle for the intercalated multi-layer stack of nanoplastics. Acta Mech. Solida Sin. 20, 317–323 (2007). https://doi.org/10.1007/s10338-007-0737-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10338-007-0737-6