Skip to main content
SpringerLink
Log in

Non-linear forced vibration of axially moving viscoelastic beams

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

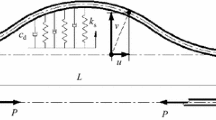
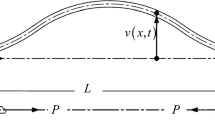
The non-linear forced vibration of axially moving viscoelastic beams excited by the vibration of the supporting foundation is investigated. A non-linear partial-differential equation governing the transverse motion is derived from the dynamical, constitutive equations and geometrical relations. By referring to the quasi-static stretch assumption, the partial-differential non-linearity is reduced to an integro-partial-differential one. The method of multiple scales is directly applied to the governing equations with the two types of non-linearity, respectively. The amplitude of near- and exact-resonant steady state is analyzed by use of the solvability condition of eliminating secular terms. Numerical results are presented to show the contributions of foundation vibration amplitude, viscoelastic damping, and nonlinearity to the response amplitude for the first and the second mode.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ulsoy A.G., Mote C.D.Jr. and Syzmani R., Principal developments in band saw vibration and stability research, Holz als Roh-und Werks, Vol.36, 1978, 273–280.

    Article  Google Scholar 

  2. Wickert J.A. and Mote C.D.Jr., Current research on the vibration and stability of axially moving materials, Shock & Vibration Digest, Vol.20, 1988, 3–13.

    Article  Google Scholar 

  3. Wickert J.A. and Mote C.D.Jr., Response and discretization methods for axially moving materials, Applied Mechanics Reviews, Vol.44,1991, S279–284.

    Article  Google Scholar 

  4. Wickert J.A. and Mote C.D.Jr., Classical vibration analysis of axially moving continua, ASME Journal of Applied Mechanics, Vol.57,1990, 738–744.

    Article  Google Scholar 

  5. Wickert J.A., Non-linear vibration of a traveling tensioned beam, International Journal of Non-linear Mechanics, Vol.27, 1992, 503–517.

    Article  Google Scholar 

  6. Pakdemirli M. and Ulsoy A.G., Stability analysis of an axially accelerating string, Journal of Sound & Vibration, Vol.203, 1997, 815–832.

    Article  Google Scholar 

  7. Öz H.R., Pakdemirli M. and Özkaya E., Transition behavior from string to beam for an axially accelerating material, Journal of Sound & Vibration, Vol.215, 1998, 571–576.

    Article  Google Scholar 

  8. Ravindra B. and Zhu W.D., Low dimensional chaotic response of axially accelerating continuum in the supercritical regime, Achieve of Applied Mechanics, Vol.68, 1998, 195–205.

    Article  Google Scholar 

  9. Öz H.R., Pakdemirli M. and Boyaci H., Non-linear vibrations and stability of an axially moving beam with time-dependent velocity, International Journal of Non-linear Mechanics, Vol.36, 2001, 107–115.

    Article  Google Scholar 

  10. Hu H.Y. and Jin D.P., Nonlinear dynamics of a suspended traveling cable subject to transverse fluid excitation, Journal of Sound and Vibration, Vol.239, No.3, 2001, 515–529.

    Article  Google Scholar 

  11. Jin D.P. and Hu H.Y., Dynamic configurations of a traveling cable subject to transverse fluid excitation, Chinese Journal of Theoretical Applied Mechanics, Vol.33, No.4, 2001, 525–530 (In Chinese).

    Google Scholar 

  12. Feng Z.H. and Hu H.Y., Dynamic stability of a slender beam with internal resonance under a large linear motion, Chinese Journal of Theoretical Applied Mechanics, Vol.34, No.3, 2001, 389–400 (In Chinese).

    Google Scholar 

  13. Chen S.H. and Huang J.L., On internal resonance of nonlinear vibration of axially moving beams, Chinese Journal of Theoretical Applied Mechanics, Vol.37, No. 1, 2005, 57–63 (In Chinese).

    MathSciNet  Google Scholar 

  14. Sze K.Y., Chen S.H. and Huang J.L., The incremental harmonic balance method for nonlinear vibration of axially moving beams, Journal of Sound and Vibration, Vol.281, 2005, 611–626.

    Article  Google Scholar 

  15. Chen L.Q., Analysis and control of transverse vibrations of axially moving strings, ASME Applied Mechanics Reviews, Vol.58, 2005, 91–116.

    Article  Google Scholar 

  16. Park S.W., Analytical modeling of viscoelastic dampers for structural and vibration control, International Journal of Solids and Structures, Vol.38, 2001, 8065–8092.

    Article  Google Scholar 

  17. Yang X.D. and Chen L.Q., Nonlinear free vibration of an axially moving beam on fixed supports, Acta Mechanica Solida Sinica, Vol.18, No.3, 2005, 242–247.

    Google Scholar 

  18. Yang X.D. and Chen L.Q., The stability of an axially accelerating beam on the simple supports with torsion springs, Acta Mechanica Solida Sinica, Vol.18, No.4, 2005, 340–347.

    MathSciNet  Google Scholar 

  19. Wickert J.A., Non-linear vibration of a traveling tensioned beam, International Journal of Non-linear Mechanics, Vol.27, 1992, 503–517.

    Article  Google Scholar 

  20. Öz H.R. and Pakdemirli M., Vibrations of an axially moving beam with time dependent velocity, Journal of Sound & Vibration, Vol.227, 1999, 279–257.

    Article  Google Scholar 

  21. Nayfeh A.H., Introduction to Perturbation Techniques, New York, Wiley, 1981.

    MATH  Google Scholar 

  22. Chen L.Q. and Yang X.D., Steady-state response of axially moving viscoelastic beams with pulsating speed: comparison of two nonlinear models, International Journal of Solids and Structures, Vol.42, No.1, 2005, 37–50.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Shenyang Institute of Aeronautical Engineering, Shenyang, 110034, China

    Xiaodong Yang

  2. Department of Mechanics, Shanghai University, Shanghai, 200436, China

    Li-Qun Chen

Authors
  1. Xiaodong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li-Qun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaodong Yang.

Additional information

Project supported by the National Natural Science Foundation of China (No. 10472060), Natural Science Foundation of Shanghai Municipality (No. 04ZR14058) and Doctor Start-up Foundation of Shenyang Institute of Aeronautical Engineering (No. 05YB04).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, X., Chen, LQ. Non-linear forced vibration of axially moving viscoelastic beams. Acta Mech. Solida Sin. 19, 365–373 (2006). https://doi.org/10.1007/s10338-006-0643-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-006-0643-3

Key words

Search

Navigation