Solubility and Surface Thermodynamics of Conducting Polymers by Inverse Gas Chromatography, IV: Polypyrrole/Titanium Oxide

Abstract

A wealth of physico-chemical information has been obtained on an insoluble and crystalline polypyrrole/titanium oxide (PPY/TiO₂) using the Inverse Gas Chromatography Method (IGC). Twenty-five solvents (test compounds) with different specific interactions were used. PPY/TiO₂ was synthesized and characterized by FTIR and DSC methods. The following characteristics of PPY/TiO₂ were explored: changes in morphology, the strength of solvent–PPy/TiO₂ interactions, dispersive surface energy, percent crystallinity, solvents and PPy/TiO₂ solubility parameters, and molar heat of sorption, mixing and evaporation ($\Delta H_{1}^{s}$, $\Delta H_{1}^{\infty }$, $\Delta H_{1}^{v}$). Interaction parameters were corrected to be free from the solvents’ chemical nature. Nonane, propyl acetate, and methyl ethyl ketone showed stronger interactions and a higher affinity to PPy/TiO₂; yet, none of these solvents can dissolve PPy/TiO₂. IGC showed that PPy/TiO₂ has 59.34 mJ/m² dispersive surface energy at 100 °C and 98% crystalline at 60 °C. Comprehensive solvents and PPy/TiO₂ solubility parameters were obtained and comparted with that of soluble and insoluble polymers.

Graphic abstract

Inverse Gas Chromatography (IGC) along with DSC and FTIR methods investigated the morphology, surface energy, degree of crystallinity and the thermodynamics of conducting polypyrrole/TiO₂. The solubility parameters were calculated for 27 solvents.

Appendix A

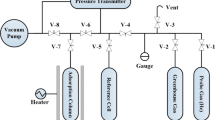
The key term in the IGC experiment is the specific retention volume V^o_g which enables the determination of thermodynamic parameters of a system under study, degree of crystallinity and the dispersive component of the surface energy. By measuring several main experimental chromatographic quantities such as; the flow rate, column temperature, retention time of test compounds, mass of the polymer, and the pressures of the carrier gas at the inlet and the outlet of the column, V^o_g can be calculated as follows:

$$V_{g}^{{^{o} }} = \frac{{273.15\Delta t.{\text{F}} . {\text{J}}}}{{w.T_{\text{c}} }}$$

(4)

J is the correction for the compressibility of the carrier gas across the chromatographic column defined by the following relation;

$$J = \frac{3}{2}\left[ {\frac{{\left( {{\raise0.7ex\hbox{${P_{\text{i}} }$} \!\mathord{\left/ {\vphantom {{P_{\text{i}} } {P_{\text{o}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${P_{\text{o}} }$}}} \right)^{2} - 1}}{{\left( {{\raise0.7ex\hbox{${P_{\text{i}} }$} \!\mathord{\left/ {\vphantom {{P_{\text{i}} } {P_{o} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${P_{o} }$}}} \right)^{3} - 1}}} \right]$$

(5)

Here, Δt = t_p − t_m is the difference between the retention time of the test compound, t_p and of the marker, t_m. Air is usually used as a marker to account for the dead volume in the chromatographic column when the thermal conductivity (TC) detector is used. The retention time of the marker must be subtracted from the test compound retention time to reflect the test compound value of the test compound retention time as Δt. F is the flow rate of the carrier gas measured at the column temperature T_c, and w is the mass of the stationary phase. J factor is calculated using P_i and P_o, the inlet and outlet pressures, respectively. P_i and P_o are measured using electronic transducers, which are interfaced at the inlet and outlet of the column. These transducers are usually calibrated using a mercury manometer. Since Δt is a function of F, it must be extrapolated to zero to reflect the true value of Δt. Then, the product of the Δt and the flow rate F may also yield a valuable quantity as a net retention volume, V_N, as follows:

$$V_{\text{N}} = \Delta t.{\text{F}}$$

(6)

V_N in Eq. (6) accounts for the retention time of test compound in terms of volume in mL and it is dependent on the mass of the polymer in the column. To be more specific, V_N can be taken a step further by dividing it by the mass of the polymer and corrected to 0 °C to become a specific retention volume of the test compound, V^o_g as in Eq. (4).

$$V_{\text{g}}^{\text{o}} = V_{\text{N}} \left( {\frac{273.15}{W.Tc}} \right)$$

(7)

V^o_g is the key term for the calculations of thermodynamic quantities. It enables the calculations of the partition coefficient, K_p, which will lead to the calculation of the molar free energy of sorption (ΔG_s) of the test compounds into the polymer layer, using the following relationship:

$$K_{\text{p}} = \frac{{V_{\text{g}}^{\text{o}} \rho T}}{273.12}$$

(8)

where ρ is the density of the polymer in the chromatographic column. Then, the relationship between K_p and the ΔG_s is well known:

$$\Delta G_{\text{s}} = - RT\ln K_{\text{p}}$$

(9)

Accordingly, the molar heat of sorption ($\Delta H_{s}^{1}$) of test compounds into the polymer layer can also be derived from IGC data as follows [23]. For a pure solvent, the liquid–vapor equilibrium is described by the Clapeyron equation:

$${\raise0.7ex\hbox{${{\text{d}}P}$} \!\mathord{\left/ {\vphantom {{{\text{d}}P} {{\text{d}}T}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{d}}T}$}} = {\raise0.7ex\hbox{${\Delta H_{\text{ad}}^{1} }$} \!\mathord{\left/ {\vphantom {{\Delta H_{\text{ad}}^{1} } {T\left( {\bar{V}_{\text{g}} - \bar{V}_{\text{l}} } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T\left( {\bar{V}_{\text{g}} - \bar{V}_{\text{l}} } \right)}$}}$$

(10)

Here $\bar{V}_{\text{g}}$ and $\bar{V}_{\text{l}}$ are partial molar volumes of the test compound gas and liquid states and $\Delta H_{s}^{1}$ is the partial molar heat of sorption of the test compound onto the polymeric surface. An analogous relationship can be derived for sorption of test compounds into the polymer layer ($\Delta H_{s}^{1}$):

$${\raise0.7ex\hbox{${{\text{d}}P_{1} }$} \!\mathord{\left/ {\vphantom {{{\text{d}}P_{1} } {{\text{d}}T}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{d}}T}$}} = {\raise0.7ex\hbox{${\Delta H_{s}^{1} }$} \!\mathord{\left/ {\vphantom {{\Delta H_{s}^{1} } {T\left( {\bar{V}_{\text{g}} - \bar{V}_{\text{l}} } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T\left( {\bar{V}_{\text{g}} - \bar{V}_{\text{l}} } \right)}$}}$$

(11)

Considering that $\bar{V}_{l}$ is negligible as compared to $\bar{V}_{\text{g}}$ and substituting the pressure of the vapor from the ideal gas equation for $P_{1} = {\raise0.7ex\hbox{${\text{RT}}$} \!\mathord{\left/ {\vphantom {{\text{RT}} {\bar{V}_{\text{g}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\bar{V}_{\text{g}} }$}}$(this is always allowed when IGC set-up is at an infinite dilution). Using V^o_g from the chromatographic quantities along with Eq. (11), the molar heat of sorption of solvents into the polymer layer can be calculated as:

$${\text{d}}\ln V_{\text{g}}^{\text{o}} .{\text{d}}\left( {\frac{1}{T}} \right) = - \frac{{\Delta H_{\text{s}}^{ 1} }}{R}$$

(12)

A plot of ln V^o_g versus the inverse of temperature will determine $\Delta H_{s}^{1}$. If the polymer surface is amorphous at the experiments’ temperature, the equilibrium between the vapor and the polymer will be established, then the slope of the linear relationship [29] can be measured from the following equation.

$$ \Delta H_{\text{s}}^{ 1} = - \left[ {\frac{{R\partial \ln V_{\text{g}}^{\text{o}} }}{{\partial \left( {\frac{1}{T}} \right)}}} \right] $$

(13)

To calculate the interaction parameters of test compounds used with PPY/TiO₂, V^o_g from Eq. (4) can also be utilized to calculate the interaction parameter of the mobile and the stationary phases as, χ₁₂, as follows:

$$ \chi_{12} = \ln \frac{{273.15R\nu_{2} }}{{V_{\text{g}}^{\text{o}} V_{1} P_{1}^{\text{o}} }} - 1 + \frac{{V_{1} }}{{M_{2} \nu_{2} }} - \frac{{B_{11} - V_{1} }}{\text{RT}}P_{1}^{o} $$

(14)

χ₁₂ parameter can reveal the strength of the specific interactions between the test compounds and the pure polymers and with the polymer pair. 1 denotes the test compound and 2 denotes the polymer under examination; υ₂ is the specific volume of the polymer at the column temperature T_c; M₁ is the molecular weight of the test compound; P^o₁ is the saturated vapor pressure of the test compound; V₁ is the molar volume of the test compound; R is the gas constant; and B₁₁ is the second virial coefficient of the test compound in the gaseous state. Equation (14) is used routinely for the calculation of χ₁₂ from IGC experiments.V^o_g can also be utilized to calculate another important thermodynamic quantity, the molar heat of mixing of solvents with PPY/TiO₂′s surface at infinite dilution, $\Delta H_{1}^{\infty }$. To accomplish this goal, the mass fraction activity coefficient,$\varOmega_{1}^{\infty }$, should be calculated [20].

$$ \varOmega_{1}^{\infty } = \ln \left[ {\frac{273.15R}{{V_{\text{g}}^{\text{o}} P_{1}^{o} M_{1} }}} \right] - \frac{{P_{1}^{o} (B_{11} - V_{1} )}}{\text{RT}} $$

(15)

The molar enthalpy of mixing $\Delta H_{1}^{\infty }$ can be calculated using Eq. (15), as follows:

$$ \Delta H_{1}^{\infty } = \frac{{R\partial \ln \varOmega_{1}^{\infty } }}{{\partial \left( {\frac{1}{T}} \right)}} $$

(16)

Similarly, the molar free energy and the molar entropy of mixing can also be calculated:

$$ \Delta G_{1}^{\infty } = {\text{RT}}\ln \varOmega_{1}^{\infty } $$

(17)

$$ \Delta S_{1}^{\infty } = \frac{{(\Delta H_{1}^{\infty } - \Delta G_{1}^{\infty } )}}{T} $$

(18)

Solubility Parameters

To calculate the Hildebrand solubility parameters for the solvent, δ₁ and the conducting PPY/TiO₂, δ₂ [44, 50, 51], the molar heat of vaporization of the solvent, ΔH^v₁ needs to be known. It is calculated using the following equation [52].

$$\Delta H_{ 1}^{\text{v}} = \Delta H_{1}^{\infty } - \Delta H_{1}^{\text{s}}$$

(19)

The solubility parameter of the solvent, δ₁ is related to ΔH^v₁ by the following equation [44]

$$\partial_{1} = \left[ {\frac{{(\Delta H_{\text{v}} - {\text{RT}})}}{{V_{1} }}} \right]^{0.5}$$

(20)

In the early 1970s, Guillet et al. [53, 54] were able to calculate solubility of the polymer, δ₂, using the IGC method, they derived the following equation utilizing Flory–Huggins parameter, χ₁₂, Eq. (14), as follows,

$$\left( {\frac{{\partial_{1}^{2} }}{\text{RT}} - \frac{{\chi_{12} }}{{V_{1} }}} \right) = \left( {\frac{{2\partial_{1} \partial_{2} }}{\text{RT}}} \right) - \left( {\frac{{\partial_{2}^{2} }}{\text{RT}}} \right)$$

(21)

δ₂ can be obtained from Eq. (21) by plotting the left-hand side of the equation versus δ₁ calculated in Eq. (20), the slope of the straight line is (2 δ₂/RT).

Dispersive Surface Energy

The total surface energy of PPY-TiO2 is the combination of several contributions depending on the nature of the solute that is interacting with the polymer surface. One of these contributions is due to the dispersive interaction forces such as those in alkanes. The dispersive forces in alkanes increase as more CH₂ group is added to its backbone. If the solute used exhibits acid–base interaction forces, it also contributes to the total value of the surface energy. When the mobile gaseous phase comes in contact with the polymeric surface, an interfacial energy will be created according to the nature of the interacting solute and whether it is polar (γ_p) and/or non-polar or dispersive (γ_d). Then, the adsorption of the solute vapor onto the polymer surface will be affected by the magnitude of the surface free energy. Since the alkane series used in this work has a uniform increase in dispersive forces, it makes it possible to calculate the dispersive component of the surface energy of PPY/TiO₂ using IGC. From the measured chromatographic quantities V^o_g can also be used to calculate the dispersive component of the surface energy of polymers using alkane test compounds [55, 56]. A complete theoretical treatment for the calculation of γ^d_s was first published by Fowkes [55]. It relates to the equilibrium constant K between the adsorbed test compound and the polymer surface, the molar free energy of adsorption, ∆G^s₁, can be calculated as follows:

$$\Delta G_{ 1}^{\text{s}} = \, - {\text{ RT }}\ln V_{\text{g}}^{\text{o}} + {\text{ C }}.$$

(22)

Equation (23) relates the energy of adsorption to the surface energy as follows:

$${\text{RT}}\ln V_{\text{g}}^{\text{o}} + C = 2Na\sqrt {\gamma_{\text{s}}^{\text{d}} \gamma_{\text{i}}^{\text{d}} }$$

(23)

γ^d_s and γ^d_i are the dispersive components of the surface energy for the solid surface and the interactive test compounds, respectively. Equation (23) can be rewritten to yield the dispersive surface energy as follows:

$$\gamma {\text{S}}^{\text{d}} { = }\left[ {\tfrac{ 1}{{ 4 { }\gamma {\text{CH}}_{ 2} }}} \right] \, \left[ {\tfrac{{ (\Delta G_{\text{a}}^{\text{CH2}} )^{2} }}{{(N. \, a_{{CH_{2} }} )^{2} }}} \right]$$

(24)

where γ_CH2 is the surface energy of a hydrocarbon consisting only of n-alkanes, a_CH2 is the area of one –CH2– group. Equation (24) usually tests the IGC method for obtaining the dispersive surface energy of polymers.