Heritability of telomere length in the Zebra Finch

Abstract

Telomere length predicts survival in birds, and many stressors that presumably reduce fitness have also been linked to telomere length. The response to selection of telomere length will be largely determined by the heritability of this trait; however, little is known about the genetic component of telomere length variation in animals other than humans. Moreover, published heritability estimates of telomere length are based on telomere measurements with techniques that do not distinguish between terminal telomeres, which are susceptible to age and stress, and the interstitial telomeric repeats, which are relatively inert. Heritability estimates that combine interstitial and terminal telomeres are difficult to interpret in species such as birds, where interstitial telomeres are often numerous. We estimated the heritability of terminal telomere length in a captive Zebra Finch population of cross-fostered (half-)siblings using data obtained with an electrophoresis technique that excludes the interstitial repeats from the measurements. We used both a Bayesian quantitative genetic ‘animal’ model and a frequentist sibling regression approach to estimate heritability. With the animal model, we estimated a high heritability of telomere length (h ² = 0.99, 95 % credible interval = 0.87–1), but had insufficient statistical power to separate parental and permanent environment effects. The frequentist approach yielded similar heritability estimates, although with large confidence intervals. We used general linear mixed models to disentangle variance components of telomere length. The relative contributions of the individual, mother and father to telomere length variation were statistically indistinguishable at 23–31 %. Chicks were cross-fostered 4-days after hatching, and no effect of rearing nest was found, indicating that any undetected environmental effects exerted their influence prior to, or soon after, hatching. Thus, we conclude that telomere length resemblance between relatives is high and proportional to their relatedness, but we cannot conclusively distinguish between genetic and other forms of inheritance.

Zusammenfassung

Erblichkeit der Telomerlänge beim Zebrafink Taeniopygia guttata Anhand der Telomerlänge sind bei Vögeln Prognosen zur Überlebensdauer möglich, und viele Stressfaktoren, welche vermutlich die Fitness verringern, konnten ebenfalls mit der Telomerlänge in Verbindung gebracht werden. Wie die Telomerlänge auf Selektion reagiert, wird hauptsächlich von der Erblichkeit dieses Merkmales abhängen, allerdings weiß man mit Ausnahme des Menschen bislang nur wenig über die genetische Komponente der Telomerlängen-Variabilität bei Tieren. Darüber hinaus basieren veröffentlichte Schätzwerte für die Erblichkeit der Telomerlänge häufig auf Messwerten, welche mit Techniken erhoben wurden, die nicht zwischen terminalen Telomeren, welche anfällig für Alter und Stress sind, und den relativ inerten interstitiellen telomerischen Sequenzen unterscheiden. Schätzwerte für die Erblichkeit, die interstitielle und terminale Telomere zusammenfassen, sind bei solchen Arten wie den Vögeln, bei denen interstitielle Telomere oft zahlreich vorhanden sind, schwer zu interpretieren. Wir schätzten die Erblichkeit der terminalen Telomerlänge bei einer Volierenpopulation von Zebrafinken- (Halb-)geschwistern, die in Pflegenestern aufgezogen worden waren, anhand von Daten, die mit einer Elektrophoresetechnik gewonnen wurden, welche die interstitiellen Wiederholungselemente von den Messungen ausschloss. Zur Schätzung der Erblichkeit verwendeten wir sowohl ein Bayes’sches quantitatives genetisches Tiermodell als auch einen frequentistischen Geschwister-Regressionsansatz. Für das Tiermodell ergaben sich hohe Schätzwerte für die Erblichkeit der Telomerlänge (h ² = 0.99, 95 %-Kredibilitätsintervall = 0.87–1), dieses hatte allerdings nur eine unzureichende statistische Aussagekraft bei der Trennung von elterlichen Faktoren und ständigen Umwelteinflüssen. Der frequentistische Ansatz ergab ähnlich Erblichkeitsschätzwerte, jedoch mit großen Konfidenzintervallen. Wir verwendeten gemischte lineare Modelle (General Linear Mixed Models, GLMM), um die Varianzkomponenten der Telomerlänge aufzuschlüsseln. Der relative Anteil, den das Individuum beziehungsweise dessen Mutter und Vater zur Telomerlängen-Variabilität beitrugen, ließ sich statistisch nicht unterscheiden und lag zwischen 23–31 %. Vier Tage nach dem Schlüpfen wurden die Küken gegen solche aus einem anderen Nest ausgetauscht, es war aber kein Effekt des Aufzugnestes festzustellen, was darauf hindeutet, dass etwaige unbemerkte Umweltfaktoren vor oder kurz nach dem Schlupf zur Wirkung kommen. Wir schlussfolgern daher, dass die Ähnlichkeit der Telomerlänge zwischen Verwandten hoch ist und in Proportion zum Verwandtschaftsgrad steht; wir können aber nicht mit Sicherheit zwischen genetischer und anderen Formen der Erblichkeit unterscheiden.

Introduction

Telomeres are non-coding repeats of the highly conserved DNA sequence 5′-TTAGGG-3′ (Meyne et al. 1989) that are important in the protection and stabilization of linear chromosomes (Blackburn 1991). Because of the end replication problem, the fact that DNA polymerase is not able to completely replicate the 3′ end of the DNA strand, and other contributing factors such as oxidative stress, telomeres tend to shorten with age (Olovnikov 1973; von Zglinicki 2002). Telomere shortening can be accelerated by various forms of stress encountered throughout life (Epel et al. 2004; Kotrschal et al. 2007; Gilley et al. 2008; Bauch et al. 2013; Boonekamp et al. 2014). Short telomeres eventually lead to replicative senescence of the cell (Blackburn 2005), and individuals with longer telomeres have a higher probability of survival in numerous species (Joeng et al. 2004; Haussmann et al. 2005; Bize et al. 2009; Salomons et al. 2009), including humans (Boonekamp et al. 2013). Furthermore, individual Zebra Finches with longer telomeres at the end of the nestling period have a longer lifespan (Heidinger et al. 2012). Therefore, telomeres have been suggested as biomarkers of the levels of stress that individuals have experienced over their lifetime (e.g. Monaghan 2014).

Given the association between telomere length and survival, it is of interest to unravel the causes of variation in telomere length. Variation in telomere length is determined by (1) initial telomere length in the zygote, (2) the rate of shortening and (3) the degree of telomere maintenance (Bischoff et al. 2005), and all three factors may be influenced by both genetic and environmental factors. Quantifying the contribution of genetics to the outcome of these processes (i.e., heritability) is important because it will determine the response to selection (Falconer and Mackay 1996; Visscher et al. 2008). New statistical methods also enable separation of individual phenotypes into genetic and environmental components (Kruuk and Hadfield 2007), allowing estimation of the importance of various factors in shaping the variation in a trait. Heritability of human telomere length has repeatedly been investigated, and heritability estimates are in the range of 0.36 to 1.28 (Table 1). Based on the largest data set, the heritability of telomere length was estimated at 0.70 (95 % CI 0.64–0.76, Broer et al. 2013), which falls close the mean of the other estimates. In five animal populations, heritability of telomere length was estimated to range from 0.09 to 1 (Table 1). The number of studies is low, however, and they differ widely in many respects (e.g., in estimate and measurement technique). Hence, our knowledge of the heritability of telomere length in non-human animals is limited.

Table 1 Published estimates of telomere length heritability

In the present paper, we report heritability estimates of telomere length in a population of captive Zebra Finches. Resemblance between relatives can have a genetic basis, but can also be due to a shared environment. In order to obtain an unbiased estimate of heritability, genetic and environmental effects need to be separated (Kruuk and Hadfield 2007). To reduce shared environment effects, we cross-fostered 75 % of the individuals 4 days after the first hatching in a nest, enabling us to separate birth and rear nest effects, at least from cross-fostering onwards. Furthermore, we used a sample containing both full siblings and half-siblings to separate covariance of different degrees of relatives statistically. Specifically, we included both maternal and paternal half-siblings to quantify parental effects. We estimated heritability with two methods. First we applied a so-called ‘animal’ model, a general linear mixed model using a pedigree of individuals in the data set, to estimate heritability (Kruuk 2004) in a Bayesian framework (Hadfield 2010). ‘Animal’ models have the advantage of using all relationships in the data set, but the disadvantage of being data consuming. Second, we used frequentist methods to calculate intraclass correlations and heritabilities comparing both full and half sibships to investigate parental effects (Falconer and Mackay 1996). Finally, we disentangled environmental and parental effects on telomere length with general linear mixed models (GLMM).

In contrast to humans, many avian species have numerous interstitial telomeric repeats, which are in addition to ‘terminal’ telomeric repeats (Delany et al. 2000; Foote et al. 2013). Terminal telomeres are susceptible to ageing and environmental factors and are involved in the protection and stabilization of the chromosomes. Although there is evidence that interstitial telomeric repeats are involved in DNA repair, chromosome stabilization and the regulation of gene transcription, the exact function is not yet fully understood (Kilburn et al. 2001; Rivero et al. 2004; Yang et al. 2011). It is also not known whether interstitial telomeric repeats change in length within an animal’s lifetime, given that this would involve two double strand breaks. The number of interstitial telomeric repeats and the length of terminal telomeres are therefore in essence different traits, despite their superficial similarity. Laboratory techniques differ in the type of telomeres included in the measurements, and published heritability estimates are based on techniques that pool interstitial and terminal telomeric repeats in one estimate (qPCR, southern blot; Table 1). Thus, it is not known to what extent published heritability estimates in species other than humans provide information on variation in interstitial versus terminal telomeres (there are few interstitial repeats in the human genome). We therefore measured telomeres with in-gel hybridization, labelling the single-stranded overhang of telomeres (Haussmann and Vleck 2002), i.e., the telomeric loop at the end of linear chromosomes that is an evolutionary, well-conserved aspect of telomere biology (Stansel et al. 2001). Hence, we measure only terminal telomeres (see “Materials and methods” for details), and our heritability estimates are specifically for terminal telomeres only.

Materials and methods

Study species and sampling

We used 125 Zebra Finches (66 females; 57 males), originating from 73 broods, reared from stock that were part of a long-term experiment, in which natal brood size and energy expenditure required for foraging were manipulated (De Coster et al. 2011; Koetsier and Verhulst 2011). With respect to the foraging cost manipulation, we only used control birds that had easy access to food. Parents were paired randomly and housed in pairs during breeding; hence, paternity was known with certainty. The inbreeding level is low in our Groningen Zebra Finch population (Forstmeier et al. 2007). Four days after the first chick of a brood hatched, we conducted a brood size manipulation, in which brood size was standardized to either 2 or 6 young (both within the natural range). Our aim was to cross-foster all individuals in this procedure, but due to logistic constraints, we cross-fostered 75 % of the chicks (N = 94).

We measured telomere lengths in DNA from red blood cells. Blood was collected from the brachial vein into heparinised capillaries. Samples were suspended in 2 % EDTA buffer, and within 2 days the red blood cells were spun down, and the pellet was stored in glycerol buffer at −80 °C after snap freezing. We used blood samples collected in 2006–2010. Storage time prior to analysis (0–6 years) did not affect telomere length (F _6,152 = 0.66, p = 0.68). The samples were analysed, divided over seven gels, and timing (batch) of analysis did not affect telomere measurements (F _6,152 = 1.48, p = 0.19). Hence, storage time and timing of analysis were not included in the analyses.

On average, individuals were 132 days old (SE = 11.6, range = 9–636) when a blood sample was collected. For 18 individuals, we analysed two to three samples, as these individuals were sampled multiple times in life, resulting in a total of 158 telomere length estimates. On average, the samples after the first sample were taken at an age of 940 days (SE = 52.5, range = 609–1572). To simplify the models for estimating heritability, and because we had repeated measurements of only a subset of all individuals (18 out of 125 individuals), we used the average telomere length as a Terminal Restriction Fragment (TRF) estimate per individual to calculate heritability. In order to estimate variance components that might influence phenotypic similarity, we used the complete data set, including repeated measurements. Because telomere length generally declines with age, we controlled for age in all analyses.

TRF assay

The TRF assay was conducted following Salomons et al. (2009). In summary, 5 μl of red blood cells were suspended in an agarose solution to form an agarose plug (0.8 %; following the manufacturer’s protocol, CHEF Mammalian Genomic DNA Plug kit, Bio-Rad Laboratories, Inc., USA). The cells in half a plug were digested overnight at 50 °C with Proteinase K. DNA was then digested overnight at 37 °C using a mixture of three restrictions enzymes, HindIII (60 U), HinfI (30 U) and MspI (60 U), in NEB2 buffer (New England Biolabs, Inc., Beverly MS, USA).

The restricted DNA and the size standards (Molecular Weight Marker XV, Roche and 1 kb DNA ladder, New England Biolabs) were electrophoresed through a 0.8 % agarose gel by pulsed field gel electrophoresis at 14 °C for 24 h (3.5 V/cm, initial switch time 0.5 s, final switch time 7.0 s). Gels were dried with a gel dryer (Bio-Rad, model 538) and hybridized overnight with ³²P-labelled oligo (5-CCCTAA-3)₄, which labelled the single-stranded overhang of the telomeres. Since the DNA was not denatured as in Southern blot techniques, no ³²P-labelled oligo marked interstitial repeats. The radioactive signal of the marker was detected by a phosphor screen (PerkinElmer Inc., USA), and analysed using a phosphor imager (Cyclone TM Storage Phosphor System, PerkinElmer).

Telomere length varies among cells and chromosomes (Lansdorp et al. 1996); and hence, the TRF assay results in a smear, instead of a clear band. The distribution of telomere lengths was calculated based on densitometry (Haussmann and Mauck 2008) in the open-source software IMAGEJ v. 1.38x (Salomons et al. 2009). The average labelled telomere length per lane was calculated as: Σ (OD _i  × L _i )/Σ (ODi), where OD _i is the optical density output at position i, and L _i is the length of the DNA (bp) at position i. OD is corrected for the background by subtracting the average grey value of non-DNA containing gel in IMAGEJ. Our lower limit was 2.3 kb, which falls within the smallest band of the 1 kb DNA ladder, which is 1 kb, and our upper limit was an extrapolated value of 80 kb based on the Molecular Weight Marker XV, which has a range of 2.4–48.5 kb, because telomere lengths of the Zebra Finches exceeded the Molecular Weight Marker XV. Note, however, that the extrapolation comprised < 1.5 cm on the gel (±7 % of the total length used), and that there was a strong correlation between calculations of telomere length based on the Molecular Weight Marker XV (up to 48.5 kb) and the same samples quantified with the extrapolated marker (up to 80 kb) (r = 0.82). Based on the repeated measures of 18 individuals, individual variation in TRF assays was 78 % of the total variance in telomere lengths. Since repeat abilities of our TRF assays are high (Jeanclos et al. 2000; Haussmann and Mauck 2008; Salomons et al. 2009) and the analysis is time consuming, all samples were run once.

Statistical analyses

We compiled a pedigree using the Groningen Zebra Finch database. Data on ancestry were available for four generations of birds, with the earliest records dating back to 2004. We used pedigree data pruned back to the 125 phenotyped individuals, plus 143 unphenotyped individuals linking the phenotyped birds. The pedigree contained 112 individuals in a full sibling relationship, 45 maternal half-siblings and 62 paternal half-siblings. Half-sibling comparison facilitated attempts to separate genetic and environmental components. We over-represented paternal half-siblings in our data collection, because females lay the eggs and may thereby potentially exert a greater environmental influence on offspring telomere length, and we were primarily interested in the genetic component of the variance. For further details of the pedigree, see Table S1 (Supplementary material).

We calculated the heritability of telomere length with an ‘animal’ model (Kruuk 2004), using a Bayesian approach (Hadfield 2010), estimating the posterior mode and 95 % credible intervals (95 % Cred. Int.) for fixed effects, variance components and heritability. In short, an ‘animal’ model uses a pedigree to calculate the proportion of the phenotypic variance that is due to additive genetic effects, by comparing the covariance due to additive genetic effects in a phenotype between relatives. We calculated heritability using the package MCMCglmm (2.15) in R 2.14.1 (Hadfield 2010; R Development Core Team 2011) with 10,000,000 iterations, a burn-in of 2500,000 and a thinning interval of 5000. Autocorrelation between sampled iterations was < 0.08. We used default priors for fixed effects, parameter expanded priors for the random variance structure (variance = 1, degree of belief = 1, prior mean = 0, prior covariance matrix = 500), and non-informative inverse-Wishart priors for the residual variance structure (variance = 1, degree of belief = 0.002). We applied several different prior distributions to confirm that our estimate of additive genetic variance was robust to prior specification.

Telomere length was normally distributed (Shapiro–Wilk W = 0.989, p = 0.25, N = 158). Exploratory analyses indicated that including sex and the logarithm of age (we log-transformed age because telomeres shorten faster early in life) as fixed effects improved our model fit. For individuals with an average telomere length of multiple TRF estimates, we used the logarithm of the average age at sampling. Because the data set did not have sufficient power to discriminate between the random variance components explaining environmental (birth nest and permanent environment, meaning an individual’s own common environment) and parental effects, we used a naïve model including only the pedigree component as a random effect. We therefore estimated the variance components as:

$$V_{\text{P}} = V_{\text{A}} + V_{\text{R}}$$

(1)

where V _P is the phenotypic variance, accounting for the fixed effects of sex and the logarithm of the age at which an individual was sampled; V _A is the additive genetic variance and V _R the residual variance. We then calculated heritability as:

$$h^{2} = \frac{{V_{\text{A}} }}{{V_{\text{P}} }}$$

(2)

We compared h ² from the ‘animal’ model with the heritability estimate based on the intraclass correlations for sibships (Falconer and Mackay 1996), to evaluate robustness of our findings. The individual least square mean estimate of telomere length was used from a model including the logarithm of age. For the full sibling comparison, we used a general linear mixed model (GLMM) with family identity as a random effect, where a family is defined as a set of full siblings. Second, we made a half-sibling comparison in a subset of the data containing half-siblings, by building a GLMM with either mother identity or father identity as a random effect. Here we used a mean value of telomere length for each birth nest, to prevent our estimate from being biased by pseudo-replication by full siblings. This approach allowed us to compare similarity between maternal- and paternal half-siblings, testing for a trans-generational effect from mother or father. Sample sizes for all sibling relationships can be found in Table 4. Some of the individuals in the full sibling comparison were also included in the maternal (N = 14) and paternal (N = 31) half-sibling comparison. Following Falconer and Mackay (1996) equation 9.8, heritability in the full sibling data set was calculated by multiplying the correlation between full siblings by two:

$$t_{\text{FS}} = \frac{{\frac{1}{2}V_{\text{A}} + \frac{1}{4}V_{\text{D}} }}{{V_{\text{P}} }}$$

(3)

where t _FS is the correlation between full siblings and V _D the dominance variance. In general V _D is relatively small compared to V _A, and hence could be ignored (Falconer and Mackay 1996). This was confirmed by the similarity of our heritability estimates of full siblings and half-siblings (see “Results”). Heritability using the half-sibling data set was calculated by multiplying the correlation between half-siblings by 4, according Falconer and Mackay (1996) (equation 9.6)

$$t_{\text{HS}} = \frac{1}{4}\frac{{V_{\text{A}} }}{{V_{\text{P}} }}$$

(4)

where t _HS is the correlation between half-siblings.

As we could not include random effects in the ‘animal’ model, nor separate variance components in the intraclass correlations, we estimated variance components that may influence phenotypic similarity in telomere length with a GLMM. We ran a GLMM with sex and the logarithm of age as fixed effects, where our response was telomere length at a given age, rather than one averaged value, and included individual as random effect in the model. In Table 2, we describe which environmental and genetic effects are embedded in each variance component. We defined phenotypic variance components as significantly different from zero if their confidence intervals (CI) did not overlap with zero.

Table 2 Separation of phenotypic variance components into genetic, environmental and parental effects

Ethics statement

The brood size manipulations and long term foraging experiment with Zebra Finches, including blood sampling, have been approved by the animal welfare ethics committee of the University of Groningen (according to Dutch law), under license number 5150.

Results

With our ‘animal’ model, we estimated a high additive genetic variance (V _A) in telomere length, with a heritability of 0.999 (95 % Cred. Int. = 0.87–1). Few repeated measures meant that we could not partition permanent environment effects, but as the chicks were cross-fostered, these are predicted to be small. Despite our study design containing various degrees of relatedness (siblings, and maternal and paternal half-siblings, Table S1), there was not enough power to partition parental (genetic and environmental) effects. Extended models including additional variance components did not converge, due to low sample sizes and a shallow pedigree. Therefore we used a naïve ‘animal’ model, and hence our estimate of heritability may be confounded by environmental or parental effects, which may have inflated our estimate. We found no sex effect and a trend of a negative logarithm of age effect on telomere length (Table 3). Telomere length generally declines with age, but our finding that age yielded only a trend in this analysis was not unexpected, since we used a cross-sectional design, and between-individual variation is large while variation in age within the data set was intentionally small.

Table 3 Mode of the posterior distribution and 95 % credible intervals for the different parameters in the ‘animal’ model

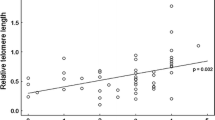
To test for robustness of our estimate, we calculated heritability with GLMMs based on cross-fostered full sibling and half-sibling intraclass correlations. Also with this approach we found high heritabilities, confirming the results of the ‘animal’ model (Table 4; Fig. 1). The three estimates were very similar, but CI were large, and only the estimate based on full siblings (with the largest sample size) yielded a 95 % CI that did not include zero. Based on this 95 % confidence interval of the full sibling estimate, the minimum estimate of the heritability is 0.46, assuming no V _D, while the maximum estimate exceeds 1.

Table 4 Heritability estimates based on the intraclass correlations of telomere length corrected for sex and age

Fig. 1

Correlations between full siblings (N = 42) (a) and half-siblings (b); closed dots maternal half-siblings (N = 8); and open dots paternal half-siblings (N = 18). Lines are linear regressions. To avoid pseudo replication due to shared maternal or paternal descent, both graphs depict a random selection of sibling pairs in cases where there were more than two phenotyped siblings, whereas in the analyses, all individuals from a family are incorporated with family as a random effect

Applying GLMMs including repeated telomere measurements enabled us to separate different variance components. In all models (Fig. 2; Table 5), we found an effect of the individual. In model two, we compared effects of the pre-cross foster natal environment (which may include parental effects) with post-cross foster rear nest environment (94 out of 125 individuals were cross-fostered). We found no effect of rear nest identity in this or any subsequent model, indicating that pre-manipulation effects (both genetic and environmental) were more important in determining telomere length than post-manipulation effects. Also, no effect of manipulated brood size was found in any of our models (e.g., in model 4, Fig. 2: F _1,55.75 = 0.18; p = 0.67). Therefore, brood size was not included in our final analyses. Birth nest includes multiple potential variance components, e.g., shared environment, maternal and paternal effects. When adding parental identity (model three), the variance explained by birth nest went down to zero, with mother and father identity taking over this effect, i.e., trans-generational parental effects were important, while characteristics of that specific breeding event explained no additional variation. Mother and father identity contributed substantially and about equally to telomere length variation, as also shown by the correlational approach in the (half) siblings (Fig. 1). Together, mother and father identity explained over two times more variation than individual identity, indicating that additive genetic and common natal environment effects were substantially more important in determining telomere length than other permanent events over the whole lifetime. Based on the log likelihood (Fig. 2) and significance of the variance components, we considered model 4 biologically most parsimonious. This implied that it is likely that the individual (which contains the additive genetic variance and a permanent environment effect), and mother and father (which contain the additive genetic variance and a parental environment effect) all contributed about equally to variation in telomere length.

Fig. 2

Variance components of telomere length, from four GLMMs. Plus depicts significant variance components for which the confidence interval (CI) does not overlap with zero and (plus) variance components for which the CI just overlaps zero (<1 %). The numbers above the bars are the log likelihoods of each model

Table 5 Estimates for percentage of phenotypic variance explained, with 95 % CI per variance component and estimates for the fixed effects (sex coded as 1 = female, 2 = male, reference is female) with standard error and p value in four different GLMMs of telomere length

Discussion

We estimated the heritability of terminal telomere length in Zebra Finches, and find it to approach 1, independent of the type of numerical approach [‘animal’ model or (half-)sibling comparison]. We found no effects of rear nest identity, suggesting that possible environmental agents exerted their effects very early in life. Most phenotyped offspring were cross-fostered at a young age, but cross-fostering of chicks does not control for parental effects arising during laying, incubation and in the few days after hatching that they spent in their natal nest. Pre-natal environmental effects on telomere length can, for example, include endocrinology aspects of egg composition (Haussmann et al. 2012), and we cannot exclude that such effects increased the resemblance between (half-)siblings in our study. On the other hand, the mother primarily determines egg characteristics, and effects of father and mother identity on offspring telomere length were indistinguishable in our study (Table 5, model 4). This argues against a large effect of egg characteristics causing telomere length resemblance between offspring, making a quantitative genetic basis of the observed resemblance between relatives more likely. Furthermore, heritability estimates based on full siblings (1.18) and paternal half-siblings (0.93) were of similar magnitude (albeit with large CI, Table 4), lending further support to the tentative conclusion that telomere length resemblance between relatives was primarily due to genetic effects. We acknowledge, however, that larger sample sizes and/or a deeper pedigree are required to more definitely draw this conclusion.

Our study distinguishes itself from earlier reports in that we specifically measured terminal telomeres, while in previous studies (Table 1), interstitial and terminal telomeres were pooled due to the technique used to measure telomere length. This is of importance, because terminal telomeres are susceptible to ageing and predictors of survival, while interstitial telomeric repeats are, as far as we know, inert within the lifetime of an individual. It is not obvious what the effect of measurement technique will be on heritability estimates, because this depends on (1) the reliability of the measurement technique, and whether this is accounted for in the analysis; and (2) contribution of the interstitial repeats versus terminal telomeres to the total variance in telomeric repeats between individuals. For example, interstitial repeats are infrequent in humans, and in this respect, the measurement technique should have little effect on telomere length heritability estimates in humans. In avian species, however, the frequency of interstitial repeats is frequently high (Foote et al. 2013), and it remains to be investigated to what extent published heritability estimates (Table 1) can be attributed to variance in interstitial repeats versus terminal telomeres. To resolve this issue, additional studies in which the heritability can specifically be assigned to either interstitial telomeric repeats and/or terminal telomeres are required.

Terminal telomeres shorten with age, and these dynamics are at least to some extent under the influence of environmental effects (e.g., Boonekamp et al. 2014). This could have increased family resemblance in our study (Rossiter 1996), because all birds were housed in similar aviaries, reducing environmental variation later in life, in particular in comparison with free-living animals. However, such homogenizing environmental effects in all likelihood did not have a large effect on our estimates, since we found no effect of rear nest, and permanent environment explained approximately one-quarter of the variance in telomere length (Table 5). Therefore, sharing the same genes and/or the pre-cross foster environment (including parental effects) were the strongest determinants of our heritability estimates. Individual differences in human telomere length persist over life (Benetos et al. 2013), and initial telomere lengths are determined in the zygote, with only a minor effect of epigenetic and/or environmental effects during life on resemblance of telomere length between relatives (Graakjaer et al. 2004). One pathway explaining the minor effect of late environment is via the telomere-elongating enzyme telomerase, which is involved in the process of maintaining telomere length in particular tissues during development. Serakinci et al. (2008) suggest that telomere dynamics in lymphocytes and mesenchymal stem cells show little random fluctuation and that telomerase possibly even further conserves the relative telomere lengths or profile between chromosome arms (Serakinci et al. 2008). It seems that specific patterns of telomere lengths are already determined in the embryo, and telomerase is an important determinant during life for resemblance of telomere lengths between relatives.

In humans (e.g. Broer et al. 2013), Kakapos (Horn et al. 2011) and King Penguins (Reichert et al. 2014), telomere length has a stronger maternal than paternal inheritance; however, in Sand Lizards (Olsson et al. 2011), stronger paternal inheritance was found, although CI overlapped (Table 1). In contrast, we found no evidence for a difference between maternal and paternal effects in our study (Tables 4, 5). The non-human studies have relatively small sample sizes compared to the human studies, and used—except for the Great Reed Warbler study, which used an ‘animal’ model—parent-offspring regression, which is unable to separate environmental variance from genetic components. The human study included both parent-offspring regression and twin studies, which also do not separate environmental factors. Furthermore, in humans, a positive association with paternal age was demonstrated, whereas this was negative in Sand Lizards. Thus, the results on parental effects are mixed, and for non-human species in particular, there is a need for more studies.