Abstract
Objective
To investigate the effect of inter-operator variability in arterial input function (AIF) definition on kinetic parameter estimates (KPEs) from dynamic contrast-enhanced (DCE) MRI in patients with high-grade gliomas.
Methods
The study included 118 DCE series from 23 patients. AIFs were measured by three domain experts (DEs), and a population AIF (pop-AIF) was constructed from the measured AIFs. The DE-AIFs, pop-AIF and AUC-normalized DE-AIFs were used for pharmacokinetic analysis with the extended Tofts model. AIF-dependence of KPEs was assessed by intraclass correlation coefficient (ICC) analysis, and the impact on relative longitudinal change in Ktrans was assessed by Fleiss’ kappa (κ).
Results
There was a moderate to substantial agreement (ICC 0.51–0.76) between KPEs when using DE-AIFs, while AUC-normalized AIFs yielded ICC 0.77–0.95 for Ktrans, kep and ve and ICC 0.70 for vp. Inclusion of the pop-AIF did not reduce agreement. Agreement in relative longitudinal change in Ktrans was moderate (κ = 0.591) using DE-AIFs, while AUC-normalized AIFs gave substantial (κ = 0.809) agreement.
Discussion
AUC-normalized AIFs can reduce the variation in kinetic parameter results originating from operator input. The pop-AIF presented in this work may be applied in absence of a satisfactory measurement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Dynamic contrast-enhanced (DCE) magnetic resonance imaging (MRI) is increasingly being used to assess microvascular properties of tissue in oncology and has proven well suited to quantify brain tumor hemodynamics and damage to the blood–brain barrier. DCE-MRI is a technique in which a series of T1-weighted images is rapidly acquired before, during and after the administration of a paramagnetic contrast agent (CA) [1]. Using pharmacokinetic (PK) modelling, these dynamic images allow for the quantification of kinetic biomarkers that are of use in the evaluation of tumors. The most commonly used PK model in high-grade glioma (HGG) diagnostics is the extended Tofts model [2], which describes the tissue by the rate constants Ktrans and kep as well as the volume fractions ve and vp.
Quantitative descriptors of tumor vasculature that—in theory—can be obtained independently of equipment and technique, would be a very powerful tool in disease management and monitoring. However, DCE-MRI suffers from a lack of reproducibility across different imaging sites. This is due to several potential sources of error, including inadequate temporal resolution, insufficient acquisition time frame [3], pre-contrast T1 measurement uncertainty [4, 5] and difficulty in determining the dynamic CA concentration in plasma (Cp)—the arterial input function (AIF) [6, 7].
Different approaches exist for determining the AIF, including fully automatic algorithms [8], semi-automatic methods [9], manual selection and the use of standard models [10]. It is generally accepted that the AIF is dependent on cardiac output, blood pressure and vascular auto-regulation in the region-of-interest []. The gold standard for DCE-MRI imaging is thus an individual AIF from each time-point in each patient measured in a feeding artery of the pathology/region-of-interest (ROI). The accuracy of this AIF varies by the temporal resolution, potential partial volume effects from low spatial resolution [11] and inter-observer variability from manual selection.
The aim of this study was to investigate the inter-observer variability, among domain experts (DEs), in AIF determination and corresponding variability in kinetic parameters obtained using the extended Tofts model in HGG patients. Further, we define a parametric form of a population-averaged AIF from brain data according to the framework previously published [10].
Methods
Patients
Study approval was obtained from the regional medical ethics committee and patients were included only if written informed consent was signed. A total of 118 DCE-MRI examinations from 23 patients (17 males, mean age 53.7 years, range 32–66 years) with histologically confirmed HGG (one grade III and 22 grade IV) were included in a prospective study of early detection of perfusion changes during radiochemotherapy [12]. Patients were imaged once before, thrice during, and up to five times for a maximum of 15 months after initiation of standard treatment regime [13]. In the present work, the initial six imaging time-points in each patient, encompassing two post-radiochemotherapy follow-ups at two and 14 weeks, were considered for inclusion. Examinations were excluded if there were no contrast-enhancing voxels (N = 2) or if DCE-MRI was not successful (N = 18), resulting in a total of 118 included examinations. A surgical debulking procedure was performed in 22 patients prior to baseline imaging, whilst the remainder received biopsy.
MRI
All imaging was performed at 3.0 T (Philips Achieva, Philips Medical Systems, Best, The Netherlands), using an eight-channel head coil. DCE images were acquired from a 3D- saturation recovery-based gradient echo sequence. The sequence was designed to minimize water exchange effects by employing a short saturation recovery delay (TD) [14]. Eleven slices covering the tumor volume were acquired with the following key sequence parameters: field of view (FoV): 240 × 240 mm2; acquisition matrix: 120 × 120; partial Fourier: 5/8; voxel size: 1.9 × 1.9 × 4 mm3; pixel bandwidth: 434 Hz; echo time (TE)/flip angle: 2.5 ms/26°; sensitivity encoding (SENSE) factor: 2.3 in the anterior–posterior phase-encoding direction. Two variants of the DCE sequence were used: one using repetition time (TR)/TD/temporal resolution: 8.2 ms/80 ms/3.4 s, 100 dynamic scans and scan time: 5:40 (variant 1) in seven patients for a total of 38 examinations, and one using TR/TD/temporal resolution: 5.1 ms/50 ms/2.1 s, 150 dynamic scans and scan time: 5:10 (variant 2) in 16 patients for a total of 80 examinations. 0.1 mmol/kg gadobutrol (Gadovist®, Bayer Schering Pharma AG, Berlin, Germany) was administered after a pre-contrast baseline duration of five timepoints using a power injector at a rate of 3 ml/s, immediately followed by a 20 ml saline flush at the same rate. The full imaging protocol included the following structural image series: sagittal 3D fluid-attenuated inversion recovery (FLAIR) images, axial 2D T2-weighted images and sagittal 3D T1-weighted gradient echo images acquired before and after CA administration. All image series were acquired before the DCE series except the CA-enhanced T1-weighted images which were acquired directly afterwards. Tumor region-of-interest (ROI) containing contrast-enhancing tissue was defined in all examinations by a radiologist (4 years of experience) using a previously described method [12, 15].
AIF extraction
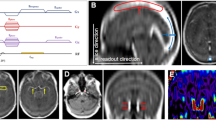
AIFs were determined independently in each DCE series by three DEs (two radiologists with 1 (J. V.) and 5 (M. Kim.) years of experience and one clinician with 10 years of experience in DCE-MRI (C. L.)) using a semi-automatic algorithm based on automated identification of most likely AIF voxels using K-means clustering from a user-defined search region, implemented in the software tool nordicICE (NordicNeuroLab, Bergen, Norway) [8]. The AIF search region was selected independently by each DE to include the large intracerebral arteries according to the tumor location and hence the available volume covered by the DCE acquisition. Since the K-means method is iterative with a random seed starting point, repeated AIF searches may not result in identical results. Hence, multiple AIF searches were performed for a selected search region and the AIF with the highest first-pass arterial signal peak and the highest signal tail during the wash-out phase was chosen. This process was repeated until the AIF was considered satisfactory by the DE. An overview of the process is given in Fig. 1. In addition, a venous output function from the large sinuses was obtained in each examination for AIF partial volume correction [3].
Outline of the arterial input function (AIF) extraction process. Top right: the search area (yellow rectangle) is placed in an area likely to contain arterial signal, and the algorithm selects the best pixels (red squares). The AIF is the mean signal of the selected pixels and is plotted in red. The venous output function is detected similarly and is plotted in blue along with mean tumor
The AIFs were supplied as single-column text files containing change in longitudinal relaxation rate \(\Delta {R}_{1}={R}_{1}\left(t\right)-{R}_{1}\left(0\right)\) from baseline for each timepoint t, which was converted to CA concentration by:
where r1 = 4.4 mM−1 s−1 is the relaxivity of gadobutrol at 3.0 T [16] and Hct is the hematocrit, set to 0.45. R1(0) of arterial blood at 3.0 T was assumed to be 0.60 s−1 [16].
This procedure resulted in a total of 354 DE-defined AIFs from 23 patients, of which 114 AIFs from seven patients were from DCE sequence variant 1 and the remaining 240 AIFs in 16 patients were from DCE sequence variant 2.
Population-averaged AIF
A population-averaged AIF (pop-AIF) was created by fitting the mean of all measured AIFs with DCE sequence variant 2 (N = 240 AIFs) to the sum of two Gaussians and an exponential modulated by a sigmoid function, as described by Parker et al. [10]:
Here, An are scaling factors, Tn are centers and σn are widths of the nth Gaussian; α and β describe the amplitude and slope of the exponential function, respectively, and s and τ are the width and center of the sigmoid. Prior to calculating the mean AIF, each individual AIF was time-shifted so that the peak occurred at the same timepoint.
Pharmacokinetic modeling
The DCE time series were analyzed using the extended Tofts model according to:
where Ct(t) is the time-dependent CA concentration in tissue, Cp(t) is the time-dependent CA concentration in blood plasma (the AIF), Ktrans is the flux of contrast agent from the intravascular space (IVS) to interstitium, kep is the flux of contrast agent back to the IVS, ve is the ratio of Ktrans and kep, denoting the fraction of extracellular, extravascular volume and vp is the fractional plasma volume.
From Eq. 3, it is evident that errors in the amplitude of \({C}_{\mathrm{p}}(t)\) will directly scale to corresponding errors in Ktrans and vp. Therefore, to assess the contribution of differences in AIF peak values, the analysis was repeated using AIFs normalized to an area under the curve (AUC) equal to the mean of all measured AIFs (600 mM s). Because each patient received the same CA dose at each imaging session, the AIF AUC is expected to remain constant, and normalization should therefore reduce variability in parameter estimates due to errors in measured peak AIF amplitudes, but at the cost of loss of absolute quantitative parameter estimates. Consequently, kinetic analysis was performed with seven different AIFs in each examination: three DE-supplied, the same three AUC-normalized and the pop-AIF obtained by fitting the mean AIF across all examinations to Eq. 2. From each analysis, the median parameter values from each tumor ROI were extracted and used for comparison. Voxels in which parameters ve or vp took an unphysiological value outside the range 0–100% was excluded from median calculation for all AIFs in that examination. The PK modelling and AIF analysis were performed in MATLAB 2020a (MathWorks, Natick, MA, United States).
Statistical analysis
AIF peak and AUC, as well as estimates of parameters Ktrans, kep, ve and vp, were used for statistical analysis. The median value of each parameter in each tumor ROI was used for analysis. AIF characteristics were assessed using Wilcoxon signed-rank test on the AIF peak and AUC of each DE-supplied AIF against each other (e.g. DE 1 vs DE 2; four combinations). Intraclass correlation coefficient (ICC) estimates with 95% confidence intervals (CI) were calculated based on an absolute-agreement, two-way random-effects model [17]. The ICC estimate evaluates the degree of inter-operator agreement in the KPE estimates within each examination, such that identical results from all AIFs in every examination would give ICC = 1. ICCs were estimated both using the complete dataset, and including only the examinations with DCE sequence variant 1 (N = 38) to assess the performance of the pop-AIF. To investigate the effect of different AIFs on predicting clinical outcome, the change in median Ktrans for each patient from the first to the sixth imaging time-point was compared using the measured DE-AIFs and the normalized variants. An increase or decrease of more than 10% was labeled as, respectively, progression or remission, and the scores were assessed with Fleiss’ kappa using linear weights. The kappa statistic was interpreted according to the Landis and Koch benchmarking scale [18]. ICC and Fleiss’ kappa statistics were performed using Stata SE 16.1 (StataCorp LLC, College Station, TX, United States) with the kappa, etc., command [19].
Results
Population-averaged AIF
Figure 2 shows the fitted population AIF together with the mean Cb(t). The fitted value for each AIF parameter (Eq. 2) is given in Table 1. The fitted AIF is seen to closely follow the mean AIF, with a first-pass peak followed by a smaller second-pass peak and subsequent washout. The standard deviation of the mean AIF demonstrates a higher variation in measured AIFs during the early phase than during washout. A comparison of the pop-AIF and DE-AIFs with resulting Ktrans maps is shown in Fig. 3.
Top: measured (left) and normalized (right) AIFs from each domain expert (DE) in a sample examination, with the time-aligned population AIF (pop-AIF) (11). Bottom: resulting tumor Ktrans maps overlaid on structural post-contrast T1 images. The Ktrans color scale ranges from 0.0 to 0.4 min−1. Median Ktrans of the whole tumor for DE 1, 2 and 3 and pop-AIF was, respectively: 0.049 min−1, 0.053 min−1, 0.044 min−1, 0.101 min−1 (measured AIFs) and 0.071 min−1, 0.067 min−1, 0.071 min−1 and 0.080 min−1 (normalized AIFs)
Statistical analysis
The AIF peaks were found to be significantly different between all domain experts (p = 0.03), while AUC was found to be different between DE 2 and 3 (p < 10–8), but not between 1 and 2 (p > 0.80) or 1 and 3 (p > 0.14).
Table 2 shows ICC for median kinetic parameter values from the 118 examinations. There is a moderate to substantial agreement for all kinetic parameters when using the measured AIFs [18]. Inclusion of the pop-AIF yields a lower agreement estimate for kep, while the other parameters are negligibly affected. The normalized AIFs give an almost perfect (0.8–1.00) agreement for parameters Ktrans and ve, while vp ‘s agreement is substantial (0.61–0.80). As expected, kep is the least affected by normalization of the AIF, as it is not sensitive to the AIF amplitude [20]. Table 3 shows the same ICC estimates calculated from only the examinations using DCE sequence variant 1 and demonstrates a similar relationship between ICC estimates with and without inclusion of the pop-AIF.
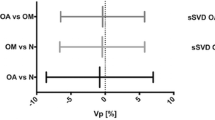
Figure 4 shows the relative Ktrans change from baseline to the sixth exam for two sample patients that demonstrate different degrees of observer dependence. Panel B represents a worst-case scenario, where different DE-AIFs produce opposing estimates of disease progression.
When change in median Ktrans is segmented into remission (< 10%), status quo (− 10% ≤ and ≤ + 10%) and progression (> + 10%), Fleiss’ kappa (3 raters, 23 subjects) is calculated as 0.595 with a 95% CI of (0.363, 0.827) for the measured AIFs, suggesting a fair to moderate agreement, while the normalized counterparts yield a kappa of 0.809 with CI (0.661, 0.958), suggesting a substantial to almost perfect agreement.
Discussion
The aim of the present work was to investigate the effect of differences in user-defined AIFs on kinetic parameters estimated from DCE using the extended Tofts model on data from HGG patients. Three experienced DEs individually produced AIFs for 118 examinations of 23 patients with HGG, following a common guideline that included the use of a semi-automatic detection algorithm. Additionally, a population-averaged AIF was fitted to a subset of the measured AIFs. A fixed T1(0) both in tissue and blood was assumed in all patients, and all analyses were performed at the same facility without input from the DEs other than their supplied AIFs. Therefore, the results of the kinetic analyses in this study should not be influenced significantly by factors other than the difference in AIFs.
The results in this study show moderate to substantial agreement in kinetic parameters estimated with AIFs from different DEs (Table 2). Agreement in estimated parameters is not substantially affected when the pop-AIF is included. This suggests that the pop-AIF represents an appropriate alternative to manually measured AIFs on a per-examination basis. The AUC-normalized DE-AIFs is seen to yield higher agreement in parameter estimates for Ktrans, ve and vp, as expected from the known sensitivity of these parameters to the AIF peak amplitude. The parameter kep depends more on the shape of the AIF [20] and is therefore virtually unaffected by the AIF normalization. This is in agreement with previous work investigating the effects of measuring the AIF for brain DCE in different vessels [21], which found a strong correlation between lower AIF peak and overestimation of all parameters except kep.
Comparing the relative change in parameter estimates over time as an indicator for disease progression shows that the use of AUC-normalized AIFs increases the agreement between DEs. The case presented in Fig. 4b represents a worst-case scenario where longitudinal change in Ktrans is labeled differently (progression, stable, remission) by each of the DE-AIFs, while all AUC-normalized DE-AIFs and the pop-AIF indicate progression. This demonstrates that a single DCE series can contain several clusters of voxels that produce subjectively acceptable, yet consequentially different AIFs. This operator-dependency is reduced with the AUC-normalized DE-AIFs and completely removed with the pop-AIF, at the cost of potential loss of relevant information.
Relative change in Ktrans in two sample patients from the first to the sixth exam estimated using AIFs from each domain expert (DE) and population AIF (pop-AIF) (11). a Patient with similar development in Ktrans with all DE-measured and population AIF. The largest absolute change with measured AIFs was − 0.016 min−1 (DE 2), and 0.0091 min−1 (DE 1) with normalized AIFs. b A patient where measured AIFs from the three DEs give diverging progression, while the normalized AIFs give a unidirectional progression. With measured AIFs from DE 1 the change is + 0.022 min−1, while normalized AIFs from DE 2 gives a change of − 0.014 min−1
The AIFs in this study were not accompanied by per-examination measurement of hematocrit, which is known to fluctuate significantly during chemotherapy treatment [22]. Hematocrit variations would lead to a true variation in AIF peak amplitude, which would not be reflected in the AUC-normalized AIF or the pop-AIF. However, if hematocrit values were available, this could be incorporated as an additional per-patient and per-examination scaling factor in the resulting AUC-normalized or population-based AIFs [23].
This study included data acquired with two slightly different DCE-MRI sequences, differing in TR, TE, TD and number of dynamic scans. The pop-AIF was derived using only data from the sequence variant with the largest number (variant 2, N = 220) of scans. To confirm that this pop-AIF was valid for both sequence variants, the ICC was compared including either all data from both sequences and only data from sequence variant 1. The results (Tables 2, 3) show that agreement is equally affected when including the pop-AIF in both datasets, indicating that the pop-AIF can be used on data acquired with sequence parameters deviating from the ones used when defining the pop-AIF.
One major challenge with the DCE-MRI field is lack of standardization between sites and studies. Although white papers suggesting standards for MRI protocol and analysis exist [2], there is still a substantial variation in both acquisition and analysis methods in the published data, making comparison of quantitative parameter estimates challenging. In treatment response studies, like the one presented here, the absolute values of the kinetic parameters may be of less importance and the emphasis should be on the ability of a given method to accurately detect parameter changes during the course of disease progression and treatment response. This is in line with previous findings in a large multicenter study concerning prostate cancer [7]. Our results suggest that this can readily be achieved through a combination of standardized and fixed protocols for AIF determination and a fixed imaging protocol over time. Further, and more importantly, our results suggest that the derivation of a population-wide AIF derived from the mean of many DCE-MRI examinations acquired on the same system provides a good alternative to the need for time-consuming identifications of individual AIFs by domain experts. It is, however, important to stress that such population AIF may need to be adjusted according to site-specific variations in MRI protocol and scanner type. Still, the population AIF obtained here, based on the same functional form as previously suggested by Parker for abdominal use [10], may form the basis for a similar pop-AIF for use in brain DCE-MRI applications.
In conclusion, normalizing the measured AIFs to a reasonable AUC can serve to reduce the variation in kinetic parameter results that stem from operator input. Further, using a parametric population AIF for the brain as presented in this study may be applied in absence of a satisfactory measurement in kinetic parameter estimation from DCE-MRI data in HGG patients.
Abbreviations
- AIF:
-
Arterial input function
- AUC:
-
Area under the curve
- CA:
-
Contrast agent
- DCE:
-
Dynamic contrast-enhanced
- DE:
-
Domain expert
- FLAIR:
-
Fluid-attenuated inversion recovery
- HGG:
-
High-grade glioma
- IVS:
-
Intravascular space
- KPE:
-
Kinetic parameter estimate
- MRI:
-
Magnetic resonance imaging
- PK:
-
Pharmacokinetic
- Pop-AIF:
-
Population-averaged AIF
- ROI:
-
Region-of-interest
- TD:
-
Saturation recovery delay
- TE:
-
Echo time
- TR:
-
Repetition time
References
Larsson HBW, Stubgaard M, Frederiksen JL, Jensen M, Henriksen O, Paulson OB (1990) Quantitation of blood-brain barrier defect by magnetic resonance imaging and gadolinium-DTPA in patients with multiple sclerosis and brain tumors. Magn Reson Med 16:117–131
Tofts PS, Brix G, Buckley DL, Evelhoch JL, Henderson E, Knopp MV, Larsson HBW, Lee TY, Mayr NA, Parker GJM, Port RE, Taylor J, Weisskoff RM (1999) Estimating kinetic parameters from dynamic contrast-enhanced T1- weighted MRI of a diffusable tracer: standardized quantities and symbols. J Magn Reson Imaging 10:223–232
Larsson C, Kleppestø M, Rasmussen I, Salo R, Vardal J, Brandal P, Bjørnerud A (2013) Sampling requirements in DCE-MRI based analysis of high grade gliomas: simulations and clinical results. J Magn Reson Imaging 37:818–829
Larsson C, Kleppestø M, Grothe I, Vardal J, Bjørnerud A (2015) T 1 in high-grade glioma and the influence of different measurement strategies on parameter estimations in DCE-MRI. J Magn Reson Imaging 42:97–104
Heye T, Boll DT, Bashir MR, Merkle EM (2012) Impact of precontrast T1 relaxation times on DCE-MRI pharmacokinetic parameters: T1 mapping versus a fixed reference value. Proc Intl Soc Mag Reson Med 20:1961
Keil VC, Mädler B, Gielen GH, Pintea B, Hiththetiya K, Gaspranova AR, Gieseke J, Simon M, Schild HH, Hadizadeh DR (2017) Intravoxel incoherent motion MRI in the brain: impact of the fitting model on perfusion fraction and lesion differentiability. J Magn Reson Imaging 46:1187–1199
Huang W, Chen Y, Fedorov A, Li XX, Jajamovich GH, Malyarenko DI, Aryal MP, Laviolette PS, Oborski MJ, O’Sullivan F, Abramson RG, Jafari-khouzani K, Afzal A, Tudorica A, Moloney B, Gupta SN, Besa C, Kalpathy-Cramer J, Mountz JM, Laymon CM, Muzi M, Kinahan PE, Schmainda K, Cao Y, Chenevert TL, Taouli B, Yankeelov TE, Fennessy F, Li XX, Sullivan FO, Abramson RG, Jafari-khouzani K, Afzal A, Tudorica A, Moloney B, Gupta SN, Besa C, Kalpathy-Cramer J, Mountz JM, Laymon CM, Muzi M, Kinahan PE, Schmainda K, Cao Y, Chenevert TL, Taouli B, Yankeelov TE, Fennessy F, Li XX (2016) The impact of arterial input function determination variations on prostate dynamic contrast-enhanced magnetic resonance imaging pharmacokinetic modeling: a multicenter data analysis challenge. Tomography 5:56–66
Mouridsen K, Christensen S, Gyldensted L, Østergaard L (2006) Automatic selection of arterial input function using cluster analysis. Magn Reson Med 55:524–531
Bjørnerud A, Emblem KE (2010) A fully automated method for quantitative cerebral hemodynamic analysis using DSC–MRI. J Cereb Blood Flow Metab 30:1066–1078
Parker GJM, Roberts C, Macdonald A, Buonaccorsi GA, Cheung S, Buckley DL, Jackson A, Watson Y, Davies K, Jayson GC (2006) Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magn Reson Med 56:993–1000
Chen J, Smith M, Frayne R (2005) The impact of partial-volume effects in dynamic susceptibility contrast magnetic resonance perfusion. J Magn Reson Imaging 22:390–399
Larsson C, Groote I, Vardal J, Kleppestø M, Odland A, Brandal P, Due-Tønnessen P, Holme SS, Hope TR, Meling TR, Fosse E, Emblem KE, Bjørnerud A (2020) Prediction of survival and progression in glioblastoma patients using temporal perfusion changes during radiochemotherapy. Magn Reson Imaging 68:106–112
Stupp R, Hegi ME, Gilbert MR, Chakravarti A (2007) Chemoradiotherapy in malignant glioma: standard of care and future directions. J Clin Oncol 25:4127–4136
Larsson HBW, Rosenbaum S, Fritz-Hansen T (2001) Quantification of the effect of water exchange in dynamic contrast MRI perfusion measurements in the brain and heart. Magn Reson Med 46:272–281
Odland A, Server A, Saxhaug C, Breivik B, Groote R, Vardal J, Larsson C, Bjørnerud A (2015) Volumetric glioma quantification: comparison of manual and semi-automatic tumor segmentation for the quantification of tumor growth. Acta radiol 56:1396–1403
Shen Y, Goerner FL, Snyder C, Morelli JN, Hao D, Hu D, Li X, Runge VM (2015) T1 relaxivities of gadolinium-based magnetic resonance. Invest Radiol 50:330–338
Koo TK, Li MY (2016) A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J Chiropr Med 15:155–163
Landis JR, Koch GG (1977) The measurement of observer agreement for categorical data. Biometrics 33:159
Klein D (2018) Implementing a general framework for assessing interrater agreement in stata. Stata J 18:871–901
Li X, Cai Y, Moloney B, Chen Y, Huang W, Woods M, Coakley FV, Rooney WD, Garzotto MG, Springer CS (2016) Relative sensitivities of DCE-MRI pharmacokinetic parameters to arterial input function (AIF) scaling. J Magn Reson 269:104–112
Keil VC, Mädler B, Gieseke J, Fimmers R, Hattingen E, Schild HH, Hadizadeh DR (2017) Effects of arterial input function selection on kinetic parameters in brain dynamic contrast-enhanced MRI. Magn Reson Imaging 40:83–90
Groopman JE, Itri LM (1999) Chemotherapy-induced anemia in adults: incidence and treatment. J Natl Cancer Inst. https://doi.org/10.1093/jnci/91.19.1616
Sahoo P, Gupta PK, Patir R, Vaishya S, Saha I, Gupta RK (2016) Comparison of actual with default hematocrit value in dynamic contrast enhanced MR perfusion quantification in grading of human glioma. Magn Reson Imaging 34:1071–1077
Funding
Open access funding provided by University of Oslo (incl Oslo University Hospital).
Author information
Authors and Affiliations
Contributions
AB: study conception and design, analysis and interpretation of data, critical revision. IRG: study conception and design, drafting of manuscript, critical revision. MK: acquisition of data, critical revision. MK: study conception and design, analysis and interpretation of data, drafting of manuscript, critical revision. CL: study conception and design, analysis and interpretation of data, drafting of manuscript, critical revision. JV: acquisition of data, critical revision.
Corresponding author
Ethics declarations
Conflict of interest
Author Atle Bjørnerud is a paid consultant of NordicNeuroLab AS. No other conflict of interest was reported from any of the authors. No funding was received for the writing of this study.
Ethical standards
Informed consent from all participants was acquired before imaging according to the ethical regional committee and the Helsinki declaration from 1964.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kleppestø, M., Bjørnerud, A., Groote, I.R. et al. Operator dependency of arterial input function in dynamic contrast-enhanced MRI. Magn Reson Mater Phy 35, 105–112 (2022). https://doi.org/10.1007/s10334-021-00926-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10334-021-00926-z