Abstract
Objective
The aim of the study is to compare structure tensor imaging (STI) with diffusion tensor imaging (DTI) of the sheep heart (approximately the same size as the human heart).
Materials and methods
MRI acquisition on three sheep ex vivo hearts was performed at 9.4 T/30 cm with a seven-element RF coil. 3D FLASH with an isotropic resolution of 150 µm and 3D spin-echo DTI at 600 µm were performed. Tensor analysis, angles extraction and segments divisions were performed on both volumes.
Results
A 3D FLASH allows for visualization of the detailed structure of the left and right ventricles. The helix angle determined using DTI and STI exhibited a smooth transmural change from the endocardium to the epicardium. Both the helix and transverse angles were similar between techniques. Sheetlet organization exhibited the same pattern in both acquisitions, but local angle differences were seen and identified in 17 segments representation.
Discussion
This study demonstrated the feasibility of high-resolution MRI for studying the myocyte and myolaminar architecture of sheep hearts. We presented the results of STI on three whole sheep ex vivo hearts and demonstrated a good correspondence between DTI and STI.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
Myocardial structure plays an important role in the normal function of the heart, by facilitating efficient contraction and significantly influencing electrical propagation [1]. Various cardiac diseases are associated with major structural remodeling, which impacts cardiac function.
The myocardium consists of branching myolaminae, or sheetlets, which are 4–6 cells thick. The long axis of the myocytes within these laminae, also referred to as fiber orientation, shows a regular low-order organization in the ventricular wall often described as a helical transmural arrangement, which was described previously in detail [2,3,4]. The laminar architecture, i.e., the orientation of the myolaminae, is, however, more complex, with rapidly branching sheetlets separated by interstices containing collagen bundles [5]. Both myofibers and myolaminar architecture are present throughout the myocardium and exhibit orthotropy along three orthogonal directions along the fiber axis, perpendicular to the fibers in the sheetlet plane, and normal to the sheetlet plane.
Various techniques have been used to visualize the myocardial architecture, including histology [6], extended confocal imaging (ECI) [7] and magnetic resonance imaging (MRI). Histology provides high-resolution (HR) images of the cardiac structure, but it is a destructive technique with limited three-dimensional (3D) volumetric reconstruction and spatial coverage, a limitation that also applies to ECI.
Different MRI techniques can provide information on myocardial–myocyte orientation and myolaminar/sheetlet structure in the intact heart. Over the last 15 years, diffusion tensor imaging (DTI) has been applied to investigate cardiac fiber orientation in vivo [8,9,10] and ex vivo in 3D [11, 12]. Several species have been studied, including rodents [2, 11], dogs [13], sheep [14], pigs [9], and humans [15]. In 2003, Köhler et al. compared diffusion-weighted MRI and T2* images, and found that there was a good agreement in the visualization of microstructure in isolated rat hearts [16]. The technique was also validated by comparison with histology [17]. Following from this earlier work, Gilbert et al. proposed and validated 3D HR MRI acquisition at an isotropic resolution of 50 µm3 to visualize and quantify cardiac microstructure in ex vivo rat hearts [18]. They demonstrated that structure tensor imaging (STI) at an isotropic resolution of 200 µm3 provided accurate information on sheetlet orientation and cardiac orthotropy and was superior to DTI [19]. Our group recently reported preliminary results on STI and DTI of one human heart [20]. However, it was only applied on a single heart, and requires further validation on post processing and visualization in large mammalian species.
The aim of this study was to present a pipeline acquisition of DTI and STI, and compare the two modalities to assessing cardiac microstructure by analysis fiber orientation and sheetlet structure on three ex vivo sheep hearts at 9.4 T with a large bore access of 30 cm.
Materials and methods
Sample preparation
Hearts (hearts 1–3) were explanted from three female sheep (weight: ~ 50 kg) via sternal thoracotomy under general anesthesia. This protocol was approved by the Animal Research Ethics Committee in accordance with the European rules for animal experimentation. The three hearts (~ 12 × 8 × 6 cm3, heart weight = 150 ± 10 g) were perfusion-fixed in 10% formaldehyde (total fixation solution of 1 L) containing 2 mL of gadoterate meglumine (Gd Dotarem), a gadolinium-based contrast agent (Dotarem; Guerbet, Paris, France) for 12 h. This method provides enhanced contrast between the myolaminae and cleavage planes and a greater signal-to-noise ratio [18]. Then, hearts were placed inside a container filled with perfusion solution and were stored in a cold room (4 °C). For MRI acquisition, first samples were removed from the solution and stored in a plastic container.; second, using a 10-mL syringe, the heart cavities were carefully filled with Fomblin (Solvay Solexis, Brussels, Belgium), which is a perfluoropolyether with no 1H detectable signal when scanned using MRI. It offers similar magnetic susceptibility to tissue such that it attenuates susceptibility artifacts at the border of the cardiac chambers [18]. Finally, whole hearts immersed in Fomblin were sealed in a plastic container.
MRI
All experiments were performed at 9.4 T (400 MHz resonance frequency for the water protons) with an open bore access of 30 cm (BioSpin MRI; Bruker, Ettlingen Germany), a 200-mm inner diameter gradient (300 mT/m), and a shim system. Hearts were placed in the center of the magnet in the base–apex axis along the gradient coil.
A dedicated RF volume coil for imaging large samples designed by Bruker was used for scanning. The RF coil was a cylindrical volume array (inner/outer diameters of 165/198 mm, respectively) including seven equally spaced overlapping loop elements (100 mm width, 175 mm length). In this design, no exactly opposing elements occur, but each element is opposed to a gap between two other elements, thus strongly reducing the degree of coupling between the critical elements without the need of reducing the loop size. Phase setting of each element was shifted of 45°–50° to avoid destructive interference. Then, scout images were obtained, 3D B1 maps were acquired within 20 min using the Bloch Siegert shift [21] method for all RF coil elements with a gradient echo sequence modified by including an off-resonance radiofrequency pulse with an offset of 6 kHz relative to water. Based upon preliminary work and our experimental experience [20], a 3D shim box was placed in the septum. Local B1+ shimming was performed by determining a set of transmit phases and amplitudes to maximize the homogeneity within the region of interest (ROI).
3D DTI
Diffusion tensor MRI was carried out using a 3D diffusion-weighted spin-echo sequence with TE = 22 ms, TR = 500 ms, FOV = 100 × 80 × 110 mm, matrix = 166 × 133 × 183 and an isotropic resolution of 600 μm. Each diffusion gradient had a duration of 4.5 ms, and gradients were separated by an 11-ms delay: three b0 maps were generated and six gradient directions were applied with a b value of 1000 s/mm2, as described previously [19], and an partial Fourier undersampling of 1.8 factor in phase direction was used, for a total acquisition time of 16 h 55 min. Raw diffusion-weighted images were processed using ParaVison 6.0 (Bruker) to compute the diffusion tensor.
For segmentation of the cardiac ventricles, N4 bias correction [22] was applied on maps with b = 0 s/mm2 to avoid the segmentation of regions showing some B1 inhomogeneity and signal drop-off associated with RF coil sensitivity profile in the region of the cardiac apex and base (Fig. 1, processing pipeline). Low and high cutoff thresholds were applied to the FA, trace, and weighted images to define a binary mask. The first diffusion tensor eigenvector has been shown to correspond to myocyte orientation DTI [6,7,8,9]. The second and third eigenvectors have been associated with sheetlet in-plane and normal directions, respectively, but their accuracy in determining tissue laminar organization is poor [19]. Computer post processing to extract the tensor and vectors from DTI acquisitions lasted less than 1 min.
Pipeline of magnetic resonance imaging (MRI) data acquisition, post-processing, and analysis for each sample inspired from [20]. Diffusion tensor (DT) spin-echo and structure tensor (ST) gradient-echo data were processed through two different pipelines yielding the helix angle (HA), transverse angle (TA), sheetlet elevation (SE) angle, and sheetlet azimuth (SA) angle. The transformation to align the long axis of the LV along the z axis was applied on angles maps. The angle maps were then registered along the short axis using rigid registration, the left ventricle (LV) was segmented, and the 17-segment American Heart Association (AHA) model was applied to quantitatively analyze 17 segments of the mid-LV.
3D STI
A 3D FLASH sequence was applied to image the whole heart volume, which was averaged 20 times, with the following settings: TE = 9 ms; TR = 30 ms; matrix size = 731 × 665 × 532; FOV = 110 × 100 × 80 mm, voxel dimensions = 150 µm isotropic, flip angle = 30°, and an accelerator factor in phase direction of 1.91. The total acquisition time for each heart was 30 h 50 min.
T1-weighted images contrast was used to determine the orientation of the sheetlet and myofibers. The following steps were applied to the FLASH images:
-
Images were reformatted in short axis view and converted into a stack of 16-bit images (Fig. 1, processing pipeline).
-
The derivatives of the image intensity (the intensity gradient) along each direction were computed: first a 5 × 5 × 5 point derivative template was defined [23]. The derivative template was applied on the full 3D images using 1D FFT convolution as described previously [18, 19]. The 5 × 5 × 5 kernel applied to 150 µm isotropic images involved a region of 750 × 750 × 750 µm. This resolution represents the size of local environment that contributes to the structure tensor at a given point.”
-
The structure tensor (the outer product of the intensity gradient vectors) was computed for each voxel and smoothed at a progressive resolution from 150 to 600 µm isotropic (731 × 665 × 532 tensors to 183 × 166 × 133 tensors). Each structure tensor component at resolution doubling was determined using level 4 binomial low-pass filters to smooth from one level of resolution to the next.
-
The principal directions of the structure tensor at each discrete point were extracted using eigenanalysis at isotropic resolution 600 µm. The 600 µm smoothed structure tensor data set was used to best-match the expected diffusion tensor resolution. (See steps in Fig. 1).
-
We used a previously described tissue coordinate reference frame [18, 19] as follows: the first eigenvector (largest magnitude eigenvalue) corresponds to the sheetlet/lamina normal direction, the second to the sheetlet/lamina in-plane direction, and the third (smallest magnitude eigenvalue) to the myocyte orientation.
-
Additionally, binary masks were created based on FA, trace, and image intensity to segment the background using low and high cutoff thresholds.
Post data treatment after acquisition to reconstruct images, and extract tensors and eigenvector lasted 1 h. The processing pipeline was implemented [19, 20] using Matlab (The MathWorks Inc., Natick, MA) and VTK libraries.
Comparison between DTI and STI
Our previous study [19] in rat hearts showed that DTI provides robust information on fiber orientation, whereas STI is more accurate in terms of sheetlet orientation. A mean of 897,181 ± 32,096 voxels was extracted for the three hearts using DTI, and 798,645 ± 33,051 voxels from FLASH images were post-processed to obtain the same resolution as DTI (isotropic resolution of 600 µm with 133 × 167 × 183 tensors).
As described previously [24], all structural information was obtained using a specific cardiac reference system (see Fig. 1 angles extraction), with an apex–base left ventricle (LV) axis running through the center of the left ventricular cavity. For each voxel in the segmented datasets, the orientations of myocytes (fibers) and sheetlets were computed in this coordinate system.
For myocyte orientation, we compared the first DTI eigenvector with the third STI eigenvector and computed the fiber helix angle (HA), which is the angle between the short axis plane and the projection of the fiber vector onto the wall tangent plane. The fiber transverse angle (TA) is the angle between the wall tangent plane (also known as the longitudinal orientation) and the projection of the fiber vector onto the transverse (also known as the short axis plane) (see Fig. 1 in angles extraction part).
For sheetlet orientation, the first STI eigenvector was compared to the third DTI eigenvector, which is assumed to be positioned normal to the sheet. The sheetlet elevation (SE) angle is the angle between the short axis plane and the projection of the vector onto the radial orientation. The sheetlet azimuth (SA) angle is the angle between the local radial orientation and the projection of the vector onto the short axis plane [11].
Each segment for each sample contains a mean of 16,032 ± 2270 voxels.
Mean transmural evolution was plotted (bin of 0.005, i.e., 200 points displayed) for each angle for 17 segments between the endocardium (normalized distance x = 0) and epicardium (normalized distance x = 1). We performed a local unwrap for pixels up to 90°.
Registration and segmentation (Fig. 1 analysis pipeline)
Short axis registration of the parametric volume maps was performed. Rigid registration using 3D Slicer (http://www.slicer.org) [25] between DTI and STI for the same heart was performed to obtain the same configuration for both acquisitions. Data from STI were then aligned across the three samples to obtain a similar alignment among hearts. The LV was manually segmented, and quantitative transmural maps were subdivided into regions defined by the 17-segment American Heart Association (AHA) model [26]. We used a polar coordinate system described previously [27], in which segments were defined as ranges of angles.
Statistical analysis and Image visualization and quantification
Scatter and Bland–Altman plots in whole three hearts using GraphPad Prism (GraphPad Software, San Diego, CA) were performed. Mean of HA angles for DTI and STI in endocardium, mid-ventricular and epicardium were calculated to analyze the reproducibility of measured between samples and similarities between methods. Statistical analysis are performed for comparison between groups using nonparametric test (Kruskal–Wallis test) with p < 0.05 are considered as statistically significant. One asterisk (*) identifies p values between 0.01 and 0.05, two asterisks (**) identify adjusted p values between 0.01 and 0.001.
Descriptive statistics from linear regression (R2 linearity and slope) and curve fitting were calculated for HA and TA transmural profile.
Bullseye representations were created using homemade program on Matlab after 17 AHA segmentation. Mean in each segment for the three hearts was visualized for DTI and STI results for HA, TA, SE and SA angles.
Image reconstruction was performed using ParaVision 6.0 (Bruker) on a workstation with 512 GB of accessible memory to process the large data matrices. Visualization of 3D volume renderings was performed using Volview and Paraview software (Kitware, Clifton Park, NY). Short axis registration of the parametric volume maps was performed using 3D Slicer software and (http://www.slicer.org) [25] and parametric maps were displayed using Advanced Normalization Tools (ANTS) libraries [28].
Results
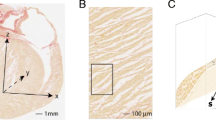
Figure 2 shows a 3D volume rendering and short and long axis slices of one of the whole hearts using contrast-enhanced FLASH acquisitions at an isotropic resolution of 150 μm3. In these images, the interstices between sheetlets, as well as vessels, appear bright due to the presence of residual Gd Dotarem. The fine details of the laminar architecture (see animated gif in https://github.com/valeryozenne/Cardiac-Structure-Database/tree/master/Article) can be seen in these images. Raw images extracted from 3D volumes after MRI acquisitions are displayed in Fig. 3 for the three hearts (hearts #1 to #3) in short axis view. The first line shows diffusion-weighted images from DTI acquisition recovered at an isotropic resolution of 600 µm. The second line presents high-resolution images at 150 µm obtained after STI acquisitions. In term of samples fixation right and left ventricles are fixed in relaxed phase, no damages or scars are observed. For STI images we can identify same structures inside the left ventricular cardiac tissue with differences of fibers orientation from the endocardium to epicardium. A bright signal in the top of the samples appears in some acquisitions, it corresponds to a residue of formaldehyde and was removed by segmentation in post-processing data pipeline. Some residues from formalin trapped in the coronaries or vessels rise to the surface and can be observed as super intense signal on images. In heart #2, a bubble is trapped between right cavities, formalin and fomblin.
The tissue FA for the first heart is extracted from the 3D DTI acquisitions. Yellow and red areas are more anisotropic than blue areas (Fig. 4a). Figure 4b shows cumulative histograms of FA (binning of 0.02 between 0 and 1 ) extracted from DTI for the three hearts by segmenting out the cardiac bases and cavities. The graph reveals mean FA values of 0.33 ± 0.16, 0.3 ± 0.17, and 0.32 ± 0.18 for samples 1, 2, and 3, respectively, in the ventricular myocardium.
HA, TA, SE and SA maps are represented in Fig. 5 for representative short and long axis slices for each heart (hearts #1 to #3).
HA, TA, SE and SA angles between − 90° and 90° from DT imaging (DTI) and ST imaging (STI) after post-processing in short axis and long axis views for hearts #1, #2 and #3—with an isotropic resolution of 600 µm. Cut planes in the images are similar to Fig. 2
A qualitative interpretation of angles maps is presented in the following part: maps are consistent across the three hearts. In general, a larger noise level is observed in the STI maps. We identify the well-known transmural profile in the LV, where the HA varied smoothly from a negative value (blue–green) at the epicardium to a positive value (red) at the endocardium. There is a smooth transition between the RV and LV in the posterior position, and an abrupt change of orientation in the same area in the anterior view.
TA maps are mainly close to zero in short axis view. The angle distribution appeared to be more heterogeneous in the septum. TA maps derived from DTI and STI appear to be similar; short axis images of the left free wall for all hearts for both acquisitions showed negative values in the same areas.
There are similarities between STI and DTI for images of the LV, with SE angles < 0° in the LV and septum. In long axis views, the SE angle is positive at the apex and negative at the base for the three hearts. On SA angle maps, STI and DTI data are similar with abrupt angle changes in the LV in short axis view but heterogeneous angle distribution in the long axis view in the septum. In the RV, some differences can be seen between DTI and STI, with negative values derived from DTI and positive values derived from STI in short axis view, especially for SE angles in all samples. Abrupt changes in short axis orientation were seen in the ventricles and also at the LV–septum–RV insertions.
Difference angles maps between DT and ST images are represented in the last column of Fig. 5, global values are close to 0° with some local discrepancies especially in the septum for HA and TA maps. Differences maps for SE and SA display more negative values in short and long axis views.
A more quantitative approach is described in the next Fig. 6. Global transmural profiles for mean and standard deviation of HA are presented in scatter plots in Fig. 6a for DTI and STI. The table in Fig. 6b presents mean and standard deviation for each heart in three areas: endocardium, mid-ventricular and epicardium for the two methods.
a Scatter plot comparison of total mean for HA angles in degree (°) divided in three areas along cardiac muscle (endocardium, mid-ventricular and epicardium) between DT and ST and between the three hearts. b Table of HA mean and SD for each heart along myocardium for hearts #1, #2 and #3. c Statistical results between three hearts and between STI and DTI methods
In the endocardium, the mean of HA is in the same range for DT with difference in mean of 3.9 ± 16.1° between hearts #1 and #2, 8.3 ± 16.2° between hearts #2 and #3 and 4.4 ± 14.9° between hearts #1 and #3. STI displays differences in mean of 12 ± 13.7°, 14.6 ± 13.4° and 2.6 ± 14.6° between hearts #1 and #2, between hearts #2 and #3 and between hearts #1 and #3, respectively.
In the mid-ventricular area, heart #2 displays higher values in DT (25.5 ± 25.6°) and ST (30.1 ± 17.3°) for HA angle in comparison with heart #1 and heart #3. In this area, higher standard deviation is calculated due to the transition of positive to negative HA angles. Then, in the epicardium, we can see that HA from DTI displays lower values (between − 27.5 ± 14.9° and − 33.8 ± 11.1°) than for STI (values between − 22.1 ± 8.9° and − 26.7 ± 14.6°). Statistical results are presented in in Fig. 6c between hearts for STI and STI. For the DTI method, no significant difference is observed with a global p > 0.12 between hearts #1 and #2, hearts #1 and #3 and hearts #2 and #3. For the STI method, the differences between samples are more pronounced: with a p = 0.02 and p = 0.003, respectively, for hearts #1 and #2 and hearts #2 and #3; no significant difference is observed in STI between hearts #1 and #3.
Transmural evolution for mean and standard deviation of HA and TA angles for three hearts are plotted between − 90° on the endocardium to 90° on the epicardium in Fig. 7 spread over 17 segments AHA model for DTI and STI (in violet and blue on the graphs, respectively). Their linearity and slope coefficient slope from LV endocardium to epicardium are summarized in Table 1. Experimental plots of angles between the endocardium and epicardium were remarkably consistent between STI and DTI for the two angles profiles in all 17 segments. For HA angles profiles, the R2 calculated ranges from 0.63 to 0.97 using DTI and from 0.66 to 0.95 for STI. Across the 17 different regions, slopes means for HA are − 129 ± 34° and − 121 ± 43° for DTI and STI, respectively. Linearity for TA is more variable across segments with R2 = 0.53 ± 0.38 for DTI and for STI R2 = 0.61 ± 0.29. A difference in slope is noticeable between STI and DTI in segment 2 and 8 in RV/LV junction. A mean difference between DT and STI slopes for TA is 10.4 ± 5.7°, and we notice a higher difference for segment 2 of 50.1° (slope(DTI) = 21.3°, slope(STI) = − 28.8°) and for segment 8 of 41.5° (slope(DTI) = 4.8°, slope(STI) = − 36.7°) between DTI and STI.
Transmural variation in myocytes orientations comparison between mean of DTI and STI for all hearts. Regions were defined by the 17-segment AHA model. Segments 1–17 are presented for DTI (violet dots) and STI (blue dots) with respective linear fit (lines). Helix angle (HA) and transverse angle (TA) are displayed. Mean of HA and TA for three hearts is shown between − 100° and 100° in y axis in function of LV wall thickness normalized between 0 and 1 corresponding to the LV epicardium and endocardium, respectively, in x axis
Figure 8 displays mean values of HA, TA, SA and SE for 17 segments of the AHA model for DTI, STI and |DTI-STI| results for all hearts. HA distribution is consistent between DTI and STI; absolute differences between modalities are below 11° in all the 17 segments.
Seventeen segment distribution of mean of HA, TA, SE, SA angles for all hearts for DT and STI in degrees (°) along the left cardiac muscle is represented in gray between − 30° and 30°. The last line represents the absolute difference map between DTI and STI in color (range between 0° and 20°) for each angles in degrees (°)
For TA distribution, difference maps between DTI and STI distribution are always below 10° except for segments 2 and 8 closed to RV with a difference higher than 15°. For SE, DTI displays globally negative values ranging for − 35.6° (segment 15) to 14.7° (segment 6). Absolute difference maps angles are close or above 20° in segments 6, 13, 16 and 17 (in red on SE difference maps with difference values of 22.5, 19.8, 42 and 45.4, respectively). For the SA angles, DTI and STI bullseye representation displays maps close to 0°. Absolute difference maps between DTI and STI displayed difference below 15° in absolute value except for in segments 2, 8, and 13 close to RV with difference of 27.9°, 24.4° and 18.4°, respectively, between |DTI-STI|.
Figure 9 presents Bland–Altman plots for all three hearts for HA, TA, SE and SA angles between DTI and STI method in the LV wall. HA are distributed between − 90° and 90° in x axis with a HADTI-STI of − 2.2 ± 17.5° (mean ± 1.96 standard deviation in y axis). TA mean varies between − 45° and 45° in x axis with TADTI-STI centered to zero of − 2.2 ± 20.0°. For sheetlet comparison, SE points tend to be negative in mean with a SEDTI-STI of − 3.6 ± 51.5°. SA mean varies between − 45° and 45° in x axis with SADTI-STI centered to zero of − 9.1 ± 30.5°.
Discussion
We presented a detailed investigation and comparison between DTI and STI on several hearts from a large mammalian species (sheep) with same age, size, and cardiac fixation and without any cardiac pathologies, to study robustness of STI acquisition and post processing on whole hearts. This allowed us to successfully analyze myocardial structure using a combination of 3D STI (150–600 µm) and 3D DTI (600 µm) within a total acquisition time of ~ 2 days.
In the current study, we have used the same acquisition and a similar post processing pipeline as those presented in the 2019 FIHM conference [20]. However, in this previous publication, STI and DTI are only briefly compared for one human heart. Access to human hearts is limited and does not allow performing a thorough analysis of the performance and robustness of the proposed methods. The novelty of the current manuscript relies on the detailed study of the robustness of cardiac sample preparation, acquisition parameters and results obtained by DTI and STI that goes well beyond the scope of preliminary data presented in our previous conference proceedings [20].
The fibers followed the widely described organization with transmural fiber rotation; whereas, sheetlets in the three ventricles appeared macroscopically to be mainly aligned along two distinct perpendicular orientations across the LV wall. Previous studies have demonstrated the utility of DTI [11, 13,14,15, 29, 30] to quantify fiber orientation in the heart. Smooth fiber angles can be seen in DTI scans, and observations from the images have already been validated using histology [31]. DTI acquisition could be improved by adding more directions (> 6) which is already described in published works [11, 12]. In this study, we used NA = 1 and 6 directions, which is the minimum to calculate the tensor from diffusion-weighted imaging data. However, we obtained smooth data and reproducible results on three ex vivo sheep hearts with good image quality (see Fig. 3). Nevertheless, the measure is indirect (water diffusion using one compartmental model), and DTI has been shown to allow only limited assessment of laminar directions [32]. With HR MRI, Gilbert et al. demonstrated that there was very good consistency between contrast in native HR images and histology in terms of following the architecture of myolaminae [18]. Acquisition of HR images can be time consuming (more than 24 h) and post-processing is challenging. However, we have recently shown that HR MRI combined with STI analysis can yield robust information on the orientation of cardiac sheetlets. To date, this has only been performed in small animal hearts, mainly due to hardware limitations. To acquire in 3D an isotropic resolution of 150 µm could be limited by gradient strength and SNR on conventional MRI [18, 19].
Comparison between DTI and STI
We demonstrated that the DTI and STI myofiber orientation exhibited similar rotation along the short and long axes, and both imaging modalities produced analogous maps of fiber orientation consistent with a previous study on rat hearts [19]. HA maps derived from both DTI and STI exhibited a smooth transmural orientation, with very high linear correlation coefficients. TA maps were close to 0° for both acquisitions. Cardiac fiber orientation was well correlated between STI and DTI.
FLASH images at 150 µm on sheep hearts at 9.4 T includes a lot of information like vessels, fiber and sheet orientation, etc. We noticed that on FLASH images, we can both identify bright and black interstices in specific area. The black interstices’ meaning remains speculative, but it could indicate either less well-perfused regions during the fixation protocol or larger extracellular clefts where less Gd is accumulated. However, it probably did not affect quantitative analysis, given the good correspondence between DTI and STI (at least in fiber orientation).
Bland–Altman (Fig. 9) plots assess the correspondence of DTI and STI measurements across the whole three hearts. These plots allow to compare the same measurements using two different techniques [33]. For fiber orientation, distribution for HA demonstrated no difference between − 60° and 60° across the left ventricle. For TA angles, we showed that the mean of TA is close to 0° across the myocardium, and a small bias is observed between two techniques. These results are in good agreement with the 17-segment representation, where the absolute difference in all segments is close to zero for HA and TA angles (see Fig. 8). Segments correlation in the AHA model has resulted in difference maps close to 0° for fibers structure. For the SE and SA angles extracted from DTI and STI, a large bias between techniques is noticed (see Fig. 8), indicating that SE and SA angles are larger for STI measurements that for DTI measurements (see also graphs for SE as SA in supplementary material S1). Indeed, for laminar structure, bullseye presentation displays a more heterogeneous differences for the two techniques. A frequent area with large differences between techniques appears in the LV/RV junction segments 2, 7 and 8. This region presents an underlying structure between the right and left ventricles. In Fig. 9, for SE, the 95% confidence interval is between 48° and − 55°, for SA between 21° and − 40°. These values are larger than for HA differences, between 15° and − 20°, and TA differences between 18° and − 22°.”
Overall, the differences between STI and DTI were larger for SE and SA (~ 6.3°) than for HA and TA (~ 2.2°). Similar results were found by Bernus et al. [19], showing in rat hearts differences up to 20° between DTI and STI sheetlet orientation due in part to eigenvectors sorting issues.
Limitation: fixation process
Mazumder et al. [34] demonstrated that formalin fixation affects molecular diffusivity by reducing FA and mean fiber length and increasing ADC. It results in structural changes including shrinkage of sheetlet interstices, and consequently, sheetlet orientations may not reflect in vivo sheetlet measurements. However, fixation does not alter the structural orientation of the fibers. This hypothesis is further supported by another study where 4 weeks of formalin fixation with a 10% neutral buffered solution resulted in decreased diffusivity in mouse brains [35]. Moreover, the type of fixation (perfusion fixation, immersion fixation or both), thickness of tissue, preparation of the fixing agent, time interval between tissue extraction and fixation, temperature of fixation, play a role in the fixation process which can affect the diffusion properties of the heart differently. In comparison, protocols for in vivo diffusion MRI are improving, but they remain resolution-limited and prone to artifacts from respiratory, cardiac motion and strain [36, 37]. Moreover, fixation before imaging fixed hearts which do not represent truly systolic or diastolic phase; a direct comparison with in vivo measurements is complicated because state of ex vivo hearts is not matched to in vivo contractile state. Pennell’s group [9, 37] measured limited changes for fibers orientation (HA angles) between in vivo cardiac phase (systolic and diastolic) and ex vivo states (relaxed and contracted). Whereas for sheetlets arrangement, they demonstrated that results are dependent on contractile state.
Limitation temperature
In this study, the three hearts were perfusion fixed in 10% formaldehyde (total fixation solution of 1 L) containing 2 mL of gadoterate meglumine (Gd Dotarem), during 12 h. Then, hearts were immersed inside container with perfusion solution and were stored in a cold room. Scanner room temperature was monitored by constant air temperature around 19 °C. For three hearts the same protocol of fixation and storage have been applied (see material and method). During acquisition, an optical temperature probe is placed close to the sample and connected to a computer, the fiber monitors change of temperature. We measure an increase of temperature of 2° ± 0.5 °C using SE DTI for 6 h of recording. No temperature variation was measured during FLASH acquisition.
Limitation B0 and B1
The acquisition of data from large-sized samples using ultra-high field HR MRI is still challenging due to B0 and B1 homogeneities. B0 could influence MR signal and create susceptibility artifacts and affect image quality. In this study, we used fomblin to avoid susceptibility effects in ventricular cavities. A 3D B0 mapping was performed, using a dual-echo steady-state sequence and performed a global shim to reach a full-width at half-maximum of 50 Hz. B1 could influence RF pulses efficiency and create signal drop-off associated with RF coil sensitivity. To achieve homogenous B1 field and excitation, B1 maps were acquired within 20 min and a shim box in 3D was placed in the septum. Local B1+ shimming was performed by determining a set of transmit phases and amplitudes that will maximize the homogeneity within a region of interest and avoid RF destructive effects. Moreover, in post-processing pipeline, a N4 filter was also used to correct low frequency intensity non-uniformity present in 3D volumes (due to coil sensitivity or B1 effect). B0 and B1 have been optimized for each acquisition. However, some studies present results a study based on SNR and the impact of DTI results on large mammalian hearts at 3 T and 7 T [12] and on ex vivo rat heart [38]; comparing different SNR and their impact on DTI and STI acquisition is outside the scope of this work.
Limitation post processing on HR MRI images
A large amount of data produced by HR 3D imaging require adequate processing hardware and dedicated software. The acquisition time to obtain 3D images of the whole hearts is several hours, and if data for both DTI and STI are acquired, the total acquisition time could exceed several days (acquisition time in this study was 2 days). Moreover, Teh et al. [33] used tensor analysis on synchrotron radiation imaging; they investigated vessel segmentation for STI data processing. They presented better sheetlet definition on SE and SA angles maps. A limitation of our approach is, therefore, the post-processing pipeline of STI, which is both complex and time consuming, but essential to reduce noise and avoid potential reconstruction errors. Indeed, statistical analysis have shown a less robust results between hearts than for DTI (see Fig. 6).
MRI allowed unprecedented visualization of cardiac structure of the ex vivo sheep heart with a high level of structural accuracy. In particular, new areas of interest, such as the RV and RV/LV junction, can be observed directly (segments 2 and 8). We also noticed that angles in the RV present abrupt orientation changes. Indeed, the importance of using an appropriate coordinate system to investigate the RV fiber and sheetlet orientations, as using an LV centroid may give rise to artifactual measurements in fiber helix/transverse angles and sheetlet orientations [30, 39].
In conclusion, results of STI on three whole ex vivo sheep hearts demonstrated a good correspondence with DTI and opens new perspectives for HR 3D structural characterization of normal/pathological cardiac structure. These results applied on healthy and pathological hearts will provide new insight for cardiac modeling research groups and it will improve developments of mathematical cardiac model. The objective is to gain a better understanding of the links between structural remodeling and electrical disorders of the heart. These results hold promise for the development of new noninvasive imaging methods to better characterize the cardiac microstructure in healthy and pathological human hearts.
Abbreviations
- 3D:
-
Three-dimensional
- DTI:
-
Diffusion tensor imaging
- FA:
-
Fractional anisotropy
- FLASH:
-
Fast low angle shot
- FOV:
-
Field of view
- Gd Dotarem:
-
Gadolinium-based contrast agent (Dotarem)
- HA:
-
Helix angle
- HR MRI:
-
High-resolution magnetic resonance imaging
- LV:
-
Left ventricle
- MRI:
-
Magnetic resonance imaging
- ROI:
-
Region of interest
- RV:
-
Right ventricle
- SA:
-
Sheet azimuth
- SE:
-
Sheet elevation
- STI:
-
Structure tensor imaging
- TA:
-
Transverse angle
References
Hooks DA, Trew ML, Caldwell BJ, Sands GB, LeGrice IJ, Smaill BH (2007) Laminar arrangement of ventricular myocytes influences electrical behavior of the heart. Circ Res 101(10):e103-112
Holmes AA, Scollan DF, Winslow RL (2000) Direct histological validation of diffusion tensor MRI in formaldehyde-fixed myocardium. Magn Reson Med 44(1):157–161
Streeter DD Jr, Spotnitz HM, Patel DP, Ross J Jr, Sonnenblick EH (1969) Fiber orientation in the canine left ventricle during diastole and systole. Circ Res 24(3):339–347
Schmid P, Jaermann T, Boesiger P, Niederer PF, Lunkenheimer PP, Cryer CW, Anderson RH (2005) Ventricular myocardial architecture as visualised in postmortem swine hearts using magnetic resonance diffusion tensor imaging. Eur J Cardiothorac Surg 27(3):468–472
Costa KD, Takayama Y, McCulloch AD, Covell JW (1999) Laminar fiber architecture and three-dimensional systolic mechanics in canine ventricular myocardium. Am J Physiol 276(2):H595-607
Burton RA, Plank G, Schneider JE, Grau V, Ahammer H, Keeling SL, Lee J, Smith NP, Gavaghan D, Trayanova N, Kohl P (2006) Three-dimensional models of individual cardiac histoanatomy: tools and challenges. Ann N Y Acad Sci 1080:301–319
LeGrice I, Sands G, Hooks D, Gerneke D, Smaill B (2004) Microscopic imaging of extended tissue volumes. Clin Exp Pharmacol Physiol 31(12):902–905
Toussaint N, Stoeck CT, Schaeffter T, Kozerke S, Sermesant M, Batchelor PG (2013) In vivo human cardiac fibre architecture estimation using shape-based diffusion tensor processing. Med Image Anal 17(8):1243–1255
Nielles-Vallespin S, Khalique Z, Ferreira PF, de Silva R, Scott AD, Kilner P, McGill LA, Giannakidis A, Gatehouse PD, Ennis D, Aliotta E, Al-Khalil M, Kellman P, Mazilu D, Balaban RS, Firmin DN, Arai AE, Pennell DJ (2017) Assessment of myocardial microstructural dynamics by in vivo diffusion tensor cardiac magnetic resonance. J Am Coll Cardiol 69(6):661–676
Nielles-Vallespin S, Scott A, Ferreira P, Khalique Z, Pennell D, Firmin D (2019) Cardiac diffusion: technique and practical applications. J Magn Reson Imaging. https://doi.org/10.1002/jmri.26912
Teh I, McClymont D, Burton RA, Maguire ML, Whittington HJ, Lygate CA, Kohl P, Schneider JE (2016) Resolving fine cardiac structures in rats with high-resolution diffusion tensor imaging. Sci Rep 6:30573
Lohr D, Terekhov M, Weng AM, Schroeder A, Walles H, Schreiber LM (2019) Spin echo based cardiac diffusion imaging at 7T: an ex vivo study of the porcine heart at 7T and 3T. PLoS ONE 14(3):e0213994
Helm PA, Tseng HJ, Younes L, McVeigh ER, Winslow RL (2005) Ex vivo 3D diffusion tensor imaging and quantification of cardiac laminar structure. Magn Reson Med 54(4):850–859
Healy LJ, Jiang Y, Hsu EW (2011) Quantitative comparison of myocardial fiber structure between mice, rabbit, and sheep using diffusion tensor cardiovascular magnetic resonance. J Cardiovasc Magn Reson 13:74
Rohmer D, Sitek A, Gullberg GT (2006) Reconstruction and visualization of fiber and sheet structure with regularized tensor diffusion MRI in the human heart. Vol LBNL-60277. Lawrence Berkeley National Laboratory
Köhler S, Hiller KH, Waller C, Bauer WR, Haase A, Jakob PM (2003) Investigation of the microstructure of the isolated rat heart: a comparison between T*2- and diffusion-weighted MRI. Magn Reson Med 50(6):1144–1150
Köhler S, Hiller KH, Waller C, Jakob PM, Bauer WR, Haase A (2003) Visualization of myocardial microstructure using high-resolution T*2 imaging at high magnetic field. Magn Reson Med 49(2):371–375
Gilbert SH, Benoist D, Benson AP, White E, Tanner SF, Holden AV, Dobrzynski H, Bernus O, Radjenovic A (2012) Visualization and quantification of whole rat heart laminar structure using high-spatial resolution contrast-enhanced MRI. Am J Physiol Heart Circ Physiol 302(1):H287-298
Bernus O, Radjenovic A, Trew ML, LeGrice IJ, Sands GB, Magee DR, Smaill BH, Gilbert SH (2015) Comparison of diffusion tensor imaging by cardiovascular magnetic resonance and gadolinium enhanced 3D image intensity approaches to investigation of structural anisotropy in explanted rat hearts. J Cardiovasc Magn Reson 17:31
Haliot K, Magat J, Ozenne V, Abell E, Dubes V, Bear L, Gilbert SH, Trew ML, Haissaguerre M, Quesson B, Bernus O (2019) 3D high resolution imaging of human heart for visualization of the cardiac structure. In: International conference on functional imaging and modeling of the heart FIMH 2019, no 11504, pp 196–207
Sacolick LI, Wiesinger F, Hancu I, Vogel MW (2010) B1 mapping by Bloch-Siegert shift. Magn Reson Med 63(5):1315–1322
Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC (2010) N4ITK: improved N3 bias correction. IEEE Trans Med Imaging 29(6):1310–1320
Farid H, Simoncelli EP (2004) Differentiation of discrete multidimensional signals. IEEE Trans Image Process 13(4):496–508
Gilbert SH, Smaill BH, Walton RD, Trew ML, Bernus O (2013) DT-MRI measurement of myolaminar structure: accuracy and sensitivity to time post-fixation, b-value and number of directions. Conf Proc IEEE Eng Med Biol Soc 2013:699–702
Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin J-C, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M, Buatti J, Aylward SR, Miller JV, Pieper S, Kikinis R (2012) 3D slicer as an image computing platform for the quantitative imaging network. Magn Reson Imaging 30(9):18
Cerqueira MD, Weissman NJ, Dilsizian V, Jacobs AK, Kaul S, Laskey WK, Pennell DJ, Rumberger JA, Ryan T, Verani MS, American Heart Association Writing Group on Myocardial S, Registration for Cardiac I (2002) Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart. A statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation 105(4):539–542
Cedilnik N, Duchateau J, Dubois R, Sacher F, Jais P, Cochet H, Sermesant M (2018) Fast personalized electrophysiological models from computed tomography images for ventricular tachycardia ablation planning. Europace 20(suppl3):iii94–iii101
Avants BB, Tustison NJ, Song G, Cook PA, Klein A, Gee JC (2011) A reproducible evaluation of ANTs similarity metric performance in brain image registration. Neuroimage 54(3):2033–2044
Helm P, Beg MF, Miller MI, Winslow RL (2005) Measuring and mapping cardiac fiber and laminar architecture using diffusion tensor MR imaging. Ann N Y Acad Sci 1047:296–307
Teh I, Burton RA, McClymont D, Capel RA, Aston D, Kohl P, Schneider JE (2016) Mapping cardiac microstructure of rabbit heart in different mechanical states by high resolution diffusion tensor imaging: a proof-of-principle study. Prog Biophys Mol Biol 121(2):85–96
Hsu EW, Muzikant AL, Matulevicius SA, Penland RC, Henriquez CS (1998) Magnetic resonance myocardial fiber-orientation mapping with direct histological correlation. Am J Physiol 274(5 Pt 2):H1627-1634
Gilbert S, Trew M, Smaill B, Radjenivic A, Bernus O (2011) Measurement of myocardial structure: 3D structure tensor analysis of high resoluion MRI quantitatively compared to DT-MRI. Paper presented at the STACOM 2012. Lecture notes in computer science, Berlin, Heidelberg
Teh I, McClymont D, Zdora MC, Whittington HJ, Davidoiu V, Lee J, Lygate CA, Rau C, Zanette I, Schneider JE (2017) Validation of diffusion tensor MRI measurements of cardiac microstructure with structure tensor synchrotron radiation imaging. J Cardiovasc Magn Reson 19(1):31
Mazumder R, Choi S, Clymer BD, White RD, Kolipaka A (2016) Diffusion tensor imaging of healthy and infarcted porcine hearts: study on the impact of formalin fixation. J Med Imaging Radiat Sci 47(1):74–85
D’Arceuil HE, de Crespigny AJ (2007) The effects of brain tissue decomposition on diffusion tensor imaging and tractography. Neuroimage 36:64–6
Nielles-Vallespin S, Mekkaoui C, Gatehouse P, Reese TG, Keegan J, Ferreira PF, Collins S, Speier P, Feiweier T, de Silva R, Jackowski MP, Pennell DJ, Sosnovik DE, Firmin D (2013) In vivo diffusion tensor MRI of the human heart: reproducibility of breath-hold and navigator-based approaches. Magn Reson Med 70(2):454–465
Ferreira PF, Kilner PJ, McGill LA, Nielles-Vallespin S, Scott AD, Ho SY, McCarthy KP, Haba MM, Ismail TF, Gatehouse PD, de Silva R, Lyon AR, Prasad SK, Firmin DN, Pennell DJ (2014) In vivo cardiovascular magnetic resonance diffusion tensor imaging shows evidence of abnormal myocardial laminar orientations and mobility in hypertrophic cardiomyopathy. J Cardiovasc Magn Reson 16:87
McClymont D, Teh I, Schneider JE (2017) The impact of signal-to-noise ratio, diffusion-weighted directions and image resolution in cardiac diffusion tensor imaging - insights from the ex-vivo rat heart. J Cardiovasc Magn Reson 19(1):90
Agger P, Ilkjaer C, Laustsen C, Smerup M, Frandsen JR, Ringgaard S, Pedersen M, Partridge JB, Anderson RH, Hjortdal V (2017) Changes in overall ventricular myocardial architecture in the setting of a porcine animal model of right ventricular dilation. J Cardiovasc Magn Reson 19(1):93
Acknowledgements
The authors thank Peter Ullmann, Johannes T Schneider and Simon Stark from Bruker for providing us a homemade RF design coil with seven elements and developing protocol to map and shim B1.
Funding
This work was supported by the National Research Agency (ANR-10-IAHU04-LIRYC) and the European Union’s FP7 research and innovation program under the Marie Sklodowska-Curie (FP7-PEOPLE-2012-IRSES), Grant Agreement No 317766—CORDIS 3D and the European Research Council (FP7/2007-2013 Grant Agreement Number 322886–SYMPHONY).
Author information
Authors and Affiliations
Contributions
JM and VO contributed equally to this work. JM: drafting of manuscript and prepared figures. JM, SHG and JN: samples preparation, acquisition of data and study conception and design. JM, SHG, VO, KH and NC: programming developments and data treatments. JM, SHG, VO, MT, BQ and OB: analysis and interpretation of data. JM, VO, NC, MS, JN, KH, SHG, MT, MH, BQ and OB: critical revision.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
Animals protocol was approved by the Animal Research Ethics Committee (Comité d’Ethique en Expérimentation Animale de Bordeaux; CEEA50) in accordance with the European rules for animal experimentation (European legislation 2010/63/UE; 2010).
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
10334_2021_913_MOESM1_ESM.tif
Supplementary file1. S1: Transmural variation in sheetlet orientations comparison between mean of DTI and STI for all hearts. Regions were defined by the 17-segment AHA model. Segments 1–17 are resented for DTI (violet dots) and STI (blue dots). Helix angle (HA) and Transverse angle (SA) are displayed. Mean of SE and SA for three hearts is shown between − 100° and 100° in y axis in function of LV wall thickness normalized between 0 and 1 corresponding to the LV epicardium and endocardium, respectively, in x axis. (TIF 78667 KB)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Magat, J., Ozenne, V., Cedilnik, N. et al. 3D MRI of explanted sheep hearts with submillimeter isotropic spatial resolution: comparison between diffusion tensor and structure tensor imaging. Magn Reson Mater Phy 34, 741–755 (2021). https://doi.org/10.1007/s10334-021-00913-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10334-021-00913-4