Introduction

Fluorine-19 (19F) magnetic resonance (MR) methods have found their application in a wide range of biomedical research areas. One branch of research is the tracking of cells, including inflammatory cells, in vivo with the help of fluorine 19F nanoparticles (NPs) [1,2,3,4,5,6,7]. 19F MR methods provide several advantages over methods employing contrast agents such as iron oxide particles that modulate proton relaxation [8, 9]. Iron oxide particles such as ultra-small iron oxide agents are potentially advantageous with regard to their MR sensitivity, but suffer from drawbacks such as signal quantification and a difficulty to distinguish the contrast which they create in the cells they label from other intrinsic tissue contrasts [8]. Due to the absence of organic 19F in living organisms, the acquired 19F MR images are free from background signal, such that 19F/1H MRI is able to localize labeled cells in vivo with complete signal selectivity and specificity. 19F MR directly detects the 19F spins in the cells labeled with 19F NPs, meaning that 19F NPs are cell labels, rather than contrast agents. The possibility of quantifying inflammatory cells by 19F MR spectroscopy is another advantage, allowing a quantitative assessment of inflammation and of anti-inflammatory strategies. However, the usefulness of 19F MR in a wide range of biomedical imaging applications is hampered by the low availability of 19F spins in the living organism. This is compounded by the fact that the signal sensitivity of current state-of-the-art MR equipment remains limited, making 19F MR measurements of fluorine compounds present at low concentrations an extremely challenging task.

Therefore, there is a need to improve the sensitivity of the measuring instrument to increase the signal-to-noise ratio (SNR). One way to improve signal sensitivity is to increase the strength of the static magnetic field (B0) [10], a strategy which has also been actively pursued for clinical application [11]. Intrinsic SNR is expected to grow at least linearly with increasing frequency and B0 strengths [12,13,14]. In early seminal studies using solenoid RF coils at frequencies (\( f \)) below 1 MHz, the maximum sensitivity was expected to be proportional to the frequency: sensitivity ∝ \( f \)1.75; this proportionality approached linearity when sample losses predominated [12, 13]. At low field strengths, the principle of reciprocity can be used to calculate the receive field (B1) sensitivity of a single channel RF coil in terms of the transmit field (B1+) that can be easily measured [15]. In the high-field domain, the increasing \( f \) and the influence of wave propagation need to be considered [10]. The homogeneity of the B1+ field is expected to decline with increasing B0, thereby influencing the overall SNR gain. An experimental study investigating SNR dependency on B0 in the human brain revealed SNR ∝ B 1.650 in the range of 3.0 T to 9.4 T [14]. A recent simulation study also showed that SNR grows super-linearly with frequency, particularly in the deeper regions of the sample; in less deep regions, the SNR versus B0 trend approached linearity [16]. Ultrahigh field imaging has proven particularly beneficial for X-nuclei imaging such as sodium MR, in which a change in B0 from 9.4 to 21.1 T resulted in an SNR gain of ~ 3 compared to a gain of ~ 2 for 1H MR [17].

Here, we studied the feasibility of 19F MRI at 21.1 T compared to 9.4 T, and the influence of the B0 change on the SNR and 19F relaxation of the compound fluoro-15-crown-5-ether (PFCE). According to theory and previously published experimental results, we postulated that SNR would increase by a factor of three to four when moving from 9.4 to 21.1 T. We therefore investigated how much of the expected sensitivity gain could be achieved in practical experiments. The rationale behind these experiments was to make use of higher B0 strengths to study inflammatory cell migration with better resolution and detail. Using 19F MRI and 19F NPs that label immune cells in vivo, we studied inflammation in experimental autoimmune encephalomyelitis (EAE), the animal model of multiple sclerosis [6, 18]. The main driving force for using higher B0 is to boost sensitivity and therefore resolution of the in vivo 19F MR images.

Materials and methods

Small animal MR scanners

All experiments were carried out on two small animal MR scanners with different magnetic field strengths: a 21.1 T vertical bore MR system operating at 900 MHz (1H) and 844.9 MHz (19F) at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee (Florida, USA) and a 9.4 T horizontal bore MR system (BioSpec 94/20, Bruker BioSpin MRI, Ettlingen) operating at 400 MHz (1H) and 376 MHz (19F) located in Berlin (Germany). The 21.1 T magnet was designed and constructed at the NHMFL [19]. It has a bore size of 105 mm and a 64-mm inner diameter imaging gradients (Resonance Research Inc, Billerica, MA) that provides a peak gradient strength of 6 mT/cm over a 64-mm diameter [20]. The 9.4 T system has a bore of 120 mm and an actively shielded B-GA12 gradient set providing gradient amplitudes of 4 mT/cm. Both MR systems are equipped with a Bruker Avance III console and operated using PV6.1 software (Bruker BioSpin, Ettlingen, Germany).

Radiofrequency (RF) coils and EMF simulations

Experiments were carried out on the 21.1 T using a linear low pass (LP) 19F/1H birdcage RF coil consisting of eight rungs: coil length = 54.5 mm, inner diameter = 33 mm, shield length = 64 mm, shield diameter = 53 mm. For experiments at the 9.4 T MR system, a linear high-pass 19F/1H RF coil of similar dimensions was used (12 rungs, coil length = 50 mm, inner diameter = 35 mm, shield length = 80 mm, shield diameter = 57 mm). To estimate the expected SNR gain, electromagnetic field (EMF) simulations were performed for both RF coils using the finite-element method (FEM) implemented in CST Microwave Studio (CST, Darmstadt, Germany). FEM was chosen over a time-domain solver because the unstructured finite-element meshes can more accurately resolve the current distributions occurring on metal structures with singular edges such as copper strips, thus leading to a more accurate loss estimation. Copper and substrate losses were calculated in the 3D domain by the FEM solver based on their respective conductivity and loss tangent values (copper conductivity σ = 5.8e7 S/m, FR4 tan δ = 0.025). Capacitors were assigned equivalent series resistances according to manufacturer datasheets, and solder losses also modeled as frequency-dependent resistors scaled to the desired frequency based on available literature data [21]. Both RF coils were loaded with a 15-ml falcon tube phantom filled with tissue equivalent material (ε = 78, σ = 0.79 S/m for 9.4 T, ε = 78, σ = 0.94 S/m for 21.1 T). Cable losses and preamplifier noise were approximated by appropriate attenuators inserted between the power source and the RF coil in the simulation; attenuation was set according to the losses at the respective frequency (9.4 T: 0.5 dB preamplifier noise figure, 2 m cable with 0.58 dB/m attenuation; 21.1 T: 1 dB preamp noise figure, 3 m cable with 0.9 dB/m attenuation). The coils were perfectly tuned and matched (|S11| < − 40 dB) and were fed with a forward power of 1 kW, which is dissipated in the system according to the noise power contribution of the different noise sources (Table 1). The average receive field (B1−) magnitude was calculated in a 5 × 5 × 5 mm cube in the isocenter of the coil. The relative estimated SNR between both systems was then calculated as follows:

$$ \frac{{{\text{SNR}}_{{21.1 {\text{T}}}} }}{{{\text{SNR}}_{{9.4 {\text{T}}}} }} = \left( {\frac{{f_{{0|21.1{\text{T}}}} }}{{f_{{0|9.4{\text{T}}}} }}} \right)^{2} \cdot \left( {\frac{{B_{{1|21.1{\text{T}}}}^{ - } }}{{B_{{1|9.4{\text{T}}}}^{ - } }}} \right), $$
(1)

where \( B_{1}^{ - } \) is the average receive field strength of each RF coil in \( \mu T/\sqrt {kW} \) [15].

Table 1 Contribution of each noise source to the total noise power
Full size table

Animal experiments

All experiments were conducted in accordance with the procedures approved by the Animal Welfare Department of the State Office of Health and Social Affairs Berlin (LAGeSo), and conformed to national and international guidelines to minimize discomfort to animals (86/609/EEC). Experimental autoimmune encephalomyelitis (EAE) was actively induced in SJL/J mice as previously described [18]. Female SJL/J mice (Janvier SAS, Le Genest-St-Isle, France) were immunized subcutaneously with 250 µg PLP139–151 purity > 95% (Pepceuticals Ltd., UK) together with Complete Freund’s Adjuvant and heat-killed Mycobacterium tuberculosis (H37Ra, Difco). On each day following immunization, mice were weighed and scored as follows: 0, no disease; 1, tail weakness and righting reflex weakness; 2, paraparesis; 3, paraplegia; 4, paraplegia with forelimb weakness or paralysis; 5, moribund or dead animal. Five days following EAE induction, mice were administered NPs containing 5 µmol of the 19F compound fluoro-15-crown-5-ether (PFCE) [18]. NPs were prepared by emulsifying 1200 mM PFCE (Fluorochem, UK) with Pluronic F-68 (Sigma-Aldrich, Germany) using a titanium sonotrode (Sonopuls GM70, Bandelin, Germany), as previously described [22]. NPs were administered daily to EAE mice from day 5 to day 10 after immunization. On day 10, the mice were transcardially perfused with 20 ml PBS followed by 20 ml 4% paraformaldehyde (PFA) following terminal anesthesia, after which the tissue was prepared for ex vivo MRI [18].

Sample preparation

In this study, we focused on PFCE since this 19F compound is commonly used to image inflammation and to track cells in vivo. We prepared (1) PFCE phantoms containing only pure PFCE (Setup 1), (2) NPs containing different concentrations of PFCE (Setup 2), (3) inflamed tissue infiltrated by inflammatory cells labeled with PFCE NPs (Setup 3). The same phantoms were used at both 9.4 T and 21.1 T B0 strengths.

For studying PFCE in pure form, we submerged an NMR tube containing pure PFCE in a 15-ml tube filled with water containing 4.5 g/L NaCl (this NaCl concentration provides the best electrodynamic loading conditions for a 15-ml tube for the RF coils used). For studying PFCE in nanoparticle form, four NMR tubes containing different PFCE concentrations (60 mM, 120 mM, 600 mM, 1200 mM PFCE) were submerged in a 50-ml tube containing 4.5 g/L NaCl. For studying PFCE in inflamed tissue, we prepared EAE mice that had been transcardially perfused with PBS and 4% PFA (see above). To examine PFCE in the inflamed central nervous system (CNS), as well as associated lymphatic tissue, the mice were cleared of the external pelt, extremities, and thoracic and abdominal tissues. Brain and spinal cord (CNS) were kept in situ within the skull and vertebral column, keeping head and neck draining lymph nodes (LNs) in the preparation. Other lymphoid tissue such as spleen was also harvested and stored separately in 2-ml tubes containing 4% PFA. All fixed tissue was stored at 4 °C. CNS/LNs preparations were transferred and secured within 15-ml tubes filled with 4% PFA. Spleens were inserted and secured within NMR tubes to maintain the longitudinal alignment of the tissue along the z-axis (B0 field) for both horizontal (9.4 T) and vertical (21.1 T) bores. The NMR tubes holding the spleens were then transferred to 15-ml tubes filled with 4.5 g/L NaCl. All 15-ml tubes (containing pure compound, CNS/LNs tissue or spleens) were positioned within a 50-ml tube.

MR measurements

To determine SNR differences in 19F measurements between the two magnetic field strengths, we made use of two of the above phantom setups (Setup 1 and Setup 2). For the 19F phantom with pure PFCE (Setup 1) we employed a 2D-FLASH technique with variable repetitions times (TRs) and flip angles (FAs): TR = 14–4000 ms, TE = 4.2 ms, FA = 5°–90°, dummy scans = 80, exc. pulse = sinc10H (3000 Hz), FOV = [32 × 32] mm2, matrix = 256 × 256, averages (NA) = 6, TA (acquisition time) = 0.5–30 min (according to TR). To quantify and compare SNR in a way more relevant for brain inflammation, we measured SNR as a function of the number of 19F atoms using phantoms containing different concentrations of 19F nanoparticles and different slice thickness (Setup 2). We acquired axial 19F MR images using 2D-RARE: TR = 4000 ms, TE = 9.1 ms, ETL (echo train length, rare factor) = 4, FOV = [30 × 30] mm2, matrix = 128 × 126, slices = 1–10 mm, NA = 1, TA = 17 min.

Parametric mapping was performed on axial slices of Setup 1 and Setup 2, as well as coronal slices of Setup 3 (EAE spleen tissue) to determine T1 and T2 of PFCE. A RARE sequence with variable repetition times (RARE-VTR) was used for T1-mapping. A multi-spin echo (MSE) technique was employed for T2-mapping. For Setup 1 (pure PFCE) we used the following parameters for RARE-VTR: 14 TRs = 29–5000 ms, TE = 5.6 ms, ETL = 4, FOV = [20 × 20] mm2, matrix = 144 × 144, slice thickness = 5 mm, NA = 2, TA = 17 min; for MSE: TR = 30 s, 40 × TEs = 160–6400 ms, FOV = [20 × 20] mm2, matrix = 96 × 96, slice thickness = 10 mm, NA = 4, TA = 3 h 12 min. For Setup 2 (PFCE nanoparticles) we used the following parameters for RARE-VTR: 15 TRs = 24–8000 ms, TE = 4.6 ms, ETL = 4, FOV = [30 × 30] mm2, matrix = 96 × 96, slice thickness = 10 mm, NA = 36, TA = 5 h 42 m; for MSE: TR = 4000 ms, 150 TEs = 7–1050 ms, FOV = [30 × 30] mm2, matrix = 96 × 96, slice thickness = 10 mm, NA = 64, TA = 6 h 49 min. For Setup 3 (spleens from EAE mice administered with nanoparticles) we acquired different repetitions of the same coronal spleen slice using RARE-VTR: 9 TRs = 50–12000 ms, TE = 6.9 ms, ETL = 4, FOV = [20 × 30] mm2, matrix = 44 × 64, slice thickness = 3.6 mm, NA = 128, TA = 15 h 50 min.

For visualizing inflammation in the EAE mouse CNS and associated lymph nodes, we acquired 1H MR images using 3D-FLASH: TR = 150 ms, TE = 7.5 ms, FOV = 30 × 20 × 20 mm, matrix = 600 × 400 × 400, NA = 2, TA = 3 h 20 min and 19F MR images at different spatial resolutions using 3D-RARE: TR = 800 ms, TE = 4.9 ms, FOV = 30 × 20 × 20 mm, NA = 256, high-resolution: matrix = 195 × 130 × 130, ETL = 33, TA = 7 h 30 min; medium-resolution: matrix = 135 × 90 × 90, ETL = 23, TA = 5 h 14 min; low-resolution: matrix = 90 × 60 × 60, ETL = 15, TA = 3 h 24 min.

Data analysis

SNR was calculated using MATLAB® (R2018a, The Mathworks, Natick, USA) by dividing the signal from magnitude images (Sm) by the standard deviation of the background (σm). For both Setup 1 and Setup 2, a single SNR value was determined from the mean signal intensity over one central circular regions of interest covering ~ 90% of visible sample and the standard deviation of the noise of four region of interests positioned at the corners of the image. SNR was corrected to compensate for the non-Gaussian distribution [23]. For both single channel RF coils used, the intensity values of the MR images are expected to follow a Rician distribution [24, 25]. We estimated the true SNR from the Sm and background σm using:

$$ {\text{SNR}} = \frac{S}{\sigma } = \frac{{S_{\text{m}} }}{{\sigma_{\text{m}} }} \cdot \frac{{f_{\text{S}} \left( {S_{\text{m}} ,\sigma_{\text{m}} } \right)}}{{1/c_{\sigma } }}, $$
(2)

where cσ is 0.655 (for Rician distribution) and the correction function fS is derived from the mean of the respective distribution [24, 26]. The noise-induced signal bias of the conventional Fourier reconstructed images was corrected [24]. All image reconstructions were thresholded to 3.5σ to distinguish between background and signal voxels. The number of 19F atoms per image pixel was estimated from the PFCE concentration and the voxel size, and plotted against the SNR. Two-factor ANOVA was used to compare SNR (dependent variable) at various numbers of fluorine atoms between the two field strengths (independent variables). GraphPad Prism v.5.01 (GraphPad Software, Inc. La Jolla, CA, USA) was used for the analysis. SNR efficiency (SNReff) for 2D-FLASH data was calculated as follows [27]:

$$ {\text{SNR}}_{\text{eff}} = \frac{\text{SNR}}{{\sqrt {{\text{NA}} \times {\text{TR}}} }}. $$
(3)

Calculations of PFCE T1 and T2 relaxation times were performed on MSE and RARE-VTR scans using parametric mapping developed in MATLAB® in-house. T1 and T2 were determined by fitting the following relation [28] to the obtained data points using least-squares optimization:

$$ S_{{\left( {\text{TR}} \right)}} = S_{0} \cdot \left( {1 - \exp \left( {\frac{{ - {\text{TR}}}}{{T_{1} }}} \right)} \right), $$
(4)
$$ S_{{\left( {\text{TE}} \right)}} = S_{0} \cdot \exp \left( {\frac{{ - {\text{TE}}}}{{T_{2} }}} \right), $$
(5)

where S(TR) and S(TE) are the signal intensity at a specific repetition time and specific echo time, respectively, S0 is the maximum signal and TR and TE are a specific repetition time and specific echo time, respectively. Depending on the experiments, relaxation times were calculated either as pixel-based data points or averaged data within specific regions of interest, corrected for the non-Gaussian noise distribution in MR magnitude images [24].

Calculations of T1 relaxation time for PFCE were also performed on 2D-FLASH acquisitions with different TRs and FAs (α). T1 was calculated from the Ernst equation [29]:

$$ S_{{\left( {{\text{TR}},\alpha } \right)}} = S_{0,\alpha } \cdot \sin \cdot \frac{{1 - { \exp }({\raise0.7ex\hbox{${ - {\text{TR}}}$} \!\mathord{\left/ {\vphantom {{ - {\text{TR}}} {T_{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T_{1} }$}})}}{{1 - \cos { \exp }({\raise0.7ex\hbox{${ - {\text{TR}}}$} \!\mathord{\left/ {\vphantom {{ - {\text{TR}}} {T_{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T_{1} }$}})}}, $$
(6)

where S(TR,α) is signal intensity at a specific repetition time and flip angle (α) and S(0,α) is the maximum signal intensity at a specific α.

For a 3D representation of 19F 1H MR image overlays of Setup 3 (EAE mouse brain and associated lymph nodes), 1H MR data were first converted to NIFTI-format in ImageJ (National Institutes of Health, USA, http://imagej.nih.gov/ij and 1H MR images of inflamed regions (CNS) and draining lymph nodes were segmented using ITK snap (version 3.4) [30].

Results

Estimation of noise contribution and SNR gain from 9.4 to 21.1 T

Prior to performing the practical experiments, we estimated the SNR gain to be expected at 21.1 T from simulations. We first studied the noise contributions for both the 9.4 T and 21.1 T MR systems. The intrinsic noise contribution of the RF coil (capacitors, copper and housing) compared to the total noise power (Table 1) showed that the 9.4 T coil was only slightly more sample noise dominated (35.5% sample vs. 32.6% intrinsic coil losses). The intrinsic noise contribution of the 21.1 T coil is lower: in contrast to the 9.4 T coil, the sample noise dominates over the coil noise contribution (37.1% sample vs. 5.4% intrinsic coil losses). At 21.1 T, the noise contributed by the total cable length (between preamplifier and coil) as well as preamplifier noise appeared to be higher, almost double that of the 9.4 T system. For birdcage coils, as used in this study, the transmit field (B1+) is expected to be approximately equal to the receive field (B1−). From the simulations we calculated an average B1− field strength of 288 μT at 9.4 T and 153 μT at 21.1 T, for a forward power of 1 kW. Using the principle of reciprocity [15], and ignoring all flip angle, sequence and relaxation-dependent effects, the expected SNR ratio was calculated as 2.68 using Eq. (1). This ratio represents a baseline estimation of the expected SNR gain, based on the information available for the specific hardware of each system. Additionally, one can estimate the SNR gain between the two systems by considering the relationship of the individual reference powers required for calibrating a 90° flip angle. The reference power required at 9.4 T and 21.1 T was 0.257 W and 0.338 W, respectively. This translates to a field magnitude of 12.3 \( \mu T/\sqrt {kW} \) at 9.4 T and 9.3 \( \mu T/\sqrt {kW} \) at 21.1 T. The ratio between the two field magnitudes (0.76) can be used as a scaling factor in Eq. (1) to calculate SNR gain from the quadratically increasing MR signal strength. This yields an estimated SNR gain of ~ 3.8, when reference power is factored into the Eq. (1).

Experimental SNR difference between 9.4 T and 21.1 T

To determine the actual SNR gain we acquired axial 19F MR scans of a nanoparticle phantom (Setup 2) containing four different concentrations of PFCE (Fig. 1a). We used a 2D-RARE sequence with variable slice thicknesses (1–10 mm, in steps of 0.5 mm). This together with the four different PFCE concentrations resulted in a total of 76 experiments to estimate SNR as a function of the number of 19F atoms per voxel for both B0 strengths. Figure 1a illustrates 20 of these SNR experiments (only 5 slice thicknesses are shown). Results of all SNR experiments were then plotted against the number of 19F atoms per voxel for both B0 strengths (Fig. 1b). There was a significant difference in the SNR for all 76 experiments between the two B0 strengths observed at varying numbers of fluorine atoms (p < 0.0001, two-factor ANOVA). A mean SNR gain of 2.1 was estimated. For these experiments, we used a long TR in the 2D-RARE method to measure SNR differences between B0 strengths.

Fig. 1
figure 1

Comparison of SNR between 21.1 and 9.4 T B0 strengths in PFCE nanoparticles using a 2D-RARE sequence. a SNR was calculated from axial images of four NMR tubes (60 mM, 120 mM, 600 mM, 1200 mM) with varying slice thicknesses (shown are MR images of 1, 2, 4, 6 and 8 mm slice thickness). SNR was calculated by dividing signal from magnitude images by the background standard deviation, and corrected to compensate for the non-Gaussian Rician distribution. b Plot of SNR versus 19F atoms per voxel. A linear fit was determined for both 21.1 T (y = 4e−19x, R2 = 0.9983) and 9.4 T (y = 2e−19x, R2 = 0.9996). A significant difference was determined between 9.4 and 21.1 T, p < 0.0001, two-factor ANOVA

Full size image

In the next experiments, we studied the dependency of the actual SNR gain on the TR and flip angle (α) at both B0 strengths. Axial 19F MR scans of the pure PFCE compound (Setup 1) were acquired using a wide range of TRs (14–4000 ms) and α (5°–90°). SNR changes over the relaxation period were studied and the T1 relaxation values for both B0 strengths determined (Fig. 2). A 2-D fit of the measured data points resulted in T1|9.4T = 788 ms (Fig. 2a) and T1|21.1T = 409 ms (Fig. 2b). The choice of TR has a direct impact on the total acquisition time. A shorter TR permits more averages to be acquired in the same time period. To take this into consideration we estimated the SNR achievable in a fixed amount of time [27] (SNR efficiency = SNR/\( \sqrt t \)) from the data obtained at 9.4 T (Fig. 2c) and 21.1 T (Fig. 2d). For all scans with TR shorter than 4 s, we calculated how many averages would be possible within the fixed acquisition time, and then added the corresponding SNR improvement, based on the theoretical relationship SNR ~ \( \sqrt {\text{NA}} \). As expected, SNR/\( \sqrt t \) favors very short TRs for both B0 strengths. The maximal SNR/\( \sqrt t \) for 9.4 T was calculated to be 96/\( \sqrt {\hbox{min} } \) at TR = 20 ms and α = 13°, while the maximal SNR/\( \sqrt t \) for 21.1 T was calculated to be 701/\( \sqrt {\hbox{min} } \) at TR = 20 ms and α = 18°. At the optimal condition for 9.4 T, i.e., TR = 20 ms and α = 13°, the SNR/\( \sqrt t \) for 21.1 T was calculated to be 668/\( \sqrt {\hbox{min} } \). The SNR/\( \sqrt t \) ratio (between 21.1 T and 9.4 T) at these conditions is therefore 6.95, while the SNR/\( \sqrt t \) ratio when comparing the best possible conditions for 21.1 T with the best possible conditions for 9.4 T is estimated to be 7.29. The SNR/\( \sqrt t \) ratio will vary between the two B0 strengths, according to the specific α and TR chosen for the particular experimental setup. Within a sensible range of α (1°–90°) and TR (15–4000 ms), the minimum SNR/\( \sqrt t \) ratio would be 5.5 (at TR = 4000 ms, α = 1°) and the maximum would be 10.0 (at TR = 15 ms, α = 90°). However, these results illustrate the SNR/\( \sqrt t \) ratio due to changes in both B0 and T1. To distinguish between both influencing factors, we modeled the SNR/\( \sqrt t \) at 21.1 T for the T1 observed at 9.4 T (T1|21.1T = T1|9.4T = 788 ms). With this we could determine the B0 effect on SNR efficiency independent of T1 effects (Fig. 3): the maximal SNR/\( \sqrt t \) for 21.1 T was calculated to be 505/\( \sqrt {\hbox{min} } \) at TR = 20 ms and α = 13°, in comparison to the 96/\( \sqrt {\hbox{min} } \) at the same TR and α for 9.4 T. This translates into an SNR/\( \sqrt t \) ratio of 5.25 in comparison to 6.95 (when T1 relaxation effects at 21.1 T were considered, T1|21.1T = 409 ms). In consequence, the T1 shortening at 21.1 T results in an additional increase in SNR efficiency by a factor of 1.3 (Fig. 3).

Fig. 2
figure 2

Comparison of SNR between 21.1 T and 9.4 T B0 strengths for pure PFCE using a 2D-FLASH sequence. SNR measurements at various repetition times (TR = 14–4000 ms) and flip angles (α = 5°–90°) for both 9.4 T (a) and 21.1 T (b) B0 strengths. 2-D fitting of these data points resulted in T1|9.4T = 778 ms and T1|21.1T = 409 ms. SNR efficiency (SNR/\( \sqrt t \)) defined as the SNR achievable in a fixed amount of time was estimated for data obtained at 9.4 T (c) and 21.1 T (d)

Full size image
Fig. 3
figure 3

SNR efficiency changes between 21.1 T and 9.4 T B0 strengths for PFCE as a result of B0 and T1 effects. The B0 factor on SNR efficiency at 21.1 T was calculated to be 5.25 after modeling SNR/\( \sqrt t \) to keep T1 between both magnetic fields constant (T1|21.1T = T1|9.4T = 788 ms). The T1 factor on SNR efficiency at 21.1 T was calculated to be 1.3

Full size image

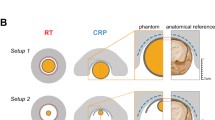
We recently reported on the sensitivity gain achieved when comparing a cryogenically cooled 19F RF probe (19F CRP) with a room temperature 19F RF coil of similar size [18]. Here, we attempted to compare the sensitivity gain achieved when moving from 9.4 T to 21.1 T with that achieved by using the 19F CRP (Fig. 4). Although the two volume resonators used in the B0 comparison were designed for the mouse body, the two RF coils used to determine SNR gains with the 19F CRP were designed for the mouse head (Fig. 4, left panels). For all four RF coil configurations, we studied the SNR of the same phantom (pure PFCE, Setup 1) employing the parameters TR = 18.4 ms and α = 15°, which are close to the conditions calculated to give the best SNR/\( \sqrt t \) for the same sequence. The 19F CRP is a transceive surface RF coil and does not achieve a spatially uniform excitation [18]. When studying the B1 characteristics of this coil, a strong FA decrease is observed with increasing distance from the 19F CRP surface [18]. In the previous experiments, we used one NMR tube with PFCE in the middle of the phantom. For the RT versus CRP comparison, we used two NMR tubes with PFCE to study the SNR gain at regions distal and proximal to the 19F CRP surface. While the factor in the SNR change for the B0 comparison was 6.59, the factor in SNR change from RT to 19F CRP was 7.49 when measuring proximal to the 19F CRP surface (upper ROI) and 0.93 when measuring distal to the 19F CRP (lower ROI) (Fig. 4).

Fig. 4
figure 4

19F MR sensitivity gain differences between the B0 comparison from 9.4 to 21.1 T and a RT versus 19F CRP comparison. Upper panel: B0 comparison between 9.4 and 21.1 T using room temperature (RT) 19F mouse body volume resonators with a diameter of 33–35 mm. Lower panel: RT versus CRP comparison using a RT 19F mouse head coil and a 19F CRP

Full size image

Relaxation times of PFCE at 9.4 T and 21.1 T

From the previous experiments, it was evident that T1 relaxation was influenced by B0. We next studied the impact of increasing B0 to 21.1 T on both the T1 and T2 relaxation for PFCE nanoparticles. Similar to other nuclei, the transverse spin–spin (T2) relaxation was decreased when moving from 9.4 T to 21.1 T (Fig. 5a). The PFCE concentration did not influence changes in the T2 values of the nanoparticles at either B0 strengths (Table 2). The longitudinal spin–lattice (T1) relaxation time of PFCE nanoparticles was substantially shorter at 21.1 T, approximately 50% compared to 9.4 T (Fig. 5b). T1 values were also not influenced by the PFCE concentration in the nanoparticles (Table 2). Shortening of the T1 at higher B0 strengths is not common for 1H, where T1 values are typically known to increase with increasing B0 [31, 32]. The shortening of T1 for PFCE at 21.1 T was consistent for different forms of the 19F compound (Table 3). The 50% decrease in T1 was observed in the pure compound (Fig. 2a), PFCE nanoparticles (Fig. 5b) and in ex vivo tissue from EAE mice administered PFCE nanoparticles (Fig. 6).

Fig. 5
figure 5

19F relaxation times for PFCE nanoparticles measured at 21.1 T and 9.4 T. aT2 relaxation of PFCE nanoparticles at 21.1 T was shorter than T2 relaxation at 9.4 T (T2|21.1T = 195 ms T2 | 9.4T = 503 ms). bT1 relaxation of PFCE nanoparticles at 21.1 T was shorter than T1 relaxation at 9.4 T (T1|21.1T = 441 ms; T1|9.4T = 913 ms)

Full size image
Table 2 No influence of PFCE concentration on T1 and T2 in 19F nanoparticles
Full size table
Table 3 T1 shortening at 21.1 T is consistent in all PFCE samples studied
Full size table
Fig. 6
figure 6

19F relaxation times for PFCE in ex vivo EAE spleen measured at 21.1 T and 9.4 T. Spleens were harvested from EAE mice that had been administered PFCE nanoparticles for 5 days during imitation of disease. a1H MR scan of the ex vivo EAE spleen positioned in an NMR tube using 3D-FLASH: TR = 1500 ms, TE = 6.5 ms, FOV = [20 × 30 × 3.6] mm3, matrix = 400 × 600 × 72, NA = 1, TA = 23 m. bT1 maps were generated on one coronal slice of the spleen using RARE-VTR: 9 × TRs = 50–12,000 ms, TE = 6.9 ms, ETL = 4, FOV = [20 × 30] mm2, matrix = 44 × 64, slice thickness = 3.6 mm, NA = 128, TA = 15 h 50 m. The averaged intensities over the coronal slice for all image series were fitted to the T1 and T2 equations

Full size image

High spatially resolved 19F MR imaging of EAE inflammation

To utilize the SNR gain observed in the above experiments to maximum advantage within the context of neuroinflammation, we investigated the feasibility of 19F MR imaging at 21.1 T to detect brain inflammation in EAE at high spatial resolutions (Fig. 7). We observed a high level of detail of immune cell distribution in the inflamed brain and accompanying draining lymph nodes. Employing a resolution of 150 μm3 at 21.1 T, 19F MR signals were observed especially localized to the brain parenchyma (Fig. 7a). At this spatial resolution, these 19F signals were not observed at 9.4 T when using a smaller room temperature coil [18]. When using the same RF coils employed in the present study to compare 19F MR images in EAE mice, we observed even larger differences between 9.4 T and 21.1 T; even at low and medium spatial resolutions (222 µm3 and 333 µm3) most 19F MR signals detected at 21.1 T were no longer identified at 9.4 T (Supplementary Figure). Given the highly homogeneous field provided by the RF coil used at 21.1 T, we could equally observe very prominent 19F MR signals within the draining lymph nodes in the ventral region of the EAE mouse head.

Fig. 7
figure 7

19F MR image of an ex vivo EAE mouse acquired at 21.1 T and at different spatial resolutions. 19F MR images were acquired using a 3D-RARE sequence acquired at three different spatial resolutions: a high: matrix = 195 × 130 × 130, resolution = 153 µm3, b medium: matrix = 135 × 90 × 90, resolution = 222 µm3, c low: matrix = 90 × 60 × 60, resolution = 333 µm3. 19F MR images (shown in red) were scaled to units of SNR (pseudocolor scale), thresholded at SNR = 4, and overlayed onto the FLASH 1H anatomical MR images (shown in grayscale). For all three spatial resolutions both horizontal (upper panel) and 3D-render (lower panel) views of the EAE mouse brain and accompanying draining lymph nodes are shown

Full size image

Discussion

In this study, we demonstrate the feasibility and increased sensitivity of 19F MR methods at 21.1 T for detecting inflammation with high spatial definition in the brain and adjacent lymphatic system in the animal model of multiple sclerosis. The potential applications of 19F MR methods to image inflammation have long been recognized [1,2,3,4,5, 7], even in autoimmune encephalomyelitis [6, 33, 34]. 19F MR methods are conceptually appealing due to the superiority of 19F nuclei over other MR-sensitive nuclei with regard to signal selectivity and specificity. However, they are constrained by sensitivity due to their typically low availability in vivo. Therefore, numerous efforts have been made to boost 19F signal, e.g., by optimizing the efficiency of the acquisition methods according to the T1 and T2 values of the specific 19F compounds [27], increasing the number of available 19F nuclei by promoting 19F nanoparticle cellular uptake [35] or by improving the sensitivity of the RF hardware by introducing cryogenically cooled RF probes [18]. Nevertheless, major challenges in signal sensitivity constraints remain. Improving 19F sensitivity using a combination of all currently available strategies, as well as developing new solutions, will be essential to realize the full potential of 19F MR.

Here, we studied the potential of increasing B0 for improving 19F MR signal sensitivity. Prior to the practical experiments, we estimated the expected SNR gain to be 2.7, when moving from 9.4 to 21.1 T, taking into account the noise contributions for both MR systems and using the principle of reciprocity [15]. When we introduced the relationship of the reference power for both MR systems into Eq. (1), we estimated an SNR gain of ~ 3.8. In our practical experiments, we realized an SNR gain of 2.1 when employing a 2D-RARE technique on different concentrations of nanoparticles. In 2D-FLASH measurements, the ratio in SNR efficiency (SNR/\( \sqrt t \) ratio) was estimated to be 7.29, when comparing the best possible conditions (optimal TR and α) at 21.1 T with those at 9.4 T and when including T1 relaxation effects. Differences between the actual SNR gains determined experimentally and those expected from theory and simulations are conceivable, due to minor inaccuracies in the assumptions made for the EMF simulations. Factors such as sample noise, RF coil geometries, receive chain losses and preamplifier noise figure may add to the confounding influences that alter the actual SNR gain. In contrast to human imaging, the measurement noise in small animal imaging is dominated by the measurement hardware and not by the sample [36]. Thus in small animal MR scanners, differences in coil geometries and detector electronics can have a larger impact on the variations from expected sensitivity gains. Our estimations showed that in contrast to the 9.4 T RF coil, the intrinsic noise contribution of the 21.1 T RF coil was much lower than the sample noise contribution. However, the noise contributed by the relative long cables needed for the probe body (~ 2 m) with the 21.1 T and preamplifier was estimated to be higher, indeed almost double those at the 9.4 T system. Therefore, the highest potential for increased SNR gains (potentially up to ~ 40%) at 21.1 T could be achieved by using the shortest cables possible (e.g., by placing the preamplifier as close to the coil as possible) or using preamplifiers with a lower noise figure.

Another factor that must be considered when investigating B0-influenced SNR changes is the potential changes in relaxation. Both spin–lattice (T1) and spin–spin (T2) relaxation times are expected to change with increasing B0 fields. The SNR gain of 3.8 derived from the simulations does not take changes in relaxation time into account. When T1 relaxation effects were removed from the experimental data, we calculated an SNR/\( \sqrt t \) ratio of 5.25 (instead of 7). It is only in the fully relaxed regime that the SNR gain is expected to be influenced primarily by B0 and not influenced by T1-weighting. Water shows a highly significant increase in T1 relaxation and decrease in T2 relaxation in different regions of the rat brain with increasing B0 in the range from 4.0 to 11.7 T [31]. Knowledge of T1 relaxation is particularly crucial for MR spectroscopy and quantification of specific compounds. Brain metabolites show a similar, but less pronounced trend as water with respect to proton relaxation. Conversely, macromolecules display a strong dependency of T1 on B0, but T2 is field independent [31]. Proton T1 relaxation of brain metabolites does not increase substantially beyond 9.4 T (up to 14 T) and any changes likely have minimal impact on sensitivity [37]. Particularly for 19F MR methods, where sensitivity is a crucial factor, it is critical to understand the mechanisms of T1 relaxation. Interestingly, T1 relaxation for 19F compounds appears to be inversely related to B0 strength. The decline in T2 at higher B0 could hamper the expected increase in 19F MR signal at 21.1 T and warrants further consideration. The decline in T1 with increasing B0 is consistent with previous studies [38, 39]. Thus far, a decrease in 19F T1 for 19F compounds has been attributed to an influence from dipole–dipole interactions and chemical shift anisotropy [38].

A decrease in T1 for 19F compounds with increasing B0 has substantial ramifications, since this suggests the opportunity to increase SNR per unit time at higher magnetic field strengths by introducing more averaging. The T1 shortening at 21.1 T observed in this study could provide one mechanism for the ratio in SNR efficiency (7.29) estimated from the 2D-FLASH experiments using optimal TRs and α specific to each B0 strength. The observations made here at 21.1 T are especially meaningful for studies that are hampered by the low availability of 19F spins and thus have a pressing need for sensitivity gains. An SNR gain could be exploited in several ways: e.g.. for a gain of 7.29, either the scan time could be reduced by a factor of 53 (e.g., from 60 to ~ 1.1 min) to obtain the original SNR or higher spatial resolution could be employed to achieve better image definition. In this study we made use of the SNR gain to acquire isotropic spatial resolutions of 150 μm3 to study neuroinflammation (19F MR signals) more precisely. At this resolution, we aimed to gain more precise information regarding inflammatory cell localization in the brain, compared to our previous studies [6]. The level of detail achieved at 21.1 T was similar to that of the 19F MR images we recently obtained with a 19F cryogenic RF probe (CRP) where we reported on a maximal SNR gain of 15 and were able to study intraparenchymal inflammation at a high isotropic resolution of 150 μm [18]. In the present study, we made the best feasible comparison of the sensitivity gains achievable between 19F CRP and a B0 increase to 21.1 T, given the current hardware limitations. Although different RF coil sizes and geometries were used to make this comparison, we measured the same sample (pure PFCE) and used the same sequence parameters. Employing the 2D-FLASH technique used in the present study, we observed an SNR gain of 6.59 at 21.1 T when compared to 9.4 T, and an SNR gain of 7.49 with the CRP when compared to a room temperature coil of similar size. As discussed previously [18], the SNR gains achieved with the 19F CRP can be attributed to several factors in addition to cooling: differences in RF coil design (birdcage vs. surface coil; quadrature versus linear), RF coil sample loading, and the specific RF pulse power adjustments all play important roles [18]. Even though the SNR gain achieved by moving from 9.4 T to 21.1 T is slightly lower than that realized at 9.4 T with a 19F CRP, the SNR gain at 21.1 T is consistent throughout the entire field of view due to the homogeneity of the RF volume coils used. This is in striking contrast to the CRP, which has an inherent limitation due to the declining gradient in the B1 field with increasing distance from the surface due to the transceive surface coil design [18]. Therefore in contrast to the 19F CRP, 19F signals in ventral regions of the head were prominently detected with a resolution of 150 μm at 21.1 T. Given the difficulty of detecting 19F signals in these distal structures, most studies of the EAE model tend to focus exclusively on imaging of the brain. The advantages gained from using volume resonators at 21.1 T will allow a more comprehensive and detailed study of immune cell dynamics within the draining lymph nodes. On the other hand, studies focusing on the brain could be enhanced by using a CRP at this field strength. A fusion of both SNR boosting strategies has the potential for realizing even greater levels of detail when studying experimental brain pathologies.