Policy measures to promote mid-summer drainage in paddy fields for a reduction in methane gas emissions: the application of a dynamic, spatial computable general equilibrium model

Abstract

Rice production is affected by climate change, while climate change is simultaneously accelerated by methane gas (CH₄) emissions from paddy fields. The rice sector must take suitable mitigation measures, such as prolonging mid-summer drainage (MSD) before the rice flowering period. To propose a mitigation policy, this study aims to demonstrate the environmental and economic effects of MSD in Japanese paddy fields by using a dynamic, spatial computable general equilibrium (CGE) model and crop model; the study also considers environmental subsidies with a carbon tax scheme to promote MSD measures. The results demonstrate that climate change under the 8.5 representative concentration pathway (RCP) scenario will reduce rice prices and rice farmers’ nominal income due to bumper harvests until the 2050s. Promoting MSD in paddy fields can prevent a decrease in farmers’ nominal income and effectively reduce CH₄ emissions if all farmers adopt this measure. However, some farmers can potentially increase their own yield by avoiding MSD under high rice prices, which would be maintained through other farmers’ participation. A strong motivation exists for some farmers to gain a “free ride,” and an environmental subsidy with a carbon tax can help motivate farmers to adopt MSD. Therefore, the policy mix of prolonging MSD and environmental subsidies can increase all farmers’ incomes by preventing “free rides” and decrease greenhouse gas emissions with a slight decrease in Japan’s GDP.

Introduction

Rice production highly depends on climate conditions, including temperature, solar radiation, and precipitation. Future climate change will affect rice production, while greenhouse gas (GHG) emissions from rice production will simultaneously accelerate the warming process. Methane (CH₄) is the second-largest GHG in terms of abundance in the Earth’s atmosphere, and CH₄ emissions from paddy fields account for more than 10% of worldwide CH₄ emissions. As these numbers are not ignorable, the rice sector must take suitable mitigation measures to decrease CH₄ emissions and tackle future climate change. Further, it is crucial to quantify the economic effects of reducing CH₄ in creating better policy measures from both the environmental and economic perspectives.

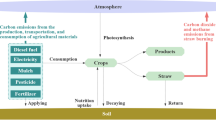
Mid-summer drainage (MSD) before the rice flowering period generates cracks in paddy fields and introduces air to the root zone (Fig. 1). Such aeration increases the rice yield and decreases the total CH₄ production from paddy fields; however, an excessively long MSD period decreases rice production, in spite of an additional reduction in CH₄ emissions (Itoh et al. 2011). This is one trade-off in prolonging MSD. Naturally, farmers are not obliged to participate in MSD, as the cultivation of rice began thousands of years ago, before the start of climate change. Additionally, ceasing rice production does not solve the problem, because most paddy fields could turn to swamp and still continue to emit CH₄. Considering this background and the trade-off effects, incentives for farmers must be introduced to encourage their cooperation.

Fig. 1

Source: Itoh et al. (2011)

MSD implementation and its effects. Note: The signs on the horizontal axis indicate the location of survey fields; “Y,” “F,” “N,” “G,” “A,” “T,” “KM,” and “KG” represent the Yamagata, Fukushima, Niigata, Gifu, Aichi, Tokushima, Kumamoto, and Kagoshima prefectures, respectively.

This study aims to quantify the effects of both prolonging the MSD period and offering environmental subsidies with a carbon tax as mitigation measures by using a dynamic, spatial computable general equilibrium (CGE) model. When future situations are simulated, (i) projection results from global climate and crop yield models are used, (ii) the trade-off effects of MSD and the compensation effects of environment subsidies with a carbon tax are concretely quantified, and (iii) regional differences are considered.

The rest of this paper is organized as follows: “Literature review and scientific questions” section reviews previous studies on CGE analyses to evaluate climate change. “Method” section explains the analytical methods. “Results” section shares the results of several simulations using the CGE model, and the final section concludes and discusses policy implications.

Literature review and scientific questions

Itoh et al. (2011) measured the trade-off effects of MSD from field surveys in several regions in Japan and compared prolonging the MSD period for one more week against the conventional period (Fig. 1). Their data indicated that an additional MSD period decreased CH₄ emissions by 30% on average (11–55%), but decreased rice yields by 5% (from a 14% decrease to a 10% increase). If all farmers assumed this MSD measure, 1.67 million tons of CH₄ could be reduced annually throughout Japan. This number is 30% of total CH₄ emissions or equal to 5.57 million tons of CO₂ from all paddy fields in Japan.

In terms of future rice production, previous studies using a rice crop model indicate that the initial high levels of rice yields will eventually decline at summer temperatures of higher than 28 °C; such a change will be especially obvious in western Japan after the 2040s (Iizumi et al. 2009). Further, Kunimitsu et al. (2015) used the rice crop model’s projection results to analyze the causative factors for total factor productivity (TFP), which is a comprehensive productivity index, in Japanese rice production under climate change conditions. Consequently, (i) temperature and solar radiation were shown to have high potential impact on rice yields, next to economies of scale, as represented by each farm organization’s farm management scale, and (ii) both climate and socioeconomic factors were shown to widen regional gaps in rice TFP over time.

The economic influences of future climate change in the global food market were analyzed by an econometric model (Furuya et al. 2014). The model’s rice yield function was estimated by considering the temperature and precipitation during the rice maturation period. The simulation results indicated that a future temperature increase would increase rice production in most Asian countries, including Japan, but excess temperatures would have negative effects. This previous study focused on future agricultural productivity, but could not fully capture the feedback effects from other markets and agents. Thus, a macroeconomic analysis with a general equilibrium framework is needed to evaluate policy measures under resource restrictions and by considering government sectors.

The CGE model depicts inter-market relations and trade flows in the economy as a whole and considers the circular flow of income and expenditures under limited resources. Therefore, CGE models are better suited for analyzing global effects on agricultural markets and policy issues, as is the case with climate change (Masui 2005; Palatnik and Roson 2012; Kunimitsu 2018). Further, Lee (2009) used a multi-sector CGE model to analyze the impact of climate change on global food prices and quantities; his analysis revealed that climate change benefited developed countries in their crop yields, but negatively influenced developing countries. Calzadilla et al. (2011) used a CGE model to analyze the effects of climate change on agriculture relative to water use. Their results indicated that climate change had mostly positive effects on social welfare in water-stressed regions, but these influences were more complicated, and mostly negative, in regions in which water was not scarce. Kunimitsu (2015) also analyzed the influences of climate change on the Japanese economy with a CGE model. This study demonstrated that until the 2040s, future climate change would increase rice production, but decrease farmers’ income due to substantial price decreases.

Regarding mitigation and adaptation measures, the CGE model was also used to evaluate carbon tax and CO₂ emissions trading. Most previous studies note that these instruments decreased carbon emissions with relatively little economic distortion (Ekins and Barker 2001), but in reality, only a few countries adopted these measures. Further, other tax reductions or environmental subsidies that use carbon tax revenues can potentially create economic profit; this is called the “double-dividend hypothesis.” Regarding Japanese environmental policy, Kawase et al. (2003) noted a positive effect from decreasing social insurance premium payments through carbon tax revenues, supporting the double-dividend hypothesis. In contrast, Takeda (2007) mentioned that a decrease in labor or income taxes through carbon tax revenues created no profits in Japan, as labor and income taxes were less distortionary than others. These different effects from the double-dividend hypothesis likely depend on the policy measures in which the carbon tax revenues are used.

As these previous studies indicate, CGE models have great potential in evaluating the effects of environmental policy measures and considering resource limitations. However, few studies focus on the economic ripple effects of the measures to decrease CH₄ emissions. As little room exists for CO₂ reduction in Japan, it is useful to consider decreasing CH₄ emissions and evaluate the use of MSD and environmental subsidies with a carbon tax as potential environmental policy measures.

Method

Structure of the recursive–dynamic spatial CGE model

The model used here is the recursive–dynamic CGE model with considering inter-regional relationships;¹ this model’s structure is based on work by Ban (2007) and Kunimitsu (2015).² The major deviations from the original model are as follows.

The cost functions, as derived from the production functions, are formed as a nested type of CES (constant elasticity of substitution) function (Fig. 2). These functions are based on the firms’ optimization behavior. The bottom part of added value composed of capital and labor is Cobb–Douglas type function which is commonly used in the previous studies. Farmland is then joined to production with consideration of low substitutability against capital and labor (Kunimitsu 2015). Intermediate inputs and value-added production create total production with Leontief type functional form. After calculating total production, imports and exports are, respectively, defined by the Armington’s function and the CET (constant elasticity of transformation) function.

Fig. 2

Structure of production inputs. Note: The s here indicates the substitution elasticities in the CES function, and s^r indicates the spatial substitution elasticities

The prices of each industry in the region are assumed to have different prices, because some products produced in different regions have discriminatory prices in the market. Hence, the same industrial goods and services produced in other regions are traded and used for production. The market’s degrees of regional differentiation depend on the flexibility of inter-regional trade, represented by the spatial substitution elasticity (s^r) as illustrated in Fig. 2. Tsuchiya et al. (2005) empirically showed these spatial substitution elasticity values were between 0.40 and 8.0, while Koike and Naka (2014) used each Japanese industry’s data to discover that these values differed according to the industry, and most had values of approximately 1. Their estimations are smaller than Armington’s substitution elasticity noted in GTAP database for foreign trade (Narayanan and Walmsley 2008). Therefore, the supply chain’s domestic structure is assumed as less flexible than the foreign trade structure.

Consumption is also defined by the nested function based on consumers’ maximization assumptions on utility (Fig. 3). The first nest is defined by the function of the LES (linear expenditure system), as derived from the Stone–Geary utility function. The second nest reflects spatial flexibility among the commodities produced in different regions with the spatial substitution elasticity (s^r). Other structures—such as government decision and taxation scheme other than carbon tax—are the same as Kunimitsu (2015) study.

Fig. 3

Structure of consumption demands. Note: The s and s^r are the same as those in Fig. 2; ε^Y denotes the income elasticity of consumption

Conjunction function of climate factors in the CGE model

Climate factors are assumed to influence rice production through the rice total factor productivity (TFP). Based on Kunimitsu et al. (2015), the TFP function to be estimated is:

$$ \begin{aligned} \ln ({\text{TFP}}_{r,t}) & = \beta_{0} + \beta_{1} \ln ({\text{MA}}_{r,t}) + \beta_{2} \ln ({\text{KK}}_{t}) + \beta_{3} \ln ({\text{CHI}}_{r,t}) \\ & \quad + \beta_{4} \ln ({\text{CQI}}_{r,t}) + \beta_{5} \ln ({\text{CFI}}_{r,t}) + \varepsilon_{r,t} + \rho \varepsilon_{r,t - 1}, \\ \end{aligned} $$

(1)

where TFP_r,t is the total factor productivity in year t and region r; MA is the management area per farm organization, representing economies of scale; KK represents the knowledge capital stocks accumulated through research and development (R&D) investments; CHI is the rice yield index; CQI is the rice quality index; CFI is the flood index caused by heavy rain; β’s are the parameters to be estimated, corresponding to elasticities of TFP; ρ is also a parameter to be estimated, representing the first-order auto-regressive process in the error term; and ε denotes the error term. Further, CHI, CQI, and CFI are estimated only by climate conditions—such as temperature, solar radiation, and precipitation—using the crop yield model, crop quality model, and extracted maximum precipitation from August to October, respectively (“Appendix”). Table 1 displays the estimation results, using panel data.

Table 1 Estimation results of TFP function (Eq. 1)

Moreover, MA and KK are assumed as constant during the simulation periods to simplify the simulation. By dividing both sides of Eq. (1) with the referenced year, which is the starting year in our simulation (t₀ = 2015), the following conjunction equation for TFP is derived:

$$ {\text{TFP}}_{r,t}/{\text{TFP}}_{{r,t_{0}}} = \left({{\text{CHI}}_{r,t}/{\text{CHI}}_{{r,t_{0}}}} \right)^{{\beta_{3}}} \cdot \left({{\text{CQI}}_{r,t}/{\text{CQI}}_{{r,t_{0}}}} \right)^{{\beta_{4}}} \cdot \left({{\text{CFI}}_{r,t}/{\text{CFI}}_{{r,t_{0}}}} \right)^{{\beta_{5}}}. $$

(2)

Resource allocation function

The total labor supply fundamentally decreases according to changes in the Japanese population, but the regional labor force as a supply source is assumed to move across regions based on wage differences. The labor supply (LS) is defined as:

$$ {\text{LS}}_{r,t}^{{}} = {\text{LS}}_{r,t - 1} \left({\frac{{w_{r,t - 1}}}{{\overline{w}_{t - 1}}}} \right)^{0.5} \frac{{{\text{POP}}_{r,t}}}{{{\text{POP}}_{r,t - 1}}}, $$

(3)

where w is the wage rate; $\overline{w}$ is the entire country’s average wage rate; ${\text{POP}}_{t}/{\text{POP}}_{t - 1}$ indicates the population’s growth rate; and 0.5 is the wage elasticity of labor supply considering the relatively inflexible Japanese labor market, which is characterized by low female labor participation rate, low mid-career adoption rate, and high persistence to the original living location (Kunimitsu et al. 2015).

Private capital stocks KP are accumulated through private investments:

$$ {\text{KP}}_{r,t} = (1 - \delta){\text{KP}}_{r,t - 1} + {\text{IP}}_{t}. $$

(4)

Here, δ is the depreciation rate and is set at an actual rate of 4.0%; this was calculated using national accounting statistics from 2005 to 2013. Further, private investments (IP) are assumed as allocated to industries according to the rate of return (ROR):

$$ {\text{IP}}_{i,r,t}^{*} = {\text{IP}}_{i,r,t - 1} \left({\frac{{{\text{PK}}_{i,r,t - 1} \cdot {\text{ROR}}_{i,r,t - 1}}}{{\overline{\text{PK}}_{r,t - 1} \cdot \overline{\text{ROR}}_{r,t - 1}}}} \right)^{0.5} \frac{{{\text{IPT}}_{r,t}}}{{{\text{IPT}}_{r,t - 1}}}, $$

(5)

$$ {\text{IP}}_{i,r,t} = \frac{{{\text{IP}}_{i,r,t}^{*}}}{{\sum\nolimits_{r} {{\text{IP}}_{i,r,t}^{*}}}}{\text{IPT}}_{r,t}, $$

(6)

The subscript i here indicates the industry; IP* is the ideal private investment; PK is the capital service price changing the real ROR to a nominal value; IPT is the total private investment, regulated by the total savings under a macroeconomic balance; and 0.5 is the price elasticity of investments, assuming an inelastic reflection of investors under the existence of transaction costs as explained by Kunimitsu et al. (2015).

Farmland has decreased under the pressure of urbanization and imported agricultural products in addition to progress of depopulation in rural areas. However, to express these pressures is difficult in a model, so the total farmland supply FS is assumed to decrease with the past trend:

$$ {\text{FS}}_{r,t} = (1 + gf_{r}/100){\text{FS}}_{r,t - 1}, $$

(7)

where gf_r is the annual change rate of farmland by regions.

Environmental subsidies with a carbon tax

To secure funds for prolonging MSD period, a carbon tax is assumed and levied on all industries to maintain the balance of national accounts. The environmental subsidy is set to match the monetary value of CH₄ reduced by prolonging the MSD period, and its value (V_CH4) is:

$$ V_{{{\text{CH}}4}} = 25 \cdot P_{{{\text{CO}}2}} \cdot O_{{{\text{CH}}4}} \cdot r_{{{\text{CH}}4}}, $$

(8)

where 25 is the carbon equivalent coefficient for CH₄ emissions; P_CO2 is the carbon price realized in the carbon trade market; O_CH4 is the total amount of CH₄ produced from paddy fields in Japan; and r_CH4 is the reduction rate by prolonging MSD period.

A carbon tax is subsequently set so that the carbon tax revenue matches to the above expenditure for environmental subsidies. The environmental tax levied on each industry (Taxc) in accordance with CO₂ emissions is:

$$ T{\text{axc}}_{i,r} = \frac{{V_{{{\text{CH}}4}}}}{{O_{{{\text{CO}}2}}}}{\text{e}}\_{\text{co}}2_{i} \cdot y_{i,r}, $$

(9)

where Oco2 is the total amount of CO₂ emitted from all industries (so that V_CH4/O_CO2 corresponds to the unit price of carbon tax); e_co2 is the emission coefficient estimated by National Institute for Environmental Study (NIES) (2019); and y is each industry’s total production value.

Data to calibrate the CGE model

A social accounting matrix was used to calibrate the model’s parameters, based on Japan’s 2014 inter-regional input–output table which was estimated from the inter-regional input–output data in 2005 (Ministry of Economy, Trade and Industry (METI) 2010). Updated inter-regional input–output data were calculated by using the RAS method, which is a mathematical procedure for balancing the columns and rows of modified input–output table, and the controlled total production that was measured from national accounts’ statistics in 2005 and 2014 (Cabinet Office of Japan 2016). Rice production was more precisely analyzed by separating the rice sector from the agricultural sector in the original table using information from the 2005 national input–output basic classification table, which included 404 × 350 sectors (Ministry of Economy, Trade and Industry (METI) 2009). The original sectors were then reassembled into 20 sectors: (1) rice paddies (pady); (2) other cultivated plants (ocpl); (3) livestock (livs); (4) agricultural services (agsv); (5) forestry, fishery, and mining (ofst); (6) rice milling (rice); (7) noodles, bread, and other milling (omil); (8) dairy and meat products (mkmt); (9) other food and drinks (ofnd); (10) chemical products (chem); (11) machinery (mach); (12) electrical equipment (elem); (13) other manufacturing (omfg); (14) construction (cnst); (15) electricity, gas, and water (elgw); (16) wholesale and retail sales (trad); (17) financial services (fina); (18) transportation and telecommunication (tpts); (19) research and education (rese); and (20) other services (sev).

Nine regions were included: Hokkaido (1hok); Tohoku (2toh); Kanto (3kan), including Niigata Prefecture; Chubu (4chb); Kinki (5kin); Chugoku (6chg); Shikoku (7sik); Kyushu (8kyu); and Okinawa (9oki) (Fig. 4).

Fig. 4

Areas used in the CGE model

The input value of farmland is not noted in the Japanese input–output table, but was estimated by each year’s areas of cultivated farmland (Ministry of Agriculture, Forestry and Fisheries (MAFF) 2009), by multiplying the areas with farmland rent. The value of this farmland was then subtracted from the operation surplus in the input–output table, and the remaining operation surplus was added to the value of capital input (the depreciation of capital stocks).

The annual change rate of farmland, gf_r, in Eq. (7) is measured using the 2008–2017 trends based on cultivated farmland statistics (Ministry of Agriculture, Forestry and Fisheries (MAFF) 2009). The concrete annual change rate is − 0.2% in Hokkaido; − 0.4% in Tohoku; − 0.5% in Chubu, Kinki, and Okinawa; − 0.6% in Kanto and Kyushu; − 0.7% in Chugoku; and − 0.9% in Shikoku.

The spatial substitution elasticities, s^r, of inter-regional trade for intermediate inputs (Fig. 1) were obtained from the empirical estimations (Koike and Naka 2014). The concrete values of spatial substitution used here were 1.22 for food processing industries (“rice,” “omil,” “mkmt,” “ofnd”), 1.32 for chemical industry (“chem”), 1.238 for machinery industry (“mach”), 1.348 for electrical equipment industry (“elem”), and 1.242 for other manufacturing industry (“omfg”). The remaining industries adopt 1 for the substitution elasticity, as it shows moderate substitutability and is close to the average of all of Koike and Naka’s estimations.

The spatial substitution elasticities in the consumption part (Fig. 2) are the same as intermediate inputs based on empirical study. The Frisch parameter for LES function is − 1.2 based on the Saito’s (1996) empirical study. Other substitution elasticities were the same as Kunimitsu (2015) which was based on GTAP database. To secure the stability of the simulation, a sensitivity analysis with ± 20% change of the most substitution elasticities was conducted. That analysis confirmed that the direction did not change although the simulation results’ levels changed.

Simulation method

The following cases are considered in measuring the influences of climate change and mitigation measures:

Case 0 (Reference case): This case represents a baseline reference situation. In this case, the TFP of rice production is set to one, indicating no technological progress and no changes in climate conditions.

Case 1 (only climate change): This case represents the future climate change that only affects rice production, but does not consider mitigation measures. The levels of future rice TFP are calculated using Eq. (2). Changes in annual climate factors are projected by the crop growth model (Eq. 10), crop quality model (Eq. 11), and maximum precipitation (Eq. 12). Regarding the inputs of these equations, the projection results for climate conditions—such as solar radiation, temperature, and precipitation—are obtained from a global climate model, MIROC version 5 (K-1 Model Developers 2004). The GHG emissions scenario involves representative concentration pathways of 8.5 (RCP 8.5), which indicates the highest increase in future temperatures among the RCP scenarios.³ The global average temperature in this scenario increases by 2.6 to 4.8 °C by 2100.

Case 2 (voluntary MSD under climate change): This case considers prolonging the MSD period under the future RCP 8.5 scenario. All rice farmers voluntarily prolong MSD by one more week and accept a 5% decrease in rice yields to decrease paddy fields’ CH₄ emissions by 30% (statistics that are based on Fig. 1).

Case 3 (MSD and environmental subsidies with a carbon tax, mixed policy): This case considers prolonging MSD and environmental subsidies with a carbon tax under climate change to motivate farmers. Environmental subsidies are provided to only farmers who decrease their paddy fields’ CH₄ emissions by prolonging MSD. Values of environmental subsidies are calculated by Eq. (8).⁴ Also, based on Eq. (9), the same amount of money, as total subsidies to decrease CH₄ emissions, is collected as carbon tax from all industries, including rice sector, in accordance with each industry’s CO₂ emission.⁵ The settings for MSD are the same as in Case 2.

Exogenous variables are set as follows in all cases: The growth rate of the population used as labor in each region is based on projections from the National Institute of Population and Social Security Research. Government savings, foreign savings, and regional money transfers are fixed at the present levels as noted in the social accounting matrix. The Japanese economy’s technological growth rate is assumed as 0% per year to simplify the simulation.

Results

The influence of climate change (Case 1 versus Case 0)

Figure 5 illustrates the chronological changes in relative TFP ratios, calculated according to Eq. (2) and used for Cases 1 to 3, from 2015 to 2065. The annual TFP levels fluctuate due to changes in climate conditions. Okinawa’s TFP was assumed to remain at the same level, as its change in rice production was negligible.

Fig. 5

Changes in regional TFP under future climate change. Note: In the legend, “1hok” is Hokkaido, “2toh” is Tohoku, “3kan” is Kanto, “4chb” is Chubu, “5kin” is Kinki, “6chg” is Chugoku, “7sik” is Shikoku, “8kyu” is Kyushu, and “9oki” is Okinawa

On average, the TFP in the northeastern regions—Hokkaido and Tohoku—increased even under climate change conditions, while the southwestern regions—Kanto, Chubu, Kinki, Chugoku, Shikoku, and Kyushu—experienced a decrease in TFP. This occurred because the temperature in the southwestern regions surpassed the threshold temperature for many years. Specifically, the degrees of decrease in Chubu and Kinki were almost the same as in Kyushu. Although Chubu and Kinki are located at higher latitudes than Kyushu, the temperature increase under climate change was relatively high, and few high temperature-resistant rice varieties are grown in these regions. The TFP fluctuations in each region signify that future climate change could involve instances of cold weather as well as excessively high temperatures.

Figure 6 illustrates the influences of climate change (Case 1–Case 0) on gross rice production corresponding to the total production quantity (q_rice); rice prices (p_rice); rice farmers’ nominal income (inc_rice)⁶; gross regional production (GRP); equivalent variation (EV) indicating the social welfare level; and CO2 emissions (CO2). For brevity, the average values of every 15-year period—noted as “early term” (2021–2035), “midterm” (2036–2050), and “later term” (2051–2065)—were plotted for these target variables.

Fig. 6

Influences of climate change by variable and region. Note: The dots indicate the average level of difference between Case 1 and Case 0 in each variable for 15 years. The characters on the horizontal axis are the same as the legend of Fig. 5. Five regions—Chubu, Kinki, Chugoku, Shikoku, and Okinawa—were merged into an “Others” group, as they have similar tendencies in variable changes, and the average values are relatively small in these regions

The entire country’s (q_rice) increased due to climate change until approximately 2050, but subsequently decreased in accordance with TFP changes. Each region’s (q_rice) increased in Hokkaido and Tohoku and chronologically declined in other regions. However, the changes in each region were canceled out and the nationwide changes lessened.

Rice prices moved almost inversely with an increase in production. As the (q_rice) includes inter-regional trade, price movements in each region were affected by neighboring regions. In particular, many imports from Tohoku occurred in the Kanto region; thus, the rice prices in this region did not increase in spite of the decrease in its own (q_rice).

Rice farmers’ nominal income (inc_rice) in most regions declined until around 2050 to reflect rice price changes, then subsequently rose, but was still lower than the present level. As rice is a type of necessary good, the price elasticity of demand is small; conversely, the change in price is large relative to the changes in demand. Therefore, rice farmers’ (inc_rice) was greatly influenced by price changes rather than rice production.

When the rice sector’s productivity increased (or decreased), this positive (or negative) influence expanded to other industries through labor and capital markets. Consequently, fluctuations in GRP, which corresponds to the total added value across all industries, became greater than the production changes in the rice sector. The average GRP growth rates in many regions—except for Tohoku and Kyushu—were positive until the midterm and became negative afterward. The GRP across the entire country (the GDP) increased due to climate change during all periods. The changes in EV exhibited a similar tendency as the GRP. CO₂ emissions showed similar changes to (q_rice), as climate change was assumed to only affect the rice production and change CO₂ emissions from this sector.

Overall, it can be posited that climate change will cause decreases in rice prices and rice farmers’ nominal income because of bumper harvests until approximately 2050.

The effects of MSD and environmental subsidies with a carbon tax (Cases 2 and 3 versus Case 1)

Figure 7 illustrates the effects of voluntary prolonging MSD under climate change (Case 2) as compared to Case 1 which only involves climate change. The values were calculated by subtracting Case 1 from Case 2 to demonstrate the policy measures’ net effects.

Fig. 7

Effects of voluntary prolonging MSD (Case 2). Note: The q_rice, p_rice, inc_rice, and GRP, respectively, signify the total rice production, rice prices, rice farmers’ nominal income, and gross regional production. The characters at the horizontal axis are the same as those in Fig. 6

Prolonging MSD caused the rice yield per area to decrease in all regions, but this measure caused a decrease in consumption due to increased rice prices, wages, and the rental prices of capital stocks. The characteristics of some farmlands changed as farmers planted other crops, and inter-regional trade increased. Consequently, the supply and demand equilibrium amounts (q_rice) decreased in all regions with regional differences, and especially in Tohoku. A large decrease in Tohoku occurred for two reasons: First, the rice production in this region was substantial, and a decrease of 5% in its rice yield, the same as in other regions, led to a significant difference in production amounts. Second, a decrease in other regions’ demand caused a decrease in inter-regional transfers from Tohoku, where the rice sector was a primary source of funds acquisition.

This voluntary measure caused rice production to decrease across the entire country and rice prices to increase. Rather than causing production volume changes, rice farmers’ nominal income increased following the same trends as the price changes. Implementing only the MSD measure caused a decrease in the nationwide GRP (GDP). Consequently, the MSD measure prevented a decrease in rice farmers’ nominal income, which was decreased by climate change, although actual production was negatively impacted.

Figure 8 illustrates the effects of the policy mix—both prolonging MSD and the environmental subsidies with a carbon tax—as simulated in Case 3. As in the previous figures, this figure calculates the difference between Cases 3 and 1 to exclude other influences.

Fig. 8

Effects of MSD and the environmental subsidy with carbon tax (Case 3). Note: The variables and characters are the same as those in Fig. 7

This policy mix reveals decreased negative impacts from only prolonging MSD (Case 2) on the production side. Further, rice production increased nationwide, and rice prices decreased. The nominal income increased across all regions owing to subsidies in spite of the price decrease. However, GDP (whole regions’ GRP total) decreased due to a carbon tax. The negative impact of carbon tax on GRP was severe in Tohoku, as many energy intensive industries are located. Even so, this policy mix eliminates the disadvantages in rice production caused by prolonging MSD, and the negative impact on GDP is not so big, accounting for only 0.004% of Japan’s total GDP.

A comparison between Figs. 7 and 8 suggests the net effects of environmental subsidies with a carbon tax, because a difference between these figures corresponds to a difference between Cases 2 and 3 and removes influences of MSD measures. From such comparison, it can be found that changes in GDP in Fig. 8 marked lower level than in Fig. 7, showing negative economic benefit in the case of only environmental subsidies with a carbon tax. Since the carbon tax decreased production in other industries, this offset the increase in rice production and reduced the changes in GDP across the entire country. As will be demonstrated later, the country’s CO₂ emissions declined. Therefore, this measure brought about positive environmental benefit, but did not yield double dividends in the Japanese economy, as is consistent with Takeda’s (2007) work.

The possibility of a “free ride” and policy measures’ environmental effects

Table 2 illustrates rice farmers’ nominal income per area. The nominal income in the “free ride” case was assumed as 1.015 times (1/0.95^0.294) that in Case 2. This number is the inverse value of the TFP change caused by the yield change, assuming that no decrease occurs in the free riders’ yield from prolonging MSD.

Table 2 Changes in farmers’ income per area due to policy measures

Table 2 notes the level of nominal income per area occurred sequentially as Case 1 < Case 2 < Free Ride < Case 3. In other words, and as Fig. 7 predicts, prolonging MSD prevented a decrease in rice farmers’ nominal income by maintaining a higher level of rice prices if all farmers participate in this measure. As the “free ride” case became superior to Cases 1 and 2, the farmers’ agreement to prolong MSD is always at risk due to the emergence of free riders. Although the concrete numbers are unknown, if several farmers become free riders and other farmers notice this change, the income level changes to Case 1, which is the least ideal for all farmers. However, it is the most beneficial for farmers to be paid subsidies by participating in the prolonging of MSD among all possible policy measures. Thus, the incentive for “free rides” could be reduced by paying environmental subsidies to rice farmers.

Table 3 illustrates the total decrease in CO₂ and CH₄ emissions as a result of policy measures; the CH₄ emissions have been converted to CO₂-equivalent amounts with the efficiency coefficient for GHG emissions.

Table 3 Nationwide environmental effects after policy measures (Case 2 or 3–Case 1)

When only comparing CO₂ emissions, the reduction in CO₂ emissions from Case 3 was greater than in Case 2 because of the carbon tax. Reductions in CH₄ emissions were the same in both cases, so the merits of prolonging MSD period and including an environmental subsidy with the carbon tax (as noted in Case 3) were environmentally superior to voluntary prolonging MSD shown by Case 2.

Summary, policy implications, and conclusion

This study used a dynamic, spatial CGE model to measure the effects of prolonging mid-summer drainage (MSD) on rice production and regional economies. Environmental subsidies from carbon tax revenues were introduced to promote this MSD measure. Future situations were then simulated according to projection results from the MIROC global climate model under an RCP 8.5 scenario, which indicated the highest increase in temperature to parallel the recent growth trends among global economies.

The results demonstrate that an increased temperature decreases both rice prices and rice farmers’ nominal income due to bumper harvests until approximately 2050. Prolonging MSD in paddy fields effectively decreases methane gas (CH₄) emissions and prevents a decrease in farmers’ income. However, some farmers can potentially increase their own incomes by avoiding MSD and gaining higher yields under higher rice prices, which are maintained by other farmers’ voluntary participation in MSD. Therefore, strong motivation exists for some farmers to “free ride” this measure.

Environmental subsidies with a carbon tax are useful in motivating farmers to adopt MSD, and this can increase farmers’ income without worsening the country’s balance sheet, although such a policy cannot create “double-dividend” effects. Farmers who adopt the MSD measure and receive environmental subsidies gain a higher income than in the case of only climate change as well as in the case of voluntary participation in MSD, while GHG emissions, such as CO₂ and CH₄, can decrease nationwide with a small decrease in Japan’s GDP.

Based on these findings, this study indicates that a mix of environmental policies, such as MSD and environmental subsidies, can be the key to obtaining environmental benefits with a simultaneous suitable economic benefit. Several trade-offs exist in environmental policies, but a combination of such policy measures can ease these contradictions. Simulations involving the CGE model play an important role in planning and designing the best policy mix.

Another issue to consider involves how to monitor MSD performance, as easy technology sometimes causes problems with control and accountability. Further research and development should be conducted to address this matter. Additionally, analyses of other measures are important in addressing climate change, such as managing systems of rice intensification (SRIs). As SRI management requires intermittent and light irrigation and can be applied in other locations, such as African countries (Kassam et al. 2011), SRI management can possibly decrease paddy fields’ CH₄ emissions more than conventional management. If field experiment data on CH₄ emissions becomes available, the CGE analysis employed here could verify SRI management’s usefulness as a worldwide mitigation measure.

Many issues also remain for further study. First, the model must be improved to simulate more realistic situations. For example, important and noteworthy issues used in the dynamic stochastic general equilibrium model include an installation of forward-looking type assumptions, which will allow consumers to prepare for these future changes in advance. It is also necessary to renew and improve MSD field data relative to other countries, and especially Asian countries, in which rice production dominates.

Appendix

The CHI and CQI are, respectively, calculated from the crop growth and crop quality models, which were both estimated by Kunimitsu et al. (2015) using climate conditions, such as temperature and solar radiation during planting periods. The CFI is calculated using the maximum precipitation from August to October; specifically,

$$ \begin{aligned} {\text{CHI}}/{\text{SR}}7\_9_{r,t} & = \beta ^{\prime}_{0} + \beta ^{\prime}_{1} {\text{TM}}7_{r,t} + \beta ^{\prime}_{2} {\text{TM}}7_{r,t}^{2} + \beta ^{\prime}_{3} {\text{TM}}8_{r,t} + \beta ^{\prime}_{4} {\text{TM}}8_{r,t}^{2} \\ & \quad + \beta ^{\prime}_{5} {\text{TM}}9_{r,t} + \beta ^{\prime}_{6} {\text{TM}}9_{r,t}^{2} + \varepsilon ^{\prime}_{r,t}, \\ \end{aligned} $$

(10)

$$ \begin{aligned} {\text{CQI}}_{r,t} & = \beta^{\prime \prime}_{0} + \beta^{\prime \prime}_{1} {\text{SR}}7_{r,t} + \beta^{\prime \prime}_{2} {\text{SR}}8_{r,t} + \beta^{\prime \prime}_{3} {\text{ABS}}(TL7\_8_{r,t} - 19.34) \\ & \quad + \beta^{\prime \prime}_{4} {\text{DYR}}_{r,t} + \varepsilon^{\prime \prime}_{r,t}, \\ \end{aligned} $$

(11)

$$ {\text{CFI}}_{r,t} = \hbox{max} \left({{\text{Rain}}89_{{r,t,{\text{day}}}}} \right), $$

(12)

where SR7_9, SR7, and SR8 are the average solar radiation from July to September, in July, and in August, respectively; TM7, TM8, TM9, and TL7_8 are the daily average temperatures in July, August, and September, and the average daily minimum temperature from July to August, respectively; DYR is the dummy variable that is 1 for the negative spikes, showing a rapid drop of − 20% in a specific year and rapid recovery the following year, and 0 otherwise; Rain89 is the daily precipitation during August and September, which is typhoon season in Japan.

The estimated coefficients of Eq. (10) from the panel data (38 prefectures, with a time series spanning from 1979 to 2010) were β′₀ = − 38.58880, β′₁ = 1.651944, β′₂ = − 0.035587, β′₃ = 1.822283, β′₄ = − 0.040967, β′₅ = 0.726466, and β′₆ = − 0.011593, indicating the quadratic curvature relative to temperature. Further, the estimated coefficients of Eq. (11) from the 38 × 31 panel data were β′′₀ = 54.79937, β′′₁ = 0.646943, β′′₂ = 0.940363, β′′₃ = − 6.703061, and β′′₄ = − 39.06254, indicating a rooftop-shaped curvature regarding temperature. All estimated coefficients in Eqs. (10) and (11) were significant compared to the t-statistic values at the 0.1% level of probability. The adjusted R-squared values were 0.69 (Eq. 10) and 0.48 (Eq. 11), the F-statistics of redundant fixed-effects tests were 39.0 (Eq. 10) and 14.3 (Eq. 11) at a 0.1% level of significance, and the Hausman’s test Chi-squared values were 212.5 (Eq. 10) and 16.5 (Eq. 11) at a 0.1% level of significance, demonstrating the fixed-effects model’s superiority.