Introduction

In a regional hydrological cycle, surface water and groundwater interact to exchange water across their common boundary. In an alluvial fan where groundwater level is adequately below the ground surface, the dominant effect of water exchange is the groundwater recharge from the surface. On the other hand, in an alluvial plain where groundwater level is relatively close to the ground surface, both groundwater recharge and groundwater discharge could occur via rivers and canals. While running from an alluvial fan to the following alluvial plain, a stream generally loses water to aquifer in certain upper reaches and gains water from aquifer in lower reaches. Even in the same reach, a stream could also switch between gaining and losing across the seasons according to the rise and fall of the difference between surface water level and groundwater level. The dynamic processes of groundwater system and stream–aquifer interaction are affected not only by geological/meteorological conditions but also by human activities such as irrigation. Studies and clear understanding of the dynamic stream–aquifer interaction would provide some guidelines for reasonable water management and ecological prevention.

One of the approaches to quantify a stream–aquifer flow is to utilize a hydrological watershed model (e.g. Hu et al. 2007; Krause and Bronstert 2007). In many hydrological watershed models, a stream–aquifer flow is usually considered as a water flux through a low-permeable streambed stratum (e.g. Rushton and Tomlinson 1979). The MODFLOW (McDonald and Harbaugh 1988) and the streamflow routing packages such as RIV (McDonald and Harbaugh 1988), STR1 (Prudic 1989) and SFR1 (Prudic 2004) have been coupled with some surface runoff models to quantify a stream–aquifer flow. Kim et al. (2008) developed SWAT-MODFLOW model and applied it to estimate groundwater drawdown and stream flow reduction by pumping groundwater out. Other hydrological watershed models (e.g. Jia et al. 2001; Korkmaz et al. 2009) have adopted the expression similar to the streamflow routing packages. Jia et al. (2001) developed the WEP model, which simulates water and energy cycles in a watershed, and applied it to project water balance change by urbanization in the future. Korkmaz et al. (2009) adopted MODCOU to reproduce the damaging flood that was caused by immense groundwater discharge. These studies suggest that the expression similar to the streamflow routing packages is useful and relevant for quantifying a stream–aquifer flow. These studies, however, make rough estimates of unsteady surface water levels in streams. The stream flow is approximated with kinematic wave flow (Jia et al. 2001) or steady uniform flow (Kim et al. 2008; Korkmaz et al. 2009).

For reliable estimation of a stream–aquifer flow, spatiotemporal variation of the surface water level should be considered, especially for a stream running in an alluvial plain. For description of the surface water flow dynamics, the complete (non-approximated) shallow water equations (i.e. unsteady open channel flow equations) are proper. Swain and Wexler (1996) developed a coupled surface water and groundwater flow model (MODBRANCH) for simulation of stream–aquifer flow. Their model links MODFLOW to BRANCH (Schaffranek et al. 1981) in which the shallow water equations are used to simulate unsteady flow dynamics in an open channel network. Thompson et al. (2004) adopted MIKE-11, which is based on the shallow water equations and is able to simulate the flow through hydraulic structures such as weirs, gates, bridges and culverts, to link it with MIKE-SHE. Their linked model was applied to low-lying wet grassland to investigate the seasonal variations of groundwater level and surface water level in a ditch. These attempts indeed vouch for the necessity of employing unsteady surface water flow model for representing stream flow which interact with aquifers, but do not deal with stream–aquifer interaction induced by irrigation and drainage practices.

In an agricultural watershed, surface water and groundwater interaction is often promoted by human-induced surface/subsurface water modifications such as irrigation and drainage. Many previous studies (e.g. Fujihara and Ohashi 2000; Liu et al. 2005; Imaizumi et al. 2006) indicated that infiltration from the irrigated paddy fields makes a large contribution to groundwater recharge. Infiltration from irrigation and drainage canals is also a non-negligible source of groundwater recharge (Fujinawa 1981; Wakasa 2006). In agricultural lowland area, drainage canals play an important role in groundwater discharge from shallow aquifers to keep soil water contents proper in crop fields. Carroll et al. (2010) developed a MODFLOW-based hydrological model in which the water exchange between drainage canals and aquifer is focused on but the canal flow is assumed to be steady and uniform. Takeuchi et al. (2009) developed a finite-volume hydro-environmental model in which the water exchange between drainage canals and aquifer is taken into account. Takeuchi et al. (2010) constructed the refined hydro-environmental watershed model (HEWM-1) that enables more reliable estimation of canal-aquifer flow with the high-resolution divisions of the watershed. Both of them make a rigid-lid assumption for water level in any canal, thus prescribing time-independent in-canal water levels as internal boundary conditions.

This study aims at developing a hydro-environmental watershed model that can simulate the dynamic canal-aquifer flow caused by the rise and fall of the difference between surface water level and groundwater level. For attaining this purpose, this study makes HEWM-1 (Takeuchi et al. 2010) free from the assumption that in-canal water levels are time-independent. The time-varying stream flow in canals is described by the complete one-dimensional (1-D) shallow water equations without any approximations. Different two effects of canal-aquifer flow are separately considered: exchange flow through canal bed that is according to the difference in hydraulic head between canal and aquifer and groundwater discharge through underdrains that is caused by removing superfluous soil water in farmlands. The presently improved model (HEWM-2) is applied to a mesoscale agricultural watershed including lowland areas to be validated. With a long-term simulation by HEWM-2, the spatiotemporal variations of canal-aquifer flow and their contribution to the overall water budget are estimated.

Model development

Model structure

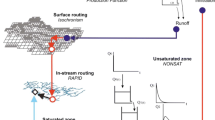
The graphical representation of the improved hydro-environmental model, HEWM-2, is shown in Fig. 1. In HEWM-2, as in HWEM-1, watershed geometry is subdivided into column cells which have triangular tops that well fit field plots and canal courses. Profile of a column cell is zoned into two: a surface zone and an unconfined aquifer zone. Hydrological process in the surface zone is expressed by combining a tank submodel and a soil moisture submodel according to Alam et al. (2006), and that in the unconfined aquifer zone is expressed by a shallow groundwater flow submodel.

Fig. 1
figure 1

Schematic of hydro-environmental watershed model (HEWM-2)

Full size image

A major improvement over HEWM-1 is made for treating flow in agricultural drainage canals as unsteady open channel flow, in lieu of steady flow with rigid-lid assumption. Another improvement is made for realistic and detailed representation of the water exchange between drainage canals and aquifer. In HEWM-2, the canal-aquifer flow rate is defined as the sum of the exchange flow rate through canal bed and the underdrain discharge.

Surface zone

The tank submodel expresses the hydrological processes on the ground surface, relating surface water storage of effective rainfall, infiltration, evaporation, inflow from upper tanks and outflow to a lower tank. In farmland areas, one tank is assigned to one set of cells identical with one field plot, whereas in other off-field areas, one tank is assigned to one cell. On a paddy field tank, the outflow from the tank is represented by an overflow through a sharp-crested weir whose height is identified to actual weir height of an outlet at a field plot. On a non-paddy field tank, the outflow from the tank is calculated in the same way as that from the standard tank model (Sugawara et al. 1986). The infiltration through the ground surface is calculated with the soil moisture submodel as described in the following paragraph. The evaporation occurs from the surface tank when the surface water storage is not null. The potential evaporation is the product of a drop coefficient and the pan evaporation, which is estimated by use of the Penman method.

A soil moisture model, which was originally developed for a lumped runoff model (Tan and O’Connor 1996), is adapted for a submodel in this distributed watershed model. The soil moisture submodel expresses the hydrological processes in the unsaturated subsurface soil, relating soil water retention, infiltration, evapotranspiration, lateral outflow and vertical percolation. The infiltration is regulated by soil water content so that the limited water infiltrates under a wet condition. The surplus water to the infiltration remains in the surface tank. The soil water content is retained to a certain capacity, and the surplus water to the capacity is separated into a lateral outflow and a vertical percolation. The evapotranspiration occurs in the subsurface soil only when the surface water storage is less than the potential evaporation. Also the evapotranspiration rate is regulated by soil water content so that the limited soil water is pulled off under a dry condition.

The lateral outflows from the ground surface and the subsurface soil are discharged into drainage canals. If a cell abuts on no canal, the outflow from the cell is given as an inflow contribution to the lowest cell amongst the neighbouring three cells. The vertical percolation from subsurface soil recharges the groundwater in the aquifer zone.

A minor improvement on HWEM-1 is made in making a distinction between snowfall and rainfall. From air temperature and relative humidity, whether precipitation is rainfall, snowfall, or sleety rainfall is inferred. The following two threshold values for relative humidity are criteria of distinction (Matsuo 1984).

$$ \begin{array}{*{20}c} {H_{\text{s}} = - 7.5T + 93} & {\left( {0.0 \le T < 5.0} \right)} \\ \end{array} $$
(1)
$$ \begin{array}{*{20}c} {H_{\text{r}} = 46\sqrt {6.2 - T} } & {\left( {1.47 \le T < 4.57} \right)} \\ \end{array} $$
(2)

where T is the air temperature (°C), H s is the threshold relative humidity (%) for distinction between snow and sleet and H r is that (%) for distinction between rain and sleet. The type of precipitation is identified to be snowfall if the air temperature is under 0°C or the relative humidity is less than H s even if the air temperature is over 0°C, or to be rainfall if the air temperature is over 5°C or the relative humidity is more than H r even if the air temperature is under 5°C. If the relative humidity is between the two threshold values, the precipitation is regarded as a half-and-half sleety mixture of snow and rain.

The melting rate of snow is essentially determined by a heat balance on a surface of snow cover. However, an empirical expression that relates the melting rate to only air temperature is usually used for estimating the amount of melting. Here, the following degree-hour method (Kojima et al. 1983) is employed.

$$ M = m\sum\limits_{i = 1}^{24} {\max \left( {0.0,T^{\text{h}}_{i} } \right)} $$
(3)

where M is the rate of snow melting (mm/day), T h is the hourly-mean air temperature (°C) and m is the melting coefficient (mm/(°C day)).

Drainage canals

The unsteady open channel flow submodel for drainage canals is described by the following set of the continuity and momentum equations, which is defined in 1-D domain Ωr.

$$ \frac{\partial A}{\partial t} + \frac{\partial Q}{\partial \zeta } = q_{\text{in}} $$
(4)
$$ \frac{\partial Q}{\partial t} + \frac{\partial }{\partial \zeta }\left( {\frac{{\beta Q^{2} }}{A}} \right) = - gA\frac{\partial }{\partial \zeta }\left( {h_{r} + z_{r} } \right) - gAS_{f} $$
(5)

with

$$ S_{\text{f}} = \frac{{n_{\text{M}}^{2} Q\left| Q \right|}}{{A^{2} R^{4/3} }} $$
(6)

where A is the wetted cross-sectional area (m2), Q is the volumetric flow rate (m3/s), ζ is the local curvilinear abscissa along the channel bed, q in is the lateral inflow per unit width (m2/s), β is the Boussinesq coefficient, h r is the water depth (m), z r is the elevation of the channel bed, g is the gravitational acceleration (m/s2), S f is the friction slope that is estimated with the Manning’s equation, n M is the Manning’s roughness coefficient and R is the hydraulic radius (m). The lateral inflow in the continuity equation is assumed to bring no momentum because its direction is considered to be at right angle to the channel flow. The sources of the lateral inflow are tributaries, intakes for irrigation water supply, surface discharge and canal-aquifer flow rate. The surface discharge is that calculated from the surface tank and soil moisture submodels. The canal-aquifer flow rate is calculated in linking the unsteady open channel flow submodel with the shallow groundwater flow submodel.

The initial condition is given as follows.

$$ \begin{array}{*{20}c} {h_{\text{r}} \left( {\zeta ,0} \right) = h_{\text{r0}} \left( \zeta \right)} & {\text{in}} & {\Upomega_{r} } \\ \end{array} $$
(7)

where h r0 is the prescribed initial water depth (m) over the whole domain Ωr. At the upstream end of the canal, the prescribed volumetric flow rate, Q up (m3/s), is given.

$$ \begin{array}{*{20}c} {Q\left( {\zeta ,t} \right) = Q^{\text{up}} \left( t \right)} \quad {\text{on}} \,\,{\Upgamma^{\text{up}} } \\ \end{array} $$
(8)

where Γup is the upstream boundary. At the downstream end of the canal, the prescribed water depth, h dwr (m), is given if flow in the canal is under the backwater influence of river or lake which communicates with it.

$$ \begin{array}{*{20}c} {h_{\text{r}} \left( {\zeta ,t} \right) = h_{\text{r}}^{\text{dw}} \left( t \right)} \quad {\text{on}} \,\, {\Upgamma_{\text{L}}^{\text{dw}} } \\ \end{array} $$
(9)

where Γ dwL is the backwater-type downstream boundary. If the canal end is a drop, the critical water depth, h dwc (m) and the null flow rate flux are given for subcritical and supercritical flows in the canal, respectively.

$$ \left\{ \begin{gathered} \begin{array}{ll} h_{\text{r}} \left({\zeta ,t} \right) = h_{\text{c}}^{\text{dw}} \left( t \right) & {\text{if}} \; h_{\text{r}} \ge h_{\text{c}}^{\text{dw}} \\ \frac{\partial Q}{\partial \zeta} = 0 & \text{if}\;h_{\text{r}} < h_{\text{c}}^{\text{dw}} \end{array}\\ \end{gathered} \right.{\text{on}}\quad \Upgamma_{\text{F}}^{\text{dw}} $$
(10)

where Γ dwF is the drop-type downstream boundary.

Gate or weir across the canal is treated as an internal boundary where the flow rate, Q g, expressed by well-defined flow rate formula, is prescribed.

$$ \begin{array}{*{20}c} {Q\left( {\zeta ,t} \right) = Q_{\text{g}} \left( t \right)} \quad {\text{on}} \,\, {\Upgamma^{\text{in}} } \\ \end{array} $$
(11)

where Γin is the internal boundary.

The 1-D shallow water equations (Eqs. 4, 5) are numerically solved with the finite difference method in space and the Runge-Kutta method in time. The spatial discretization of the canals is adjusted to that of the surface zone so that length of a subdivided canal is identical to that of a side of a triangular cell. The convection term in the momentum equation that, if it is dominant, may render the solution oscillatory is numerically approximated resorting to the upwind scheme, adding an artificial viscosity into the equation (Asai and Hosoda 1999).

Aquifer zone

The shallow groundwater flow submodel expresses the unsteady groundwater flow in the unconfined aquifer zone that lies on a low-permeable layer. The shallow groundwater flow dynamics is predominantly two-dimensional and expressed by the following equation with the Dupuit’s assumption.

$$ n_{\text{e}} \frac{{\partial H_{\text{g}} }}{\partial t} = - \nabla \cdot \left( { - \left( {H_{\text{g}} - z_{\text{b}} } \right)K\nabla H_{\text{g}} } \right) + r_{\text{g}} \left( {{\mathbf{x}},t - t_{\text{d}} } \right) - l - q_{\text{dc}} - q_{\text{ud}} $$
(12)

where n e is the effective porosity, H g is the groundwater level (m), z b is the elevation (m) of the low-permeable layer, K is the saturated hydraulic conductivity (m/s), r g is the recharge (m/s) from the surface zone, t d is the time lag, l is the leakage (m/s) to a deeper layer which is assumed to be proportional to the water depth in the aquifer zone, q dc is the exchange flow rate (m/s) through canal bed per unit wetted-area (positive and negative values indicate the flow into and out of the canal, respectively), q ud is the underdrain discharge (m/s) per unit surface-cell area and \( {{\mathbf{x}}} = \left( {x,y} \right)^{T} \) is the Cartesian coordinate system.

The exchange flow rate through canal bed is expressed as a water flux through a low-permeable streambed stratum. The water flux is calculated on the basis of the Darcy’s law, represented by a product of hydraulic conductivity of the low-permeable streambed stratum and hydraulic gradient between top and bottom of the stratum (Prickett and Lonnquist 1971).

$$ {\text{If}}\;h_{\text{r}} > 0, $$
$$ q_{\text{dc}} = \left\{\begin{gathered} \begin{array}{ll} K_{\text{zr}} \frac{{\left( {H_{\text{g}} - H_{\text{r}} } \right)}}{L_{\text{zr}}}, & \text{if} \; {z_{\text{c}} \le H_{\text{g}}}\\ K_{\text{zr}} \frac{{\left(z_{\text{c}} - H_{\text{r}} \right)}}{{L_{\text{zr}} }}, & \text{if} \; H_{\text{g}} < z_{\text{c}} \end{array}\end{gathered} \right. $$
(13)
$$ {\text{If}}\;h_{\text{r}} = 0, $$
$$ q_{\text{dc}} = \left\{ \begin{gathered} \begin{array}{ll} K_{\text{zr}} \frac{{\left({H_{\text{g}} - z_{\text{r}} } \right)}}{{L_{\text{zr}} }}, & {\text{if}} \; {z_{\text{r}} \le H_{\text{g}} } \\ 0, & {\text{if}} \; H_{\text{g} < z_{\text{r}}} \end{array}\end{gathered} \right.$$
(14)

where H r (\( = h_{\text{r}} + z_{\text{r}} \)) is the surface water level (m) in the canal, L zr is the thickness (m) of the low-permeable canal bed stratum that is hypothetically placed, K zr is the hydraulic conductivity (m/s) of the low-permeable canal bed stratum and z c is the bottom elevation (m) of the canal bed stratum. Values of L zr and K zr are those to be identified through calibration of the model (Prudic 2004). It is assumed that canals with concrete-lined bed have no exchange flow through their beds. As Eq. 13 states, the exchange flow rate, q dc, becomes independent of the time-dependent groundwater level when \( H_{\text{g}} < z_{\text{c}} \) (or the groundwater table drops below the streambed-stratum bottom), but still varies in time since H r is that obtained from unsteady streamflow routing.

The underdrain discharge can be expressed as

$$ q_{\text{ud}} = \left\{ {\begin{array}{lll} {\kappa K\left( {H_{\text{g}} - H_{\text{r}} } \right),} & {\text{if}} & {z_{\text{u}} \le H_{\text{r}} ,H_{\text{g}} } \\ {\kappa K\left( {H_{\text{g}} - z_{\text{u}} } \right),} & {\text{if}} & {H_{\text{r}} < z_{\text{u}} \le H_{\text{g}} } \\ {0,} & {\text{if}} & {H_{\text{g}} < z_{\text{u}} \le H_{\text{r}} } \\ {0,} & {\text{if}} & {H_{\text{r}} ,H_{\text{g}} < z_{\text{u}} } \\ \end{array} } \right. $$
(15)

where z u is the elevation (m) of the underdrain and κ is the discharge coefficient (m−1) denoting drainage performance of the underdrain. Eq. 15 is only applied to farmlands provided with underdrains for soil moisture control.

As an example, all possible situations caused under a typical condition of for \( h_{\text{r}} > 0 \) and \( H_{\text{r}} < z_{\text{u}} \) are illustrated in Fig. 2. The first three and the last denote the situations in that surface water and groundwater are connected and disconnected, respectively. As Eq. 13 states, surface water and groundwater are hydraulically connected and thus q dc is a function of the difference between the surface water level and the groundwater level, when \( H_{\text{g}} > z_{\text{c}} \). When \( H_{\text{g}} < z_{\text{c}} \), groundwater is regarded as being hydraulically disconnected with surface water (Sophocleous 2002) and thus q dc becomes independent of the time-dependent groundwater level. The relation of the canal-aquifer flow rate and the groundwater level for all the four conditions is shown in Fig. 3. In Cases (a) to (c), the canal-aquifer flow rate is proportional to the groundwater level. In Case (d), the canal-aquifer flow rate is independent of the groundwater level.

Fig. 2
figure 2

Interactive canal-aquifer flow. (a–c connected conditions, d disconnected condition)

Full size image
Fig. 3
figure 3

Canal-aquifer flow rate as a function of groundwater level

Full size image

The following initial and boundary conditions are given for the unambiguous solution to the above equation.

$$ \begin{array}{*{20}c} {H_{\text{g}} \left( {{\mathbf{x}},0} \right) = H_{{{\text{g}}0}} \left( {\mathbf{x}} \right)} & {\text{in}} \,\, {\Upomega_{\text{g}} } \\ \end{array} $$
(16)
$$ \begin{array}{*{20}c} {H_{\text{g}} \left( {{\mathbf{x}},t} \right) = H_{\text{g}}^{\text{D}} \left( {{\mathbf{x}},t} \right)} & {\text{on}} \,\, {\Upgamma^{\text{D}}_{\text{wg}} } \\ \end{array} $$
(17)
$$ \begin{array}{*{20}c} { - \left( {H_{\text{g}} - z_{\text{b}} } \right)K\frac{{\partial H_{\text{g}} }}{{\partial \nu_{\text{wg}} }} = q_{\text{wg}} \left( {{\mathbf{x}},t} \right)} & {\text{on}} \,\, {\Upgamma^{\text{N}}_{\text{wg}} } \\ \end{array} $$
(18)

where H g0 is the prescribed initial groundwater level (m) over the whole domain Ωg, H Dg is the prescribed groundwater level (m) on the Dirichlet boundary Γ Dwg , q wg is the prescribed water flux per unit width (m2/s) through the Neumann boundary Γ Nwg and ν wg is the unit vector outward normal to Γ Nwg .

The shallow groundwater flow equation is numerically solved with the cell-based finite-volume method in space and the backward Euler method in time. When a computed groundwater level becomes higher than the ground level, the groundwater level is equalized to the ground level, and the surplus water is regarded as spring. The spring water is discharged to the drainage canals or the external boundaries. If a cell abuts on no canal, the spring water is given as an inflow contribution to the lowest cell amongst the neighbouring three cells.

Application

Study area

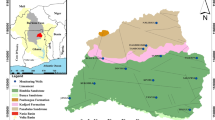
The study area is a part of Takashima City in Shiga Prefecture, Japan, being located on the northwestern side of Lake Biwa, as illustrated in Fig. 4. The area is in the Japan Sea climatic zone and has the average annual precipitation of 1,812 mm, 17% of which is snowfall (Japan Meteorological Agency 2011). The annual evapotranspiration is estimated at about 690 mm/y (Lake Biwa Research Institute 1988).

Fig. 4
figure 4

Study area

Full size image

The study area of 12.7 km2 wide is bordered with the Sakai River and the Ishida River on the northern and southern sides, respectively. The western boundary is the ridge separating watersheds, and the eastern is the shore of Lake Biwa. In the area, a variety of landforms can be found including forested hills (300–400 m AMSL), an alluvial fan formed by the Sakai River, river terraces along the Ishida River, valley floors and a nearly level alluvial plain (90 m AMSL). Figure 5 shows the hydrogeological profile, obtained from the core borings and the groundwater level observation, along the Line A depicted in Fig. 4. The inclination of the ground surface in the alluvial fan is about 0.04 and that in the alluvial plain is smaller than 0.01. Depth of the groundwater table below the ground surface is 8–15 m in the alluvial fan, while only 2 m or less in the alluvial plain. The groundwater table in the fan is, for the most part, along the ground surface, and getting close to the ground surface towards the foot of the fan. The geological columns of the boring cores for the alluvial fan mainly consist of sandy gravel, silt and clay, while for the alluvial plain mainly consist of humus silt and silt. The in situ permeability tests indicated that the sandy gravel in the alluvial fan has high hydraulic conductivity of 10−3 cm/s and the humus silt in the alluvial plain has low hydraulic conductivity of 10−4 cm/s.

Fig. 5
figure 5

Hydrogeological profile along Line A

Full size image

The farmlands in the fan area were not suitable for rice cropping because subsurface water quickly percolates and runs through the aquifer without supplying sufficient water to crops. The farmlands on the alluvial plain had been in ill-drained condition because of high groundwater level and backwater in canal from Lake Biwa. From 1970s to 1990s, the small field plots were altered to the large rectangular plots, the drainage canals were separated from the irrigation canals to improve drainage performance, and the underdrains were put to get rid of excess water in soil and keep low level of groundwater. In addition, the dredging of the main drainage canal which runs in the middle of the study area improved the drainage performance all over the area, and provided sufficient flow capacity against 10-year flood.

Forests, rice fields and other crop fields account for 33%, 33% and 10% of the entire area, respectively. The rice fields in the western part of the area are irrigated with water withdrawn from a branch of the Ishida River, some irrigation tanks, spring and a deep aquifer. The drainage water from those fields is collected into the main drainage canal. The water flowing down in the main drainage canal is reused as irrigation water for the rice fields in the eastern part of the area, which is also irrigated with return water pumped up from Lake Biwa.

Materials

The values of rainfall and pan evaporation on each cell were interpolated from those available at the monitoring points by the method of inverse squared distance weighting (Brath et al. 2004). The air temperature on each cell was firstly estimated with linear interpolation and then revised with the temperature lapse rate of 0.065°C/m. The following rule for water management in paddy fields was considered. During an irrigation period of April 24 to July 31, all the paddy fields are ponded with an appropriate water depth except for a mid-summer drainage period. If the depth is reduced to 30 mm, irrigation water is supplemented considering the water requirements of 30 mm/day and 20 mm/day for rice paddies on the fan and the plain, respectively.

The ground surface elevation of each cell was identified from the digital map of 50 × 50 m grid. The surface geology was zoned with five soil types on the basis of the geological map (Nakae and Yoshioka 1998; Nakae et al. 2001), as shown in Fig. 6. The elevation of low-permeable layer, z b, was assumed to vary according to the elevation of the ground surface so that the aquifer is 1.5 m thick in the forested hill and gradually becomes 5.5 m thick at the shore of the lake. For exception, the aquifer was assumed to be 10 m or more thick in the fan and the river terraces. The elevation of channel bed, z r, was assumed to be 1.0–2.5 m lower than the ground surface on the basis of the survey results. The underdrain was assumed to be set only in the H zone (shown in Fig. 6), and its elevation, z u, was assumed to be 1.0–2.0 m lower than the ground surface. The land use distribution is shown in Fig. 7, classified into forest, rice field and other crop field which includes the field converted from a rice field, housing land, irrigation tank and others.

Fig. 6
figure 6

Geological zoning

Full size image
Fig. 7
figure 7

Land use distribution in 2009

Full size image

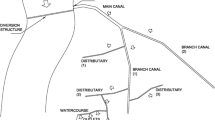
The surface zone in the whole study area was meshed with 9,775 cells of triangular shape. The drainage canals shown in Fig. 7 were discretized into a total of 1,603 segments. For the open channel flow submodel, the external boundary conditions were given as follows. The volumetric flow rate given at the upstream end of drainage canal is that obtained from the in situ measurement. If the drainage canal feeds Lake Biwa, its end is regarded as the backwater-type downstream boundary, and otherwise, as the drop-type downstream boundary. A total of 6 diversion weirs, built across the main drainage canal for irrigation water intake, were treated as internal boundaries. The aquifer zone is discretized into 9,775 triangular cells and 1,603 rectangular cells. In the shallow groundwater flow submodel, the external boundaries formed by the ridge were treated as zero-flux Neumann boundaries, and those formed by the rivers and the lake shore were treated as Dirichlet boundaries with their water levels. The water levels of the rivers were assumed to correspond to their bed elevations with disregard for temporal variations of the water levels. The water levels of the lake were obtained from the web site of the Biwa Lake authority.

The initial conditions for all the submodels were provided by a warming-up calculation which is executed over the period of April 2008 to March 2009. The initial condition for the groundwater flow submodel, which is shown in Fig. 8, qualitatively consists with the actual distribution of the ground water level. In Fig. 8a, the inclination of the groundwater level is about 0.04 in the fan and is smaller than 0.01 in the plain. This is consistent with the observation aforementioned and shown in Fig. 5. In Fig. 8b, the depth to the groundwater table below the ground surface, the ‘groundwater depth’ mentioned here, is likely to be more than 3 m in the fan, while less than 2 m in the plain. The groundwater level reaches the ground surface along the mountain streams and the fringe of the forested hills. This is consistent with the fact that spring spots are found here and there in these areas.

Fig. 8
figure 8

Initial condition for groundwater level. (a groundwater level elevation [m AMSL], b depth to groundwater table below ground surface [m])

Full size image

Calibration and verification

The values of the model parameters common to both of the previously developed HEWM-1 and the presently improved HEWM-2 were identified to those given in the earlier study (Takeuchi et al. 2010). The values of the conceptual model parameters in the tank and soil moisture submodels were determined, considering their physical meanings and referring to the published studies (Alam et al. 2006; Nakagiri et al. 1998). Their values were finally identified through calibration of the model, so that the reported amounts of evapotranspiration and groundwater recharge (Lake Biwa Research Institute 1988; Mitsuno and Nagahori 1987) were reproduced by the model. The values of the physical model parameters in the shallow groundwater submodel, the two left columns in Table 1, were inferred from field tests, laboratory tests and the literatures. The hydraulic conductivities for the two soil types in the alluvial fan and the alluvial plain (GSS and H zones shown in Fig. 6) were in situ measured as aforementioned, and their porosities were estimated from the core samples as well. The values of the hydraulic conductivity and the porosity for other soil types were estimated referring to Linsley et al. (1958) and Domenico and Mifflin (1965).

Table 1 Parameters of groundwater flow submodel
Full size table

The values of the model parameters newly introduced in this study were identified in the following manner. The values of the melting coefficient, m, estimated by Kojima et al. (1983) were employed as they are 0.14 mm/(°C h) from November to January and 0.21 mm/(°C h) from February to March. In the open channel flow submodel, the Manning’s roughness coefficient, n M, was estimated from the literature and model calibration, as shown in Table 2: 0.016 for concrete-lined canals and 0.020 for unlined canals. In the groundwater submodel, the thickness and the hydraulic conductivity of the canal bed stratum, L zr and K zr, were inferred through model calibration, as shown in Table 1. Since the elevation of stratum bottom is a critical level at which surface water and groundwater becomes disconnected, the stratum thickness is thought to be larger than an air entry pressure head of the aquifer soil. The value of L zr on the H zone (shown in Fig. 6) was identified to be 0.2 m, while that on the GSS zone to be 0.1 m. The value of K zr was identified to be 30% of K: 2.3 × 10−4 cm/s for the canals on the H zone and 5.4 × 10−4 cm/s on the GSS zone. The discharge coefficient for the underdrains, κ, was identified as 1.0 with model calibration, as shown in Table 1.

Table 2 Parameters of open channel flow submodel
Full size table

The parameter identifications, executed above, resulted from calibrating the model by comparison of the computed and observed flow rates in the drainage canal and that of the computed and observed groundwater levels. In calibration, the reproducibility of the computed result was measured in terms of statistics, and a particular simulation run which minimizes the residuals was found on a trial and error basis. For the calibration, the simulations were run with the data from April 2010 to November 2010, because the data of the canal flow rate before April 2010 were not available at all. Using the identified parameter values, verification of those values was done with the data of another time period from April 2009 to March 2010.

Figure 9 comparatively illustrates the time-varying computed and observed canal flow rates at the observation point (depicted in Fig. 7). It shows some interruptions in the observed flow rates, because the observed data are often lacked. The values of the calibration performance measures that are integrated over the four broken sub-periods (denoted in Fig. 9) are listed in Table 3. The values of RMS (Root Mean Square), SRMS (Scaled RMS), SRMFS (Scaled Root Mean Fraction Square) and SMSR (Scaled Mean Sum of Residuals) are sufficiently low, and the value of correlation coefficient, r, is adequately high. The temporal distribution of the residuals (the difference between observed and computed levels) is also checked with a scattergram of observed and computed flow rates, as shown in Fig. 10. It suggests that peak flow rates tend to be under-predicted with this model, especially when the flow rate is over 1.0 m3/s.

Fig. 9
figure 9

Computed and observed volumetric flow rates in canal

Full size image
Table 3 Statistics for the calibration/verification performance
Full size table
Fig. 10
figure 10

Scattergram of observed versus computed flow rates

Full size image

Figure 11 comparatively illustrates the time-varying computed and observed groundwater levels at the observation well. It shows that the computed groundwater level roughly trace the observed one. The values of SRMS, SRMFS and SMSR are over 10%, and the value of r is not high, as shown in Table 3. The scattergram (Fig. 12) indicates that the residuals are adequately low over the whole period except for April, 2009. The over-predicted groundwater levels in April, 2009, which resulted from an over-predicted initial condition, might cause the poor values of the performance measures above mentioned. Although there is still room for improvement, the results of model calibration are generally acceptable. For better model calibration performance, some additional data are needed to give information about the spatial distributions of groundwater level and canal flow rate.

Fig. 11
figure 11

Computed and observed groundwater levels

Full size image
Fig. 12
figure 12

Scattergram of observed versus computed groundwater levels. a Calibration period, b Verification period

Full size image

Results and discussion

Table 4 shows the annual water budget over the whole area, which was calculated from the result of the numerical flow simulation during the 1-year period of April 2009 to March 2010. The net income to the surface zone, obtained from deduction of the evapotranspiration loss from the total water supply by rainfall/snowfall and irrigation (or the sum of the values with a superscript (a) in Table 4), is 1,367 mm/y. Since the recharge from the surface zone to the aquifer zone (superscript (b)) is 920 mm/y, it accounts for 67% of the net income on the surface zone. The corresponding percentage of the recharge was 61% in the earlier study (Takeuchi et al. 2010) which applied HEWM-1 for the other period of April 2006 to March 2007. On the aquifer zone, the surface-to-aquifer recharge (920 mm/y, superscript (c)) account for 92% of the total groundwater recharge to the aquifer (1,002 mm/y, superscript (d)). The similar percentage, 96%, was obtained in the earlier study (Takeuchi et al. 2010). The water returning from the aquifer to the surface zone, which consists of the spring and the discharge to the canals and the rivers (or the sum of the values with a superscript (e), 499 mm/y), accounts for 54% of the recharge (920 mm/y, superscript (c)). According to Sato et al. (2007), who developed the water quality model consisting of surface water and groundwater submodels, the simulation result for the whole Lake Biwa watershed showed that annual groundwater recharge accounts for 60% of the net income (deduction of evapotranspiration from sum of rainfall and irrigation). Their study also shows that the water returning from the aquifer to the surface is 39% of the groundwater recharge. Our result in water budget is nearly consistent with their result despite many differences between the two models.

Table 4 Annual water budget in whole area
Full size table

Figure 13 compares the cumulative surface water and groundwater discharges to canals over-a-year. Note that the groundwater discharge corresponds to the canal-aquifer flow rate, which is the sum of the exchange flow rate through canal bed and the underdrain discharge. The surface discharge is highly susceptible to erratic rainfall/snowfall, while the groundwater discharge is rather subject to gradual rise and fall of the groundwater table 43% of the gross discharge throughout-a-year (1.1 × 107 m3/y) is of groundwater origin.

Fig. 13
figure 13

Cumulative surface water/groundwater discharge

Full size image

The interactive canal-aquifer flow dynamics, integrated over all the drainage canals, is illustrated in Fig. 14. It includes annual variations of the aquifer-to-canal discharge, the canal-to-aquifer recharge (reverse or negative discharges) and the net aquifer-to-canal discharge. The discharge peaks late after the termination of the irrigation period and reaches the bottom in autumn. This annual variation of the discharge corresponds to that of the groundwater level. The temporal increasing events of the recharge are thought to be caused by sharp rises of in-canal water level, because they were not found in the simulation with HEWM-1 (Takeuchi et al. 2010). The effect of canal rise on recharge can be simulated with HEWM-2 because of the open channel flow submodel newly introduces.

Fig. 14
figure 14

Time-varying canal-aquifer flow

Full size image

Figure 15 visualizes the spatial distributions of the groundwater depth and the canal-aquifer flow rate, in winter (November) and summer (July) seasons. The discharge reach indicates a reach of the canal which gains groundwater discharged from aquifer. The recharge reach is a reach which loses stream water to recharge groundwater. In both the seasons, the groundwater depth is likely to be more than 3 m in the fan, while less than 2 m in the plain. The drainage canals in the fan and the plain mostly serve as losing and gaining canals, respectively. At the upstream side of the diversion weirs, the canal loses water despite high groundwater level, because the weirs keep the in-canal water level higher than the groundwater level. In summer when groundwater depth becomes less than 1.5 m in a wide area of the plain, most of the drainage canals gain the discharge of 2–3 m3/d/m. For better model application, the physical properties (e.g. depth, inclination and permeability of bottom sediment) of all canals need to be investigated.

Fig. 15
figure 15

Distributions of groundwater depth and canal-aquifer flow rate. a November, 2009, b July, 2010

Full size image

Conclusion

This study improves HEWM-1 so that the improved model, HEWM-2, can simulate the dynamic canal-aquifer interaction caused by the rise and fall of the difference between surface water level and groundwater level. In HEWM-2, the time-varying surface water level is computed to determine the direction (discharging or recharging) and the rate of the canal-aquifer flow for any canal at each time step. HEWM-2 has the following improvements on HEWM-1:

  • Open channel flow submodel is introduced in which the stream flow in the canals is represented by the complete 1-D shallow water equations.

  • Different two effects of canal-aquifer flow are explicitly represented. The exchange flow through canal bed is represented with Eqs. 13 and 14, and the underdrain discharge is done with Eq. 15.

  • In meteorological description, an empirical snow melting model is introduced so that snowfall is distinguished from rainfall to melt and infiltrate soil with some lags.

With an integrated operation of the four submodels, the hydro-environmental aspects of a watershed can be investigated numerically at a field-plot-scale resolution.

The validity of HEWM-2 was qualitatively shown, though it is difficult to verify the simulation results with the spatial distributions of groundwater level and canal-aquifer interaction because of the limitation of available observation data. This model is efficacious for assessing irrigation impacts on hydrological cycle in detail and for implementing integrated management of agricultural canal systems. The model could also be a useful tool for identifying whether any drainage canal is gaining or losing water in relation to groundwater level, and at the same time for estimating the canal-aquifer flow rate. If maps of such canal attributes associated with canal-aquifer interaction are provided, as shown for the application example, these could assist in conserving a complex network of drainage canals which is biological corridor for aquatic animals like fishes.