Abstract
Ionosphere Associate Analysis Centers (IAACs) of the International GNSS Service (IGS) independently produce global ionosphere maps (GIMs) of the total electron content (TEC). The GIMs are based on different modeling techniques, resulting in different TEC levels and accuracies. In this study, we evaluated the accuracy and consistency of the IAAC GIMs during high (2014) and low (2018) solar activity periods of the 24th solar cycle. In our study, we applied two different evaluation methods. First, we carried out a comparison of the GIM-derived slant TEC (STEC) with carrier phase geometry-free combination of GNSS signals obtained from 25 globally distributed stations. Second, vertical TEC (VTEC) from GIMs was compared to altimetry-derived VTEC obtained from the Jason-2 and Jason-3 satellites and complemented for plasmaspheric TEC. The analyzed GIMs obtained STEC RMS values reaching from 1.98 to 3.00 TECU and from 0.96 to 1.29 TECU during 2014 and 2018, respectively. The comparison to altimetry data resulted in VTEC STD values that varied from 3.61 to 5.97 TECU and from 1.92 to 2.78 TECU during 2014 and 2018, respectively. The results show that among the IAACs, the Center for Orbit Determination in Europe global maps performed best in low and high solar activity periods. However, the highest accuracy was obtained by a non-IGS product—UQRG GIMs provided by Universitat Politècnica de Catalunya. It was also shown that the best results were obtained using a modified single layer model mapping function and that the map time interval has a relatively small influence on the resulting map accuracy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
For over two decades, one of the most important GNSS applications has been the remote sensing of the ionosphere. The ionospheric total electron content (TEC) derived from dual-frequency measurements is used to obtain global ionosphere maps (GIMs). GIMs are applied to a wide range of applications, like precise GNSS positioning and navigation. For example, single-frequency precise point positioning (PPP) is often supported by GIMs (van Bree and Tiberius 2012; Cai et al. 2017). GIMs are also used in relative positioning to derive double-differenced ionospheric corrections (Grejner-Brzezinska et al. 2007). Since the ionosphere is the region of the atmosphere that is directly affected by solar activity, the GIMs are also applied to space weather and climate analysis (Jin et al. 2017). Additionally, space weather studies use empirical ionosphere models, such as NeQuick 2 or the International Reference Ionosphere (IRI), which are often updated/validated using GIMs (Nava et al. 2011; Liu et al. 2019).
Therefore, the International GNSS Service (IGS) has provided ionosphere products since 1998, when the Ionosphere Working Group was established (Hernández-Pajares et al. 2009). Currently, there are seven Ionosphere-Associated Analysis Centers (IAACs), which produce their own GIMs. Each center applies different datasets and modeling techniques, resulting in different levels of GIM accuracy. Given that these ionosphere models serve as a reference for the actual state of the ionosphere, it is important to model them reliably. Therefore, there is a need to evaluate their empirical accuracy levels.
There are several methods of assessing the GIMs accuracy. Some authors have investigated the quality of GIMs against reference TEC derived from GPS data (Li et al. 2015; Chen et al. 2020). However, one has to keep in mind that the reference GPS TEC is usually based on carrier-to-code leveled (CCL) observations presenting the accuracy of 2–10 TECU depending on station latitude and solar activity (Ciraolo et al. 2007; Brunini and Azpilicueta 2010). Other authors have evaluated GIMs in positioning applications. For instance, Rovira-Garcia et al. (2020) have studied their own fast-PPP ionosphere model together with IGSG (IGS global maps) and UQRG (global maps from Ion-SAT group based on kriging) in a single-frequency PPP application. A similar approach was used by Ghoddousi-Fard and Lahaye (2016), who have analyzed IAAC GIMs during the selected nine quiet and stormy days of 2014 and 2015. It should be noted that this is a unique study, which also evaluates the influence of the commonly used ionospheric mapping functions. Another approach to validation of the GIM accuracy is the comparison to precise ground GNSS data. This approach is often called self-consistency analysis (Orús 2005). It is based on precise carrier phase measurements and according to Feltens et al. (2011), its typical accuracy is about 0.1 TECU. The self-consistency analysis is divided into two similar techniques. The first one is based on slant TEC time differences (dSTEC) between two observations with a similar elevation in the phase-continuous data arc (Orús et al. 2005). The second, which is a more popular technique, calculates differences with respect to a reference observation having the highest elevation in the analyzed arc (Feltens et al. 2011). In this contribution, however, we apply our own version of the self-consistency analysis, which is based on carrier phase data fitting into GIM STEC and post-fit residual analysis (Krypiak-Gregorczyk et al. 2017).
Another popular and independent validation method is the comparison with vertical TEC (VTEC) derived from dual-frequency altimeters (here: ALT_VTEC). Hernández-Pajares et al. (2017) have compared both self-consistency analysis and altimetry-based validation methods confirming that these approaches are consistent, and therefore, they highly recommend using both approaches simultaneously. One example of applying both methods is the study published by Roma-Dollase et al. (2018). The authors of that study evaluated all IAACs & UQRG GIMs focusing on the comparison between classic, new and resumed IAACs. Their investigation was made against 15 years of altimetry measurements and four selected days of GPS observations. UQRG accuracy has been additionally evaluated with respect to altimetry data using different map intervals, i.e., 15, 60 and 120 min. Another example is the study published by Ren et al. (2019), who made comparisons of GIMs including dSTEC and ALT_VTEC data, focusing on the evaluation of the newest real-time GIMs during the low solar activity period.
However, none of these studies combines consistent analysis of IAAC GIMs with respect to different solar conditions, geographical regions, mapping functions and map interval using the same dataset and methodology. Therefore, in our study, we verify the accuracy of ionosphere maps addressing the above-mentioned factors and using the two most popular evaluation methods—self-consistency analysis and comparison to altimetry TEC data. However, we modified both approaches to make the investigation more reliable. For the self-consistency study, we carefully selected GNSS tracking stations uniformly covering the globe, which were not used in generating any GIMs (based on the information provided in IONEX files). In comparison with VTEC derived from altimetry missions, we used Jason-2 and Jason-3 satellite data. However, probably for the first time, the observed ALT_VTEC was complemented with model-derived plasmaspheric TEC. Both methods were applied during the full years of 2014 and 2018. These periods were chosen to analyze the GIM accuracy during both solar maximum and minimum conditions and its annual variation. In our investigation, we evaluated all IAAC GIMs and also UQRG GIM. In addition, we analyzed the influence of the applied mapping functions and GIM interval.
Analyzed global ionosphere maps
In our study, we tested the final GIMs, providing grids of vertical TEC values with a spatial resolution of longitude 5° and latitude 2.5°, respectively. Their temporal resolution ranged from 15 min to 2 h, depending on the model used (Table 1). The following GIMs provided by seven IGS IAACs were investigated:
-
CASG GIM from the Chinese Academy of Sciences (Beijing, China);
-
CODG GIM from the Center for Orbit Determination in Europe (Bern, Switzerland);
-
EMRG GIM from the Natural Resources Canada (Ottawa, Canada);
-
ESAG GIM from the European Space Agency/European Space Operations Centre (Darmstadt, Germany);
-
JPLG GIM from the Jet Propulsion Laboratory (Pasadena, United States);
-
UPCG GIM from the Polytechnic University of Catalonia (Barcelona, Spain);
-
WHUG GIM from Wuhan University (Wuhan, China).
In addition, we investigated the UQRG GIM provided by the Ion-SAT group from the Polytechnic University of Catalonia (UPC) because of its higher temporal resolution (15 min) and the final combined IGS product. All of these models are described in more detail below.
The Chinese Academy of Sciences (CAS) joined the IGS as an Ionosphere Associate Analysis Center in 2016. They generate global ionosphere maps using the Spherical Harmonics function plus generalized Trigonometric Series (SHPTS). In this approach, the GIM product is generated using the following two steps. Firstly, the variation of ionospheric TEC is modeled using the Spherical Harmonic (SH) function on a global scale and the Generalized Trigonometric Series function on a regional scale. In the following step, the GIM product is calculated using the improved DADS (different areas, different stations) method. The SHPTS method adopts a single-layer model with a layer height of 450 km. CAS provides ionospheric products in the IONosphere map EXchange (IONEX) format (Schaer et al. 1998), consisting of 49 maps with a 30-min temporal resolution (Li et al. 2015).
The CODE has been a member of the Ionosphere Working Group since its inception in 1998. To generate daily VTEC maps, it uses GPS/GLONASS data from about 300 globally distributed stations. SH expansion is used to parameterize vertical TEC in a solar-geomagnetic frame. Slant TEC is converted into VTEC using a modified single-layer model mapping function.t approximates the JPL extended slab model mapping function. The final CODE GIM results correspond to the results for the middle of the day of a 3-day combination analysis. In the combination 73 × 256, or 18,688 VTEC parameters and 3 daily sets of differential code bias (DCB) constants are solved. In this way, discontinuities at the borders of the day can be minimized. The CODE ionospheric product is based on double-difference data, and it is provided in the IONEX format. Each IONEX file includes 25 VTEC maps with a time spacing of 1 h (Schaer 1999).
The Canadian Geodetic Survey (CGS) of Natural Resources Canada (NRCan) was a member of the Ionosphere Working Group from its inception until 2003, and it resumed the provision of ionosphere products in April 2015. The global ionosphere maps are generated on a daily basis using GPS data (from 2016, also GLONASS). The TEC is modeled with SH up to a degree and order of 15, adopting a single-layer model in a geomagnetic reference frame. Every day, twenty five hourly maps are derived from the data recorded by about 350 IGS stations (Ghoddousi‐Fard et al. 2011).
The IGS Analysis Centre of the European Space Agency (ESA) is located at the European Space Operations Centre (ESOC) in Darmstadt, Germany. The ESA/ESOC, which has been involved in the Ionosphere Working Group since its establishment in 1998, develops its global ionospheric maps using a single-layer approach (layer height 450 km) in a solar-geomagnetic reference frame. The vertical TEC is modeled by spherical harmonics in combination with a daily receiver and satellite DCBs. Ionosphere products are delivered in the final mode with a 2-h time resolution and rapid mode with 2-h and 1-h time resolutions. In 2013, the ESOC ionosphere processing software IONMON (Ionosphere Monitoring Facility) became an integral part of ESOC NAPEOS (Navigation Package for Earth Orbiting Satellites) software. Since then, GLONASS data have been processed in combination with GPS data (Feltens 2007).
The Jet Propulsion Laboratory (JPL) in Pasadena (USA) has been part of the Ionosphere Working Group since 1998. The global ionosphere maps are produced using GPS data. In the IONEX format, ionosphere products consist of 13 VTEC maps with a 2 h temporal resolution. At the beginning of the twenty-first century, a three-shell model was introduced instead of a common single-shell model. In this model, the layers are placed at fixed altitudes of 250, 450, and 800 km. However, single-shell maps are provided to the IGS. The JPL product is a data-driven model that uses a Kalman filter-based approach to fit slanted TEC observables derived from GPS data into the model (Mannucci et al. 1998).
The Polytechnic University of Catalonia (UPC) has contributed to the Ionosphere Working Group since its inception in 1998. Ionosphere maps are generated using Tomographic Ionosphere model software (TOMION) with spline interpolation. Instead of a single-layer approximation, the UPC uses a 2-layer voxel model. To derive raw information from GNSS signals, they use only carrier phase observables, whose ambiguities are estimated with a Kalman filter. IONEX products consist of thirteen 2-hourly ionosphere maps (Hernández-Pajares et al. 1999). UPC also provides an additional UQRG high-resolution model, which uses kriging interpolation instead of splines. It contains 97 TEC maps with a time spacing of 15 min. UQRG is not an official IGS product, but it was also evaluated in this study (Orús et al. 2005).
Wuhan University is the second new contributor to the Ionosphere Working Group since 2016. They provide ionosphere products containing rapid and final GIMs (labeled WHRG and WHUG). To represent global ionospheric maps, they use SH expansion. The global ionospheric maps are based on a single-layer model. Wuhan University uses a new algorithm, called inequality-constraints least squares adjustment, to reconstruct VTEC models. Each IONEX product with thirteen 2-h ionosphere maps is provided in IONEX format (Zhang et al. 2013).
Finally, the final IGS product is a combination of individual products provided by IAACs (Hernández-Pajares et al. 2009). However, IGS IONEX files provided for 2014 are based on CODE, JPL, and ESA GIMs only, and for 2018, they are based on CODE and JPL GIMs.
Comparison with GPS STEC data: self-consistency analysis
One of the methods to evaluate the quality of GIMs is the direct comparison to ground GNSS observations. The computation process is based on the extraction of slant TEC (STEC) data from the geometry-free linear combination of carrier-phase observables:
where k and i are the satellite and receiver indexes, respectively; \(\xi_{GF} = 1 - \xi = 1 - \frac{{f_{1}^{2} }}{{f_{2}^{2} }} \approx - 0.647\) is a factor that converts the ionospheric delay \(\left( {\Delta I_{i}^{k} } \right)\) at the LGF signal to the delay related to L1; f1, f2 are the L1 and L2 signal frequencies; \(B_{iGF}^{k}\) is the carrier phase bias; \(\lambda_{1} \;{\text{and}}\;\lambda_{2}\) are signal wavelengths; N stands for the carrier phase ambiguities; and b denotes hardware delays.
As it was already mentioned, in this study, we used our own approach for the self-consistency analysis, as presented by Krypiak-Gregorczyk et al. (2017). In this method, GIMs were used independently to calibrate the carrier phase bias \(\left( {B_{iGF}^{k} } \right)\) for each continuous carrier phase observational arc. As the raw STEC values from GNSS measurements are biased by unknown carrier phase bias, the bias has to be removed by the following STEC calibration procedure (see Fig. 1):
-
Geometry-free linear combination of carrier phase observations \(\left( {L_{iGF}^{k} } \right)\) was formed for each continuous data arc (red line in Fig. 1-left panel);
-
VTEC values from each GIM were interpolated for each data arc using the method recommended in the technical note by Schaer et al. (1998);
-
Interpolated VTEC data were converted to STEC (denoted GIM_STEC, blue line in Fig. 1-left panel) values using the single-layer model (SLM) mapping function presented by Schaer (1999);
-
Carrier phase bias was estimated by fitting carrier phase data (LGF) into GIM_STEC, which resulted in the determination of calibrated STEC data (denoted GNSS_STEC, red line in Fig. 1-middle panel);
-
Then, post-fit residuals were used to calculate RMS, which served as a consistency metric (blue line in Fig. 1-right panel).
Since GNSS_STEC values are based on real GNSS observations, they precisely reflect actual ionospheric STEC variations and, therefore, may serve as a reference for GIM_STEC. However, one has to note that the absolute level of GNSS_STEC is driven by the TEC level from a particular GIM used for calibration.
In order to validate GIMs by GNSS_STEC, 25 globally distributed stations were selected (Fig. 2). The geographical distribution of the stations enabled the analysis of the accuracy of GIMs in three geomagnetic regions: a low-latitude region (from 30° S to 30° N), a mid-latitude region (from 30° to 60° in both hemispheres), and a high-latitude region (from 60° to 90° in both hemispheres). In the analysis, GPS carrier phase L1 and L2 observables with 30-s intervals and 25° elevation cut-off were used.
The RMS values of post-fit residuals between GIM_STEC and GNSS_STEC were calculated for each PRN, station, and day. Some examples of GIM_STEC, GNSS_STEC, and post-fit residuals for IGSG and UQRG for a quiet day are shown in Figs. 3 and 4 (January 5, 2014, max Kp = 1o). Two stations, ABOO and KATO, were selected, corresponding to low-latitude and mid-latitude regions, respectively. Continuous GPS data arcs observed by both stations were selected for the same time of day, roughly between 8:00 and 14:00 local time. A significant difference in residual values between the two selected stations located at the abovementioned regions can be observed. For station KATO, residuals did not exceed ± 2 TECU, while at ABOO station, they reached up to ± 10 TECU.
It is known that the TEC level is driven by the solar activity level and geomagnetic conditions. Hence, Fig. 5 presents another example under the most difficult conditions, such as a low-latitude region (ABOO station), a high solar activity period (year 2014), and the most geomagnetically disturbed day (February 19, 2014, max Kp = 6). This resulted in very high residuals reaching almost 30 TECU. Since 1 TECU causes 0.162 m of L1 signal delay, a bias of 30 TECU may cause a bias of over 4.5 m in ionospheric corrections.
The daily RMS values in the two analyzed years, 2014 and 2018, are presented in Figs. 6 and 7, respectively. In 2014, eight models were tested. Since EMRG resumed its IAAC activity in 2015, nine models were tested in 2018. During the high solar activity period (2014), the daily RMS for each GIM ranged from approximately 1.0 to 4.5 TECU. Based on daily RMS, a mean annual RMS was calculated for each GIM (Table 2). Among all analyzed models, the lowest annual RMS, and the only one below 2 TECU, was derived for the UQRG model, while among the IAAC models, the lowest RMS was obtained for the CODG model (2.44 TECU; see Table 2). The highest annual RMS was obtained for the ESAG model (3.00 TECU). For any tested GIMs, the highest daily RMS values were observed around the beginning of March and October (about 60 and 300 DOY, respectively), which may be related to the equinox periods. Similar behavior was observed by Orús-Pérez (2019), who studied the accuracy of the Galileo NeQuick model over the whole year of 2017. It is worth noting that the UQRG model, even at these two RMS peaks, did not exceed 3 TECU with few exceptions.
In 2014, the daily solar flux F10.7 index ranged from 89 to 253 sfu. As shown in Fig. 6, there is a significant correlation between the GIM accuracy and F10.7 index. It can be seen that the daily RMS is correlated with ~ 30-day Solar rotation period. On the other hand, there is no clear dependency between the RMS and geomagnetic conditions. During the three most geomagnetically disturbed days in 2014—DOY 50 with ∑Kp = 34o; DOY 159 with ∑Kp = 33o; DOY 51 with ∑Kp = 32−—the average daily RMS from all GIMs amounted to 3.34, 2.02 and 3.15 TECU, respectively. However, the average daily RMS exceeded 3.50 TECU thirteen times during this year, reaching its highest value of 3.83 TECU on a geomagnetically quiet day (DOY 95, ∑Kp = 19−). This is because the daily RMS is a global indicator, and the most disruptive storm effects usually have a regional character. Moreover, the duration of storms also has an impact on RMS. For example, if a storm starts in the evening, its influence on the daily RMS is less pronounced.
In our study, we also examined the impact of the most popular ionospheric mapping function on the self-consistency analysis results. The mapping function used to convert VTEC into STEC values was derived from Schaer (1999):
where z is the zenith distance at the receiver’s location; R is the mean earth radius; H is the height of the single layer; and α is a correction factor.
The standard SLM mapping function applies R = 6371 km, H = 450 km, and α = 1, while the Modified Single Layer Model (MSLM) mapping function applies R = 6371 km, H = 506.7 km, and α = 0.9782 (Feltens et al. 2018). Most of the IAACs, e.g., CODE, ESA, and NRCan, use the MSLM mapping function, which is the best fit to extended slab model mapping function used by JPL (Coster et al. 1992). The SLM mapping function is used by only a few IAACs, e.g., CAS, but UPC also recommends it for both GIMs – UQRG and UPCG. On the other hand, all IAACs define H = 450 km in the IONEX headers. In our opinion, this suggests using the SLM mapping function for IAAC GIMs. Nevertheless, we additionally calculated the self-consistency analysis with GIM_STEC derived using the MSLM mapping functions. As shown in Table 2, for any tested GIMs, the MSLM mapping function results in lower annual RMS. The most noticeable improvement in the annual RMS was obtained for JPLG GIM—5.5%, while the smallest one being 1.9% was achieved for ESAG GIM. In the study by Ghoddousi-Fard and Lahaye (2016), the MSLM mapping function also performed better in a single-frequency PPP solution supported by various IAAC GIMs.
Another factor that may affect the GIMs accuracy is their temporal resolution. The IAAC GIMs provide their IONEX files with a varied interval, which has changed over the years and currently ranges from 15 min to 2 h (see Table 1). Therefore, in order to analyze the impact of GIMs interval, we reduced the time resolution of each higher-resolution GIM to 2 h. In 2014, only UQRG GIM was provided with 15-min interval. As shown in Table 2 UQRG GIM in their original form performed the best among all tested GIMs. Although reducing the interval worsened the annual RMS by about 16%, UQRG GIM still has the lowest annual RMS (Table 2, last row), indicating that the underlying methodology has a greater impact on the GIM accuracy. This confirms findings presented by Roma-Dollase et al. (2018).
In the second analyzed year, corresponding to the solar minimum, the daily and annual RMS values were clearly lower (Fig. 7). The daily RMS for each model ranged from approximately 0.7–1.6 TECU. Similar to 2014, there were increased RMS values around equinox periods, but this phenomenon was less pronounced. In 2018, in turn, the UQRG model was characterized by the lowest annual RMS value, but the CODG GIM also performed very well (Table 3). These two models were the only ones reaching annual RMS no higher than TECU, amounting to 0.96 and 1.00 TECU, respectively. The highest RMS value of 1.29 TECU was derived for the EMRG maps.
In 2018, the daily solar flux F10.7 index ranged from 65 to 85 sfu, presenting much lower amplitude than in 2014. Therefore, during the solar minimum, the correlation with RMS is less pronounced (Fig. 7). There is also no clear dependency of the RMS on geomagnetic conditions. For example, the average daily RMS from all GIMs amounted to 1.31 TECU on the most disturbed day (August 26 with ∑Kp = 42+), while the highest average RMS of 1.44 TECU was obtained on May 6 (∑Kp = 30−). However, the second highest RMS was obtained on the second most disturbed day (April 20). This shows that in some cases, strong geomagnetic disturbances affect the accuracy of GIMs, but this is not the general rule.
Similarly to the 2014 case, the application of the MSLM mapping function increases the accuracy of STEC from all analyzed GIMs. The improvement ranged from 1.0% for CASG and EMRG to 5.9% for JPLG (Table 3). For all GIMs except JPL, this improvement was slightly lower compared to the 2014 results.
In 2015 CAS, CODE and NRCan started to provide IONEX files with higher temporal resolution (see Table 1). Therefore, these GIMs were analyzed with their interval reduced to 120 min to match the other maps. Reducing the interval increased the annual RMS by around 2%, 9%, 7%, and 11% for CASG, CODG, EMRG, and UQRG, respectively. Considering the tests with 2-h temporal resolution, UQRG and CODG still performed the best, similarly to their higher resolution versions.
To analyze the performance of GIMs over different geomagnetic regions, we have also evaluated the annual RMS for each of the three distinctive regions (Fig. 8). In both 2014 and 2018, the analyzed models reached quite similar levels of RMS in the mid- and high-latitude regions. However, in 2014, most GIMs have slightly higher RMS in the high-latitude region than in the mid-latitude region. This is because dense networks of GNSS stations cover the mid-latitude region, and also, the ionosphere is the most stable there (Hunsucker and Hargreaves 2002). As expected, RMS values in the low-latitude region were significantly higher. These differences were greater during the solar maximum period, reaching about 1.5 TECU. One can observe that the modeling in low-latitude region is still a challenging task due to the highest TEC level being present around the equatorial anomaly and also due to the large ocean areas with less dense GNSS station networks. Again, for each of the analyzed regions, the UQRG model presented the highest accuracy.
A summary of the RMS analysis is given in Fig. 9. The results confirm a clear RMS dependency on different periods of the solar activity cycle. By comparing the RMS values of each model for the two analyzed years, we found a significant deterioration of model accuracy during the high solar activity period (2014). In each of the available models, the level of RMS differed between 2014 and 2018 by approximately 1–2 TECU. Comparing to 2014, the annual RMS in 2018 was lower by more than 50%.
Table 4 presents the relative accuracy of the analyzed GIMs, based on the ratio of the residuals to the analyzed GIM STEC level. It can be observed that the overall relative STEC accuracy ranged from 5.9% (UQRG) to 10.7% (WHUG) in 2014. In 2018, due to the generally much lower TEC level, the relative error ranged from 7.9% (UQRG) to 23.9% (ESAG). In the case of ESAG, this error increased almost threefold. This increase is caused by generally very low TEC level, often under 1 TECU, at northern high-latitudes in Winter months in ESA GIMs. In general, our relative errors are clearly lower than those provided by Roma-Dollase et al. (2018), where the authors reported errors of 20–30%. Note, however, that in our study, better results come from a different approach to self-consistency analysis. Nevertheless, the rank of the GIMs is consistent in both studies.
Comparisons with altimetry-derived VTEC
Nowadays, several altimetry satellites are equipped with dual-frequency radar altimeters that scan almost the whole ionosphere in the nadir direction. Using two frequencies enables the determination of the ionospheric signal delay below the satellite orbit. Therefore, the ionospheric delays in the range can be used for TEC determination by a reverse formula:
where f is the frequency in Hz and dR is the ionospheric range correction.
Altimetric VTEC measurements are limited to sea/ocean areas. Therefore, altimetry-derived TEC (ALT_VTEC) is an important source of validation for GNSS TEC models over oceans, where the number of GNSS stations is limited. TEC values from different global models (GIM_VTEC) can then be compared with ALT_VTEC over the oceans. However, TEC values derived from altimetric ranging are affected by significant noise, and a smoothing process has to be applied. The random character of the noise and its size result in the accuracy typically being slightly worse than 1–2 TECU, so a filter based on the median is often sufficient (Hernández-Pajares et al. 2017). This study applied data from Jason-2 and Jason-3, which carry Poseidon-type dual-frequency radar altimeters that emit pulses at two frequencies: 13.6 and 5.3 GHz. Both missions operate at an altitude of around 1340 km. An example of a daily ground track of Jason-2 is presented in Fig. 10.
Since altimetric measurements provide VTEC data only up to satellite orbital height, i.e., slightly over 1300 km, direct ALT_VTEC data do not include plasmaspheric TEC values. On the other hand, each of the IAACs provides GIM_VTEC data up to the GPS satellite orbit (20,200 km). This difference in the upper boundary between ALT_VTEC and GIM_VTEC can significantly affect the analysis results. Therefore, in our investigation, we complemented the observed ALT_VTEC data with model-derived plasmaspheric TEC data to achieve consistency with GIM_VTEC. Here, plasmaspheric TEC values were derived from the NeQuick 2 model, which is the latest version of the NeQuick ionosphere electron density model (Nava et al. 2008). According to the NeQuick 2 model, TEC values above the altimeter orbit vary from 0.2 TECU to 4.7 TECU for the analyzed data.
To validate the analyzed GIMs, we calculated the differences between ALT_VTEC and GIM_VTEC data. Then, we calculated the daily mean bias, RMS, and STD values of the differences. Since ALT_VTEC data are also affected by unknown instrumental bias, we focused our analysis on the STD parameter. This approach has also been recommended by Roma-Dollase et al. (2018). An example of a comparison of ALT_VTEC from orbit #171 to GIM_VTEC derived from four selected GIMs is presented in Fig. 11.
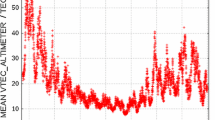
During the year of 2014, corresponding to the solar maximum, daily and annual STDs with respect to the Jason-2 VTEC are presented in Fig. 12 and Table 5, respectively. The resulting STD for all analyzed models is clearly higher than the RMS in the GNSS_STEC analysis. The daily STD of all GIMs ranges from about 2 to nearly 12 TECU. Despite the greater variation, the distribution of the daily STD is very similar to that provided in Fig. 6 with even more evident peaks around the equinox periods. Again, the UQRG model performed best. This is the only model that obtained an annual STD below 4 TECU. The ESAG model differed significantly from the other GIMs. This model obtained the highest annual STD value of almost 6 TECU, while the other models did not exceed 5 TECU.
The results presented in Table 5 show that the addition of the plasmasphere to raw ALT_VTEC data results in an improvement in the consistency with GIM_VTEC data (STD) by 1–6%. A clearer improvement was observed in the bias that ranges from − 2.1 TECU (JPLG) to 0.8 TECU (ESAG). It should be noted that CASG, UPCG and UQRG have bias even close to 0 TECU. The bias with no plasmaspheric correction, however, ranged from − 3.9 TECU (JPLG) to − 1.0 TECU (ESAG). As we already mentioned, ALT_VTEC consists of an altimeter hardware bias of a few TECU. Hence, zero bias with respect to GIM_VTEC does not necessarily means the highest accuracy. In such comparisons, STD is still the most important indicator of GIM quality.
The GIM_VTEC accuracy was also analyzed with respect to the map interval (see Table 5, last row). When reducing the temporal resolution to 120 min, the annual STD for UQRG increased by around 5%, and negligible differences were observed in the bias level. Despite reducing the interval, UQRG still performed best.
During the solar minimum (2018), the same study was performed. However, we processed data from two altimetric satellites: Jason-2 and Jason-3 (Fig. 13). Note that for the Jason-2 satellite, there were some data gaps due to orbital changes related to the end of the mission. Nevertheless, there was a high level of consistency between the results of the two analyzed satellites. There were STD peaks at the same periods of the year for both satellites, similar to the results from 2014. The daily STD of each analyzed model for Jason-2 as well as Jason-3 ranged from approximately 1.5 to 4 TECU, with a few exceptions. In terms of the annual STD, among IAAC members, the UPCG model obtained the best result—2.04 TECU for Jason-2 and 2.20 TECU for Jason-3 (see Tables 6, 7). However, once again, the UQRG model reached the lowest annual STD from all the analyzed maps, which amounted to 1.92 and 2.09 TECU for Jason-2 and Jason-3, respectively. Similar to the UPCG and UQRG GIMs, all analyzed models reached slightly higher annual STD values for Jason-3 than for Jason-2. For both altimeters, the highest annual STD was obtained for the ESAG model.
Again, the plasmaspheric corrections reduced STD for all GIMS by around 0.2–0.3 TECU for both Jason-2 and Jason-3 (from 7% for UPCG to 11% for JPLG). However, in 2018, adding the plasmaspheric corrections to Jason-2 data resulted in increased bias between ALT_VTEC and GIM_VTEC by around 0.8 TECU for all GIMs. On the other hand, adding these corrections to Jason-3 data reduced the bias on average by 0.9 TECU, with ESAG bias being close to 0 TECU. Interestingly, the bias between Jason 2 and Jason 3 VTEC data is around 2.25 TECU.
During the low solar activity period, four higher-resolution IAAC GIMs were analyzed with the interval reduced to 120 min. The results for both Jason-2 and Jason-3 satellites are shown in Tables 6 and 7, respectively. For Jason-2 satellite, the application of 2-h interval increased the annual STD by only 0.3%, 0.6%, 0.8% and 1.3%, whereas for Jason-3 by 0.1%, 1.0%, 0.5% and 1.5% for CASG, CODG, EMRG and UQRG, respectively. In comparison to 2014, the increase of STD was much lower. Again, GIM interval had negligible impact on the bias.
Altimetry data were also evaluated with respect to the three selected geomagnetic regions (Fig. 14). In both 2014 and 2018, the highest STD value occurred in the low-latitude region for all GIMs. In 2014, the annual STD for the low-latitude region amounted to 4.6–7.1 TECU, and it was ~ 90% higher than that for mid-latitudes. However, in 2018, it amounted to 2.2–2.9 TECU and was higher than that for mid-latitudes by around 20%. STD for the high-latitude region was the lowest for both 2014 and 2018. Comparing to the GNSS_STEC RMS analysis, the STD at the high-latitude area are clearly lower than at mid-latitudes. This may be caused by the fact that altimeter footprints reach only ± 66° latitude, while selected GNSS stations spread from – 86° to + 80°, and therefore, GNSS probes more varied higher-latitude ionosphere. Again, in 2014, the lowest annual STD value for the three geomagnetic regions was obtained with the UQRG model. In 2018, the annual STD for the low-latitude region was also the lowest for the UQRG GIMs. However, for the mid- and high-latitude regions, the UPCG product obtained the best or the same results as UQRG.
Annual GIM_VTEC STD values for low-, mid-, and high-latitude regions for all analyzed GIMs based on comparisons with the Jason-2 satellite data for 2014, and with the Jason-2 and Jason-3 data for 2018 (from top to bottom). The superscripts mean: aEMRG is available since April 2015; bUQRG is not an official International GNSS Service (IGS) product
A summary of the annual STD data for both Jason-2 and Jason-3 is given in Fig. 15. Comparing the data from two analyzed years, we can observe a significant increase in the annual STD during the high solar activity period (2014). Between 2014 and 2018, the annual STD differed by around 1.5 to 3.3 TECU. For each analyzed GIM, the annual STD value obtained from the new Jason-3 satellite was slightly greater than that from the Jason-2 satellite.
Summary and conclusions
This study validated the GIMs provided by seven IGS IAACs, IGS combined products, and UQRG high-resolution maps provided by the UPC. The study was performed during high (2014) and low (2018) solar activity periods with the use of two different approaches. First, we compared GIM_STEC to GNSS_STEC derived from 25 globally distributed GNSS-tracking stations. In this approach, we also evaluated GIMs using the two most popular ionospheric mapping functions—SLM and MSLM. Second, GIM_VTEC was compared with the altimetry-derived and plasmasphere-complemented ALT_VTEC data from Jason-2 and Jason-3 satellites. The GIM comparisons to both GNSS_STEC and ALT_VTEC were carried out with respect to three geomagnetic regions. In addition, we analyzed higher-resolution GIMs with a reduced interval to 120 min.
We observed a good consistency between different GIMs (Figs. 9, 15). Furthermore, there was a good agreement in terms of the rank of the models, whether GIMs were compared to GNSS_STEC or to ALT_VTEC. In both comparisons, the results confirm a clear dependency of model accuracy on the 11-year solar activity cycle. In general, the accuracy of GIMs was found to be around two times lower during the high solar activity period compared with the low activity one. The validation with GNSS data showed that the annual RMS varied from 0.96 to 1.29 TECU during the low solar activity period and from 1.98 to 3.00 TECU during the high solar activity period. In comparison with altimeter data, the annual STD varied from 1.92 to 2.78 TECU and from 3.61 to 5.97 TECU during the solar minimum and maximum periods, respectively. It is interesting to see that the application of MSLM mapping function always provided more accurate results. This suggests that MSLM may be recommended to be used with IAAC IONEX data over the standard SLM mapping function.
Increasing map interval increased the annual RMS by 2% to 16% for CASG in 2018 and UQRG in 2014, respectively. In comparison to ALT_VTEC data, increased GIM interval also increased the resulting STD, but to a lesser extent—from 0.1 to 5.5%. Note that in the case of UQRG we reduced the GIM temporal resolution eightfold, but the resulting accuracy is reduced up to 16% only. In the case of CASG, reducing map resolution has a very small impact on the results. Moreover, the CASG maps provided for 2018 have the second-highest temporal resolution (30-min), but their results were not better than those of, e.g., CODG provided with 60-min resolution. This suggests that the underlying methodology has a greater impact on the map accuracy than the map interval.
When the performance of the GIMs was considered in relation to the three geomagnetic regions, it was shown that the low-latitude region was modeled with the lowest accuracy. Modeling in this region is still a challenging task due to the higher TEC over the equatorial anomaly as well as the limited amount of data due to ocean areas. GNSS_STEC comparisons showed that the GIM_STEC RMS value for the low-latitude region is usually two times higher than that for mid- or high-latitude ones, regardless of the solar activity. In the case of GIM_VTEC, the low-latitude region presented an STD value around 90% higher than that of other regions during periods of high solar activity. However, during the low solar activity period, the annual STD value was only around 20% higher for this region.
The highest accuracy level for both GNSS and altimetry comparisons was obtained for UQRG, even with the increased interval, which may indicate some advantage of the stochastic approach (kriging). From the IAAC GIMs, usually, the best results were obtained with the CODG product. Since, currently, the final IGS maps do not include all IAAC GIMs, it may be expected that future inclusion of the remaining GIMs into the final IGS GIM will improve their accuracy.
Data availability
Products containing ionosphere VTEC maps are accessible from the NASA’s CDDIS ftp server (ftp://cddis.nasa.gov/gnss/products/ionex/) in the IONEX format. RINEX files are accessible from the SOPAC (ftp://garner.ucsd.edu/archive/garner/rinex/), UNAVCO (ftp://data-out.unavco.org/pub/rinex/obs/) and SONEL (ftp://ftp.sonel.org/gps/data/) ftp servers. Altimeter data are accessible from the NOAA ftp server (ftp://ftp.nodc.noaa.gov/pub/data.nodc/).
References
Brunini C, Azpilicueta F (2010) GPS slant total electron content accuracy using the single layer model under different geomagnetic regions and ionospheric conditions. J Geodesy 84(5):293–304. https://doi.org/10.1007/s00190-010-0367-5
Cai C, Gong Y, Gao Y, Kuang C (2017) An approach to speed up single-frequency PPP convergence with quad-constellation GNSS and GIM. Sensors 17(6):1302. https://doi.org/10.3390/s17061302
Chen P, Liu H, Ma Y, Zheng N (2020) Accuracy and consistency of different global ionospheric maps released by IGS ionosphere associate analysis centers. Adv Space Res 65(1):163–174. https://doi.org/10.1016/j.asr.2019.09.042
Ciraolo L, Azpilicueta F, Brunini C, Meza A, Radicella SM (2007) Calibration errors on experimental slant total electron content (TEC) determined with GPS. J Geodesy 81(2):111–120. https://doi.org/10.1007/s00190-006-0093-1
Coster AJ, Gaposchkin EM, Thornton LE (1992) Real-time ionospheric monitoring system using GPS. Navigation 39(2):191–204. https://doi.org/10.1002/j.2161-4296.1992.tb01874.x
Feltens J (2007) Development of a new three-dimensional mathematical ionosphere model at European Space Agency/European Space Operations Centre. Space Weather 5(12):1–17. https://doi.org/10.1029/2006SW000294
Feltens J, Angling M, Jackson-Booth N, Jakowski N, Hoque M, Hernández-Pajares M, Aragón-Àngel A, Orús R, Zandbergen R (2011) Comparative testing of four ionospheric models driven with GPS measurements. Radio Sci 46(06):1–11. https://doi.org/10.1029/2010RS004584
Feltens J, Bellei G, Springer T, Kints MV, Zandbergen R, Budnik F, Schönemann E (2018) Tropospheric and ionospheric media calibrations based on global navigation satellite system observation data. J Space Weather Space Clim 8:A30. https://doi.org/10.1051/swsc/2018016
Ghoddousi-Fard R, Lahaye F (2016) Evaluation of single frequency GPS precise point positioning assisted with external ionosphere sources. Adv Space Res 57(10):2154–2166. https://doi.org/10.1016/j.asr.2016.02.017
Ghoddousi-Fard R, Héroux P, Danskin D, Boteler D (2011) Developing a GPS TEC mapping service over Canada. Space Weather. https://doi.org/10.1029/2010SW000621
Grejner-Brzezinska DA, Kashani I, Wielgosz P, Smith DA, Spencer PSJ, Robertson DS, Mader GL (2007) Efficiency and reliability of ambiguity resolution in network-based real-time kinematic GPS. J Surv Eng 133(2):56–65. https://doi.org/10.1061/(ASCE)0733-9453(2007)133:2(56)
Hernández-Pajares M, Juan JM, Sanz J (1999) New approaches in global ionospheric determination using ground GPS data. J Atmos Sol Terr Phys 61(16):1237–1247. https://doi.org/10.1016/S1364-6826(99)00054-1
Hernández-Pajares M, Juan JM, Sanz J, Orus R, Garcia-Rigo A, Feltens J, Komjathy A, Schaer SC, Krankowski A (2009) The IGS VTEC maps: a reliable source of ionospheric information since 1998. J Geodesy 83(3–4):263–275. https://doi.org/10.1007/s00190-008-0266-1
Hernández-Pajares M, Roma-Dollase D, Krankowski A, García-Rigo A, Orús-Pérez R (2017) Methodology and consistency of slant and vertical assessments for ionospheric electron content models. J Geodesy 91(12):1405–1414. https://doi.org/10.1007/s00190-017-1032-z
Hunsucker R, Hargreaves J (2002) The high-latitude ionosphere and its effects on radio propagation. Cambridge University Press. https://doi.org/10.1017/CBO9780511535758
Jin S, Jin R, Kutoglu H (2017) Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. J Geodesy 91(6):613–626. https://doi.org/10.1007/s00190-016-0988-4
Krypiak-Gregorczyk A, Wielgosz P, Borkowski A (2017) Ionosphere model for European region based on multi-GNSS data and TPS interpolation. Remote Sens 9(12):1221. https://doi.org/10.3390/rs9121221
Li Z, Yuan Y, Wang N, Hernández-Pajares M, Huo X (2015) SHPTS: towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J Geodesy 89(4):331–345. https://doi.org/10.1007/s00190-014-0778-9
Liu L, Yao Y, Zou S, Kong J, Shan L, Zhai C, Zhao C, Wang Y (2019) Ingestion of GIM-derived TEC data for updating IRI-2016 driven by effective IG indices over the European region. J Geodesy 93(10):1911–1930. https://doi.org/10.1007/s00190-019-01291-5
Mannucci AJ, Wilson BD, Yuan DN, Ho CH, Lindqwister UJ, Runge TF (1998) A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci 33(3):565–582. https://doi.org/10.1029/97RS02707
Nava B, Coïsson P, Radicella SM (2008) A new version of the NeQuick ionosphere electron density model. J Atmos Sol Terr Phys 70(15):1856–1862. https://doi.org/10.1016/j.jastp.2008.01.015
Nava B, Radicella SM, Azpilicueta F (2011) Data ingestion into NeQuick 2. Radio Sci 46(06):1–8. https://doi.org/10.1029/2010RS004635
Orús R (2005) Contributions on the improvement, assessment and application of the global ionospheric VTEC maps computed with GPS data. Ph.D. dissertation. Universitat Politècnica de Catalunya, Barcelona, Spain
Orús R, Hernández-Pajares M, Juan JM, Sanz J (2005) Improvement of global ionospheric VTEC maps by using kriging interpolation technique. J Atmos Sol Terr Phys 67(16):1598–1609. https://doi.org/10.1016/j.jastp.2005.07.017
Orús-Pérez R (2019) Using TensorFlow-based Neural Network to estimate GNSS single frequency ionospheric delay (IONONet). Adv Space Res 63(5):1607–1618. https://doi.org/10.1016/j.asr.2018.11.011
Ren X, Chen J, Li X, Zhang X, Freeshah M (2019) Performance evaluation of real-time global ionospheric maps provided by different IGS analysis centers. GPS Solut 23(4):113. https://doi.org/10.1007/s10291-019-0904-5
Roma-Dollase D et al (2018) Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J Geodesy 92(6):691–706. https://doi.org/10.1007/s00190-017-1088-9
Rovira-Garcia A, Ibáñez-Segura D, Orús-Perez R, Juan JM, Sanz J, González-Casado G (2020) Assessing the quality of ionospheric models through GNSS positioning error: methodology and results. GPS Solut 24(1):4. https://doi.org/10.1007/s10291-019-0918-z
Schaer S (1999) Mapping and predicting the Earth's ionosphere using the global positioning system. Ph.D. thesis, Ph.D. dissertation. University of Bern, Bern
Schaer S, Gurtner W, Feltens J (1998) IONEX: the ionosphere map exchange format version 1. In: Proceedings of the IGS AC workshop, IGS technical note, Darmstadt, Germany, vol 9, no 11
van Bree RJP, Tiberius CCJM (2012) Real-time single-frequency precise point positioning: accuracy assessment. GPS Solut 16(2):259–266. https://doi.org/10.1007/s10291-011-0228-6
Zhang H, Xu P, Han W, Ge M, Shi C (2013) Eliminating negative VTEC in global ionosphere maps using inequality-constrained least squares. Adv Space Res 51(6):988–1000. https://doi.org/10.1016/j.asr.2012.06.026
Acknowledgements
The study is supported by Grant No. UMO-2017/27/B/ST10/02219 from the Polish National Center of Science. The authors would like to thank anonymous reviewers whose comments helped us to improve this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wielgosz, P., Milanowska, B., Krypiak-Gregorczyk, A. et al. Validation of GNSS-derived global ionosphere maps for different solar activity levels: case studies for years 2014 and 2018. GPS Solut 25, 103 (2021). https://doi.org/10.1007/s10291-021-01142-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-021-01142-x