Introduction

The performance of any GNSS strongly relies on clocks adopted by the system, both at the ground and space segments. In particular, the clocks onboard the satellites must meet rigorous requirements in terms of mass, cost, volume and power consumption and, at the same time, exhibit high-frequency stability capabilities to ensure the positioning and synchronization accuracies to the end-users (Rochat et al. 2012; Maciuk 2019). Sub-meter accuracy in the positioning signal is becoming of interest for a growing number of civilian applications, from autonomous driving to unmanned agriculture, just to mention some examples (Joubert et al. 2020; Winterhalter et al. 2020).

It is interesting to derive a typical GNSS specification, Galileo, for example, from a very qualitative point of view. The GNSS receiver obtains the position information by retrieving the propagation time of the incoming signals traveling through space at the speed of light, according to the satellite and receiver local clocks. Assuming as a target a fraction of a meter, the time on the satellites has to be known within Δt = 1 ns. The task of the onboard clocks is then to guarantee this level of uncertainty for an as long as possible time interval t, at least 100,000 s, which is equivalent to a couple of synchronizations and revolutions of the satellite around the earth (Fig. 1).

Fig. 1
figure 1

A GNSS satellite in orbit around the Earth takes tens of thousands of seconds to make a revolution and to re-synchronize. In the meanwhile, it has to carry the time information with minimal perturbation from temperature (T(t)) and magnetic field fluctuations (\(\overrightarrow{B}(t)\))

Full size image

Roughly speaking, the onboard clock requires fractional frequency stability (Rubiola 2011) \(y\equiv \frac{\Delta \nu }{\nu }=\frac{\Delta t}{t}\) = 1 × 10−14 for an averaging time of the order of one day, being ν the nominal clock frequency and Δν its fluctuation. As shown in Fig. 2, a high-performing Rubidium Atomic Frequency Standard (RAFS) satisfies this requirement. Its stability, expressed in terms of Allan deviation, scales as τ−1/2 up to averaging times τ of the order of 104 s. This white frequency noise region is usually followed by a flicker floor component. For even longer τ, the RAFS stability is affected by a linear frequency drift.

Fig. 2
figure 2

Qualitatively derivation of Galileo specification for what concerns the frequency stability of onboard clocks and their sensitivity to temperature and magnetic field

Full size image

In addition, a RAFS suited for GNSS has to carry the time, i.e., the phase time information, with minimal perturbation from temperature and magnetic field fluctuations. Onboard clocks, particularly their electronics and optics packages, have also to be radiation hardened to operate in space without failures and/or performance degradation (see section Issues related to a space implementation of the POP clock).

It has been recognized that lamp-pumped RAFS is a mature technology satisfying these requirements. For example, the RAFSs used in the GPS Block IIF satellites exhibit a short-term stability better than 1 × 10−12 τ−1/2, with a drift of units of 10−15 per day (Vannicola et al. 2010). A new type of physics package designed and realized in Hao et al. 2016 achieved short-term stability of 2.4 × 10−13 τ−1/2, a considerable result for a RAFS. More recently, a space-borne rubidium atomic clocks for the BeiDou III navigation satellite system has been reported in Mei et al. 2021; this clock exhibits short-term stability of 6.1 × 10−13, reaching the level of 4 × 10−15 for one day of measurement time.

However, new laser-based clock technologies have been recently studied and proposed, offering the perspective of better results in a device similar, for certain aspects, to a RAFS (Vanier et al. 2007, Bandi et al. 2014). In this regard, a Rb vapor-cell clock based on laser optical pumping has been implemented and characterized at INRIM since 2012 (Micalizio et al. 2012a).

Compared to a traditional lamp-pumped Rb clock where the atoms interact simultaneously with light and microwave radiation, in the pulsed optical pumping (POP) approach developed at INRIM, atom preparation, microwave interrogation and detection phases take place at different times, with a significant benefit for the clock frequency stability. Specifically, the most performing POP clock developed at INRIM exhibits a frequency stability (Allan deviation) of 1.7 × 10−13 at 1 s and at the level of few 10−15 for integration times of 104 s has been measured (Micalizio et al. 2012b). In the paper, we refer to this clock as Prototype 1.

More recently, we investigated the possibility of reducing the size of the clock’s physics package, but still keeping the short-term stability below the 10−12 level. A second clock setup (Prototype 2) based on a loaded cavity-cell arrangement has been then implemented.

After resuming the physical principles on the basis of the POP clock operation, the paper describes the realization and the results obtained with Prototype 1 and the ongoing activity related to Prototype 2. Some of the issues connected to a space implementation of the POP clock are also discussed.

We finally present the preliminary results of a space-qualified prototype under development by Leonardo SpA in collaboration with INRIM. The aim of this partnership is the implementation of a stable, space-qualified, atomic clock based on the Rb POP concept and intended for GNSS application.

Principle of operation

Currently used Rb clocks are based on the double resonance (DR) approach where the atoms simultaneously experience resonant light and microwave field (Camparo 2007). The light is generated by a lamp and is used for optical pumping purposes: a population inversion between the two clock levels is in fact required in order to have a significant signal-to-noise ratio. The atoms are sealed in a cell housed in a microwave cavity where the atoms experience a resonant microwave field and make the clock transition (Vanier and Audoin 1989). Specifically, the resonant absorption of microwave radiation is manifested by a decrease in the transmitted light intensity.

As in the DR approach, in the POP technique the atoms also interact with light and microwave radiation, but with two important differences. First, the optical pumping operation is performed by a laser; this guarantees a highly efficient population inversion between the two ground-state levels defining the clock transition, with a consequent benefit for the signal-to-noise ratio. Second, the clock works in a pulsed regime, i.e., laser and microwave fields are not simultaneously applied but they act on the atomic sample alternately. In this way, the mutual influence of light and microwave signals is greatly reduced (Godone et al. 2004); specifically, light shift is strongly suppressed, leading to a medium/long-term stability that can also achieve the 10−15 region.

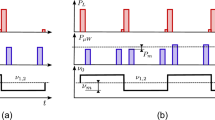
Other advantages characterize the pulsed operation. In particular, the clock interrogation is performed according to the Ramsey interaction scheme: 1) (Fig. 3) a strong laser pulse prepares the atoms in one of the two clock levels; 2) the atoms experience a couple of resonant microwave pulses of duration t1 separated in time by T and finally 3) a weak laser pulse (duration td) is sent to probe the clock transition which appears as an interference pattern on the absorption signal: the Ramsey fringes (Micalizio et al. 2009). In other words, the POP clock operation is similar to that of an atomic fountain but with a cycle time much faster, of the order of a few millisecond, being the Ramsey time T limited by the relaxation processes taking place inside the cell (Levi et al. 2014, Wynands et al. 2005).

Fig. 3
figure 3

Principle of operation of the POP technique. A strong laser pulse changes the thermal equilibrium in the ground state of a 87Rb sample, completely inverting the atomic population. The atoms then interact with a couple of microwave pulses according to the Ramsey scheme and make the clock transition. A weak laser pulse is used to probe the atoms during the detection phase. Γ* is the relaxation rate of the excited state. Typical durations are tp = 0.4 ms, t1 = 0.4 ms, T = 3.0 ms and td = 0.15 ms, with a total cycle time of 4.35 ms

Full size image

The central Ramsey fringe represents the reference atomic signal that is used to discipline the local oscillator. Its linewidth (full width at half maximum, FWHM) Δν1/2 can be approximated by the relation:

$$\Delta \nu _{{1/2}} \approx \frac{1}{{2T}}$$
(1)

and is almost insensitive to any laser/microwave power broadening, being dependent on the Ramsey time T only.

Prototype 1: a POP Rb clock with optical detection

Figure 4 shows the setup of our laboratory prototype that implements the principle of operation described in the previous section. Basically, a POP clock can be divided into three subsystems: physics package, optics and electronics.

Fig. 4
figure 4

Schematic of the POP clock setup. The three packages, optics (OP), physics (PP), and electronics (EP) are indicated with dashed frames

Full size image

The clock physics package (PP) is the structure containing the atoms in a properly shielded and controlled environment and includes the apparatus for the clock transition detection (we observe that conventionally PP of Rubidium clocks consists of both the light source and cavity along with related optics; however, in this case we prefer to distinguish the optics module from the PP. This distinction is functional to the implementation of the POP clock where it is more convenient to envisage the clock as composed of different modules that, if needed, can be replaced. Also, in the space implementation of the POP clock pursued by Leonardo, laser and the optical components have a dedicated development phase). The optical system provides the laser radiation used to shine the Rb vapor in the pumping and detection phases. The electronic system includes the low-phase-noise microwave synthesis, starting from a quartz oscillator. Moreover, it is devoted to clock control, including the pattern generation, signal acquisition and stabilization loops (laser locking, quartz locking, temperature stabilization, quantization magnetic field, etc.).

The POP physics package is not different in principle from that of a traditional Rb clock. It is a layer structure whose core is the cell filled with 87Rb atoms. A buffer gas is also added to the cell to localize the atoms avoiding a fast spin depolarization. However, the buffer gas produces a linear temperature-dependent shift of the clock frequency. Therefore, it is a common practice to use a mixture of buffer gases (typically Ar and N2) with opposite temperature coefficients so that an inversion point is introduced for the frequency shift as a function of temperature. By operating close to this specific set point, the temperature sensitivity turns out to be only quadratic (Vanier et al. 1982) and the transfer of temperature fluctuations to the clock frequency is minimized. Specifically, in our implementation, the total buffer gas pressure is 25 Torr with a pressure ratio Ar/N2 of 1.6. The inversion point is around 65 °C, where the Rb vapor density is optimal for clock operation.

Rubidium collisions with buffer gas atoms/molecules cause a relaxation of the atomic observables. For our buffer gas composition and at the operational temperature of 65 °C the relaxation rates of atomic population and coherence in the ground state are γ1 = 360 s−1 and γ2 = 300 s−1, respectively. In this way, the signal decay time is of the order of 3 ms, limiting the duration of the Ramsey time. As a consequence, according to (1), linewidths as narrow as 160 Hz can be obtained.

The cell has a radius R = 10 mm and a length L = 20 mm, with a long stem used as a cold point outside the microwave cavity where the metallic Rb atoms condensate.

The cell is placed inside a resonant microwave cavity tuned to the TE011 mode (Godone et al. 2011); the cavity allows the atoms to interact with a highly uniform microwave field. This is important in order to maximize the signal contrast, reducing at the same time the effect of neighboring transitions.

A solenoid outside the cavity produces a uniform quantization magnetic field (also called C-field) of the order of 15 mG. A series of magnetic shields and heaters aimed at reducing the clock frequency sensitivity to environmental variations completes the physical package. The temperature sensitivity of the cell clock is indeed a crucial aspect, and a long-term stability of hundreds of microkelvins is required to achieve clock stability in the 10−15 range (see Table 1). In addition, to eliminate barometric pressure sensitivity (Micalizio et al. 2012b; Moreno et al. 2018), the POP physics package is kept in a vacuum chamber.

Table 1 Sensitivity of the POP-clock cell to the main parameters of influence and the stability required to the latter to support frequency stability of 10−14 and 10−15. Sensitivities are mainly from Micalizio et al. 2010 and Micalizio et al. 2012b
Full size table

The optical system required for the POP operation is relatively simple. It is composed of a single laser diode (either at 780 or at 795 nm), typically a distributed-feedback (DFB) diode, frequency locked to the Rb optical transition. The laser then passes through an acousto-optic modulator (AOM) that acts as an optical switch for the pulsed operation and as an amplitude modulator to have high power for pumping and low power for detection.

At the entrance of the cell, the laser can deliver up to 15 mW peak powers; the laser beam shape is Gaussian (TEM00) and, after collimation, the diameter is about 10 mm.

A lens focuses the laser transmitted through the cell onto the detection photodiode placed outside the cavity; a trans-impedance amplifier then transforms the detected atomic absorption in a reference signal for clock purposes.

Even if highly integrated into a single package, the clock electronic system can be divided into three major functional parts:

  1. (1)

    Synthesis chain.

  2. (2)

    Clock cycle management.

  3. (3)

    Stabilization loops.

The synthesis chain provides the main output at 6.834 GHz, with the possibility to generate phase-coherent microwave pulses as required by the Ramsey interaction scheme. It is made starting from a 10 MHz OCXO as the local oscillator (LO). The details of its implementation are reported in Micalizio et al. 2012a, b.

The phase noise at 6.834 GHz is − 107 dB rad2/Hz at 200 Hz from the carrier; this noise affects the clock signal via the well-known Dick effect (Dick 1987; Santarelli et al. 1998; Lo Presti et al. 1998). Basically, the phase noise of the interrogating signal appears as a random "end-to-end phase difference," thereby introducing frequency noise in the loop. In frequency standards with a pulsed operation, the phase noise around even harmonics of the pulse rate is down-converted by aliasing to baseband. Taking into account the typical timing of the POP clock cycle, the Dick effect gives a contribution of 7 × 10−14 at 1 s to the clock stability budget. The synthesis chain architecture has been more recently updated, resulting is an even lower Dick effect, at the level of 2 × 10−14 at 1 s. (François et al. 2015).

A custom digital board guarantees the pulsed operation, where a single field-programmable-gate-array (FPGA) drives, among the other, two direct-digital synthesizers (DDS), one analog-to-digital converter (ADC) and one digital-to-analog converter (DAC): (1) the first DDS generates the baseband version of the two microwave pulses required by the Ramsey scheme; the second DDS drives the AOM for generating the pumping and the detection laser pulses, (3) the ADC acquires the atomic signal and (4) the DAC continuously corrects the OCXO so that its frequency is locked to the atoms. This architecture makes extensive use of digital components. In view of a possible space application, we report the availability on the market of space-qualified 16-bit DACs at tens of MHz and 14-bit DACs at hundreds of MHz; we then do not expect major criticalities in this regard.

In separate custom boards, we implemented the temperature controllers for the physics package, the trans-impedance amplifier for the detection photodiode and the low-noise current generator that drives the C-field coils. Instead, laser temperature and frequency controllers, as well as the current driver are based on commercial instrumentation. The digital nature of the electronic implementation based on an FPGA gives great flexibility for implementing new functionalities.

The experimental behavior of the clock has been extensively described in Micalizio et al. 2012a, b, here we report the main results only. In Fig. 5, we show typical Ramsey fringes obtained using the same timing reported in Fig. 3. The central Ramsey fringe represents the reference signal; it has a contrast of 28% and a linewidth of 160 Hz, corresponding to a quality factor of 4.2 × 107.

Fig. 5
figure 5

Ramsey fringes observed on the optical transmitted signal, according to the principle of operation shown in Fig. 3. The laser power during pumping (detection) is 4 mW (200 μW)

Full size image

A typical stability of the POP clock, when all internal and external parameters are optimized is reported in Fig. 6. A short-term stability of 1.7 × 10−13 τ−1/2 is observed with a clear white frequency noise signature up to 1000 s; after this time, a flicker floor around 6 × 10−15 is reached. The plot of Fig. 6 is representative of the medium-term performances of the POP clock and has been obtained selecting 2 days of data from a 10 day run. A long-term drift around -6 × 10−15/day has been measured over the complete data set (due to its small entity the drift has not been removed from the plot). Figure 6 clearly shows that Prototype 1 is compliant with the specifications of the Galileo PHM, one of the most performing space-qualified clocks (Droz et al. 2009). In order to characterize the medium-long term behavior, it is important to investigate the clock frequency sensitivity to fluctuations of internal and external parameters (Micalizio et al. 2010). In particular, the clock frequency is sensitive to a combination of environmental parameters (like barometric pressure (Huang et al. 2010), temperature, humidity, magnetic fields) and operational parameters (like microwave power, laser frequency, amplitude, polarization and pointing, internal temperature and gradients (Calosso et al. 2012), cavity Q, buffer gas and others).

Fig. 6
figure 6

Measured frequency stability of the POP Rb clock obtained in the same conditions of Fig. 5. An active H-maser has been used as a reference (continuous line). The dashed line represents the specification of the Galileo PHM. The small stability bump at 250 s is due to periodic thermal fluctuation induced by the laboratory air conditioning and transmitted to the PP through thermal bridges (cables, connectors, etc.…)

Full size image

Table 1 lists the main influence parameters and the related sensitivities of the clock at the cell level, and then it derives the stability that is required for these parameters to target a clock frequency stability consistent with current (10−14) and improved (10−15) GNSS specifications. A clock stability target at the level of 10−14 can be considered not particularly demanding for the POP clock. The overall thermal sensitivity is of the order of 10−11/K and a stabilization of the cell temperature at the mK level through a double oven is sufficient. The environment magnetic field fluctuations can be reduced by means of magnetic shields (three in our prototype), provided that the effect of the apertures for feeding the laser and the cables are minimized and that the current generator feeding the C-field coil has a fractional stability better than few ppm.

Concerning other parameters, thanks to the intrinsic low sensitivity of the POP clock to laser and to microwave powers, it is possible to reach the 10−14 level without any particularly demanding stabilization. The laser frequency stabilization to the external cell only requires a few Hz-bandwidth.

In case of a target in the 10−15 region, for example for next-generation more performing clocks, the requirements on the parameters of influence become much more stringent and their fulfillment has a significant impact on the clock design. At this level of performance, an active stabilization of laser and microwave powers, a high-performance laser frequency stabilization, and careful magnetic shielding design and additional temperature shields would be necessary.

Adding these new functionalities is in principle not trivial: a careful measurement of these parameters as perceived by the atoms would be required and high performing controllers compensating for their fluctuations should be implemented. In our case, we adopt a new approach based on the possibility of extracting directly from the atoms the information about the perturbing parameters. For example, we implemented and use routinely a technique based on the so-called Rabi oscillations to stabilize the amplitude of the microwave field (Gozzelino et al. 2018). In other words, we exploit the pulsed regime and the possibility to program arbitrarily long clock sequences to use the atoms themselves as microwave amplitude discriminators. In this way, apart from stabilizing the output power of the synthesis chain, it is possible to significantly mitigate cavity-aging effects, such as a frequency drift of the cavity and/or the relaxation of its quality factor. Specifically, in the case of prototype 1, the drift was reduced from 3 × 10–14/day to a negligible level with beneficial impact in the long-term of Fig. 6.

This approach can be extended to stabilize other quantities of interest, still subject of investigation, like the quantization magnetic field, or to compensate for the light shift, (Sanner et al. 2018; Hafiz et al. 2018). It is also possible to stabilize the laser frequency using the clock cell itself, without the need for any external reference. Thanks to the low-noise detection chain, we obtained preliminary clock stability results at the level of 1 × 10−14, corresponding to a fractional frequency stability for the laser below 1.7 × 10−9 (Calosso et al. 2017, 2019). Definitely, this approach results in a set of advantageous techniques that, thanks to the flexibility of our digital electronics, improve the clock performance with minimal or no additional hardware. Moreover, in some cases, like the stabilization of the laser frequency to the clock cell, a significant part of the setup could be removed with a consequent clock simplification, a great benefit for a possible space application.

Prototype 2: the miniaturization process

As mentioned above, reducing size and weight is of crucial importance for any device intended for space applications. It is sufficient to think that the cost to send a satellite in orbit is 20–30 k€/kg. However, it is not only a matter of cost. Reducing the size also implies a better ability to control the temperature of all the system.

The POP clock has already a rather compact structure, as the physics package can occupy less than 2.5 L for a laboratory setup and a complete experiment can be filled in less than 9-L volume (Arpesi et al. 2019). However, further optimization of the clock architecture is possible without compromising the stability performances. Regarding the physics package, recently there have been efforts to redesign the core of the structure and in particular novel solutions for the microwave cavity were introduced (Kang et al. 2015; Gozzelino et al. 2020). Miniaturization can possibly be aided by the improving capabilities of additive manufacturing (Affolderbach et al. 2018). Once the core volume is reduced, the thermal and magnetic shields can be scaled down, with considerable reductions of weight, size and power consumption.

The slotted-tube resonator (or ''magnetron cavity'') was introduced to have comparable field properties and to excite the clock transition with a more compact resonator (Stefanucci et al. 2012). Indeed, the resonance frequency of a TE011-like mode can be properly modified by choosing the number and geometry of the electrodes. External volume reduction up to a factor of 4 has been recently achieved by using a structure with 4 electrodes (Hao et al. 2019).

An alternative strategy to reduce the cavity footprint is to load the resonator volume with a dielectric (Williams et al. 1983, Howe et al. 1983, Wang 2008, Li et al. 2013). In prototype 2, a simple design has been introduced in Gozzelino et al. (2021) by using high-purity alumina (Al2O3) as loading material. The assembly is shown in Fig. 7 where we can observe that the cylindrical symmetry is preserved.

Fig. 7
figure 7

a Loaded cavity-cell arrangement used in the miniaturized clock experiment; b comparison between the cavity used in Prototype 2 clock (left) and the one used in Prototype 1 (right)

Full size image

The cavity still works on the TE011 mode even if its spatial distribution and resonance frequency are modified by the alumina. The cavity resonates at 6.834 GHz for an operational temperature of 60 °C. The inner volume is reduced by a factor of 10 with respect to the un-loaded cylindrical design, with a cell volume reduction of a factor of 8. Two below cut-off waveguides allow the laser beam to access the clock cell and a Si-photodiode detects the light transmission through the clock cell. The dielectric also acts as a holder for the vapor cell. This feature is favorable for possible space applications, as, in principle, it ensures better mechanical stability and resilience to vibrations, as opposed to gluing the cell to the metallic walls. The field uniformity inside the cell volume is even better than in the case of the traditional un-loaded cavity because of proper engineering of the loading material shape.

The final physics package structure will be different if intended for operation in vacuum or (on the ground) at atmospheric pressure. Given that the reduction in the cavity outer volume is a factor of 5 compared to Prototype 1, we expect a reduction of (at least) a factor of 2 in total volume, mass and heating power for the physics package.

The design of Fig. 7 applied to a POP experiment demonstrated clock spectroscopy with high contrast and high atomic-line quality factor.

In Fig. 8, we present preliminary short-term stability results for Prototype2, using a cell containing a mixture of Kr-N2 as a buffer gas, at the total pressure of 40 Torr and in the pressure ratio 0.96. As explained in Gozzelino et al. (2020), this mixture is able to reduce by more than one order of magnitude the barometric and temperature sensitivities of the clock frequency. The prototype has been tested at ambient pressure. With a Ramsey time of 1.1 ms and a cavity temperature of 58 °C, we obtained σy(1 s) = 6 × 10−13, still compliant with current GNSS requirements.

Fig. 8
figure 8

Measured frequency stability of the mini-POP Rb clock. The continuous line represents the H-maser stability used as the reference oscillator

Full size image

We observe that the cavity operates 2 °C below its tuning temperature, corresponding to 1 MHz of cavity detuning with respect to the atomic line. Given that the loaded quality factor of the microwave cavity is less than 200, this is not a major issue. Of course, seeking the best performance, a fine tuning of the cavity is foreseen but could not be done “a-priori” before a first determination of the operational temperature set by the buffer-gas content.

Medium-long-term is under investigation as the thermal stability of the setup is being upgraded. Also, optimization of long–term performances could require under vacuum characterization tests.

Issues related to a space implementation of the POP clock

Neither of the two POP clock prototypes previously described contains space-qualified components. However, since space engineering is currently undertaken by Leonardo S.p.A. (see next section), it is interesting to briefly discuss some issues to be faced in order to manufacture a reliable and performing device.

Space is a harsh environment. During the revolution around the earth, the satellite modifies its exposure to the sun and the temperature of the external surface can change from + 100 °C when it is illuminated to − 100 °C when it is in shadow (Martinez 2013, p. 141). The strong external temperature fluctuations affect the baseplate of the onboard clocks at the level of + / − 1 K, and, consequently, the temperature sensitivity of the signal delivered by the clock must be lower than 1 × 10−14/K.

Moreover, the satellite is under the influence of the terrestrial magnetic field, whose value changes when the satellite moves along the orbit. The maximum variation at 29,994 km from the center of the earth is of the order of 10 mG peak to peak.

To this value, the internally generated magnetic field has to be added, mainly due to the magnetorquer used to maintain the satellite’s orientation. The latter can be as high as 0.1 G. For this reason, the clock requires a sensitivity to the magnetic field below 10−13/G.

Besides experiencing significant temperature and magnetic-field fluctuations, the satellite is continuously bombarded by radiations of different nature (Steinberger et al. 2017). Specifically, three main ionizing radiation sources have to be considered: galactic cosmic rays (GCR), solar particle events, and trapped particles. In the following, we refer to Marcello G et al. (2015).

GCR originates from outside our solar system and approximately are composed of 85% protons, 14% He nuclei, 1% heavy nuclei. They have an energy up to 10 GeV/ amu, but some of them can have much higher energy. They are very penetrating and it is virtually impossible to shield them with reasonable amounts of material. In addition, they are anti-correlated with solar activity: solar flux scatters incoming charged particles. GCR fluxes are in the order of a few particles per square centimeter per second.

The solar particle flux is a stream of charged particles released from the upper atmosphere of the sun, called the corona. This plasma mostly consists of electrons, protons and alpha particles. This flux is dependent on the solar cycle and can reach > 105 particles/cm2 /s with energy > 10 meV/nucleon. Solar wind and flares depend on the solar activity.

Trapped particles are due to the earth’s magnetic field which is able to capture charged particles. These particles, once confined, move in a spiral, bouncing from one pole to the other and form two belts: the outer belt made for the most part of electrons and the inner belt consisting of both electrons and protons. Fluxes of electrons with energy above 1 meV can reach 106 particles/cm2/s, those of trapped protons can be as high as 105 particles/cm2/s (Walt 1995). A peculiar feature is the South Atlantic Anomaly (SAA), where the radiation belts come closest to earth. The SAA is caused by the fact that the magnetic field axis forms an 11° angle with respect to the North–South axis, and its center is not located at the Earth center but it is about 500 km far from it, causing a dip in the magnetic field over the South Atlantic area. The SAA is the area where most errors and malfunctions occur in satellites placed in low orbits.

A possible design and implementation of a space POP frequency standard should take into account all these effects. We point out, however, that the POP clock shares many features with other clocks that already have a space realization. For instance, the POP physics package and electronics are in principle similar to those used in RAFSs or H-masers already used onboard GPS/Galileo satellites (Batori et al. 2020, Riley 2019).

The main issues are then related to the optics package, laser source and optical components, especially if a lifetime of the order of 10 years is required. To our knowledge, only one atomic clock using lasers has been launched in space (Cold Atom Clock Experiment in Space, CACES), but it was mainly a proof of principle experiment based on cold atoms with no real timing purposes and operated for only 15 months (Liu et al. 2018).

However, laser diodes are increasingly used for space applications (Guilhot and Ribes-Pleguezuelo 2019, Tolker-Nielsen and Guillen 1998). The number of instruments requiring diode lasers is rapidly growing, including (but not limited to) sources for pumping solid-state lasers or for LIDAR experiment, like ALADIN (Cosentino et al. 2015), or also for spectroscopic purposes like in PHARAO to be used in the ACES experiment (Minec-Dube 2006). In this regard, several studies as cited below have been devoted to investigating the effect of radiations on the performance of different diode lasers. Exposure to ionizing radiation may lead to material degradation due to displacement damage ionization effects. Defects are detrimental for photonic devices as they modify the optical properties of a material by introducing absorption bands or color centers. Recent results would suggest that a DFB diode laser can be made relatively robust against gamma radiation and flash X-rays (Timmons and Stoner 2011). In Esquivias et al. (2011), the effects of proton and gamma irradiation have been evaluated on the performance of GaSb-based 2.1 μm diode lasers for space applications. No significant radiation damage has been found. On the other hand, radiation effects on diode lasers can be quite peculiar (Camparo et al. 1992), and further studies need to be carried out.

Definitely, due to the fundamental role played by the laser in the POP clock operation, it is mandatory to foresee a redundancy of the laser source in the clock design phase.

Discussion and conclusion

In recent years, several high-performing vapor-cell clocks have been developed in different laboratories. For a review, see Godone et al. (2015). Not only do these clocks adopt efficient laser sources, but also innovative techniques to prepare and detect the atoms, reduce the transfer of laser noise to the atoms, and to improve the signal-to-noise ratio. We can mention, for instance, clocks based on advanced coherent population trapping (CPT) techniques (Yun et al. 2017; Abdel Hafiz et al. 2017) or even vapor-cell clock based on cold atoms (Esnault et al. 2010; Langlois et al. 2018).

Even if these devices reach frequency stabilities in the 10−13 at 1 s and in some cases achieve units of 10−15 in the long term, they are rather complex, especially in terms of the optics package used to generate the required radiations. The POP approach, instead, joints similar stabilities performances with a much simpler implementation, only one laser is used to alternatively pump and detect the atoms. The effectiveness of the POP technique is also demonstrated by the interest of several other laboratories that, following the seminal works done at INRIM, have undertaken the realization of a POP clock (Baryshev et al. 2017; Dong et al. 2017; Monahan et al. 2019), obtaining in some cases outstanding results not far from those achieved by INRIM (Almat et al. 2020; Shen et al. 2020).

For a possible space implementation, it is of crucial importance to reduce the clock size and complexity. For this reason, we have also investigated the possibility of using a loaded cavity to shrink the physics package dimensions. We successfully demonstrated that, despite a reduced signal-to-noise ratio, the clock is still able to reach very good frequency stability performances. In addition, digital techniques foresee the stabilization of the laser frequency directly to the clock cell with a very significant simplification of the optical setup.

We conclude this overview of the POP Rb clock by briefly mentioning an ongoing space-implementation activity. Based on the results achieved with Prototype 1, INRIM and Leonardo Company SpA have been collaborating since 2016 for the engineering of the POP clock. Specifically, ESA appointed Leonardo jointly with INRIM to develop a space-qualified POP clock suitable to be embarked in an experimental flight within the Galileo Transition Satellites program. Table 2 shows a comparison between RAFS, PHM and POP clock in terms of performances, size, weight and power consumption (SWaP).

Table 2 Comparison between the expected performances and SWaP of the POP Rb clock and the specifications of Galileo PHM and RAFS. Data are
Full size table

The POP clock is expected to have size and power consumption between the RAFS and the PHM but with a short-term frequency stability at least one order of magnitude better than that of the RAFS.

As a first step, Leonardo implemented a physics package of POP clock, see Fig. 9. The Leonardo physics package has been completely characterized at INRIM facilities in terms of physics behavior, including thermal and magnetic sensitivities. At ambient pressure, it demonstrated frequency stability of 1.8 × 10−13 at 1 s (Arpesi et al. 2019), a result comparable to that of Fig. 6. In addition, the physics package successfully passed vibration and shock tests. These results, together with medium-long term characterization and under vacuum tests, will be presented in detail in a forthcoming work.

Fig. 9
figure 9

POP physics package implemented by Leonardo and tested at INRIM (courtesy of Leonardo SpA). The package includes the cavity-cell arrangement, magnetic and thermal shields, whereas the laser, its stabilization, and the AOM are part of another module. As a benchmark, a one Euro coin has been added (diameter 23.25 mm)

Full size image

The optical bench used to characterize the Leonardo physics package is the same used for Prototypes 1 and 2. No space-qualified component has been then used, including the laser diode. As mentioned in the previous section, the reliability and lifetime of the laser module are an issue for the POP clock. The aging of DFB lasers emitting at 780 nm and used for ground Rb clocks has been studied in Matthey et al. 2011, where diode lasers have been observed for 9 months. The results show that DFB lasers can be used in laser-pumped clocks with an acceptable variation of their power and frequency, even extrapolating the data to a projected clock lifetime of 20 years. Also, laser diodes with a wavelength close to D lines of 87Rb are predicted to have a median time to failure of approximately 8 years at a room temperature of 40 °C (Gale 2008). Compact and robust diode laser emitting at 780 nm and specifically suited for quantum optics experiments in space have been developed in Wicht et al. 2017. These data are encouraging for the realization of a space qualified laser module to be used in the POP clock.

Definitely, regarding its near-term deployment on board of Galileo satellites, the POP clock looks very promising, having unique strengths in terms of compactness jointly to outstanding frequency stability performances (Camparo et al. 2015, Jaduszliwer et al. 2021).

The implementation of this new technology at the industrial level is then expected to well match GNSS requirements and provide advantages reducing in orbit maintenance needs, increasing re-alignment intervals with a simultaneous reduction of size, mass and power consumption while providing frequency stability performance competitive with the passive hydrogen maser.