Introduction

The International GNSS Service (IGS) has been routinely producing precise orbits and clocks for geodetic and timing applications since 1998 (Beutler et al. 1999). IGS products are typically computed using batches of 24 h, and hence, the estimates of adjacent days are independent. As a consequence, IGS products exhibit day-boundary discontinuities (DBDs), most noticeable in the clock solutions, up to 1 ns in magnitude (Ray and Senior 2003). DBDs are reduced from 10 to 30% by increasing rate of the IGS clock products from 300 to 30 s (Yao and Levine 2013). DBDs reflect inaccuracies on the estimation processes which are mainly due to the noise present in the code pseudorange measurements used to compute the IGS clock products (Defraigne and Guyennon 2008). Moreover, other physical unmodeled effects such as hardware issues at the antenna, cables or temperature dependencies also contribute to clock errors (Ray and Senior 2005).

DBDs do not severely affect Precise Point Positioning (PPP) technique (Malys and Jensen 1990) using IGS precise products (Zumberge et al. 1997; Kouba and Héroux 2001) because the clocks and orbits are consistent on each batch. PPP uses dual-frequency code and carrier phase measurements to build the so-called ionospheric free (IF) combination that cancels 99.9% of the refractive ionospheric delay (Sanz et al. 2013). The receiver clock is estimated simultaneously with the estimation of the float phase ambiguities and other parameters such as the tropospheric delay and station coordinates. Hence, pseudorange measurements decorrelate initial phase ambiguities and clocks in the parameter estimation. The noise present in such code observations determines which part of the hardware delay and the receiver clock is absorbed by the initial phase ambiguity (Dach et al. 2003). The precision of the time transfer solutions using PPP can be improved with integer ambiguity resolution (IAR) techniques (Ge et al. 2008; Collins et al. 2010). Petit et al. (2015) estimated typical uncertainties with floated PPP about 1 × 10−15 and 1 × 10−16 when averaging at 1 and 30 d, respectively, whereas the uncertainty of PPP with IAR was estimated at the level of 1 × 10−16 when averaging 5 d.

However, DBDs do limit the stability of time transfer solutions obtained with geodetic techniques. The mitigation of DBD on clock estimates has been extensively addressed by the timing community, proposing several methods to attenuate their effect on clock determinations. One option is to increase the length of the computation batch and perform network processing (Zhang et al. 2020). Another option is to use a sliding batch (Yao and Levine 2013). In this sense, Guyennon et al. (2009) reduced the DBD to less than 0.1 ns with sliding batches up to 3 or 30 d. Another option is to concatenate independent ambiguities estimated in daily batches to restore the continuity of the clock estimates, the ambiguities or the instrumental biases occurring at the receiver and satellite (Dach et al. 2006; Petit et al. 2015).

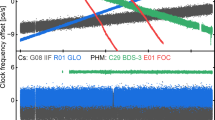
The aim of the present contribution is to propose a strategy to estimate the satellite and receiver clock offsets that is capable to reduce the DBD observed in different analysis centers (ACs) contributing to IGS and to its multi-GNSS experiment (MGEX) (Montembruck et al. 2017). Figure 1 depicts different examples of DBDs present in the clock products computed by the ACs Center for Orbit Determination in Europe (CODE) and European Space Operation Center (ESOC). The magnitude of the DBDs is not the same for the three satellites computed by CODE or the two satellites computed by ESOC. Thus, the DBDs cannot be explained as a result of a change in the reference clock selected during these two consecutive days. This observation is confirmed in the DBDs shown at the bottom panel, as the ESOC estimates were computed using the same reference clock (receiver BRUX) during both adjacent days.

Fig. 1
figure 1

DBDs between day 292 and 293 of 2017, present in the satellite clock solutions estimated by CODE and ESOC in the top and bottom panel, respectively

Full size image

The proposed strategy relies on the use of unambiguous carrier phase measurements collected by a network of permanent receivers on ground. The method considers the carrier phase hardware delays and assumes their possible variations along time. After performing IAR, our daily data processing guarantees the continuity of the unambiguous carrier phase measurements over multiple days. This continuity can be achieved even if data are processed with daily batches. The proposed method can process several GNSS constellations and all of their frequencies in an uncombined manner, i.e., without building the usual IF combination of carrier phases and pseudoranges.

In the next section, we describe the data used in the study and the IGS products used to compare our estimates. Then, we explain the key points of the strategy for obtaining unambiguous carrier phases and clock estimates, which are compared with other clock solutions available from the IGS MGEX. We conclude the manuscript with a summary and a discussion of the results.

Data set

In order to address the feasibility of the strategy, we have gathered RINEX files at a 30 s sampling rate from 150 permanent stations belonging to IGS, as depicted in Fig. 2. The temporal campaign comprised the period from day of year (DoY) 285 to 301 in 2017. The permanent station CEBR, equipped with passive hydrogen maser (PHM) frequency standard, was chosen as the reference clock.

Fig. 2
figure 2

Distribution of 150 permanent stations (squares) from the IGS network used in the present study to determine phase biases and integer ambiguities. Fifty of them are used to estimate satellite and receiver clocks (blue dots). The reference clock CEBR is depicted with a filled red square

Full size image

We have used the precise orbit and clock products “repro3” from ESOC, which include GPS and Galileo satellites. The clock estimates computed by the methodology presented in the next section have been compared with the clock solutions from different IGS AC:

  • GBM: the multi-GNSS product from Deutsches GeoForschungsZentrum (GFZ).

  • COM: the un-reprocessed product from CODE.

  • ESOC: the “repro4” product from ESOC. ESOC “repro4” is a refined version of “repro3,” where the same receiver BRUX was used for the entire dataset. However, ESOC “repro4” does not include clock products for GPS satellites, but only Galileo satellites.

Methodology

The fundamental equations for the GNSS measurements, i.e., carrier phase L and pseudorange P, at a frequency fm collected by a permanent receiver i and transmitted by a satellite j, can be written according to chapter 4.1.1 of Sanz et al. (2013):

$${L_{m}}_{i}^{j} = \rho_{i }^{j} + c\left( {T_{i} - T^{j} } \right) + Trop_{i}^{j} - \alpha_{m} \left( {I_{i}^{j} + D_{m_{{\large i}}} + {D_{m}}^{j} } \right) + \lambda_{m} \left( {\delta_{m_{{\large i}}} + {\delta_{m}}^{j} + {N_{m}}_{i}^{j} } \right) + \in$$
(1)
$${P_{m}}_{i}^{j} = \rho_{i }^{j} + c\left( {T_{i} - T^{j} } \right) + Trop_{i}^{j} + \alpha_{m} \left( {I_{i}^{j} + D_{m_{{\large i}}} + {D_{m}}^{j} } \right) + \varepsilon$$
(2)

where ρ is the geometric range between satellite and antenna phase centers (APCs) assuming that the station and satellite coordinates are known. \(T_{i}\) and \(T^{j}\) are the receiver and satellite clock offsets. Trop accounts for the slant tropospheric delay. I is the slant ionosphere delay expressed in total electron content units (TECUs). \(D_{m_{{\large i}}}\) and \({D_{m}}^{j}\) account for the receiver and satellite hardware delays of the code measurements at frequency \(f_{m}\), whereas \(\delta_{m_{{\large i}}}\) and \({\delta_{m}}^{j}\) are the receiver and satellite hardware bias of carrier phase measurements at frequency \(f_{m}\), in the form of a fraction of one cycle. \(N_{m}\) is the integer carrier phase ambiguity at frequency \(f_{m}\). \(\varepsilon\) and \(\in\) account for the thermal noise and multipath of code and carrier phase. \(\alpha_{m}\) is the conversion factor between TECU and the meters of delay at the frequency \(f_{m}\):

$$\alpha_{m} = \frac{{40.3 \times 10^{16} }}{{f_{m}^{2} }}$$
(3)

Notice that there is a one to one correlation between hardware biases \(D_{m}\) and the device clocks, for both satellites and receivers. Therefore, one has to define a reference clock with null hardware bias, linked to the measurements at a frequency or at a combination of frequencies. Typically, it is taken as a reference the IF combination at frequencies \(f_{m}\) and \(f_{n}\), which is equivalent to assume \(D_{m}\) = \(D_{n}\). Indeed, this common instrumental bias for the two frequencies disappears, along with the ionospheric effect I, when the IF combination is built from (1). In this sense, these biases would correspond to the differential code bias (DCB) of any of the two frequencies with respect to the IF combination.

Carrier phase measurements have been corrected in (1) from the satellite wind-up (Wu et al. 1993). Therefore, the main differences between the modeling of (1) and (2) are the opposite sign of the ionospheric delay, the carrier phase instrumental delay \(\delta\) and the carrier phase ambiguity N. In order to have small values of \(\delta\) and N, carrier phase measurements are prealigned to the code pseudorange measurements by adding an integer number of wavelengths as part of the pre-processing stage. In what remains of the section, we detail the step-by-step procedure to estimate \(\delta\) and N. As we will see, once the phase delays are computed, the ambiguities can be resolved to integer values, ultimately obtaining continuous carrier phase measurements in (1) on the boundary between two adjacent days.

Wide Lane processing

The first step of the proposed IAR process employs the Hatch-Melbourne-Wübenna (HMW) combination (Hatch 1982). That is, the difference of the wide lane (WL) combination of carrier phases and the narrow lane (NL) combination of code pseudoranges:

$$HMW_{mn} = WL_{mn} - NL_{mn} = \frac{{f_{m} L_{m} - f_{n} L_{n} }}{{f_{m} - f_{n} }} - \frac{{f_{m} P_{m} + f_{n} P_{n} }}{{f_{m} + f_{n} }}$$
(4)

where m and n refer to one pair of frequencies, which in our study correspond to f1 and f2 for GPS and f1 and f5 for Galileo. Substituting (1) and (2) into (4), the HMW combination is expressed in terms of differences of phase biases \(\delta\) and differences of integer ambiguities \(N\):

$${HMW_{mn}}^{j}_{i} = \frac{c}{{f_{m} - f_{n} }}\left( {\delta_{m_{{\large i}}} - \delta_{n_{{\large i}}} + {\delta_{m}}^{j} - {\delta_{n}}^{j} + {N_{m}}_{i}^{j} - {N_{n}}_{i}^{j} } \right) + \in_{NL_{{\large mn}}}$$
(5)

The advantage of the HMW combination in (5) is that only depends on slow-varying and constant parameters δ and N, which eases their estimation. In contrast, the drawback is that (5) contains the noise of the NL combination of pseudorange measurements, \(\varepsilon_{NL_{{\large mn}}}\). However, the wavelength of the WL combination, \(\lambda_{WL} = \frac{c}{{f_{m} - f_{n} }}\), is 86 cm in GPS and  75 cm in Galileo, large enough to allow a robust estimation of δ and N most of the time.

Raw WL phase biases

The procedure starts by selecting one receiver as a reference, e.g., CEBR in our study, in which the values of its phase biases and of its integer ambiguities are taken as zero, i.e., \(\delta_{m_{{\large ref}}} = \delta_{n_{{\large ref}}} = {N_{m}}_{ref}^{j} = {N_{n}}_{ref}^{j} = 0\). In this first step, the phase biases of every “j” satellite in view from the reference receiver are determined directly with the HMW combination of the reference receiver:

$${HMW_{mn}}_{ref}^{j} = \lambda_{WL} \left( {{\delta_{m}}^{j} - {\delta_{n}}^{j} } \right)$$
(6)

Note that the phase biases can be greater than one cycle, but the absolute value has no actual meaning. Then, the process continues with a second receiver “i” close to the reference station. This is a reason to have multiple receivers within the network depicted with empty squares in Fig. 2. At every epoch, we use the satellite phase biases derived in (6) to compute as many differences of HMW combinations, as the number of satellites in common view with the reference receiver:

$${HMW_{mn}}_{i}^{j} - \lambda_{WL} \left( {{\delta_{m}}^{j} - {\delta_{n}}^{j} } \right) = \lambda_{WL} \left( {{\delta_{m_{{\large i}}}} - \delta_{n_{{\large i}}} + {N_{m}}_{i}^{j} -{N_{n}}_{i}^{j} } \right) + \in_{NL_{{\large mn}}}$$
(7)

In such “ith” receiver, in order to eliminate the ambiguity term \({N_{m}}_{i}^{j} - {N_{n}}_{i}^{j}\), we perform the modulo \(\lambda_{WL}\) operation, resulting in:

$${HMW_{mn}}_{i}^{j} - \lambda_{WL} \left( { {\delta_{m}}^{j} - {\delta_{n}}^{j} } \right) = \lambda_{WL} \left( {\delta_{m_{{\large i}}} - \delta_{n_{{\large i}}} } \right) + \in_{NL_{{\large mn}}}$$
(8)

From (8), the receiver phase bias \(\delta_{m_{{\large i}}} - \delta_{n_{{\large i}}}\) can be determined with the common satellites in view with the reference receiver. For a “k” satellite not in view by CEBR, we use the receiver phase bias estimated in (8) to determine the satellite phase value \({\delta_{m}}^{k} - {\delta_{n}}^{k}\):

$${HMW_{mn}}_{i}^{k} - \lambda_{WL} \left( {\delta_{m_{{\large i}}} - \delta_{n_{{\large i}}} } \right) = \lambda_{WL} \left( { {\delta_{m}}^{k} - {\delta_{n}}^{k} } \right) + \in_{NL_{{\large mn}}}$$
(9)

The process described by (7)–(9) continues for all the 150 receivers within the network of Fig. 2. In this regard, the first phase biases are estimated for receivers located close to the reference receiver and once the phase biases for these nearby receivers are estimated, they are used as references for estimating the phase biases of further receivers within the network. The last step is to average the instantaneous estimates of the whole network into a single value per satellite and a single value per receiver, in order to increase the robustness of the estimation and to reduce its noise.

Figure 3 illustrates the phase biases of the WL combination for the receiver BRUX in the bottom panel and two satellites in the top panel; G10 from GPS and E03 from Galileo. The red and blue points in the bottom panel correspond to the left-hand side of (8), for all satellites in view from BRUX at every epoch. The HMW combinations are HMW12 for GPS and HMW15 for Galileo, respectively. Every 900 s, all those instantaneous values from those satellites seen from BRUX are averaged into a single value, depicted with a black and a green line with squares, to provide an accurate estimate of the receiver phase bias \(\delta_{1_{{\large BRUX}}} - \delta_{2_{{\large BRUX}}}\) and \(\delta_{1_{{\large BRUX}}} - \delta_{5_{{\large BRUX}}}\), with errors clearly below 1 cycle. The same reasoning applies to the top panel of Fig. 3, illustrating the left-hand side of (6) and (9) for the GPS satellite G10 and the Galileo satellite E03 with, respectively, red and blue points. As in the case of the receivers, the dispersion of the satellite phase biases is quite below 1 cycle, and the average every 900 s, shown with green and black lines with squares, provides a robust estimation of \(\delta_{1}^{G10} - \delta_{2}^{G10}\) and \(\delta_{1}^{E03} - \delta_{5}^{E03}\).

Fig. 3
figure 3

Phase biases for the WL combination. The bottom panel depicts the receiver phase biases of BRUX. In red and blue, the BRUX phase biases were computed for all the GPS and Galileo satellites in view and the corresponding averaged value in black and green lines. The top panel depicts the satellite phase biases of the Galileo satellite E03 and the GPS satellite G10. In red and blue, the phase biases were computed for all the receivers collecting data from G10 and E03 and the corresponding averaged value in black and green lines

Full size image

Undifferenced WL IAR

Once the satellite and receiver phase biases are determined from (6) to (9), we can subtract such estimates to (5), in order to resolve the WL ambiguity:

$${HMW_{mn}}_{i}^{j} - \lambda_{WL} \left( {\delta_{m_{{\large i}}} - \delta_{n_{{\large i}}} + {\delta_{m}}^{j} - {\delta_{n}}^{j} } \right) = {N_{m}}_{i}^{j} - {N_{n}}_{i}^{j} + \in_{NL_{{\large mn}}}$$
(10)

where note that the HMW carrier phase measurements have not been differenced. Figure 4 illustrates the left-hand side of (10), for all the satellites in view from receiver HRAG. It can be seen how the float values of \({N_{m}}_{i}^{j} - {N_{n}}_{i}^{j}\) are very close to integer values, provided that the noise \(\in_{NL_{{\large mn}}}\) is small enough. IAR in (10) is performed for all observations within one day and for all the receivers within the network.

Fig. 4
figure 4

WL float ambiguities before IAR in undifferenced mode, after the satellite and receiver phase biases are determined and removed

Full size image

Assuring the continuity of the WL phase biases

Although the carrier phase ambiguities are resolved in each daily solution, IAR in (10) does not guarantee that the same integer values for the ambiguities are obtained every day, thus producing possible integer jumps between the batches (Petit et al. 2015). As it can be seen in the example of Fig. 5, DBDs are produced on the WL biases \(\delta_{1}^{E19} - \delta_{5}^{E19}\) for the Galileo satellite E19. The phase bias for this satellite is close to 0.5 cycles, which produces that consecutive daily estimations can differ in \(\pm 1\) cycle (\(\pm 0.75\) m). As commented in the introduction, the noise present in the code pseudorange measurements is responsible for the different integers that produce the DBDs. In a daily basis estimation, this is unimportant, however, if this is not corrected it would produce discontinuities of 1 cycle at the day boundaries.

Fig. 5
figure 5

Phase biases for the WL combination for the Galileo satellite E19. Most of the days, the phase biases are around +0.5 cycles, but three days exhibit a phase biases of -0.5 cycle. It is therefore necessary to correct these three days to avoid DBDs

Full size image

It is therefore necessary to study a long-enough temporal series of the satellite and receiver phase biases to select a unique value for the entire data set. Note that this task can be performed in a real-time operation environment, after an initialization period. For instance, the most repeated value in Fig. 5 during about a month is close to +0.5 cycle, and then, the phase biases of the days close to -0.5 cycle are aligned by adding +1 cycle to have a continuous series of phase biases. Note that we could have also chosen the least repeated value to perform the alignment of the rest of the phase biases. What must be ensured is that we align to the same value, no matter which, to avoid jumps caused by the pseudorange noise. The approach is similar to Dach et al. (2006), but our reconnection takes place on the phase biases and not on the clock estimates or the ambiguities. Therefore, our procedure can be applied to undifferenced measurements and can be done without using estimates of ambiguities or clocks from the previous day.

L1/E1 processing

Once the WL ambiguities are resolved to integer values on daily batches, and the continuity of the WL phase biases is assured, we proceed to resolve the L1/E1 ambiguities. Unlike the IAR of the WL that uses only raw measurements, i.e., code pseudoranges and carrier phases, in order to determine the L1/E1 ambiguities, we need externally computed precise orbits and clocks. As mentioned in the section “Data Set,” we used the “repro3” products from ESOC.

The process starts by building the IF combination of carrier phases, \(L_{IF} ,\) and code pseudoranges, \(P_{IF}\), and applying well-known geodetic models of PPP to correct such measurements from the different effects on the GNSS signals:

$${{(L_{IF} )_{mn}}_{i}^{j} { } = \frac{{f_{m}^{2} {L_{m}}_{i}^{j} - f_{n}^{2} {L_{n}}_{i}^{j} }}{{f_{m}^{2} - f_{n}^{2} }} = \rho_{{i{ }}}^{j} + c\left( {T_{i} - T^{j} } \right) + Trop_{i}^{j} + {(B_{IF} )_{mn}}_{i}^{j} } \\$$
(11)
$${(P_{IF} )_{mn}}_{i}^{j} { } = \frac{{f_{m}^{2} {P_{m}}_{i}^{j} - f_{n}^{2} {P_{n}}_{i}^{j} }}{{f_{m}^{2} - f_{n}^{2} }} = \rho_{{i{ }}}^{j} + c\left( {T_{i} - T^{j} } \right) + Trop_{i}^{j}$$
(12)

The only new term in (11) and (12) with respect to the description of (1) and (2) is \(B_{IF}\); a real-value combination of the receiver phase bias, the satellite phase bias and the integer ambiguities at frequencies fm and fn. The float value of \(B_{IF}\) is estimated using the aforementioned PPP technique and precise orbits and clocks, together with the wet tropospheric delay and station clocks. The coordinates of the receiver and the satellites are not estimated. The estimation starts few hours in the day before the day of interest.

The next step is to relate the floated estimate of the IF ambiguity with the integer ambiguities of the WL combination \({N_{m}}_{i}^{j} - {N_{n}}_{i}^{j}\), which have already been resolved. We use the relation in (Sanz et al. 2013):

$$\frac{{ {(B_{IF} )_{mn}}_{i}^{j} }}{{\lambda_{NL} }} - \frac{{f_{n} }}{{f_{m} - f_{n} }}\left( {{N_{m}}_{i}^{j} - {N_{n}}_{i}^{j} } \right) = \frac{{f_{m} \delta_{m_{{\large i}}} - f_{n} \delta_{n_{{\large i}}} }}{{f_{m} - f_{n} }} + \frac{{f_{m} {\delta_{m}}^{j} - f_{n} {\delta_{n}}^{j} }}{{f_{m} - f_{n} }} + {N_{m}}_{i}^{j}$$
(13)

where \(\lambda_{NL} = \frac{c}{{f_{m} + f_{n} }}\) is the wavelength of the NL combination and is equal to approximately 11 cm for both the GPS frequencies f1 and f2 or the Galileo frequencies f1 and f5.

The procedure to resolve \({N_{m}}_{i}^{j}\) to an integer value in (13) repeats the previous steps (6) to (10). That is, first, we assume that the phase biases and ambiguities of the reference receiver are zero: \(\delta_{m_{{\large ref}}} = \delta_{n_{{\large ref}}} ={N_{m}}_{ref}^{j}= 0.\) That choice determines the satellite phase biases \(\frac{{f_{m} \delta_{m}^{j} - f_{n} \delta_{n}^{j} }}{{f_{m} - f_{n} }}\), of the satellites in view by the reference receiver:

$$\frac{{ {(B_{IF} )_{mn}}_{ref}^{j} }}{{\lambda_{NL} }} = \frac{{f_{m} {\delta_{m}}^{j} - f_{n} {\delta_{n}}^{j} }}{{f_{m} - f_{n} }}$$
(14)

The difference of phase biases estimated in (14) is propagated to nearby receivers:

$$\frac{{ {(B_{IF} )_{mn}}_{i}^{j} }}{{\lambda_{NL} }} - \frac{{f_{n} }}{{f_{m} - f_{n} }}\left( {{N_{m}}_{i}^{j} - {N_{n}}_{i}^{j} } \right) - \frac{{f_{m} {\delta_{m}}^{j} - f_{n} {\delta_{n}}^{j} }}{{f_{m} - f_{n} }} = \frac{{f_{m} \delta_{m_{{\large i}}} - f_{n} \delta_{n_{{\large i}}} }}{{f_{m} - f_{n} }} + {N_{m}}_{i}^{j}$$
(15)

Again we eliminate the ambiguity \({N_{m}}_{i}^{j}\) performing a modulo \(\lambda_{NL}\) operation:

$$\frac{{ {(B_{IF} )_{mn}}_{i}^{j} }}{{\lambda_{NL} }} - \frac{{f_{n} }}{{f_{m} - f_{n} }}\left( {{N_{m}}_{i}^{j} - {N_{n}}_{i}^{j} } \right) - \frac{{f_{m} {\delta_{m}}^{j} - f_{n} {\delta_{n}}^{j} }}{{f_{m} - f_{n} }} = \frac{{f_{m} \delta_{m_{{\large i}}} - f_{n} \delta_{n_{{\large i}}} }}{{f_{m} - f_{n} }}$$
(16)

From which the receiver phase biases of all permanent stations within the network are estimated using (16). For a “k” satellite not in view by the reference station, its satellite phase bias is determined using the estimate of the receiver phase bias:

$$\frac{{ {(B_{IF} )_{mn}}_{i}^{k} }}{{\lambda_{NL} }} - \frac{{f_{n} }}{{f_{m} - f_{n} }}\left( {{N_{m}}_{i}^{k} - {N_{n}}_{i}^{k} } \right) - \frac{{f_{m} \delta_{m_{{\large i}}} - f_{n} \delta_{n_{{\large i}}} }}{{f_{m} - f_{n} }} = \frac{{f_{m} {\delta_{m}}^{k} - f_{n} {\delta_{n}}^{k} }}{{f_{m} - f_{n} }}$$
(17)

The result of applying the steps (14)–(17) consists on the estimation of the phase biases of the receivers \(\frac{{f_{m} \delta_{m_{{\large i}}} - f_{n} \delta_{n_{{\large i}}} }}{{f_{m} - f_{n} }}\) and satellites \(\frac{{f_{m} {\delta_{m}}^{j} - f_{n} {\delta_{n}}^{j} }}{{f_{m} - f_{n} }}\). As in the case of the WL phase biases, all the instantaneous estimates are averaged into a single value per satellite and a single value per receiver. The averaging reduces the noise of the estimation which, in turn, is driven by the mis-modelings in (17). In this manner, the method exploits the redundancy that several stations track the same satellite, and conversely, one receiver tracks many satellites simultaneously.

Figure 6 depicts an example of the estimated phase biases in L1/E1 for satellites and receivers in the top and bottom panel, respectively. The values of the L1/E1 phase biases are clearly more scattered than these previously estimated for the WL combinations, see Fig. 5. The reason is that the determination of these L1/E1 phase biases relies on the accuracy of externally computed orbits and clocks. Hence, any error or DBD present in such precise products is absorbed by the float \(B_{IF}\) ambiguities and it is propagated into (14)–(17), deteriorating the L1/E1 estimates. Conversely, if the external products have enough accuracy, the phase bias can be estimated confidently.

Fig. 6
figure 6

Phase biases for the L1/E1 frequency. The bottom panel depicts the receiver phase biases of BRUX. In red and green, the BRUX L1/E1 phase biases were computed for all the GPS and Galileo satellites in view and the corresponding averaged value in black and blue lines. The top panel depicts the satellite phase biases of the Galileo satellite E03 and the GPS satellite G10. In red and blue, the phase biases were computed for all the receivers collecting data from G10 and E03 and the corresponding averaged value in black and green lines

Full size image

Figure 7 depicts the satellite phase biases for the Galileo E14 for multiple days. We can observe two types of discontinuities. The first category corresponds to few DBDs occurring as a result of using precise orbits and clocks in (17). DBDs on the phase biases do not have any consequence as long as the discontinuities are lower than 0.5 cycles of L1, because such DBDs do not change the integer values of the L1 ambiguity. The second category corresponds to jumps occurring in the middle of the day, see for instance day 296. These discontinuities are actual rapid variations of the phase biases, averaged every 900 s.

Fig. 7
figure 7

L1 satellite phase biases for Galileo satellite E14. Some discontinuities can be observed on the day change and within the day

Full size image

Undifferenced L1/E1 IAR

Once the satellite and receiver phase biases are determined in (14)–(17), we subtract such estimates to (13), in order to resolve the \({N_{m}}_{i}^{j}\) ambiguity:

$$\frac{{ {(B_{IF} )_{mn}}_{i}^{j} }}{{\lambda_{NL} }} - \frac{{f_{n} }}{{f_{m} - f_{n} }}\left( {{N_{m}}_{i}^{j}- {N_{n}}_{i}^{j} } \right) -\frac{{f_{m} \delta_{m_{{\large i}}} - f_{n} \delta_{n_{{\large i}}} }}{{f_{m} - f_{n} }}- \frac{{f_{m} {\delta_{m}}^{j} - f_{n} {\delta_{n}}^{j} }}{{f_{m} - f_{n} }} ={N_{m}}_{i}^{j}$$
(18)

where again is noted that we are using combinations of ambiguities that have not been differenced. Figure 8 illustrates the left-hand side of (18), for all the satellites in view from receiver MGUE. It can be seen how the float values of \({N_{1}}_{MGUE}^{j}\) are close to an integer value.

Fig. 8
figure 8

L1/E1 float ambiguities before IAR, in undifferenced mode, after satellite and receiver phase biases are determined and removed

Full size image

In general, the L1/E1 ambiguity can be resolved for about 90% of time for all satellites and receivers of the network depicted in Fig. 2. The percentage of unresolved ambiguities is not as important as the location of the station that cannot perform IAR successfully. In areas, where the satellite clocks are determined with few and isolated stations, e.g., in the Pacific Ocean, a reduction in the number of receivers with resolved ambiguities deteriorates the estimation of the satellites clocks tracked in those areas. In contrast, if the lack of resolved ambiguities occurs for a receiver well surrounded by other stations, e.g., within a continent, the effect on the clock estimation is irrelevant.

Continuous and unambiguous measurements

Once the integer value of \({N_{m}}_{i}^{j}\) is known for each satellite-receiver arc of continuous data, one can compute the integer values for the frequency n using the integer values of the WL combination of ambiguities, \({N_{m}}_{i}^{j} - {N_{n}}_{i}^{j}\). Then, these integer values can be subtracted to the carrier phase measurements in (1) obtaining:

$${L_{m}}_{i}^{j} = \rho_{i }^{j} + c\left( {T_{i} - T^{j} } \right) + Trop_{i}^{j} - \alpha_{m} \left( {I_{i}^{j} + k_{m_{{\large i}}} + {k_{m}}^{j} } \right)$$
(19)

where the phase biases \(\delta_{m_{{\large i}}}\) and \({\delta_{m}}^{j}\) in (1) are redefined to include the code hardware delays \(D_{m_{{\large i}}}\) and \({D_{m}}^{j}\):

$$\begin{aligned} & k_{m_{{\large i}}} = D_{m_{{\large i}}} - \frac{1}{{\alpha_{m} }}\delta_{m_{{\large i}}} \\ & {k_{m}}^{j} ={D_{m}}^{j} - \frac{1}{{\alpha_{m} }}{\delta_{m}}^{j} \\ \end{aligned}$$
(20)

Except for the sign in the ionospheric term, the model for the carrier phase measurements described in (19) is equivalent to the model described in (2) for the pseudorange measurements. Therefore, once the integer part of the carrier phase ambiguities is solved, carrier phases can be treated as precise pseudoranges.

Estimating receiver and satellite clocks

The precise, absolute, undifferenced and uncombined carrier phase measurements in (19) can be used to estimate the satellite and receiver clocks, the ionospheric slant delay, and refined phase biases or even to re-estimate orbit parameters. For such a purpose, we use the sub-network of 50 receivers depicted with blue dots in Fig. 2. The estimation could also be performed to the entire network of 150 receivers, but the clock results do not show any improvement, compared to the increased computation time.

Instead of using the standard IF combination, the proposed approach applies the geodetic models of PPP to the raw, i.e., uncombined, carrier phases in (19) to eliminate all non-dispersive effects of the GNSS signals and the slant tropospheric wet delay estimated from the PPP processing in (11)–(12). This difference is termed carrier phase residuals and is computed in the left-hand side of:

$${L_{m}}_{i}^{j} - \rho_{i }^{j} - {\widehat{Trop}}_{i}^{j} = c\left( {T_{i} - T^{j} } \right) - \alpha_{m} \left( {I_{i}^{j} + k_{m_{{\large i}}} + {k_{m}}^{j} } \right)$$
(21)

where \(\rho\) includes the satellite-receiver geometric distance, solid tide corrections, APC corrections, dry tropospheric delay, among other PPP model terms. \(\widehat{Trop}\) accounts for the wet tropospheric residual already estimated simultaneously with the \(B_{IF}\) in (11). In this manner, (21) can use all frequencies available in every GNSS, instead of being limited to just the two involved in the IF combination. This allows studying the variation of the biases of a third frequency (Juan et al. 2020).

To estimate the five type of parameters on the right-hand side of (21), we apply a Kalman filter on a daily basis, i.e., the data of each day are processed independently, with noise processes for each parameter as follows:

  • Satellite and receiver clocks (\(T_{i}\) and \(T^{j}\)) are estimated as white noise processes.

  • Slant Ionospheric delays (\(I_{i}^{j}\)) are also estimated as white noise processes.

  • Refined satellite and receiver biases (\(k_{m_{{\large i}}} \;{\text{and}}\;{ }{k_{m}}^{j}\)) are estimated as random walk processes. In this manner, it is possible to take into account the dependency on the temperature reported in (Nie et al. 2018).

Figure 9 illustrates the unambiguous and undifferenced carrier phase residuals for the receiver BRUX and three different satellites (G12, E01 and E09) during the DoYs 292 and 293 in 2017. In order to better depict the continuity of the residuals, one linear model, the same for both days, has been subtracted from the residuals in (21). It can be seen that after the IAR process, such detrended residuals are continuous regardless of the day change. The different noise levels observed are related to the satellite clocks, being the GPS residuals noisier than these of Galileo.

Fig. 9
figure 9

Carrier phase residuals on L1 after IAR, linearly detrended to eliminate the variations of the satellite and clocks, evidencing its continuity on the day change

Full size image

Results

The satellite clocks estimated from (21) have been compared to the clock determinations of ESOC, GFZ and CODE. Note that those IGS ACs also perform IAR to compute the clocks, as in the present methodology. However, such solutions are obtained without requiring continuity of the phase biases over the day change. The absolute value of such phase biases is arbitrary because it is determined by the code pseudorange noise (Collins et al. 2010). Thus, the absolute value of the phase biases can change from day to day, producing DBD in conventional daily computations.

In this sense, the advantage of the present approach is emphasized when clocks are to be studied during periods longer than one day, as it was the original objective of the project GREAT (Juan et al. 2020). In contrast, when the comparisons are performed within the same day, the results of our clock estimates should be similar to those obtained by the conventional methods used within the IGS ACs, as our approach does not present any advantage for periods shorter than one day.

The test consists on using one hour of clock solutions during the last hour of one day to fit a linear model using least squares. Then, this linear model is propagated one hour forward into the following day. Finally, differences of satellite clocks are computed from the linear model predictions and the actual clock estimates over the first hour of the following day. In this manner, such extrapolation errors assess the stability of the clock solutions. Of course, this test is more meaningful for stable clocks such as those on-board of Galileo satellites.

Table 1 summarizes the extrapolation errors, computed for three IGS ACs and the approach presented in the present contribution, termed as “gAGE.” We can observe that for gAGE and GFZ, the extrapolation errors of Galileo are lower than these of GPS. This observation is attributable to the higher stability of clocks on-board Galileo satellites. Both 68th and 95th percentiles obtained with the proposed approach “gAGE” are lower than these of the other ACs. For instance, gAGE approach reduces about 39% and 24% the 68th and 95th percentiles of the extrapolation errors computed by ESOC. This confirms the advantage of using continuous measurements over the day change to determine the clocks. Surprisingly, CODE presents lower extrapolation errors for GPS clocks than for Galileo, despite Galileo clocks should be more predictable than these of GPS, as occurs for the other solutions. Assuming that each AC applies the same procedure to estimate Galileo and GPS clocks, a possible reason for explaining the degradation of the Galileo results in the case of CODE is that the algorithms applied by CODE are more sensitive the minor number of GAL satellites than the case of gAGE or GFZ.

Table 1 Extrapolation errors from DOY 292 to 301 in 2017, for the clocks computed by different ACs of IGS and the proposed approach, labeled as gAGE
Full size table

Figure 10 depicts a histogram with the extrapolation errors of all Galileo and GPS satellite clocks in the top and the bottom panel, respectively. The higher stability of Galileo clocks compared to GPS magnifies the differences between the extrapolation errors of the proposed approach and the extrapolation errors observed in clocks computed by the other ACs. In other words, the histograms in GPS clocks look more similar than these of Galileo due to the low stability of GPS clocks. In both panels, it can be seen that the highest peaks in the histograms correspond to the proposed approach gAGE. This observation confirms that the DBDs observed in Fig. 1 are clearly reduced by the IAR procedure described in the present contribution.

Fig. 10
figure 10

Histogram depicting the extrapolation errors from DOY 292 to 301 in 2017, for Galileo and GPS satellites in the top and bottom panels, respectively. The bin size is 5 mm

Full size image

Conclusions

DBDs in clock determinations are a long-standing issue in time transfer analyses using carrier phase measurements and geodetic techniques. The present contribution proposes a methodology to obtain continuous carrier phase measurements that largely mitigates DBDs and, ultimately, improves daily clock estimates. The procedure uses the well-known IF and WL combinations of undifferenced measurements to estimate the receiver and satellite phase biases, ultimately allowing the IAR on daily batches. Such daily process can produce DBD on the phase biases estimates, but the DBDs can be easily detected and removed. The obtained precise, absolute, undifferenced and uncombined carrier phase measurements can be exploited to estimate very precisely parameters such as orbits and clocks. As an application, we have used this methodology to estimate satellite clocks. The results show a clear reduction of the extrapolation errors between clock determinations of adjacent days, thus reducing the DBDs observed in the state-of-the-art products available in IGS.