Abstract
A single geodetic GNSS station placed at the coast has the capability of a traditional tide gauge for sea-level measurements, with the additional advantage of simultaneously obtaining vertical land motions. The sea-level measurements are obtained using GNSS signals that have reflected off the water, using analysis of the signal-to-noise ratio (SNR) data. For the first time, we apply this technique to detect extreme weather-induced sea-level fluctuations, i.e., storm surges. We first derive 1-year sea-level measurements under normal weather conditions, for a GNSS station located in Hong Kong, and compare them with traditional tide-gauge data to validate its performance. Our results show that the RMS difference between the individual GNSS sea-level measurements and tide-gauge records is about 12.6 cm. Second, we focus on the two recent extreme events, Typhoon Hato of 2017 and Typhoon Mangkhut of 2018, that are ranked the third and second most powerful typhoons hitting Hong Kong since 1954 in terms of maximum sea level. We use GNSS SNR data from two coastal stations to produce sea-level measurements during the two typhoon events. Referenced to predicted astronomical tides, the storm surges caused by the two events are evident in the sea-level time series generated from the SNR data, and the results also agree with tide-gauge records. Our results demonstrate that this technique has the potential to provide a new approach to monitor storm surges that complement existing tide-gauge networks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Storm surges, the abnormal rise of sea levels as a result of wind and air pressure changes associated with a storm, are one of the main drivers of coastal flooding. The most extreme of these events normally occur when tropical cyclones coincide with astronomical high tides. Storm tides reaching up to 6 m have been reported, with devastating consequences to coastal communities (Fritz et al. 2007; Soria et al. 2016; Wang et al. 2014). Accurate modeling and forecasts of these surges are important for reducing the damaging impacts of such surges.
A key component in storm surge modeling is performance validation, which is usually achieved by comparison to tide-gauge data (Li et al. 2018a, b; Madsen et al. 2015; Soria et al. 2016; Spencer et al. 2015; Wadey et al. 2014). Satellite altimetry has also been shown to be capable of observing storm surges, and of contributing to understanding the forcing behind them (Chen et al. 2014; Li et al. 2018; Scharroo et al. 2005). However, due to the limitations of the spatial–temporal sampling of conventional nadir-pointing altimeters, including difficulties in accurately observing coastal sea levels (Cazenave et al. 2018), satellite altimetry has been of only modest benefit so far.
Tide gauges are installed close to water, putting them at high risk of getting damaged by the sharp fluctuations of water levels caused by storm surges. Historically, there are many examples showing that, during major storms, including Hurricane Katrina (Fritz et al. 2008a), Cyclone Gonu (Fritz et al. 2010), and Super Typhoon Haiyan (Soria et al. 2016), tide gauges failed to record the peak water level due to breakdown or interruption of electricity. In addition, the largest extremes may not always be represented adequately in the tide-gauge data. These events are rare, and when they do happen the highest sea level may not occur exactly at the tide-gauge station, but at some distance along the coast (Pugh and Woodworth 2014).
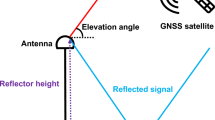
The Global Navigation Satellite System-Interferometric Reflectometry (GNSS-IR) technique is emerging as an in situ sea-level monitoring technique that uses data from geodetic-quality GNSS instruments for sensing the near-field environment, with the advantage of simultaneously providing continuous weather-independent sea-level information and vertical land motions (Larson et al. 2013a). In contrast to the well-recognized applications of GNSS in positioning, timing and atmospheric sounding that make use of the direct satellite signals received by GNSS stations, GNSS-IR for water-level monitoring uses satellite signals reflected off the nearby water surface that is delayed with respect to the direct satellite signals. These reflected signals cause measurable interference in the form of oscillation of the recorded GNSS signal-to-noise ratio (SNR) data. By analyzing the frequency of the SNR oscillation, we can estimate the vertical distance from the water surface to the GNSS antenna phase center. It has been demonstrated that the retrieved water levels from a single geodetic GNSS receiver have comparable accuracy to traditional tide gauges (Larson et al. 2013b, 2017; Löfgren et al. 2014; Roussel et al. 2015). GNSS-IR can sense larger areas (tens to hundreds of meters from the station) than traditional tide gauges, and may thus capture sea-level extremes occurring at some distance along the coast. Furthermore, GNSS stations sometimes have the advantage of being installed at a relatively high location, e.g., on top of a building, so they have a reduced risk of being damaged or destroyed during the most energetic storms.
To investigate the potential of using GNSS-IR to detect the sharp fluctuations of water level caused by storms, we retrieve sea levels using SNR data from two GNSS stations in Hong Kong that are installed on top of buildings near the water surface, with a focus on the two recent major events—Super Typhoons Hato (August 23, 2017) and Mangkhut (September 16, 2018). In terms of maximum sea level, Mangkhut and Hato have ranked the second and third strongest typhoons to hit Hong Kong since 1954. A maximum sea level (above chart datum) of 4.6 m, with corresponding maximum storm surge (above astronomical tide) of 2.4 m, was recorded at Tsim Bei Tsui during Hato; and a maximum sea level of 4.7 m, with corresponding maximum storm surge of 3.4 m, was recorded at Tao Po Kau during Mangkhut. Many key tide gauges near Hong Kong became non-functional during these two major typhoon events. For example, all tide gauges in Macau failed to record the peak water level during Hato (Li et al. 2018a, b), and tide-gauge records at Shenzhen station have a gap in observations during Mangkhut.
GNSS and tide-gauge data
The Hong Kong Satellite Positioning Reference Station Network (SatRef) consists of 18 continuously operating GNSS reference stations. Two SatRef stations, HKPC and HKQT, were installed on top of buildings that are close to the sea. The locations are given in Figs. 1 and 2. The GNSS antennas at those two stations can receive both direct signals from the GNSS satellites and the reflected signals from the nearby sea surface, so we can use their data to examine the potential of GNSS-IR for detecting extreme weather-induced water-level fluctuations. In addition, a tide-gauge station Quarry Bay is co-located with GNSS station HKQT, providing an independent dataset to validate the retrieved water levels from GNSS-IR.
HKPC and HKQT are equipped with a LEICA GR50 receiver and a TRIMBLE NETR5 receiver, respectively, receiving satellite signals from GPS, GLONASS, Beidou, Galileo, and the Japanese QZSS. Despite the receivers’ multi-constellation capability, we only used GPS signals in this study. The receivers at both stations were configured to simultaneously track GPS L1-C/A (L1 hereafter), L2P, L2C and L5 signals. Among the four types of signal, L1 (civilian signal) and L2P (encrypted signal) are the legacy signals that GPS satellites have transmitted from the beginning; L2C and L5 are the second and the third civilian GPS signals, designed specifically to meet commercial needs and high-performance applications. In terms of effective power indicated in the SNR data, L5 is strongest, while L2P is weakest due to the fact that the techniques used to access the encrypted L2P signal introduce a degradation. We show a comparison of the L1, L2P, L2C and L5 SNR data at low elevation angles in Fig. 3.
We obtained GNSS data in the RINEX3 format (Receiver Independent Exchange Format) at 5-s sampling intervals from the Survey and Mapping Office (SMO) of the Hong Kong Lands Department, hourly tide-gauge records from the University of Hawaii Sea Level Center, and real-time tide-gauge information at 1-min sampling intervals from the Intergovernmental Oceanographic Commission.
SNR data analysis
As shown in Fig. 4, when a satellite travels along its arc, the land-based GNSS antenna receives both the direct line-of-sight satellite signal and the reflected signal off the nearby water surface. Those two signals interfere with each other, creating a characteristic oscillating pattern overlain on a long-time trend in the SNR data. The frequency of these oscillations is related to the reflector height \(H\). To estimate \(H\), we first translate the SNR data from units of decibels–hertz on a logarithmic scale to volt per volt on a linear scale, assuming a 1-Hz bandwidth, and then use a second-order polynomial to remove the trend. We model the SNR residuals \(\delta\) as (Larson et al. 2013a)
where \(\lambda\) is the GNSS wavelength, \(\theta\) the elevation angle, \(A\) the amplitude, and \(\varphi\) is the phase offset. We estimate the dominant multipath frequency \(\left( {\frac{{2H}}{\lambda }} \right)\) using the Lomb–Scargle periodogram (LSP) with an oversampling interval that results in a precision of 1 mm.
Sea level is constantly changing, so a height-rate correction is needed as (1) assumes that the water surface is stationary during a rising or setting satellite arc. We follow Larson et al. (2013b) to correct the bias caused by this effect. The equation is expressed below:
where \(d\) (\(d=2H\sin \theta\)) is the propagation delay of a reflection with respect to the direct path. Under normal weather conditions, the temporal variability in sea levels over a satellite arc is mainly from the change of astronomical tidal levels. We use the Oregon State University TPXO8-atlas global tide model to predict astronomical tides at the selected GNSS sites for calculating \(\dot {H}\) in (2).
Due to the tropospheric delay, the measured reflector heights are always smaller than the true geometric heights. Williams and Nievinski (2017) demonstrated that ignoring the tropospheric delay in GNSS-IR induces a scale error in the reflector heights. We use a combination of astronomical refraction (Bennett 1982) and the Global Pressure and Temperature 2 (GPT2) Wet model (Böhm et al. 2015) to correct tropospheric delay. The expression for the elevation angle correction \(\Delta \theta\) is described as
where \(\Theta =~\theta +{7.31^\prime }/\left( {\theta +{{4.4}^ \circ }} \right)\), \(\theta\) in units of degree, \({\varvec{\Delta}}\theta\) in units of minute, \(T\) the temperature in units of Celsius degree, and \(P\) is the pressure in a unit of hPa.
GNSS reflection sensing zones
Whereas traditional tide gauges measure coastal sea levels at a particular location, GNSS-IR senses the near-field environment. The size of the sensing zone depends on the reflector height, the elevation angle, and the azimuth of a satellite. Figure 5 shows the reflection areas that can be sensed by the two GNSS antennas at HKPC and HKQT. As both stations were originally installed for serving the needs of geodetic surveys, they are not at strategically selected locations for sea-level monitoring. We can see from the figure that the view of the water from the two stations is limited, and to avoid including reflections from the land we need to define an azimuth and elevation angle mask. For HKPC, we choose data with elevation angles between 3° and 7°. Azimuthally, the location of this particular site allows data from only 190° to 310°. For HKQT, we apply an elevation mask angle between 4° and 9°, and azimuth between − 60° and 105°. The GPS satellite tracks shown in the figure are those after the mask has been applied. The empty region at HKQT, shown in yellow, is due to the spatial coverage of the GPS constellation, i.e., there are no GPS satellites passing across that region.
Locations of the two GNSS stations HKPC and HKQT (yellow dots), and the corresponding reflection areas (white ellipses), which were approximated by the first Fresnel zone for a reflector height of 20 m and 6 m for HKPC and HKQT, respectively. The white ellipses for each satellite track are the sensing zones for GPS observations for elevation angles 3° (longest ellipse), 5° (second ellipse), and 7° (shortest ellipse) for HKPC, and for elevation angles 4° (longest ellipse), 6° (second ellipse), and 9° (shortest ellipse) for HKQT. We made the figures using Google Earth
Validation of SNR-derived sea levels
Since HKPC and HKQT were not originally installed for sea-level monitoring, before proceeding to demonstrate the potential of GNSS-IR to detect storm surges, we first validate performance under normal weather conditions by comparing sea levels retrieved from SNR data for station HKQT with tide-gauge records from Quarry Bay. We chose data from June 13, 2015 to June 12, 2016 to examine the SNR-derived sea levels, because during this period (1) none of the L1, L2C and L5 SNR data were missing in the RINEX files provided by SMO; (2) no extreme events occurred; and (3) tide-gauge records with research quality data are available for comparison. We did not use L2P SNR data since (1) the L2P signal is relatively weak compared to L1, L2C and L5 signals, and (2) L2P SNR data exhibit double peaks in the LSP (not shown). Roesler and Larson (2018) indicated that the second peak is expected because the geodetic receiver must cross-correlate with the L1 signal to extract the L2P data.
We can see from Fig. 5 that at HKQT the number of GPS tracks that cover the water area is limited due to the particular location of the antenna. Taking April 5, 2016 as an example, a total of 30, 21, and 15 rising or setting GPS satellite tracks for the L1, L2C and L5 signals were useful for further analysis after applying the azimuth and elevation angle mask. To report a valid reflector height, we impose the following quality control measures: (1) the time span of a satellite arc must be > 12 min and < 30 min, (2) the normalized spectrogram peak must be > 5 volts/volts, (3) the peak-to-noise ratio must be > 3, and (4) we discard non-physical reflector height peaks (i.e., \(H\) > 10 m or \(H\) < 3 m). After imposing those measures, we could produce 25, 18, and 14 sea-level retrievals from the L1, L2C, and L5 SNR data, respectively.
During the period of June 13, 2015–June 12, 2016, we retrieve, on average, 25, 18 and 13 measurements per day from the L1, L2C and L5 SNR data. Sampling intervals in the retrieved sea levels are not uniform, and the temporal resolution, especially at L5 frequency, is not sufficient to perform tidal decomposition as some studies showed previously (Larson et al. 2017; Löfgren et al. 2014). We instead use the Van de Casteele test (Miguez et al. 2008) to validate the SNR-derived sea levels. To directly compare the sea-level measurements from GNSS-IR with tide-gauge data, we translate the hourly tide-gauge records to the time-tags of the SNR-derived sea-level time series through a cubic interpolation.
Figure 6 shows the Van de Casteele diagrams for the sea-level measurements generated by L1, L2C and L5 SNR data. We can see in the figure that the three diagrams for the L1, L2C and L5 frequencies are all centered around zero difference, indicating that there is no systematic shift between the sea-level measurements from GNSS-IR and tide-gauge records. Among the L1, L2C and L5 signals, sea levels retrieved from L5 SNR data best agree with tide-gauge data. The root-mean-square (RMS) differences between sea levels produced from L1, L2C and L5 SNR data and tide-gauge data are 18.4 cm, 15.6 cm, and 12.6 cm, respectively. If the effect of height change was not corrected, the RMS differences are 20.5 cm, 18.1 cm, and 15.3 cm for L1, L2C and L5 signals, respectively. We also examined the effect of tropospheric delay on our estimates of reflector heights and the corresponding sea levels. Our results show that the scale error on reflector heights caused by this effect is 10 cm: on average, the reflector height generated from L5 SNR data is 6.33 m if the effect was not corrected, and the average value is 6.43 m if tropospheric delay correction was applied. However, after the reflector heights were converted to sea levels, this effect is negligible as it only resulted in 0.1 cm larger RMS difference with respect to tide-gauge records.
As shown in Fig. 5, more than half of the view from the HKQT antenna is buildings or roads, and there is a hole in the reflection areas that cover water due to the limited spatial coverage of the GPS constellation at this particular location. As a consequence, the temporal resolution of SNR-derived sea levels is relatively poor. To test if the SNR-based technique for retrieving water levels is able to capture the daily maximum sea level under such conditions, we compare the daily highest water level from SNR-derived measurements and hourly tide-gauge records (Fig. 7).
Compared to tide-gauge records, the daily maximum sea levels produced from L1 and L2C SNR data are seen in Fig. 7 to be biased high, with a median offset of 15.4 cm and 3.2 cm. In contrast, daily highest sea levels generated by L5 SNR data are biased low, with a median offset of −4.8 cm. Because the errors in the sea-level measurements from GNSS-IR are much larger than the tide-gauge errors, the highest values from each day in the sea-level measurements from GNSS-IR will nearly always be biased high if the temporal resolution is sufficient. However, SNR-derived daily maximum sea levels at L5 frequencies are generally smaller than those from tide-gauge data. This is likely because L5 signals have the least spatial coverage among the L1, L2C and L5 signals; on average, only 13 measurements per day were produced from L5 SNR data, and those measurements are not evenly sampled in time, while the sampling interval of tide-gauge records is uniformly 1 h. The RMS differences of daily maximum sea levels between tide-gauge records and sea-level measurements produced by L1, L2C and L5 SNR data are 20.5 cm, 11.0 cm and 9.2 cm, respectively. Those values are comparable to the single measurement accuracy with respect to tide-gauge data, demonstrating that GNSS-IR at HKQT can be used for detecting daily/sub-daily sea-level extremes.
Storm surges caused by Hato and Mangkhut at HKQT
Based on the tide-gauge record for Quarry Bay, the storm surge caused by Hato lasted about 7 h. Sea level at this location started to exceed the highest tidal level of the day at 23:00 (August 22), reached a peak at 02:27 (August 23), and returned to normal water level at 06:00 (August 23). Note we use UTC times. During the 7 h of the storm surge, nine GPS satellites passed across the water area that can be sensed by the HKQT antenna (Table 1).
A storm surge is an abnormal rise in sea water level during a storm, measured as the height of the water above normal predicted astronomical tide. The surge is caused primarily by a storm’s strong winds pushing water onshore. Löfgren et al. (2014) demonstrated that sea levels based on L1 SNR data from a single geodetic receiver do not appear to be affected by an increase in wind speed, but higher wind speeds will increase sea-surface roughness and, therefore, result in a decrease in the reflected signal power. Consequently, the amplitude of the SNR oscillations will decrease as they depend on both the direct and reflected signal power. Wind speeds during Hato reached up to 28.3 m/s in Hong Kong, which is much larger than the maximum wind speed of 18 m/s in the study of Löfgren et al. (2014). We, therefore, impose less rigorous quality control measures in reporting valid reflector heights. The criterion of the minimum normalized spectrogram peak is reduced from 5 volts/volts to 4 volts/volts, and the requirement of a minimum peak-to-noise ratio of 3 is decreased to 2. After quality control measures are applied, we have 7, 4 and 6 sea-level measurements produced by the L1, L2C and L5 SNR data, respectively, during the 7 h of the storm surge. From Table 1, when wind speeds reached the maximum, we only obtained valid sea-level retrieval from L5 SNR data.
Depending on the magnitude, astronomical tides may no longer be the major contributor to coastal water levels during storms. We thus did not apply the correction of height change for such events, which may cause larger errors in SNR-derived sea levels. We demonstrated that the RMS difference with respect to tide-gauge data is about 3 cm larger if the effect of height change is not corrected. But compared to the errors in the sea-level measurements from GNSS-IR, such differences should not significantly affect the final results before and after the storms. For post-processing, if temporal resolution is sufficient, it is possible to correct the effect of height change during the storms iteratively using harmonic analysis based on the SNR-derived reflector heights. However, this is not the case in this study. Also, we did not correct tropospheric delay as both temperature and pressure from GPT2 could be largely biased under such abnormal and extreme weather conditions. However, this would not bias the SNR-derived sea levels as we demonstrated that the effect of tropospheric delay at this particular site is negligible.
Figure 8 shows the sea-level measurements from the tide gauge and GNSS-IR before, during and after Hato. We also superimpose predicted astronomical tide for the same period in the figure to highlight out the surges caused by this extreme event and Severe Tropical Storm Pakhar that hit Hong Kong on September 27. The sea-level measurements from GNSS-IR illustrated in the figure are combined results from L1, L2C and L5 SNR data. We first convert reflector heights (\({H_{\text{f}}}\), \(f\) represents frequency L1, L2C and L5) to relative sea levels \({h_{\text{f}}}\). Second, we average \(h_{{L1}}^{s}\left( t \right)\), \(h_{{L2C}}^{s}\left( t \right)\) and \(~h_{{L5}}^{s}\left( t \right)\) at time \(t\) from the same satellite track \(s\) to obtain relative sea level \(h\left( t \right)\) as the combined results from the three frequencies. For a satellite track at time \(t^{\prime}\), if sea-level retrieval is only valid from SNR data at one frequency, i.e., we only have one measurement instead of three measurements at time \(t^{\prime}\), then \(h\left( {t^{\prime}} \right)={h_f}\left( {t^{\prime}} \right)\). We assume the phase center offset among L1, L2C and L5 frequencies is negligible. We understand that errors in sea-level measurements are different depending on carrier frequency; however, the differences in errors are much smaller than the errors themselves. Therefore, combining measurements from the three frequencies is unlikely to affect the final results, but it can improve temporal sampling during storm surges.
Typhoon Mangkhut hit Hong Kong on September 16, 2018 and the surge caused by this event lasted about 12 h. Sea level at HKQT started to exceed the highest tidal level of the day at 00:10, reached a peak at 06:42, and returned to normal water level at 12:00. During that period, 14 GPS satellites passed across the water area that can be sensed by the HKQT antenna (Table 2). We impose the same quality control measures as Hato to report valid reflector heights during Mangkhut.
Comparing Tables 1 and 2 for the two events, we find that wind speed during Mangkhut was generally higher than that during Hato, resulting in even weaker reflected signal power. There are, therefore, less satellite tracks for which we are able to retrieve sea levels from the SNR data. Also, Hato coincided with a high tidal level, whereas Mangkhut occurred at low tidal level. The sea surface was, therefore, even rougher during Mangkhut than during Hato, although the storm tides caused by the two events are not that different. In addition, the sea-surface roughness effect on the reflected signal is not linearly dependent on the wind speed (Drennan et al. 2005), so we successfully retrieved sea levels for some satellite tracks (e.g., PRN 25) with high wind speed, but we were not able to derive valid reflector heights for some satellite tracks (e.g., PRN 10) with lower wind speed. Figure 9 shows the sea-level measurements from the tide gauge and GNSS-IR before, during and after Mangkhut, and the predicted astronomical tide. The GNSS-IR measurements in the figures are the results combined from the three frequencies. Together Fig. 9 with Fig. 8 demonstrates that GNSS-IR is able to capture the fluctuations in water levels caused by such extreme weather.
Storm surges caused by Hato and Mangkhut at HKPC
HKPC is located about 18 km west of HKQT. There is no tide gauge co-located with this site. We thus use the TPXO8-atlas model to predict the astronomical tide at this location. As HKPC is on land, we used a nearby offshore location to predict the astronomical tide.
Compared to the GNSS antenna at HKQT, the GNSS antenna at HKPC was installed on a taller building (the average reflector height is 19.7 m; at HKQT, it is 6.4 m) and further away from the water (about 25 m, horizontal distance; and HKQT is approximately 2 m). Thus, there are fewer GPS satellite tracks that cover the water area and we need to use SNR data at even lower elevation angles to exclude onshore reflections. For comparison, we take the same day (April 5, 2016) we used for HKQT as an example, after applying the azimuth and elevation angle mask: a total of 16, 11, 6 rising or setting GPS satellite tracks for L1, L2C and L5 signals, which are about half of the number of satellite tracks at HKQT, were useful for further analysis. After imposing the same quality control measures that we defined for HKQT (for removing non-physical reflector height, we used \(H\) > 22 m or \(H\) < 17 m for HKPC), we obtained 12, 10 and 6 sea-level measurements from L1, L2C and L5 SNR data, respectively.
Examining L2P SNR data at HKPC, we find that it does not exhibit double peaks in the LSP (not shown). This is due to receiver type, i.e., the receivers use different techniques to access the L2P signal (Teunissen and Montenbruck 2017; Roesler and Larson 2018). Regardless, the L2P signal at HKPC is still weaker than L1, L2C and L5 signals in terms of effective power, and also for being consistent with our analysis for HKQT, we did not use it for sea-level retrievals.
Figure 10 shows sea-level measurements from GNSS-IR superimposed with the predicted astronomical tide before, during and after Hato and Mangkut, respectively. Sea levels displayed in the two panels are combined results from the L1, L2C and L5 frequencies. It should be noted that the sensing zones of the HKPC antenna are within Peng Chau public ferry pier; ships coming and going may disturb the reflected signals, causing more outliers and/or larger errors in the sea-level measurements from GNSS-IR.
Storm surges caused by the two events are evident from Fig. 10. Excluding the two surge periods, the SNR-derived sea levels are generally smaller than the astronomical tide. Possible reasons could be large errors in the GNSS-IR measurements, the inverse barometer effect which causes variations in sea-surface height due to atmospheric loading, or both. In addition, we can see in the top panel of Fig. 10 that the sea-level measurements from GNSS-IR are much larger than the astronomical tide on September 27 compared to other periods; this is a true storm surge caused by Severe Tropical Storm Pakhar.
Discussion
Monitoring storm surges requires the equipment to be robust against storms and able to produce valid measurements under extreme weather, i.e., heavy rains and strong winds. Tide gauges can continuously record sea levels under strong winds, but they are at high risk of being damaged by sharp fluctuations of sea level caused by severe storms as they need to be installed at the coast and close to the water. In contrast, GNSS-IR stations have the advantage of being installed at high locations and horizontally set back from the water. Therefore, they are less likely to get destroyed. Along the same line of thinking, GNSS-IR also has the potential for monitoring tsunami waves. The time series of tsunami waveforms recorded by tide gauges are key to validating tsunami models, with the potential to give a great deal of information about the source of the tsunami (Lorito et al. 2008; Romano et al. 2016; Titov et al. 2005). However, as with extreme typhoon events, it is common for tide gauges to suffer damage during major tsunami events, as reported by Mori et al. (2011) during the 2011 Tohoku-oki tsunami and by Fritz et al. (2008b) during the 2007 Peru tsunami.
Based on the available data for the two major events Hato and Mangkut, the L1, L2C and L5 SNR data all show the potential to capture the sharp fluctuations of sea level. Generally, the higher the wind speed, the weaker the reflected signal power. However, no matter how weak the power is, the reflected signal will still interfere with the direct signal, creating oscillations in the SNR data; and sea levels can be estimated through analysis of the oscillations that meet the criteria mentioned earlier. In terms of effective power, the L5 signal is the strongest compared to the L1 and L2 signals. Our results indicate that the oscillations in the L5 SNR data are less likely to be impacted by strong winds. According to the information from the US government GPS web page, the full constellation of GPS satellites will transmit the modernized civil signals by December 31, 2020. That is to say, by then there will be 5 to 12 more GPS satellites transmitting L5 signals, which would certainly improve the possibility of using GNSS-IR for extreme sea-level monitoring as well as providing a better temporal sampling.
Examining the GLONASS SNR data, we found that the reflected signal power is generally smaller than that from GPS satellites, and the reflector heights produced by GLONASS SNR data contain more outliers, i.e., non-physical reflector heights, and are also noisier (not shown). Therefore, we only used GPS satellite signals. The origin of the issue with GLONASS SNR data is beyond the scope of this study. However, combining results from multi-constellations would help to solve the problem of temporal resolution that sea-level retrievals from only GPS satellite signals are currently facing, because in future there could be more than 100 navigation satellites (including GPS, GLONASS, Beidou, Galileo, QZSS, etc.). Our future work will incorporate other navigation systems for using GNSS-IR to investigate both short-term and long-term sea-level changes and their driving mechanisms.
We have mentioned that both HKPC and HKQT were originally installed for geodetic survey purposes, not for sea-level monitoring. Even so, the antennas at those two locations are still able to sense the sea-level changes from the nearby water and to successfully capture the storm surges caused by Super Typhoons Hato and Mangkhut. If we install GNSS stations at strategically selected locations for monitoring such events, more satellite tracks that cover water area would be expected. Furthermore, GNSS-IR does not require high-precision orbit products; we used the broadcast ephemeris, which is simultaneously obtained with GNSS measurements, to calculate the positions of the GPS satellites and the subsequent azimuth and elevation angles. Therefore, it is technically possible to make GNSS-IR operational in near real-time, which could provide useful information for coastal flooding planning and warning systems, especially in the case that tide gauges failed to continuously record sea levels, and/or in areas where no traditional tide gauges are available.
Conclusions
We first investigated the performance of sea-level measurements from GPS SNR data at HKQT under normal weather conditions and demonstrated that in terms of individual measurement from L1, L2C and L5 signals, L5 SNR data produced observations of sea level best agree with tide-gauge data. Second, we applied the same techniques to retrieve sea levels during the periods when Super Typhoons Hato (2017) and Mangkut (2018) hit Hong Kong. Our results showed that GNSS-IR is able to produce valid sea-level measurements in strong wind conditions. Referenced to predicted astronomical tides, the storm surges caused by the two events are evident in the sea-level time series produced by GNSS-IR at both HKQT and HKPC. We also superimposed tide-gauge records from Quarry Bay that is co-located with HKQT to prove that the surges measured by GNSS-IR are real. This is the first time that GNSS-IR has been used for storm surge monitoring. The successful demonstration in this study highlights the potential of GNSS-IR application in detecting extreme sea levels caused by weather, tsunami, etc. We anticipate the technique will have broad applications, especially in the near future when all GNSS signals can be used in the data analysis.
References
Bennett G (1982) The calculation of astronomical refraction in marine navigation. J Navig 35(2):255–259
Böhm J, Möller G, Schindelegger M, Pain G, Weber R (2015) Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut 19(3):433–441
Cazenave A, Palanisamy H, Ablain M (2018) Contemporary sea level changes from satellite altimetry: what have we learned? What are the new challenges? Adv Space Res 62(7):1639–1653
Chen N, Han G, Yang J, Chen D (2014) Hurricane Sandy storm surges observed by HY-2A satellite altimetry and tide gauges. J Geophys Res: Oceans 119(7):4542–4548
Drennan WM, Taylor PK, Yelland MJ (2005) Parameterizing the sea surface roughness. J Phys Oceanogr 35(5):835–848
Fritz HM, Blount C, Sokoloski R, Singleton J, Fuggle A, McAdoo BG, Moore A, Grass C, Tate B (2007) Hurricane Katrina storm surge distribution and field observations on the Mississippi Barrier Islands Estuarine. Coast Shelf Sci 74(1–2):12–20
Fritz HM, Blount C, Sokoloski R, Singleton J, Fuggle A, McAdoo Brian G, Moore A, Grass C, Tate B (2008a) Hurricane Katrina storm surge reconnaissance. J Geotech Geoenviron Eng 134(5):644–656
Fritz HM, Kalligeris N, Borrero JC, Broncano P, Ortega E (2008b) The 15 August 2007 Peru tsunami runup observations and modeling. Geophys Res Lett 35:L10604
Fritz HM, Blount CD, Albusaidi FB, Al-Harthy AHM (2010) Cyclone Gonu storm surge in Oman Estuarine. Coast Shelf Sci 86(1):102–106
Larson KM, Löfgren JS, Haas R (2013a) Coastal sea level measurements using a single geodetic GPS receiver. Adv Space Res 51(8):1301–1310
Larson KM, Ray RD, Nievinski FG, Freymueller JT (2013b) The accidental tide gauge: a GPS reflection case study from Kachemak Bay, Alaska. IEEE Geosci Remote Sens Lett 10(5):1200–1204
Larson KM, Ray RD, Williams SD (2017) A 10-year comparison of water levels measured with a geodetic GPS receiver versus a conventional tide gauge. J Atmos Ocean Technol 34(2):295–307
Li L, Yang J, Lin C-Y, Chua CT, Wang Y, Zhao K, Wu Y-T, Liu PL-F, Switzer DS, Mok KM, Wang P, Peng D (2018a) Field survey of the 2017 Typhoon Hato and a comparison with storm surge modeling in Macau. Nat Hazards Earth Syst Sci 18(12):3167–3178
Li X, Han G, Yang J, Chen D, Zheng G, Chen N (2018b) Using satellite altimetry to calibrate the simulation of typhoon Seth Storm Surge off Southeast China. Remote Sens 10(4):1–15
Löfgren JS, Haas R, Scherneck H-G (2014) Sea level time series and ocean tide analysis from multipath signals at five GPS sites in different parts of the world. J Geodyn 80:66–80
Lorito S, Romano F, Piatanesi A, Boschi E (2008) Source process of the september 12, 2007, Mw 8.4 southern Sumatra earthquake from tsunami tide gauge record inversion. Geophys Res Lett 35:L02310
Madsen KS, Høyer JL, Fu W, Donlon C (2015) Blending of satellite and tide gauge sea level observations and its assimilation in a storm surge model of the North Sea and Baltic Sea. J Geophy Res: Oceans 120(9):6405–6418
Miguez BM, Testut L, Wöppelmann G (2008) The Van de Casteele test revisited: an efficient approach to tide gauge error characterization. J Atmos Ocean Technol 25(7):1238–1244
Mori N, Takahashi T, Yasuda T, Yanagisawa H (2011) Survey of 2011 Tohoku earthquake tsunami inundation and run-up. Geophys Res Lett 38:L00G14
Pugh D, Woodworth PL (2014) Sea-level science: understanding tides, surges, tsunamis and mean sea-level changes. Cambridge University Press, Cambridge
Roesler C, Larson KM (2018) Software tools for GNSS interferometric reflectometry (GNSS-IR). GPS Solut 22(3):80
Romano F, Piatanesi A, Lorito S, Tolomei C, Atzori S, Murphy S (2016) Optimal time alignment of tide-gauge tsunami waveforms in nonlinear inversions: application to the 2015 Illapel (Chile) earthquake. Geophys Res Lett 43(21):11226–11235
Roussel N, Ramillien G, Frappart F, Darrozes J, Gay A, Biancale R, Striebig N, Hanquiez V, Bertin X, Allain D (2015) Sea level monitoring and sea state estimate using a single geodetic receiver. Rem sens Environ 171:261–277
Scharroo R, Smith WH, Lillibridge JL (2005) Satellite altimetry and the intensification of Hurricane Katrina. Eos Trans Am Geophys Union 86(40):366–366
Soria JLA, Switzer AD, Villanoy CL, Fritz HM, Bilgera PHT, Cabrera OC, Siringan FP, Maria YY-S, Ramos RD, Fernandez IQ (2016) Repeat storm surge disasters of Typhoon Haiyan and its 1897 predecessor in the Philippines. Bull Am Meteor Soc 97(1):31–48
Spencer T, Brooks SM, Evans BR, Tempest JA, Möller I (2015) Southern North Sea storm surge event of 5 December 2013: water levels, waves and coastal impacts. Earth Sci Rev 146:120–145
Teunissen P, Montenbruck O (eds) (2017) Springer handbook of global navigation satellite systems. Springer, Berlin
Titov VV, González FI, Bernard EN, Eble MC, Mofjeld HO, Newman JC, Venturato AJ (2005) Real-time tsunami forecasting: challenges and solutions. Nat Hazards 35(1):35–41
Wadey M, Haigh I, Brown J (2014) A century of sea level data and the UK’s 2013/14 storm surges: an assessment of extremes and clustering using the Newlyn tide gauge record. Ocean Sci 10(6):1031–1045
Wang HV, Loftis JD, Liu Z, Forrest D, Zhang J (2014) The storm surge and sub-grid inundation modeling in New York City during Hurricane Sandy. J Mar Sci Eng 2(1):226–246
Wessel P, Smith WH (1998) New, improved version of generic mapping tools released. Eos Trans Am Geophys Union 79(47):579–579
Williams S, Nievinski F (2017) Tropospheric delays in ground-based GNSS multipath reflectometry—experimental evidence from coastal sites. J Geophys Res: Solid Earth 122(3):2310–2327
Acknowledgements
We are grateful to two anonymous reviewers for their suggestions that improved the manuscript. We thank the Survey and Mapping Office of Hong Kong Lands Department for providing GNSS data, and the University of Hawaii Sea-Level Center and the Intergovernmental Oceanographic Commission for providing tide-gauge records. We used the Generic Mapping Tools (Wessel and Smith 1998) and the toolbox provided by Roesler and Larson (2018) to make Figs. 1 and 5, respectively. ADS thanks the support of Scor Re. This research was supported by Singapore Ministry of Education Academic Research Fund Tier 2 (MOE 2016-T2-2-041), and by the Earth Observatory of Singapore and the National Research Foundation Singapore and the Singapore Ministry of Education under the Research Centres of Excellence initiative. This research is a contribution to IGCP639 project Sea level change from minutes to millennia. This is the Earth Observatory of Singapore paper number 208.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Peng, D., Hill, E.M., Li, L. et al. Application of GNSS interferometric reflectometry for detecting storm surges. GPS Solut 23, 47 (2019). https://doi.org/10.1007/s10291-019-0838-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-019-0838-y