Abstract
GNSS-R interferometric reflectometry (also known as GNSS-IR, or GPS-IR for GPS signals) is a technique that uses data from geodetic-quality GNSS instruments for sensing the near-field environment. In contrast to positioning, atmospheric, and timing applications of GNSS, GNSS-IR uses the signal-to-noise ratio (SNR) data. Software is provided to translate GNSS files, map GNSS-IR reflection zones, calculate GNSS-IR Nyquist frequencies, and estimate changes in the height of a reflecting surface from GNSS SNR data.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
GNSS-IR is a method for estimating environmental parameters around a geodetic-quality GNSS site. Unlike other reflection techniques, where an antenna is designed to measure reflection signals (Löfgren et al. 2011; Camps et al. 2013) or a geodetic antenna is rotated to improve its ability to measure reflections (Anderson 2000), GNSS-IR uses data collected with (nominally) multipath-suppressing geodetic-quality GNSS antennas in an upright orientation. GNSS-IR has been demonstrated and validated for measuring surface soil moisture (Larson et al. 2008), snow depth (Larson et al. 2009; Nievinski and Larson 2014c, d), permafrost melt (Liu and Larson 2018), tides (Larson et al. 2013, 2017; Löfgren et al. 2014; Roussel et al. 2015), ice-up (Strandberg et al. 2017), firn density (Larson et al. 2015), and vegetation water content (Wei et al. 2015). In addition to these practical demonstrations, Felipe Nievinski developed a simulator that allows a user to test the reflection characteristics for different experimental configurations and surfaces (Nievinski and Larson 2014a, b).
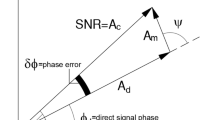
At some level, all GNSS-IR studies are based on the analysis of SNR patterns created by the interference of direct and reflected (or multipath) GNSS signals. There is significant literature on the inherent frequencies in GNSS multipath, and we will not repeat it here (Georgiadou and Kleusberg 1988; Ge et al. 2000; Ray and Cannon 2001; Axelrad et al. 2005; Bilich and Larson 2007). While the multipath frequencies for a planar reflector change as a satellite rises or sets, Axelrad et al. (2005) proposed a simple change of variable (using \(\sin e\) rather than e) that yields one multipath frequency per rising/setting satellite arc. Ignoring the direct signal contribution, SNR data for a single satellite and receiver can be modeled as:
where e is the GNSS satellite elevation angle with respect to the horizon, \(\lambda\) is the GNSS wavelength, \(\phi\) is a phase constant, HR is the vertical distance between the GNSS antenna phase center and the horizontal reflecting surface, and A(e) represents the amplitude of the SNR data. To be clear, this representation of SNR data is time dependent because e is a function of time. A fuller discussion of the contributions to A(e) can be found in Nievinski and Larson (2014a).
When HR is fixed, surface soil moisture can be derived from the estimated changes in \(\phi\) (Larson et al. 2008; Chew et al. 2016). Using similar assumptions, A can be used to measure vegetation water content (Wei et al. 2015). Changes in A are also important for applications such as sea ice detection (Strandberg et al. 2017). In this short note we ignore A and \(\phi\) and focus on the inherent multipath frequency, \(2{H_{\text{R}}}/\lambda\). By estimating the multipath frequency, we have a simple way to determine HR. This has also been called the reflector height (Larson and Nievinski 2013), although to be clear, it is not a “height” in a geodetic sense. Here, we will mostly use HR so as to limit the confusion between HR and orthometric and ellipsoidal heights. In the next sections, we will discuss our software for GNSS-IR frequency relationships. In particular, we are providing software to do the following:
-
Translate GNSS data files stored in the RINEX format.
-
Map GNSS-IR reflection zones.
-
Calculate the average Nyquist frequency for a GNSS-IR installation.
-
Estimate dominant frequencies (and thus HR) from GNSS SNR data.
Extracting SNR observations needed for GNSS-IR from a RINEX file
Most GNSS networks provide carrier phase and pseudorange data to users in the RINEX format (Gurtner and Estey 2007). These dual-frequency ranging observations are then used with high-precision geodetic or surveying software, with precise ephemerides, to compute daily (or more frequent) Cartesian positions. Unfortunately, the parameters needed for GNSS-IR cannot always be easily extracted from the outputs of high-precision geodetic or surveying software. Here we provide Fortran 77 code that translates the GPS (and more generally GNSS) observations stored in a RINEX file into a format usable for reflections research. In the first (RinexSNR), the elevation and azimuth angles of GPS satellites with respect to the local horizon are computed using the GPS navigation message. The latter is also stored in the RINEX format. The times of the observations (in GPS time, seconds of the day) are also extracted and the SNR observations on the L1, L2, and L5 frequencies are saved. The output format is in columns and thus the data can be easily loaded using other programming languages such as Matlab and python. The current version of the code only reads RINEX version 2.11 format and files with no more than 15 observation types. Signals from non-GPS constellations are ignored.
To support GNSS-IR, we have provided a separate piece of Fortran code (RinexSNR_GNSS) that extracts GNSS SNR observations from a RINEX file. The main difference between the two programs is that the first uses real-time navigation messages to compute satellite ephemerides and the second uses precise ephemerides. The current constellations supported are GPS, GLONASS, GALILEO, and BEIDOU. Because all GNSS constellations nominally number their satellites the same way, we rename the non-GPS satellites by adding 100 (GLONASS), 200 (GALILEO), or 300 (BEIDOU). Additional instructions are provided in the readme file.
Both Fortran translation programs use the Cartesian station location in the RINEX header to compute the satellite/station elevation angle. If the RINEX file doesn’t have station coordinates, the code stops. It is not necessary that the station location be extremely accurate—but we suggest it be within 50 m of its true position. Most RINEX files created by geodesists and surveyors have much better station coordinates than this, with the exception of some data from the cryosphere. In these cases, the archives often use a single station location for all station files, even though the station is moving rapidly (e.g., hundreds of meters per year). For these users, we allow time-varying receiver coordinates to be read from an external text file. The user should input a Cartesian position at a given epoch and a Cartesian velocity, in meters and meters/year, respectively. This option is not necessary for other GNSS-IR sites.
GNSS-IR reflection zones
The equations for a Fresnel zone near the surface of the Earth are given in the appendix of Larson and Nievinski (2013). The sizes of these elliptical sensing zones are directly sensitive to HR, the satellite elevation angle (e) and the GNSS transmitter frequency (L1, L2, or L5). The orientation of the Fresnel zone with respect to the GNSS antenna depends on the azimuth angle of the satellite. The Fresnel zones gets smaller and closer to the antenna as the elevation angles increase.
We provide two sets of Matlab codes to facilitate mapping the reflection zones. The first, mapview_fresnel_toolbox.m, plots the Fresnel zones for a given GNSS site in a plain “horizontal” map view. Figure 1 shows example L1 Fresnel zones for a GNSS station located in Boulder, Colorado. Two values of HR are used to demonstrate the fundamental relationship to this quantity. The second code, googleEarthFresnel.m, provides similar information, with an output kml file that can be loaded into Google Earth. Figure 2 shows a screen view from Google Earth for the Boulder, Colorado example. Figure 3 shows a screen view for a GNSS site in Alaska. This particular GNSS site is far above sea level, about 68 m, and the input HR value used reflects that.
Both mapview_fresnel_toolbox.m and googleEarthFresnel.m need to know the approximate azimuth of the rising and setting satellites for the GNSS station in question. If the user does not know this information, values can be computed using a separate piece of Matlab code: do_azims.m. The googleEarthFresnel.m code allows the user to either manually set HR or to use mean sea level as the reflecting surface. If desiring mean sea level, the code uses the ellipsoidal GNSS station height and the EGM96 geoid correction (Lemoine et al. 1998). For more information on Fresnel zones in GNSS-IR, the reader is directed to Roussel et al. (2014) and Nievinski et al. (2016).
Frequency extraction from GNSS-IR: theoretical discussion
Although a GNSS receiver will track signals at even time intervals, the interval between 2 samplings of sin(e(t)) will be uneven during any given observing window. Furthermore, different satellite tracks will have different sampling intervals, as GNSS satellites that stay low in the sky move more slowly than others that pass higher in the sky. Figure 4 shows how sample data intervals vary for a site in Greenland. We use the Lomb Scargle Periodogram (hereafter LSP), designed to detect periodic signals with unevenly spaced observations, to extract the SNR spectral content (Lomb 1976; Press et al. 1992). To express the SNR spectral frequencies directly in terms of H in meters, we scale the sampling variable sin(e(t)) by a wavelength factor. The code lomb.m computes the normalized periodogram of a sequence of SNR data sampled at X(t) = 2sin(e(t))/λ, during an arc over a given elevation angle range [emin emax].
A LSP requires the user to provide the highest frequency factor (hifac) and an oversampling factor (ofac). We have recast these inputs into variables that are more intuitive for a GNSS-IR analyst. Instead of hifac and ofac, the user chooses the maximum value of H to be calculated and the desired precision, both in meters. Thus, the Lomb normalized periodogram is calculated at the frequencies H = [0: desired Precision: maxHeight]. These two user inputs are then converted into hifac and ofac for input to lomb.m. More details can be found in the Matlab code get_ofac_hifac.m.
The spectral grid can be as large and fine as you want at the expense of longer computation time. A user may want to compute frequencies up to the pseudo-Nyquist limit (see the next section). For a 1-s GPS sampling rate the pseudo-Nyquist limit is ~ 450 m with N = 1800 samples collected in a 30 min arc. Using a grid precision of 1 cm, the number of frequencies would be Nf = 45,000. The scaling of the lomb.m algorithm, provided in this GPS Toolbox contribution, is of the order of Nf ↔N ~ = 108. For a 5-s GPS sampling rate, this value is reduced by 25 but is still quite large. Instead, for snow accumulation, we have prior knowledge of the frequency range from which to expect a spectral peak. For a GNSS antenna initially set at 2 m, we might select a maximum grid frequency maxHeight of 6 m. Note that faster implementations of the LSP exist if you would like to check all frequencies (Press and Rybicki 1989).
There is no guarantee that the highest peak corresponds to the best frequency HR. And even if you are on the correct peak, the grid spacing is not the precision of the spectral peak. For instance, the spectral resolution scales inversely to the length W of the GNSS type observing window, where W = 2(sin(emax)–sin(emin))/λ in units of inverse meters. It is advisable to have at least one cycle of SNR data in your survey window. Significant frequencies below 1/W need to be analyzed carefully as they could be low-frequency residuals from an imperfect removal of the direct SNR signal. Finally, the peak estimate from one LSP may not be statistically reliable, but by taking the daily average or median over tens to hundreds of tracks one can increase the quality of the HR estimate over a region.
For even sampling, any frequency above the Nyquist frequency will be folded back (aliased) into the lower frequencies. With uneven sampling, the Nyquist-like limit, the limit beyond which no further information from the spectral content of the sampled signal can be extracted, can be much larger than the “Average-Nyquist” frequency computed for the same number of data uniformly sampled during the same time span. This makes intuitive sense because when the spacing varies we collect extra information in the space between two even samples and this can remove the aliasing ambiguity (Press et al. 1992; VanderPlas 2017).
In the context of GNSS SNR data, the samples in the observing window are structured, i.e., they are not random. Any structure in the sampling interval will be reflected in the LSP of the signal. Qualitatively the LSP patterns can be represented as the convolution between the window spectrum and the spectrum of the true signal. To discuss a Nyquist-like limit, we will look at the spectral characteristics of the observing windows. We provide this discussion so that potential GNSS-users will have an understanding of what GNSS time sampling interval to use to appropriately resolve HR from their SNR data. Figure 5d shows L2C SNR observations from the GNSS station GLS2. Operators of the station set its receiver-sampling rate to 15 s and there was no elevation mask. Figure 5e shows three tracks with the same SNR characteristics but with different survey windows in the elevation angle range [5°–20°]. The window spectra are computed up to H of 300 m (To estimate the form of the window power, compute a LSP on a series of unit measurements, but turn off the automatic pre-centering of the data in lomb.m).
Effect of GNSS type survey window with uneven sampling on the LSP of SNR data. Three windows for L2C data are shown spanning the elevation range [5–20] from the GNSS station GLS2. The latter has a receiver sampling-rate of 15 s. Satellite 27’s southeast track (blue) has nearly uniform samplings. Satellite 30’s northeast track (green) has moderately uneven samplings. Satellite 27’s northeast track (red) has the most uneven samplings found at this site. a LSP of SNR data between 0 and 300 m. b LSP of sampling windows. c Zoom of LSP of SNR data between 0 and 6 m. d SNR data with the same characteristics, as a function of the sampling variable X(t) = 2sin(e(t))/λ in units of inverse meters. e Interval between observations dX as a function of X. Note that in this figure we use X as the variable because it is this sampling variable which expresses the spectral frequencies directly in meters
As shown in Fig. 5e, the southeast track for satellite 27 has a nearly uniform sampling. This results in a power spectrum of the window close to regularly narrow spaced spikes with a cadence of 69 m (Fig. 5a). Yet as the frequency H increases, the shape of the peaks changes. The spikes slightly decrease in power and their tail end spreads. As the sampling becomes less uniform the distortion increases. For the most severe case of uneven sampling found at GLS2 (satellite 27 northeast track) the window spectrum becomes noise-like after 250 m. This window structure is reflected in the LSP of the SNR (red traces in Fig. 5a, b).
The distance (cadence) between two spikes stays relatively constant. We will use half of this distance as the pseudo-Nyquist frequency. Any single frequency above this limit will be an imperfect version folded back into the lower frequencies, with a spectrum spread distortion depending on the degree of unevenness in the samplings. For moderately uneven to strong uneven sampled noisy data, the interaction of high-frequency noise bands with the convolution window can be complex with an increased spectral background noise level and eventually create spurious high-leveled peaks. Figure 5c shows that SNR power spectrums for the three tracks in the range [0–6 m] are similar. This is because there is no significant high-frequency noise folded back into this region.
We should clarify that with this type of LSP window, when the power of the second spike is less than ~ half the power of the zero-frequency peak, one should be able to detect significant spectral peaks beyond this pseudo-Nyquist frequency, and the true Nyquist-like limit is much larger. For further qualitative details on the effect of uneven-sampling and understanding the LSP the reader is referred to VanderPlas 2017.
To conclude, the exact structure of the LSP window will vary with each site, track, elevation range, L-band frequency and GPS receiver sampling rate, but the window LSP signature will vary between the 2 extremes mentioned above. This is one reason for the quality of the LSP across sites and tracks, especially in the presence of noise. We can get an approximate order of magnitude pseudo-Nyquist frequency using the average-Nyquist frequency, which is around 30–50 m for GLS2, using a GNSS sampling rate of 15 s at the L2 frequency (Table 1). For a survey window of length W and N observations the average-Nyquist frequency is N/2W.
Matlab code median_avg_nyquist.m is provided to allow a user to calculate the median average-Nyquist frequency. The user provides a receiver sampling interval (in seconds), the station location, GPS frequency, and elevation angle limits. The code simulates rising and setting satellite information for that GNSS site and outputs the median average-Nyquist frequency in meters.
GNSS-IR examples
Finally, we provide Matlab code to compute GNSS-IR results (sample_gnss_ir.m). The GNSS stations are chosen from Greenland, Antarctica, Alaska, and the western U.S. The GNSS sites have one thing in common: they were deployed without any thought that they could be used for GNSS-IR. Although we refer to GNSS here, these particular sites only tracked GPS satellites. Before discussing the output of this code, we will first describe the various steps within it.
-
1.
Because this is a set of tutorial codes, the user is asked to choose a GPS frequency. The L1 GPS signal generated with the C/A code, or L1C, has the advantage that it is almost always available in RINEX files and it is tracked for all satellites. There can be issues with quality, particularly for some receivers; some of these issues were discussed previously by Larson and Nievinski (2013). The L2 GPS GPS signal currently has two codes. The public code (L2C) is far superior to L2P for GNSS-IR. Unfortunately, it is not always tracked at GNSS sites. As of 2016, L2C is available on 18 GPS satellites. For the sample data files we provided, we strongly recommend using L1 or L2C (when available). None of the example GNSS sites in this tutorial tracked L5 signals, but as with L2C, these new data are excellent for GNSS-IR applications (Tabibi et al. 2015).
-
2.
Various defaults have been set. As discussed in the previous section, two LSP parameters need to be defined. The LSP precision is set to 5 mm and the maximum HR allowed is 8 m. HR values smaller than 0.4 m are not allowed, as GNSS-IR breaks down for small values of HR (Nievinski and Larson 2014c). For tower applications, users must change the maximum allowed value of HR.
-
3.
The code needs to know the rising and setting satellite arcs for each site. Rather than predefine these values, the tutorial codes search for all available satellite data within 45-degree azimuth bins. Once the observations for a particular satellite in a given azimuth bin are found, the SNR data are converted to linear units (from dB-Hz to volts/volts) and a low-order polynomial is removed. The latter represents the direct signal component which is of no interest for GNSS-IR. A LSP is then produced from these “flattened” SNR traces. The user can change the polynomial order by modifying the code directly.
-
4.
After a LSP is computed for a given rising or setting arc, the code must decide whether the peak in the LSP is significant. Here we have used a simple peak/noise ratio test. This is certainly not the only- or the best-way to compute the significance of a peak. The code allows the user to define over which frequencies the noise metric is computed and what ratio between the peak and noise is required. Other quality control metrics that could be used include a simple amplitude minimum value, the number of points (which would depend on the sampling interval), and the elevation angle difference.
-
5.
The tutorial code generates two kinds of output. The significant HR results are printed to a text file. Plots can be automatically generated either as a summary for all azimuths or in separate azimuth bins. This is currently set to 45-degree azimuth bins. However, this can be changed by the user.
-
6.
Figures 6 and 7 give you an overview of the GNSS-IR steps used for GLS2, the sample GNSS site in Greenland. In contrast to the Fresnel zones in the Boulder, Colorado case, which had a void in the north, there is 360-degree azimuthal coverage at GLS2. This is typical for GNSS sites in polar regions. Figure 6 shows SNR data for satellite 30, which rose and set twice at GLS2. This means there are four satellite arcs, one in each geographic quadrant. Figure 7 shows the corresponding LSP for these SNR data. Note that at this site the quality of the oscillations is poorer at higher elevation angles. The user can restrict the analysis accordingly. The reflection signal at GLS2 below 10° is quite strong, which serves as a reminder to station operators that elevation masks hinder GNSS-IR applications.
-
7.
sample_gnss_ir.m can be run with six sample files. Here we will only discuss three of the sites: P038, GLS2, and SG27. Figure 8 shows L2C GNSS-IR results for station P038. This station is located at an airport in New Mexico with little or no terrain relief. We used the “Separate plots by azimuth bin” option and show LSP output for azimuths between 180° and 225°. You can see that the peaks of the LSP are very consistent with a horizontal planar surface. Figure 8 also shows complete GNSS-IR results for a GLS2 data record. In this example, we opted to show all azimuths together and the code calculates the median of the peak values, yielding a HR of 2.95 m.
Lomb Scargle Periodograms for the SNR data shown in Fig. 6
Figure 9 shows sample LSP results for GNSS site SG27 in Barrow, Alaska. Only the southeast quadrant is shown, as this region is unobstructed and planar (Liu and Larson 2018). The L1C LSP results produce a median HR value of 3.60 m. Figure 9 also shows LSP results for L2P. Instead of a single significant peak, there appear to be strong peaks at both the L1 peak and at ~ 4.6 m. The second peak is located at 3.60 multiplied by the ratio of the L2 and L1 wavelengths (0.244 and 0.19 m, respectively). This second peak is to be expected given that geodetic receivers must cross correlate to extract the L2P data. While the secondary peak is straightforward to observe and exclude, we caution that the peaks will be much more difficult to separate at smaller values of HR. We have also provided options in sample_gnss_ir.m so that you can evaluate your own GNSS site and/or modify default assumptions.
Our goal for distributing this software is to make it easier for you to visually understand what reflected GNSS signals look like in SNR data. You cannot immediately use the codes in an operational sense, but they can easily be modified for that use. The main change you will need is to convert sample_gnss_ir.m into a function. Most typically at this stage all plots would be turned off, and this new function would be called with, e.g., station name, year, day of year, frequencies, elevation angles limits, desired precision, maximum HR, and azimuth ranges. One reason we think it is useful to start out evaluating SNR data visually is so that you can see which azimuth and elevation angles are generating usable reflection data. The reflection zone mapping software we have provided earlier gives you a way to validate these azimuth and elevation angle choices. While it is certainly possible to automate the azimuth and elevation angle choices, as we did for PBO H2O (Larson 2016), you will be able to develop a better automation scheme if you start with the raw SNR data. Visually inspecting GNSS-IR periodograms will also encourage you to think about how to decide which LSP retrievals are significant and which are not. The Fortran and MATLAB code for this software, and the sample data, can be accessed via the GPS Toolbox website at http://www.ngs.noaa.gov/gps-toolbox.
Final remarks
We hope that this software will provide guidance for new users of GNSS-IR. The technique is particularly straightforward to use in the cryosphere (Shean et al. 2017; Siegfried et al. 2017). With excellent azimuthal coverage at the poles and large planar surfaces, several hundred GNSS-IR reflection retrievals can easily be made per day, yielding an extremely robust daily average. GNSS receivers/antennas on towers can also provide accurate measurements of the surface over a large spatial region. If the GNSS antenna pole is set in ice, GNSS-IR and traditional GNSS vertical measurements can be used to simultaneously constrain the density of the firn layer and snow accumulation (Larson et al. 2015). Liu and Larson (2018) recently demonstrated that GNSS-IR can also be used to measure the deformation of the transition zone in permafrost regions.
The GNSS-IR technique is increasingly being used as a tide gauge (Larson et al. 2017). The motivation for doing so is primarily its simultaneous ability to measure changes in the water surface and the antenna phase center in a terrestrial reference frame (Santamaría-Gómez and Watson 2017). For the tide gauge application, additional corrections are needed and codes for those corrections are not provided in this GPS Toolbox contribution. First, a correction is needed if the water height changes significantly during a rising or setting satellite arc (Larson et al. 2013), i.e., the so-called \({\dot {H}_{\text{R}}}\) term. Second, a refraction correction must be made. The reader is directed to Williams and Nievinski (2017) for more discussion of refraction in GNSS-IR and how to correct for it. Because the tide gauge application requires subdaily measurements, significant efforts have been made to improve the resolution of a single HR value. We direct the reader to Strandberg et al. (2016), Reinking (2016), and Wang et al. (2018) for additional information on these efforts.
As a final note, we encourage GNSS-IR enthusiasts to take advantage of GNSS-IR simulators such as Nievinski and Larson (2014d) and Roussel et al. (2014) and the mapping/Nyquist tools provided here to properly design new GNSS-IR sites. At a minimum, one should:
-
1.
Track all frequencies.
-
2.
Track all codes (i.e. L2C, L5).
-
3.
Track all constellations.
-
4.
Remove elevation angle masks.
If there are significant cost issues related to telemetry, one can choose a receiver sampling interval that both limits those costs and allows reflection monitoring. We also encourage those station operators that need to place their GNSS antennas on buildings to consider placing them near the edge of the roof so as to enable reflection science.
References
Anderson KD (2000) Determination of water level and tides using interferometric observations of GPS signals. J Atmos Oceanic Technol 17(8):1118–1127
Axelrad P, Larson KM, Jones B (2005) Use of the Correct Satellite Repeat Period to Characterize and Reduce Multipath Errors, Institute of Navigation GNSS. In: 18th International Technical Meeting of the Satellite Division, Long Beach, 13–16 September, 2005, pp 2638–2648
Bilich A, Larson KM (2007) Mapping the GPS Multipath Environment Using the Signal-to-Noise Ratio (SNR). Radio Sci 42:RS6003. https://doi.org/10.1029/2007RS003652
Camps A, Rodriguez-Alvarez N, Valencia E, Forte G, Ramos I, Alonso-Arroyo A, Bosch-Lluis X (2013) Land monitoring using GNSS-R techniques: a review of recent advances. In: 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 4026–4029. IGARSS.2013.6723716
Chew CC, Small EE, Larson KM (2016) An algorithm for soil moisture estimation using GPS interferometric reflectometry for bare and vegetated Soil. GPS Solut 20(3):525–537. https://doi.org/10.1007/s10291-015-0462-4
Ge L, Han S, Rizos C (2000) Multipath mitigation of continuous GPS measurements using an adaptive filter. GPS Solut 4(2):19–30
Georgiadou Y, Kleusberg A (1988) On carrier signal multipath effects in relative GPS positioning. Manuscr Geod 13:172–179
Gurtner W, Estey L (2007) RINEX: the receiver independent exchange format version 2.11. http://igs.org/pub/data/format/rinex211.txt. Accessed 22 Feb 2018
Larson KM (2016) GPS interferometric reflectometry: applications to surface soil moisture, snow depth, and vegetation water content in the Western United States. WIREs Water 3:775–787. https://doi.org/10.1002/wat2.1167
Larson KM, Nievinski FG (2013) GPS snow sensing: results from the earthscope plate boundary observatory. GPS Solut 17(1):41–52. https://doi.org/10.1007/s10291-012-0259-7
Larson KM, Small EE, Gutmann E, Bilich A, Braun J, Zavorotny V (2008) Use of GPS receivers as a soil moisture network for water cycle studies. Geophys Res Lett 35:L24405. https://doi.org/10.1029/2008GL036013
Larson KM, Gutmann E, Zavorotny VU, Braun JJ, Williams M, Nievinski FG (2009) Can we measure snow depth with GPS receivers? Geophys Res Lett 36:L17502. https://doi.org/10.1029/2009GL039430
Larson KM, Ray RD, Nievinski FG, Freymueller JT (2013) The Accidental Tide Gauge: A GPS Reflections Case Study from Kachemak Bay, Alaska. IEEE Geosci Remote Sens Lett 10(5):1200–1204. https://doi.org/10.1109/LGRS.2012.2236075
Larson KM, Wahr J, Kuipers Munneke P (2015) Constraints on snow accumulation and firn density in Greenland using GPS receivers. J Glaciology 61(225):101–115. https://doi.org/10.3189/2015JoG14J130
Larson KM, Ray RD, Williams SDP (2017) A ten year comparison of water levels measured with a geodetic GPS receiver versus a conventional tide gauge. J Atmos Ocean Technol 34(2):295–307. https://doi.org/10.1175/JTECH-D-16-0101.1
Lemoine FG, Kenyon SC, Factor JK, Trimmer RG, Pavlis NK, Chinn DS, Cox CM, Klosko SM, Luthcke SB, Torrence MH, Wang YM, Williamson RG, Pavlis EC, Rapp RH, Olson TR (1998) The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96. NASA/TP-1998-206861, July 1998
Liu L, Larson KM (2018) Decadal changes of surface elevation over permafrost area estimated using reflected GPS signals. The Cryosphere 12:477–489. https://doi.org/10.5194/tc-12-477-2018
Löfgren JS, Haas R, Scherneck HG, Bos MS (2011) Three months of local sea level derived from reflected GNSS signals. Radio Sci 46:RS0C05, https://doi.org/10.1029/2011RS004693
Löfgren JR, Haas R, Scherneck HG (2014) Sea level time series and ocean tide analysis from multipath signals at five GPS sites in different parts of the world. J Geodyn 80:66–80
Lomb NR (1976) Least-squares frequency-Analysis of unequally spaced data. Astrophys Space Sci 39(2):447–462
Nievinski FG, Larson KM (2014a) Forward modeling of GPS multipath for near-surface reflectometry and positioning applications. GPS Solut 18(2):309–322. https://doi.org/10.1007/s10291-013-0331-y
Nievinski FG, Larson KM (2014b) An Open Source GPS Multipath Simulator in Matlab/Octave. GPS Solut 18(3):473–481. https://doi.org/10.1007/s10291-014-0370-z
Nievinski FG, Larson KM (2014c) Forward and Inverse modeling of GPS multipath for snow depth estimation, part I: formulation and simulations. IEEE Trans Geosci Remote Sens 52(10):6555–6563. https://doi.org/10.1109/TGRS.2013.2297681
Nievinski FG, Larson KM (2014d) Forward and Inverse modeling of GPS multipath for snow depth estimation, part II: application and validation. IEEE Trans Geosci Remote Sens 52(10):6564–6573. https://doi.org/10.1109/TGRS.2013.2297688
Nievinski FG, Silva MF, Boniface K, Monico JFG (2016) GPS Diffractive Reflectometry: Footprint of a Coherent Radio Reflection Inferred From the Sensitivity Kernel of Multipath SNR. IEEE J Sel Topics Appl Earth Observ 9(10):4884–4891
Press WH, Rybicki GB (1989) Fast algorithm for spectral analysis of unevenly sampled data. Astrophys J 338:277–280. https://doi.org/10.1086/167197
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in fortran 77, vol 1, 2nd edn. Cambridge University Press, New York, pp 569–573
Ray JK, Cannon ME (2001) Synergy between Global Positioning System code, carrier, and signal-to-noise ratio multipath errors. J Guid Contr Dyn 24:54–63
Reinking J (2016) GNSS-SNR water level using global optimization based on interval analysis. J Geod Sci 6:80–92. https://doi.org/10.1515/jogs-2016-0006
Roussel N, Frappart F, Ramillien G, Darrozes J, Desjardins C, Gegout P, Pérosanz P, Biancale R (2014) Simulations of direct and reflected wave trajectories for ground-based GNSS-R experiments. Geosci Model Dev 7(5):2261–2279
Roussel N, Ramillien G, Frappart F, Darrozes J, Gay A, Biancale R, Striebig N, Hanquiez V, Bertin X, Allain A (2015) Sea level monitoring and sea state estimate using a single geodetic receiver. Remote Sens Environ 171:261–277
Santamaría-Gómez A, Watson C (2017) Remote leveling of tide gauges using GNSS reflectometry: Case study at Spring Bay, Australia. GPS Solut 21(2):451–459
Shean D, Christiansen K, Larson KM, Ligtenberg SRM, Joughin IR, Smith BE, Stevens CM, Bushuk M, Holland DM (2017) GPS-derived estimates of surface mass balance and ocean-induced basal melt for Pine Island Glacier ice shelf, Antarctica. The Cryosphere 11:2655–2674. https://doi.org/10.5194/tc-11-2655-2017
Siegfried MR, Medley B, Larson KM, Fricker HA, Tulaczyk S (2017) Snow accumulation variability on a west Antarctic ice sheet observed with GPS reflectometry, 2007–2017. Geophys Res Lett 44(15):7808–7816. https://doi.org/10.1002/2017GL074039
Strandberg J, Hobiger T, Haas R (2016) Improving GNSS-R sea level determination through inverse modeling of SNR data. Radio Sci 51:1286–1296. https://doi.org/10.1002/2016RS006057
Strandberg J, Hobiger T, Haas R (2017) Coastal Sea Ice Detection Using Ground-Based GNSS-R. IEEE Geosci Remote Sens Lett 14(9):1552–1556. https://doi.org/10.1109/LGRS.2017.2722041
Tabibi S, Nievinski FG, van Dam T, Monico G (2015) Assessment of modernized L5 SNR for ground-based multipath reflectometry applications. Adv Space Res. https://doi.org/10.1016/j.asr.2014.11.019
VanderPlas JT (2017) Understanding the Lomb Scargle Periodogram. https://arxiv.org/pdf/1703.09824.pdf. Accessed 27 Feb 2018
Wang X, Zhang Q, Zhang S (2018) Water levels measured with SNR using wavelet decomposition and Lomb-Scargle periodogram. GPS Solut 22:22. https://doi.org/10.1007/s10291-017-0684-8
Wei W, Larson KM, Small EE, Chew CC, Braun JJ (2015) Using GPS Receivers to Measure Vegetation Water Content. GPS Solut 19(2):237–248. https://doi.org/10.1007/s10291-014-0383-7
Williams SDP, Nievinski FG (2017) Tropospheric delays in ground- based GNSS multipath reflectometry—experimental evidence from coastal sites. J Geophys Res 122:2310–2327. https://doi.org/10.1002/2016JB013612.
Acknowledgements
KL acknowledges her GNSS-IR colleagues Eric Small, Clara Chew, Felipe Nievinski, Valery Zavorotny, and John Braun. Kevin Choi helped decipher the Google Earth maps. At UNAVCO we thank Fran Boler, Karl Feaux, John Galetzka, Dave Maggert, Thomas Nylen, and Jim Normandeau. We thank Kai Borre, Dmitry Savransky and many others for providing open access MATLAB code. This research is currently supported by NSF Atmospheric Sciences, EarthScope, and Hydrologic Sciences (Grant AGS 1449554) and NASA NNX14AQ14G; reflectometry research at CU was previously supported by the NASA Earth Surface and Interior program via NNX12AK21G.
Author information
Authors and Affiliations
Corresponding author
Additional information
The GPS Tool Box is a column dedicated to highlighting algorithms and source code utilized by GPS engineers and scientists. If you have an interesting program or software package you would like to share with our readers, please pass it along; e-mail it to us at gpstoolbox@ngs.noaa.gov. To comment on any of the source code discussed here, or to download source code, visit our website at http://www.ngs.noaa.gov/gps-toolbox. This column is edited by Stephen Hilla, National Geodetic Survey, NOAA, Silver Spring, Maryland, and Mike Craymer, Geodetic Survey Division, Natural Resources Canada, Ottawa, Ontario, Canada.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Roesler, C., Larson, K.M. Software tools for GNSS interferometric reflectometry (GNSS-IR). GPS Solut 22, 80 (2018). https://doi.org/10.1007/s10291-018-0744-8
Published:
DOI: https://doi.org/10.1007/s10291-018-0744-8