Cylindrical overbounding for quadratic integrity monitors with non-Gaussian inputs

Abstract

We develop tools for conservatively approximating the missed-detection probability of quadratic integrity monitors, commonly used for safety-critical navigation, for example, in the signal deformation monitor for global positioning system satellites. A derivation is presented that guarantees that a cylindrical overbounding approach conservatively approximates the true worst-case missed-detection probability for a quadratic monitor. A simulation study demonstrates that the cylindrical overbound is a relatively accurate bound, with mild overconservatism, within 5% of the correct answer for two-dimensional vector spaces with moderate-sized faults. Overconservatism increases somewhat for high-dimensional vector spaces and large fault-induced biases.

Appendices

Appendix 1: Example warping function

The idea of transforming, or warping, one distribution into another distribution is a well-understood concept in probability theory. Warping can be used, for example, to convert a set of samples created by a uniform random number generator into a set of samples characterized by an entirely different PDF, such as a χ ² PDF.

A useful principle in converting one distribution to another is to match their CDFs (Ludeman 2003). The matching process integrates two PDFs to obtain CDFs and finds the arguments that result in matching probabilities. For example, consider a pair of two-dimensional, spherically symmetric PDFs: an exponential PDF $p_{e} \left( {\mathbf{x}} \right)$ and a Gaussian PDF $p_{g} \left( {\mathbf{y}} \right)$.

$$\begin{aligned} p_{e} \left( {\mathbf{x}} \right) = \frac{1}{{2\pi L^{2} }}e^{{ - \tfrac{1}{L}\left\| {\mathbf{x}} \right\|}} \hfill \\ p_{\text{g}} \left( {\mathbf{y}} \right) = \frac{1}{{2\pi \sigma^{2} }}e^{{ - \tfrac{1}{{2\sigma^{2} }}\left( {{\mathbf{y}}^{T} {\mathbf{y}}} \right)}} \hfill \\ \end{aligned}$$

(27)

Here, the parameter L is the scaling parameter for the exponential distribution, and the parameter σ is the standard deviation of the Gaussian distribution. After converting to polar coordinates with r _e the radius for the exponential and r _g the radius for the Gaussian, both PDFs can be decomposed into a product of a uniform marginal PDF, $p\left( \theta \right) = \tfrac{1}{2\pi }$, and a radial conditional PDF, either p _e(r _e|θ) or p _g(r _g|θ), where

$$\begin{aligned} p_{\text{e}} \left( {r_{\text{e}} |\theta } \right) = \tfrac{1}{{L^{2} }}e^{{\tfrac{{ - r_{\text{e}} }}{L}}} \hfill \\ p_{g} \left( {r_{\text{g}} |\theta } \right) = \tfrac{1}{{\sigma^{2} }}e^{{\tfrac{{ - r_{\text{g}}^{2} }}{{2\sigma^{2} }}}} \hfill \\ \end{aligned}$$

(28)

Integrating both radial conditionals against the radial element of integration in two dimensions gives a probability per unit angle. Now integrate the exponential PDF to a limit R, and integrate the Gaussian PDF to a limit f(R), such that the two integrated probabilities per unit angle are equal.

$$\int\limits_{{r_{e} = 0}}^{R} {p_{\text{e}} \left( {r_{\text{e}} |\theta } \right)r_{\text{e}} {\text{d}}r_{\text{e}} } = \int\limits_{{r_{\text{g}} = 0}}^{f(R)} {p_{\text{g}} \left( {r_{\text{g}} |\theta } \right)r_{g} {\text{d}}r_{\text{g}} }$$

(29)

In the special case of this example, both integrals are analytic, and the above equation can be integrated to give

$$1 - \left( {1 + \frac{R}{L}} \right)e^{{\frac{ - R}{L}}} = 1 - e^{{\frac{{ - f^{2} (R)}}{{2\sigma^{2} }}}}$$

(30)

Solving for f(R) results in the warping function:

$$f(R) = \sigma \sqrt 2 \sqrt {\frac{R}{L} - \ln \left( {1 + \frac{R}{L}} \right)}$$

(31)

This warping function (31) is illustrated in Fig. 6, as the curve labeled N = 2.

Fig. 6

Converting the radial limit for an exponential CDF into an equivalent radial limit for a Gaussian CDF. Different warping functions are shown for spatial dimensions of N = {1,2,4,8}. The dashed reference line is the identity warping function, which maps a Gaussian CDF to itself

Although the derivation of this warping function f(R) was purposefully conducted in two dimensions to ensure the warping function was analytic, a similar warping function can be generated in higher dimensions as well. For instance, in three dimensions, the conditional CDF balance is

$$\int\limits_{{r_{\text{e}} = 0}}^{R} {p_{\text{e}} \left( {r_{\text{e}} |\theta } \right)r_{\text{e}}^{2} {\text{d}}r_{\text{e}} } = \int\limits_{{r_{\text{g}} = 0}}^{f(R)} {p_{\text{g}} \left( {r_{\text{g}} |\theta } \right)r_{\text{g}}^{2} {\text{d}}r_{\text{g}} }$$

(32)

Evaluating both sides to obtain the 3D analogy to (30) gives

$$1 - \left( {1 + \frac{R}{L} + \frac{{R^{2} }}{{2L^{2} }}} \right)e^{{\frac{ - R}{L}}} = 2P_{g1} \left( {\tfrac{f\left( R \right)}{\sigma }} \right) - 1 - \frac{2f\left( R \right)}{{\sqrt {2\pi } \sigma }}e^{{\frac{{ - f^{2} (R)}}{{2\sigma^{2} }}}}$$

(33)

It is not possible to solve Eq. (33) to obtain an analytic solution for f(R), so instead it is necessary to use an interpolation process to relate f(R) to R. Because an analytic form is not feasible, it is preferable to integrate (5) numerically, particularly in higher dimensions, where the analogy to (30) and (33) is expansive. The numeric approach, moreover, works on any distribution, so that other candidate distributions can easily be substituted for p _e when a numerical solution is applied.

For the sake of comparison, a numerical solution was used to obtain the warping function f(R) relating the exponential distribution to the Gaussian distribution for dimensions up to N = 8. A subset of these warping functions is illustrated in Fig. 6, as the curves labeled N = 1 through N = 8. In the figure, the dashed reference line indicates the identity warping function that relates a Gaussian CDF to itself. Not surprisingly, the family of exponential warping functions is all below the reference line, indicating the exponential CDF’s heavy tails.

Appendix 2: Monotonicity of warped radius

This section provides a proof that the warped radius increases monotonically for angles moving toward ϕ ₁ = ϕ _* along the inner threshold surface and for angles moving away from ϕ ₁ = ϕ _* along the outer threshold surface.

Lemma

Consider the surface Λ _w created by warping a hypersphere with radius $\sqrt T$, with center displaced from the origin by b, and with $b > \sqrt T$. The derivative of the warped inner radius f(R _i )with respect to ϕ ₁ is positive, and the derivative of the warped outer radius $\bar{f}(R_{o} )$ with respect to ϕ ₁ is negative. In other words,

$$\frac{{\partial \underline{f} (R_{i} )}}{{\partial \phi_{i} }} \ge 0\,\,\,\,{\text{and }}\,\,\,\frac{{\partial \bar{f}(R_{o} )}}{{\partial \phi_{i} }} \le 0$$

(34)

Proof

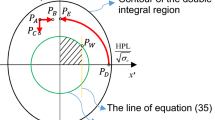
Consider the triangle geometry shown in Fig. 1 (top). From the law of cosines:

$$T = b^{2} + R^{2} - 2Rb\cos \phi_{1}$$

(35)

The ray at any angle ϕ ₁ ≤ ϕ _* intersects the bounding sphere (dashed contour in Fig. 1, top) at two locations. These locations can be obtained by solving the above quadratic equation for R and labeling the two solutions R _i and R _o , corresponding to the distances to the inner and outer intersections points, respectively. Equations for both solutions are given by (11). Equations (11) can be rewritten slightly by substituting (9) to give:

$$\begin{aligned} R_{i} \left( {\phi_{1} } \right) = b\cos \phi_{1} - b\sqrt {\sin^{2} \phi_{*} - \sin^{2} \phi_{1} } \hfill \\ R_{o} \left( {\phi_{1} } \right) = b\cos \phi_{1} + b\sqrt {\sin^{2} \phi_{*} - \sin^{2} \phi_{1} } \hfill \\ \end{aligned}$$

(36)

The limiting angle ϕ ₁ = ϕ _* is a special case where the two intersection points converge to the same location, such that R _i  = R _o . For small perturbations ɛ from the critical angle, such that ϕ ₁ = ϕ _* + ɛ, the small angle approximation for (36) is

$$\begin{aligned} R_{i} \left( {\phi_{1} } \right) = b\cos \phi_{*} - b\sin \phi_{*} \left| {\sin \varepsilon } \right| \hfill \\ R_{o} \left( {\phi_{1} } \right) = b\cos \phi_{*} + b\sin \phi_{*} \left| {\sin \varepsilon } \right| \hfill \\ \end{aligned}$$

(37)

For any small perturbation ɛ → 0, noting that the sine and cosine terms are positive on the range of possible ϕ _* values, it can be concluded by inspection that

$$\begin{aligned} \frac{{\partial R_{i} }}{\partial \varepsilon } \le 0 \hfill \\ \frac{{\partial R_{o} }}{\partial \varepsilon } > 0 \hfill \\ \end{aligned}$$

(38)

To analyze larger perturbations from the critical angle ϕ _*, take the derivative of (35) with respect to ϕ ₁ for fixed b and T:

$$0 = 2R\frac{\partial R}{{\partial \phi_{1} }} - 2b\left( {\frac{\partial R}{{\partial \phi_{1} }}\cos \phi_{1} - R\sin \phi_{1} } \right)$$

(39)

Rearranging terms, it is possible to show that

$$\frac{\partial R}{{\partial \phi_{1} }} = \frac{{ - Rb\sin \phi_{1} }}{{\left( {R - b\cos \phi_{1} } \right)}}$$

(40)

Substituting (36) into (40), gives

$$\frac{{\partial R_{i} }}{{\partial \phi_{1} }} = \frac{{R_{i} \sin \phi_{1} }}{{\sqrt {\sin^{2} \phi_{*} - \sin^{2} \phi_{1} } }}$$

(41)

and

$$\frac{{\partial R_{o} }}{{\partial \phi_{1} }} = - \frac{{\partial R_{i} }}{{\partial \phi_{1} }}$$

(42)

The denominator of (41) diverges at the critical angle ϕ ₁ = ϕ _*, but we have already analyzed the derivative at the critical angle using the small perturbation analysis to obtain (38). For angles other than the critical angle, on the domain $0 \le \phi_{1} < \phi_{*} < \tfrac{1}{2}\pi$, Eq. (41) must be positive because sin ϕ ₁ is positive, sin ² ϕ _* > sin ² ϕ ₁, and R _i is everywhere positive. If (41) is everywhere positive then (42) must be everywhere negative on the domain away from ϕ ₁ = ϕ _*,

$$\begin{array}{*{20}c} {\frac{{\partial R_{i} }}{{\partial \phi_{1} }} \le 0} \\ {\frac{{\partial R_{o} }}{{\partial \phi_{1} }} \ge 0} \\ \end{array} \quad \quad \forall \left\{ {\phi_{1} \left| {0 \le \phi_{1} < \phi_{*} < \tfrac{1}{2}\pi } \right.} \right\}$$

(43)

Now consider the derivatives of the warping functions f(R _i ) and $\bar{f}(R_{o} )$. Using the product rule,

$$\begin{aligned} \frac{{\partial \underline{f} (R_{i} )}}{{\partial \phi_{1} }} = \frac{{\partial \underline{f} (R_{i} )}}{{\partial R_{i} }}\frac{{\partial R_{i} }}{{\partial \phi_{1} }} \hfill \\ \frac{{\partial \bar{f}(R_{o} )}}{{\partial \phi_{1} }} = \frac{{\partial \bar{f}(R_{o} )}}{{\partial R_{o} }}\frac{{\partial R_{o} }}{{\partial \phi_{1} }} \hfill \\ \end{aligned}$$

(44)

The functions f(R _i ) and $\bar{f}(R_{o} )$ increase monotonically with their respective arguments, since the warping functions are compound functions of two monotonically increasing functions: a CDF and an inverse CDF. Hence the derivatives of the warping functions in (44) with respect to their own arguments are positive. Thus, the derivatives in (44) match the sign of the derivatives of the radii with respect to ϕ ₁, which according to (38) and (43) imply that on the domain $0 \le \phi_{1} \le \phi_{*} < \tfrac{1}{2}\pi$,

$$\frac{{\partial f(R_{i} )}}{{\partial \phi_{i} }} \ge 0\,\,\,{\text{and}}\,\,\,\,\frac{{\partial f(R_{o} )}}{{\partial \phi_{i} }} \le 0$$

(45)

QED