Abstract
Strong ionospheric electron content gradients may lead to fast and unpredictable fluctuations in the phase and amplitude of the signals from Global Navigation Satellite Systems (GNSS). This phenomenon, known as ionospheric scintillation, is capable of deteriorating the tracking performance of a GNSS receiver, leading to increased phase and Doppler errors, cycle slips and also to complete losses of signal lock. In order to mitigate scintillation effects at receiver level, the robustness of the carrier tracking loop, the receiver weakest link under scintillation, must be enhanced. Kalman filter (KF)-based tracking algorithms are particularly suitable to cope with the variable working conditions imposed by scintillation. However, the effectiveness of this tracking approach strongly depends on the accuracy of the assumed dynamic model, which can quickly become inaccurate under randomly variable situations. This study first shows how inaccurate dynamic models can lead to a KF suboptimum solution or divergence, when both strong phase and amplitude scintillation are present. Then, to overcome this issue, it proposes two self-tuning KF-based carrier tracking algorithms, which self-tune their dynamic models by exploiting the knowledge about scintillation that can be achieved through scintillation monitoring. The algorithms have been assessed with live equatorial data affected by strong scintillation. Results show that the algorithms are able to maintain the signal lock and provide reliable scintillation indices when classical architectures and commercial ionospheric scintillation monitoring receivers fail.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Under disturbed conditions, turbulences and small-scale irregularities in the ionosphere can constructively and de-constructively interfere with GNSS signals, leading to random and fast variations of signal amplitude and phase (Rino 1979). This phenomenon, known as ionospheric scintillation, is particularly challenging for the carrier tracking stage of a GNSS receiver, the receiver link most sensitive to platform dynamics and signal attenuations. Even if scintillation usually involves just a portion of the sky, it can affect several satellite links at the same time, leading to outages in positioning and navigation. In the case of Ionospheric Scintillation Monitoring Receivers (ISMRs), designed to provide information about ionospheric disturbances by estimating a number of scintillation parameters, a decrease in the tracking performance will translate into poor scintillation monitoring capabilities. This is why ISMRs are usually based on high-grade geodetic receivers, heavily relying on the carrier phase information.
Traditionally the carrier phase is obtained through a closed tracking loop, the phase-locked loop (PLL), which extracts the carrier phase measurements from the signal input. For this purpose, a local carrier replica is generated by the numerical controlled oscillator (NCO) and correlated with the input signal (Kaplan and Hegarty 2006). The correlator outputs are then input into the discriminator, a nonlinear device that estimates the error in the parameters to be tracked. Then the tracking error is filtered by the loop filter and used to adjust the NCO, generating a new carrier replica to minimize the tracking error. The PLL robustness is given by its capability of maintaining the signal lock also in non-nominal conditions, as in the presence of weak signals or high dynamics such as produced by ionospheric scintillation. In order to cope with weak signals, narrow loop bandwidths or longer filter memory is usually employed, whereas with fast signal dynamics one prefers wide loop values or shorter filter memory. Robust GNSS tracking is particularly challenging under equatorial scintillation, which is characterized by canonical fades, namely simultaneous deep signal fading of up to 25 dB and abrupt phase variations (Hinks et al. 2008). If the Doppler shift produced by phase scintillation is wider than the PLL bandwidth, then the tracking stage may not be able to follow the signal fast dynamics, leading to the occurrence of cycle slips or losses of lock. Also weak signals due to amplitude scintillation may bring the signal power below the limit required to maintain the signal tracking. One way to avoid the above design dilemma typical of closed-loop tracking architectures is to use an open-loop architecture; see, i.e., Curran et al. (2014). This architecture does not rely on feedback information and, consequently, does not lose the signal lock, ensuring increased robustness at the cost of a higher complexity. Another possible approach is to replace the PLL with a frequency-locked loop (FLL), which is more robust under harsh situations but also less accurate. When high accuracy is required, the FLL can be used as a backup solution to replace the PLL in case of loss of lock (Fantinato et al. 2012). Alternatively, FLL-assisted PLL techniques can be employed (Xu et al. 2015). They allow estimating the frequency and phase errors which are then combined to adjust the NCO (Chiou et al. 2007). Furthermore, adaptive tracking schemes (Skone et al. 2005) represent a suitable solution to optimize the tracking parameters in the presence of variable GNSS signal conditions. Research has shown that Kalman filter (KF) tracking schemes are particularly useful to cope with fast dynamics and deep fading seen in GNSS signals due to ionospheric scintillation (Macabiau et al. 2012; Psiaki et al. 2007). However, not much work has been done to optimize and tune the KF-based GNSS tracking schemes under scintillation. Indeed, the effectiveness of the KF tracking loop is strictly related to the accuracy of the dynamic model employed, which is usually defined a priori. When the working conditions quickly change over time, the initially assumed dynamic model may be no longer valid, leading to a suboptimum solution or a filter divergence. This study first shows that when very strong phase and amplitude scintillation are simultaneously present, the KF tracking loop can fail if not properly tuned. Then it proposes two self-tuning KF tracking algorithms, which continuously monitor a number of scintillation parameters to adapt their covariance matrix. A first scheme, referred to as scintillation-based adaptive KF (SAKF1), uses the scintillation spectral parameters p (the slope of the phase power spectral density) and T (the spectral strength of the phase noise at 1 Hz) to model the scintillation phase error contribution to its covariance matrix. This algorithm is an extension of the one proposed in Susi et al. (2014a, b), where the KF was used to replace only the PLL filter. In this newly proposed solution, the KF replaces both the DLL and PLL filters. A further variation is introduced in the form of a scaling factor that depends on the filter residuals and is applied to the measurement noise. The second algorithm, referred to as SAKF2, has been proposed to reduce the computation cost of SAKF1. It requires only the simpler computation of the phase scintillation index Phi60. The SAKF2 algorithm first detects the level of phase scintillation and then selects the most suitable dynamic model among four pre-defined options. The algorithms presented herein were implemented as part of a GNSS software receiver and have been assessed by using live equatorial data affected by strong scintillation. As a by-product of this work, an improved algorithm for the computation of scintillation indices has been developed. This algorithm can provide continuous scintillation indices information even when commercial ISMRs fail.
Ionospheric scintillation and its effects on a GNSS receiver
The term scintillation refers to the random modulation of wave signals due to refractive index variation in the propagation medium. When GNSS signals travel through the ionosphere, scintillation may occur due to random electron density fluctuations inside the ionosphere (Rino 1979). Ionospheric scintillation affects mainly polar and equatorial regions. Since the morphology of the ionosphere is different at these two regions, the physical processes determining the occurrence of scintillation are also different. At high latitudes, scintillation is characterized by strong phase fluctuations and weak amplitude variations in the signal, whereas at equatorial regions scintillation can show both significant phase and amplitude fluctuations. This is why the equatorial region, analyzed further in this research, is the most critical for the receiver tracking. A generic GNSS signal affected by scintillation at the receiver input can be modeled as follows
where d(t) is the data sequence modulating the received signal, C′ = CδC with C and δC representing the nominal signal amplitude and the amplitude signal variation due to scintillation, and \(\varphi_{\text{RF}}^{\prime } = \varphi_{\text{d}} + \varphi_{\text{s}} + \varphi_{\text{o}}\) is the phase of the received GPS signal, including the contribution due to satellite and platform dynamics (φ d), phase scintillation (φ s) and other effects such as the oscillator noise (φ o). Also, c(t) is the spreading code and n(t) is the zero-mean additive white gaussian noise (AWGN) with spectral density N 0 (W/Hz).
Conventionally two indices are used to quantify the level of scintillation, namely S4 and σ φ (Van Dierendonck et al. 1993). S4 indicates the level of amplitude scintillation and is computed as the standard deviation of the received power normalized by its mean value, and σ φ quantifies the phase scintillation and is obtained by computing the standard deviation of the detrended carrier phase, averaged over a specific temporal window, which usually corresponds to 1 min of data. The temporal duration of the window used to perform the average defines the version of σ φ . The most used version is 60 s, referred to as Phi60. Scintillation affects the receiver tracking loop by increasing the signal noise and by increasing the phase error. The power spectral density (PSD) of the phase error due to scintillation can be modeled as in Rino (1979), by the following inverse power law
where T is the spectral strength of the phase noise at 1 Hz and p is the spectral slope of the phase PSD, f is the frequency of phase fluctuations, f 0 is the frequency of the maximum irregularity size present in the ionosphere. Assuming that f ≫ f 0, Eq. (2) can be approximated by S δφ (f) = Tf −p (Conker et al. 2003). The PSD of the scintillation can be related to Phi60 by the following nonlinear expression (Aquino et al. 2007),
where the lower limit of the integration is given by the cutoff frequency of the detrending filter, generally set equal to 0.1 Hz, while the upper limit is given by half of the sampling frequency, which is usually equal to 50 Hz for the commercial ISMRs case.
Linear KF-based tracking loop
The continuous GPS signal in (1), after being received by the GNSS receiver antenna, is then amplified, filtered, down converted to an intermediate frequency (IF) and sampled by the front-end. The resulting signal can be expressed by:
where \(\varphi_{\text{IF }}^{\prime }\) is the carrier phase of the received signal at IF and T ADC is the sample period. The signal is then processed by the acquisition stage providing a rough estimate of the initial Doppler shift and pseudorandom noise (PRN) code phase. After the acquisition, the tracking stage has the purpose to refine the coarse estimates of carrier phase and code phase, providing also an estimate of the carrier frequency. Conventional GNSS receivers generally employ two concatenated tracking loops to estimate the signal parameters. The delay-locked loop (DLL) is used to track delay variations while a PLL or/and an FLL allow estimating phase and frequency variations.
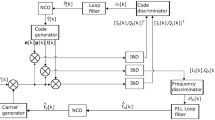
Kalman filtering offers several advantages under harsh tracking conditions when carrier phase information is continuously required. Indeed, a KF allows minimizing the mean square error (MSE) of the tracking filter by exploiting a dynamic and a statistical model to predict and estimate the parameters of interest representing the filter states. In this work, to design an optimum tracking scheme, a KF has also been used to replace both DLL and PLL filters. The KF state vector which is the minimum information necessary to describe the system time evolution (Brown and Hwang 1997) has been defined as an error vector of four parameters. They are the code delay error Δτ, the carrier phase error Δφ, the carrier Doppler frequency shift Δf and the Doppler frequency rate Δa. The state vector at the instant k can be represented as
Once the state vector is determined, the implementation of the KF requires the definition of the system dynamic and the measurements models. The system dynamic model describes the state evolution over time and allows predicting the (k + 1)th state vector at the instant t k . Then, the measurement model is exploited to correct the above prediction through the evaluation of the actual measurements. The system dynamic model is defined as
where A k is the transition matrix
with β representing the factor used to convert cycles in units of code chips and T s indicating the time of integration. The term \(\varvec{w}_{k} \;\sim\;N\left( {0,\varvec{Q}_{k} } \right)\) in Eq. (6) is an additive zero-mean and uncorrelated Gaussian noise process vector. Q k is the discrete transition noise covariance matrix which models the processes noises affecting the states. The measurement model can be defined following two main approaches. The first methodology is to directly use the correlator output as measurements. In this case, the relationship between measurements and parameters to be estimated is highly nonlinear and the KF replaces both discriminators and loop filters. To cope with this nonlinearity, an extended KF (EKF) should be used (O’Driscoll et al. 2011). The alternative approach adopted in this study is to use the discriminator output as measurements so that the KF replaces only the loop filters. The carrier and code discriminators provide an estimate of the phase and code errors over the time of integration, indicated, respectively, as \(\overline{\delta \varphi }\) and \(\overline{\delta \tau }\) herein. The measurement model is so described
where \(\varvec{z}_{k} = \left[ {\begin{array}{*{20}c} {\overline{\delta \varphi } } \\ {\overline{\delta \tau } } \\ \end{array} } \right]\) and H k is the observation matrix describing the relationship between measurements and filter states and so defined:
In Eq. (8), v k \(\sim\;N\left( {0,\varvec{R}_{k} } \right)\) indicates a zero-mean and uncorrelated Gaussian noise process uncorrelated with w k , where R k is the covariance matrix of the measurement noise. Assuming the code and the carrier measurements as independent, the matrix R k can be represented as a diagonal matrix whose elements are the variances of the carrier and code discriminator output σ 2 δφ and σ 2 δτ ,
For their pull-in range performance cost and effectiveness at low C/N 0 (Del Peral-Rosado et al. 2010), the early minus late envelope and the four-quadrant arctangent have been selected as code and carrier discriminators. The carrier and code measurement variances for the above discriminators are given by
where d is the code delay, and c/n 0 is the carrier-to-noise ratio given by \(10^{{0.1C/N_{0} }}\), with C/N 0 continuously computed as in Kaplan and Hegarty (2006). Once the linear dynamic and measurements models are defined, the KF can be implemented by applying the recursive prediction and correction steps summarized by the following equations (Brown and Hwang 1997):
Prediction steps
where \(\hat{\varvec{x}}_{k + 1}^{ - }\) is the a priori state estimated computed by projecting the state estimate through the transition matrix \(\varvec{A}_{k + 1}\) and \(\varvec{P}_{{\varvec{k} + 1}}^{ - }\) is the a priori estimated covariance matrix obtained by projecting the error covariance ahead.
Correction steps
\(\varvec{K}_{k}\) is the four-element vector of the KF gains, weighting the error between the real measurements and the predicted ones. The KF gains are then exploited to estimate the state a posteriori estimate \(\hat{\varvec{x}}_{\varvec{k}}\) by including the measurement \(\varvec{z}_{\varvec{k}}\) in the a priori state estimate, as shown by (16). The a posteriori estimate of the covariance matrix can be obtained from its a priori estimate by applying (17). Finally, the discrepancy between actual and estimated measurements is indicated as residual and computed as
The adaptive nature of the KF is given by the variation of the above gains. If the measurements are very noisy, the gains are lowered to down-weight the measurements contribution, which is unreliable. Otherwise, if the measurements are not noisy, the gain values increase indicating more reliable measurements. The KF equivalent filter bandwidth can be estimated by these gains as shown in Tang et al. (2015). Indeed, in steady state, when the KF gains reach constant values, the KF is equivalent to a discrete filter with same order and equivalent bandwidth. The design of the KF requires a careful selection of the process noise covariance matrix Q and the measurement noise matrix R. In a standard KF tracking architecture, these matrices are fixed a priori. Traditionally, in order to define the above matrices, the dominant error contributions are taken into account as in Macchi-Gernot et al. (2010). Under the assumption of uncorrelated noise sources Q, which is the continuous version of Q k in (14), can be defined as a diagonal matrix with the diagonal elements given by the spectral densities of each processes noise \(\left[ {\begin{array}{*{20}c} {S_{\Delta \tau } } & {S_{\Delta \varphi } } & {S_{\Delta f} } & {S_{\Delta a} } \\ \end{array} } \right]\). The relationship between continuous and discrete domain can be found in Macchi-Gernot et al. (2010). S Δτ represents the power spectral density of the carrier/code divergence, which is produced by propagation through the ionosphere. S Δφ and S Δf , the power spectral densities of the expected error on the phase and frequency, are conventionally considered due to the receiver oscillator error, which is assumed to be the dominant error source. The spectral densities of the clock bias and drift can be computed as (Brown and Hwang 1997)
where h 0 and h −2 depend on the type of oscillator and f L1 is the frequency of the GPS L1 signal here considered. Typical values of these parameters for different types of oscillators can be found in Brown and Hwang (1997). S Δa is the spectral density of the expected phase acceleration which is mainly driven by the dynamics along the line of sight between receiver and satellite. For this work, the receiver is assumed to be stationary or with low dynamics, and therefore, user motion and related effects were not modeled.
Covariance matrix tuning under scintillation
Even when the assumed dynamics do not correspond to reality due to variations in the GNSS signal working conditions, the KF may still continue the state estimation process. However, if these variations are too strong and the discrepancy between the model and the actual dynamics is too big, the KF could lead to a wrong solution or diverge. For instance, scintillation could cause quick and random variations beyond the tolerance limit of the filter, which, consequently, may lead to the a priori fixed noise model being no longer valid. Therefore, in this study, the scintillation noise contribution is continuously estimated and included in the definition of the process noise. Clearly, under severe scintillation the ionospheric contribution should be no longer neglected. Especially in the case of ISMRs, where low-noise oscillators are generally used to capture the phase variations due to ionospheric scintillation, the ionospheric error contribution can be higher than the oscillator’s. Therefore, the spectral densities of the process noise related to the phase and the frequency errors are computed as
In Eqs. (21) and (22), the sum operation is valid because the receiver oscillator and the scintillation noise contributions are independently generated by different physical processes. The scintillation phase noise power spectral density can be estimated as S Δφscint(f) = Tf −p by using the approximation introduced above. The frequency noise PSD is derived by the phase noise PSD as S Δfscint = f 2 S Δφscint (Chiou et al. 2007), where f represents the frequency corresponding to the ionospheric irregularity size, which is set equal to 0.19 Hz. This is a suitable value for the equatorial scintillation cases (Forte and Radicella 2002) analyzed herein. The proposed KF tracking schemes adapt their covariance matrix according to the working conditions determined by the level of detected scintillation. SAKF1 continuously monitors T and p and exploits these parameters to self-tune its covariance matrix. SAKF2 first detects the level of phase scintillation by monitoring Phi60 and then according to the level of phase scintillation selects a dynamic model among four a priori defined ones. The models correspond to absent, weak, moderate and severe scintillation cases.
The \(S_{\Delta \tau }\) and \(S_{\Delta \tau }\) elements in the covariance matrix for each of the above cases were defined by using values of p and T obtained experimentally and reported in Table 1. The approach is justified by the theoretical relationship between Phi60, p and T defined in (3). \(S_{\Delta \tau }\) and S Δa are kept constant and modeled as in Macchi-Gernot et al. (2010).
Measurement noise matrix tuning
In order to tune the measurement noise according to the signal intensity, the C/N 0 is estimated as in Van Dierendonck et al. (1993) and used to estimate the discriminator variance output in Eqs. (11) and (12). In this way, the KF gains, and consequently the loop equivalent bandwidth, change according to the signal intensity. In case of signal fading, the loop noise is decreased to filter out as much as possible the noise affecting the signal parameter estimation. However, there could be cases when, even if C/N 0 is low, the bandwidth should not be too much decreased to follow the fast signal dynamics due to phase scintillation. To further enhance the robustness of the measurement noise estimation, a weighting factor is applied to the measurement noise matrix. The measurement noise matrix is estimated as suggested by Yang and Gao (2006), in order to make the actual value of the covariance of residuals as close as possible to its theoretical value. The covariance of residuals, averaged within a fixed window M to reduce the noise, can be defined as:
where M has been empirically selected equal to 10 samples so to allow averaging the noise without removing useful information.
The theoretical covariance is given by
Considering that the predicted innovation covariance should match the one computed by the innovation values, any discrepancy between the two covariance matrices should be attributed to a mismodeling of P or/and R. It can be shown (Yang and Gao 2006) that, assuming Q as properly defined, the degree of mismatch between the theoretical and the actual covariance can be compensated by multiplying R by a scaling factor
with \(\alpha_{k} = \frac{{{\text{trace}}\left( {\varvec{C}_{\varvec{k}} } \right)}}{{{\text{trace}}\left( {\bar{\varvec{C}}_{\varvec{k}} } \right)}}\).
The general structure of the SAKF1 and SAKF2 algorithms is reported in Fig. 1. It is shown how the parameters p, T and C/N 0 are computed by dedicated blocks, and fed into the KF replacing the traditional PLL and DLL filters. SAKF1 directly estimates p and T, while SAKF2 selects them from a set of a priori defined values according to the detected Phi60 values.
Experimental setup and results
The performance of the proposed algorithms has been assessed using real data affected by equatorial scintillation. The data, provided by the Joint Research Centre of the European Commission, has been collected by installing a radio-frequency (RF) data acquisition system based on a Universal Software Radio Peripheral (USRP) N200 in Hanoi, Vietnam. In its nominal architecture, the USRP includes a temperature-controlled crystal oscillator (TCXO), which is not optimal for scintillation monitoring. Indeed, to capture the phase fluctuations due to scintillation it is necessary to minimize the clock error contribution by using a low phase noise clock. Consequently, an external 10 MHz rubidium oscillator has been used to drive the front-end. The data were collected at 5 M samples/s in the L1/E1 band each day after sunset local time in order to monitor the peak of the ionospheric disturbances. Then, through a replay process of the USRP logged data, scintillation indices and 50 Hz in-phase (I) and in-quadrature (Q) samples, were obtained from a commercial ISMR used as benchmark. A data set affected by strong scintillation, collected on April 16, 2013, has been selected for the SAKF1 and SAKF2 algorithm assessment. The skyplot for this data set is shown in Fig. 2, while the amplitude and phase scintillation indices, S4 and Phi60, are reported in Figs. 3 and 4, respectively.
For the selected data set, 10 satellites are available, of which 6 are affected by scintillation.
To assess the algorithms, four satellite links with different levels of scintillation have been selected. They are SV1, SV7, SV8, and SV28. As shown in Figs. 3 and 4, SV1 is affected by moderate/strong amplitude scintillation and weak phase scintillation while SV7 and SV8 are affected by both very strong amplitude and phase scintillation. Finally, apart from the first 2 min, SV28 is almost scintillation-free. This satellite has been selected to observe the algorithm performance also under quiet conditions. For SV7, namely the satellite link affected by the most severe scintillation level, no Phi60 values are provided by the commercial ISMR from minute 6–11. This is due to temporary losses of lock on the aforementioned receiver, which induce the phase detrending filter to reset, producing, as a consequence, gaps in the output Phi60. Indeed, it takes up to four minutes for this filter to converge. Consequently, to ensure reliable and continuous scintillation monitoring capabilities the losses of lock and cycle slips must be minimized.
The IF data have been processed by using the different tracking architectures detailed in Table 2. They are:
-
Conventional tracking schemes with fixed bandwidth;
-
The proposed SAKF1 and SAKF2; and
-
Conventional adaptive KF tracking schemes, indicated as AKF1 and AKF2.
AKF1 is a classical adaptive KF tracking with Q a priori fixed, as in Macchi-Gernot et al. (2010), and with the elements of R obtained as in (11) and (12). AKF2 has the same characteristics as AKF1, but additionally, it applies the scaling factor to R as shown by Eq. (25). AKF2 has been included to assist in better analyzing the single contribution given by tuning the covariance matrix and the measurement noise to the performance improvement.
In order to compare the tracking performance of the above algorithms, the phase jitter for SV7 was selected as an example case because this satellite was affected by the most severe level of scintillation. The computed result is shown in Fig. 5. The phase jitter, namely the standard deviation of the phase discriminator output, has been computed over temporal windows of 4 s. As it can be seen in Fig. 5, SAKF1 and SAKF2 show the best performance in terms of phase jitter reduction. On the other hand, AKF1 shows poor performance and indeed, after the minute 7 the AKF1 model fails, leading to various losses of lock occurring when the phase jitter is over 15°, which is the 1 sigma phase error threshold for the carrier phase tracking commonly used for commercial GNSS receivers. Due to bad modeling, the AKF1 shows even worse performance than the traditional tracking with fixed bandwidth and T s = 20 ms.
Finally, SAKF1 and SAKF2 outperform also the commercial ISMR. The two algorithms achieve very close performance, but at the minute 10, the SAKF2’s phase jitter goes above the 15° tracking threshold while in the SAKF1 case, the phase jitter is never above the tracking limit.
In Fig. 6, Phi60 and the strength of the phase scintillation spectrum at 1 Hz (T) for SV7, computed by the SAKF1 to adjust the KF covariance matrix, are shown.
It is interesting to observe the clear correlation between the two parameters over time. Both parameters, as well as the slope of the phase scintillation spectrum p, have been computed by using 1-min sliding windows updated at each time of integration (T s ). T has been estimated by evaluating the PSD of the detrended accumulated carrier phase FFT at 1 Hz. The parameter p has been estimated by computing the slope of a straight line obtained by a linear fit to the detrended accumulated carrier phase PSD (Aquino et al. 2007). It is worth underlining that the use of sliding windows provides various advantages if compared with the non-overlapping windows generally exploited by commercial ISMRs. First of all, it allows catching fast variations of the estimated parameter, and then, it offers an increased robustness due to the higher number of estimated samples.
To assess the carrier tracking performance of the algorithms, the phase lock indicator (PLI) has also been computed. This tracking indicator, which is proportional to the cosine of twice the phase error, is estimated by exploiting in-phase (I) and in-quadrature (Q) components as
where M has been selected equal to 100 samples.
A value of PLI below 0.86 corresponds to a phase error larger than the threshold of 15°, representing the tracking limit. In Fig. 7, the percentages of PLI samples below 0.86 are shown for the various tracking algorithms for SV1, SV7, SV8 and SV28. SAKF1 and SAKF2 achieve the best performance for the satellites affected by both strong phase and amplitude scintillation, namely for SV7 and for SV8. In the case of SV1, where the amplitude scintillation is dominant, the performances of the KF-based algorithms and also of the commercial receivers are very close.
To better quantify the advantage of using the proposed algorithms, Table 3 demonstrates the improvement percentages in terms of reduction in the occurrence of PLI samples below 0.86, achieved by the SAKF1 algorithm with respect to the other tracking schemes. It is clear that SAKF1 outperforms all the other classical tracking schemes in the presence of strong scintillation. Finally, as shown in the last column of Table 3, SAKF1 performs slightly better than the SAKF2 algorithm but at cost of a higher computational cost. Indeed, SAKF2 allows avoiding the spectrum parameters p and T computation which require the estimation of the phase PSD through the application of the computational demanding fast Fourier transform (FFT).
The Doppler shift, shown in Fig. 8 for all algorithms, allows comparing the tracking performance in terms of agility in following the signal dynamics.
All KF-based tracking schemes outperform the classical fixed bandwidth PLL/DLL in terms of Doppler noise reduction. Moreover, a loss of lock for the scheme with fixed bandwidth and T s = 10 ms can be observed around minute 10 in the time series. In Fig. 9, the mean values of the Doppler shift standard deviations, computed over the observation period, are reported for SV1, SV7, SV8 and SV28. In this case, all KF-based tracking schemes achieve close values, outperforming the algorithms with fixed bandwidth.
By applying the approach in Tang et al. (2015), the equivalent carrier bandwidth for SV7, the satellite link affected by the strongest level of scintillation, is reported in Fig. 10 for AKF1, SAKF1, SAKF2. It is worth underlining that 4 min is required to the SAKF1 and SAKF2 to start computing the parameters necessary to tune their dynamic models. After the fourth minute, the effect of the dynamic model adjustment is reflected in the increase of the bandwidth values with respect to the values of AKF1. For SAKF2, the variations in the bandwidth values are less marked due to the use of the four pre-defined dynamic models. Both SAKF1 and SAKF2 increase their equivalent bandwidth to achieve higher agility in following the dynamics when the phase variation is stronger, thanks to the fact that the covariance matrix includes the phase scintillation contribution. At the same time, the deep fading in the bandwidth values shows also the good response of SAKF1 and SAKF2 to the C/N 0 variations. On the contrary, the AKF1 bandwidth values are much lower due to the fact that it is only adjusted according to the C/N 0 variations. These lower values do not allow following the signal dynamics producing lower tracking performance in the presence of strong phase scintillation.
Furthermore, the correlator outputs and the accumulated phase obtained by the proposed tracking schemes have been used to compute the scintillation indices S4 and Phi60 as in Van Dierendonck (1993). As an example, the scintillation indices computed for SV7 are shown in Fig. 11 along with their counterparts provided by the high-grade commercial ISMR used as benchmark. The S4 values obtained by the KF tracking schemes are in good agreement with the values provided by the commercial ISMR. Due to temporary losses of lock, the commercial ISMR shows data gaps in the Phi60 values. Figure 11 (bottom plot) shows the comparison for Phi60 between the commercial ISMR and the implemented tracking schemes.
The first 4 min of data is missing since this is the convergence time of the filter used to estimate Phi60.
For the implemented tracking schemes, the Phi60 is computed by a 1-min sliding window at every integration time, while for standard commercial ISMRs the computation is performed on non-overlapping windows. The use of sliding windows allows increasing the number of available samples within the period making the algorithm more robust to temporary losses of lock. Indeed, if there is not a sufficient number of samples for the convergence of the filter necessary to the Phi60 computation, the filter will need to be reset producing data gaps in the Phi60, as visible in Fig. 11 in the case of the commercial ISMR.
The Phi60 values for AKF1, SAKF1 and SAKF2 shown are actually an average of the Phi60 values computed during 1 min and presented at the end of each minute. As shown in Fig. 11, in this way it is possible to get continuous information on Phi60 not only for SAKF1 and SAKF2, which present higher tracking performance, but also for AKF1, which, on the contrary, experiences several losses of lock. Although for AKF1 more losses of lock occurred than for the ISMR, by computing Phi60 using sliding windows, the scintillation monitoring capabilities of the algorithms are not affected and no Phi60 samples are missed.
Conclusions
It has been shown how a classical a priori fixed dynamic model KF tracking algorithm can fail under strong phase and amplitude variations associated with ionospheric scintillation. Two KF-based tracking schemes (SAKF1 and SAKF2) have been proposed. They self-tune their covariance matrices according to the detected level of scintillation and self-adapt their measurement noise model to cope with simultaneous phase and amplitude variations. SAKF1 requires a continuous computation of phase scintillation spectral parameters, whereas SAKF2 selects the dynamic model for the specific case from a set of a priori defined options according to the detected Phi60 values. SAKF2 allows achieving performance comparable to SAKF1 while reducing the computational cost. Both algorithms outperform the classical adaptive KF, traditional PLL/DLL tracking algorithms with fixed bandwidth and even a high-grade commercial ISMR when severe amplitude and phase variations occur simultaneously. It has also been shown that by computing phase scintillation indices using sliding windows, it is possible to get a higher number of samples, reducing the probability of having data gaps in the Phi60 computation when losses of lock occur. This approach allows achieving scintillation monitoring performance capabilities higher than with the commercial ISMR used as benchmark.
References
Aquino M, Andreotti M, Dodson A, Strangeways H (2007) On the use of ionospheric scintillation indices as input to receiver tracking models. Adv Space Res 40(3):426–435. doi:10.1016/j.asr.2007.05.035
Brown RG, Hwang PY (1997) Introduction to random signal and applied Kalman filtering, 3rd edn. Wiley, New York
Chiou T, Gebre-Egziabher D, Walter T, Enge P (2007) Model analysis on the performance for an inertial aided FLL-assisted-PLL carrier-tracking loop in the presence of ionospheric Scintillation. In: Proceedings of ION-NTM-2007, Institute of Navigation, San Diego, CA, USA, Jan 22–24, pp 1276–1295
Conker RS, El-Arini MB, Hegarty CJ, Hsiao T (2003) Modelling the effects of ionospheric scintillation on GPS/satellite-based augmentation system availability. Radio Sci 38(1):1001. doi:10.1029/2000RS00260
Curran JT, Bavaro M, Fortuny J (2014) An open-loop vector receiver architecture for GNSS-based scintillation monitoring. In: Proceedings of European Navigation Conference (ENC-GNSS), Rotterdam, pp 1–12
Del Peral-Rosado JA, Lopez-Salcedo G, Seco-Granados JM, López-Almansa J (2010) Kalman Filter based architecture for robust and high-sensitivity tracking in GNSS receivers. In: Proceedings of the satellite navigation technologies and European Workshop on GNSS signals and signal processing, (NAVITEC), 2010 5th ESA Workshop, Noordwijk, pp 1–8
Fantinato S, Rovelli D, Crosta P (2012) The switching carrier tracking loop under severe ionospheric scintillation. In: Proceedings of the satellite navigation technologies and European Workshop on GNSS signals and signal processing, (NAVITEC), 2012 6th ESA Workshop, Noordwijk, pp. 1–6
Forte B, Radicella SM (2002) Problems in data treatment for ionospheric scintillation measurements. Radio Sci 37(6):1096. doi:10.1029/2001RS002508
Hinks JC, Humphreys TE, O’Hanlon BW, Psiaki ML, Kintner PM (2008) Evaluating GPS receiver robustness to ionospheric scintillation. In: Proceedings of ION GNSS 2008, Institute of Navigation, Savannah, Georgia, September 16–19, pp. 309–320
Kaplan ED, Hegarty C (2006) Understanding GPS principles and applications, 2nd edn. Artech House, Norwood
Macabiau C, Barreau V, Valette JJ, Artaud G, Ries L (2012) Kalman filter based robust GNSS signal tracking algorithm in presence of ionospheric scintillations. In: Proceedings of ION GNSS 2012, Institute of Navigation, Nashville, TN, September 17–21, pp 1–8
Macchi-Gernot F, Petovello MG, Lachapelle G (2010) Combined acquisition and tracking methods for GPS L1 C/A and L1C signals. Int J Navig Obs, Article ID 190465. doi:10.1155/2010/190465
O’Driscoll C, Petovello MG, Lachapelle G (2011) Choosing the coherent integration time for Kalman filter-based carrier-phase tracking of GNSS signals. GPS Solut 15(4):345–356
Psiaki M, Humphreys T, Cerruti AC, Powell S, Kintner P (2007) Tracking L1 C/A and L2C signals through ionospheric scintillations. In: Proceedings of ION GNSS 2007, Institute of Navigation, Fort Worth, TX, pp 246–248
Rino CL (1979) A power law phase screen model for ionospheric scintillation: 1. Weak scatter. Radio Sci 14(6):1135–1145. doi:10.1029/RS014i006p01135
Skone S, Lachapelle G, Yao D (2005) Investigating the impact of ionospheric scintillation using a GPS software receiver. In: Proceedings of ION-GNSS-2005, Institute of Navigation, Long Beach, CA, USA, Sept 13–16, pp 1126–1137
Susi M, Andreotti M, Aquino M (2014) Kalman filter based PLL Robust against ionospheric scintillation, mitigation of ionospheric threats to GNSS: an appraisal of the scientific and technological outputs of the TRANSMIT project. Dr. Riccardo Notarpietro (ed), ISBN: 978-953-51-1642-4, InTech. doi:10.5772/58769
Susi M, Aquino M, Romero R001, Dovis F, Andreotti M (2014) Design of a robust receiver architecture for scintillation monitoring. In: Proceedings of PLANS 2014, Institute of Navigation, May 5–8, Monterey, California, USA, pp 73–81
Tang X, Falco G, Falletti E, Lo Presti L (2015) Theoretical analysis and tuning criteria of the Kalman _filter-based tracking loop’’. GPS Solut 19(3):489–503
Van Dierendonck AJ, Klobuchar J, Hua Q (1993) Ionospheric scintillation monitoring using commercial single frequency C/A code receivers. In: Proceedings of ION GPS-93, Institute of Navigation, Salt Lake City, UT, pp 1333–1342
Xu R, Zhizhao L, Chen W (2015) Improved FLL-assisted PLL with in-phase pre-filtering to mitigate amplitude scintillation effects. GPS Solut 19(2):263–276. doi:10.1007/s10291-014-0385-5
Yang Y, Gao W (2006) An optimal adaptive Kalman filter. J Geod 80(4):177–183
Acknowledgements
The authors wish to thank Joaquim Fortuny (Joint Research Centre) for providing the real data affected by scintillation used in this work. This research work is undertaken under the framework of the TRANSMIT ITN funded by the Research Executive Agency within the 7th Framework Program of the European Commission, People Program, Initial Training Network, Marie Curie Actions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Susi, M., Andreotti, M., Aquino, M. et al. Tuning a Kalman filter carrier tracking algorithm in the presence of ionospheric scintillation. GPS Solut 21, 1149–1160 (2017). https://doi.org/10.1007/s10291-016-0597-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10291-016-0597-y