Abstract
The study presents the influence of strong total electron content (TEC) fluctuations occurring at high latitudes on rapid static positioning. The authors propose an algorithm mitigating the impact of dynamic temporal changes in electron content using the rate of TEC corrections. It consists of modifying the observations using the measured rate of TEC variations and hence allows reducing the number of parameters to one ionospheric delay of a reference epoch per satellite and per session. An analysis was carried out for a typical quiet day in solar minimum on September 6, 2009 and a disturbed day during high solar activity on March 17, 2013. For a standard geometry-based relative model with weighted ionosphere and troposphere, the results confirmed the dramatic drop of ambiguity resolution efficiency during a violent space weather event. The results obtained for the new algorithm, however, demonstrate its wide applicability and a 10-fold improvement in ambiguity success rate during the disturbed day.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The global navigation satellite system (GNSS) positioning is currently one of the fastest developing measurement techniques, having applications in daily life and scientific research, including wide usage in navigation and surveying (Teunissen et al. 2011; Popielarczyk and Templin 2014). In most cases, which involve both real-time and post-processing applications, positions can be determined with subcentimeter accuracy in relative mode. The feasibility of obtaining such precision is strongly associated with the processing algorithms used and biases that affect observations. One of the most crucial factors that deteriorate the precision of GNSS positioning is refraction of radio waves in the ionosphere. Due to the correlation of ionospheric parameters and ambiguity parameters, the mitigation of the former is essential for good integer ambiguity resolution performance. On the other hand, the inter-frequency relationship of the ionospheric delay allows for monitoring the state of the ionosphere. In comparison with other techniques, the worldwide network of GNSS receivers allows global monitoring of total electron content (TEC) with subdaily resolution (Komjathy et al. 2005; Hernandez-Pajares et al. 2009 and references therein). Corresponding research limited to a specified area is also conducted with GNSS data for many regional or national networks (Wielgosz et al. 2008; Jakowski et al. 2011; Bergeot et al. 2014).
Precise relative GNSS positioning is most frequently performed with dual-frequency pseudorange and phase observations. This allows the application of advanced positioning algorithms, using both raw observations and linear combinations. The applied methodology for precise positioning depends predominantly on the length of the baseline and the observing session and is mainly connected with ionospheric conditions. In precise relative positioning, the ionospheric delay can be neglected for short baselines of up to several kilometers (Kleusberg 1986). In this case, double-differenced (DD) ionospheric delays do not deteriorate integer ambiguity resolution since they are small in comparison with GNSS signal wavelengths. With regard to medium and long baseline positionings, the algorithms depend on session length. At this point, it should be noted that dual-frequency observations allow elimination of the first order of ionospheric refraction through the ionosphere-free combination. On the other hand, the resulting ambiguity term is no longer an integer value, and this solution can be considered only as float one (Hofmann-Wellenhof et al. 2001).
Post-processing applications usually cover relatively long time spans and are often characterized by baseline lengths of several hundred kilometers. For such applications, two strategies are generally implemented to mitigate the impact of ionosphere. The first one is based on two linear combinations of the dual-frequency data: wide line and ionosphere-free (Blewitt 1989). In this strategy, the first combination is used for fixing the wide-line ambiguity, which constitutes the basis for searching the narrow-line L 1 ambiguity. With regard to reliable code measurements, the wide-line observations can be replaced by the Hatch–Melbourne–Wübbena linear combination (Hatch 1982; Melbourne 1985; Wübbena 1985). The second algorithm is termed quasi-ionospheric-free (QIF) ambiguity resolution strategy and was implemented in Bernese GPS Software (Mervart 1995; Dach et al. 2007). The ambiguity searching process minimizes the difference between the real values of ambiguities retrieved from ionospheric-free observations and the analyzed pairs of their integer equivalents. Both strategies are widely applied in the processing of global or regional networks (Ge et al. 2005; Steigenberger et al. 2006).
In recent years, fast positioning has become a major GNSS application. Therefore, the scientific community has put extensive effort into the development of new algorithms for ionospheric delay mitigation in precise rapid positioning. These advances have led to the development of a geometry-based ionosphere-weighted model supported with network-derived ionospheric corrections (Teunissen 1997; Odijk 2000a, b; Julien et al. 2004; Hu et al. 2005; Wielgosz 2010; Paziewski and Wielgosz 2014). This approach, often performed in the multi-baseline mode, allows reliable positioning even up to several tens of kilometers. Unfortunately, the feasibility of ambiguity resolution in precise positioning is still related to the state of the ionosphere and can be affected by ionospheric disturbances of different scales (Wielgosz et al. 2005; Jacobsen and Schäfer 2012; Lejeune et al. 2012). Thus, ionospheric refraction mitigation is still an open problem in precise positioning. Here, we introduce a new approach allowing for the mitigation of high ionospheric disturbances in precise positioning. The methodology of this new approach relies on the correction of raw dual-frequency observations using rate of TEC (ROT) formulae. The application of ROT corrections allows the ionosphere-weighted functional model to be modified through a reduction in epoch-varying ionospheric parameters to just a single parameter. Positioning tests were performed at high latitudes, where strong TEC fluctuations are observed (Sieradzki 2015; Cherniak et al. 2014).
The next section is devoted to the analysis of ionospheric conditions and their impact on GNSS observations. It starts from a global view of TEC fluctuations around the North Geomagnetic Pole, goes through the view of ionospheric conditions observed at collocated stations, and finally demonstrates the differences in ionospheric delays at specified epochs. We then introduce the details of ROT corrections algorithm together with a modified ionosphere-weighted functional model for precise positioning. Subsequently, performance analysis of the proposed methodology for precise rapid static positioning is presented. The last section contains conclusions and future research.
Detection of TEC fluctuations using GNSS observations
The GNSS-based monitoring of ionospheric disturbances is usually performed using parameters of signal phase or amplitude variability. In the case of receivers collecting observations with 30-s interval, the information on TEC fluctuations is retrieved from geometry-free linear combination
where λ 1 and λ 2 correspond to the signal wavelengths, φ 1 and φ 2 are the carrier phase observations for satellite m and station k at epoch i. The L 4 function (1) contains only an ionospheric delay \(I_{{k,4,t_{i} }}^{m}\) and phase ambiguities \(N_{{k,1,t_{i} }}^{m}\) and \(N_{{k,2,t_{i} }}^{m}\):
where \(I_{{k,4,t_{i} }}^{m}\) equals the difference in ionospheric delays on respective phase observations
The difference in L 4 over consecutive epochs i and j, denoted by \(\widetilde{\text{ROT}}_{k}^{m}\), constitutes a change in the ionospheric delay for satellite m at station k, provided that the ambiguities are constant. For our application, the following equation is given in the units of meters,
According to (4), it is possible to detect the relative fluctuations of TEC for a specific satellite. It should be noted that in the case of ionospheric research, ROT is usually expressed in TECU/min,
The intensity of TEC fluctuations is usually described with the rate of TEC index (ROTI) proposed by Pi et al. (1997). This parameter is defined as standard deviation of ROT values in a 5- to 10-min time span and refers to TEC fluctuations caused by the presence of ionospheric irregularities.
The ROT and ROTI parameters are used in our study to demonstrate the ionospheric conditions during quiet and disturbed periods. For testing purposes, 2 days were chosen, September 6, 2009 and March 17, 2013. The first day corresponds to typical conditions during an exceptionally long minimum of the solar activity cycle. The second day represents the response of the circumpolar ionosphere to the coronal mass ejection (CME) which hit the earth magnetic field at 6:00 UTC, on March 17, 2013. During this period, a moderate geomagnetic storm was observed (Kp = 6). In order to present the global difference between the intensity of TEC fluctuations for both days, observations were processed from about 180 stations, participating in different networks or projects (EUREF Permanent Network, International GNSS Service and Plate Boundary Observatory; Bruyninx 2004; Dow et al. 2009). Figure 1 presents the distribution of ROTI values around the North Geomagnetic Pole as a function of geomagnetic latitude and magnetic local time (MLT). More information on the used algorithm can be found in Sieradzki et al. (2013). The results clearly demonstrate the difference in latitudinal range of the irregularities oval and amplitudes of TEC fluctuations registered by GNSS permanent stations. The ionospheric disturbances for the quiet conditions were observed above 78°N and 70°N of geomagnetic latitude, on the dayside and the nightside, respectively (Fig. 1, top). During the active geomagnetic conditions, the outside boundaries were detected correspondingly at 65°N and 60°N. It implies that the presented effect could strongly affect the functionality of GNSS networks in Scandinavian and Canadian sectors (Fig. 1, bottom).
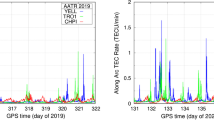
In the context of precise relative positioning, the most important feature of the ionosphere that deteriorates ambiguity fixing is the TEC gradient between simultaneous GNSS observations. It is related to the amplitude of TEC changes. The results retrieved for the disturbed day show that ROTI values often reach 2 TECU/min or even more. For an example for a quiet day, the typical ROTI values equal 0.3–0.5 and 0.1–0.3 TECU/min on the dayside and nightside, respectively. In order to demonstrate a more useful analysis in the context of precise positioning, Fig. 2 shows 1-min ROT values calculated using data from stations HJOR, LYNS, TREO, and KBUG (Table 1) for both days analyzed; the same data were subsequently used in a positioning test. The stations are located at about 72°N and 46°E geomagnetic latitude and longitude, respectively. The figure depicts the changes in TEC observed for each satellite separately. The zero level of TEC fluctuations for each satellite is defined as a horizontal line passing through the corresponding PRN on the left Y-axis. For quiet ionospheric conditions (left), the retrieved results were close to 0, excluding the short time span between 04:00 and 05:00 UTC. This means that the outside boundary of the oval was located at higher latitudes, and the results of the positioning tests should not be affected by the ionosphere. The changes in TEC observed during the disturbed day (right) are strongly amplified. In this case, ROT values even reached 5 TECU/min, which corresponds to 0.8 m of L 1 signal delay and practically disenables robust ambiguity fixing. The initial phase of ionospheric response can be easily identified in the ROT time series, and it is well correlated with the CME arrival time. The strongest changes in electron content were observed for 08:00–10:00 and 16:00–18:00 UTC. Considering the ionospheric conditions and its monitoring with 1-h time span, one can observe the high correlation between the dynamic changes at the individual stations. The similarity of ROT graphs for all stations is evident. However, in the context of relative positioning, the difference between the ionospheric delays observed in different stations at a same epoch is most crucial.
The geometry-free linear combination (2) was used in order to capture the absolute values of ionospheric delay fluctuations at each station. Its changes directly correspond to the impact of ionosphere provided that the ambiguity parameters are constant. Due to the individual character of the ambiguity terms, the comparison of results obtained for each receiver must be preceded by a levelling process. In the case of monitoring ionospheric disturbances, this process usually consists of filtering or differencing (Wautelet and Warnant 2014; Hernández-Pajares et al. 2011). We used the differences between the individual geometry-free values and their minimal value observed in the time span analyzed for a specified receiver. The first results (Fig. 3, top two panels) demonstrate the impact of the ionosphere on measurements of GPS satellites PRN 26 and 30 during the quiet day. The curves for the different receivers have practically the same shape, and more importantly, the difference between them is close to 0. The magnification of the worst cases shows a discrepancy level of 0.02 and 0.06–0.07 m for satellite PRN 26 and 30, respectively. During the disturbed day, the ionospheric fluctuations between consecutive epochs were very dynamic (bottom two panels). The comparison of TEC time series retrieved from different stations demonstrates the complex nature of the ionosphere at high latitudes. The strong discrepancies are highly visible for the entirety of the periods. Generally, the observed effects are twofold. The first one is depicted as a systematic shift between values obtained for selected stations. The shift is characterized by a relatively long time span (10 min or more). Typical examples of this effect are those observed for satellite 12, station KJOR during 17:40–18:40 UTC, or for the same satellite and station KBUG in the period 19:00–19:25 UTC. The shifts in these cases are about 0.4 and 0.3 m. The second effect is associated with ionospheric irregularities, clearly visible in the zoomed rectangles. They lead to the permanent occurrence of a strong discrepancy between total ionospheric delays at specified stations. The amplitude of this highly variable effect can reach 0.5 m. Precise relative positioning is practically impossible in such conditions without any advanced algorithms to reduce the impact of ionosphere.
Precise positioning in the presence of ionospheric fluctuations
The presented study clearly suggests the challenge for obtaining reliable, fast GNSS positioning at high latitudes depending on the state of the ionosphere. The following section will introduce an approach which allows for substantial mitigation of the impact of ionospheric disturbances on rapid positioning. Furthermore, the performance of the new approach is compared to the geometry-based ionosphere-weighted model in different ionospheric conditions.
Functional model of precise positioning
The starting point for precise positioning is the geometry-based relative model with weighted ionosphere. The initial research was conducted by Teunissen (1997) and Odijk (2000a, b). Since the details may be found in several publications (Julien et al. 2004; Wielgosz 2010; Paziewski and Wielgosz 2014), only a brief description is presented here.
In precise relative positioning, we can distinguish between two approaches for ionospheric delay parametrization: ionosphere-fixed model and ionosphere-float model. In case of the former, the DD ionospheric delays are not estimated as parameters in the adjustment. The second approach—ionosphere-float model—relies on parametrization of the ionospheric delays, although without introduction of a priori information about the value of delay. The ionosphere-weighted model can be treated as the generalized approach of the ionospheric parametrization. In this model, the DD ionospheric delays are treated as stochastic parameters. The a priori values of the DD ionospheric corrections are weighted in the adjustment, i.e., the a priori DD ionospheric delays are considered pseudo-observations (Odijk 2002).
The geometry-based relative model with weighted ionosphere and troposphere relies on a double-difference dual-frequency observations and pseudo-observations. The equations are
The subscripts k, l and superscripts m, n denote stations and satellites, respectively. The observations are the DD carrier phase φ and pseudorange P. In addition, we have the geometric range ρ, the zenith tropospheric delays ZTD at the station, the troposphere mapping function coefficient α, the integer phase ambiguities N, the ionospheric delay I, and the carrier frequency f.
Additionally, the described model is supplemented with pseudo-observations, which allow imposing of constraints on selected parameters through the a priori variance factors. The pseudo-observations for ionospheric and tropospheric parameters can be written as follows:
In this equation, I mn kl and ZTD k are estimated parameters. The right side of (7) represents a priori values of DD ionospheric delays \(I_{kl}^{mn\prime }\) and tropospheric delays at specific stations \({\text{ZTD}}_{k}^{\prime }\). These values can be derived from any external sources or result from appropriate assumptions. In this study, the a priori values of DD ionospheric delays were set to zero. In the case of tropospheric delays, the constraints are applied to estimated residual zenith tropospheric delays after correction by an empirical model.
The above functional model was implemented in the in-house developed GNSS processing software (Paziewski 2012, 2015). In this implementation, the model parameters are estimated with the least squares adjustment with a priori parameter constraints (Leick 2004; Xu 2007). The ionosphere and troposphere parameter weights correspond to the accuracy of the tropospheric and ionospheric a priori values. In the composition of the weight matrix, all mathematical correlations between the observations are taken into account. The MLAMBDA algorithm is applied for ambiguity resolution (Chang et al. 2005). The UNB3m model is used for a priori tropospheric delays computations (Leandro et al. 2008).
Rate of TEC corrections algorithm
Standard ionosphere-weighted approach implies treating stochastic ionospheric parameters as epoch-varying. In the new approach, the ionospheric corrections based on the ROT are used in order to eliminate the variations in DD ionospheric delay between epochs. According to (4), \(\widetilde{\text{ROT}}_{k}^{m}\) represents a change in the ionospheric delay on the L 4 signal \(I_{{k,4,t_{ji} }}^{m}\) between two epochs i and j for satellite m as long as no-cycle slips occur. The derived change can be converted to a corresponding one for the base signal L 1 as:
Applying this correction to phase and pseudorange observations at epoch i results in identical ionospheric delays at both epoch i and j,
As a consequence, the modified observations \(\widetilde{L}_{{k, 1,t_{i} }}^{m}\) and \(\widetilde{P}_{{k, 1,t_{i} }}^{m}\) at epoch i are affected by ionospheric delay originally present in observations at epoch j (\(I_{{k,1,t_{j} }}^{m}\)).
Correspondingly, all measurements for a specific arc of observations can be corrected, and as a result, they all contain the same ionospheric delay, which was originally at epoch j. Thus, considering the modified observations, we have \(\widetilde{{\Delta I}}_{{k, 1,t_{ji} }}^{m} = 0\) between any two epochs i and j. Similarly, one can calculate the observations related to the L 2 signal. Since the undifferenced GNSS signals are characterized by a constant ionospheric delay, albeit still unknown, the DD observations used in precise relative positioning are biased with a constant unknown ionospheric delay as well. As a result, the new DD ionospheric delays are session-dependent parameters, and the influence of strong TEC fluctuations is eliminated. The other advantage of the proposed algorithm is the feasibility of choosing a different reference epoch for each satellite in the entire session to minimize the ionospheric term in DD phase equations. It should be mentioned that this approach does not eliminate all the ionospheric delay. After applying the corrections, the observations are biased by a new constant ionospheric delay which may not be the smallest in relation to the original epoch-dependent delay. In this study, the levelling process was performed using the minimal values of the geometry-free combination for each session, which can be considered as the most probable approximation of relatively stable background TEC values. The results shown in the next section prove that this way is efficient; however, finding the optimal reference epoch for each satellite is still under consideration.
An example of an effect introduced by the rate of TEC corrections (RTC) algorithm into the phase equations is presented in Fig. 4. The top panel shows DD ionospheric delays obtained from the geometry-free solution with fixed ambiguities. These values can be regarded as “true” DD ionospheric delays which deteriorate GNSS positioning reliability and are present in both the DD carrier phase and pseudorange observations. They were computed for the TREO–LYNS baseline of 59 km during strong ionospheric fluctuations occurrence (March 17, 2013). The top panel depicts high DD ionospheric variability reaching over ±0.75 m observed at original observations. The bottom figure presents the same DD ionospheric delays after applying the developed algorithm to the original observations in 10-min sessions. It can be clearly seen that in each session, the DD ionospheric delays are reduced to a constant value.
This confirms the legitimacy of our approach of treating the DD ionospheric delays as constant parameter per session for each observation arc. It can also be observed that the proposed algorithm is particularly efficient in the case of short peaks of ionospheric delays. Regarding the aforementioned two effects detected in the geometry-free time series (Fig. 3), the application of RTC corrections should allow for a significant mitigation of impact connected with different scale irregularities. The stable shift between TEC observed at collocated stations cannot be eliminated in such a way.
Precise positioning performance
The impact of strong ionospheric disturbances on standard and improved positioning algorithms was analyzed for 2 days, characterized by different ionospheric conditions. The performance of the new RTC algorithm was evaluated and compared to the performance of the standard ionosphere-weighted approach. In particular, two processing strategies were applied:
-
1.
Ionosphere-weighted model (IW approach);
-
2.
ROT correction algorithm with enhanced ionosphere-weighted model (RTC approach).
Both approaches were applied for fast static positioning in multi-baseline mode. In specific, 10-min-long sessions with 30-s interval were processed. Thus, every 10 min, the session was reinitialized and resolved independently. The elevation mask was set at a level of 15°. In order to test the network in fairly quiet ionospheric conditions, the analysis for the first day (September 6, 2009) was limited to the time of 06:00–18:00 UTC. It allowed the retrieval of the true level of positioning precision indicators in the absence of ionospheric irregularities.
For testing purposes, we used GPS data from four stations located in Greenland. Stations KBUG, TREO, and HJOR served as reference stations, and station LYNS served as a user rover receiver. The baselines length ranged from 59 to 122 km (Fig. 5). The approximate coordinates of the stations are presented in Table 1. The maximal height difference is observed at baseline HJOR–LYNS and reaches 591 m. All stations were occupied by Trimble NETRS with TRM29659.00 antenna.
Due to the very intensive TEC fluctuations during the disturbed day, it was impossible to obtain solution with correctly fixed ambiguities in the reference network processing. Thus, no network ionospheric corrections were generated and used in the rover solution. For ionospheric pseudo-observables, the variance factors of 15 cm were introduced. These values were adopted on the basis of empirical studies (Wielgosz et al. 2005). A priori values of the zenith tropospheric delays obtained from UNB3m model were constrained with 1-cm variance factor.
Several performance indicators for ambiguity resolution and coordinate domains were analyzed. In specific, the standard deviations and mean coordinate residuals served as indicators of quality of positioning. These residuals were based on the repeatability of the rover solution in relation to the reference coordinates. The ratio of sessions with correctly resolved ambiguities with respect to the number of all processed sessions—ambiguity success rate (ASR)—served as an indicator of ambiguity resolution performance.
Table 2 presents the statistics of the rapid static positioning performed with both approaches for quiet and disturbed days. The coordinate statistics were calculated on the basis of fixed ambiguity solutions. During the selected 12 h for the quiet day, the results for the introduced strategies are comparable in both ambiguity resolution and coordinate domains. The ambiguity resolution success rate reached 93.1 % for both strategies. Similar values of coordinates bias and precision indicators were observed as well. The standard deviations of the rover coordinates reached 0.3, 0.2, 1.0 cm for N, E, U in both cases. Thus, it can be concluded that the new approach has no visible impact on positioning results during quiet ionospheric conditions.
The results obtained for the second day are characterized by strong discrepancies between both approaches. Their comparison, summarized in Table 2, shows a significant improvement in the ambiguity resolution domain in the case of the RTC algorithm. The application of the reference IW model produced the ASR parameter at a level of only 6.3 %. Thus, the performance of precise positioning in such conditions can be regarded as very poor. On the other hand, we obtained an almost 10-fold improvement in the ratio of successfully resolved sessions for the RTC algorithm. In this strategy, the ASR reached 59.0 %. While this value is lower than during the quiet day, the algorithm has proven its usage and applicability for the mitigation of strong TEC fluctuations. It can be also seen that the residual effect of disturbed ionospheric conditions has affected the bias and precision indicators, which is clearly visible in the height component. One can observe more than 1 cm shift in the means of height between both approaches and worse precision obtained for the RTC algorithm. However, it should be noted that these indicators were computed only for fixed sessions. Hence, the dynamic ionospheric conditions, which make the ambiguity solution impossible in the reference IW model, did not influence the results in this case.
The left panel of Fig. 6 presents the spatial distribution of horizontal coordinates and time series of the vertical component obtained for both strategies during the quiet day. It confirms a good agreement between the approaches and proves that RTC corrections do not exert any substantial effect on the reliability of the standard IW model. The right panel presents the corresponding distribution of GNSS positioning performance for the disturbed day. According to the indicators summarized in Table 2, the RTC results are characterized by more significant deviations observed for all coordinates. These strong discrepancies are primarily observed during intensive TEC fluctuations and can be treated as their residual effect. In addition, the time series of the height component clearly demonstrate that after the impact of CME (06:00 UTC), no session was fixed using the standard IW strategy. The worse performance of this approach can be observed for the first hours (00:00–04:00 UTC), also affected by ionospheric disturbances (Fig. 2). In the case of the RTC algorithm, the problems with ambiguity fixing were mainly detected for the highly disturbed period 08:00–10:00 UTC.
In order to test the efficiency of both algorithms in the ambiguity domain, the cumulative solution was also analyzed. The application of the developed RTC algorithm results in the growth of correctly resolved sessions from about 20 to 59 % with extending session length from 1 to 20 epoch cumulative solution. It should be noted that except for two epoch sessions, the progression in ASR can be observed, and the correct solution is not lost. On the other hand, the strong TEC fluctuations distort the ionosphere-weighted model solution so seriously that even the ASR ratio decreases with session duration (Fig. 7).
Summary and conclusions
A new algorithm for mitigating the impact of TEC fluctuations on precise relative positioning was proposed. It assumes the modification of raw observations using the ROT corrections and ensures that the ionospheric delay variations can be leveled to the reference epoch. The elimination of temporal TEC fluctuations allows treating the ionosphere parameters as constant during the entire session in the ionosphere-weighted positioning model.
The applicability of the algorithm was evaluated on the basis of static multi-baseline positioning performed for different ionosphere conditions. During a quiet day, the ionosphere-weighted model and its proposed modification provide almost the same results. With regard to the disturbed period, the occurrence of strong TEC fluctuations makes ambiguity fixing for the standard positioning algorithms practically impossible (the ambiguities were fixed in only 6.3 % of the sessions). The comparison of GNSS positioning reliability during the quiet and disturbed days clearly depicts the scale of possible effects introduced by electron content disturbances at high latitudes. The application of the proposed RTC algorithm resulted in a significant improvement of the ambiguity resolution success rate of almost 10 times on the disturbed day. However, the comparison of results for quiet and disturbed ionospheres (ASR equals 93.1 and 59.0 %, respectively) shows that the applied corrections do not eliminate the entire impact of the ionosphere. Furthermore, the analysis demonstrates that with the no-cycle-slip condition, the solution is stable, which led to the continuous increase in ASR depending on session length. On the other hand, it should remembered that such a highly active ionosphere leads to frequent cycle slips, and this aspect may need further investigation.
The developed algorithm can be also applied to longer sessions as well. The major advantage of the new approach is the leveling of temporal changes in ionospheric delay to one selected epoch. Thus, the future research will focus on choosing this reference epoch, which should improve the efficiency of ASR and shorten the time for fixing the ambiguities as well.
Finally, the promising statistics of GNSS positioning supported by the ROT corrections suggests the applicability of the proposed approach for other regions (mid and low latitudes) and processing strategies.
References
Bergeot N, Chevalier J-M, Bruyninx C, Pottiaux E, Aerts W, Baire Q, Legrand J, Defraigne P, Huang W (2014) Near real-time ionospheric monitoring over Europe at the Royal Observatory of Belgium using GNSS data. J Space Weather Space Clim. doi:10.1051/swsc/2014028
Blewitt G (1989) Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km. J Geophys Res 94(10):187–283. doi:10.1029/JB094iB08p10187
Bruyninx C (2004) The EUREF Permanent Network: a multi-disciplinary network serving surveyors as well as scientists. GeoInformatics 7:32–35
Chang X-W, Yang X, Zhou T (2005) MLAMBDA: a modified LAMBDA method for integer least-squares estimation. J Geod 79(9):552–565. doi:10.1007/s00190-005-0004-x
Cherniak I, Krankowski A, Zakharenkova I (2014) Observation of the ionospheric irregularities over the Northern Hemisphere: methodology and service. Radio Sci. doi:10.1002/2014RS005433
Dach R, Hugentobler U, Fridez P, Meindl M (2007) Bernese GPS software version 5.0, user guide. Astronomical Institute, University of Bern
Dow JM, Neilan RE, Rizos C (2009) The international GNSS service in a changing landscape of global navigation satellite systems. J Geod 83(3–4):191–198. doi:10.1007/s00190-008-0300-3
Ge M, Gendt G, Dick G, Zhang FP (2005) Improving carrier-phase ambiguity resolution in global GPS network solutions. J Geod 79:103–110. doi:10.1007/s00190-005-0447-0
Hatch R (1982) The synergism of GPS code and carrier measurements. In: Proceedings of the third international symposium on satellite doppler positioning at Physical Sciences Laboratory of New Mexico State University. Feb. 8–12, vol 2, pp 1213–1231
Hernandez-Pajares M, Juan JM, Sanz J, Orus R, Garcia-Rigo A, Feltens J, Komjathy A, Schaer SC, Krankowski A (2009) The IGSVTEC maps: a reliable source of ionospheric information since 1998. J Geod 83(3–4):263–275. doi:10.1007/s00190-008-0266-1
Hernández-Pajares M, Miguel J, Sanz J, Aragón-Àngel À, Garcia-Rigo A, Salazar D, Escudero M (2011) The ionosphere: effects, GPS modeling and the benefits for space geodetic techniques. J Geod 85(12):887–907. doi:10.1007/s00190-011-0508-5
Hofmann-Wellenhof B, Lichtenegger H, Collins J (2001) Global positioning system: theory and practice, 5th edn. Springer, Berlin
Hu G, Abbey DA, Castleden WE, Earls C, Ovstedal O, Weihing D (2005) An approach for instantaneous ambiguity resolution for medium- to long-range multiple reference station. GPS Solut 9(1):1–11. doi:10.1007/s10291-004-0120-8
Jacobsen KS, Schäfer S (2012) Observed effects of a geomagnetic storm on an RTK positioning network at high latitudes. J Space Weather Space Clim. doi:10.1051/swsc/2012013
Jakowski N, Mayer C, Hoque MM, Wilken V (2011) Total electron content models and their use in ionosphere monitoring. Radio Sci. doi:10.1029/2010RS004620
Julien O, Alves P, Cannon ME, Lachapelle G (2004) Improved triple-frequency GPS/Galileo carrier phase ambiguity resolution using a stochastic ionosphere modeling. In: Proceedings of ION-NTM-2004, Institute of Navigation, San Diego, California, pp 441–452
Kleusberg A (1986) Ionospheric propagation effects in geodetic relative GPS positioning. Manuscr Geod 11:256–261
Komjathy A, Sparks L, Wilson BD, Mannucci AJ (2005) Automated daily processing of more than 1000 ground-based GPS receivers for studying intense ionospheric storms. Radio Sci. doi:10.1029/2005RS003279
Leandro RF, Langley RB, Santos MC (2008) UNB3m_pack: a neutral atmosphere delay package for GNSS. GPS Solut 12(1):65–70
Leick A (2004) GPS satellite surveying, 3rd edn. Wiley, New Jersey
Lejeune S, Wautelet G, Warnant R (2012) Ionospheric effects on relative positioning within a dense GPS network. GPS Solut 16(1):105–116. doi:10.1007/s10291-011-0212-1
Melbourne WG (1985) The case for ranging in GPS based geodetic systems. In: Proceedings of the 1st international symposium on precise positioning with the global positioning system, US Department of Commerce, Rockville, Maryland, pp 373–386
Mervart L (1995). Ambiguity resolution techniques in geodetic and geodynamic applications of the global positioning system. Ph.D. thesis. Astronomical Institute, University of Berne Switzerland
Odijk D (2000a) Stochastic modelling of the ionosphere for fast GPS ambiguity resolution. In: Proceedings of Geodesy beyond 2000: the challenges of the first decade, IAG General Assembly, Birmingham, UK, July 19–30, vol. 121, pp 387–392. doi: 10.1007/978-3-642-59742-8_63
Odijk D (2000b) Improving ambiguity resolution by applying ionosphere corrections from a permanent GPS array. Earth Planets Space 10(52):675–680
Odijk D (2002) Fast precise GPS positioning in the presence of ionospheric delays. Ph.D. dissertation, Publications on Geodesy, 52, Netherlands
Paziewski J (2012) New algorithms for precise positioning with use of Galileo and EGNOS European satellite navigation systems. Ph.D. dissertation, University of Warmia and Mazury in Olsztyn (in Polish)
Paziewski J (2015) Precise GNSS single epoch positioning with multiple receiver configuration for medium-length baselines: methodology and performance analysis. Meas Sci Technol 26(3):035002. doi:10.1088/0957-0233/26/3/035002
Paziewski J, Wielgosz P (2014) Assessment of GPS+ Galileo and multi-frequency Galileo single-epoch precise positioning with network corrections. GPS Solut 18(4):571–579. doi:10.1007/s10291-013-0355-3
Pi X, Mannucci AJ, Lindqwister UJ, Ho CM (1997) Monitoring of global ionospheric irregularities using the worldwide GPS network. Geophys Res Lett. doi:10.1029/97GL02273
Popielarczyk D, Templin T (2014) Application of integrated GNSS/hydroacoustic measurements and GIS geodatabase models for bottom analysis of Lake Hancza: the deepest inland reservoir in Poland. Pure Appl Geophys 171(6):997–1011. doi:10.1007/s00024-013-0683-9
Sieradzki R (2015) An analysis of selected aspects of irregularities oval monitoring using GNSS observations. J Atmos Sol-Terr Phy 129:87–98. doi:10.1016/j.jastp.2015.04.017
Sieradzki R, Cherniak Iu, Krankowski A (2013) Near-real time monitoring of the TEC fluctuations over the northern hemisphere using GNSS permanent networks. Adv Space Res. doi:10.1016/j.asr.2013.03.036
Steigenberger P, Rothacher M, Dietrich R, Fritsche M, Rülke A, Vey S (2006) Reprocessing of a global GPS network. J Geophys Res. doi:10.1029/2005JB003747
Teunissen PJG (1997) The geometry-free GPS ambiguity search space with a weighted ionosphere. J Geod 71(6):370–383. doi:10.1007/s001900050105
Teunissen PJG, Giorgi G, Buist PJ (2011) Testing of a new single-frequency GNSS carrier-phase attitude determination method: land ship and aircraft experiments. GPS Solut 15(1):15–28. doi:10.1007/s10291-010-0164-x
Wautelet G, Warnant R (2014) Climatological study of ionospheric irregularities over the European mid-latitude sector with GPS. J Geod 88(3):223–240. doi:10.1007/s00190-013-0678-4
Wielgosz P (2010) Quality assessment of GPS rapid static positioning with weighted ionospheric parameters in generalized least squares. GPS Solut 15(2):89–99. doi:10.1007/s10291-010-0168-6
Wielgosz P, Kashani I, Grejner-Brzezinska DA (2005) Analysis of long-range network RTK during severe ionospheric storm. J Geod 79(9):524–531. doi:10.1007/s00190-005-0003-y
Wielgosz P, Krankowski A, Sieradzki R, Grejner-Brzezińska DA (2008) Application of predictive regional ionosphere model to medium range RTK positioning. Acta Geophys 56:1147–1161. doi:10.2478/s11600-008-0059-1
Wübbena G (1985) Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements. In: Proceedings first international symposium on precise positioning with the global positioning system, US Department of Commerce, Rockville, Maryland, pp. 403–412
Xu G (2007) GPS: theory, algorithms and applications, 2nd edn. Springer, Berlin
Acknowledgments
The authors are grateful for GNSS data provided by International GNSS Service, EUREF Permanent Network, and UNAVCO.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sieradzki, R., Paziewski, J. Study on reliable GNSS positioning with intense TEC fluctuations at high latitudes. GPS Solut 20, 553–563 (2016). https://doi.org/10.1007/s10291-015-0466-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10291-015-0466-0