Abstract
This paper demonstrates a geometry-free GNSS measurement analysis approach and presents results of single frequency GPS, EGNOS and GIOVE short and zero baseline measurements. The purpose is to separate the different contributions to the measurement noise of pseudo range code and carrier phase observations at the receiver. The influence of multipath on the different combinations of observations is also determined. Quantitative results are presented for the thermal code and phase measurement noise and for the correlation between the observations. Comparison of the results with theoretical approximations confirms the validity of the used approach. Results from field measurements clearly show less thermal noise on the Galileo E1BC observations than on the GPS L1C/A observations due to the new signal modulation. The feasibility of ambiguity resolution with a geometry-free model is also discussed including the significant impact of multipath thereon.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
This paper compares several methods, using the geometry-free model, to analyze thermal measurement noise on the code and phase observations as well as the effects of multipath. Also the feasibility of integer carrier phase ambiguity resolution with the geometry-free model is explored. The analysis techniques are demonstrated with recently collected short baseline (SB) and zero baseline (ZB) multi-constellation GNSS measurements including the Galileo test satellites GIOVE A and B. This research is opportunity driven as these are some of the earliest datasets collected in the field with both GIOVE A and B.
Measurement campaign
On the 6th and 10th of July 2008 a short and zero baseline were measured, respectively, with two identical Septentrio AsteRx1 single frequency receivers with Galileo enabled firmware. The SB was measured, in a fairly benign radio environment, in a field near Delft with virtually no obstacles within a radius of a few kilometers. The receivers were connected to two identical Septentrio PolaNt survey antennas that were placed equally oriented on tripods at 4 m distance from each other. More details can be found in Tiberius et al. (2008). The ZB was measured on a flat roof in Delft on top of a four story building with both receivers connected through a signal splitter to a single Septentrio PolaNt antenna. Sky visibility on the roof was unobstructed down to the horizon, but due to the roof significant multipath effects occurred. The multipath mitigation technique of the receivers was not applied during this measurement campaign. Table 1 summarizes important properties of the antennas and receivers.
During the measurement campaign GPS, EGNOS (European Geostationary Navigation Overlay Service) and Galileo satellites were tracked by the receivers with a measurement rate of 1 Hz. A minimum of eight GPS satellites were visible during the entire measurement period. Galileo, the European GNSS, so far has two test satellites in orbit: GIOVE A and B (indicated in the graphs by E32 and E31, respectively). Both GIOVE satellites were visible simultaneously for over 1.5 h during the SB measurements and for over 2.5 h during the ZB measurements. The E1BC signal from the GIOVE satellites was tracked with a pure Binary Offset Carrier BOC(1,1) replica, not multiplexed BOC (for GIOVE-B), but the corresponding loss is less than 1 dB (Hein et al. 2006). The GIOVE satellites did not transmit usable navigation messages during the measurement campaign. EGNOS, the European space-based augmentation system, uses three geostationary satellites of which two were tracked during the measurement campaign (S120 and S126). Figures 1 and 2 show the sky plots for the short and zero baseline measurements, respectively.
Table 2 summarizes important properties of the tracked signals. It is important to note that the geostationary EGNOS satellites by definition move very little with respect to a stationary receiver on Earth, so the multipath delay also changes very little. The received signal strength is different for the three systems. However, as all results in this paper are presented with respect to a carrier-to-noise density ratio (C/N0) of 45 dB-Hz, this does not influence the conclusions.
Observation equations
The equations for single frequency observations of one satellite expressed in units of range are:
with C the pseudo range code observation, L the carrier phase observation, \( \left| {\left| {x^{\text{s}} - x_{\text{r}} } \right|} \right| \) the geometric range, c the speed of light, δt r the receiver clock error, δt s the satellite clock error, T the tropospheric delay, I the ionospheric delay, MP C the code multipath, MP L the phase multipath, λ the carrier wavelength, A the phase ambiguity, ξ C the instrumental code delay, ξ L the instrumental phase delay, ε C and ε L random code and phase measurement errors, respectively, with expectation equal to zero (E{ε} ≡ 0).
Geometry-free model
At the time of the measurement campaign there was no publicly available GIOVE orbit data with sufficient accuracy. Therefore, the so-called geometry-free model was used for this early analysis (see, e.g., Odijk 2008). In the geometry-free model the first four terms (\( \left| {\left| {x^{\text{s}} -x_{\text{r}} } \right|} \right| + c\delta t_{\text{r}} - c\delta t^{\text{s}} + T \)) at the right-hand side of (1) are equal for all observables and can be denoted by g:
To visualize the influence of different conditions, receiver performance is often shown versus the satellite elevation. In this paper the measured C/N0 is used instead, because the received signal strength is different for each GNSS. For comparison, the C/N0 versus satellite elevation is presented in Figs. 3 and 4 for the short and zero baseline, respectively. The elevation of the GIOVE satellites was computed from NASA two-line elements. For GPS the C/N0, presented in the figures for both receivers at the baseline, is averaged over all satellites. The variation of the C/N0 with elevation is mainly due to the receiver antenna gain pattern and multipath. Other influences are the distance to the satellite, the satellite antenna gain pattern and the atmospheric losses. The transmitted power of individual GPS satellites can also differ slightly. The differences between the short and zero baseline results are due to the different multipath environments. The ZB measurements show multipath that slowly changes with satellite elevation. This could be a result of a reflective surface, in this case the roof, very close to the antenna. The antenna was mounted only 0.1 m above the roof. The SB measurements show multipath that changes more rapidly with satellite elevation. This could be a result of a reflective surface, in this case the ground, further away from the antenna. The figures clearly show that, for the same elevation, the measured C/N0 for one component of the GIOVE E1BC signal is 3–4 dB-Hz lower than for the GPS C/A signal. This effect is mainly due to the specified received power, which is lower for the GIOVE signal component than for the GPS C/A signal and the actual transmitted power of the GPS satellites that tends to be above specifications.
Code-minus-phase
A linear combination that can be used to determine the code noise is the so-called code-minus-phase:
In this combination, the lumped parameter g (geometric range, receiver and satellite clock and tropospheric delay) is eliminated from the observation equation. The phase noise and phase multipath are assumed to be an order of magnitude smaller than the code noise and code multipath, respectively, and they are consequently neglected.
Stand alone receiver
This section presents two methods to determine the code noise from the code-minus-phase measurements of a single receiver. The first is by fitting a low-order polynomial to the data and then subtracting this polynomial from the data. The second, called time differencing, is by taking the differences between measurements from consecutive epochs.
Low-order polynomial fitting
By fitting a low-order polynomial to the code-minus-phase data, the slowly changing components can be removed from the data. This includes the instrumental delays (Liu et al. 2004), the constant ambiguities, the low frequency multipath and the low frequency ionospheric delay. This leaves twice the high frequency ionospheric delay, the high frequency code multipath and the code noise. The expectation E and dispersion D of the code-minus-phase observations are:
where p(t) is the low-order polynomial, σ C the standard deviation of the code measurement noise, dI and dMP C are the residual ionospheric and multipath delay, respectively. The polynomial is estimated from many data points and hence its uncertainty can be neglected in the dispersion of (4). The top pane of Fig. 5 shows the code-minus-phase combination in blue and the fitted polynomial in red for GPS PRN18 and the bottom pane shows the measured C/N0. The periodic effect that is clearly visible in both panes is most likely caused by multipath. PRN18 was selected for its distinct multipath pattern, but other satellites show similar results. The figure shows that the polynomial does not follow the multipath variations and consequently the multipath is not removed when the polynomial is subtracted from the code-minus-phase observations.
Stand alone receiver code-minus-phase observations for GPS PRN18 on SB (top undifferenced; middle time differenced; bottom measured C/N0). Both the undifferenced observations and the measured C/N0 show a periodic effect, most likely caused by multipath. The time differenced observations do not show these delays, but the variance of the noise changes with the C/N0
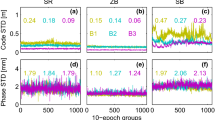
The standard deviation of the code-minus-phase observations after subtraction of the polynomial is presented in Fig. 6 versus the measured C/N0 for each GNSS. Each data point represents 120 epochs. For each GNSS the mean standard deviation of the observations for a C/N0 of 45 dB-Hz is estimated by fitting a line to the data that describes the standard deviation as a function of the measured C/N0. The slope of these lines follows from the inversely proportional relation between the C/N0 (as ratio-Hz) and the variance of the noise (see, e.g., Braasch and van Dierendonck 1999) and fits well with the data. These results together with results from other analysis techniques are also provided in Table 3 (there called 1Rx-UD short for single Receiver Undifferenced). It is clear that the GIOVE satellites perform better than the GPS satellites for the same measured C/N0, because of the different signal modulation. The EGNOS satellites show a larger standard deviation than both the GPS and GIOVE satellites, mainly due to the smaller transmit bandwidth.
Time difference
In the difference between two epochs, the phase ambiguity is removed and the ionospheric delay, multipath and instrumental delays are reduced. The expectation and dispersion of the time differenced code-minus-phase observations are:
where Δ indicates the time difference and ρ Δ is the time correlation coefficient (|ρ Δ| < 1) between two consecutive code observations. The standard deviation of the code measurements is assumed to be constant from one epoch to the next. The middle pane in Fig. 5 shows the time differenced code-minus-phase observations for GPS PRN18. The multipath delays, present in the undifferenced code-minus-phase observations (top pane), are removed in the time differenced observations (ΔMP C is small). The variations in the measured C/N0 due to multipath (bottom pane) do still influence the variance of the time differenced code-minus-phase observations; careful inspection of Fig. 5 shows that the variation in the middle pane is larger when the C/N0 is smaller. For the time differenced observations the standard deviation for a C/N0 of 45 dB-Hz has again been estimated by fitting a line to the 120 s data segments. This fitting of the data is very similar for each combination of observations and therefore no more figures like Fig. 6 are presented. Results are provided in Table 3 (1Rx-ΔUD) after normalization to the undifferenced levels by division of the standard deviation by √2. This is the factor by which the standard deviation increases by differencing if there is no correlation.
Between receiver difference
Measurements from two receivers tracking the same satellites can be combined to remove common errors from the measurements. Traditionally, the main purpose of taking the between receiver single difference (SD) is to eliminate the satellite clocks from the observation equations, but these are already removed in the geometry-free code-minus-phase combination. Now the fractional part of the phase ambiguity and the instrumental delay at the satellite are removed. For a SB the ionospheric delay is also removed because the differential ionospheric delay can be neglected for a SB (here only 4 m). The antenna hardware delays are reduced in the SD if the same antenna type is used at both ends of a SB which is true for this measurement campaign. For a ZB the ionospheric delay, the multipath errors and the antenna hardware delays are removed because they are the same for both receivers. The resulting observations contain the SD phase ambiguity, the remaining SD hardware delay, the SD code noise and, for the SB, the SD multipath error. The expectation and dispersion of the SD code-minus-phase observations are:
where ρSD is the correlation coefficient between the code observations of the two receivers. For the SB it is assumed that there is very little correlation between measurement noise of the two receivers ([ρ SD]SB ≈ 0), but for the ZB a large part of the noise is the same for both receivers (Gourevitch 1996) giving a high correlation ([ρ SD]ZB ≠ 0). Therefore, an increase of the variance of the noise by a factor two is only a good assumption for the SD SB observations. For multipath it is the other way round, multipath is absent for the ZB ([MPSD]ZB ≈ 0), but not for the SB ([MPSD]SB ≠ 0).
Subtraction of the mean value from the observations removes the phase ambiguity, which is constant if there are no cycle slips, and reduces the remaining hardware delay. Figure 7 again shows the undifferenced code-minus-phase observations for GPS PRN18 in the top pane and the measured C/N0 in the bottom pane, but now for both receivers in the SB setup. The multipath effects for the two receivers are similar but not the same. The middle pane shows the SD code-minus-phase observations. These observations still contain multipath in the same order of magnitude as the undifferenced code-minus-phase observations. For the SD observations the estimated standard deviation for a C/N0 of 45 dB-Hz is again provided in Table 3 (SB-SD and ZB-SD) after normalization to the undifferenced levels.
Time difference
By taking the difference between the SD observations of two epochs, the phase ambiguity is eliminated and the remaining hardware delay and multipath are reduced. This gives the following expectation and dispersion for the time differenced SD code-minus-phase observations:
The variance of the time differenced SD measurements is dependent on both the time correlation between two epochs and the correlation between the observations from the two receivers. Results for the estimated standard deviation of the time differenced SD observations for a C/N0 of 45 dB-Hz are provided in Table 3 (SB-ΔSD and ZB-ΔSD) after normalization to the undifferenced levels.
Double difference
Subtracting the measurements to one reference satellite from the measurements to all other satellites removes all common terms from the measurements. Traditionally, the main purpose of taking the between satellite difference is to eliminate the receiver clocks from the observation equations, but these are already removed in the geometry-free code-minus-phase combination. Now the fractional part of the phase ambiguity and the instrumental delay at the receiver are removed. By taking the between satellite difference and the between receiver difference the so-called double differences (DD) are formed. All terms that are removed in the SD are also removed in the DD. This leaves the DD phase ambiguity, the DD code noise and, for the SB only, the DD multipath error. The variance of the code noise increases by a factor four if there is no correlation between the observations. The noise on the observations made to different satellites is assumed to be uncorrelated. As pointed out with the SD, for the SB the observations of the two receivers to the same satellite are also assumed to be uncorrelated, but this is not true for the ZB. The expectation and dispersion of the DD code-minus-phase observations is:
Because all fractional parts of the phase ambiguities are removed the resulting DD ambiguities have an integer value (indicated by N).
Between satellite difference C/N0
As we have to combine two satellites for the between satellite differences, a pseudo C/N0 is computed with the following equation:
where (C/N0)12 is the between satellite difference carrier-to-noise density ratio; (C/N0)1 and (C/N0)2 are, respectively, the carrier-to-noise density ratios of the reference satellite and the second satellite forming the satellite pair. This equation follows from the inverse relation between the variance and the carrier-to-noise density ratio when expressed in ratio-Hertz. A factor of one half is added to normalize the C/N0 to the undifferenced levels. A certain value of the pseudo C/N0 can be interpreted as following from the difference between two observations with this same value of the C/N0. Table 3 shows the results for the standard deviation of the DD code-minus-phase observations for a C/N0 of 45 dB-Hz, for both the short and zero baseline (SB-DD and ZB-DD).
Ambiguity resolution
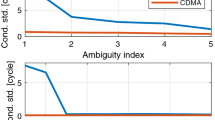
The DD phase ambiguities are expected to be integer numbers. This integer number does not change as long as the receivers keep tracking the satellite pair and no cycle slip occurs. Because the expectation value of the code noise is zero it follows from expression (8) that averaging the DD code-minus-phase observations over many epochs leaves multipath and the DD phase ambiguity. From this average the integer phase ambiguity can be determined unless there is significant MP that does not average out to zero or there are undetected cycle slips in the data. The necessary length of a data segment to determine the ambiguity correctly depends mostly on the standard deviation of the code noise and the multipath. To assess the performance of geometry-free ambiguity resolution, the GPS data have been processed with a geometry-based model to solve the DD ambiguities and the solution is taken as truth. For the Galileo data the geometry-free ambiguity based on the entire dataset is taken as truth. Then the dataset has been split into shorter data segments and the geometry-free ambiguities based on these shorter data segments have been compared to these ‘true’ values. Figure 8 shows the results for the ZB with data segments of 2 min versus the pseudo C/N0. If the DD code-minus-phase averaged over a data segment is within half a cycle of the true ambiguity, then rounding to the nearest integer provides the correct solution. For the ZB this is true for more than 99% of the data segments. The performance for the mixed system (GPS-Galileo) ambiguities is very similar to the performance for single system ambiguities. This means that there either is no intersystem bias, or that it is canceled out by the use of identical equipment at both ends of the baseline.
Figure 9 shows the results for the SB with data segments of 1 h. There are still three satellite combinations where rounding to the nearest integer does not provide the correct ambiguity. This shows that the multipath, present in the DD SB observations, does not average out to zero. For single frequency data, processed with a geometry-free model, this is not an unexpected result and it could probably be improved by using high-end (choke ring) antennas. To further validate the SB GIOVE ambiguity, the complete dataset of 1.5 h has been split into four equal parts and the ambiguity has been computed for each segment. Because this provides the same integer value for each segment, it gives confidence that a Galileo ambiguity for a SB has been solved correctly for the first time.
Time difference
In the time difference between the DD observations of two epochs (also called triple difference), the phase ambiguity is eliminated and the multipath is reduced. This gives the following expectation and dispersion for the time differenced DD code-minus-phase observations:
The expectation value is very close to zero especially for the ZB setup. Results for the estimated standard deviation of the measurement noise are again provided in Table 3 (SB-ΔDD and ZB-ΔDD).
Carrier phase analysis
In all the analyses so far the carrier phase acted as an accurate reference in the code-minus-phase combination. The noise of the carrier phase itself can be analyzed along similar lines using the DD carrier phase observations. A low-order polynomial must be fitted to the DD carrier phase segments in between cycle slips and receiver clock jumps in order to remove carrier phase ambiguities, DD geometric range and clock synchronization effects. For the SB this leaves the carrier phase measurement noise and the carrier phase multipath. For the ZB multipath is removed in the between receiver difference so this leaves mainly the phase noise. For the ZB the measurement noise of the phase observations of the two receivers is correlated (Gourevitch 1996), giving the following expectation value and dispersion:
The polynomial p(t) is again based on enough data points to safely neglect its uncertainty in the dispersion of (11). Results for the standard deviation of the DD phase observations for a C/N0 of 45 dB-Hz are presented in Table 5 for both the short and zero baseline (SB-DD and ZB-DD). Because the results are very similar for each GNSS, no distinction is made in Table 5 between the different systems. This is inline with expectations since the standard deviation of the carrier phase depends only on the C/N0 and not on the signal modulation. Because the geometric effect of the receiver clock offset is not completely removed by the polynomial fitting, there remains a small effect on the DD phase observations proportional to the Doppler offset. As a result the stationary EGNOS satellites perform slightly better than the other satellites.
Time difference
In the triple difference phase observations the DD geometric range and the geometric effects of the clock offsets are reduced and the carrier phase ambiguities are eliminated. In addition, most of the phase multipath is removed leaving mainly the phase noise. There is little time correlation between the phase measurements, giving the following expectation value and dispersion:
Figure 10 shows the ΔDD phase observations for 120 s data segments for each GNSS for the SB observations. From this figure it can be concluded that the standard deviation of the phase observations as a function of the C/N0 is the same for each GNSS. Therefore, the standard deviation for a C/N0 of 45 dB-Hz has been estimated from all observations simultaneously (see Table 5 SB-ΔDD and ZB-ΔDD).
Comparison with theory
Table 3 shows the standard deviation of the observations for each of the discussed combinations for a C/N0 of 45 dB-Hz. These standard deviations have been normalized to the undifferenced levels. To clarify the similarities and differences in the normalized standard deviations of the code noise for the different combinations of the observables, an analysis is presented here, with special attention for three effects that influence the computed standard deviations. These are: multipath, time correlation of the observations (resulting from the tracking loops) and correlation resulting from both receivers tracking the same signal traveling through the atmosphere, antenna and low noise amplifier (LNA) in the ZB setup (Gourevitch 1996). In Table 3 the different observation combinations are grouped based on how they deal with these three effects. The first group (single receiver, SB-SD and SB-DD) does not remove the multipath from the observations. Therefore, it is expected that the computed noise for this group is larger than the theoretical thermal noise. The second group (single receiver time difference, SB time difference SD and SB time difference DD) removes most of the multipath from the measurements. In addition, the standard deviation of the noise is further reduced if the measurements are positively correlated in time. Therefore, it is expected that the computed noise is smaller than the theoretical thermal noise if the correlation is positive. The third group (ZB SD and ZB DD) also removes the multipath from the measurements. In addition, the standard deviation of the noise is further reduced because the measurements of the two receivers are correlated as a result of being connected to the same antenna and LNA ([ρ SD]ZB = ρ LNA ≠ 0). Therefore, it is expected that the computed noise is smaller than the theoretical thermal noise. The noise levels of group two and three cannot easily be compared. The fourth group (ZB time difference SD and ZB time difference DD) also removes the multipath from the measurements. In addition, the computed standard deviation of the code noise is further reduced by both the time correlation and the correlation resulting from the antenna and LNA and so it is expected that this group has the smallest standard deviation of the noise. The values in Table 3 are very close to each other within each group with the exception of group one. This is an expected result, because the multipath is very different for the field and roof environment.
Using results of groups three and four, the time correlation of the observations can be determined by solving the following relation for the time correlation coefficient ρ Δ:
where σ and σ Δ are the (not normalized) standard deviations of the code noise of group three and the corresponding time differenced code noise of group four, respectively. When the correlation has been determined, the undifferenced thermal code noise (σ) can be estimated by applying Equation (13) to the standard deviation of group two (σ Δ). Here, it is assumed that the tracking loop time correlation is the same for the short and zero baselines (Amiri-Simkooei and Tiberius 2007 showed that this is a good assumption for the baseline components). The resulting estimated code noise represents thermal noise (without multipath and without underestimation due to time correlation or correlation due to the LNA in the ZB measurements). In a similar way using results of groups two and four the correlation between the ZB measurements mostly due to the LNA can be determined ([ρ SD]ZB = ρ LNA). Table 4 shows the results of these computations for each GNSS as well as theoretical thermal noise values for C/N0 = 45 dB-Hz that have been determined with the formulas presented in Sleewaegen et al. (2004) and the receiver and signal properties, which are given in Tables 1 and 2. For the integration time the symbol duration has been used and a common narrow correlator spacing has been assumed for GPS and Galileo. For EGNOS a correlator spacing of one half chip/of half of a chip has been assumed. The measured results are very close to the theoretical values for GPS and Galileo. For EGNOS the measured values are slightly higher than the theoretical values.
The same technique has been used to compute the time correlation, the correlation due to the LNA and the thermal noise of the phase observations. The results of these calculations are presented in Tables 5 and 6. The results are very similar for each GNSS and no distinction is made in the tables between the different systems. The measured values are quite close to the theoretical value determined with the formula presented in Sleewaegen et al. (2004), and the receiver and signal properties, which are given in Tables 1 and 2.
Conclusions
The different contributions of the code and phase measurement noise have been investigated with a geometry-free model using single frequency, multi-GNSS, short and zero baseline measurements. Using the single, double and time differences of the code-minus-phase combination, the code noise, code multipath delays and correlation between the code observations have been quantified. From these investigations a good estimate of the undifferenced code noise without multipath has been made. This estimate is very close to the theoretical values for the thermal noise. The results show that the improvement in performance of the new GIOVE E1BC signal with respect to the GPS L1 C/A signal is close to the theoretical expectations.
The measurements show that the multipath delay of the two receivers in the SB setup is almost uncorrelated even for a very SB (4 m) in an open field. This leads to SD observations with multipath in the same order of magnitude as the multipath of the undifferenced observations.
In the ZB setup, the multipath is removed in the SD observations. In the time differenced observations the multipath is also greatly reduced. However, in both cases the correlation between the observations should be taken into account. The results show significant correlation between the code observations made by two receivers in the ZB setup as well as significant time correlation between code observations of consecutive epochs which cannot be neglected. Not taking this into account may lead to an over optimistic stochastic model. The observations made to two different satellites are almost uncorrelated as expected.
From the DD code-minus-phase observations the phase ambiguities have been solved by averaging over a data segment and rounding to the nearest integer. The results show that without multipath (ZB) this gives the correct integer for a data segment of only 2 min more than 99% of the time. However, with multipath (SB) this still gives an incorrect integer for a data segment of an hour 21% of the time. This clearly shows that multipath does not quickly ‘even out’ for this dataset. These results for the SB may improve when using high-end (choke ring) antennas.
Despite this impact of multipath on SB ambiguity resolution, additional validation of the GIOVE results gives confidence that a Galileo ambiguity has been solved correctly from field measurements for the first time.
The phase noise and phase multipath have also been studied from the DD phase observations. The results show that the estimated phase noise is close to the theoretical thermal noise and almost equal for each GNSS as expected. Just like the code observations, the phase observations made by two receivers in the ZB setup are highly correlated. Unlike the code observations the phase observations show very little time correlation at a sampling rate of 1 Hz. The small difference in time of observation between the two receivers should be taken into account with the geometry-free model. In a standard geometry-based approach the satellite positions are evaluated for both receivers individually, thereby respecting the (slightly) different times of observation.
Geometry-free short and zero baseline processing is a valuable (and fairly simple) way to determine the different noise contributions of the code and phase observations as well as the correlation between the different observations. This in turn is very useful when setting up a stochastic model to accompany the functional model for positioning algorithms with the final goal of improving the positioning results.
Abbreviations
- UD:
-
Undifferenced
- SD:
-
Between receiver single difference
- DD:
-
Double difference
- Δ:
-
Time difference
- SB:
-
Short baseline
- ZB:
-
Zero baseline
- Rx:
-
Receiver
- LNA:
-
Low noise amplifier
References
Amiri-Simkooei AR, Tiberius CCJM (2007) Assessing receiver noise using GPS short baseline time series. GPS Solut 11(1):21–35. doi:10.1007/s10291-006-0026-8
Braasch MS, van Dierendonck AJ (1999) GPS receiver architectures and measurements. Proc IEEE 87(1):48–64
Gourevitch S (1996) Measuring GPS receiver performance: a new approach. GPS World 7(10):56–62
Hein GW, Avila-Rodriguez J-A, Wallner S et al. (2006) MBOC: the new optimized spreading modulation recommended for GALILEO L1 OS and GPS L1C. In: IEEE/ION PLANS 2006, pp 883–892
Liu X, Tiberius CCJM, de Jong K (2004) Modelling of differential single difference receiver clock bias for precise positioning. GPS Solut 7(4):209–221
Odijk D (2008) What does “geometry-based” and “geometry-free” mean in the context of GNSS? In: Column: GNSS solutions. Inside GNSS March/April 2008, pp 22–24
Sleewaegen J-M, de Wilde W, Hollreiser M (2004) Galileo Alt-BOC receiver. In: Proceedings of the European Navigation Conference (GNSS ‘04)
Tiberius CCJM, van der Marel H, Sleewaegen J-M, Boon F (2008) Galileo down to a millimeter: analyzing the GIOVE-A/B double difference. Inside GNSS September/October 2008, pp 40–44
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
de Bakker, P.F., van der Marel, H. & Tiberius, C.C.J.M. Geometry-free undifferenced, single and double differenced analysis of single frequency GPS, EGNOS and GIOVE-A/B measurements. GPS Solut 13, 305–314 (2009). https://doi.org/10.1007/s10291-009-0123-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10291-009-0123-6