Advantage of velocity measurements on instantaneous RTK positioning

Abstract

Instantaneous real-time kinematic (RTK) techniques are one approach to achieving real-time high-accuracy positioning. The object of this paper is to show the advantage of adding velocity information to instantaneous RTK positioning. In this paper, velocity from Doppler frequency measurements is used to help resolve integer ambiguities in the LAMBDA method. In urban areas, pseudorange measurements can suffer from significant errors due to strong multipath, despite the use of advanced multipath-mitigation techniques. However, Doppler frequency measurements do not deteriorate as much as pseudoranges, because the multipath error on Doppler frequency measurements is only in the range of several centimeters. Our proposed method has been tested by both static and moving users in sub-urban environments. Single-epoch ambiguity fixing performance was improved compared to conventional ambiguity resolution without velocity information.

Introduction

Intelligent transportation systems (ITS) are used to address road traffic problems, such as traffic accidents and congestion, by facilitating communication between people, vehicles, and roads using state-of-the-art telecommunications technology. Synchronization between traffic-information services, car-navigation systems, automatic-charge-payment systems, and bus-location systems has been demonstrated. In fact, such systems are now widely used in Japan. Future ITS services will include autonomous ground-vehicle navigation and dynamic prevention of traffic accidents. Although it is difficult for an autonomous ground vehicle to be put into practical use in the near future, one key technology to make this possible is real-time high-accuracy positioning to within 10 cm.

The object of this paper is to reveal the advantage of velocity information on instantaneous RTK positioning. Single-epoch determination of carrier-phase integer ambiguities is essential for RTK technology to be used in a vehicle because “nuisance” cycle slips that might intrude upon multi-epoch fixing can be neglected. GPS satellite signals can be shaded or momentarily blocked in urban areas. When this occurs, integer values are usually lost and must be re-determined, which makes it important to be able to reacquire the integers quickly. The key issues related to fast ambiguity resolution have been discussed by several researchers (Hatch 1991; Han 1997; de Jonge P et al. 2000).

Using the well-known LAMBDA method for ambiguity resolution (Teunissen and Verhagen 2007), the probability of successful fixing in a single epoch with a dual-frequency GPS receiver is over 99% when the separation between reference and user antennas is within several kilometers and the user antenna is installed such that no multipath is present (Teunissen 1995; Kubo and Yasuda 2007). However, it is generally accepted that this performance cannot be achieved in urban areas. There are two main reasons for this. One is the presence of significant multipath error, and the second is that the number of visible satellites decreases (Kubo and Yasuda 2007). In terms of the number of visible satellites, at least four visible satellites are required in order to attempt to fix ambiguities in a single epoch regardless of whether or not the attempt succeeds.

Although high-sensitivity GPS receivers are better able to output measurements for more satellites (even in urban areas) compared with typical dual-frequency receivers, the resulting accuracy is generally insufficient to fix ambiguities correctly. However, it should be noted that high-sensitivity receivers can use Doppler measurements produced from a robust frequency lock loop (FLL) to aid positioning (Kaplan and Hegarty 2006). It is well known that the accuracy of Doppler measurements is better than the accuracy of pseudoranges, especially when strong multipath is present. The advantages of using Doppler measurements in an odometer are also pointed out in (Wieser 2007).

In the author’s previous work, the improvement of single-epoch ambiguity fixing using user velocity information has been demonstrated (Kubo and Pullen 2008). However, the standard deviation of the float solutions deduced from updating the accurate previous position with velocity information was set to a constant value (around 10 cm). This was conservative especially in the case of using a high-accuracy receiver because the accuracy of Doppler frequency from this type of receiver was usually less than 5 cm. In this paper, the standard deviation of the float solutions was set according to the estimated FLL tracking loop jitter due to thermal noise.

Although several papers using constrained ambiguity resolution have been discussed (Teunissen 2006; Monikes et al. 2005), these were for two antennas located very close together in a rover vehicle, such as the “GPS Compass” used for attitude determination. Constrained ambiguity resolution methods regarding positioning domain test have also been discussed (Kubo and Yasuda 2007; Monikes et al. 2005). Our proposed method can be implemented with the standard single-baseline model using only raw GPS measurements. The proposed algorithm of single-epoch RTK positioning is the same as described in (Kubo and Pullen 2008). After obtaining carrier phase, pseudorange, and Doppler measurements, ambiguity resolution is conducted. The LAMBDA method was used for ambiguity searching. In the LAMBDA method, the position estimate deduced from velocity information is used for computing the “float” solution in order to strengthen the model before the search step. As a result, the probability of incorrect fixing due to large pseudorange multipath error is reduced. In other words, the resulting ambiguity fixing performance is no longer strongly dependent on pseudorange accuracy. These algorithms have been tested by static and moving users subjected to several different multipath conditions. In all experiments conducted to date, single-epoch ambiguity fixing performance was improved compared to conventional ambiguity resolution without velocity information. Furthermore, applying the new less-conservative proposed standard deviation of the float solutions was also effective in improving integer ambiguity resolution.

Ambiguity resolution using user velocity

In this section, the conventional LAMBDA method and velocity estimation are introduced briefly. After that, the LAMBDA method including user velocity is introduced (Misra and Enge 2006; Teunissen and Verhagen 2007; Teunissen 1999).

LAMBDA method

The linear equation obtained from single- or dual-frequency measurements in the GNSS baseline model is as follows

$$ {\mathbf{y}} = G\delta {\mathbf{x}} + {\mathbf{N}} + \varepsilon $$

(1)

where y denotes the difference between the measured and computed carrier phase double differences for the initial position estimate; G is the observation matrix characterizing the double-difference user-reference station-satellite geometry; δ x is the error in the initial position estimate; N is the vector of double-difference integer ambiguities to be estimated; and ε is the carrier phase double-difference measurement errors. We have to find δ x and N which minimize the cost function

$$ \begin{aligned} {\text{C}}{\mathbf{w}} (\delta {\mathbf{x}} , {\mathbf{N}} ) &= ||{\mathbf{y}} - {\mathbf{G}}\delta {\mathbf{x}} - {\mathbf{N}} | |_{{\mathbf{W}}}^{2} \hfill \\ & = ({\mathbf{y}} - {\text{G}}\delta {\mathbf{x}} - {\mathbf{N}})^{T} {\mathbf{W}} ({\mathbf{y}} - {\mathbf{G}}\delta {\mathbf{x}} - {\mathbf{N}} )\hfill \\ \end{aligned} $$

(2)

which uses the inverse of the noise covariance matrix W to give different weights to the contributions of the double-difference residuals. The standard LAMBDA method can then be divided into three steps.

Step 1

To obtain float solutions disregard the integer constraint on the ambiguities and obtain solutions for δ x and N which minimizes the cost function (2). In the LAMBDA method, this is only the first step, and it ends with the float solution for the position and ambiguities and their covariance matrix written in block from as $[\delta {\hat{\mathbf{x}}},{\hat{\mathbf{N}}}]$

$$ {\text{Cov}}\left[ \begin{gathered} \delta {\hat{\mathbf{x}}} \hfill \\ {{\hat{\mathbf{N}}}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\sum_{{\delta {\hat{\mathbf{x}}}}} } & {\sum_{{\delta {\hat{\mathbf{x}}} ,{\hat{\mathbf{N}}}}} } \\ {\sum_{{\delta {\hat{\mathbf{x}}} ,{\hat{\mathbf{N}}}}} } & {\sum_{{{\hat{\mathbf{N}}}}} } \\ \end{array} } \right] $$

(3)

where $\delta {\hat{\mathbf{x}}}$ and ${\hat{\mathbf{N}}}$ are the float solutions; $\sum_{{\delta {\hat{\mathbf{x}}}}}$ and $\sum_{{^{{^{{{\hat{\mathbf{N}}}}} }} }}$ are the corresponding covariance matrices; and $\sum_{{\delta {\hat{\mathbf{x}}} ,{\hat{\mathbf{N}}}}}$ gives the cross-correlations between the two solutions.

Step 2

Find the integer vector N which minimizes the cost function:

$$ c({\mathbf{N}}) = ({\mathbf{N}} - {\hat{\mathbf{N}}})^{T} {\mathbf{W}}_{{\mathbf{N}}} ({\mathbf{N}} - {\hat{\mathbf{N}}}) $$

(4)

where ${\hat{\mathbf{N}}}$ is the float solution from Step 1, and the weight matrix W _N is the inverse of its covariance matrix: ${\mathbf{W}}_{{\mathbf{N}}} = \sum_{{\widehat{{\mathbf{N}}}}}^{ - 1}$ Step 2 is at the heart of LAMBDA method. The measure of distance of an integer vector to $\widehat{\text{N}}$ is given by (4). The contour of points with a constant value of the cost function is an ellipse in two dimensions and an ellipsoid in higher dimensions, centered at $\widehat{\text{N}}$. The search space is delimited by selecting the size of the ellipsoid to be searched via a parameter value c > 0. Therefore, the inequality

$$ ({\mathbf{N}} - \widehat{{\mathbf{N}}} )^{T} {\mathbf{w}}_{{\mathbf{N}}} ({\mathbf{N}} - {\mathbf{N}}) \le c $$

(5)

defines the integer vectors N which are candidates for the solution. The search space consists of the integer grid points inside the ellipsoid defined by (5). Ideally, this search space must be large enough to contain the right answer and small enough to be searched quickly. LAMBDA would be a simple algorithm if W _N could be diagonalized. LAMBDA involves many subtle steps to transform W _N into a matrix that is as nearly diagonal as possible.

Step 3

Obtain the “fixed solution” δ x from (1) after fixing the integer ambiguities to N found in Step 2. In Step 3, several tests have been proposed in the literature to decide whether or not to accept the resulting integer solution. The ratio test is one of the most commonly-used tests.

Velocity estimation

Typically, a well-designed GPS receiver carrier-tracking loop will “close the loop” with a dynamically-robust wideband FLL. Then it will gradually reduce the carrier-tracking-loop bandwidth and transition into a wideband s (PLL). If the signal being tracked is blocked, or if interference exists in the environment, the FLL may be able to track when the PLL cannot. Similarly, a delay lock loop (DLL) is used to track the code signal from each GPS satellite. A GPS receiver tracks the distinct and sharp peak of the code auto-correlation function. The resulting pseudorange estimate is unambiguous (Kaplan and Hegarty 2006; Misra and Enge 2006).

If the satellite velocity vector is approximately known, Doppler measurements can be used to estimate user velocity. Doppler measurements, which are measurements of range rate, can be written as the projection of the relative velocity vector onto the satellite line-of-sight vector. There are three types of range-rate measurements, and their approximate accuracies are as follows. More accurate results can be obtained using a high-quality receiver.

• 1. Delta carrier phases obtained from PLL (≈1 cm).

• 2. Delta pseudoranges obtained from DLL (≈100 cm).

• 3. Doppler measurements obtained from FLL (≈10 cm).

In this paper, Doppler measurements obtained from a FLL are used to obtain range rates. The model for determining range rate is given by the following equation.

$$ \begin{aligned} \dot \rho^{({\text{k}})} & = \dot{\text{r}}^{ ( {\text{k)}}} + (\dot{\text{b}} - \dot{\text{b}}^{ ( {\text{k)}}}) + \dot{\text{I}}^{ ( {\text{k)}}} + \dot{\text{T}}^{ ( {\text{k)}}} \\ & = ({\text{\bf{v}}}^{ ( {\text{k)}}} - {\text{\bf{v}}}){\text{I}}^{({\text{k}})} + \dot{\text{b}} + \varepsilon_{\dot \varphi}^{({\text{k}})} \\ \end{aligned} $$

(6)

where v ^(k) is the satellite velocity vector, obtained from the navigation data message broadcast by the satellite, and v is the user velocity to be estimated. Both v ^(k) and v are expressed in the ECEF coordinate frame. The user-to-satellite line-of-sight unit vector l ^(k) is determined from a rough estimate of the user position (user position for this purpose is derived from single-point positioning using raw pseudorange at the user); $\dot{\text{r}}^{ ( {\text{k)}}}$ is the rate of change in the actual (unknown) distance from satellite to user, $\dot{b}$ and $\dot{b}^{{({\text{k}})}}$ are the rates of change in the receiver and satellite clocks, respectively, $\dot{\text{I}}^{ ( {\text{k)}}}$ and $\dot{\text{T}}^{ ( {\text{k)}}}$ are the rates of change in the ionospheric and tropospheric delays; and $\varepsilon_{{\dot{\varphi }}}^{{({\text{k}})}}$ denotes the combined error due to changes in the satellite clock, ionosphere, and troposphere during the measurement interval.

Note that the velocity of an object attached to the earth is zero in the ECEF coordinate frame. Errors due to changes during the measurement interval in ionospheric and tropospheric delays and in multipath are also generally small. For moderate user speeds, the main source of error in velocity estimation is the error in the predicted satellite position and velocity. Problems can also arise if the user dynamics are high, as the range–rate estimate computed from (6) gives only an average velocity over the measurement time interval. High accelerations and jerks would clearly create difficulties for this method (Misra and Enge 2006).

LAMBDA method applying user velocity

When user velocity is applied to aid ambiguity resolution, we focus on the first step defined above, that is, the float solution in the LAMBDA method. In other words, in this paper, the calculation of the float solution is modified by incorporating user velocity.

When the “float solution” is calculated, double-differenced pseudoranges are typically used as mentioned in equation (3). If multi-epoch data can be used, not only pseudorange but carrier-phase measurements can be used to smooth the pseudorange noise. However, multi-epoch data cannot be used in this paper because single-epoch ambiguity resolution is required. Generally speaking, using multi-epoch data will be difficult for a moving platform in urban areas due to frequent signal blocking. As a result, the probability of correct ambiguity fixing strongly depends on pseudorange accuracy. If pseudorange accuracy suffers from large multipath error, it will be difficult to resolve correct ambiguities, even if the LAMBDA method is used. The reason is that the LAMBDA method cannot easily adapt to the additional bias (as opposed to variance) errors that occur when significant multipath is introduced.

The proposed method can mitigate this problem by taking advantage of user velocity information. Specifically, the “float solution” is calculated by updating an accurate previous position fix with velocity information. Accurate previous position is critical here. In order to decide if the previous epoch was fixed correctly or not, the LAMBDA ratio test is used. If the previous epoch passed the ratio test, the previous position is regarded as the result of correct ambiguities. Although the ratio test itself is not an optimal test (Teunissen and Verhagen 2007), it is well known that the ratio test is suitable for this purpose. The threshold for this ratio test is set to 3. Once the correct ambiguities are resolved, the “float solution” in the next epoch will be very accurate and reliable. This is very important to strengthen the mathematical model because, as noted above, the LAMBDA method itself is not strong against bias errors.

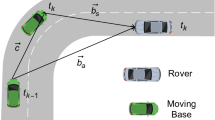
The method to use user velocity at each epoch is as follows. In a static condition, the center of the search space, which gives the expected position, is the previous fixed position updated by the previous velocity estimate, as described above. However, for a moving platform such as a car, a certain degree of acceleration has to be considered. Thus, the expected position is the previous fixed position updated by adding half of the present velocity estimate and half of the previous velocity estimate. The equation for our proposed float solution is given by the following heuristic equation.

$$ \delta \widehat{{\mathbf{x}}} (t ) = \delta {\mathbf{x}} (t - N ) + \sum\limits_{n = 1}^{N} {({\mathbf{v}}(t - n + 1) + {\mathbf{v}} (t - n ) )T / 2} $$

(7)

where $\delta \widehat{{\mathbf{x}}}$ is the proposed float solution, δx is the previous fixed position, and t is the time of epoch. N is the number of epochs, and T is the measurement time interval. Parentheses are used to distinguish a specific time epoch. In our proposed method, both float ambiguities and the corresponding covariance matrices are calculated according to the following flowchart in Fig. 1.

Fig. 1

Flowchart for AR

Standard deviation of float solution

As mentioned in the “Introduction”, in the author’s previous work, the standard deviation of the proposed float solutions (deduced from updating the accurate previous position with velocity information) was set to a constant value of about 10 cm. In fact, this value was conservative, especially in the case of using the Doppler frequency from a high-accuracy receiver, because the accuracy of velocity information from such receivers usually is less than 5 cm. The accuracy of the proposed float solution depends on the accuracy of the Doppler frequency, which is based on the FLL tracking loop measurement error. This measurement error was used to calculate the standard deviation of our proposed float solution in this paper. The FLL tracking loop jitter due to thermal noise is (Kaplan and Hegarty 2006):

$$ \sigma_{{t{\text{FLL}}}} = \frac{\lambda L}{2\pi T}\sqrt {\frac{{4F{\mathbf{B}}_{n} }}{{C/N_{ 0} }}\left[ {1 + \frac{1}{{TC /N_{ 0} }}} \right]} \,({\text{m}}/{\text{s}}) $$

(8)

where B _n is the frequency loop noise bandwidth (Hz).

C/N ₀ is calculated by the $10\frac{{(C/N_{0} ){\text{dB}}}}{10}$ for (C/N ₀)dB expressed in dB-Hz. T is the predetection integration time (s). λ _n is GPS L band carrier wavelength (m). F is equal to 1 at high C/N ₀ or 2 near the threshold of minimum signal power that can be tracked by the FLL.

The 3D velocity vector deduced from Doppler frequency was investigated under good (low-multipath) static conditions using both a high-accuracy receiver and a high-sensitivity receiver. The data period was 1 h. The 1-sigma error of the 3D velocity vector magnitude was 3.3 cm/s for the high-accuracy receiver and 13.7 cm/s for the high-sensitivity receiver. The similar results of velocity vector are mentioned in (Wieser 2007). The average PDOP value during this test was around 2.0.

Since a representative value for C/N ₀ has to be established in order to determine the standard deviation of our proposed float solution, the average C/N ₀ of all the visible satellites in each epoch is used. If consecutive velocity information is used; i.e., N > 1 in (7), the standard deviation is enlarged according to the law of error propagation. The flowchart of our proposed method is shown in Fig. 1.

Experimental results

The proposed ambiguity resolution method using velocity updates has been investigated using actual GPS data collected under both static and moving conditions. In this section, the details of these experiments and their results are introduced.

Static testing under strong multipath conditions

Static GPS test data was collected for 75 min at a 2-Hz rate in the courtyard of the Terman building at Stanford University in July 2008 (this building is adjacent to the Durand building, where the reference antenna was sited). The reference station was equipped with a NovAtel OEM3 GPS receiver and a NovAtel GPS702 antenna. At the rover station, a NovAtel OEMV receiver and NovAtel GPS702 antenna were used. The separation between reference and user receiver antennas was 135 m. The rover’s mask angle was set to be 10° and the code loop bandwidth in the GPS receiver was set to be 0.01 Hz. The method of choosing or changing satellites was based on signal strength and other quality parameters within the GPS receiver.

The period of data-taking was selected in order to fulfill the following two requirements. The first requirement is that the minimum number of visible satellites is at least four, and the second requirement is to capture cases where strong specular multipath is present. For this test, the rover antenna was installed on an antenna rod and was surrounded by nearby buildings made of concrete and glass. This location is shown in Fig. 2. From this figure, it can be seen that the GPS-signals from the direction opposite to the wall of the building will be strongly reflected by the wall. The average number of visible satellites at the rover station was 5.9 during the 75-min period. The total number of epochs in this test meets the above first requirements was 8,757.

Fig. 2

Location of GPS rover antenna

In this analysis, the performance of ambiguity resolution was evaluated based on two indicators. The first of these is the number of epochs that the ratio value in the LAMBDA ratio test is more than 3 or 2. Although the use of the ratio test in recent literature most commonly applies a threshold value of 3, a threshold of 2 was also examined in this paper because several past papers have applied this value (Teunissen and Verhagen 2007). When the threshold for the ratio test is set to 2, the detection of whether or not the previous epoch is correct is also based on a test threshold of 2. The second indicator is the number of epochs in which ambiguity fixing is possible. “Potential Fix” in the following results refers to this quantity. Generally speaking, it is almost always possible to find four correct ambiguities needed for positioning “artificially” in real time as long as the number of visible satellites remains 4 or more, although the software implementation will be complicated. More specifically, one or several epochs for which the ratio test is not passed can be linked together using the correct ambiguities that did pass the ratio test earlier (based on a test threshold of 3). On the other hand, when the number of visible satellites was less than four in the previous epoch, it will be impossible to find four correct ambiguities. The number of potential fixed epochs includes these types of “artificial” correctly-fixed epochs.

The horizontal DGPS positioning errors for this test (using all epochs of data) are shown in Fig. 3. The DGPS horizontal and vertical error standard deviations were 2.64 and 4.58 m, respectively, and the respective mean horizontal and vertical errors were 0.29 and 2.59 m. The overall performance of the single-epoch correct fix rate is shown in Table 1. As can be seen from Figs. 2 and 3, the rover station was strongly affected by short-delay multipath. Despite the fact that the data period only lasted for 75 min, several large horizontal DGPS error deviations of over 4 m can be seen. Table 1 shows the summary of the ambiguity resolution results. The second column shows the results of the conventional LAMBDA method. The third column shows the results of the proposed LAMBDA method with the constant standard deviation of the float solution. The fourth column shows the results of the proposed LAMBDA method with the new standard deviation of the float solution.

Fig. 3

Horizontal DGPS positioning errors

Table 1 Ambiguity resolution summary (total epochs: 8,757)

As can be seen in Table 1, both of the proposed LAMBDA methods with user velocity did much better than the conventional LAMBDA method. The greater number of epochs that passed the ratio test indicates that both availability and reliability were improved by using the proposed method. It is also clearly shown that the improvement of “Proposed2” over “Proposed1” is significant. One of the reasons why the fix rate of the conventional LAMBDA method is fairly low is large pseudorange multipath error. It is well understood that the continued strong multipath error in a static condition strongly degrades the performance of ambiguity resolution. Although strong multipath can be observed occasionally in the case of moving platform in urban areas, this type of situation does not last long when the vehicle is moving.

Table 2 shows the standard deviations of the 3D velocity vector components, deduced from the Doppler measurements using all epochs in each period. As can be seen from this table, Doppler measurements were not affected heavily by multipath, and this fact results in the excellent performance of the proposed techniques. Although they are not shown in the tables, wrong fixes were not seen in any methods in the case where the ratio-test threshold was set to 3. In static conditions, it is not difficult to resolve ambiguities perfectly using position information from previous epochs as long as the number of visible satellites remains at four or more. In this case, the number of visible satellites was five or six for all epochs in this test.

Table 2 Standard deviation of velocity vector components

Road testing

Raw GPS test data was collected at 2 and 4 Hz rates in Palo Alto, CA (near the Stanford campus) by a moving car. The reason for using different data rates was in recognition of the fact that the accuracy of the position estimation deduced from the velocity information depends on the sampling interval over which position extrapolation takes place. If we use higher-rate velocity information, we should be able to reduce errors due to user dynamics.

In this test, not only a high-accuracy dual-frequency receiver but also a high-sensitivity single-frequency receiver was used to examine the proposed method because the high-sensitivity receiver is able to produce Doppler measurements for more GPS satellites at a given time. In other words, high-sensitivity receivers can continue to output velocity information during periods when high-accuracy receivers are not able to do so. If velocity information is available from a high-sensitivity receiver during a period when fewer than four visible satellites are tracked by a high-accuracy receiver, the “float solution” can be estimated using consecutive epoch of velocity information from the high-sensitivity receiver. This is an important means of performance improvement in moving application because, as shown above, the float solution deduced from velocity information is much more reliable and accurate than the float solution using only pseudorange measurements when relatively few satellites are visible.

The configuration of this road testing was the same as that of the previous static test except that a high-sensitivity receiver was added. In the rover automobile, a NovAtel OEMV, which is a representative high-accuracy receiver, a u-blox AEK-4T, which is a representative high-sensitivity receiver, and a NovAtel GPS702 antenna were used. The maximum speed of the car was under 50 km/h in all of the following tests.

Road testing in Palo Alto (2-Hz rate)

Raw GPS data was collected twice for about 15 min each at a data rate of 2 Hz using a car in downtown Palo Alto in July 2008. The course was same in each period (at all points, this course lies within 3 km of the reference station on the Durand building), but the time slot was different. For this test, the rover antenna was installed on the rooftop of the car. Several streets along the course were narrow and were surrounded by many nearby trees and buildings, but the buildings were not so high. Several pictures of the test course are shown in Fig. 4.

Fig. 4

Pictures of the test course

The precise position fixes for all epochs with four or more visible satellites were post-processed perfectly in order to check if the positions determined by real-time integer-fixing were correct or not. The average number of visible satellites at the rover station during the two data-taking periods was 6.7 and 5.3, respectively. There were many epochs where the number of visible satellites was less than four, especially in the second period. In this analysis, the performance of ambiguity resolution was evaluated in the same manner as in the previous static testing.

Table 3 summarizes the performance achieved during the first 15-min period of data collection, while Table 4 summarizes the performance achieved during the second 15-min period. Both of these tables use the same format as Table 2. Each percentage in these two tables is calculated from the number of epochs that passed the ratio test divided by the total number of epochs with four or more satellites given above. The total number of epochs in which the number of visible satellites was four or more was 1,763 and 1,346, respectively. The “Potential Fix” row shows the total number of possible correct epochs in real time, as mentioned earlier.

Table 3 Ambiguity resolution summary (first period) (total epochs: 1,763)

Table 4 Ambiguity resolution summary (second period) (total epochs: 1,346)

As can be seen from Tables 3 and 4, both of the proposed LAMBDA methods with user velocity did much better than the conventional LAMBDA method. This means that the float solutions deduced from the two proposed methods were reliable and accurate. As a result, the probability of passing the ratio test increases, and this has the synergistic effect of increasing the overall fix rate in ambiguity resolution. Furthermore, the effects of using the proposed standard deviations can be seen clearly when comparing the results of “Proposed1” with those of “Proposed2”. Wrong integer fixes were seen a few times even when the ratio-test was passed (based on a test threshold of 3). The number of epochs with wrong fixes was three in the first period and two in the second period, respectively. This suggests that wrong fixes cannot be avoided in moving applications, even if the ratio-test threshold is set to three. Figure 5 shows the vertical dimension (height) profile of a typical “wrong fix” case during the first data period. In this case, the number of visible satellites was four, and the ratio-test value was 3.2. In other words, the number of visible satellites was almost not enough during this specific period. Most “wrong fix” cases occur when the number of visible satellites increases to four or more or it decreases below four in the next epoch. This suggests that the quality of carrier phase tends to degrade soon after re-acquisition or right before losing satellites.

Fig. 5

Height profile in a typical “Wrong Fix” case

Figures 6 and 7 show the temporal ratio values of all epochs in the first and second data periods, respectively. The results of the “Proposed” in these figures represent the “Proposed1” (constant standard deviation) method. From these figures, it is clear that the ratio-test values deduced from the proposed method were overwhelmingly higher than the values deduced from the conventional method in almost all epochs.

Fig. 6

Comparison of ratio-test values in the first period

Fig. 7

Comparison of ratio-test values in the second period

Figure 8 shows one successful example of the “Proposed1” method during the second period of data collection. In this case, the threshold for the ratio test was set at 3. The fixed position in 409,627 was established as the origin of the plot. Four types of horizontal results from epochs 409,627–409,630 are included in this figure. The number of visible satellites that the carrier phase can be used at each epoch is shown in parenthesis. The points labeled “FIX1” are horizontal positions from the standard LAMBDA method when the ratio-test statistic is over 3. The points labeled “FLOAT1” are horizontal positions computed from DGPS pseudoranges. The points labeled “FIX2” are horizontal positions from the LAMBDA method aided by user velocity when the ratio-test statistic is over 3. The points labeled “FLOAT2” show the previous fixed position updated by velocity estimates. In “Float2” the previous position was updated by using velocity estimates while the number of visible satellites was less than four. As can be seen in Fig. 8, the float solutions deduced from the proposed method were much more accurate than the float solutions derived from conventional DGPS. This explains why the conventional LAMBDA method did not pass the ratio test at epochs 409,628, 409,628.5, and 409,630, and was not able to produce a solution. In fact, the solutions with minimum residuals in the conventional LAMBDA method in the above three epochs were also wrong. On the other hand, the proposed LAMBDA method with user velocity passed the ratio test and was able to produce correct solutions.

Fig. 8

Successful example of the proposed method

In terms of “Potential Fix”, the difference between the two methods (LAMBDA and Proposed1) was relatively small in the first period (see Table 3) because the number of visible satellites was relatively high during this period. On the other hand, there was a significant difference in the second period (see Table 4) because cases similar to the example shown in Fig. 8 were seen more frequently. This indicates that the proposed method is useful when the number of visible satellites returns to four or more from an insufficient number to support positioning. This advantage is gained mostly from the use of a high-sensitivity receiver.

Road testing in Palo Alto (4-Hz rate)

In order to investigate the effects of a higher data rate, raw GPS data was taken for about 17 min at a rate of 4 Hz in October 2008. The test course was the same as in the previous road test. The average number of visible satellites at the rover car was 6.4. In this analysis, the performance of ambiguity resolution and the differences between the results at 4 Hz and the results at 2 Hz were investigated in detail. Note that the 2 Hz results were generated from the same raw data by decimating the 4-Hz data down to 2 Hz.

Table 5 summarizes the resulting performance using the 4-Hz data, while Table 6 summarizes the resulting performance using the decimated 2-Hz data. The total number of epochs in which that the number of visible satellites was four or more was 4,169 and 2,084, respectively. Compared with the first period in the previous road test, the overall performance was improved a little in spite of the fact that the average number of visible satellites was a little lower. This is because the satellite configuration in this more-recent test was much better overall, and the number of visible satellites did not change as much as in the previous test. Comparing the results at 4 Hz with those at 2 Hz, a slight but significant improvement can be seen in the 4 Hz results. This is expected because, as mentioned earlier, the higher sampling rate should theoretically reduce errors due to user dynamics.

Table 5 Ambiguity resolution summary (4 Hz) (total epochs: 4,169)

Table 6 Ambiguity resolution summary (2 Hz) (total epochs: 2,084)

In order to reveal the accuracy of the proposed float solutions for the different data rates, actual differences between the proposed float solutions and the fixed-integer position solutions (based on a ratio-test threshold of 3) were analyzed. Float solutions based only on the fixed positions of the immediately-preceding epoch were used in order to avoid accumulated errors due to the use of consecutive velocity information. Temporal position differences between the proposed float solutions and the fixed solutions for both 2 and 4 Hz data rates are shown in Fig. 9.

Fig. 9

Temporal position difference between proposed float solutions and fixed solutions

The standard deviations of the temporal position differences were 3.6 cm for 4-Hz data and 4.8 cm for 2-Hz data, respectively. The accuracy of the fixed position itself is expected to be within 1 cm during most of test period. This strongly suggests that the accuracy of the float solutions is better at 4 Hz than at 2 Hz. It was also noticed that errors increased rapidly at traffic intersections for both data rates. There were 14 turns in this period (not counting entering and exiting the parking lot). The arrows corresponding to these turns are shown just below the x-axis of Fig. 9.

Conclusion

Carrier-phase integer ambiguity resolution with Doppler frequency measurements has been evaluated in this paper. In urban areas, pseudorange measurements can suffer from large errors due to multipath, but Doppler measurements are not affected nearly as much. Velocity errors from Doppler measurements will be under 10 cm/s in most cases. This characteristic can significantly improve the performance of integer ambiguity resolution.

This proposed method described in this paper has been evaluated by several static and mobile data sets acquired under different multipath conditions. Commercial GPS receivers were used to collect GPS data at the Stanford University campus and in nearby downtown Palo Alto. Single-epoch ambiguity fixing performance improved dramatically using the proposed method when compared to conventional ambiguity resolution. In addition, the proposed method for real-time determination of standard deviations for the float solutions was effective in further improving ambiguity resolution. Under the static condition tested, the single-epoch fix rate was improved dramatically using the proposed method. Even in road testing using a moving car, the proposed LAMBDA method was effective. The proposed LAMBDA method with the new standard deviations achieved the best performance in both static and moving conditions. It can be concluded that having reliable and accurate float solutions makes it possible not only to find correct fixed solutions, but also to maintain high ratio-test-statistic values, which provide assurance to users that their fixed solutions are correct.

In this paper, both a high-accuracy receiver and a high-sensitivity receiver were used to estimate Doppler frequency. Although the Doppler frequency output from a high-sensitivity receiver is not very accurate, it greatly contributes to robust ambiguity resolution under moving conditions. The high-sensitivity receiver contributes mostly by providing velocity information during periods when the high-accuracy receiver tracks fewer than four satellites.