Does import competition drive productivity growth? Evidence from Hungary’s pre-accession import tariffs

Abstract

This paper studies the effect of increased competition from imports on the productivity of firms. It proposes an empirical model that estimates productivity from sales revenue. The model addresses concerns associated with unobserved prices and demand conditions in revenue productivity. Unlike De Loecker (Econometrica 79(5):1407–1451, 2011), the model builds on recent evidence on the effect of exporting on firm-level prices by distinguishing between the export and domestic demand markets and integrating both in the supply function of firms. It applies this framework to study the effect that tariffs reduction on EU imports had on the efficiency of manufacturing firms in Hungary during the period 1996–2003, and finds that a 10-percentage point reduction in import tariffs on similar products manufactured by a firm raises the firm’s productivity by 1.40%. This is in contrast to 2.35% when revenue productivity is used. The proposed model provides a simple framework that improves productivity estimates from sales data.

1 Introduction

How do manufacturing firms react when faced with increased competition from imports? Do they tend to eliminate inefficiencies in order to be competitive when faced with such competition? While most existing papers focus on the effects of exporting or imported intermediate inputs on firm-level outcomes,¹ only very few papers have studied the effect of increased competition from imports. An example is De Loecker (2011), which studied the effect of import competition, arising from import quota reduction, on efficiency of Belgian textile manufacturers. However, it is not clear whether import competition arising from tariffs reduction will be similar to that arising from quota reduction, as tariffs reduction reduces trade costs which may have a direct impact on market prices. Additionally, it is also not clear whether the effect of import competition on firms in a developed country (i.e. Belgium) will be the same as the case of an emerging economy.

Another issue with most existing studies is with the method productivity is estimated from sales revenue data. Most papers² typically rely on productivity estimates from a revenue production function as sales quantity is unobserved. In these studies, firm-level prices are unobserved, so firm-level sales revenue is deflated using an industry price index and used as the dependent variable in the productivity estimation. This leads to estimates of efficiency with two shortcomings (Levinsohn & Melitz, 2002; De Loecker, 2011). First, the coefficients of the inputs may be biased if the price error defined as the difference between a firm’s price and the industry’s price index is correlated with any production input. This price error is expected to be larger in industries with larger scope of product differentiation. Second, even if this bias is absent, the productivity estimates will reflect true efficiency and components of unobserved prices and demand conditions which may bias the true productivity.

In this paper, we offer two contributions to the literature. First, we study the impact of the gradual reduction in import tariffs charged on EU imports on manufacturing firm’s efficiency in Hungary during the period (1996–2003) leading to Hungary’s accession into the EU. Second, we propose an empirical model that offers less noisy estimates of productivity from revenue data, thus improving on the drawbacks from revenue productivity already mentioned above.

The proposed model nests De Loecker (2011) empirical model³ and revenue productivity model, and we show that each of these models is a special case of our framework under certain conditions, thus offering a more general empirical model for estimating physical productivity from revenue data. The key difference between our model and De Loecker (2011) is that we extend their framework by integrating both the domestic and foreign markets demand conditions (i.e. foreign and domestic demand shocks) to the supply function of the firm, while De Loecker (2011) makes no distinction between foreign and domestic demand shock. This is particularly important given the recent empirical evidence on the strong relationship between exporting and firm-level prices (Garcia-Marin and Voigtländer, 2019). Infact, we show that neglecting the export markets may bias productivity estimates for exporters.⁴

Our paper offers better identification of the effects of import competition on productivity. Unlike other similar studies that identify tariffs at the industry level and argues for exogeneity of tariffs, we identify import tariffs at the firm-product level. In reality, it is difficult to argue that average industry level tariffs negotiations are exogenous (i.e. not influenced by industrial policies, or lobbying by organized sectors etc.), so we leverage on our approach by constructing firm-level exposure to tariffs on imports from the EU and control for time-varying industry effects. This is necessary in our setting for two reasons. First, since export and import tariffs are likely correlated at the industry-level (Trefler, 2004), the industry-year fixed effects, controls for the industry-level export and import tariffs at the 2-digit level. Second, it is possible that some industries received subsidies during this period or were protected due to political lobbying or other unobserved considerations. Thus, our approach enables us control for unobserved time-varying industry effects which may bias our results.

By applying our empirical model, we recover the productivity estimates which we call quality-adjusted productivity (QA productivity).⁵ For comparison, we also recover revenue productivity and productivity from De Loecker (2011) model. Our findings imply that a 10 percentage point reduction in import tariffs⁶ increase QA productivity by 1.40%. We show that De Loecker (2011) model offers a more precise estimate of the effect of import competition on productivity than revenue productivity; however, both models overstate this effect when compared to our framework.

Our empirical model consists of conventional variables (labour, capital, material inputs) and a proxy for unobserved firm-level prices—domestic market share in its industry. We verify that our price proxy replicates similar pattern in studies that observe firm-level prices. In the spirit of Foster et al. (2008), we examine the correlation between our price proxy, revenue productivity and quality-adjusted productivity. While we find a strong positive correlation between our proxy for prices and revenue productivity, the correlation between the proxy and quality-adjusted productivity is negative, consistent with Foster et al. (2008) in their study for the US.

We begin our analysis in Sect. 2 where we present our simple empirical setup and derive a new structural econometric equation for the estimation of productivity from revenue data. We consider the demand side of a two-country world—home and foreign with a representative consumer in each that faces a standard CES utility function and chooses varieties to consume subject to a budget constraint. The usual demand system for each variety emerges which depends negatively on the price and positively on quality of the variety. On the supply side, we consider a firm which produces with a Cobb-Douglas technology, sells in the domestic market and then decides whether to export. The firm’s problem is to choose prices in domestic and export markets (if it exports). We derive the total revenue that emerges in equilibrium and show how to recover productivity. Our productivity estimate is the conventional revenue productivity adjusted with the domestic market share of the firm within its industry.

In Sect. 3, we present our data and discuss several cleaning procedures and restrictions on our sample. We also provide detailed descriptive statistics of the datasets. While in Sect. 4, we estimate our empirical model, the standard revenue productivity model, and De Loecker (2011) model using standard proxy methods pioneered by Olley and Pakes (1996) and extended in Levinsohn and Petrin (2000) and Ackerberg et al. (2015) (henceforth OP, LP and ACF respectively).

In Sect. 5, we estimate the effect of the reduction in import tariffs charged on EU imports on the efficiency of Hungarian manufacturing firms. One of the main strengths of our methodology is that we construct variations in tariffs at the firm-level. By doing this, we are able to control for possible unobserved time-varying industry (NACE 2 digits) effects that jointly affect average industry tariffs and productivity. However, our analysis in this section poses a potential shortcoming. We focus only on exporters because we do not observe products sold by non-exporters. So, we assume that products sold in the export markets are the same as those sold in the domestic market. If exporters have different product mix in the export and domestic markets, it is likely that such patterns exist at a highly disaggregated level of product definition.⁷. This assumption is not likely a concern given the evidence that firms sell same products, but of different quality (taste) across markets (Manova and Zhang, 2012; Crozet et al., 2012).

We identify the tariffs faced by a firm by computing the simple average of the tariffs on products the firm produced and sold in the domestic market in each period,⁸ and employ two empirical strategies. The first strategy is a direct method as in Fernandes (2007) where we estimate the effect of tariffs on productivity directly in a single production function estimation.⁹ The second strategy which we call the two-step approach follows a non-parametric form where we start with estimating the productivity as residuals from a production function estimation and then we project the productivity estimates on tariffs while controlling for some variables of interest as discussed later. We sum up the discussions in Sect. 6 and provide additional information and results in both the online appendix and supplementary online appendix.

1.1 Literature review

We build on the vast and growing literature on production function estimation at the firm level. Starting with Olley and Pakes (1996) (OP) which shows how to control for the simultaneity bias when estimating production functions by relying on investments as proxy for unobserved productivity. Given the lumpy nature of investment data, Levinsohn and Petrin (2000) (LP) showed that material inputs (which are less lumpy) could be used as proxy for productivity in the Olley and Pakes (1996) framework. Their work has been extended by Ackerberg et al. (2015) (ACF) which argued that the coefficient of labor cannot be identified in the first stage of OP and LP framework and shows how to identify labor in the second stage. Other literatures have proposed an adjustment to this framework. For example, Bond and Söderbom ((2005)) have shown (for the Cobb-Douglas production function) that under the scaler unobservable assumptions in the LP and OP framework, using gross output function cannot identify coefficients of perfectly variable inputs without input price variation except further assumptions are imposed. Thus, they propose estimation of a value-added production function. De Loecker (2013) suggests including lagged export dummy in the productivity process of the OP and LP procedure, as lag of export status may be correlated with lag of productivity. These literatures typically rely on deflating sales revenue with industry price index which poses a threat to identification of production inputs and may bias productivity estimates in industries with high scope of product differentiation. Relative to these literatures, we propose a new production function estimation equation that controls for unobserved prices and demand shifters.

Our paper is not the first to integrate the demand-side of the economy to the supply-side in estimating a production function. Klette and Griliches (1996) developed the framework to integrate the demand-side with the supply-side of the economy, thus, addressing the problems caused by deflated sales proxy for firm-level production function estimation in differentiated products. Their focus was on estimating the returns to scale and not productivity. Levinsohn and Melitz (2002) build on this framework, to obtain and interpret credible estimates of productivity. They show that productivity estimates based solely on sales revenue are bias as they reflects price and demand shifters, however they offer no application to their procedure. De Loecker (2011) is the first to apply this methodology in the study of the effect of quota reduction on efficiency of Belgian textile manufacturers. Their estimating equation is a reduced form expression of deflated sales revenue on production inputs (capital, labour and materials), industry output, unobserved demand shifter and productivity. They recover the elasticity of substitution from the coefficient of industry output which they use to back-out quantity productivity from their reduced-form estimates of productivity. Their framework assumes that the unobserved demand shifter can be summarised by a product and sector fixed effect, a proxy for prices and an unobserved error term which they assume to be exogenous. They exploit the multi-products nature of their data and construct a proxy for prices which reflects the extent to which a firm is exposed to the rapid easing of quotas in the EU during the period 1994 to 2002. They find that their methodology predicts weaker effect of trade liberalization on firm-level productivity compared to revenue productivity. Relative to these papers, we offer a general framework for addressing this problem of unobserved prices. Our model nests De Loecker (2011)’s model and shows that their main estimating equation is a special case of ours under the assumption that firms do not export. By allowing for exporting, we show that our estimating equation is equivalent to De Loecker (2011) model with an additional term which reflects the firms’ export intensity. Unlike their framework, ours do not rely on estimates of the industry elasticity of substitution or precise observation of industry output variable to back out physical productivity.

Our paper is also related to Rho and Rodrigue (2016). The main similarity is that both papers estimate a model-consistent productivity under the assumption that firms endogenously respond to idiosyncratic demand shocks in the foreign market. While their paper focuses on understanding the impact of investment on exporting, we focus on how increased import competition faced by firms affects physical productivity. In addition, they normalize domestic demand shocks to one, while we assume it to be different across firms and time. This is important in our setting as our objective is to investigate the relationship between firm-level variation in domestic demand shocks and productivity. Demidova et al. (2012) use a similar estimation approach as ours in studying the effects of productivity and country-specific export demand shocks on export destination. While theirs introduces destination-specific export demand shocks non-parametrically in their material function, we incorporate both domestic and export demand shocks addressed to a firm in a structural empirical model. Besides, our focus is different from theirs. While we are interested in a more precise estimate of productivity and how import competition impacts it, they focus on the effects of interaction between productivity and country-specific export demand shocks on a firm’s export destination.

Our paper is also related to Foster et al. (2008) which investigates the distinction between quantity and revenue productivity. In their framework, they observed both physical output and sales revenue at the firm level in addition to input variables. They estimate quantity and revenue productivity and perform a number of comparative analysis between their estimates. One finding that emerges from their study is that the correlation between plant prices and revenue productivity is positive with a correlation coefficient of 0.16, however this correlation with physical productivity is negative with a coefficient of $-0.54$. The findings in our paper is consistent with theirs. Our proxy for prices is negatively correlated with quality-adjusted productivity and positively correlated with revenue productivity. The similarity between both findings supports the notion that revenue productivity may reflect rising firm-level prices and also implies that domestic market shares of a firm within its industry is strongly correlated with unobserved prices.

This paper is also related to the vast and growing literature studying the impact of trade liberalization on productivity of firms (Topalova and Khandelwal, 2011)—Indian firms; Fernandes (2007)—Colombian firms; Lileeva and Trefler (2010)—Canadian firms; Bustos (2011)—Argentine firms; De Loecker et al. (2016)—Indian firms; Trefler (2004)—Canadian firms; among many). Some of these papers use either revenue productivity (Topalova and Khandelwal 2011; Fernandes 2007) or labor productivity (Trefler, 2004) and find a positive effect of trade liberalization on productivity. We argue that using revenue productivity may overestimate the effect of trade liberalization, and we introduce a methodology that corrects for this potential bias.

A number of recent studies have analyzed the impact of import competition on firm-level or firm-product efficiency (Bräuer et al., 2019)—German manufacturing firms; Dhyne et al. (2017)—Belgian manufacturing firms; etc.). In these studies, import competition is measured as a firm’s exposure to imports of similar products that they manufacture; and find efficiency gains from import competition. We differ from these studies in the measurement of import competition and a focus on an emerging economy. Shu and Steinwender (2019) provide a detailed review of the empirical literature on the impact of trade shocks (import competition, export opportunities, access to imported intermediate inputs, and foreign input competition) on firm-level efficiency.

Some other studies analyzed the effect of import competition on product quality and prices such as Amiti and Khandelwal (2013) and Bas and Strauss-Kahn (2015); both find a positive effect of import competition on quality upgrading. McManus and Schaur (2016) find a positive effect of import competition on workplace injury rates in the US. Our paper differs as we focus on physical productivity. This work is also related to Khandelwal (2010). Both papers use market shares as proxy for quality conditional on prices¹⁰ and investigate different questions.

To our knowledge, this paper is the first to consider the effect of foreign demand shocks on firm-level productivity estimates using sales revenue data.

2 Empirical framework

In this section, we start with a model of demand and supply side, derive the estimating equation of interest and discuss the advantages of the framework.

2.1 Demand

Consider a world consisting of two countries home h and foreign f, and a representative industry with many firms producing differentiated goods. Our analysis is focused on firms in the home country. Consumers in both countries have the constant elasticity of substitution (CES) preferences with same industry elasticity of substitution between varieties denoted by $\sigma >1$. Consumers in country $i=\{h,f\}$ spend $R_{i}$ in nominal terms on varieties in the industry. A representative consumer in each country i maximizes its utility given by:

$$\begin{aligned} U_{i}=\bigg [ \int _{\omega \in \Omega } \tilde{q_{i}}(\omega )^{\frac{\sigma - 1}{\sigma }}d\omega \bigg ]^{\frac{\sigma }{\sigma - 1}} \text {for } i\in \{h, f \} \end{aligned}$$

(1)

We assume $U_i$ to be differentiable and quasi-concave. The quantity of each consumed variety is denoted by $\tilde{q_i}(\omega )$ which is measured in units of utility. For each industry, we assume that all varieties are measured in similar physical units such that $\tilde{q_i}(\omega )$ can be seperated into a demand shifter $\zeta _h(\omega )$ which we call quality and physical units $q_i(\omega )$ such that $\tilde{q_i}(\omega ) = \zeta _h(\omega )q_i(\omega )$. The product quality $\zeta _h(\omega )$ can be seen as a single dimensional metric of the representative consumer’s valuation of product characteristics in one physical unit of the product (Johnson 2012). Thus, product quality acts as a demand shifter for physical quantities. Changes in $\zeta _h(\omega )$ across time could result from either changes in the quality embodied from the good or changes in consumer’s relative valuation of the product. For foreign consumers, we assume $\zeta _f(\omega )=\zeta _h(\omega )\nu _f$ such that $\nu _f\ge 0$ is the foreign demand shock. This allows for changes in idiosyncratic preferences for product $\omega$ across countries. Consumers in both countries are subject to the budget constraint: $\int _{\omega \in \Omega }p_{i}(\omega ) q_{i}(\omega )d\omega = R_{i}$, where $p_{i}(\omega )$ and $R_i$ are the price of variety $\omega$ and income in country i respectively. This setup generates the usual demand system faced by each firm i as :

$$\begin{aligned} q_{i}(\omega )=\zeta _{i}(\omega )^{\sigma -1}\chi _{i}p_{i}(\omega )^{-\sigma } \end{aligned}$$

(2)

where $\chi _{i}=P_{i}^{\sigma -1}R_{i}$ is the aggregate level of demand in the sector in country i , this can be interpreted as the position of the demand curve common to all firms and $P_{i}=[\int _{w \in \Omega } \zeta _{i}(\omega )^{\sigma -1}p_{i}(\omega )^{1-\sigma }d\omega ]^{\frac{1}{1-\sigma }}$ is a summary of the prices of all available varieties in an industry in country i. We assume that firms are small relative to the industry they belong to, so they have no power to exert any influence on this industry price index $P_{i}$ and take it as given.

2.2 Supply

We assume that all firms j are heterogeneous in their productivity levels $A_{j}$ and produce a single variety j under monopolistic competition. To avoid the abuse of notations we henceforth denote j in place of $\omega$ such that $q_{i}(\omega )\equiv q_{ij}$. Firms produce with a Cobb-Douglas technology using labor $L_{j}$, physical capital $K_{j}$ and material inputs $M_{j}$. We follow the literature and assume that labor $L_j$ and capital $K_j$ are predetermined (Halpern et al., 2015) and material is a perfectly variable input with price normalised to 1¹¹ and can be freely adjusted at any point in time. Firm $j's$ production function in the current period is:

$$\begin{aligned}q_{j} = A_{j}K_{j}^{\alpha _k} L_{j}^{\alpha _l} M_{j}^{\alpha _m} \end{aligned}$$

where $A_j=exp(a_j + \mu _j)$ and $\mu _j$ is the measurement error and idiosyncratic shock to production. Our assumption on $M_j$ implies that the total variable cost is given by :

$$\begin{aligned} TVC_{j} = q_{j}^{\frac{1}{\alpha _m}} A_{j}^{-\frac{1}{\alpha _m}}K_{j}^{-\frac{\alpha _k}{\alpha _m}}L_{j}^{-\frac{\alpha _l}{\alpha _m}} \end{aligned}$$

Note here that we do not assume any specific marginal cost structure. Firms may export some of their output to the foreign market by paying a fixed export cost $f_{f}$ which reflects additional cost incurred by doing business abroad. We assume that the price which exporters receive ($p_{jf}$) is different from that paid by foreign consumers such that $p_{jf}^*=p_{jf}\tau _j$, where $\tau _{j}>1$ is the import tariff or shipping cost. The firm’s problem is to maximize profits choosing prices in both domestic and foreign markets subject to the demand curve in Eq. (2). We can rewrite this problem as:

$$\begin{aligned} \max _{q_{jh} q_{jf}}\bigg \{ q_{jh}^{\frac{\sigma - 1}{\sigma }}(\zeta _{jh}^{\sigma -1} \chi _{h})^{\frac{1}{\sigma }} + \frac{q_{jf}^{\frac{\sigma - 1}{\sigma }}(\zeta _{jf}^{\sigma -1} \chi _{f})^{\frac{1}{\sigma }}}{\tau _{j}}- \frac{(q_{jh} + q_{jf})^{\frac{1}{\alpha _m}}}{A_{j}^{\frac{1}{\alpha _m}}K_{j}^{\frac{\alpha _k}{\alpha _m}}L_{j}^{\frac{\alpha _l}{\alpha _m}}} - f_{h}- f_{f}\bigg \} \end{aligned}$$

(3)

where $f_h$ is the fixed cost of selling at home. This yields the price equation:

$$\begin{aligned} p_{jh}=\bigg (\frac{\sigma }{\sigma - 1}\bigg )^V \bigg [\frac{1}{\alpha _{m}} (A_jK_j^{\alpha _k} L_j^{\alpha _l})^{-\frac{1}{\alpha _m}}\bigg ]^V \zeta _{jh}^{1- \frac{V}{\alpha _m}} (\chi _h + \tau ^{-\sigma } \nu _f^{\sigma - 1} \chi _f)^{\frac{V(1-\alpha _m)}{\alpha _m}} \end{aligned}$$

(4)

where $V=\frac{\alpha _m}{\alpha _m - \sigma (\alpha _m-1)}$. Provided $\alpha _m \ne 1$, a change in the demand shifter has an effect on prices. Foreign demand shock has an effect on unobserved firm level prices ($p_{jh}$) making it imperative to integrate the foreign demand system into the supply function of the firm. We derive the firm-level domestic, foreign, and total revenue that emerges from this framework (see supplementary online appendix) respectively below:

$$\begin{aligned} R_{jh}&= Z^{V(\sigma -1)}(A_{j} K_{j}^{\alpha _k} L_{j}^{\alpha _l})^{\frac{V(\sigma -1)}{\alpha _m}} \zeta _{jh}^{\frac{V(\sigma -1)}{\alpha _m}}\chi _{h}(\chi _{h} + \tau _{j}^{-\sigma } \nu _{jf}^{\sigma -1}\chi _{f})^{\frac{V}{\alpha _m}-1} \end{aligned}$$

(5)

$$\begin{aligned} R_{jf} &= Z^{V(\sigma -1)}(A_{j} K_{j}^{\alpha _k} L_{j}^{\alpha _l})^{\frac{V(\sigma -1)}{\alpha _m}} \zeta _{jh}^{\frac{V(\sigma -1)}{\alpha _m}}\chi _{f}\nu _{jf}^{\sigma -1} \tau _{j}^{-\sigma }(\chi _{h} + \tau _{j}^{-\sigma } \nu _{jf}^{\sigma -1}\chi _{f})^{\frac{V}{\alpha _m}-1} \end{aligned}$$

(6)

$$R_{{jT}} = \left\{ {\begin{array}{*{20}l} {Z^{{V(\sigma - 1)}} (A_{j} K_{j}^{{\alpha _{k} }} L_{j}^{{\alpha _{l} }} )^{{\frac{{V(\sigma - 1)}}{{\alpha _{m} }}}} (\zeta _{{jh}}^{{\sigma - 1}} \chi _{h} )^{{\frac{V}{{\alpha _{m} }}}} } \hfill & {{\text{if firm sells at home}}} \hfill \\ {Z^{{V(\sigma - 1)}} (A_{j} K_{j}^{{\alpha _{k} }} L_{j}^{{\alpha _{l} }} )^{{\frac{{V(\sigma - 1)}}{{\alpha _{m} }}}} \zeta _{{jh}}^{{\frac{{V(\sigma - 1)}}{{\alpha _{m} }}}} (\chi _{h} + \tau _{j}^{{ - \sigma }} \nu _{{jf}}^{{\sigma - 1}} \chi _{f} )^{{\frac{V}{{\alpha _{m} }}}} } \hfill & {{\text{if firm sells in both}}} \hfill \\ \end{array} } \right.$$

(7)

where T denotes total and $Z=(\frac{\sigma -1}{\sigma })\alpha _m$. Our aim in this exercise is to derive an empirical equation which estimates physical productivity from total revenue data. There are 3 unobservable variables in Eq. (7b)—$\zeta _{jh}$, $\tau _j$ and $\nu _{jf}$. We can reduce the unobservables by dividing Eq. (5) by (6)

$$\begin{aligned} \nu _{jf}^{\sigma -1}\tau _j^{-\sigma }=\frac{R_{jf}\chi _h}{R_{jh}\chi _f}=\frac{R_{jf}/P_{sf}^{\sigma -1} R_{sf}}{ R_{jh}/P_{sh}^{\sigma -1} R_{sh}} \end{aligned}$$

(8)

where s denotes the sector/industry. Equation (8) can be interpreted as the competitiveness of a firm in the export market relative to the domestic market. This relative competitiveness can be increasing due to either a decrease in the tariffs faced by a firm or an increase in the export demand. We substitute Eq. (8) in (7) and simplify to obtain:

$$\begin{aligned} \frac{(R_{jh} + R_{jf})}{P_{sh}}= A_j K_{j}^{\alpha _k}L_{j}^{\alpha _l}M_{j}^{\alpha _m}\zeta _{jh}\bigg (\frac{R_{jh}}{R_{sh}}\bigg )^{\frac{1}{|\sigma - 1 | }} \end{aligned}$$

(9)

Denote $D_{jh}=\frac{R_{jh}}{R_{sh}}$ the domestic market share of the firm j within its industry s; $\frac{1}{|\sigma -1 | }$ yields an estimate of the industry elasticity of demand. Taking logs of Eq. 9 and including a time subscript we derive:

$$\begin{aligned} {\tilde{r}}_{jt}= \alpha _l l_{jt} + \alpha _k k_{jt} + \alpha _m m_{jt} + \beta d_{jt} + ln \zeta _{jht}+ a_{jt} + \mu _{jt} \end{aligned}$$

(10)

Equation (10) is our new production function estimation equation, where $\beta =\frac{1}{|\sigma -1| }$ and all lower-case variables are in log terms. The demand shifter $\zeta _{jh}$ is unobserved, but positively correlated with domestic market shares $d_{jt}$¹². Therefore, part (but not all) of the variation in quality $\zeta _{jh}$ is captured by variations in the domestic market shares ($d_{jt}$). In addition, $d_{jt}$ also captures variation in prices not related to product quality.¹³ Note, $\alpha _l$, $\alpha _k$ and $\alpha _m$ are structural parameters of the production function, and the industry elasticity of substitution can be recovered from $\beta =\frac{1}{|\sigma -1|}$. In section A1 and A2 of the online appendix, we compare our estimating Eq. 10 with standard revenue productivity equation and De Loecker (2011) quantity productivity equation.

3 Data

In this section, we describe our data sources and cleaning procedure, and present some descriptive statistics.

We use 3 datasets from Hungary. The first is production data which is a panel of the universe of Hungarian firms’ balance sheet data for the period 1993–2003. The second is a panel of export data consisting of firm-product and export destination information for the period 1993–2003. The third is data on import tariffs charged on EU imports for the period 1996–2003. We also complement this with data on producer price index (PPI) by industry publicly available at the online database of Hungarian statistical office. We briefly describe the datasets and provide additional details in the supplementary online appendix.

3.1 Production data

The production dataset comes from Hungarian Tax Authority (APEH) and includes balance sheet and income statement information such as net value of sales and exports, fixed assets, wage bills, costs of goods and material inputs, and average annual employment, among others. For the purpose of this paper, we focus on manufacturing firms¹⁴ with at least one employee and positive sales value, and delete observations from non-manufacturing firms and manufacturing firms with less than one employee and zero sales revenue. The data consists of 95033 unique firms and 605056 observations. Out of these, there are 239361 observations for which total exports is greater than total sales. We drop these observations as we consider them a reporting error and we are unsure about how to treat them.¹⁵ We merge the data with industry producer price index (PPI) at the 2-digit NACE identifier and create new variables for deflated total sales, exports sales and material inputs using the PPI. We construct domestic sales by subtracting exports from total sales. In the supplementary online appendix, we discuss a number of data cleaning procedure and treatment of missing values for sales, capital, employment and material inputs. After the cleaning, the manufacturing sectors consist of 64979 unique firms and 324351 firm-year observations. Out of these, approximately 40% of firms exported at least once throughout our sample period. We classify these firms as exporters. Table 1 shows some descriptive statistics of the production data. We observe an increasing pattern for total sales, exports and material inputs throughout the sample period. The fraction of exporters ranges between 0.42 to 0.54, however these exporter’s share of total sales lie between 93 and 96% of total sales. This suggests that the impact of import competition on exporting firms can be generalised to all firms considering the weight of exporter’s total sales in aggregate output. In column (9), We show that the average annual growth of wage per worker increased over the time period studied with decline in some periods. Overall, the observed patterns are consistent with existing studies.

Since the domestic market share of a firm within its industry is crucial in this work, we describe the patterns of this variable over time. We proceed by computing the fraction of domestic sales within an industry attributed to the top 1%, 5% and 10% of firms in each year. The top 1%, 5% and 10% of firms are defined in terms of their yearly domestic sales within an industry. We then summarise its distribution across industries in Table 2. For example under Top 1%, in 1993, the minimum across industries for the fraction of domestic market share attributed to the top 1% of firms within an industry is 20%, the maximum is 38.5% and the median is 29%. The table shows that in the median industry, the top 10%, 5% and 1% of firms contributed 73.5%, 60.5% and 29% of total domestic sales in 1993. This pattern is consistent across all the years in our data. The results imply that the domestic sales within an industry is heavily concentrated in very few number of large firms—superstar firms using the parlance in Mayer and Ottaviano (2008). In Table (S2), we present the share of total sales and number of firms attributed to the top 1%, 5%, and 10% of firms in terms of the total sales. As expected, the top 1% of firms accounts for between 56% to 68% of total sales, while the top 10% of firms account for over 89% of total sales.

Table 1 Summary statistics of production data

3.2 Trade data

This dataset comes from Hungarian statistical Office and assembled from customs declarations. It consists of a complete set of firm-level transactions on exports in Hungary at a highly disaggregated level (Combined Nomenclature-10). That is, we observed the range of products exported by a firm, the export destination, quantity and sales value. The total number of observations is 2,466,408.¹⁶ Table 3 shows a summary statistics of the trade data. We see that the largest fraction of Hungarian manufacturing exports goes to the EU/EFTA during the period covered in our data. This is also true for Hungarian imports from the EU/EFTA as shown in Fig. 1. Between 73 and 79% of Hungarian manufacturing export destination is the EU, and between 55 and 66% of imports are from the EU during the period 1996–2003. Clearly, the EU/EFTA is Hungary’s biggest trading partner during the period 1996–2003. The second export destination are a group of countries consisting mainly of Central and Eastern European countries (see notes in Table 3).

Table 2 Summary statistics for domestic market share

Fig. 1

Total imports and share of imports from the EU/EFTA (1992–2003)

3.3 Tariff data

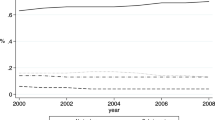
Our tariffs dataset comes from Hungarian trade office. The data consists of raw files of highly disaggregated (CN-10) product tariffs charged on EU imports, bilateral product tariffs with members of Central European Free Trade Association (CEFTA) and tariffs charged on other Central European countries, Israel and Turkey during the period 1996–2003. This tariffs capture the differential exposure of Hungarian products to different tariffs with the EU and other countries. We aggregate the tariffs with the EU/EFTA countries¹⁷ by taking simple averages at the HS-6 level for each year. Column (6) of Table 3 shows the average import tariffs charged on EU/EFTA imports. Clearly, tariffs are reducing during the period leading to Hungary’s entry into the EU. Average tariffs fell by over 75% between 1996–2003.¹⁸ In Fig. 2, we plot the average tariffs (in percentages) on imports from the EU/EFTA and Group 2 countries. The figure shows a strong positive co-movements between both tariffs. It also suggests that any of these tariffs can be used as a measure of import competition. Since Hungary’s biggest trading partner is the EU/EFTA, we choose the tariffs with the EU/EFTA in our analysis.

We merge these datasets. Our final sample contains 39128 observations and 11038 unique firm identifiers. During the late nineties, a large number of firms were part of the supply chain for large firms in the EU, thus domestic sales may not matter to them. These export platforms are pronounced in the auto manufacturing industry and may have little presence in other industries. Since we do not observe these firms in the data, and in order to address this potential concern, we create a sub-sample by excluding firms in Motor vehicles, trailers and semi-trailers and Other transport equipments industries (NACE 2 industry 34 and 35), and firms with over 70% of export share from our sample. This new subsample consists of 27829 observations and 9071 unique firm identifiers. This will be our main sample. We provide detailed discussions on the merging procedure in section (S2.2) of the supplementary online appendix.

Table 3 Share of Hungarian exports across different destinations

Fig. 2

Import tariffs. See notes below Table 3 for a list of countries under Group 2

4 Estimation strategy

In this section, we describe the estimation procedure and identification that provides estimates of productivity. Our procedure relies on the proxy methods developed in Olley and Pakes (1996) and extended by Levinsohn and Petrin (2000) and Ackerberg et al. (2015). The main estimating equation is given by:

$$\begin{aligned} {\tilde{r}}_{jt}= \alpha _l l_{jt} + \alpha _k k_{jt} + \alpha _m m_{jt} + \beta d_{jt} + a_{jt} + ln\zeta _{jht} + \mu _{jt} \end{aligned}$$

(11)

All variables are as defined in Sect. 2. Our goal here is to obtain consistent estimates of the firm-level productivity. Since we do not observe the demand shifter $\zeta _{jht}$, we need to construct a variable which approximates it. As already mentioned, changes in $\zeta _{jht}$ across time could result from either changes in the quality embodied in the good or changes in consumer’s relative valuation of the product. We already assumed that firms are endowed with quality (as in Johnson, 2012), so that any variation in $\zeta _{jht}$ will result from consumer’s relative valuation of the product.¹⁹ We argue that the variation in demand addressed to a product will depend on the availability of substitutes. As the decline in tariffs on EU imports is likely to increase the net number of competing varieties addressed to a firm (Melitz 2003), $\zeta _{jht}$ will reflect a firm’s exposure to the prevailing import tariffs.²⁰ We approximate $\zeta _{jht}$ with an industry dummy $\alpha _s$, year dummy $\alpha _t$, average tariffs faced by a firm ${\bar{\tau }}_{jt}$, a dummy for whether a firm used imported inputs $imp_{jt}$²¹ and an unobservable firm-specific demand shock ${\tilde{\zeta }}_{jht}$ which we assume to be independent and identically distributed (iid) across firms over time. That is:

$$\begin{aligned} \zeta _{jht} = \alpha _s + \alpha _t + \rho {\bar{\tau }}_{jt} + imp_{jt} + {\tilde{\zeta }}_{jht} \end{aligned}$$

(12)

The highly disaggregated nature of our data makes it possible to construct each producer’s exposure to trade policy in each time period. In some specification, we control for industry-time dummies instead of a separate industry and time fixed effects to address a potential concern that industry export and import tariffs may be correlated. The industry-time dummies controls for any time-variant industry effects that maybe correlated with firm level characteristics such as unobserved industrial policies such as subsidies, tax preferences, average industry tariffs, endogeneity of industry level tariffs etc. We then rewrite our main estimating equation as:

$$\begin{aligned} {\tilde{r}}_{jt}= \alpha _l l_{jt} + \alpha _k k_{jt} + \alpha _m m_{jt} + \beta d_{jt} + a_{jt} + \alpha _s+ \alpha _t + \rho {\bar{\tau }}_{jt} + imp_{jt} + \mu _{jt}^*\end{aligned}$$

(13)

where $\mu _{jt}^*=\mu _{jt} + {\tilde{\zeta }}_{jht}$ is the zero-mean shocks that are uncorrelated with the regressors. To study the effect of import competition on productivity, we can estimate Eq. (13) directly or we employ a two-step method where we estimate ${\tilde{r}}_{jt}= \alpha _l l_{jt} + \alpha _k k_{jt} + \alpha _m m_{jt} + \beta d_{jt} + a_{jt} + \mu _{jt}$ and recover the productivity estimates $a_{jt}$ in a first step, and then regress the recovered productivity on average tariffs ${\bar{\tau }}_{jt}$ whilst controlling for some covariates in the second step. We provide a detailed discussion on this in Sect. 5. We estimate Eq. 13 borrowing insights from Ackerberg et al. (2015)

We use firm-level sales revenue data deflated by NACE 2-digit industry-specific price indices as the dependent variable and we also deflate other nominal variables using same price indices. We specify an endogenous process for productivity which depends on lagged productivity. The law of motion of productivity is assumed to follow a first-order markov process as defined below:

$$\begin{aligned} a_{jt} = f(a_{jt-1}) + \xi _{jt} \end{aligned}$$

(14)

where $\xi _{jt}$ is the innovation term. This specification ensures that we control for any time-invariant effects that may be correlated with unobserved productivity and inputs. The innovation term $\xi _{jt}$ is by OP/LP assumption uncorrelated with the firm’s lagged choice variables.

We commence by assuming that materials $m_{jt}$ is directly related to unobserved productivity, labor input, import tariffs, and our proxy for price and demand shifter—domestic market shares. Specifically, as assumed in OP/LP, capital in period t is determined through its choice of investment in period $t-1$ (i.e. $k_{jt}$=g($k_{jt-1}, i_{jt-1}$) ), and as in ACF, $l_{jt}$ is chosen either in period $t-1$, $t-q$ (such that $0<q<1$) or t. The crucial thing here is that material inputs is chosen conditional on $l_{it}$. What is new here is that we introduce a new variable to the ACF framework by assuming that the firm observes its domestic demand in either period t or $t-q$ before choosing its material inputs. In otherwords, material inputs are chosen conditional on $k_{jt}, l_{jt}, d_{jt}, a_{jt}, {\bar{\tau }}_{jt}$.²² This gives rise to the function of material inputs as:

$$\begin{aligned} m_{jt}=g_t(k_{jt}, l_{jt}, d_{jt}, a_{jt}, {\bar{\tau }}_{jt}) \end{aligned}$$

(15)

This relies on the assumption that input demand is monotonically increasing in productivity under monopolistic competition²³ conditional on $k_{jt}, l_{jt}, d_{jt},$ and ${\bar{\tau }}_{jt}$. With the monotonicity assumption, we can invert Eq. (15) and derive a function that proxies for productivity as:

$$\begin{aligned} a_{jt}=g_t^{-1}(k_{jt}, l_{jt}, d_{jt}, m_{jt}, {\bar{\tau }}_{jt})=h_t(k_{jt}, l_{jt}, d_{jt}, m_{jt}, {\bar{\tau }}_{jt}) \end{aligned}$$

(16)

The estimation consists of two stages as in Ackerberg et al. (2015) except for the fact that we obtain both demand and supply parameters in the second stage. In the first stage of the procedure, we estimate the equation of the form:

$$\begin{aligned} {\tilde{r}}_{jt}= \phi _t( k_{jt} ,l_{jt}, d_{jt}, m_{jt}, {\bar{\tau }}_{jt}) + \alpha _s + \alpha _t + imp_{jt} + \mu ^*_{jt} \end{aligned}$$

(17)

where $\phi _t(k_{jt} ,l_{jt}, d_{jt}, m_{jt}, {\bar{\tau }}_{jt}) = \alpha _k k_{jt} + \alpha _l l_{jt} + \alpha _m m_{jt} + \beta d_{jt} + \rho {\bar{\tau }}_{jt} +h_t(m_{jt}, k_{jt}, l_{jt}, d_{jt},{\bar{\tau }}_{jt})$. In some specifications, we control for industry-year dummies to ensure that any unobservable industry level time-varying effects which may be jointly correlated with import tariffs do not bias our results. Foreign firms are more productive than domestic firms (Halpern et al., 2015). In an unlikely scenario where ownership status is correlated with import competition, our estimates of ${\bar{\tau }}_{jt}$ will be biased. So, we also include foreign ownership dummy in the material function in some specifications, where a firm is classified as foreign-owned if foreigners own over 50% of the firm’s equity.

In principle, none of the input variables can be identified in the first stage. We compute $\hat{\phi _t}(.)$ from first stage estimation where $h_t(m_{jt}, k_{jt}, l_{jt}, d_{jt}, {\bar{\tau }}_{jt})$ is proxied by a third-order polynomial function of its components. In the second stage, we provide moment conditions to identify the parameters of interest after obtaining the innovation term. We commence by using $\hat{\phi _t}(.)$ and together with initial guess of the coefficient vector $\varvec{\alpha _z}=\{\alpha _k, \alpha _l , \alpha _m, \beta , \rho \}$ and for any other candidate vector of $\varvec{\tilde{\alpha _z}}$, productivity is computed as:

$$\begin{aligned}a_{jt}(\varvec{\tilde{\alpha _z}})= \hat{\phi _t}(.) - (\tilde{\alpha _k} k_{jt} - \tilde{\alpha _{l}}l_{jt}-\tilde{\alpha _{m}}m_{jt} -{\tilde{\beta }}d_{jt} -{\tilde{\rho }}{\bar{\tau }}_{jt})\end{aligned}$$

We use our productivity process (Eq. 14) to recover the innovation term $\xi _{jt}$ by a non-parametric regression of $a_{jt}(\varvec{\tilde{\alpha _z}})$ on its own lag $a_{jt-1}(\varvec{\tilde{\alpha _z}})$. We define the moment condition below and iterate over candidate vector $\varvec{\tilde{\alpha _z}}$

$$\begin{aligned} {\varvec{E}}\left \{ \xi _{jt} (\tilde{\alpha _k}, \tilde{\alpha _m}, \tilde{\alpha _m}, {\tilde{\beta }}, {\tilde{\rho }}) \left( \begin{array}{c} k_{jt} \\ l_{jt-1} \\ m_{jt-1} \\ d_{jt-1} \\ {\bar{\tau }}_{jt-1}\end{array} \right) \right \}=0 \end{aligned}$$

(18)

Thus, Eq. (18) states that for the optimal $\varvec{\tilde{\alpha _z}}$, the innovation term $\xi _{jt}$ is uncorrelated with our instruments ($k_{jt}$ $l_{jt-1}$ $m_{jt-1}$ $d_{jt-1},{\bar{\tau }}_{jt-1}$ )$^\prime$. The optimal value of $\varvec{\tilde{\alpha _z}}$ gives us our coefficient of interest.²⁴

We also estimate both revenue productivity (using similar procedure as above) and quantity productivity from De Loecker (2011).²⁵ We recover the productivity measures using the estimated parameters ${\hat{\alpha }}_l,{\hat{\alpha }}_k, {\hat{\alpha }}_m,$ and ${\hat{\beta }}$ and perform a number of comparative analysis in Section A3 of the online appendix.

5 Effects of import competition on productivity

In this section, we study the impact of import competition measured as reduction in tariffs charged on imports from the EU on firm level productivity during the period between 1996 and 2003. We focus on firms with at least two observations during the period studied.

Our data limitation poses two potential shortcomings. First, we do not observe the product mix of non-exporters so we cannot match our tariff information to non-exporters. However, this is not an issue as total sales attributed to exporting firms ranges between 93% to 96% of total sales of all firms during the period 1996–2003 (see Table 1). Second, we observe products exported by exporting firms but we do not know whether exporters have different product mix in the domestic and foreign markets. This is clearly not a concern if products mix in domestic and foreign markets are differentiated at a highly disaggregated level (HS-6 and above).²⁶ This assumption is somewhat consistent with existing literature which finds that firms sells same products but of different quality (taste) across markets (Manova and Zhang, 2012; Crozet et al., 2012).²⁷ Thus, we remind the reader about these caveats in the interpretation of our results.

After estimating the impact of import competition on quality-adjusted productivity, we compare the estimates with that obtained when revenue productivity and physical productivity estimates based on De Loecker (2011);—subsequently, we call it DEL productivity. We also examine whether foreign-owned firms benefit more or less from import competition compared to domestic firms.

As already discussed in Sect. 4, we employ two estimation strategies—two-steps strategy and direct method. In the first step of the two-steps strategy, we separately estimate the three productivity measures using the methods described in Sect. 4. In the second step, we project the recovered productivity estimates against the tariffs faced by each firm. While the quality-adjusted productivity allows the productivity response to be isolated from the foreign and domestic demand response, DEL productivity isolates only the domestic demand response, and revenue productivity does not isolate any demand response. Before proceeding to the regression equation, we remind the reader about the underlying assumption that the tariff setting process is exogenous to the firm. This assumption is plausible given that the chances that a single firm in Hungary influenced trade decisions at the EU level is quite slim.

The second stage involves a regression of the form:

$$\begin{aligned} \omega _{jt}^i = k + \rho {\bar{\tau }}_{jt} + \alpha _{st} + \beta X_{jt} + \epsilon _{jt}, i\in \{C,N, D\} \end{aligned}$$

(19)

where we now denote productivity by $\omega _{jt}^i$, where superscripts C, N and D denote revenue, QA and DEL productivity respectively. $\alpha _{st}$ is an industry time fixed effect which controls for any industry-level time-variant heterogeneity that are simultaneously correlated with import tariffs and productivity. Such heterogeneity may include endogeneity from organized industry lobbying for preferential protection. ${\bar{\tau }}_{jt}$ is the average import tariffs at the 6-digits product level, and $X_{jt}$ are controls such as lagged productivity or ownership dummy. Our main coefficient of interest is $\rho$ which measures the effects of import competition on productivity. Since $\omega _{jt}^C=\omega _{jt}^N + (p_{jt} - P_{sht} - \zeta _{jht})$, Eq. (19) implies that regressing revenue productivity on tariffs rely on the strong assumption that firm-level tariffs are uncorrelated with prices. This clearly overstates the effect of import competition on revenue productivity²⁸ and sheds some light on the importance of integrating the demand system in production function estimation if sales quantity is unobserved. In the estimation, we use either contemporaneous or lagged tariff variables.

The second estimation strategy is the direct method which we already described in Sect. 4. Here, the effects of import competition on productivity is estimated in a single production function equation.

5.1 Estimation results

The results are presented in Tables 4, 5 and 6 using both contemporaneous and lagged average tariffs.²⁹ We proceed with the direct approach by comparing the results for the quality-adjusted, revenue, and DEL productivity in Table 4. Clearly, import competition (i.e. coefficient of tariffs in Table 4) is associated with an increase in firm-level productivity across all specifications, however, our methodology offers the most modest impact (columns 1 and 2), followed by DEL productivity (columns 5 and 6), and revenue productivity (columns 3 and 4), consistent with the theory presented in Sect. 2.³⁰

We now turn to our preferred specification in Table 5 where we present the results of the direct approach estimates for quality-adjusted and revenue productivity, controlling for industry-time fixed effects.³¹ The results imply that a 10 percentage point reduction in tariffs is associated with an increase in firm-level productivity by 1.4% when QA productivity is used. However, same 10 percentage point reduction in tariffs is associated with an increase in revenue productivity by 2.35%. This pattern is consistent even when we control for importers dummy and foreign ownership dummy (Table 4). The average import tariffs during our period of study declined from 8.13% in 1996 to 1.99% in 2003 (Table 3)—a drop by 6.14 percentage points. Hence, our results suggest that import competition increased productivity by 0.84%. In sum, these findings imply that import competition increased firm-level efficiency, and its effect is overstated when revenue productivity is used as the measure of efficiency. In addition, our results imply that productivity measurements from sales revenue data can be improved if export markets are integrated into the supply function of firms.

We now present the results for the two-steps approach, starting with the first stage estimates in Table (S3) of the supplementary online appendix, and the second-stage estimates (Eq. 19) in Table 6 panels I, II and III for QA, Revenue and DEL Productivity respectively, using both contemporaneous (columns 1–2) and lagged tariffs (columns 3–7). Similar to the findings in the direct approach, the results in the two-steps approach show that import competition is associated with an increase in firm-level productivity across all specifications. However, QA productivity offers the most modest estimate when compared with revenue and DEL productivity.

Our preferred specification is in column 2 of Table 6 where we controlled for industry-year fixed effects. The estimates from this specification suggest that a 10 percentage points reduction in tariffs on imports from the EU is associated with an increase in quality-adjusted productivity by 1.3%. This estimated effect rises to 1.7% if DEL productivity was used, and to 1.8% if revenue productivity was used.

We now explore heterogeneity in efficiency gains along the lines of ownership type (i.e. domestic-owned vs foreign-owned firms). If firms are eliminating internal inefficiency as a result of increased competition, we should expect higher efficiency gains from domestic-owned firms than from foreign-owned firms. This is because foreign-owned firms could be more exposed to foreign competition and may have eliminated most inefficiencies prior to the trade policy. In column (6) of Table 6, we interact tariffs with a dummy that takes the value of 1 if the firm is a foreign firm and 0 if otherwise. Our estimates for QA productivity imply that a 10 percentage points reduction in tariffs on imports from the EU is associated with an increase in QA productivity by 0.59% for domestic firms, and 0.13% for foreign firms, suggesting that efficiency gains from import competition are weaker for foreign-owned firms compared to domestic firms. This pattern is consistent for both revenue and DEL productivity.

Our results are similar in magnitude with some developing countries studies (Topalova and Khandelwal, 2011; Fernandes, 2007), however, it differs from developed countries studies (De Loecker, 2011; Trefler, 2004). For example, while our results using DEL productivity framework imply an average productivity increase of 1.6% for a 10 percentage point increase in import competition, De Loecker (2011) finds weak and insignificant average effects of 0.2% productivity increase for Belgian textile manufacturers for same 10 percentage point increase in import competition. One possible explanation is that Hungary was an emerging economy in the process of integrating with the developed EU, and domestic firms that were less efficient may have taken drastic steps in eliminating inefficiencies in order to compete with EU firms, while Belgium is a developed economy and firms were already efficient before the easing of EU-15 textile quotas. Another possible explanation is that Belgian textile manufacturers faced competition from textile producers in low-wage countries, while the source of import competition in Hungary was from the EU. The latter explanation is consistent with Bräuer et al. (2019), which finds productivity gains from import competition in German manufacturing firms if the sources of import competition are high-income countries, and no productivity gains if the sources are from low-income countries.

Table 4 Effects of import competition on productivity: direct approach

Table 5 Effects of import competition on productivity: direct approach

Table 6 Effects of import competition on productivity: two-steps approach

A potential shortcoming of our estimated pro-competitive effects lies in the omission of import tariffs on intermediate inputs. As Hungary was an emerging economy in the process of integration with the EU, import tariff liberalization with the EU may have also contributed to productivity growth via improved access to foreign inputs and technology (Halpern et al., 2015). If output tariffs are strongly correlated with input tariffs, this poses an identification issue to the empirical strategy. While previous literature suggests a strong correlation between input and output tariffs at the sector level (Topalova and Khandelwal, 2011; Trefler, 2004), we argue that such correlation is unlikely in our setup as we identify output tariffs exposure at the firm-level instead of sector-level. In Topalova and Khandelwal (2011), the input tariff of a focal industry is the summation of the output tariffs of all industries (inclusive of the focal industry’s output tariffs) weighted by the fraction of the industry’s output used by the focal industry as inputs. Since most industries often use a large fraction of their output as production inputs as observed in input-output tables, the correlation between input and output tariffs in previous studies may be driven by this phenomenon.

Nevertheless, we have included a dummy that takes the value 1 if a firm imported an input and 0 if otherwise, and we also included a 2-digit sector-year fixed effects. The imported inputs dummy controls for average productivity growth attributed to imported inputs, while the sector-year fixed effects, amongst other things, controls for industry output and input tariffs at the 2-digit level. An ideal strategy that ensures consistency with the literature, is to include both the 4-digit industry output and input tariffs in order to isolate the pro-competitive effects from productivity gains due to intermediate input tariff liberalization with the EU. Unfortunately, we do not observe firms at their 4-digit level industry. However, we observe the imports of each importing firm at the 10-digit CN level in each time period. We then construct 2 different measures of imported inputs tariffs and use them in the analysis. In the first measure, we take simple averages of 6-digit tariffs on the products that each firm imports from the EU in each year, similar to the construction of the output tariffs. We use the average import tariffs directly as a proxy for input tariffs, and we compute the effective rate of protection (ERP) by substracting the firms’ import tariffs from its output tariffs.³² The main concern with this approach lies in not observing whether the imports are used as intermediate inputs or for other unobserved purposes.³³ To address this concern, we construct another measure of input tariffs by considering only imported items that are classified as either intermediate inputs or as capital according to the BEC classification³⁴ and compute the ERP in a similar way as above. The result from the first measure of input tariffs is presented in Table (7), while that of the second measure is presented in Table (A3) of the online appendix.

In columns (1)–(3) of Table 7, we present the results for the case where ERP is the main dependent variable, and in columns (4)–(6) we present the case where both the input and output tariffs are the main dependent variables using the full datasets.³⁵ In all specifications, we find that import competition is strongly associated with productivity growth. The coefficients of both the lagged ERP and output tariffs are negative and statistically significant across all specifications with the exception of the case where we control for firm and year fixed effects. We also find that the relationship between import tariffs and productivity to be insignificant across the three specifications. In Table (A3), we find very similar estimates to that in Table 7 across all specifications, thereby providing additional support to the estimated pro-competitive effects.

Table 7 Effects of import competition on productivity

We conduct some robustness checks to test the sensitivity of our results to a slightly modified specification and data restrictions. This includes using weighted average tariffs as the measure of import competition, clustering standard errors at the firm level, dropping importer’s dummy and using the full sample etc. In all checks, the results are similar to our main results. We present the details of these sensitivity checks in the online appendix and supplementary online appendix.

6 Conclusion

This paper provides new evidence on the effect of import competition on manufacturing firm’s productivity in Hungary. By exploiting tariffs reduction on imports from the EU during the periods leading to Hungary’s EU accession, we make important contributions to the literature.

First, we propose an empirical model for estimating productivity from sales revenue data. The proposed framework integrates the demand-system of the domestic and foreign markets with the firm’s supply-side, and derives a new productivity estimation equation which nests revenue productivity equation and the estimation equation proposed in De Loecker (2011). This framework was introduced to overcome estimation bias associated with revenue productivity when firms are exporters and can be easily adapted to other settings where productivity is estimated from sales revenue data.

Second, we apply the model to our data. While most related studies approximate firm-level average tariffs with a 3- or 4-digits industry level tariffs, we use highly disaggregated dataset and construct average firm-level tariffs using tariffs on 6-digit products manufactured by the firm. This unique dataset enables us to control for industry-time fixed effects while exploiting the variation in average firm-level exposure to import tariffs reduction on productivity. This strategy offers better identification as it overcomes some potential endogeneity concerns in existing studies.³⁶.

We find that import competition has a strong effect on productivity, even after controlling for unobserved firm-fixed effect, time-varying industry effects, average input tariffs, and general economic conditions that affect all firms. We also find that this effect is stronger when we use revenue productivity as our measure of efficiency compared to when quality-adjusted productivity is used. In addition, we find that this effect is in general weaker for foreign firms compared to domestic firms.

Further work on the underlying mechanisms would be an interesting direction for future studies. Existing studies highlights the importance of competition on managerial practices which in turn improves efficiency (Bloom et al., 2015).