How preferences shape the welfare and employment effects of trade

Abstract

We set up a trade model with two countries, two sectors, and one production factor, which features a home-market effect due to the existence of trade costs. We consider search frictions and firm-level wage bargaining in the sector producing differentiated goods and a perfectly competitive labor market in the sector producing a homogeneous good. Consumers have price-independent generalized-linear preferences over the two types of goods, covering homothetic and quasi-homothetic preferences as two limiting cases. Due to the specific functional forms of indirect utility, homothetic preferences lead to risk aversion, while quasi-homothetic preferences lead to risk neutrality in our model. We show that trade between two countries that differ in their population size leads to an expansion of the differentiated goods sector and a contraction of the homogeneous good sector in the larger economy. This induces the larger country to net-export differentiated goods at the cost of a higher economy-wide rate of unemployment in the open economy (with the effects reversed for the smaller country). The welfare effects of trade depend on the preference structure. Looking at the two limiting cases, we show that the larger country is likely to benefit from trade if preferences are homothetic, whereas losses from trade are possible if preferences are quasi-homothetic. The opposite is true in the smaller country. This reveals an important role of preferences for the welfare effects of trade in the presence of labor market imperfection, a result we further elaborate on by considering more general preferences as well as differences of countries in their per-capita income levels.

1 Introduction

The question of how labor market imperfection shapes the welfare and employment effects of trade has played a prominent role in economic research since Brecher’s (1974) seminal contribution on the role of minimum wages in a Heckscher-Ohlin model. Due to strong public discontent about the negative consequences of globalization for domestic workers, this question has gained momentum over the last 15 years. Whereas recent theoretical work on the matter acknowledges new developments in trade theory (see Krugman, 1979, 1980) and labor economics (see Pissarides, 2000), the reallocation of workers between sectors that differ in their labor market distortions continues to play a prominent role for explaining the effects of trade on employment and welfare in open economies. It is thereby well understood from existing research that trade generates welfare effects if it changes the allocation of labor between sectors, with the sign of these effects being a priori unclear, because the utility gain of workers newly employed in high-wage jobs of sectors featuring a stronger labor market distortion is typically counteracted by a utility loss of newly unemployed workers. We argue in this paper that it depends on the specific form of consumer preferences which of these two counteracting effects dominates, thereby pointing to a determinant of economy-wide welfare that has been largely ignored by the existing literature.

To analyze how preferences shape the employment and welfare effects from a trade-induced reallocation of labor between sectors featuring different labor market distortions, we propose a model with two countries, two sectors of production, and labor as the only input factor. Following Helpman and Krugman (1985), we assume that one sector produces differentiated goods under monopolistic competition, whose exports are subject to trade costs in the open economy. The other sector produces a homogeneous good under perfect competition that can be shipped to the foreign country at zero costs. This model has become a workhorse in modern trade theory for studying home-market effects and it is widely used as well for analyzing the consequences of trade in the presence of labor market distortions (see, for instance, Davis, 1998b; Helpman and Itskhoki, 2010).¹ As it is common in the literature, we capture labor market distortions by search frictions and individual wage bargaining (cf. Helpman et al., 2010; Felbermayr et al., 2011). To keep the analysis simple, we assume that the labor market distortion is confined to the differentiated goods industry.

The existence of wage bargaining in only one industry generates a wage premium, whose realization comes at the cost of a higher risk of unemployment from the perspective of workers. This feature of our model is akin to the distinction of good and bad jobs in Acemoglu (2001) and it has the important consequence that the probability to find employment in the sector of differentiated goods is directly linked to the wage premium paid in this industry by an indifference condition that makes applying for jobs in the two sectors equally attractive for workers prior to the revelation of who is successfully matched with a firm.² The exact link between the wage premium and the employment probability established by this indifference condition depends on household preferences or, more specifically, on the underlying risk attitudes. To study the role of risk attitudes in a systematic way, we refer to price-independent generalized-linear (so-called PIGL) preferences as the most general class of preferences that admit a representative consumer and therefore avoid complications from aggregating consumer demand over heterogeneous households (Muellbauer, 1975, 1976). The subclass of parametric PIGL preferences considered in our analysis has the advantage of delivering an explicit solution for the direct utility function (see Boppart, 2014), which is particularly useful to avoid an otherwise potentially complicated integrability problem.³ Whereas the preferences do not have Gorman form in general, they cover a specific type of homothetic (log-transformed Cobb-Douglas) preferences and a specific type of quasi-homothetic (while not homothetic) preferences as limiting cases.

These limiting cases are particularly useful for our purposes, because they allow us to illustrate the role of risk attitudes for the employment and welfare effects of trade in a simple way. The more general case of preferences not having Gorman form provides the additional insight on how changes in the distribution of income that are triggered by the between-sector reallocation of labor can alter our results. Thereby, the association of quasi-homothetic and homothetic preferences with different risk attitudes is in our model a consequence of the functional form of indirect utility. Monotonic transformations of these preferences can change the risk attitudes, and hence it is the specific form of indirect utility functions in the two limiting cases of PIGL preferences that is important for our analysis. If households have quasi-homothetic preferences, their indirect utility is linear in income, and they are therefore classified as risk neutral. As a consequence of risk neutrality, the employment probability can be comparably small for a given wage premium to render job search attractive in the sector of differentiated goods, despite a risk of unemployment. In the case of homothetic preferences, the indirect utility of households is logarithmic in income, making them risk averse. In this case, the employment probability must be comparably high for a given wage premium in order to compensate workers for the risk of unemployment and to make job search in the sector of differentiated goods attractive. Due to differences in the risk attitudes, a given change in the fraction of workers applying for jobs in the sector of differentiated goods can have quite different effects on nominal income for the two types of preferences. With the employment probability unchanged, a higher fraction of workers seeking employment in the sector of differentiated goods will reduce income if preferences are quasi-homothetic, whereas it increases income under homothetic preferences, provided that the unemployment compensation for those who do not find a job is not too generous.

With this fundamental insight at hand, we then turn to the open economy and consider trade between two countries that are fully symmetric except for their population sizes. In line with the literature on home-market effects, we show that the sector of differentiated goods expands in the larger country and contracts in the smaller country, with the opposite being true for the sector producing the homogeneous good. As a consequence, the larger country will net-export the differentiated good and net-import the homogeneous good in the open economy. With a larger fraction of workers seeking employment in the sector of differentiated goods, the larger country experiences an increase in economy-wide unemployment. This is, because the risk of unemployment for an individual worker seeking employment in the sector of differentiated goods is the same in the closed and the open economy, whereas the fraction of workers prone to this risk has increased in the larger country. However, the increase in unemployment does not necessarily imply a welfare loss. We can distinguish three effects: First, households in both economies benefit from lower import prices (which in the case of a movement from the closed to the open economy fall from infinity to a finite positive value). Second, provided that an increase in the fraction of workers seeking employment in the sector producing differentiated goods is associated with an increase in nominal income, trade generates an income gain in the larger and an income loss in the smaller country. This is the case if preferences are homothetic and unemployment compensation is not too generous, whereas the opposite is true if preferences are quasi-homothetic. Third, welfare is influenced by a variety effect, which can be decomposed into two partial effects, namely an increase in the fraction of firms producing differentiated goods in the larger country and an increase or decrease in the global mass of firms producing differentiated goods. The combined variety effect is positively linked to the effect of trade on nominal income and can therefore also be positive or negative for either economy.

Taking stock, our model produces the well-known result that lower trade costs exhibit a direct positive welfare effect in both countries by lowering the costs of imports. In contrast, the income and variety effects differ in the two economies and can only be positive for one of them. If preferences are quasi-homothetic, the income and variety effects are to the detriment of the larger economy and it is possible that these negative effects dominate the gains associated with a fall in the costs of imports so that the larger country loses from trade. In this case, the larger country experiences double losses, because, as outlined above, its economy-wide rate of employment decreases as well. Things are different in the smaller country, which due to its specialization on the production of the homogeneous good will experience double gains from trade if preferences are quasi-homothetic. However, if preferences are homothetic and unemployment compensation is not too generous, welfare gains are guaranteed in the larger country, despite an increase in the economy-wide rate of unemployment. At the same time, the smaller country can be worse off in the open economy, despite a decrease in the economy-wide rate of unemployment. This points to an important role of preferences (and more specifically the risk attitudes implied by these preferences) for determining the welfare effects of trade in settings featuring labor market imperfection.⁴ If labor markets were undistorted, the effect of trade on nominal income would vanish, so that, irrespective of the preferences, there would be gains from trade liberalization for both countries due to a fall in the import price of differentiated goods.

We generalize these results by extending our analysis to non-Gorman preferences, rendering income dispersion a key determinant of market demand. Associating differentiated goods with luxuries whose consumption is increasing in household expenditure with an elasticity larger than one and associating the homogeneous good with a necessity whose consumption is increasing in household expenditures with an elasticity smaller than one, a larger income dispersion increases demand for differentiated goods and lowers demand for the homogeneous good. This leads to new entry of firms in the now larger market for differentiated goods which increases welfare due to the households’ love of variety. For the determination of welfare effects it has to be acknowledged that the representative consumer loses its normative interpretation if preferences do not have Gorman form, so that the choice of a proper welfare function is a priori not clear. Taking a utilitarian perspective, we show that welfare exhibits social inequality aversion, implying that an increase in income dispersion lowers social welfare. This direct welfare loss counteracts the indirect welfare gain from firm entry. Since trade changes the dispersion of disposable household income, it exerts additional welfare effects as compared to the benchmark model. As a consequence of this, a higher level of income is no longer sufficient for gains from trade to materialize in the larger country. This confirms our insight from the limiting cases of homothetic and quasi-homothetic utility that the form of preferences is crucial for the welfare consequences of trade.

In a further application of our model, we consider differences of the two countries in their per-capita income levels. Thereby, a priori differences in per-capita income exist due to differences of the two countries in the labor endowments of households, while in contrast to the benchmark model symmetry in the total effective labor supply of the two economies is assumed (and achieved by compensating differences in population size). For the thus changed setting, we show that trade does not affect labor allocation in the two economies if preferences are homothetic. This is the case, because for the class of homothetic preferences differences in per-capita income are immaterial for market demand, provided that economy-wide income is held constant. As a consequence, the production structure in the closed economy is the same for the two countries, so that trade leaves labor allocation and, in extension, the economy-wide rate of unemployment unaffected in the two economies. Gains from trade exist, however, due to a fall in the price of imported goods. Things are different if preferences are quasi-homothetic. In this case, the richer country has a larger market for differentiated goods and therefore net-exports these goods in exchange for the homogeneous good in the open economy. The reallocation of labor towards the production of differentiated goods leads to an increase in economy-wide unemployment and can induce an overall welfare loss in the richer economy.

Assessing the effects of trade in a setting that features search frictions in the sector producing differentiated goods, our model contributes to a sizable literature dealing with labor market distortions in open economies. Starting with Brecher (1974), this literature has aimed at improving our understanding about the role of labor market institutions as a determinant of international trade flows and as an important factor influencing the effects of trade on employment and welfare (cf. Davidson et al., 1988; Davis, 1998a; Kreickemeier and Nelson, 2006). Whereas the focus in recent years has shifted towards models featuring heterogeneous firms and only a single sector of production (cf. Egger and Kreickemeier, 2009, 2012; Amiti and Davis, 2012), advancements have also been made in trade models with multiple sectors and differences of these sectors in their labor market institutions (cf. Bastos and Kreickemeier, 2009; Egger et al., 2015). Most closely related to our model in this respect is Helpman and Itskhoki (2010) who consider, as we do, a two-sector trade model featuring a home-market effect.⁵ However, similar to other existing work, they do not look at the role of preferences for the employment and welfare effects of trade.

Pointing to potential welfare loss from trade, the analysis in this paper adds to an old and well established debate about the conditions, under which such losses can materialize (see Graham, 1923, for an early example and Helpman, 1984, for a thorough literature review). In multi-sector models disadvantageous specialization in the open economy is usually put forward as a key explanation of why trade can be to the detriment of an economy. Whereas the results from our model are well in line with this argument, we deviate from the widespread view that disadvantageous specialization requires external economies of scale in at least one industry. Excluding external economies of scale, we show that losses from trade can also be the result of a labor market distortion and may exist even if a country expands the sector offering ‘good jobs’ (in the terminology of, Acemoglu, 2001) . Provided that specialization in the open economy leads to an expansion of a sector prone to unemployment, increasing the number of good jobs may come at the cost of a higher fraction of workers not finding a job at all. This can generate welfare loss, with preferences playing a crucial role for such disadvantageous specialization to materialize in our model.

Postulating that households have PIGL preferences, this paper also contributes to a strand of literature, which points out that important new insights on the motives for trade, its structure, and consequences can be obtained when deviating from the widespread assumption of homothetic utility. Building on the insight of Linder (1961) that demand-side factors are important determinants of international trade flows, Krugman (1979, 1980), Markusen (1986), and Flam and Helpman (1987) have provided first theoretical accounts of the role of preferences. The main insight from this early research is that a substantial fraction of trade remains unexplained when only considering supply-side motives for its existence (see Markusen, 2013). Matsuyama (2000), Fajgelbaum et al. (2011), and Foellmi et al. (2018) have further contributed to the analysis by distinguishing high- and low-quality goods and by adding a discrete choice element to allow for an aggregation of consumer demand over heterogeneous households even if preferences do not have Gorman form.⁶ Fieler (2011) and Caron et al. (2014) consider generalized CES preferences, whereas Bertoletti and Etro (2017) and Matsuyama (2015, 2019) consider a class of preferences that establish a “generalized separable” demand system (see Pollak 1972). These preferences have the particular advantage to allow for aggregation of demand over various industries with differing price elasticities and are therefore well equipped for studying quantitative general equilibrium trade models. Lacking a representative consumer, the preferences are, however, less suited for aggregating consumer demand over households with differing income levels.⁷

The remainder of the paper is organized as follows. In Sect. 2, we discuss the building blocks of our model and in Sect. 3, we analyze the main mechanisms in the closed economy. In Sect. 4, we investigate trade between two countries that differ in their population size and study the effects of trade on production structure, economy-wide employment, and welfare. In Sect. 5, we investigate the effects of trade in rich and poor countries. Section 6 concludes with a summary of our results.

2 The model: basics

2.1 Endowment and preferences

We consider a static economy that is populated by a continuum of households with mass H, which in their role as workers inelastically supply $\lambda >1$ units of labor input for the production of goods. We can interpret $\lambda$ as worker productivity which is the same for all households. Households have price-independent generalized-linear (so-called PIGL) preferences over two goods, which are represented by a direct utility function of the form

$$\begin{aligned} {\mathcal {U}}\left( X_i,Y_i\right) =\frac{1}{\varepsilon }\left( \frac{\beta X_i}{Y_i}\right) ^\varepsilon \left[ \left( \frac{Y_i}{\beta }\right) ^{\frac{\varepsilon }{1-\varepsilon }}-\beta \right] ^{1-\varepsilon }-\frac{1-\beta }{\varepsilon }, \end{aligned}$$

(1)

where $\varepsilon ,\beta \in (0,1)$ are two constants, $Y_i$ is a homogeneous good, and $X_i$ is a CES aggregate over a continuum of differentiated goods:

$$\begin{aligned} X_i=\left[ \int _{\omega \in \Omega } x_i(\omega )^{\frac{\sigma -1}{\sigma }}d\omega \right] ^{\frac{\sigma }{\sigma -1}}, \end{aligned}$$

(2)

with $x_i(\omega )$ being the consumption level of variety $\omega$ and $\sigma >1$ being the constant elasticity of substitution between the varieties from set $\Omega$. The utility function in Eq. (1) is well-defined only if $X_i>0$. As pointed out by Muellbauer (1975, 1976), PIGL preferences are the most general class of preferences that deliver a representative consumer and therefore avoid an aggregation problem over households with differing levels of income. Whereas PIGL preferences are usually represented by an indirect utility function, for the subclass of parametric PIGL preferences considered here, an explicit solution for the direct utility function exists. As pointed out by Egger and Habermeyer (2019), the utility function in Eq. (1) has the particularly nice feature of covering homothetic (log-transformed Cobb-Douglas) preferences and quasi-homothetic (while not homothetic) preferences by the limiting cases of $\varepsilon \rightarrow 0$ and $\varepsilon \rightarrow 1$, respectively.⁸

Solving the standard protocol of utility maximization delivers individual demand functions

$$\begin{aligned} Y_i=\beta \left( \frac{e_i}{P_Y}\right) ^{1-\varepsilon }\quad \text {and}\quad x_i(\omega ) =\frac{e_i}{P_X}\left( \frac{p(\omega )}{P_X}\right) ^{-\sigma }\left[ 1-\beta \left( \frac{e_i}{P_Y}\right) ^{-\varepsilon }\right] , \end{aligned}$$

(3)

respectively, where $e_i$ is the disposable income (expenditure) of household i, $P_Y$ is the price of the homogeneous good, $p(\omega )$ is the price of variety $\omega$ of the differentiated good, and $P_X\equiv \left[ \int _{\omega \in \Omega }p(\omega )^{1-\sigma }d\omega \right] ^{\frac{1}{1-\sigma }}$ is a CES index over the prices of all these varieties. Throughout our analysis we focus on a parameter domain with a positive consumption level of both goods. Making use of Eq. (2), we can express the CES composite of differentiated goods as $X_i =\frac{e_i}{P_X}\Big [1-\beta \left( \frac{e_i}{P_Y}\right) ^{-\varepsilon }\Big ]$, where $\beta \left( \frac{e_i}{P_Y}\right) ^{-\varepsilon }$ corresponds to the expenditure share for the homogeneous good, and we compute the income elasticities

$$\begin{aligned} \frac{\partial Y_i}{\partial e_i}\frac{e_i}{Y_i} = 1-\varepsilon , \qquad \frac{\partial X_i}{\partial e_i}\frac{e_i}{X_i}=1+\varepsilon \frac{P_YY_i}{P_XX_i}. \end{aligned}$$

(4)

The income elasticities in Eq. (4) shape the Engel curves for the two goods, with preference parameter $\varepsilon$ being decisive for their form. If $\varepsilon \in (0,1)$ preferences do not have Gorman form. In this case, the income elasticity is smaller than one for $Y_i$, making the corresponding Engel curve concave and the homogeneous good a necessity. In contrast, the income elasticity is larger than one for the CES composite $X_i$, making the corresponding Engel curve convex and the differentiated good a luxury.⁹ If $\varepsilon \rightarrow 1$, preferences are quasi-homothetic and the income elasticity of $Y_i$ falls to zero, whereas the income elasticity of composite $X_i$ increases to $e_i/(P_XX_i)$. In this limiting case, the Engel curve for the CES composite $X_i$ is linear in household income, while the Engel curve of $Y_i$ is given by $\beta$ and therefore independent of household income. While this shows close resemblance to the case of quasilinear preferences, the quasi-homothetic preferences considered here have the additional property that demand for homogeneous good $Y_i$ is also independent of price $P_Y$. In the polar case of $\varepsilon \rightarrow 0$, preferences are homothetic and the income elasticities of both goods are equal to one, making the Engel curves of $X_i$ and $Y_i$ linear.

Aggregating $Y_i$ and $x_i(\omega )$ over households, gives market demand functions

$$\begin{aligned} Y&=\int _{i\in {\mathcal {H}}} Y_idi=\beta \frac{H{\bar{e}}}{P_Y}\left( \frac{{\bar{e}}}{P_Y}\right) ^{-\varepsilon }\psi ,\end{aligned}$$

(5)

$$\begin{aligned} x(\omega )&=\int _{i\in {\mathcal {H}}}x_i(\omega )di=\frac{H{\bar{e}}}{P_X}\left( \frac{p(\omega )}{P_X}\right) ^{-\sigma }\left[ 1-\beta \left( \frac{{\bar{e}}}{P_Y}\right) ^{-\varepsilon }\psi \right] , \end{aligned}$$

(6)

where $\bar{e}\equiv H^{-1}\int _{i\in {\mathcal {H}}}e_idi$ is the average disposable income of households and $\psi \equiv H^{-1}\int _{i\in {\mathcal {H}}}\left( e_i/\bar{e}\right) ^{1-\varepsilon }di$ is a dispersion index that is defined on the unit interval and captures how the distribution of disposable household income affects economy-wide consumption. The dispersion index reaches a maximum level of one if the distribution of expenditures is egalitarian or if the distribution of household income is irrelevant for aggregate demand because preferences have Gorman form.

2.2 Technology and the firms’ problem

Firms in the sector of the homogeneous good enter the market at zero cost and hire workers at a common wage rate $w_Y$ per unit of labor input. Workers need one unit of their labor input to produce one unit of the homogeneous good, which is sold under perfect competition. This establishes $w_Y=P_Y$. Firms producing differentiated goods have to develop a blueprint, which comes at the cost of f units of the homogeneous good and gives them access to a unique variety that can be sold under monopolistic competition. To produce their output firms hire workers, who manufacture one unit of the differentiated good with each unit of their labor input. Hiring and wage setting in the sector of differentiated goods is a two-stage problem. At stage one, firms install vacancies at the cost of one unit of the homogeneous good and search for workers filling these vacancies. There are search frictions and the assignment of workers to jobs is solved through random matching (cf. Pissarides, 2000; Helpman and Itskhoki, 2010; Felbermayr and Prat, 2011). For those vacancies successfully filled, firms and workers form a bilateral monopoly at stage two and distribute the production surplus generated in the workplace through Stole and Zwiebel (1996) bargaining.¹⁰ As formally shown in the Appendix, the solution to the bargaining problem can be summarized as

$$\begin{aligned} w_X(\omega )=\frac{\alpha +\gamma \lambda q }{\lambda q} w_Y ,\qquad \Pi (\omega )=\frac{\rho r(\omega )}{\sigma }-P_Yf, \end{aligned}$$

(7)

where $\rho \equiv \sigma /[\sigma +\alpha (\sigma -1)]<1$ is the constant share of revenues appropriated by firms in the process of wage bargaining, $\alpha >0$ denotes relative bargaining power of workers in the wage negotiation with the firm and $\gamma \in (0,1)$ is a common replacement rate that links the unemployment benefit of workers $\gamma \lambda w_Y$ to the wage they would have received when employed in the production of the homogeneous good. Unemployment compensation is a transfer payment that is financed by a proportional tax $\tau$ on all forms of labor income, including unemployment compensation (see Egger and Kreickemeier 2012). Thereby, tax rate $\tau$ is endogenously determined by the condition of a balanced budget of the government that equates tax revenues and transfer payments. Since all firms producing differentiated goods employ the same technology and pay the same wage, they are symmetric producers. This allows us to drop firm index $\omega$ from now on.

2.3 Industry-wide outcome in the sector of differentiated goods

Equation (7) has been derived under the assumption that firms producing differentiated goods can attract the intended mass of applicants at a wage rate $w_X$. To see under which condition this is the case, we have to determine the labor market outcome in the sector of differentiated goods. For this purpose, we note that the supply of workers in the sector of differentiated goods is given by the product of the mass of households, H, and the fraction of these households seeking employment in the sector of differentiated goods, h. The ratio between the mass of workers seeking employment, hH, and the total mass of vacancies installed, Q, is pinned down by a Cobb-Douglas matching function and given by $hH/Q=m(1-u)^{-1}$, where m is a positive constant that measures matching efficiency, and $1-u$ is the share of workers successfully matched to a firm and thus the employment rate in the sector of differentiated goods. The probability of filling a vacancy is given by $q=hH(1-u)/Q=m$ and thus independent of the employment rate in our model. Setting $m=\lambda ^{-1}$ proves particularly useful for our purposes, because it allows us to get rid of uninteresting constants. This additional simplification generates a negative relationship between matching efficiency and labor productivity, which can be justified by assuming that workers with higher and more specialized abilities are more difficult to place in the labor market.¹¹

With this matching technology at hand, we can solve for the employment rate in the sector of differentiated goods, using the indifference condition for production workers, who can either enter the sector of the homogeneous good, which promises an income of $w_Y$ per unit of labor input, or enter the sector of differentiated goods, which promises for each unit of labor input an income $w_X=(\alpha +\gamma )w_Y$ with probability $1-u$ and an unemployment compensation of $\gamma w_Y$ with probability u.¹² Considering the utility function in Eq. (1) and individual demand functions in Eq. (3), we can solve the indifference condition of workers for

$$\begin{aligned} 1-u= \frac{1-\gamma ^\varepsilon }{(\alpha +\gamma )^\varepsilon -\gamma ^\varepsilon }, \end{aligned}$$

(8)

where $w_X=(\alpha +\gamma )w_Y$ and $q=m=\lambda ^{-1}$ have been used. Eq. (8) reveals that an interior solution with $0<u<1$ requires $\alpha >1-\gamma$, and hence that the sector of differentiated goods offers a wage premium ${\tilde{\alpha }}\equiv \alpha +\gamma >1$. Provided that such an outcome exists, a higher relative bargaining power of workers, $\alpha$, increases the wage premium, and therefore the employment rate has to fall in order to restore indifference of workers to enter the two sectors. The limiting case of ${\tilde{\alpha }}=1$ (and thus $\alpha =1-\gamma$) refers to an outcome with full employment, $u=0$, and thus to an outcome, in which the labor market in the differentiated goods industry is undistorted. Setting $q=\lambda ^{-1}$, it follows from Eq. (7) that full employment is achieved if wages are equalized between the two sectors, establishing $w_X=w_Y$. We complete the characterization of the industry equilibrium by noting that free entry of firms into the sector of differentiated goods establishes the zero-profit condition $\rho r=\sigma P_Yf$.

2.4 Production structure and disposable labor income

We finish the discussion of the main building blocks of our model by elaborating on how changes in the production structure affect the average level and dispersion of disposable household income. Due to taxation, only a fraction $1-\tau$ of household income is disposable for consumption expenditures. Average disposable household income is given by

$$\begin{aligned} {\overline{e}}=w_Y\lambda \left\{ 1+h[(1-u){\tilde{\alpha }} -1]\right\} . \end{aligned}$$

(9)

Eq. (9) points to a trade-off, an increase in the fraction of workers producing differentiated goods has on average disposable income. On the one hand, a higher h leads to an increase in the fraction of workers receiving the wage premium offered by luxury producers. On the other hand, it increases the economy-wide rate of unemployment, uh, and thus the share of labor input not productively used in the economy. In general, $(1-u) {\tilde{\alpha }}>,=,<1$ is possible, so that allocating more workers to the sector of differentiated goods can have a positive or negative effect on average disposable household income, depending on whether the first or the second effect dominates. Since the effect that changes in the fraction of workers seeking employment in the production of differentiated goods have on average disposable labor income is essential for the welfare effects of trade, it is useful to shed light on the role of preferences for the ranking of $(1-u) {\tilde{\alpha }}>,=,<1$. The following lemma summarizes this role.

Lemma 1

If preferences are quasi-homothetic, we have $(1-u) \tilde{\alpha }<1$. In all other cases $(1-u) {\tilde{\alpha }}>,=,<1$ is possible, with $(1-u) {\tilde{\alpha }}>1$ achieved for sufficiently high levels of $\alpha$. In the limiting case of homothetic preferences, $(1-u) {\tilde{\alpha }}>1$ extends to all possible $\alpha >1-\gamma$ if $\gamma <\exp [-1]$.

Proof

Formal proof in the Appendix $\square$

Whereas production of differentiated goods promises a wage premium if households are successfully matched with firms, applying for jobs in the sector producing differentiated goods comes at the risk of being not successfully matched and receiving only unemployment compensation. The households’ risk attitudes and hence the evaluation of the risk of job loss depend on their preferences (or, more specifically, on preference parameter $\varepsilon$). If $\varepsilon \rightarrow 1$ preferences are quasi-homothetic and households are risk neutral. In this case, the constraint in Eq. (8), which makes workers indifferent between the two sectors, reduces to a condition equalizing the expected disposable income from job search in the two sectors: $(1-u){\tilde{\alpha }} w_Y+u\gamma w_Y=w_Y$. Because of their risk neutrality, households accept a relatively low probability of a successful match and thus a relatively high rate of unemployment, when seeking employment in the sector of differentiated goods, leading to $(1-u){\tilde{\alpha }}<1$. Things are different if households are risk averse due to $\varepsilon <1$, with the degree of risk aversion maximized in our model if $\varepsilon \rightarrow 0$ makes preferences homothetic. In this case, households applying for jobs in the sector producing differentiated goods must be compensated for accepting the risk of unemployment. With the wage premium ${\tilde{\alpha }}>1$ fixed, risk aversion leads to a fall in the unemployment rate, thereby increasing $(1-u){\tilde{\alpha }}$. In the case of homothetic preferences $(1-u){\tilde{\alpha }}>1$ is achieved for all ${\tilde{\alpha }}>1$ and thus for all $\alpha >1-\gamma$, if unemployment compensation is not too generous, i.e if $\gamma <\exp [-1]$.¹³ This is the parameter domain we focus on in the subsequent analysis in order to emphasize the important role played by the degree of risk aversion when contrasting the two limiting cases of quasi-homothetic and homothetic preferences.

With the insights regarding the relationship of production structure and average disposable household income at hand, we now turn to the dispersion index. As formally shown in the Appendix, we compute

$$\begin{aligned} \psi&=\frac{1+h\left[ (1-u)\tilde{\alpha }^{1-\varepsilon } +u\gamma ^{1-\varepsilon }-1\right] }{\left\{ 1+h\left[ (1-u){\tilde{\alpha }} +u\gamma -1\right] \right\} ^{1-\varepsilon }}, \end{aligned}$$

(10)

where $\psi =1$ holds in the case of Gorman form preferences. This points to the important result that higher degrees of risk aversion do not exert a monotonic effect on dispersion index $\psi$. This is, because the dispersion index does not capture the second moment of income distribution but the impact of income distribution on the structure of consumer demand. With quasi-homothetic or homothetic preferences, aggregate consumer demand does not depend on the distribution of disposable household income – provided that even the households with the lowest income consume both goods. To ensure that this is the case, condition $(1-\tau )\gamma \lambda >\beta ^{1/\varepsilon }$ must be fulfilled. This condition depends on the endogenous tax rate $\tau$ and thus on the, yet to be determined, fraction of workers seeking employment in the production of differentiated goods, h, which is different for the closed and the open economy.

3 The closed economy

To determine the fraction of workers seeking employment in the sector of differentiated goods, h, we can make use of two important insights from our analysis. The first one combines the solution to wage bargaining with constant markup pricing of firms to compute the wage bill of firms as $\lambda l w_X=\lambda l \gamma w_Y+ \rho r \alpha (\sigma -1)/\sigma$ (see the Appendix A.2). Noting that M firms enter and $hH(1-u)$ workers find a job, allows us to determine a positive link between the share of workers seeking employment in the sector of differentiated goods and the mass of firms producing them according to

$$\begin{aligned} h H\lambda w_Y (1-u)&= \frac{\sigma -1}{\sigma } \rho Mr, \end{aligned}$$

(11)

where $w_X=(\alpha +\gamma )w_Y$ has been considered. A second relationship between h and M follows from the market clearing condition for differentiated goods, can be derived from Eq. (6), and is given by

$$\begin{aligned} H\lambda w_Y\left( 1-\beta \lambda ^{-\varepsilon }\right) + H\lambda w_Y B(h)=Mr, \end{aligned}$$

(12)

where $B(h)\equiv h\big [(1-u){\tilde{\alpha }}-1\big ]+\beta \lambda ^{-\varepsilon }\big [1-T(h)\big ]$ is derived in the Appendix and captures the additional effect on consumer demand from the labor market distortion and the tax-transfer scheme implemented to compensate the unemployed. Rent-sharing increases market income of an endogenous fraction of $h(1-u)$ workers, who find employment in the sector of differentiated goods and therefore benefit from a wage premium ${\tilde{\alpha }}>1$. This gives term $h\big [(1-u){\tilde{\alpha }}-1\big ]$ as a first component of B(h). The second component captures the demand effect through endogenous changes in the dispersion of disposable household income, because workers seeking employment in the sector of differentiated goods can experience higher or lower income than in the homogeneous goods sector, depending on their employment status, and because the tax-transfer system makes disposable income more egalitarian. The combined dispersion effect is captured by $\beta \lambda ^{-\varepsilon }\big [1- T(h)\big ]$. Whereas the general solution of T(h) is of no further interest for our analysis and thus delegated to the Appendix, we get a simple and intuitive result if either $\varepsilon \rightarrow 0$ or $\varepsilon \rightarrow 1$.

As noted above, quasi-homothetic preferences make households risk neutral in our model, so that the expected labor income is equalized between the two sectors. In this case, income dispersion is immaterial for the goods market equilibrium, implying $T(h)=1$ and in extension $B(h)=h[(1-u){\tilde{\alpha }}-1]$. In contrast, homothetic preferences make households risk averse, and hence the expected labor income must be higher in the sector of differentiated goods to compensate workers for the risk of getting unemployed. In this case, the existence of a risk premium changes income dispersion and distorts the goods market equilibrium. This establishes $T(h)=1+h[(1-u){\tilde{\alpha }}-1]>1$ and thus $B(h)=h[(1-u){\tilde{\alpha }}-1](1-\beta )$. In both cases, B(h) captures a pure efficiency effect due to changes in the level of average disposable household income. However, this efficiency effect is not the same for homothetic and quasi-homothetic preferences. As pointed out by Lemma 1, in the case of quasi-homothetic preferences $(1-u){\tilde{\alpha }}<1$ holds for all possible parameter configurations, and hence the demand for differentiated goods is reduced by the labor market distortion, because the negative employment effect dominates the positive wage effect of those successfully matched to firms. In contrast, with homothetic preferences, $(1-u){\tilde{\alpha }}>1$ is achieved for all possible $\alpha >1-\gamma$ if unemployment compensation is not too generous, establishing $B(h)>0$. If preferences do not have Gorman form, demand for differentiated goods is furthermore influenced by the dispersion of disposable household income, because demand for the CES composite $X_i$ is not linear in household income if $\varepsilon \in (0,1)$. Whereas this complicates the analysis considerably, the model remains nicely tractable for $\varepsilon =1/2$. Finally, in the limiting case of $\tilde{\alpha }=1$ (and thus $\alpha =1-\gamma$) our model lacks a labor market distortion, implying that $B(h)=0$.

Combining Eqs. (11) and (12) allows us to solve for the equilibrium fraction of workers seeking employment in the sector of differentiated goods. The respective solution is given by the condition $\Gamma (h)=0$, with

$$\begin{aligned} \Gamma (h)\equiv 1-h\left[ 1+\left( \frac{\sigma }{\sigma -1}-\gamma \right) (1-u)\right] -\beta \lambda ^{-\varepsilon } T(h). \end{aligned}$$

(13)

We show in the Appendix that $\Gamma (h)=0$ has a unique solution in h. In the two polar cases of homothetic and quasi-homothetic preferences, we can compute explicit solutions for h, which are given by

$$\begin{aligned} h=\frac{\frac{1-\beta }{1-u}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }-\frac{1-\beta }{1-u}\left[ (1-u){\tilde{\alpha }}-1\right] },\qquad h=\frac{\frac{\lambda -\beta }{\lambda (1-u)}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }-\frac{1}{1-u}\left[ (1-u){\tilde{\alpha }}-1\right] }, \end{aligned}$$

(14)

respectively. To determine the equilibrium mass of firms producing differentiated goods, M, we can combine the zero-profit condition $\rho r=\sigma P_Yf$ with Eq. (11) and substitute $P_Y=w_Y$. This gives $M=hH\lambda (1-u)/[(\sigma -1)f]$.

Higher levels of per-capita labor endowment $\lambda$ make for a given allocation of workers all households richer and increase the expenditures for differentiated goods. In the case of homothetic preferences the expenditure shares of differentiated goods are independent of $\lambda$, so that the now higher demand for differentiated goods is offset by the now higher supply of labor producing them, leaving the fraction of workers seeking employment in the sector of differentiated goods, h, unaffected. Things are different in the case of quasi-homothetic preferences. With expenditure shares for differentiated goods increasing in $\lambda$, more workers are needed in the sector of differentiated goods to fulfill the now higher consumer demand for these goods. As a consequence, h has to increase to restore market clearing. Irrespective of the preferences, more firms will enter the now larger market for differentiated goods.

A higher relative bargaining power of workers $\alpha$ can increase or decrease the fraction of workers seeking employment in the sector of differentiated goods. A higher $\alpha$ must lower employment rate $1-u$ to restore indifference of workers between the two sectors. All other things equal, a higher fraction of workers must therefore seek employment in the sector of differentiated goods to fulfill a given demand. This effect can be counteracted if an increase in average disposable household income, due to an increase in $(1-u){\tilde{\alpha }}$, induces households to increase their demand for the homogeneous good, causing a reallocation of labor away from the sector of differentiated goods. This second effect needs not to work against the first one, because average disposable household income can fall in $\alpha$ and because with quasi-homothetic preferences income changes leave demand for the homogeneous good unaffected, according to Eq. (3). However, in general it is a priori not clear, which of the two effects dominates, so that $dh/d\alpha$ can be positive or negative. Whereas we cannot rule out positive effects of a stronger labor market distortion on the fraction of workers seeking employment in the sector of differentiated goods, the mass of firms producing them, M, unambiguously decreases in $\alpha$ in the two limiting cases captured by Eq. (14). This is, because a higher wage premium increases the costs of production, and therefore makes entry less attractive for firms. Whereas an increase in average disposable household income would counteract this effect, it does not dominate because the respective demand stimulus is mitigated by an income loss of those workers becoming newly unemployed in the sector of differentiated goods.

Changes in the fraction of workers seeking employment in the sector of differentiated goods and changes in the mass of firms producing them are important determinants of welfare effects. In the two limiting cases of $\varepsilon \rightarrow 0$ and $\varepsilon \rightarrow 1$ preferences have Gorman form, giving the representative consumer a normative interpretation. This allows us to consider utility of the representative consumer as a proper welfare function, establishing¹⁴

$$\begin{aligned} V_{CD}\left( {{\overline{e}}},P_Y,P_X\right) \equiv \ln \left( \frac{\overline{e}}{P_Y^\beta P_X^{1-\beta }}\right) , \qquad V_{QH}\left( \overline{e},P_Y,P_X\right) \equiv \frac{\overline{e}}{P_X}-\beta \frac{P_Y}{P_X}-1+\beta \end{aligned}$$

(15)

for the limiting cases of homothetic (log-transformed Cobb-Douglas) and quasi-homothetic preferences, respectively. Substituting Eqs. (9), (14), and $M=hH\lambda (1-u)/[(\sigma -1)f]$, and accounting for $P_X=\frac{\sigma }{\sigma -1}\frac{w_Y}{\rho } M^{\frac{1}{1-\sigma }}$, we can express welfare as a function of $\lambda$ and $\alpha$. Intuitively, welfare increases with per-capita labor endowment $\lambda$ for two reasons: On the one hand, an increase in per-capita labor endowment makes all households richer. In the case of quasi-homothetic preferences this direct effect is counteracted by an indirect effect, because the reallocation of labor towards the production of differentiated goods leads to an aggregate income loss. However, differentiating ${{\overline{e}}}$, it is easily verified that the indirect effect cannot dominate. On the other hand, a higher $\lambda$ induces more firms to enter the sector of differentiated goods, which leads to a fall in the CES price index $P_X$ and thereby stimulates welfare. Therefore, a higher per-capita labor endowment increases welfare under homothetic as well as quasi-homothetic preferences, and the positive welfare effect of a higher $\lambda$ also exists in our model if labor markets are undistorted, due to ${\tilde{\alpha }}=1$ (and thus $\alpha =1-\gamma$). Regarding the effect of a higher wage premium, we show in the Appendix that welfare unambiguously decreases in $\alpha$ if preferences are quasi-homothetic. This is, because a stronger labor market distortion decreases average disposable household income, lowers the mass of firms producing differentiated goods, and increases the prices charged by the remaining firms. All three effects are detrimental for social welfare. If preferences are homothetic, average disposable household income can increase in $\alpha$, thereby counteracting negative effects from a lower mass of firms and higher prices for each differentiated variety. In this case, a stronger labor market distortion can be a stimulus for social welfare.

Whereas specifying a welfare function in the case of Gorman preferences is straightforward, choosing a proper welfare function is less obvious if preferences do not have Gorman form, because the representative consumer does not bear a normative interpretation in this case (see Muellbauer 1975, 1976). One possibility put forward by Egger and Habermeyer (2019) is to take a utilitarian perspective and we follow this approach in Sect. 4.3, where we discuss how the results from our analysis change when $\varepsilon \in (0,1)$. This completes the discussion of the closed economy.

4 The open economy for two countries with differing population size

In the open economy, we consider trade between two countries that are symmetric in all respects, except for their population size: $H\ne H^*$, where an asterisk is used to indicate foreign variables and to distinguish them from home variables. Trade in the homogeneous good is free of costs, and hence wage $w_Y$ is the same in the two economies, provided that production is diversified in either of the two economies. We discuss the parameter domain supporting diversification below. Trade in differentiated goods is subject to iceberg trade costs, implying that $t^{\frac{1}{\sigma -1}}>1$ units of the good must be shipped in order for one unit to arrive in the foreign country.

4.1 Characterization of the open economy equilibrium

Under diversification, the open economy equilibrium can be characterized by combining the outcome of wage bargaining with the zero-profit conditions and goods market clearing for differentiated goods in the two economies. Since wage bargaining and price setting are unaffected by trade, the link between h and M established by these two conditions for the open economy is equivalent to the respective link for the closed economy shown in Eq. (11), with a structurally similar expression in place for the foreign country. Furthermore, firm-level revenues in home and foreign, r and $r^*$, respectively, are linked by the zero-profit conditions $\rho r=\sigma P_Y f$, $\rho r^*=\sigma P_Y f$. Accordingly, firm-level revenues are the same in the two economies, provided that production is diversified and that trade of the homogeneous good is costless. Market clearing in the sector of differentiated goods gives for home and foreign

$$\begin{aligned} \begin{aligned} H\lambda w_Y\left( 1-\beta \lambda ^{-\varepsilon }\right) +H\lambda w_Y B(h)&= \frac{Mrt}{1+t}+\frac{M^*r^*}{1+t}, \\ H^*\lambda w_Y\left( 1-\beta \lambda ^{-\varepsilon }\right) + H^*\lambda w_Y B(h^*)&= \frac{M^*r^*t}{1+t}+ \frac{Mr}{1+t}, \end{aligned} \end{aligned}$$

(16)

respectively.

Combining Eqs. (11) and (16) and accounting for the zero-profit conditions, we can solve for the equilibrium values of h and $h^*$ in the open economy. These values are determined by a system of two equations

$$\begin{aligned} h^*&= \frac{1}{\eta }\Phi (h), \qquad h=\eta \Phi (h^*), \end{aligned}$$

(17)

with $\eta \equiv H^*/H$,

$$\begin{aligned} \Phi (x)\equiv x+\frac{\sigma -1}{\sigma }\frac{\rho (1+t)}{1-u}\Gamma (x), \quad x=h,h^*, \end{aligned}$$

(18)

and $\Gamma (\cdot )$ being defined in Eq. (13). The first expression in (17) makes use of market clearing for differentiated goods at home and therefore gives the response of h to changes in $h^*$ that is necessary to restore market clearing in home. The second expression in (17) makes use of market clearing for differentiated goods abroad and therefore gives the response of $h^*$ to changes in h that is necessary to restore market clearing in foreign.

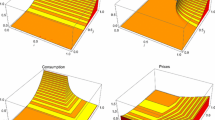
As a point of departure, we capture the open economy equilibrium for the case of symmetric countries ($\eta =1$) in Fig. 1. There, we depict in $(h,h^*)$-space the two equations in (17) by curves $\Phi (h)$ and $\Phi (h^*)$, respectively. As formally shown in the Appendix, under the assumption of sufficiently high trade costs the two curves $\Phi (h)$ and $\Phi (h^*)$ are negatively sloped and have an intersection point at the 45$^\circ$ line, which we denote by A. Point A characterizes a unique interior equilibrium in the open economy whose location at the 45$^\circ$-line implies that the fraction of workers seeking employment in the sector of differentiated goods is the same for the two symmetric countries and equal to the autarky level. We have $h=h^*=h_a$, with subscript a used to indicate an autarky variable. Stability of the open economy equilibrium in point A follows from its uniqueness and is indicated by the grey arrows in Fig.  1.¹⁵

Fig. 1

Equilibrium in the open economy with symmetric countries

The open economy equilibrium is no longer symmetric, however, if the two countries differ in their population size. For instance, if the foreign country is larger than the domestic one, we have $\eta >1$, and in this case the foreign country features a larger market for differentiated goods. This case is illustrated in Fig. 2. In the closed economy, the additional demand for labor from a larger population size is offset by a larger labor supply, leaving the fraction of workers seeking employment in the sector of differentiated goods unaffected. Accordingly, the autarky equilibrium remains to be given by point A, irrespective of the prevailing differences in population size. Things are different in the open economy. From previous work on home-market effects (cf. Helpman and Krugman 1985), we know that in a setting as ours “a country whose share of demand for a good is larger than average will have – ceteris paribus – a more than proportionally larger-than average share of world production of that good” (Crozet and Trionfetti 2008, p.309). Therefore, in the open economy the fraction of workers seeking employment in the production of differentiated goods increases in foreign and decreases in home if $\eta >1$. In Fig. 2 the relative increase in foreign market size leads to a counter-clockwise rotation of locus $\Phi (h)$ and locus $\Phi (h^*)$ in their respective intercepts $f_2(t)$. These intercepts are unaffected because they capture the local market clearing conditions of a country if worldwide production of differentiated goods is concentrated there. Accordingly, relative country size differences are irrelevant for the positions of these intercepts. Things are different for intercepts $f_1(t)$, which reflect the local market-clearing conditions of a country if no local production is left. In this case, relative country size differences exhibit the largest effect. Figure 2 shows a new open economy equilibrium in point ${\tilde{A}}$ and illustrates that access to trade leads to an expansion of the production of differentiated goods in the country with the initially larger market for these goods and to a contraction of the production of differentiated goods in the other economy.

Fig. 2

Equilibrium in the open economy with asymmetric countries

For a better understanding of how trade affects the allocation of labor, we can determine the effects of marginal changes in trade cost parameter t on h and $h^*$. These effects are illustrated in Fig. 3. Starting point is the open economy equilibrium for asymmetric countries depicted by point ${\tilde{A}}$. Due to our assumption that foreign is larger than home, this equilibrium corresponds to a production pattern with ${\tilde{h}}^*> {\tilde{h}}$. The autarky equilibrium is depicted by point A and leads to a symmetric outcome in the two economies regarding the fraction of workers seeking employment in the sector of differentiated goods: $h=h^*=h_a$. An increase in the trade cost parameter from t to $t^\prime$ rotates locus $\frac{1}{\eta }\Phi (h)$ clockwise in point C. A clockwise rotation of $\frac{1}{\eta }\Phi (h)$ depicts that higher trade costs make the home market more relevant for firms and shield domestic producers in their home market from competition with foreign ones. As a consequence, for higher levels of t an increase in foreign production (reflected by an increase in $h^*$) induces a smaller production decrease at home (reflected by a less pronounced decline in h) to restore market clearing there. This makes locus $\frac{1}{\eta }\Phi (h)$ steeper. Locus $\frac{1}{\eta }\Phi (h)$ rotates in point C, because in this point the fraction of workers seeking employment in the sector of differentiated goods at home is at its autarky level: $h=h_a$. This establishes $\Gamma (h)=0$, and we can conclude from Eq. (17) that in this case changes in t do not affect $h^*$ for a given level of h. Using the same reasoning, it follows that $\eta \Phi (h^*)$ rotates counter-clockwise in point $C^*$, implying that higher trade costs bring the fraction of workers seeking employment in the sector of differentiated goods closer to the autarky levels of the two economies. To put it differently, higher trade costs lower the scope for specialization in the open economy.

Fig. 3

Increase in trade cost parameter from t to $t^\prime$

With the solution for h and $h^*$ at hand, we can make use of the outcome of wage bargaining and price setting in Eq. (11) and a structurally similar expression for the foreign country as well as the zero-profit conditions $\rho r=\rho r^*=\sigma P_Yf$ to solve for the equilibrium masses of domestic and foreign producers of differentiated goods, M and $M^*$, respectively. As pointed out above, $h=h^*$ holds under autarky, irrespective of prevailing size differences of the two economies. Whereas the fraction of workers seeking employment in the sector of differentiated goods is the same, the two countries differ in the mass of firms producing differentiated goods in the closed economy. Since the market for differentiated goods is larger in foreign than in home if $\eta >1$, we have $M^*>M$ in this case. Because wage bargaining plus constant markup pricing establishes for either country a positive link between the fraction of workers seeking employment in the sector of differentiated goods and the mass of firms producing them, we can conclude from the graphical analysis in Fig. 2 that trade leads to firm entry in the larger country and to firm exit in the smaller one, thereby augmenting pre-existing differences in the mass of local firms producing differentiated goods. From Fig. 3, we can further conclude that higher trade costs bring the masses of firms closer to their respective autarky levels, reducing the differences in the local mass of firms producing differentiated goods. This completes the characterization of the open economy equilibrium.

4.2 Trade pattern, unemployment, and welfare

With the mass of firms determined in the previous section, we can now make use of the zero-profit conditions and compute home’s total exports and imports of differentiated goods according to

$$\begin{aligned} EX_X&=M \frac{1}{1+t} \frac{\sigma P_Y f}{\rho }, \qquad IM_X=M^* \frac{1}{1+t} \frac{\sigma P_Y f}{\rho }, \end{aligned}$$

(19)

respectively. This implies that home is a net-importer of differentiated goods, $EX_X<IM_X$, if the foreign to domestic firm ratio $\mu \equiv M^*/M$ is larger than one. This is the case, if foreign is the larger economy, $\eta >1$, and therefore offers the larger home market for differentiated goods. The opposite is true if home is the larger economy. In this case, $\eta <1$ establishes $\mu <1$ and thus $EX_X>IM_X$. This trade structure is well in line with other models featuring a home-market effect (see Helpman and Krugman 1985). Assuming that households in the case of indifference purchase the domestic product, we have $IM_Y=0$ and $EX_Y=IM_X-EX_X$ if $\eta >1$ and therefore $\sum _j(EX_j+IM_j)=2IM_X$, where $j\in \{X,Y\}$ is an industry index. In contrast, $\eta <1$ gives $EX_Y=0$ and $IM_Y=EX_X-IM_X$ and thus $\sum _j(EX_j+IM_j)=2EX_X$. Also, higher trade costs lower the mass of firms that are active in the larger economy, thereby reducing the volume of trade.

The trade structure in our model is directly linked to the employment effects of trade. From the analysis in the closed economy, we know that only a fraction $1-u$ of workers seeking employment in the sector of differentiated goods is successfully matched with a firm. Since employment probability $1-u$ is pinned down by the condition that under diversification workers must be indifferent between employment in the production of the homogeneous or the differentiated good and since this indifference condition is given by Eq. (8) and thus the same in the closed and the open economy, the economy-wide rate of unemployment, uh, can be affected by trade only through adjustments in the fraction of workers seeking employment in the sector producing differentiated goods, h. This establishes the following proposition.

Proposition 1

In the open economy, the larger country is net-exporter of differentiated goods and suffers from a higher rate of unemployment. An increase in trade costs lowers the export of differentiated goods in the larger and the import of differentiated goods in the smaller economy. The economy-wide rate of unemployment decreases in the larger and increases in the smaller economy.

Proof

The proposition follows from the analysis above. $\square$

The link between trade structure and unemployment established in Proposition 1 is a direct consequence of associating employment in the sector of differentiated goods with a higher risk of unemployment. This property of our model is akin to the distinction put forward by Acemoglu (2001) between good jobs offering high wages at the cost of a longer duration of unemployment to wait for the respective offer and bad jobs associated with low wages and a shorter duration of unemployment. The link between unemployment and wages is also well in line with the observation from the US that manufacturing, while offering higher hourly earnings than the average workplace according to data from Bureau of Labor Statistics, is prone to longer durations of unemployment (see Chien & Morris, 2016).¹⁶

Since the large country is net-exporter of differentiated goods, it experiences an increase in the rate of unemployment in the open economy. However, this does not mean that trade is to the detriment of the larger economy. To see this, we can determine the welfare effects of trade. As pointed out in the analysis of the closed economy, the representative consumer in the case of PIGL preferences does not have a normative interpretation in general, implying that the choice of a proper welfare function is a priori not clear. This is different if preferences have Gorman form, and we therefore focus on the two limiting cases of homothetic and quasi-homothetic preferences for now, while discussing the case of $\varepsilon \in (0,1)$ in Sect. 4.3.

If households have Gorman form preferences, we can combine Eqs. (11) and (16) to compute an explicit solution for the ratio of foreign to domestic firms $\mu$ as a function of the relative foreign population size $\eta$ and trade cost parameter t. This gives for homothetic and quasi-homothetic preferences

$$\begin{aligned} \mu&=\frac{\eta \delta (t)-1}{ \delta (t)-\eta }, \qquad \mu =\frac{\eta {\hat{\delta }}(t)-1}{{\hat{\delta }}(t)-\eta }, \end{aligned}$$

(20)

respectively, with

$$\begin{aligned} \delta (t)\equiv t-\frac{\sigma -1}{\sigma }\frac{\rho (1+t)}{1-u}\left[ (1-u){\tilde{\alpha }}-1\right] (1-\beta ), \quad {\hat{\delta }}(t)\equiv t-\frac{\sigma -1}{\sigma }\frac{\rho (1+t)}{1-u}\left[ (1-u){\tilde{\alpha }}-1\right] . \end{aligned}$$

(21)

Furthermore, using the definition of $\mu$ in Eq. (16) and accounting for the solution of wage bargaining and markup pricing in Eq. (11) as well as the zero-profit condition $\rho r=\sigma P_Yf$, we can determine the fraction of workers seeking employment in the sector of differentiated goods in home. For the polar cases of homothetic and quasi-homothetic preferences, we compute

$$\begin{aligned} h=\frac{\frac{1-\beta }{1-u}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1-\beta }{1-u}[(1-u){\tilde{\alpha }}-1]}, \qquad h=\frac{\frac{\lambda -\beta }{\lambda (1-u)}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1}{1-u}[(1-u){\tilde{\alpha }}-1]}, \end{aligned}$$

(22)

respectively, whereas the mass of domestic firms can be computed by the unchanged condition $M=hH\lambda (1-u)/[(\sigma -1)f]$. Using Eq. (15), we can then formulate the following proposition.

Proposition 2

Let us assume that preferences have Gorman form and let us consider an open economy equilibrium with diversified production in both economies. Then, a decline in the trade cost parameter increases welfare in the larger economy, while it can increase or decrease welfare in the smaller economy if $(1-u){\tilde{\alpha }}>1$. Things are different if $(1-u){\tilde{\alpha }}<1$. In this case, a decline in the trade cost parameter increases welfare in the smaller economy, whereas it can increase or decrease welfare in the larger economy.

Proof

See the Appendix. $\square$

To provide an intuition for the welfare effects described in Proposition 2, we can distinguish three channels through which a decline in trade costs impacts welfare in our model. The first one is a fall in the price of differentiated goods imported from the foreign economy. This effect is captured by an increase in $(1+t)/t$ in price index $P_X=\frac{\sigma }{\sigma -1}\frac{w_Y}{\rho }\Big (M\frac{\mu +t}{1+t}\frac{1+t}{t}\Big )^{\frac{1}{1-\sigma }}$, and it also exists if countries are symmetric and hence in cases in which $\eta =1$ and the fraction of workers seeking employment in the sector of differentiated goods as well as the mass of firms producing them remain at their autarky levels. If countries differ in their population size, there are two additional effects. The first one is a disposable income effect, which materializes through changes in ${{\overline{e}}}=w_Y\lambda \{1+h[(1-u){\tilde{\alpha }}-1]\}$ and can be positive or negative. It is positive for the larger country net-exporting differentiated goods if $(1-u){\tilde{\alpha }}>1$, because in this case the wage premium received by workers newly employed by firms producing differentiated goods dominates the income loss of the newly unemployed. The opposite is true if $(1-u){\tilde{\alpha }}<1$. Disposable income effects in the two countries go into opposite directions, because the fraction of workers seeking employment in the sector of differentiated goods increases in the larger and decreases in the smaller economy.

Finally, there exists a variety effect, because existing firms change the location of production (captured by changes in $\mu$ for a given total mass of producers, $M+M^*$) and because firms enter or exit the market (captured by changes in the total mass of producers, $M+M^*$, for a given $\mu$). This variety effect materializes through adjustments in price index $P_X=\frac{\sigma }{\sigma -1}\frac{w_Y}{\rho }\Big (M\frac{\mu +t}{1+t}\frac{1+t}{t}\Big )^{\frac{1}{1-\sigma }}$ that are triggered by changes in the composite term $M\frac{\mu +t}{1+t}$ and it can be positive or negative. In the larger country, which net-exports differentiated goods, the mass of domestic producers increases. However, the mass of foreign firms decreases and the former dominates the latter only if trade increases average disposable household income, i.e. if $(1-u){\tilde{\alpha }}>1$. In this case, the larger country net-exporting differentiated goods unambiguously benefits from a fall in the trade cost parameter. Things are different if $(1-u){\tilde{\alpha }}<1$. In this case, a negative disposable income effect and a negative variety effect counteract the positive effect of cheaper access to foreign imports, and we show in the Appendix that they can dominate if $\sigma$ is sufficiently large, because for high levels of $\sigma$ both the positive price effect for imported goods as well as the negative variety effect are relatively small compared to the negative income effect.

While Proposition 2 is valid for both types of Gorman form preferences, there is a difference regarding the expected trade effects for homothetic and quasi-homothetic preferences. As pointed out by Lemma 1, quasi-homothetic preferences establish $(1-u){\tilde{\alpha }}<1$ for all possible $\alpha >1-\gamma$. This is, because in the limiting case of $\varepsilon \rightarrow 1$ households are risk neutral and hence they find it attractive to seek employment in the sector of differentiated goods and accept a lower probability of finding a job whenever this causes an increase in their expected income. This leads to a relatively low employment rate in the sector of differentiated goods, implying that the impact of trade on economy-wide unemployment is fairly strong. As a consequence, average disposable labor income falls in the country expanding production of differentiated goods, so that the larger country is at risk of double losses from trade due to an increase in the economy-wide unemployment and a decrease in the representative consumer’s welfare level if preferences are quasi-homothetic. Things are different in the case of homothetic (log-transformed Cobb-Douglas) preferences, because households are risk averse and thus expect a compensation for the possibility of ending up in an unfavorable state of unemployment when applying for jobs in the sector of differentiated goods. For a given wage premium offered by firms producing differentiated goods, this results in a higher employment rate $1-u$, and thus in a moderate increase in unemployment when exporting in the open economy increases the fraction of workers seeking employment in the sector of differentiated goods, h. As put forward by Lemma 1, $(1-u){\tilde{\alpha }}>1$ is guaranteed for all $\alpha >1-\gamma$ if $\gamma <\exp [-1]$. This implies that if preferences are homothetic and unemployment compensation is not too generous, trade is to the benefit of the larger economy, but may be detrimental for the smaller country. Double losses from trade are not possible in this case.

To complete the analysis in this section, we finally look at the case of undistorted labor markets. As outlined above, this can be captured by setting ${\tilde{\alpha }}=1$ (and thus $\alpha =1-\gamma$) in our model. If the sector of differentiated goods does not offer a wage premium, we have $w_X=w_Y$ and $u=0$. This implies $(1-u){\tilde{\alpha }}=1$ and leaves only one channel through which the reallocation of labor impacts economy-wide welfare, namely adjustments in the CES price index $P_X$. Noting from the analysis above that the composite term $M\frac{\mu +t}{1+t}$ is unaffected by trade cost changes if $(1-u){\tilde{\alpha }}=1$, it is only the direct effect of lower trade costs captured by adjustments in $(1+t)/t$ that is welfare relevant. Since lower trade costs reduce the prices of imports, both countries will therefore benefit from trade liberalization if labor markets are undistorted. This highlights the importance of a labor market distortion for the existence of losses from trade in our model.¹⁷

4.3 Welfare effects of trade if preferences do not have Gorman form

The welfare effects in Proposition 2 have been derived under the assumption of Gorman form preferences. We now deviate from this assumption and consider a case in which preferences do not have Gorman form. As pointed out above, the representative consumer in our model does not have a normative interpretation if $\varepsilon \in (0,1)$. This makes the choice of a social welfare function somewhat arbitrary. Egger and Habermeyer (2019) suggest to take a utilitarian perspective and to use average household utility as a social welfare function. This establishes

$$\begin{aligned} V\left( {{\overline{e}}} ,P_Y,P_X,{\hat{\psi }}\right)&\equiv \frac{1}{\varepsilon }\left( \frac{P_Y}{P_X}\right) ^{\varepsilon }\left[ \left( \frac{\overline{e}}{P_Y}\right) ^\varepsilon {\hat{\psi }}-\beta \right] -\frac{1-\beta }{\varepsilon }, \end{aligned}$$

(23)

where ${\hat{\psi }}\equiv H^{-1}\int _{i\in {\mathcal {H}}}\left( e_i/\bar{e}\right) ^{\varepsilon }di$ is a dispersion index, which is equal to $\psi$ only if $\varepsilon =1/2$. Eq. (23) is a natural candidate for our welfare analysis and it converges to $V_{CD}({{\overline{e}}},P_Y,P_X)$ and $V_{QH}({{\overline{e}}},P_Y,P_X)$ in the limiting cases of $\varepsilon \rightarrow 0$ and $\varepsilon \rightarrow 1$, respectively. As extensively discussed in Egger and Habermeyer (2019), the welfare function in Eq. (23) features social inequality aversion (through ${\hat{\psi }}<1$), which, however, is not the consequence of a prioritarian social planner but is rooted in the risk aversion of households imposed by the preferences in Eq. (1). Thus, the welfare function in Eq. (23) would associate a market outcome with the same level but a higher dispersion of disposable household income with a lower level of welfare, providing scope for achieving a welfare gain through redistribution of income from richer to poorer households.

In comparison to the limiting cases of homothetic and quasi-homothetic preferences studied in the previous section, the assumption of non-Gorman form preferences opens an additional channel through which trade affects welfare in the open economy, namely through changes in the dispersion of disposable household income. Thereby, changes in the dispersion of disposable household income influence welfare through a direct and an indirect effect. The direct effect works through the social income inequality aversion and implies that welfare decreases if trade lowers $\hat{\psi }$. The indirect effect works through changes in firm entry. Because the Engel curves for luxuries are convex, while the Engel curve for the necessity is concave, an increase in the dispersion of disposable household income increases consumer demand for differentiated goods and therefore leads to additional firm entry through a decline in $\psi$. This firm entry lowers price index $P_X$ relative to price $P_Y$ with positive welfare implications, according to Eq. (23). To keep things simple, we look at the case of $\varepsilon =1/2$, implying that the two dispersion measures are equal: $\psi ={\hat{\psi }}$. In this case, we have $(1-u)\sqrt{{\tilde{\alpha }}}+u\sqrt{\gamma }=1$ from Eq. (8) and thus

$$\begin{aligned} \sqrt{\frac{\overline{e}}{P_Y}}\psi =\sqrt{\lambda \frac{1+h[(1-u){\tilde{\alpha }}-1]}{1+h[(1-u){\tilde{\alpha }}+u\gamma -1]}}, \end{aligned}$$

where $T(h)=\sqrt{\frac{1+h[(1-u){\tilde{\alpha }}-1]}{1+h[(1-u){\tilde{\alpha }}+u\gamma -1]}}$, with $T^\prime (h)<0$, follows for $\varepsilon =1/2$ from the general solution of T(h) in Appendix A.5. Furthermore, making use of the solution for tax rate $\tau$ in Appendix A.4 the constraint that even unemployed households consume the differentiated good, $(1-\tau )\lambda \gamma >\beta ^2$, establishes $\sqrt{{{\overline{e}}}/P_Y}\psi =\sqrt{\lambda } T(h)>\beta$. Combining the market clearing condition in Eq. (16) with the zero-profit condition $\rho r=\sigma P_Y f$, we further compute

$$\begin{aligned} M\frac{\mu +t}{1+t}=\frac{H\lambda \rho }{\sigma f}\left\{ 1+h\left[ (1-u){\tilde{\alpha }}-1\right] -\beta \left( \sqrt{\lambda }\right) ^{-1} T(h)\right\} . \end{aligned}$$

Substituting into the price index for differentiated goods, we then obtain the welfare function

$$\begin{aligned} V(\cdot )=2\left( \sqrt{\frac{\sigma }{\sigma -1}\frac{1}{\rho }}\right) ^{-1}\left( \frac{H\lambda \rho }{\sigma f}\right) ^{\frac{1}{2(\sigma -1)}} {\hat{V}}(h)-2(1-\beta ), \end{aligned}$$

(24)

with

$$\begin{aligned} {\hat{V}}(h) \equiv \left\{ \Big [1+h[(1-u){\tilde{\alpha }}-1]-\beta \left( \sqrt{\lambda }\right) ^{-1} T(h)\Big ]\frac{1+t}{t}\right\} ^{\frac{1}{2(\sigma -1)}}\left[ \sqrt{\lambda }T(h)-\beta \right] . \end{aligned}$$

Noting from Fig. 3 that $dh/dt<0$ if home is a net-exporter of differentiated goods, we can conclude that $(1-u){\tilde{\alpha }}>1$ is no longer sufficient for gains from trade in the larger economy. If $\sigma$ is sufficiently large, the detrimental impact of trade on the level and dispersion of disposable household income (captured by a lower $\sqrt{\lambda }T(h)-\beta$) may dominate the gains from a lower import price and a positive variety effect. This strengthens our insights from above that the specific form of preferences plays a crucial role for the welfare effects of trade in our model.

5 Trade effects in the case of rich and poor countries

We now consider trade between two countries that differ in the labor endowments of households but feature the same total effective labor supply, $H\lambda =H^*\lambda ^*$. Households with a larger labor endowment receive higher disposable income and their country is thus associated with the richer economy. With differences in the households’ labor endowments, the outcome of wage bargaining plus constant markup pricing remains to be given by expressions equal to Eq. (11) for home and foreign, respectively, whereas the market clearing conditions for differentiated goods change to

$$\begin{aligned} \begin{aligned} H\lambda w_Y\left( 1-\beta \lambda ^{-\varepsilon }\right) +H\lambda w_Y B(h)&= \frac{Mrt}{1+t}+\frac{M^*r^*}{1+t}, \\ H^*\lambda ^*w_Y\left( 1-\beta (\lambda ^*)^{-\varepsilon }\right) + H^*\lambda ^*w_Y B^*(h^*)&= \frac{M^*r^*t}{1+t}+ \frac{Mr}{1+t}, \end{aligned} \qquad \qquad (16^\prime ) \end{aligned}$$

respectively, where $B^*(h^*)$ is defined in analogy to B(h) with $\lambda ^*$ replacing $\lambda$. Combining Eqs. (11) and $(16^\prime )$, we compute

$$\begin{aligned} h^*&= \Phi (h), \qquad h=\Phi ^*(h^*), \qquad \qquad \qquad \qquad \qquad (17^\prime ) \end{aligned}$$

with $\Phi (h)$ given by Eq. (18), $\Phi ^*(h^*)\equiv h^*+\frac{\sigma -1}{\sigma }\frac{\rho (1+t)}{1-u}\Gamma ^*(h^*)$, and $\Gamma ^*(h^*)$ defined in analogy to $\Gamma (h)$, with $\lambda ^*$ replacing $\lambda$.

System $(17^\prime )$ gives two equations in two unknowns, which can be combined to solve for the equilibrium values of h and $h^*$ in the open economy. For this purpose, we make use of Fig. 4, where the open economy equilibrium for the case of two symmetric countries is given by point A (similar to Fig. 1). A richer labor endowment of households in the foreign country ($\lambda ^*>\lambda$) increases the home market for differentiated goods there, provided that higher average disposable household income increases demand for differentiated goods, which is the case if $\varepsilon >0$. Then, the fraction of workers producing differentiated goods is already under autarky higher in foreign than at home, which can be seen from contrasting $h_a^*$ in point $A^\prime$ with $h_a$ in point A. In the open economy equilibrium (point ${\tilde{A}}$), the difference between h and $h^*$ is further increased, because foreign specializes in the production of differentiated goods in line with the idea of a home-market effect put forward by Helpman and Krugman (1985).¹⁸

Fig. 4

Open economy equilibrium if foreign is richer than home ($\lambda ^*>\lambda$)

With the equilibrium labor allocation at hand, we can derive the mass of firms producing differentiated goods, making use of $M=hH\lambda (1-u)/[(\sigma -1)f]$ and $M^*=h^*H^*\lambda ^*(1-u)/[(\sigma -1)f]$. Provided that $\varepsilon >0$, the richer country hosts a larger mass of firms producing differentiated goods, and hence becomes net-exporter of these goods in the open economy. Similar to the baseline scenario with country asymmetries rooted in different population sizes, net-exporting differentiated goods comes at the cost of a higher economy-wide unemployment rate. To determine the welfare effects of trade, we proceed as in Sect. 4.2 and focus on the two limiting cases representing Gorman form preferences. From Eq. (22), we see that for symmetry of the two countries in aggregate labor supply $H\lambda =H^*\lambda ^*$, h and in extension M are the same in the two economies and do not differ from their autarky levels (due to $\mu =1$) if preferences are homothetic. In this case, trade leaves unemployment unaffected and increases welfare in both economies, according to Eq. (15). With quasi-homothetic preferences, differences in the households’ labor endowments generate differences of the two economies in their demand for differentiated goods. This establishes $h^*>h$ and $M^*>M$ if $\lambda ^*>\lambda$, implying that the richer country net-exporting differentiated goods not only suffers from an increase in the economy-wide rate of unemployment but may also experience welfare losses from trade if $\sigma$ is sufficiently large (see the Appendix).

6 Conclusion

We have developed a two-country model of trade with differentiated and homogeneous goods using labor as the only production input. The model features a home-market effect due to trade costs of differentiated goods. Whereas the labor market in the homogeneous goods sector is perfectly competitive, there are search frictions and firm-level wage bargaining in the sector of differentiated goods. This generates involuntary unemployment, whose extent at the economy-wide level is linked to the fraction of workers seeking employment in the sector of differentiated goods. The exact form of this link depends on consumer preferences, which are assumed to be from the PIGL class and cover homothetic and quasi-homothetic preferences as two limiting cases.

In the open economy, the larger of the two countries specializes on the production of differentiated goods and net-exports these goods. Since seeking employment in the sector of differentiated goods is prone to the risk of unemployment, trade increases the economy-wide rate of unemployment in the larger economy. If preferences quasi-homothetic, households are risk neutral and in this case trade lowers average disposable household income and exerts a negative variety effect in the larger country, so that social welfare can be reduced there, although the prices of imported goods are reduced. Things are different in the smaller country, which benefits from trade. If preferences are homothetic, households are risk averse and trade induces an increase of average disposable household income and generates a positive variety effect in the larger economy, provided that unemployment compensation is not too generous. This adds to the gains from lower import prices, implying that the larger country benefits from trade, despite an increase in the economy-wide rate of unemployment. At the same time, the smaller country can lose from trade, because the negative income and variety effects work against the gains from lower import prices.

We also look at non-Gorman preferences and show that in this case changes in the dispersion of income exert an additional welfare effect, which is missing under homothetic and quasi-homothetic preferences. The impact of changes in the dispersion of income is twofold. On the one hand, a higher income dispersion increases demand for differentiated goods, which are luxuries in our model. This implies that higher income dispersion leads to firm entry and therefore induces indirect welfare gains due to a love-of-variety effect. On the other hand, from a utilitarian perspective welfare exhibits social inequality aversion, so that higher income dispersion reduces welfare through a direct effect. In the open economy, the assumption of non-Gorman preferences implies that an increase in the level of income is no longer sufficient for welfare gains from trade. We finally consider differences of the two countries in their per-capita labor endowments and show that such differences may lead to welfare loss in the richer economy if preferences are quasi-homothetic. In contrast, welfare gains are guaranteed for both countries if preferences are homothetic, because with homothetic utility per-capita income levels do not matter for aggregate consumer demand, implying that trade does not change the production structure in the open economy.

To improve the exposition of our analysis, we have imposed several simplifying assumptions. For instance, allowing for differentiated goods in only one sector and associating output of the other sector with a homogeneous good is useful for the analysis of asymmetric countries. However, studying the effects of trade in a setting with differentiated products in both sectors may provide additional relevant insights on the link between preference, trade structure and welfare. Also, allowing for heterogeneous firms and size-wage premia in the production of differentiated goods would be a worthwhile task. Finally, extending the model to one with country-specific forms of labor market distortion could provide a more nuanced picture of the link between population size and the rate of economy-wide unemployment. Whereas extensions in all these directions are promising, they are clearly beyond the scope of this paper.

Appendix: Theoretical appendix

1.1 Discussion of the utility function in Eq. (1)

Boppart (2014) introduces a subclass of PIGL preferences that are represented by a parametric indirect utility function of the following form:

$$\begin{aligned} v\left( P_X,P_Y,e_i\right) =\frac{1}{\varepsilon } \left( \frac{e_i}{P_X}\right) ^\varepsilon -\frac{\beta }{\gamma }\left( \frac{P_Y}{P_X}\right) ^\gamma -\frac{1}{\varepsilon }+\frac{\beta }{\gamma }, \end{aligned}$$

(A.1)

where $P_X$, $P_Y$ are prices of goods X and Y, $e_i$ is expenditure of household i, and $\beta$, $\varepsilon$, $\gamma$ are three preference parameters, where $\beta \in (0,1)$ and $0\le \varepsilon \le \gamma <1$. We consider the special case of $\varepsilon =\gamma$, which gives

$$\begin{aligned} v\left( P_X,P_Y,e_i\right) =\frac{1}{\varepsilon }\left( \frac{e_i}{P_X}\right) ^\varepsilon -\frac{\beta }{\varepsilon }\left( \frac{P_Y}{P_X}\right) ^\varepsilon -\frac{1-\beta }{\varepsilon }. \end{aligned}$$

(A.2)

Applying Roy’s identity to Eq. (A.2), we can compute the Marshallian demand functions, which can then be used to substitute for $P_Y/P_X$ and $e_i/P_X$ in order to derive the direct utility function in Eq. (1). Moreover, we compute indirect utility for the limiting case of quasi-homothetic preferences according to $\lim _{\varepsilon \rightarrow 1} v(P_X,P_Y,e_i)=e_i/P_X-\beta P_Y/P_X-1+\beta$, while we compute the indirect utility function for the limiting case of homothetic preferences according to

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} v\left( P_X,P_Y,e_i\right) =\lim _{\varepsilon \rightarrow 0}\frac{\left( \frac{e_i}{P_X}\right) ^\varepsilon -\beta \left( \frac{P_Y}{P_X}\right) ^\varepsilon -1+\beta }{\varepsilon }=\ln \left( \frac{e_i}{P_X}\right) -\beta \ln \left( \frac{P_Y}{P_X}\right) , \end{aligned}$$

(A.3)

where the second equality sign follows from applying the rule of L’Hôpital. Eq. (A.3) also shows that for indirect utility in Eq. (A.2) to converge to log-transformed Cobb-Douglas preferences in the limiting case of $\varepsilon \rightarrow 0$, the additive constant $(1-\beta )/\varepsilon$ plays a crucial role.

1.2 Derivation details for Eq. (7)

To derive Eq. (7), we solve the firm’s hiring and wage setting problem through backward induction and begin with stage two. Following Stole and Zwiebel (1996), we can characterize the solution of the bargaining problem by a splitting rule, which determines how the production surplus achieved by an agreement is distributed between the bargaining parties; and an aggregation rule, describing how infra-marginal production surpluses add up to the firm’s total surplus from multilateral bargaining with all of its workers. Bargaining with a mass $l(\omega )$ of workers, firm $\omega$’s total bargaining surplus is given by

$$\begin{aligned} \pi (\omega )=\int _{0}^{l(\omega )}\kappa [\ell | l(\omega )]{\hat{r}}(\ell )d\ell , \end{aligned}$$

(A.4)

where ${\hat{r}}(\ell )=D^{\frac{1}{\sigma }} (\lambda \ell )^{1-\frac{1}{\sigma }}$ are revenues achieved with employment level $\ell$, D is a common demand shifter, and

$$\begin{aligned} \kappa [\ell | l(\omega )]\equiv \frac{1}{\alpha \ell }\left( \frac{\ell }{l(\omega )}\right) ^{\frac{1}{\alpha }} \end{aligned}$$

(A.5)

is a probability measure that determines the fraction of infra-marginal production surplus the firm can acquire in its wage negotiation with workers. This probability measure declines in the workers’ relative bargaining power $\alpha >0$. Solving the integral in Eq. (A.4) gives

$$\begin{aligned} \pi (\omega )=\frac{\sigma }{\sigma +\alpha (\sigma -1)} D^{\frac{1}{\sigma }}\left[ \lambda l(\omega )\right] ^{1-\frac{1}{\sigma }}=\frac{\sigma }{\sigma +\alpha (\sigma -1)}r(\omega ), \end{aligned}$$

(A.6)

where the second equality sign uses the definition $r(\omega )\equiv {\hat{r}}[l(\omega )]$.

If an agreement in the wage negotiation between the firm and a worker is not achieved, the worker receives an unemployment compensation of $\gamma \lambda w_Y$, where $\gamma \in (0,1)$. The influence of unemployment compensation on wages is reflected in the splitting rule determining how to distribute the production surplus between the firm and its workers. This splitting rule is given by

$$\begin{aligned} \frac{\partial \pi (\omega )}{\partial l(\omega )}=\lambda \frac{w_X(\omega )-\gamma w_Y}{\alpha }, \end{aligned}$$

(A.7)

where $w_X(\omega )$ is the wage rate for each unit of labor input paid by firm $\omega$. Eqs. (A.6) and (A.7) jointly determine the solution for the firm’s bargaining problem at stage two. Thereby, firms accrue a constant fraction $\rho \equiv \sigma /[\sigma +\alpha (\sigma -1)]<1$. Eqs. (A.6) and (A.7) can be combined to compute $[(\sigma -1)/\sigma ]\rho r(\omega )/l(\omega )=\lambda [w_X(\omega )-\gamma w_Y]/\alpha$, which in turn can be solved for the wage bill: $\lambda l(\omega ) w_X(\omega )=\lambda l(\omega ) \gamma w_Y+ \rho r(\omega ) \alpha (\sigma -1)/\sigma$.

Equipped with the solution for the bargaining problem, we next determine the outcome of the firm’s hiring problem. Recollecting from above that firms have to invest f units of the homogeneous good to start production and one unit of the homogeneous good for each vacancy installed, this solution is found by maximizing profits $\Pi (\omega )\equiv \rho r(\omega )-q^{-1}P_Yl (\omega )-P_Yf$ with respect to $l(\omega )$, where $q<1$ is the probability that a vacancy can be filled, which in the case of random matching is exogenous to the individual firm and the same for all producers. The first-order condition for the firm’s profit-maximizing choice of $l(\omega )$ is given by

$$\begin{aligned} \frac{d\Pi (\omega )}{dl(\omega )}=\frac{\sigma -1}{\sigma }\frac{\rho r(\omega )}{l(\omega )}-\frac{P_Y}{q}=0. \end{aligned}$$

(A.8)

Accounting for Eqs. (A.6), (A.7), and recollecting that $P_Y=w_Y$ then gives the outcome of hiring and wage-setting for firms producing differentiated goods in Eq. (7).

1.3 Proof of Lemma 1

Multiplying Eq. (8) by ${\tilde{\alpha }}$ gives $(1-u){\tilde{\alpha }}={\tilde{\alpha }}(1-\gamma ^\varepsilon )/(\tilde{\alpha }^\varepsilon -\gamma ^\varepsilon )$ and thus $(1-u){\tilde{\alpha }}-1= {\tilde{\alpha }}[(1-\gamma ^\varepsilon )/(\tilde{\alpha }^\varepsilon -\gamma ^\varepsilon )]-1\equiv \Psi ({\tilde{\alpha }})$. We compute $\Psi (1)=0$, $\lim _{{\tilde{\alpha }}\rightarrow \infty }\Psi ({\tilde{\alpha }})=\infty$, and

$$\begin{aligned} \Psi ^\prime ({\tilde{\alpha }})=\frac{\Psi ({\tilde{\alpha }})+1}{{\tilde{\alpha }}}\left[ 1-\frac{\varepsilon {\tilde{\alpha }}^\varepsilon }{{\tilde{\alpha }}^\varepsilon -\gamma ^\varepsilon }\right] , \qquad \Psi ^{\prime \prime }({\tilde{\alpha }})=-\frac{\varepsilon \tilde{\alpha }^\varepsilon }{{\tilde{\alpha }}({\tilde{\alpha }}^\varepsilon -\gamma ^\varepsilon )}\Psi ^\prime ({\tilde{\alpha }})+\frac{\varepsilon ^2{\tilde{\alpha }}^\varepsilon \gamma ^\varepsilon [\Psi ({\tilde{\alpha }})+1]}{{\tilde{\alpha }}^2({\tilde{\alpha }}^\varepsilon -\gamma ^\varepsilon )^2}. \end{aligned}$$

(A.9)

From the derivatives of $\Psi ({\tilde{\alpha }})$, we can safely conclude that if $\Psi ({\tilde{\alpha }})$ has an extremum at ${\tilde{\alpha }}>1$, this extremum must be unique and a minimum, implying that $\Psi ({\tilde{\alpha }})>0$ holds for sufficiently high levels of $\alpha$ (with $\alpha ={\tilde{\alpha }}-\gamma$). Furthermore $\Psi ^\prime (1)\ge 0$ follows if $\gamma \le (1-\varepsilon )^{\frac{1}{\varepsilon }}\equiv {\underline{\gamma }}(\varepsilon )$ and, in this case, $\Psi ^\prime ({\tilde{\alpha }})>0$ and thus $\Psi ({\tilde{\alpha }})>0$ holds for all ${\tilde{\alpha }}>1$ or, equivalently, for all $\alpha >1-\gamma$. Accounting for $\underline{\gamma }^\prime (\varepsilon )<0$, $\lim _{\varepsilon \rightarrow 0}\underline{\gamma }(\varepsilon )=\exp [-1]$, and $\lim _{\varepsilon \rightarrow 1}{\underline{\gamma }}(\varepsilon )=0$ then establishes Lemma 1.

1.4 Derivation of Eq. (10)

Making use of definition $\psi \equiv H^{-1}\int _{i\in \mathcal H}\left( e_i/{\bar{e}}\right) ^{1-\varepsilon }di$, the dispersion index of disposable household income can be expressed as

$$\begin{aligned} \psi =\left[ \frac{(1-\tau )w_Y\lambda }{\overline{e}}\right] ^{1-\varepsilon } \left\{ 1+h\left[ (1-u){\tilde{\alpha }}^{1-\varepsilon }+u\gamma ^{1-\varepsilon }-1\right] \right\} \end{aligned}$$

(A.10)

where $\tau \in (0,1)$ is the common income tax rate that is determined by the condition of a balanced budget of the government:

$$\begin{aligned} \tau =\frac{h u\gamma }{1+h\left[ (1-u)\tilde{\alpha }+u\gamma -1\right] }. \end{aligned}$$

(A.11)

Substituting Eqs. (9) and (A.11) for ${{\overline{e}}}$ and $\tau$, respectively, we can rewrite Eq. (A.10) as Eq. (10).

1.5 Derivations details for B(h) and Eq. (12)

From Eq. (6) it follows that total expenditures for differentiated goods are equal to

$$\begin{aligned} \int _{\omega \in \Omega }p(\omega )x(\omega )d\omega =H\overline{e}\left[ 1-\beta \left( \frac{\overline{e}}{P_Y}\right) ^{-\varepsilon }\psi \right] . \end{aligned}$$

(A.12)

Substituting Eq. (9) for ${{\overline{e}}}$ and Eq. (10) for $\psi$, we can express economy-wide demand for differentiated goods as

$$\begin{aligned} \int _{\omega \in \Omega }p(\omega )x(\omega )d\omega&=Hw_Y\lambda \left\{ 1+h[(1-u){\tilde{\alpha }}-1]\right\} -\beta Hw_Y\lambda ^{1-\varepsilon }T(h)\nonumber \\&=Hw_Y\lambda (1-\beta \lambda ^{-\varepsilon })+Hw_Y\lambda B(h), \end{aligned}$$

(A.13)

where the first equality sign uses the definition of

$$\begin{aligned} T(h)\equiv \left\{ 1+h\left[ (1-u){\tilde{\alpha }}^{1-\varepsilon }+u\gamma ^{1-\varepsilon }-1\right] \right\} \left( \frac{1+h[(1-u){\tilde{\alpha }}-1]}{1+h[(1-u){\tilde{\alpha }}+u\gamma -1]}\right) ^{1-\varepsilon }, \end{aligned}$$

(A.14)

while the second equality sign uses the definition of B(h) in the main text. Setting $\int _{\omega \in \Omega }p(\omega )x(\omega )d\omega =Mr$ finally establishes the market clearing condition in Eq. (12). This completes the proof.

1.6 Determination of h in the closed economy

In the main text, we argue that $\Gamma (h)=0$ has a unique solution on the unit interval. To see this, we can make use of the definition of $\Gamma (h)$ in Eq. (13) and first note that $\Gamma (0)=1-\beta \lambda ^{-\varepsilon }>0$ and that $\Gamma (1)=-\big (\frac{\sigma }{\sigma -1}-\gamma \big )(1-u)-\beta \lambda ^{-\varepsilon } T(1)<0$. Making use of the Intermediate Value Theorem, we can thus safely conclude that $\Gamma (h)=0$ has a solution in $h\in (0,1)$. In the two limiting cases of $\varepsilon \rightarrow 0$ and $\varepsilon \rightarrow 1$, we have $T(h)=1+h\left[ (1-u){\tilde{\alpha }} -1\right]$ and $T(h)=1$, implying that $\Gamma (h)=0$ has an explicit and unique solution in $h\in (0,1)$. The solutions for the two limiting cases are given by Eq. (14). Things are less obvious if $\varepsilon \in (0,1)$. Since uniqueness of the solution $\Gamma (h)=0$ is tedious to show for this more general case, we delegate the formal proof of this result to an Online Appendix.

1.7 Welfare effects of an increase in $\alpha$ in the closed economy

We first consider the case of homothetic (log-transformed Cobb-Douglas) preferences, so that welfare is given by $V_{CD}({{\overline{e}}}, P_Y,P_X)$ in Eq. (15). Substituting $P_X=\frac{\sigma }{\sigma -1}\frac{w_Y}{\rho } M^{\frac{1}{1-\sigma }}$ and ${{\overline{e}}}=w_Y\lambda \big \{1+h[(1-u){\tilde{\alpha }}-1]\big \}$, and accounting the relevant h from Eq. (14) and $M=hH\lambda (1-u)/[(\sigma -1)f]$, we compute $V_{CD}(\cdot )=\ln \lambda +\frac{1-\beta }{\sigma -1}\ln \left( \frac{(1-\beta )H\lambda }{(\sigma -1) f}\right) +\ln \left[ V_0(\alpha )\right]$, with

$$\begin{aligned} V_0(\alpha )=\left( \frac{\sigma }{\sigma -1}\frac{1}{\rho }\right) ^\beta \left\{ \frac{\sigma }{\sigma -1}\frac{1}{\rho }-\frac{1-\beta }{1-u} \left[ (1-u){\tilde{\alpha }}-1\right] \right\} ^{-\frac{\sigma -\beta }{\sigma -1}}. \end{aligned}$$

$dV_{CD}(\cdot )/d\lambda >0$ is immediate. Furthermore, acknowledging $\rho =\frac{\sigma }{\sigma +\alpha (\sigma -1)}$, ${\tilde{\alpha }}=\alpha +\gamma$ and $1-u=-\frac{\ln \gamma }{\ln {\tilde{\alpha }}-\ln \gamma }$, the derivative of $V_0(\alpha )$ can be computed according to

$$\begin{aligned} V_0^\prime (\alpha )=V_0(\alpha )\left\{ \frac{\beta }{\frac{\sigma }{\sigma -1}\frac{1}{\rho }}-\frac{\sigma -\beta }{\sigma -1}\frac{\beta -(1-\beta )\frac{1}{{\tilde{\alpha }}\ln \gamma }}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }-\frac{1-\beta }{1-u}\left[ (1-u){\tilde{\alpha }}-1\right] }\right\} . \end{aligned}$$

(A.15)

Evaluated at $\alpha =1-\gamma$ (and thus ${\tilde{\alpha }}=1$), we compute $V_0^\prime (1-\gamma )<0$. For higher levels of $\alpha$, the marginal effect is however not clear. For instance, setting parameter values $\sigma =2$, $\beta =0.8$, and $\gamma =0.98$, $V_0( \alpha )$ has a local minimum at $\alpha =6.46$.

Let us now turn to the limiting case of $\varepsilon \rightarrow 1$. Accounting for the relevant h from Eq. (14) and $M=hH\lambda (1-u)/[(\sigma -1)f]$, we can express welfare by $V_{QH}(\cdot )=(\lambda -\beta )^{\frac{\sigma }{\sigma -1}}\left[ \frac{H}{(\sigma -1)f}\right] ^{\frac{1}{\sigma -1}}{\hat{V}}_0(\alpha )^{\frac{\sigma }{\sigma -1}}-1+\beta$, with

$$\begin{aligned} {\hat{V}}_0(\alpha )=\left\{ \frac{\sigma }{\sigma -1}\frac{1}{\rho }-\frac{1}{1-u}\left[ (1-u){\tilde{\alpha }}-1\right] \right\} ^{-1}=\left( \frac{\sigma }{\sigma -1}-\gamma +\frac{\alpha }{1-\gamma }\right) ^{-1}. \end{aligned}$$

(A.16)

Thereby, the second equality sign makes use of the definition of $\rho$ and $1-u=\frac{1-\gamma }{\alpha }$ from Eq. (8). From these computations, we can conclude that $V_{QH}(\cdot )$ increases in $\lambda$ and decreases in $\alpha$. This completes the proof.

1.8 Characterization of a unique interior equilibrium in Fig. 1

In Fig. 1, $\Phi (h)$ has an intercept with the vertical axis at $\Phi (0)=\frac{\sigma -1}{\sigma }\frac{\rho (1+t)}{1-u}(1-\beta \lambda ^{-\varepsilon })$ and this intercept is denoted by $f_1(t)$, with $f_1^\prime (t)>0$. Due to symmetry of the two trading partners, the intercept of $\Phi (h^*)$ with the horizontal axis is also given by $f_1(t)$. Furthermore, $\Phi (h)$ has an intercept with the horizontal axis if $h+\frac{\sigma -1}{\sigma }\frac{\rho (1+t)}{1-u}\Gamma (h)=0$ has a solution in h. For $-\frac{1-u}{1+t}\left[ t\big (\frac{\sigma }{\sigma -1}-\gamma \big )-{\tilde{\alpha }}\right] -\beta \lambda ^{-\varepsilon } T(1)\equiv I(t)<0$ a solution exists and it lies on the unit interval.¹⁹ Noting that $\lim _{t\rightarrow \infty }I(t)=-\big (\frac{\sigma }{\sigma -1}-\gamma \big )(1-u)-\beta \lambda ^{-\varepsilon } T(1)\equiv \Gamma (1)$ and recollecting $\Gamma (1)<0$ from Appendix A.6, it follows that $I(t)<0$ and thus a solution $\Phi (h)=0$ in the unit interval is achieved for sufficiently high levels of t. We denote this solution by $f_2(t)$, with $f_2^\prime (t)<0$, with uniqueness of $f_2(t)$ ensured if $\Phi (h)$ has a negative slope (see below).

Let us next define a critical trade cost level

$$\begin{aligned} {\underline{t}}(x)\equiv -\frac{2\sigma }{\sigma -1}\frac{1-u}{\rho } \Gamma ^\prime (x)^{-1}-1, \quad x=h,h^* \end{aligned}$$

(A.17)

such that $\Phi ^\prime (h)<-1$ holds if $t>{\underline{t}}(h)$, whereas $\Phi ^\prime (h^*)<-1$ holds if $t>{\underline{t}}(h^*)$. Noting that $t>\max \left\{ {\underline{t}}(0),{\underline{t}}(1)\right\}$ is sufficient for $\Phi ^\prime (h)<-1$ to extend to all $h\in (0,1)$ and for $\Phi ^\prime (h^*)<-1$ to extend to all $h^*\in (0,1)$,²⁰ it follows from $t>\max \left\{ \underline{t}(0),{\underline{t}}(1)\right\}$ that both loci $\Phi (h)$, $\Phi (h^*)$ are negatively sloped with curve $\Phi (h)$ being steeper than curve $\Phi (h^*)$ in Fig. 1. From the definitions of $f_1(t), f_2(t)$, we can then infer that a unique intersection point of $\Phi (h)$, $\Phi (h^*)$ exists, which in turn must be located at the $45^\circ$-line due to our assumption of two symmetric countries. Taking stock, the analysis above proves existence of the unique intersection point A in Fig. 1 if trade costs t are sufficiently high.

1.9 Proof of Proposition 2

Let us first consider the limiting case of homothetic (log-transformed Cobb-Douglas) preferences, with welfare given by $V_{CD}({{\overline{e}}},P_Y,P_X)$ in Eq. (15). Substituting the relevant h from Eq. (22) and $M=hH\lambda (1-u)/[(\sigma -1)f]$ into $\overline{e}=w_Y\lambda \{1+h[(1-u){\tilde{\alpha }}-1]\}$ and $P_X=\frac{\sigma }{\sigma -1}\frac{w_Y}{\rho }\Big (M\frac{\mu +t}{1+t}\frac{1+t}{t}\Big )^{\frac{1}{1-\sigma }}$, we can compute

$$\begin{aligned} \overline{e}&=w_Y\lambda \frac{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1-\beta }{1-u}[(1-u){\tilde{\alpha }}-1]}, \end{aligned}$$

(A.18)

$$\begin{aligned} P_X&=\frac{\sigma }{\sigma -1}\frac{w_Y}{\rho }\left( \frac{(1-\beta )H\lambda \rho }{\sigma f}\right) ^{\frac{1}{1-\sigma }}\left( \frac{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1-\beta }{1-u}[(1-u){\tilde{\alpha }}-1]}\frac{1+t}{t}\right) ^{\frac{1}{1-\sigma }}. \end{aligned}$$

(A.19)

Substituting into $V_{CD}({{\overline{e}}},P_Y,P_X)$, then gives $V_{CD}(\cdot )=-(1-\beta )\ln \left( \frac{\sigma }{\sigma -1}\frac{1}{\rho }\right) +\ln \lambda +\frac{1-\beta }{\sigma -1}\ln \left( \frac{(1-\beta )H\lambda \rho }{\sigma f}\right) +\ln \left[ V_1(t)\right]$,

$$\begin{aligned} V_1(t)&=\left( \frac{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1-\beta }{1-u}[(1-u){\tilde{\alpha }}-1]}\right) ^{\frac{\sigma -\beta }{\sigma -1}}\left( \frac{1+t}{t}\right) ^{\frac{1-\beta }{\sigma -1}}, \end{aligned}$$

(A.20)

where $\mu$ is given by Eq. (20). Differentiating $f(t)\equiv \frac{\mu +t}{1+t}$ establishes

$$\begin{aligned} f^\prime (t)=\frac{1-\mu }{(1+t)^2}+\frac{d\mu }{dt}\frac{1}{1+t}=\frac{1}{1+t}\left[ \frac{1-\mu }{1+t}+\frac{1-\eta ^2}{[\delta (t)-\eta ]^2}\delta ^\prime (t)\right] . \end{aligned}$$

(A.21)

Noting that $\mu >,=,<1$ if $\eta >,=,<1$ from Eq. (20) and that $\delta ^\prime (t)>0$ from Eq. (21), we can safely conclude that $f^\prime (t)>,=,<0$ if $1>,=,<\eta$. Furthermore, differentiating $V_1(t)$ gives

$$\begin{aligned} V_1^\prime (t)=V_1(t)\left[ -\frac{\sigma -\beta }{\sigma -1}\frac{\frac{1-\beta }{1-u}[(1-u){\tilde{\alpha }}-1]\frac{1+t}{\mu +t}f^\prime (t)}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1-\beta }{1-u}[(1-u){\tilde{\alpha }}-1]}-\frac{1-\beta }{\sigma -1}\frac{1}{t(1+t)}\right] . \end{aligned}$$

(A.22)

This derivative is unambiguously negative if either $1>\eta$ (home net-exporting differentiated goods) and $(1-u){\tilde{\alpha }}>1$ or $1<\eta$ (home net-importing differentiated goods) and $(1-u){\tilde{\alpha }}<1$. In contrast,

$$\begin{aligned} \lim _{\sigma \rightarrow \infty }V_1^\prime (t)=-\frac{(1+\alpha )\frac{1-\beta }{1-u}[(1-u){\tilde{\alpha }}-1]f^\prime (t)}{\left\{ (1+\alpha )\frac{\mu +t}{1+t}-\frac{1-\beta }{1-u}[(1-u){\tilde{\alpha }}-1]\right\} ^2} \end{aligned}$$

(A.23)

is positive if $1>\eta$ (home net-exporting differentiated goods) and $(1-u){\tilde{\alpha }}<1$ or if $1<\eta$ (home net-importing differentiated goods) and $(1-u){\tilde{\alpha }}>1$. This completes the proof of Proposition 2 for the limiting case of $\varepsilon \rightarrow 0$.

If preferences are quasi-homothetic, welfare is given by $V_{QH}({{\overline{e}}},P_Y,P_X)$ in Eq. (15). Substituting the relevant h from Eq. (22) and $M=hH\lambda (1-u)/[(\sigma -1)f]$ into $\overline{e}=w_Y\lambda \{1+h[(1-u){\tilde{\alpha }}-1]\}$ and $P_X=\frac{\sigma }{\sigma -1}\frac{w_Y}{\rho }\Big (M\frac{\mu +t}{1+t}\frac{1+t}{t}\Big )^{\frac{1}{1-\sigma }}$, we can compute

$$\begin{aligned} \frac{\overline{e}}{P_Y}-\beta&=\frac{(\lambda -\beta )\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{ 1}{1-u}[(1-u){\tilde{\alpha }}-1]}, \end{aligned}$$

(A.24)

$$\begin{aligned} P_X&=\frac{\sigma }{\sigma -1}\frac{w_Y}{\rho }\left( \frac{H\rho }{\sigma f}\right) ^{\frac{1}{1-\sigma }}\left( \frac{(\lambda -\beta )\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1}{1-u}[(1-u){\tilde{\alpha }}-1]}\frac{1+t}{t}\right) ^{\frac{1}{1-\sigma }}. \end{aligned}$$

(A.25)

This allows us to determine $V_{QH}(\cdot )=\left( \frac{\sigma }{\sigma -1}\frac{1}{\rho }\right) ^{-1}\left( \frac{H\rho }{\sigma f}\right) ^{\frac{1}{\sigma -1}} {\hat{V}}_1(t)-1+\beta$, with

$$\begin{aligned} {\hat{V}}_1(t)&=\left( \frac{(\lambda -\beta )\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1}{1-u}[(1-u){\tilde{\alpha }}-1]}\right) ^{\frac{\sigma }{\sigma -1}}\left( \frac{1+t}{t}\right) ^{\frac{1}{\sigma -1}}. \end{aligned}$$

(A.26)

Differentiation with respect to t gives

$$\begin{aligned} {\hat{V}}_1^\prime (t)={\hat{V}}_1(t)\left[ -\frac{\sigma }{\sigma -1}\frac{\frac{1}{1-u}[(1-u){\tilde{\alpha }}-1]\frac{1+t}{\mu +t}{\hat{f}}^\prime (t)}{\frac{\sigma }{\sigma -1}\frac{1}{\rho }\frac{\mu +t}{1+t}-\frac{1}{1-u}[(1-u){\tilde{\alpha }}-1]}-\frac{1}{\sigma -1}\frac{1}{t(1+t)}\right] , \end{aligned}$$

(A.27)

where ${\hat{f}}(t)\equiv \frac{\mu +t}{1+t}$ and $\mu =\frac{\eta \hat{\delta }(t)-1}{{\hat{\delta }}(t)-\eta }$ have been considered. In analogy to the case of homothetic preferences, we find that this derivative is unambiguously negative if $1<\eta$ (home net-importing differentiated goods) and $(1-u){\tilde{\alpha }}<1$. In contrast, we find that $\lim _{\sigma \rightarrow \infty }{\hat{V}}_1^\prime (t)$ is positive if $1>\eta$ (home net-exporting differentiated goods) and $(1-u){\tilde{\alpha }}<1$. This completes the proof of Proposition 2 for the limiting case of $\varepsilon \rightarrow 1$.

1.10 Formal details for the analysis in Sect. 5

Let us consider the limiting case of $\varepsilon \rightarrow 1$ and focus on an interior solution with $h,h^*\in (0,1)$. Then, accounting for the definition of ${\hat{\delta }}(t)$ in Eq. (21), we can follow the steps from the main text to compute

$$\begin{aligned} \mu =\frac{{\hat{\eta }} {\hat{\delta }}(t)-1}{{\hat{\delta }}(t)-{\hat{\eta }}} , \qquad {\hat{\eta \equiv }} \frac{\lambda ^*-\beta }{\lambda ^*}\frac{\lambda }{\lambda -\beta }. \end{aligned}$$

(A.28)

Thereby, $\mu >,=,<1$ if $\lambda ^*>,=,<\lambda$ and thus ${\hat{\eta }}>,=,<1$. Noting that the relevant h is given in Eq. (22) and $M=hH\lambda (1-u)/[(\sigma -1)f]$ and following the derivation details from Appendix A.9, we can compute $V_{QH}(\cdot )=\left( \frac{\sigma }{\sigma -1}\frac{1}{\rho }\right) ^{-1}\left( \frac{H\rho }{\sigma f}\right) ^{\frac{1}{\sigma -1}} {\hat{V}}_1(t) -1+\beta$, with ${\hat{V}}_1(t)$ given by Eq. (A.26). The welfare effects of trade discussed in Sect. 5 then follow from the proof of Proposition 2.