Tariff scheme choice

Abstract

This paper examines the determinants of the probability that an exporter chooses between a most-favored nation (MFN) scheme and multiple regional trade agreement (RTA) schemes. We estimate a discrete choice model using transaction-level import data for Thailand in 2014. We find that RTA schemes are more likely to be chosen, given a larger transaction value. Among RTA schemes, the ones with less restrictive rules of origin or lower tariff rates are more likely to be selected. We also conduct simulation analysis to provide quantitative policy implications.

1 Introduction

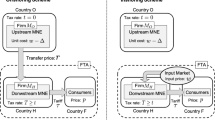
During the 2010s, regional trade agreements (RTAs) were negotiated among numerous countries to reap the benefits of trade liberalization. RTAs with many countries are called “mega” RTAs. Recent examples of mega RTAs include the Comprehensive and Progressive Agreement for Trans-Pacific Partnership (CPTPP); the Transatlantic Trade and Investment Partnership; and the Regional Comprehensive Economic Partnership (RCEP). RTA networks between each country pair will likely overlap with mega RTAs. For example, Mexico entered into the North American Free Trade Agreement (NAFTA) with Canada and the U.S., which overlaps with the CPTPP. Mexican firms must choose between a most-favored-nation (MFN) scheme and multiple RTA schemes (NAFTA or CPTPP) when they export to Canada. As this example indicates, firms increasingly face decisions between multiple RTA schemes as the number of mega RTAs has increased.

With multiple RTA schemes available, firms find it difficult to choose a tariff scheme.¹ Firms are required to adhere to the rules of origin (RoO) and obtain certificates of origin (CoO) when they use RTA tariff schemes. To certify the origin of goods, exporters must collect the required documents, such as a list of inputs, a production flowchart, production instructions, invoices for each input, and contract documents. This process arises as an exporter’s fixed cost for RTA utilization. When exporters choose between an MFN and RTA scheme, they examine whether the benefit of RTA tariff rates, which are generally lower than MFN rates, exceeds the fixed costs for RTA utilization. However, given multiple RTA schemes, exporters must consider the distinction among them, which stem from tariff rates and RoO. Exporters compare tariff rates and RoO across RTA schemes to select the best one. Furthermore, a change in tariff rates in one RTA influences the probability not only that this RTA is chosen but also that other RTAs are chosen. As the number of overlapping RTAs increases, such interaction effects are more likely to be present.

This study empirically investigates the determinants of choosing a tariff scheme when multiple RTA schemes are available. We use data on Thailand imports from other Association of Southeast Asian Nations (ASEAN) countries in 2014 for two primary reasons.² First, the data allows us to identify the tariff schemes (e.g., MFN or RTA) used in each transaction. We obtained the data, which covers all commodity imports, from the Customs Office of the Kingdom of Thailand. Product coverage is important for our study because we need sufficient variation in the tariff rates and the RoO across products.³ Second, at least seven tariff schemes were available for Thai imports from ASEAN countries in 2014: an MFN scheme, the ASEAN Trade in Goods Agreement (ATIGA), the ASEAN–Australia–New Zealand Free Trade Agreement (AANZFTA), the ASEAN–China FTA (ACFTA), the ASEAN–India FTA (AIFTA), the ASEAN–Japan Comprehensive Economic Partnership (AJCEP), and the ASEAN–Korea FTA (AKFTA). Exporters from ASEAN to Thailand can apply any of these seven schemes for any product. By examining this trade flow in 2014, we can investigate how firms choose tariff schemes, given multiple RTA schemes.

Our study contributes to the literature in three ways. First, we use discrete choice models, which are tractable in expanding the set of alternatives, i.e., the number of RTA schemes. Studies on the determinants of choosing preference schemes typically explore cases where a single preference scheme is available in addition to an MFN clause (e.g., Ju and Krishna 2005; Cadot et al. 2006; Cadot and de Melo 2007; Francois et al. 2006; Manchin 2006; Hakobyan 2015). Similar studies have been conducted with two preferential schemes and an MFN scheme (e.g., Bureau et al. 2007; Hayakawa 2014; Hayakawa et al. 2019). However, the empirical method we propose in this study is the nested logit model with two stages, which is based on a theoretical study on a firm’s tariff scheme choice (Demidova and Krishna 2008; Cherkashin et al. 2015) and can easily expand the number of alternatives (i.e., RTAs). Thus, our methodology ensures a more flexible framework. The upper stage includes two nests and describes the choice between the MFN and RTA schemes, while the lower stage describes a specific tariff scheme. As a natural extension, we also estimate the mixed logit model, which is more flexible in terms of substitution among alternatives than the nested logit model.⁴

Another advantage of using the discrete choice model is that it enables us to conduct the following three quantitative analyses. First, we examine how changes in tariff rates in one tariff scheme influence choice probabilities of this and other tariff schemes. Specifically, this study computes the elasticities of the probability of choosing each scheme in terms of tariff rates. Thereafter, it quantitatively demonstrates how differently the tariff reduction in one RTA influences the choice between this, other RTAs, and an MFN scheme. This analysis reveals the detailed interaction effects of tariff rates on the choice probability of each tariff scheme. The second analysis is to estimate the elasticity with respect to transaction values according to export countries. This provides an insight into the difference in the magnitude of fixed costs for RTA utilization across countries because larger transaction values lead to larger benefits to cover the associated fixed costs; thus, elasticity is expected to be higher when fixed costs are lower.⁵ The third analysis is indicating the extent to which scheduled tariff reduction influences the choice probability of each tariff scheme. Furthermore, we investigate how this choice probability changes if the RoO in all RTAs are set to the least restrictive type. These simulation analyses will help predict each RTA’s utilization in the final year of tariff reduction and the impacts of revising RoO to a relatively more business-friendly type on RTA utilization.

Our paper’s second contribution is to examine the role of a most disaggregated measure on transaction sizes. The existing studies have used aggregated trade values to examine the “size” effect on preference utilization. Examples of the measures used in the literature include country-level annual trade values (e.g., Hakobyan 2015) or the district-level monthly average of trade values (e.g., Keck and Lendle 2012). These aggregated measures mask the difference in transaction sizes across exporting firms. We utilized transaction-level import data. For example, one firm may import one product from one country multiple times even within one day. We identify these observations of multiple transactions and then examine how the transaction size affects a firm’s tariff scheme choice.

The use of transaction-level data is crucial when examining an exporting firm’s choice on tariff schemes. Because the information on tariff schemes used in international trade is collected in the customs of importing countries and not in exporting countries, it is a usual limitation to rely on import data. However, in our study, we do not use aggregated data like firm-level data on annual imports because they are not necessarily associated with the characteristics or decisions of a specific exporting firm, especially when a firm imports from multiple exporting firms. Only at the transaction level, can the trade information be linked with a specific exporting/importing firm. In sum, using transaction-level data is the desirable strategy for examining exporting firms’ decisions from import-side data. Our estimation results indicate that RTA schemes are likely to be chosen rather than the MFN scheme when our disaggregated measure of transaction size is larger.

Our third contribution is to improve the empirical identification strategy when examining the role of tariff rates and RoO. Unlike the framework in the literature (e.g., Carrere and de Melo 2006), our analysis is a cross-RTA analysis with regard to a product rather than a cross-product analysis within an RTA scheme. In other words, we elucidate the difference in RoO for one product across RTAs, whereas the literature uses the difference in RoO in an RTA across products. In the latter, the difference in the effect of the RoO on RTA utilization depends on not only the difference in RoO per se but also the difference in product characteristics. In particular, if product characteristics (e.g., export competitiveness) affect both the selection of RoO and the tariff scheme choice, the estimates will be biased. In our study, we directly compare RoO in each product, and our results on the effect of the RoO are not driven by differences in product characteristics. Indeed, our results on the magnitude order of the negative effects across RoO differ from those obtained in previous studies. Furthermore, thanks to the richer variation of RoO in our study RTAs, we can examine the effects of more types of RoO than previous studies.

The remainder of this paper is organized in the following manner. Section 2 specifies the nested logit model for empirical analyses. Section 3 explains the data sources and presents a brief overview of RTAs in Thailand. Section 4 discusses the estimation results. Section 5 provides some quantitative interpretation of our estimation results, and Sect. 6 concludes our study.

2 Empirical framework

We derive a nested logit model based on the exporter’s choice of tariff schemes.⁶ The model considers the case of multiple available RTA schemes in addition to an MFN. Each exporter has a firm-specific parameter that positively depends on elements such as productivity or production capability. When a firm exports a product to a country, the exporter’s decision is split into two steps. First, a firm decides whether to use an MFN ($M$) scheme or an RTA scheme ($R\left( r \right),{ }r = 1, \cdots ,N^{R}$) by comparing the export profit under the MFN scheme with the largest export profit among the RTA schemes. $N^{R}$ denotes the number of RTA schemes available for a firm. In any case, they need to pay the fixed costs for exports. Then, the exporter selects the most profitable RTA scheme if a firm decides to use RTA schemes. This two-step decision occurs because RTA schemes qualitatively differ from an MFN scheme as firms have to pay fixed costs for RTA utilization, which is not required for the latter. Indeed, this supposition will be supported in our empirical analysis.

Tariff schemes differ from each other, and tariff rates differ across tariff schemes. In particular, rates in any RTA are not higher than MFN tariff rates. In addition, when exporting under RTA schemes, firms must incur the costs of procurement adjustment to comply with RoO. Various rules exist in RoO: change in chapter (CC), change in heading (CH), change in subheading (CS), wholly obtained (WO), regional value content (RVC), and specific process (SP). For example, CC requires exported products to have different two-digit harmonized system (HS) codes from inputs imported from non-RTA member countries while such transformation is required at a six-digit level for a CS. Here CC potentially requires exporters to drastically adjust their production and input sources compared with CS. RoO are set for each product in each RTA. Therefore, the procurement adjustment cost of a product differs across RTAs.

Further, fixed costs differ between MFN and RTA schemes. As mentioned in the introductory section, when exporting under RTA schemes, exporters incur additional fixed costs for RTA utilization. Thus, the total amount of fixed costs is greater under RTA schemes than an MFN scheme. In our theoretical foundation, we assume that fixed costs for RTA utilization are identical across RTA schemes to derive a nested logit equation to estimate the conditional RTA scheme choice.⁷ Similar assumptions were employed in studies on the FDI location choice (e.g., Head and Mayer 2004; Amiti and Javorcik 2008; Mayer et al. 2010).

To specify our nested logit model for tariff scheme choice, we assume that the exporter’s unobservable production cost follows a generalized extreme value (GEV) distribution. The probability that each producer chooses alternative $Alt$ in $Nest$ is

$${\mathbb{P}}_{Alt} = {\mathbb{P}}_{Alt|Nest} {\mathbb{P}}_{Nest} ,$$

(1)

where $Nest = MFN,RTA$. There is only one alternative $M$ in the MFN nest, i.e., a degenerate nest. In contrast, as listed later, there are six alternatives in the RTA nest. Thus, $Alt = R\left( 1 \right), \cdots ,R\left( 6 \right)$, given that $RTA$ is chosen for $Nest$. ${\mathbb{P}}_{Alt|Nest}$ is the probability that an exporter chooses $Alt$, given that the exporter has chosen $Nest$. The probability that an exporter chooses $Nest$ is denoted by ${\mathbb{P}}_{Nest}$, and ${\mathbb{P}}_{MFN}$ equals $1 - {\mathbb{P}}_{RTA}$ as the number of nests in our study is two.

The standard nested logit model can be applied assuming that an agent’s utility is described by the linear combination of observable and stochastic portions, and the stochastic portion of the utility follows the GEV distribution.⁸ Under these two assumptions, ${\mathbb{P}}_{Nest}$ and ${\mathbb{P}}_{Alt|Nest}$ are the following, respectively:

$${\mathbb{P}}_{Nest} = {\exp}\left\{ {X_{Nest} + \lambda_{Nest} IV_{Nest} - \widetilde{IV}} \right\},$$

(2)

$${\mathbb{P}}_{Alt|Nest} = {\exp}\left\{ {\frac{{Q_{Alt} }}{{\lambda_{Nest} }} - IV_{Nest} } \right\},$$

(3)

where $X_{Nest}$ comprises the nest-specific determinants that explain the choice between nests, and $Q_{Alt}$ comprises alternative-specific determinants. Using matrix notation, these scalars can be written as the following:

$$X_{Nest} = {{\varvec{\upalpha}}}\left[ {{\mathbf{x}}_{Nest} } \right]^{{\varvec{T}}} = \left[ {\begin{array}{*{20}c} {\alpha_{1} } & \cdots & {\alpha_{m} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1,Nest} } \\ \vdots \\ {x_{m,Nest} } \\ \end{array} } \right],$$

$$Q_{Alt} = {{\varvec{\upgamma}}}\left[ {{\mathbf{q}}_{Alt} } \right]^{{\varvec{T}}} = \left[ {\begin{array}{*{20}c} {\gamma_{1} } & \cdots & {\gamma_{n} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {q_{1,Alt} } \\ \vdots \\ {q_{n,Alt} } \\ \end{array} } \right],$$

where ${{\varvec{\upalpha}}}$ and ${{\varvec{\upgamma}}}$ are coefficient vectors, and $m$ and $n$ are the numbers of nest- and alternative-specific variables, respectively. ${\mathbf{x}}_{Nest}$ and ${\mathbf{q}}_{Alt}$ are vectors of nest- and alternative-specific determinants, respectively.

$\lambda_{Nest}$ is the log-sum coefficient or inclusive value (IV) parameter, which is inversely related to the correlation of stochastic utility factors within each nest. $IV_{Nest}$ is the IV of a respective nest, given by:

$$IV_{Nest} \equiv \ln \mathop \sum \limits_{Alt \in Nest}^{{}} {\exp}\left\{ {\frac{{Q_{Alt} }}{{\lambda_{Nest} }}} \right\}.$$

$\widetilde{IV}$ is the expected profit from the available nests:

$$\widetilde{IV} \equiv \ln \mathop \sum \limits_{Nest}^{{}} {\exp}\left\{ {X_{Nest} + \lambda_{Nest} IV_{Nest} } \right\}.$$

Because our framework meets the above two assumptions, we can employ the standard nested logit model to examine the determinants of choice probability of each tariff scheme.

The variables in nest-specific determinants (${\mathbf{x}}_{Nest}$) include the elements that influence the decision to choose a particular RTA scheme. We first include the value of a related transaction. This value contains information on specific elements, such as an exporter-specific cost parameter (e.g., exporter’s production capability), export country-product-specific cost parameter (e.g., wages), physical transportation costs,⁹ and the importer’s product-specific demand. Obviously, an exporter’s higher production capability, a lower export country-product-specific cost parameter, lower transportation costs, and larger product-specific demand of an importer engender a larger transaction value. As a larger transaction value enables exporters to likely obtain export profits under RTA schemes to cover the fixed costs for RTA utilization, the transaction value is expected to be positively related to the probability of choosing any RTA rather than an MFN scheme.

Second, based on our theoretical foundation (see Appendix A), we explicitly introduce some of the specific elements in addition to the transaction value. We capture the importer’s size by firm-product-level import values. To control for transportation costs, we use a transaction-level dummy variable that equals 1 for land transportation (truck or railway) and 0 otherwise (sea or air). The export country-product level cost parameter is captured by the average export price at a country’s HS six-digit level.¹⁰ As a result, the remaining variation in the transaction value will correspond to an exporter-specific production capability. Kropf and Sauré (2014) and Hornok and Koren (2015) demonstrated that the transaction value increases with the exporter’s productivity. Therefore, in our specification, the transaction value is expected to be positively related to the probability of choosing any RTA scheme rather than an MFN scheme.

The determinants specific to each alternative, conditional on the nest chosen, are comprised of ${\mathbf{q}}_{Alt}$. These include the variable cost for RoO compliance and the preferential tariff rate of a particular RTA scheme if the RTA nest is chosen. The variable costs for RoO compliance are captured by introducing dummy variables according to the RoO type (see the next section for details). For an MFN nest, which is a degenerate nest, the MFN tariff rates are included. Because no RoO compliance costs are incurred here, all RoO dummy variables take the value 0 in an alternative of an MFN scheme. Consequently, an RTA scheme with less restrictive RoO or lower preferential tariff rates will be likely chosen.

3 Data

This section introduces our data sources, taking brief overviews of our sample RTAs.

3.1 Data sources

Our dataset contains the customs clearing date, HS eight-digit code, exporting country, firm identification code, tariff scheme, and import values in Thai Baht. Some firms import the same product from the same country multiple times on the same date, which we regard as different transactions. Tariff schemes comprise three categories: MFN, RTA, and the other schemes. Tariff payments for imports under “the other schemes” are exempted on the basis of five aspects: bonded warehouses, free zones, investment promotion, duty drawback for raw materials imported for the production of exports, and duty drawback for re-exportation. In our study, we drop import transactions under these other schemes.

As of 2014, seven tariff schemes are available when Thailand firms import from ASEAN countries: an MFN and six RTA schemes. Among the latter, the ATIGA was introduced in 2010 by revising the ASEAN Free Trade Area (AFTA) agreement that was effective among the 10 ASEAN countries (Brunei, Cambodia, Indonesia, Malaysia, Myanmar, Laos, the Philippines, Singapore, Thailand, and Vietnam) since the 1990s. In addition, Thailand, together with the other ASEAN members, has concluded five plurilateral RTAs, called ASEAN + 1 RTAs. The ACFTA was introduced in 2005 among the 10 ASEAN countries and China after signing the Framework Agreement on China–ASEAN Comprehensive Economic Cooperation at the sixth China–ASEAN Summit in November 2002. The AJCEP was introduced in 2008 among some of the ASEAN member countries and Japan, coming into effect in Brunei, Malaysia, Thailand, and Cambodia in 2009, and subsequently, in the Philippines in 2010. Importantly, its effectuation for Indonesia is pending. Thus, we do not include import transactions from Indonesia in our estimation since the number of available tariff schemes is different.¹¹ The AKFTA on trade in goods was introduced among some of the ASEAN member countries and Korea in 2007, coming into force in Brunei, Laos, Cambodia, and the Philippines in 2008, and Thailand in 2010. The AANZFTA was introduced in 2010 among some of the ASEAN member countries, Australia, and New Zealand. It came into effect in Laos and Cambodia in 2011 and in Indonesia in 2012. The AIFTA was introduced in 2010 among some of the ASEAN member countries and India, becoming effective in Laos, Cambodia, and the Philippines in 2011. The eligibility and preferential rates in Thailand are common across ASEAN countries, i.e., our sample exporting countries.

An important point is that “availability” differs from “eligibility.” In our study, “products in which RTA tariff rates are lower than MFN rates” are called “eligible products” while RTA schemes per se can be claimed, i.e., available, in all products. Firms have to pay MFN rates when claiming RTA schemes for ineligible products. In this sense, a set of alternatives, i.e., tariff schemes, is common across sample countries and products. However, in our robustness checks, we exclude trade in products with zero MFN rates because the motivation of choosing a tariff scheme for firms might be different between products with zero and positive MFN rates.

The difference between alternative RTAs primarily stems from preferential tariff rates and RoO type. Several types of tariff reduction or elimination exist in ASEAN RTAs, e.g., immediate elimination, gradual reduction, late start, and partial reduction.¹² The difference in preferential tariff rates across RTAs is yielded by the abovementioned difference in entry years, and the typical tariff reduction is not necessarily “immediate elimination.” For example, in the AJCEP in Thailand, 43% of tariff-line products follow a “gradual reduction,” whereas “immediate elimination” is found in only 26% of tariff-line products. Consequently, preferential tariff rates are likely to differ by RTA and years. As we will observe later (i.e., Table 2), RoO differ across RTAs because these were negotiated among member countries.¹³

As mentioned in the previous section, the operational certification procedures, which are related to additional fixed costs for RTA utilization, are the same across our sample RTAs in most aspects. For example, the cumulation rule, back-to-back CoO, and the third country invoice are allowed in all six RTAs; and the third-party certification system is adopted in all six RTAs.¹⁴ The commission charge for CoO differs across countries but is same across RTAs in each country (see Hayakawa et al. 2016, Table 1). One notable difference is the availability of the De Minimis rule,¹⁵ which is available in the AJCEP, AKFTA, ATIGA, and AANZFTA but not in the ACFTA and AIFTA. However, we believe that this difference is much less significant than the qualitative difference between an MFN and RTA, supporting our assumption of common fixed costs for RTA utilization across alternative RTAs in our empirical framework.¹⁶

Table 1 Preferential status and tariff rates by RTA schemes in 2014. Source: Authors’ computation using the legal text of each RTA

Our data sources for independent variables are as follows. The data on RTA preferential rates and RoO were obtained from the legal text of each RTA. The data on MFN rates were obtained from the Customs Office of Thailand. In Thailand, tariff rates are set at an HS eight-digit level, which includes 9,557 tariff lines. The RoO in all RTAs are set at an HS six-digit level, which includes 5,204 codes. The HS version in our analysis is HS 2012. The data on the transportation mode and the firm-product level import values are obtained from our transaction-level import data. The average export price is constructed using the import data obtained from UN Comtrade. Specifically, we first compute unit export prices (export prices per kilogram) for each country pair at an HS six-digit level in 2014. Then, we aggregate those prices by an arithmetic average according to export countries. In this aggregation, we do not include export prices to Thailand.

3.2 Data overview

Before presenting our estimation results, we briefly overview the RTAs in Thailand. Table 1 reports preferential status and tariff rates by RTA scheme in 2014, when the arithmetic average of MFN rates in Thailand was 11.5%. “Number” indicates the number of tariff-line products wherein the RTA rates are lower than the MFN rates (i.e., the number of lines eligible to each RTA). The “Share in Total line” and “Share in Dutiable line” denote the shares of that number in all tariff-line products and in products with positive MFN rates, respectively. “Average RTA rates” indicates the arithmetic average of tariff rates among all products. For products ineligible to RTA schemes, we use MFN rates when computing the average RTA rates.

Table 1 shows that the ATIGA has the highest liberalization level partly because it was introduced in the earliest period among member countries (previously the AFTA, which became effective in Thailand in 1993). All products have either zero MFN rates or ATIGA preferential rates lower than MFN rates. Consequently, the average ATIGA tariff rates are almost zero. Despite relatively later effectuation, the AANZFTA has a high liberalization level. As of 2014, over 90% of all products already have either zero MFN rates or low AANZFTA preferential rates. In contrast, the AIFTA has the lowest liberalization level. The average RTA rates in AIFTA are still over 5%.

Table 2 reports the distribution of the RoO by RTA schemes at a HS six-digit level, indicating various types and combinations. The typical RoO are CH/RVC for ATIGA, AANZFTA, AJCEP, and AKFTA; RVC for the ACFTA; and CS & RVC for the AIFTA. There is a relatively large number of CC in AJCEP. Notably, in the estimation, we construct dummy variables for the RoO based on a broader classification to keep a sufficient number of observations for each type of RoO. Such RoO are shown in the “Simplified” column. Specifically, CC, CH, and CS are categorized into change in tariff classification (CTC). Furthermore, RoO with a very small number of observations are dropped or simplified. For example, products with “SP” in any RTAs are dropped (as indicated in Table 2, such observations exist for AANZFTA). For RoO combined with SP, we ignore a component of SP. For example, CTC & SP and CTC/SP are simplified to CTC.¹⁷

Table 2 RoOs by RTA schemes at an HS six-digit level. Source: Authors’ computation using the legal text of each RTA

Table 3 reports the number and value of imports from eight ASEAN countries according to the tariff schemes in 2014. Both the number of transactions and import firm-product pairs are largest for the MFN, followed by the ATIGA. The frequency of these two schemes is much larger than other schemes. Accordingly, large imports exist for these two schemes.¹⁸ AANZFTA has the third largest imports. These findings comport with our observations in Table 1, which shows high liberalization levels in AANZFTA and ATIGA. Alternatively, AIFTA, AJCEP, and AKFTA are utilized less frequently. In particular, there were only six transactions under AIFTA when importing from eight ASEAN countries in 2014. In addition, compared with the number of transactions, the number of import firm-product pairs is obviously small, implying that some import firm-product pairs have multiple transactions; i.e., firms import one product from many countries and/or many times from one country.

Table 3 Number and value of imports according to tariff scheme in 2014 (Million THB). Source: Authors’ computation using transaction-level import data from Thailand Customs

4 Empirical results

This section reports our estimation results. After presenting our baseline results, we introduce the results of additional estimations. Table 4 provides basic statistics.¹⁹

Table 4 Basic statistics. Source: Authors’ computation using transaction-level import data from Thailand Customs

Table 5 displays our results from the nested logit model.²⁰ Column (I) contains only the inclusive value in the upper stage estimation. We report standard errors clustered by import firm–product pair because firms may import a given product several times or from multiple countries; hence, standard errors might be correlated within an import firm–product pair. As is consistent with our expectation, the coefficients for tariff rates and the RoO dummy variables are significantly negative. This indicates that tariff schemes with higher tariff rates or those required to comply with RoO are less likely to be chosen. The estimated IV parameter lies between 0 and 1. This implies that our model meets a sufficient condition for global consistency with the random utility model in discrete choice analysis.

Table 5 Estimation results: nested logit model

The order of absolute magnitude of coefficients for the RoO dummy variables is worth discussing. Our results indicate that the negative effects become more serious in the order of CTC & RVC, WO, CTC, RVC, and CTC/RVC. This result comports with a fundamental rule that adhering to all multiple types of RoO (i.e., RoO with “&”) is more restrictive than adhering to one RoO type. It also comports with the rule that adhering to either one among multiple types of RoO (i.e., RoO with “/”) is as restrictive as or less restrictive than adhering to a particular one among multiple types of RoO. The choice probability is lower for CTC & RVC than for WO. WO is known as the most restrictive RoO type because an exported product must be entirely produced or cultivated in RTA member countries. One reason is that in our sample of RTAs, almost all cases with WO are found in agricultural goods; thus, it is not technically difficult to fulfill the WO criteria for the production of agricultural goods.

Our result that the choice probability is lower for CTC than for RVC is another important finding. Carrere and de Melo (2006) found the opposite in the analysis of NAFTA utilization rates, though the results are not directly comparable due to the difference in the empirical model.²¹ As mentioned in the introductory section, our results are based on a cross-RoO analysis within a product, whereas Carrere and de Melo (2006) use a cross-product analysis. Therefore, we believe that our results indicate a more precise order of effects of alternative RoO types on the choice probability. Nevertheless, we should be careful regarding generalizing this result because the share of labor costs, local material costs, and miscellaneous expenses, all of which are costs for “originating inputs,” out of total production costs are high in Asia.²² Therefore, at least in Asia, it might be easy to adhere to a conventional cutoff in RVC (e.g., 40%).

The results in the other two columns are as follows. In Column (II), we add a log of transaction value. As is consistent with our expectation, its coefficient is estimated to be significantly positive, implying that RTA schemes are likely to be chosen, given larger transactions. The results for tariff rates and the RoO dummy variables are qualitatively unchanged in terms of signs and significance. Column (III) includes all the variables explained in the previous section. The estimation results for tariffs and the RoO are slightly changed. The coefficient for total imports is significantly positive, indicating that RTA schemes are likely to be chosen by the larger-sized importers in terms of total import values. While the coefficient for the land transportation dummy is insignificant, that for the average export price is significantly negative. The latter result implies that lower production costs lead to a higher probability of choosing RTA schemes because exporting profits under RTAs are more likely to cover the costs for RTA utilization. Even after controlling for these elements, we still see a significantly positive coefficient for transaction values. Thus, the remaining elements, such as exporter’s production capability, significantly positively impact the probability of choosing RTA schemes.

Appendix C reports additional estimation results. First, we introduce an additional explanatory variable to capture the role of cumulation rules in the second stage. Second, we focus on trade in which firms cannot enjoy cumulation rules by restricting sample products only to finished products as they are utilized when the intermediate inputs of imports are cumulated. Third, we exclude trade in products with zero MFN rates because the motivation of choosing a tariff scheme for firms might differ between products with zero and positive MFN rates. Fourth, we add observations of Indonesia’s exports to our estimation sample. Fifth, we account for possible differences in inter-industry fixed costs by introducing interaction terms of transaction values with industry dummy variables. The results indicate that as is consistent with our previous results, the coefficients for tariff rates and RoO dummy variables are negatively significant. The RTA schemes are also more likely to be chosen, given larger transactions.²³

5 Quantitative interpretation

This section quantitatively interprets our estimation results. We also estimate a mixed logit model, which is more flexible than a nested logit model in terms of substitution among alternatives. Finally, we conduct a simulation analysis.

5.1 Elasticities: nested logit model

Following Greene (2012), we compute the elasticities of the probability of choosing each tariff scheme based on the estimation results of Table 5, Column (III). First, we examine the extent to which the probabilities change when tariff rates in each scheme change by 1%. The elasticity of probability that each firm chooses alternative $Alt$ with respect to $\tilde{n}$th alternative-specific determinant of alternative $\widetilde{Alt}$, which is represented by $q_{{\tilde{n},\widetilde{Alt}}}$, is

$$\frac{{\partial \ln {\mathbb{P}}_{Alt} }}{{\partial q_{{\tilde{n},\widetilde{Alt}}} }} = \left\{ {d_{1} \left[ {d_{2} - {\mathbb{P}}_{{\widetilde{Alt}|Nest}} } \right] + \lambda_{Nest} \left[ {d_{1} - {\mathbb{P}}_{Nest} } \right]{\mathbb{P}}_{{\widetilde{Alt}|Nest}} } \right\}\gamma_{{\tilde{n}}} ,\quad \tilde{n} = 1, \cdots ,n.$$

(4)

$d_{1}$ is a binary variable equal to 1 when a nest of $\widetilde{Alt}$ is the same as that of $Alt$, and 0 is otherwise. Similarly, $d_{2}$ is a binary variable equal to 1 when the alternative $\widetilde{Alt}$ is the same as alternative $Alt$, and 0 is otherwise. Specifically, we examine the elasticity with respect to tariff rates. In our simulation, we assume that the other elements remain constant, although the change of tariff rates may affect other variables, especially transaction values and total imports. This is inevitable because we are not able to examine more fundamental firm-characteristics (e.g., productivity) due to data limitation.

Table 6 displays the results. There are two noteworthy findings. First, the effect of tariff rates on the probability of choosing that scheme is negative, i.e., the own effect. The absolute magnitude of this effect is much larger in RTAs than in the MFN. In particular, the magnitude is largest in AIFTA. In terms of elasticity, a 1% reduction in AIFTA tariff rates increases the probability of choosing the AIFTA by 70%. These results are obtained partly because the probability of choosing any RTA scheme (${\mathbb{P}}_{Nest}$) and its conditional probability, given that RTA nest (${\mathbb{P}}_{{\widetilde{Alt}|Nest}}$) is selected, is small compared with the probability of choosing the MFN scheme, as implied from Table 3.²⁴ As indicated in Eq. (4), these probabilities are negatively related to the own effect.

Table 6 Elasticities with respect to tariff rates (mean)

Second, the effect of tariff rates on the probability of choosing other schemes is positive, i.e., the cross effect. Importantly, the cross effects of tariff rates in an RTA are common across the other RTAs but differ between an RTA and an MFN scheme. This stems from the nature of nested logit models and has an advantage over conditional logit models. Table 6 indicates that the reduction in tariff rates in an RTA scheme decreases the probability of choosing other RTA schemes rather than choosing the MFN scheme. This result is partly because an IV parameter is estimated to be less than the value 1 and near 0, which implies more similarity among RTA schemes than between RTA and MFN schemes.

Next, we compute the elasticity of probability that each firm chooses alternative $Alt$ with respect to the $\tilde{m}$th nest-specific determinant of nest $\widetilde{Nest}$, which is represented by $x_{{\tilde{m},\widetilde{Nest}}}$. The elasticity is

$$\frac{{\partial \ln {\mathbb{P}}_{Alt} }}{{\partial x_{{\tilde{m},\widetilde{Nest}}} }} = \alpha_{{\tilde{m}}} \left( {d_{3} - {\mathbb{P}}_{{\widetilde{Nest}}} } \right),\quad \tilde{m} = 1, \cdots ,m.$$

$d_{3}$ is a binary variable equal to 1 when $Alt$ belongs to the nest $\widetilde{Nest}$, and 0 is otherwise. We examine the elasticity with respect to the transaction value, which indicates the extent to which the probability of choosing any RTA scheme increases with a 1% increase in the transaction value. Because exporters with a larger transaction are more likely to cover additional fixed costs for RTA utilization, this elasticity is related at least partly to the fixed costs.²⁵

Table 7 indicates the mean of elasticities according to the export country. We find that the mean of the elasticities is relatively high for relatively developed countries, including Singapore (0.24), the Philippines (0.24), and Malaysia (0.22). This result highlights that developed countries are supposed to have better knowledge and experience in dealing with documentation for RTA utilization and thus lower fixed costs. Alternatively, the three least developed countries, i.e., Cambodia (0.15), Laos (0.16), and Myanmar (0.14), have lower elasticities.

Table 7 Elasticities with respect to transaction values according to export country

5.2 Elasticities: mixed logit model

Next, we again compute the elasticity with respect to tariff rates using the estimation results of a mixed logit model. The nested logit model produces common cross effects of tariff rates in an RTA scheme across the other RTA schemes, as shown in Table 6. However, cross effects may differ across the other RTA schemes. To examine this possibility, we estimate mixed logit models, which are more flexible in terms of substitution among alternatives than the nested logit model. The specification takes a random coefficients form. We assume that all variables have normally distributed coefficients. This flexibility in coefficients enables us to examine the possibility that cross effects differ across RTA schemes. Table 8 reports the estimation results of the mixed logit models. All variables have significant coefficients with the expected signs. Except for the model specified in column (I), the order of coefficients for the RoO dummy variables is unchanged from the previous results.²⁶

Table 8 Estimation results: mixed logit model

Table 9 shows the mean elasticities of probability of choosing each tariff scheme with respect to tariff rates.²⁷ Unlike in the nested logit models, the cross effects of tariff rates in an RTA scheme differs not only between an RTA and an MFN scheme but also across RTA schemes. Two more interesting results: (1) a 1% reduction in MFN rates decreases the probabilities of choosing ACFTA (by 13%) and AIFTA (by 14%) more than the probability of choosing the other RTAs. (2) a 1% reduction in ATIGA tariff rates reduces the probability of choosing AANZFTA (by 0.38%), AJCEP (by 0.31%), and AKFTA (by 0.49%), which is more than choosing the other RTAs (i.e., ACFTA and AIFTA) and the MFN scheme. These results indicate that ACFTA and AIFTA belong to a group different from the other RTAs. One possible explanation is that the RoO in ACFTA and AIFTA are relatively restrictive compared with the other RTAs. Another explanation might be a difference in fixed costs between the two groups. As mentioned in Sect. 3.1, the De Minimis rule is not available in the ACFTA and AIFTA; thus, the reduction in MFN rates induces ACFTA/AIFTA users to switch to the MFN scheme.²⁸

Table 9 Elasticities with respect to tariff rates (mean): mixed logit model

5.3 Simulation

Here, we conduct two types of simulation analysis using the estimated results of Table 5, Column (III).²⁹ First, we demonstrate how the probability changes when the scheduled tariff reduction is completed in all RTAs. In other words, we calculate the expected changes in the choice probability of each RTA scheme from 2014 to the final year of tariff reduction. In some products, tariff reduction further continues after 2014 because the rates are scheduled to be reduced gradually or to begin several years after the enactment of RTAs (Appendix B, Table B1). The official final implementation years of ATIGA, AKFTA, ACFTA, AJCEP, AIFTA, and AANZFTA are 2015, 2017, 2018, 2018, 2020, and 2020, respectively. Table 10 reports the magnitude and number of remaining tariff reduction in each RTA. “G” is the difference between the final preferential rate and the preferential rate in 2014. The largest number of products with further tariff reduction can be found in AIFTA, whereas no further reduction occurs in ATIGA.

Table 10 Remaining tariff reduction in each RTA

We indicate the percentage points by which the probability changes between 2014 and the final year. We first calculate the predicted probabilities in the base scenario. Second, we replace the level of the 2014 tariff variable with the tariff rates scheduled in the final year of each RTA and calculate the predicted probabilities in the alternative scenario. Third, we calculate the mean difference between the two probabilities. The results are displayed in the “Tariffs” column of Table 11. The AANZFTA (0.38 percentage points) and the AJCEP (0.80 percentage points) are expected to experience an increased probability from 2014 to the final year. This is because further reduction remains in a relatively large number of products in those two RTAs (see Table 10). Although the AIFTA also has a large number of products with further tariff reduction, the restrictive RoO in AIFTA dampen any increased probability. The largest decline is found in ATIGA (− 0.80 percentage points) since the tariff reduction was already completed in 2014 (see Table 10).

Table 11 Probability change: tariff reduction in final year and least restrictive RoOs (percentage points)

Second, we indicate the percentage points of probability change if the RoO in all RTAs are set to the least restrictive type. As found in the previous estimation results, the RoO are restrictive in the order of CTC & RVC, WO, CTC, RVC, and CTC/RVC. Therefore, we set the RoO in all RTAs to CTC/RVC, calculate the predicted probabilities in the alternative scenario, and compute the mean difference according to tariff schemes. The results are shown in the “RoO” column of Table 11. In most cases, the absolute magnitude in this simulation is larger than that in the previous simulation, i.e., “Tariffs.” The ACFTA (1.35 percentage points) and the AIFTA (2.69 percentage points) experience a notably high probability increase. This is plausible, given that these two RTAs have a relatively restrictive RoO (see Table 2). The most restrictive RoO, i.e., CTC & RVC, are originally set in all products in AIFTA, whereas the least restrictive RoO, i.e., CTC/RVC, are set in few products in ACFTA. The probability of choosing the other RTAs (except for AJCEP) is expected to decline. The largest decline is found in ATIGA (2.67 percentage points) since the least restrictive RoO are already set in almost all products in ATIGA (see Table 2).

6 Conclusion

This study examined the determinants of choice probability of tariff schemes between an MFN and multiple RTA schemes. Specifically, we used transaction-level data of Thai imports from other ASEAN countries in 2014. In this flow, seven tariff schemes, including six RTA schemes and one MFN scheme, are available. By estimating theoretically consistent nested logit models with this data, we found that tariff schemes with lower tariff rates are more likely to be chosen. Further, we found that RTA schemes with more restrictive RoO are less likely to be chosen. In particular, tariff schemes with a “WO rule” or a “CTC and RVC rule” are less likely to be chosen, while firms are more likely to choose tariff schemes with a “CTC or RVC rule.” Moreover, any RTA scheme is likely to be chosen, given large transactions.

Using the estimates, we conducted additional quantitative analyses. Specifically, we calculated the change in probability of choosing each scheme when tariff rates decline by 1% and the change in probability of choosing any RTA scheme when transaction values increase by 1%. In the latter analysis, we found a relatively substantial effect when exporting from Singapore, the Philippines, and Malaysia, which are relatively developed nations. We also calculated the probability change when the scheduled tariff reduction is completed in all RTAs or if the RoO in all RTAs are set to the least restrictive type, i.e., CTC/RVC. The largest increase of choice probability from 2014 to the final year is found in the AJCEP, since further reduction is scheduled for a relatively large number of products. The change in RoO to the least restrictive type increases the probability of choosing the ACFTA and AIFTA because these two RTAs originally have relatively restrictive RoO.

Although we focused on Thailand, the issue we examined should be of interest for companies and policy makers in many countries involved in complicated RTA networks. Specifically, our findings imply that firms choose the best tariff scheme according to tariff rates and the RoO. Therefore, firms face a choice problem when the number of available RTAs increases. This issue might be one form of the spaghetti bowl phenomenon (Bhagwati et al. 1998). If one RTA scheme has the lowest preferential tariff rates and the most business-friendly RoO (e.g., CTC or RVC) in all tariff lines, then firms do not need to make a choice regarding tariff schemes. In the context of Asia, RCEP covers all of our sample RTAs (i.e., ATIGA and the five ASEAN + 1 RTAs) in terms of member countries. Therefore, RTA utilization costs will be reduced, and the spaghetti bowl phenomena may disappear if the RCEP is designed to provide the lowest preferential tariff rates and the most business-friendly RoO in each tariff line among the existing six RTAs.