1 Introduction

Critical node or edge detection problems are a family of optimization problems defined on graphs, where one is required to remove a limited number of nodes and/or edges in order to minimize some measure of the connectivity of the residual graph, or, in a complementary form, one is asked to reduce the connectivity of the graph to at most a prescribed value by removing the smallest number of nodes and/or edges. This class of problems has attracted the interest of many researchers in the last two decades, because of its relevance in a number of practical applications, including computational biology Boginski and Commander (2009); Tomaino et al. (2012), transportation problems Jenelius et al. (2006), network immunization problems He et al. (2011); Kuhlman et al. (2013); Cohen et al. (2003); Kuhlman et al. (2010), the analysis of complex networks Fan and Pardalos (2010); Borgatti (2006), and security/vulnerability issues in networks Veremyev et al. (2015); Dinh et al. (2010); Nguyen et al. (2013); Shen et al. (2012, 2013). We refer the interested reader to the survey Lalou et al. (2018) for a detailed overview of the applications as well as of the other aspects discussed below.

The choice of the connectivity measure is of course a central element in a critical node or edge detection problem. Indeed, several different connectivity measures have been proposed in the literature. In this paper we consider the pairwise connectivity between nodes, formalized in Arulselvan et al. (2009) and studied, e.g., also in Addis et al. (2013, 2016); Aringhieri et al. (2016a, 2016b, 2019); Boginski and Commander (2009); Di Summa et al. (2011); Di Summa et al. (2012); Dinh et al. (2010); Fan and Pardalos (2010); Pullan (2015); Purevsuren et al. (2017, 2016); Shen et al. (2013); Tomaino et al. (2012); Ventresca (2012); Veremyev et al. (2014), which is defined as the number of pairs of nodes belonging to the same connected component. This can be naturally generalized to the total cost of the pairs of nodes that belong to the same component, if connection costs are assigned for each pair of nodes, as well as to distance-based measures Aringhieri et al. (2019); Veremyev et al. (2015). Among the other connectivity measures introduced in the literature, we mention the number of connected components (which should be maximized in order to fragment the graph) Addis et al. (2013); Aringhieri et al. (2016a); Berger et al. (2014); Shen and Smith (2012); Shen et al. (2012); Veremyev et al. (2014); Furini et al. (2020), the size of the largest connected components (to be minimized) Addis et al. (2013); Aringhieri et al. (2016a); Lalou et al. (2016); Nguyen et al. (2013); Pullan (2015); Shen and Smith (2012); Shen et al. (2012); Veremyev et al. (2014), the minimum cost to reconnect the graph Shen et al. (2012), and the graph information entropy Veremyev et al. (2014). Recent variants include a combination of the measures based on the number and size of the connected component, in which the minimum number of components with bounded size should be obtained Furini et al. (2021), and extensions to hypergraphs Bastubbe and Lübbecke (2019).

Since problems of this type usually turn out to be NP-hard for general graphs, and often also for quite special classes of graphs Shen et al. (2013); Addis et al. (2013); Di Summa et al. (2011); Shen et al. (2012); Shen and Smith (2012), several heuristic approaches as well as methods based on integer programming formulations have been proposed in the literature; see, e.g., Nguyen et al. (2013); Arulselvan et al. (2009); Addis et al. (2016); Aringhieri et al. (2016b); Pullan (2015); Ventresca (2012); Aringhieri et al. (2016a); Purevsuren et al. (2016, 2017); Di Summa et al. (2012); Furini et al. (2020, 2021); Bastubbe and Lübbecke (2019). Polynomial-time algorithms are instead available only for some particular cases, which are usually limited to graphs with bounded treewidth, in particular trees and series-parallel graphs Addis et al. (2013); Berger et al. (2014); Di Summa et al. (2011); Lalou et al. (2016); Shen and Smith (2012); Aringhieri et al. (2019). In this paper we are interested in providing polynomial-time algorithms for some more node/edge detection problems.

1.1 The problems that we study

According to the pairwise connectivity measure mentioned above, the Critical Node Detection Problem (CNDP) is formally stated as follows:

Problem 1

(CNDP) Given an undirected graph \(G=(V,E)\), a weight \(w_v\ge 0\) for every \(v\in V\), a connection cost \(c_{uv}\ge 0\) for all \(u,v\in V\), and a weight limit \(W\ge 0\), find \(S\subseteq V\) such that the total weight of the nodes in S is at most W and the total cost of the pairs of nodes that are connected in \(G-S\) is minimized.

Here \(G-S\) denotes the graph obtained after removing from G the nodes in S, i.e., the subgraph of G induced by \(V\setminus S\). Furthermore, in the above problem as well in all variants considered below, the connection costs will be always implicitly assumed to be symmetric (i.e., \(c_{uv}=c_{vu}\) for every \(u,v\in V\)) and to satisfy \(c_{vv}=0\) for every \(v\in V\).

For this and the other problems that we study, we will be particularly interested in the case in which G is a tree. Already under this assumption, CNDP is NP-hard, even if \(w_v=1\) for every \(v\in V\) and \(c_{uv}\in \{0,1\}\) for every \(u,v\in V\)Di Summa et al. (2011). However, still assuming that G is a tree, the problem admits a polynomial-time algorithm if the \(c_{uv}\)’s are all equal to 1 (with no restriction on the \(w_v\)’s) Di Summa et al. (2011).

In this paper we further investigate the complexity of CNDP on a tree, and consider some natural variants in which edges or both nodes and edges can be removed from the graph. Indeed, most of the literature seems to focus on problems where only nodes or edges can be deleted. (See, e.g., Veremyev et al. (2014) for a discussion about this aspect.) Problems where both nodes and edges can be removed subject to a joint weight limit have been also considered in Veremyev et al. (2014), where a general integer programming framework is presented for several types of connectivity measures. A different version of this problem has been studied in He et al. (2011).

In order to simplify the description of the problems that we analyze, it is worthwhile to introduce some simple notation. Given an undirected graph \(G=(V,E)\) and a subset \(S\subseteq V\cup E\) of nodes and/or edges of G, \(G-S\) will denote the graph obtained after removing from G the elements in S. More formally, \(G-S=(V',E')\) with \(V'=V\setminus S\) and \(E'=\{uv\in E\setminus S:u,v\in V'\}\). If connection costs \(c_{uv}\) are given for all \(u,v\in V\), we use the shorthand \(c(G-S)\) to denote the total cost of the pairs of nodes that are connected in \(G-S\). When weights \(w_v\) and/or \(w_e\) are given for all nodes \(v\in V\) and/or all edges \(e\in E\), w(S) will denote the total weight of the elements in S. (Note that there is no confusion in denoting both node and edge weights with a similar symbol, i.e., \(w_v\) and \(w_e\), as the different nature of the subscript —a node or an edge— removes any ambiguity. In other words, w can be viewed as a function of the form \(w:V\cup E\rightarrow \mathbb R_+\).)

The above notation allows us to restate CNDP slightly more compactly:

Problem 2

(CNDP, restated) Given an undirected graph \(G=(V,E)\), a weight \(w_v\ge 0\) for every \(v\in V\), a connection cost \(c_{uv}\ge 0\) for all \(u,v\in V\), and a weight limit \(W\ge 0\), find \(S\subseteq V\) such that \(w(S)\le W\) and \(c(G-S)\) is minimized.

As already mentioned, we are interested in some variants of CNDP (mainly on trees) in which edges or both nodes and edges can be removed. The variants that we analyze are the following:

  • the Critical Edge Detection Problem (CEDP), which is formulated as CNDP, except that edges have to be removed instead of nodes;

  • the Critical Node/Edge Detection Problem with a single weight limit (CNEDP-1), where a cumulative weight limit for the removal of nodes and edges is given;

  • the Critical Node/Edge Detection Problem with two weight limits (CNEDP-2), where two separate weight limits are assigned for nodes and edges.

These problems are formalized below:

Problem 3

(CEDP) Given an undirected graph \(G=(V,E)\), a weight \(w_e\ge 0\) for every \(e\in E\), a connection cost \(c_{uv}\ge 0\) for all \(u,v\in V\), and a weight limit \(W\ge 0\), find \(S\subseteq E\) such that \(w(S)\le W\) and \(c(G-S)\) is minimized.

Problem 4

(CNEDP-1) Given an undirected graph \(G=(V,E)\), a weight \(w_v\ge 0\) for every \(v\in V\), a weight \(w_e\ge 0\) for every \(e\in E\), a connection cost \(c_{uv}\ge 0\) for all \(u,v\in V\), and a weight limit \(W\ge 0\), find \(S\subseteq V\cup E\) such that \(w(S)\le W\) and \(c(G-S)\) is minimized.

Problem 5

(CNEDP-2) Given an undirected graph \(G=(V,E)\), a weight \(w_v\ge 0\) for every \(v\in V\), a weight \(w_e\ge 0\) for every \(e\in E\), a connection cost \(c_{uv}\ge 0\) for all \(u,v\in V\), and weight limits \(W_V,W_E\ge 0\), find \(S\subseteq V\cup E\) such that \(w(S\cap V)\le W_V\), \(w(S\cap E)\le W_E\), and \(c(G-S)\) is minimized.

It is immediate to see that CNDP and CEDP are special cases of each of CNEDP-1 and CNEDP-2. Indeed, an instance of CNDP (respectively, CEDP) can be reduced to an instance of CNEDP-1 by giving weight \(W+1\) to all edges (respectively, nodes) in order to forbid their removal. Furthermore, an instance of CNDP (respectively, CEDP) can be reduced to an instance of CNEDP-2 by setting \(W_V=W\) and \(W_E=0\) (respectively, \(W_E=W\) and \(W_V=0\)).

We also observe that CNEDP-1 reduces to CNDP when the weights are all equal to 1, or more generally, whenever the weight of every edge is at least as large as that of its endpoints; Indeed, in this case removing an edge cannot be more convenient than removing a node. However, it is easy to see that with arbitrary weights it may be cheaper to remove some edges.

1.2 Our results

In the following, we let G be a tree. It is simple to see that, similar to CNDP, Problems 3–5 are all NP-hard already under the assumptions that the node/edge weights are unitary and the connection costs are 0/1 (Observation 1). For this reason, we will initially consider the case of unit connection costs, i.e., \(c_{uv}=1\) for every \(u,v\in V\) with \(u\ne v\). We have already recalled that CNDP can be solved in polynomial time in this situation, without any restriction on the weights. We will see that the same holds for CEDP and CNEDP-1 (Corollary 1), while for CNEDP-2 we have a polynomial-time algorithm only if we further assume that the node and edge weights are all equal to 1 (Proposition 3). On the contrary, if the connection costs are unitary but the node and edge weights are general nonnegative numbers, CNEDP-2 is NP-hard to approximate within any factor, even when G is a path (Proposition 2).

We will also see in Proposition 1 that the above polynomial-time algorithms actually apply to a more general case, in which the connection costs are 0/1 and have the following special structure: there exists \(I\subseteq V\) such that

$$\begin{aligned} c_{uv}= {\left\{ \begin{array}{ll} 1 &{} \hbox {if } u,v\in I \hbox { and } u\ne v,\\ 0 &{} \hbox {otherwise.} \end{array}\right. } \end{aligned}$$
(1)

When the connection costs are of this form, we call them square 0/1 connection costs, because if these \(c_{uv}\)’s are represented via a 0/1 matrix, the support of the matrix is, up to permutation of rows and columns, a square (without one of its diagonals).

Although in this paper we are mainly interested in theoretical results, we mention that the case of square 0/1 connection costs has also some practical interest. Indeed, the role of the subset I is easy to understand: The elements in I are the nodes that we would really like to disconnect from each other, while the other nodes are part of the graph and it may be important to remove some of them to reduce the connectivity as much as possible, but they do not count in the evaluation of the objective function.

We then study our problems when the number of leaves of the tree is bounded by a constant, which is not treated as part of the input. In this case, the assumption of unit or square 0/1 connection costs can be relaxed. Indeed, we show that CNDP, CEDP, and CNEDP-1 on a tree with arbitrary 0/1 connection costs and general nonnegative node/edge weights can be solved in polynomial time under this assumption (Proposition 4). This is in contrast to the case of general trees, for which these variants are NP-hard, as mentioned above. The same positive result holds for CNEDP-2, but only if the node and edge weights are assumed to be unitary (Proposition 5). Indeed, we recall that without this further restriction CNEDP-2 is NP-hard already on a path (even with unit connection costs), i.e., on a tree with exactly two leaves (Proposition 2).

The polynomial-time algorithms that we obtain in this paper take inspiration from the dynamic programming strategies proposed in Di Summa et al. (2011) for CNDP on a tree with unit connection costs and in Aringhieri et al. (2019) for some distance-based versions of CNDP on a tree.

2 Complexity of CEDP, CNEDP- 1, and CNEDP- 2

2.1 Hardness results for 0/1 connection costs

Di Summa, Grosso, and Locatelli Di Summa et al. (2011) proved that CNDP on a tree is NP-hard even if the node weights are all equal to 1 and the connection costs are 0/1. Their proof is via a reduction from the decision version of (unweighted) Multicut in trees, which is known to be NP-complete Garg et al. (1997) and is recalled here.

Problem 6

(Multicut in trees, decision version) Given a tree \(G=(V,E)\), a list of pairs of nodes \((u_1,v_1),\dots ,(u_k,v_k)\), and a bound M, decide whether there exists \(S\subseteq E\) with \(|S|\le M\) such that \(u_i\) and \(v_i\) are disconnected in \(G-S\) for every \(i\in \{1,\dots ,k\}\).

It is easy to see that Multicut in trees also reduces to each of CEDP, CNEDP-1, and CNEDP-2 on trees, as we observe below.

Observation 1

CEDP, CNEDP-1, and CNEDP-2 are NP-hard even on a tree with unit node/edge weights and 0/1 connection costs.

Proof

Given an instance of Multicut in trees with input as in Problem 6, we can reduce it to an instance of CEDP on the same tree, where (using the notation of Problem 3) \(w_e=1\) for all \(e\in E\), \(W=M\), \(c_{u_iv_i}=1\) for every \(i\in \{1,\dots ,k\}\), and all other connection costs are equal to zero. Clearly a subset \(S\subseteq E\) is feasible for the given instance of Multicut in trees if and only if the optimal value of the corresponding instance of CEDP is zero. This shows that CEDP is NP-hard even on a tree with unit node/edge weights and 0/1 connection costs. Since, as observed in the introduction, each of CNEDP-1 and CNEDP-2 subsumes CNDP and CEDP, we deduce the same result for CNEDP-1 and CNEDP-2. \(\square \)

2.2 Solving CEDP and CNEDP- 1 on a tree with unit connection costs

In order to prove that CEDP and CNEDP-1 can be solved in polynomial time when the underlying graph is a tree and the connection costs are all unitary, we first show a simple reduction that applies to instances on general graphs. Furthermore, it will be convenient to work with square 0/1 connection costs instead of all-one connection costs (which are of course a special case of square 0/1 connection costs).

Lemma 1

CNEDP-1 on a general graph G with square 0/1 connection costs can be polynomially reduced to CNDP with square 0/1 connection costs. Furthermore, when G is a tree the reduced instance is also defined on a tree.

Proof

Let an instance of CNEDP-1 be given, with input as in Problem 4, where the connection costs are as in (1) for some \(I\subseteq V\). Let \(G'\) be the graph obtained by subdividing every edge of G, i.e., every edge uv of G is replaced with two edges uz and zv, where z is a new node adjacent only to u and v. Formally, \(G'=(V',E')\) with \(V'=V\cup E\) and \(E'=\{ve:v\in V,\,e\in E,\,e{ isincidentwith}v\}\).

We construct an instance of CNDP on \(G'\) with the following data. For \(u,v\in V'\), the connection cost is \(c'_{uv}=1\) if \(u,v\in I\) and \(u\ne v\), and \(c'_{uv}=0\) otherwise. Note that these are square 0/1 connection costs. The weights of the elements of \(V'=V\cup E\) are defined by setting \(w'_v=w_v\) for \(v\in V\) and \(w'_e=w_e\) for \(e\in E\). The weight limit is the same as in the given instance of CNEDP-1, i.e., \(W'=W\).

Given any \(S\subseteq V\cup E=V'\), it is immediate to verify that \(c(G-S)=c'(G'-S)\). Thus the optimal solutions of the instance of CNDP with square 0/1 connection costs constructed above are precisely the optimal solutions of the given instance of CNEDP-1. It is also clear that \(G'\) is a tree whenever G is a tree. \(\square \)

We now show how to solve CNDP on a tree with square 0/1 connection costs in polynomial time, by means of a modification of the dynamic programming algorithm described in Di Summa et al. (2011). Because of the above lemma, this will also give a polynomial algorithm for CNEDP-1 on a tree with square 0/1 connection costs.

Let \(G=(V,E)\) be a tree with \(|V|=n\), and let the input data be denoted as in Problem 4, where the connection costs are as in (1) for some \(I\subseteq V\). Recall that in this problem we are interested in the number of connected pairs consisting of nodes in I.

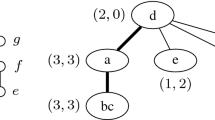
Given any subgraph H of G, we denote by V(H) the set of vertices of H. We root the tree G at any of its nodes, say \(r\in V\). Given \(a\in V\), we denote by \(G_a\) the subtree of G rooted at a. If a is not a leaf of G, we assume that an arbitrary order of its children is specified. If a has s children \(a_1,\dots ,a_s\) (listed according to the order mentioned above), for every \(i\in \{1,\dots ,s\}\) we define \(G_{a,i}\) as the subtree of G induced by \(\{a\}\cup V(G_{a_i})\cup \dots \cup V(G_{a_s})\); see Fig. 1. (Note that s depend on a, but to simplify notation we will always keep this dependence implicit.)

Fig. 1
figure 1

Node a has four children \(a_1,\dots ,a_4\). The outer rectangle represents \(G_a\). The two inner rectangles represent \(G_{a_1}\) (on the left) and \(G_{a,2}\) (on the right)

Full size image

We will calculate recursively the following values:

  • \(f_a(k,m)\) for all \(a\in V\) and all integers k, m such that \(0\le k\le n(n-1)/2\) and \(0\le m\le n\): \(f_a(k,m)\) is the minimum total weight of a subset of nodes \(S\subseteq V(G_a)\) such that \(c(G_a-S)=k\) and a is connected to exactly m nodes in \(V(G_a-S)\cap I\) (including a itself);

  • \(g_{a,i}(k,m,t)\) for all non-leaf nodes \(a\in V\), all \(i\in \{1,\dots ,s\}\), all integers k, m such that \(0\le k\le n(n-1)/2\) and \(0\le m\le n\), and \(t\in \{0,1\}\): \(g_{a,i}(k,m,t)\) is the minimum total weight of a subset of nodes \(S\subseteq V(G_{a,i})\) such that \(c(G_{a,i}-S)=k\), a is connected to exactly m nodes in \(V(G_{a,i}-S)\cap I\) (including a itself), and \(a\in S\) if and only if \(t=1\).

When \(a\in S\), the number of nodes in \(V(G_a-S)\cap I\) connected to a is intended to be zero. Furthermore, whenever the conditions in one of the above definitions cannot be satisfied, we set the value of the function to infinity. To simplify the recursive formulas below, it will be convenient to accept \(k<0\) in \(f_a(k,m)\) and \(g_{a,i}(k,m,t)\); in this case, we assume again that the function values are infinite.

The values of \(f_a\) and \(g_{a,i}\) are calculated in this order:

  • we determine \(f_a\) for every leaf a;

  • for a non-leaf node a, assuming that the \(f_{a'}\) and \(g_{a',i}\) have been already found for all \(a'\in V(G_a)\) and all i, we calculate \(g_{a,s},g_{a,s-1},\dots ,g_{a,1}\), and then \(f_a\).

At the end of the recursion, we can return the optimal value of the problem, which is

$$\begin{aligned}\min \{k:f_r(k,m)\le W,\,0\le k\le n(n-1)/2,\,0\le m\le n\},\end{aligned}$$

as \(G_r=G\). As usual in dynamic programming, an optimal solution can be reconstructed by backtracking.

We now provide the explicit formulas and then a justification for each of them. For every leaf a, we have

$$\begin{aligned} f_a(k,m)= {\left\{ \begin{array}{ll} w_a&{}\hbox {if } k=0, m=0, a\in I,\\ 0&{}\hbox {if } (k=0, m=0, a\notin I) \hbox { or }(k=0, m=1, a\in I),\\ \infty &{}\hbox {otherwise}, \end{array}\right. } \end{aligned}$$
(2)

while for a non-leaf node a the formula is

$$\begin{aligned} f_a(k,m)=\min \{g_{a,1}(k,m,0),g_{a,1}(k,m,1)\}. \end{aligned}$$
(3)

To calculate \(g_{a,i}(k,m,t)\), where a is a non-leaf node, if \(i=s\) we use the formula

$$\begin{aligned} g_{a,s}(k,m,t)= {\left\{ \begin{array}{ll} f_{a_s}(k,0)&{}\hbox {if } t=0, m=0,\\ f_{a_s}(k,m)&{}\hbox {if } t=0, m>0, a\notin I,\\ f_{a_s}(k-m+1,m-1)&{}\hbox {if } t=0, m>0, a\in I,\\ w_a+\min \{f_{a_s}(k,q):0\le q\le |V(G_{a_{s}})\cap I|\}&{}\text{ if } t=1, m=0,\\ \infty &{}\text{ if } t=1, m>0, \end{array}\right. }\nonumber \\ \end{aligned}$$
(4)

while for \(i<s\) the value of \(g_{a,i}(k,m,t)\) is calculated as follows:

$$\begin{aligned} g_{a,i}(k,m,t)= {\left\{ \begin{array}{ll} \min \{f_{a_i}(p,0)+g_{a,i+1}(k-p,0,0): 0\le p\le k\}&{}\text{ if } t=0, m=0,\\ \min \{f_{a_i}(p,q)+g_{a,i+1}(k-p-q(m-q),m-q,0):\\ \quad \qquad 0\le p\le k,\,0\le q\le m\}&{}\text{ if } t=0, m>0,\\ \min \{f_{a_i}(p,q)+g_{a,i+1}(k-p,0,1):\\ \qquad \quad 0\le p\le k,\,0\le q\le |V(G_{a_i})\cap I|\}&{}\text{ if } t=1, m=0,\\ \infty &{}\text{ if } t=1, m>0. \end{array}\right. } \end{aligned}$$
(5)

We now give a justification for the above formulas. We denote by S a subset of nodes attaining the minimum value of \(f_{a}(k,m)\) or \(g_{a,i}(k,m,t)\) (depending on which formula we are illustrating).

Formula (2) reflects the fact that when the subtree consists of just a leaf, the decision to make is whether to remove the leaf or not, and in both cases k must be zero. The value of m can be one only if the leaf belongs to I and is not removed.

Equation (3) is an immediate consequence of the observation that \(G_a=G_{a,1}\) for every non-leaf node a.

When a is a non-leaf node, in the formula for \(g_{a,s}(k,m,t)\) (Eq. (4)) there is a first distinction based on whether node a is removed (\(t=1\)) or not (\(t=0\)). In the former case, m is necessarily equal to zero, and we are on the fourth line of the formula, where the weight of node a is added to the minimum weight of a subset of nodes \(S'\) that should be removed from \(G_{a_s}\) to have k connected pairs consisting of nodes in I; note that q (the number of nodes in \(V(G_{a_s}-S')\cap I\) that are connected to \(a_s\)) is arbitrary, as this value does not affect the number of nodes connected to a, as a is removed in this case. For the other case, i.e., when a is not removed (\(t=0\)), one needs to know whether \(m=0\) or not. When \(m=0\), all of the k connected pairs are contained in \(G_{a_s}\), and no node in \(V(G_{a_s}-S)\cap I\) can be connected to \(a_s\), as otherwise it would be connected to a, as well (first line of the formula). When, \(m>0\) and \(a\notin I\), the value of \(g_{a,s}(k,m,t)\) is obtained by requiring m nodes in \(V(G_{a_s}-S)\cap I\) connected to \(a_s\) (as these nodes will be in turn connected to a) and a total connection cost of k in \(G_{a_s}-S\). Finally, if \(m>0\) and \(a\in I\), only \(m-1\) nodes in \(V(G_{a_s}-S)\cap I\) will be connected to \(a_s\), as a is also counted as connected to itself. Since these \(m-1\) connections contribute to the total connection cost k in \(G_a-S\), the total connection cost in \(G_{a_s}-S\) must be \(k-m+1\).

Formula (5) is based on a similar case distinction, except that one does not need to know whether \(a\in I\) or not. We only illustrate in detail the second case of the formula: \(t=0\) (i.e., node a is not removed) and \(m>0\). The formula is based on the observation that k must be the total cost of the connections surviving in each of the subtrees \(G_{a_i}\) and \(G_{a,i+1}\), plus the cost of the connections between the two subtrees. This last term is given by \(q(m-q)\), where q is the number of nodes in \(V(G_{a_i}-S)\cap I\) connected to \(a_i\) and, consequently, \(m-q\) is the number of nodes in \(V(G_{a,i+1}-S)\cap I\) connected to a. Thus, if p connected pairs survive in \(G_{a_i}\), \(k-p-q(m-q)\) survive in \(G_{a,i+1}\). (For a correct interpretation of the formula, it is important to keep in mind that \(G_{a_i}\) is rooted at \(a_i\), while \(G_{a,i+1}\) is rooted at a.)

We obtain the following result.

Proposition 1

CNDP, CEDP, and CNEDP-1 can be solved in polynomial time when the underlying graph is a tree and 0/1 square connection costs are given.

Proof

By the above discussion, the proposed dynamic programming algorithm correctly solves CNDP when the underlying graph is a tree and 0/1 square connection costs are given. The polynomiality is immediate to check, as a, i, k, m and t can take only a polynomial number of values, and the computation of each formula can be carried out in polynomial time.

Lemma 1 implies that CNEDP-1 can also be solved in polynomial time, under the same assumptions. Finally, the observation that CEDP is a special case of CNEDP-1 (see the introduction) proves the same result for CEDP.

An immediate corollary is the following. (For the sake of completenes, we include CNDP in the statement below, although the correspnding result was shown in Di Summa et al. (2011).)

Corollary 1

CNDP, CEDP and CNEDP-1 can be solved in polynomial time when the underlying graph is a tree and the connection costs are all unitary.

2.3 Complexity of CNEDP-2

Unlike CNEDP-1, CNEDP-2 with unit connection costs is NP-hard even on a path. We actually show a stronger result: it is NP-hard to approximate this problem within any factor. (We recall that given \(\alpha \ge 1\), an \(\alpha \)-approximation algorithm for a minimization problem is required to return a solution whose objective value is at most \(\alpha \) times the optimal value; see, e.g., Vazirani (2013).)

Proposition 2

Unless \(P=NP\), CNEDP-2 on a path with unit connection costs cannot be approximated within any factor.

Proof

We prove the result via a reduction from Partition, which is known to be NP-complete (see Garey and Johnson (1979)):

Partition: Given \(n\in \mathbb N\) and \(a_1,\dots ,a_n\in \mathbb N\), determine whether there exists \(J\subseteq \{1,\dots ,n\}\) such that \(\sum _{i\in J}a_i=\sum _{i\notin J}a_i\).

Given an instance of Partition as above, we define \(A=\sum _{i=1}^na_i\). We construct an instance of CNEDP-2 on a path as follows:

  • \(G=(V,E)\) is a path with \(2n+1\) vertices, denoted by \(u_1,v_1,u_2,v_2,\dots ,u_n,v_n,u_{n+1}\) (in the order they appear on the path);

  • the node weights are \(w_{v_i}=a_i\) for every \(i\in \{1,\dots ,n\}\), and \(w_{u_i}=A/2+1\) for every \(i\in \{1,\dots ,n+1\}\);

  • the edge weights are \(w_{u_iv_i}=a_i\) and \(w_{v_iu_{i+1}}=0\) for every \(i\in \{1,\dots ,n\}\);

  • the weight limits are \(W_V=W_E=A/2\).

We show that the given instance of Partition has a solution if and only if the optimal value of the above instance of CNEDP-2 is zero. Since, by definition, an approximation algorithm always recognizes the instances with optimal value equal to zero, this will prove the result.

Assume that the instance of Partition has a solution, i.e., there exists \(J\subseteq \{1,\dots ,n\}\) such that \(\sum _{i\in J}a_i=\sum _{i\notin J}a_i=A/2\). Define \(S\subseteq V\cup E\) as follows:

$$\begin{aligned}S=\{v_i:i\in J\}\cup \{u_iv_i:i\notin J\}\cup \{v_iu_{i+1}:i\in \{1,\dots ,n\}\}.\end{aligned}$$

This choice yields a feasible solution to the instance of CNEDP-2, as \(w(S\cap V)=w(S\cap E)=A/2=W_V=W_E\). Furthermore, as \(G-S\) contains only isolated nodes, \(c(G-S)=0\). Thus the optimal value of the instance of CNEDP-2 is zero.

For the converse, assume that the instance of CNEDP-2 has a solution with objective value zero, i.e., there exists \(S\subseteq V\cup E\) such that \(w(S\cap V)\le A/2\), \(w(S\cap E)\le A/2\), and \(c(G-S)=0\) (which means that there are only isolated nodes in \(G-S\)). Without loss of generality, we can assume that \(v_iu_{i+1}\in S\) for every \(i\in \{1,\dots ,n\}\), as these edges have zero weight. In other words, we can imagine that the original graph only contains the edges \(u_1v_1,\dots ,u_nv_n\). Furthermore, \(u_i\notin S\) for every i, as otherwise the node weight limit would be exceeded. Then the fact that \(G-S\) has only isolated nodes implies that, for every \(i\in \{1,\dots ,n\}\), S contains \(v_i\) or \(u_iv_i\). As \(w_{v_i}=w_{u_iv_i}=a_i\) for every i, we obtain \(w(S)\ge A\). Since the weight limits are \(W_V=W_E=A/2\), we necessarily have \(w(S\cap V)=w(S\cap E)=A/2\). Thus the instance of Partition has the solution \(J=S\cap V\). \(\square \)

Despite the above negative result, we now show that if the node and edge weights are fixed to 1 (as well as the connection costs), CNEDP-2 admits a polynomial-time algorithm. We use the same tree and subtree notation as in the previous section, and calculate recursively the following values:

  • \(f_a(k_V,k_E,m)\) for all \(a\in V\) and all integers \(k_V,k_E,m\) such that \(0\le k_V\le W_V\), \(0\le k_E\le W_E\), and \(0\le m\le n\): \(f_a(k_V,k_E,m)\) is the minimum cardinality of a subset \(S\subseteq V(G_a)\cup E(G_a)\) such that \(|S\cap V|\le k_V\), \(|S\cap E|\le k_E\), and a is connected to exactly m nodes in \(V(G_a-S)\) (including a itself);

  • \(g_{a,i}(k_V,k_E,m)\) for all non-leaf nodes \(a\in V\), all \(i\in \{1,\dots ,s\}\), and all integers \(k_V,k_E,m\) such that \(0\le k_V\le W_V\), \(0\le k_E\le W_E\), and \(0\le m\le n\): \(g_{a,i}(k_V,k_E,m)\) is the minimum cardinality of a subset \(S\subseteq V(G_{a,i})\cup E(G_{a,i})\) such that \(|S\cap V|\le k_V\), \(|S\cap E|\le k_E\), and a is connected to exactly m nodes in \(V(G_{a,i}-S)\) (including a itself).

We let the function values be infinity whenever the conditions cannot be satisfied.

For every leaf a we have

$$\begin{aligned} f_a(k_V,k_E,m)= {\left\{ \begin{array}{ll} 0&{}\text{ if } (k_V=k_E=0, m=1) \hbox { or } (k_V=1, k_E=m=0),\\ \infty &{}\text{ otherwise }, \end{array}\right. } \end{aligned}$$
(6)

while the formula for a non-leaf node a is

$$\begin{aligned} f_a(k_V,k_E,m)=g_{a,1}(k_V,k_E,m). \end{aligned}$$
(7)

If a is a non-leaf node, we also have

$$\begin{aligned}&g_{a,s}(k_V,k_E,m) \nonumber \\&\quad ={\left\{ \begin{array}{ll} \min \{f_{a_s}(k_V-1,k_E,q):0\le q\le |V(G_{a_s})|\}&{}\text{ if } m=0,\\ \min \big \{f_{a_s}(k_V,k_E,0),\min \{f_{a_s}(k_V,k_E-1,q):0\le q\le |V(G_{a_s})|\}\big \}&{}\text{ if } m=1,\\ f_{a_s}(k_V,k_E,m-1)+m-1&{}\text{ if } m>1, \end{array}\right. } \end{aligned}$$
(8)

while, for \(i<s\),

$$\begin{aligned}&g_{a,i}(k_V,k_E,m)\nonumber \\&\quad = {\left\{ \begin{array}{ll} \min \{f_{a_i}(p_V,p_E,q)+g_{a,i+1}(k_V-p_V,k_E-p_E,0):\\ \quad \qquad 0\le p_V\le k_V-1,\,0\le p_E\le k_E,\,0\le q\le |V(G_{a_i})|\}&{}\text{ if } m=0,\\ \min \big \{\min \{f_{a_i}(p_V,p_E,q)+g_{a,i+1}(k_V-p_V,k_E-p_E-1,m):\\ \quad \qquad \qquad \quad 0\le p_V\le k_V,\,0\le p_E\le k_E-1,\,0\le q\le |V(G_{a_i})|\},\\ \qquad \,\,\,\min \{f_{a_i}(p_V,p_E,q)+g_{a,i+1}(k_V-p_V,k_E-p_E,m-q)+q(m-q):\\ \quad \qquad \qquad \quad 0\le p_V\le k_V,\,0\le p_E\le k_E,\,0\le q\le m\}\big \}&{}\text{ if } m>0. \end{array}\right. } \end{aligned}$$
(9)

The optimal value is calculated as follows:

$$\begin{aligned} \min \{f_r(k_V,k_E,m):0\le k_V\le W_V,\,0\le k_E\le W_E,\,0\le m\le n\}. \end{aligned}$$
(10)

Formulas (6) and (7) are immediate.

In (8) we assume that if \(a\in S\) then \(aa_s\notin S\): This is without loss of generality, as if \(aa_s\in S\), we obtain the same objective value by removing the elements in \(S\setminus \{aa_s\}\). The case \(m=0\) corresponds to \(a\in S\), which leads to the formula on the first line. The case \(m=1\) occurs when \(a_s\in S\) (first argument of the outer minimum on the second line) or \(aa_s\in S\) (second argument of the outer minimum). Finally, \(m>1\) is the case in which \(a,aa_s\notin S\).

Similar to (8), in (9) we assume that if \(a\in S\) then \(aa_i\notin S\). The first case (\(m=0\)) corresponds to having \(a\in S\). In this situation, we take the sum of the optimal values that we can obtain in each of the two subtrees \(G_{a_i}\) and \(G_{a,i+1}\). For the second case (\(m>0\)), in which \(a\notin S\), we take the better of two possibilities, which correspond to the two arguments of the outer minimum. For the first possibility, which is when \(aa_i\in S\), we take again the sum of the optimal values in each of the two subtrees \(G_{a_i}\) and \(G_{a,i+1}\). For the second possibility (\(aa_i\notin S\)), we have to add the connections between the two subtrees.

The formula for the optimal value (10) is immediate, as \(G=G_r\).

We obtain the following result.

Proposition 3

CNEDP-2 on a tree with unit connection costs and unit node/edge weights can be solved in polynomial time.

Proof

The above algorithm is polynomial because one can take \(W_V\le |V|\) and \(W_E\le |E|\) without loss of generality, as the weights are all equal to one. \(\square \)

One can verify that the above result extends to square 0/1 connection costs.

3 Bounded number of leaves

In this section we consider trees in which the number of leaves is bounded by a given constant (which is not treated as part of the input). We show that if the connection costs take general 0/1 values, each of CNDP, CEDP, and CNEDP-1 can be solved in polynomial time. Note that, unless \(P=NP\), this result cannot hold for CNEDP-2, as shown by Proposition 2. However, we will see that a polynomial-time algorithm can be found for this problem if, in addition, the node and edge weights are assumed to be unitary.

The positive results in this section are in contrast with with the case of general trees, for which the assumption of general 0/1 connection costs makes the problems NP-hard. Indeed, the interest in trees with bounded number of leaves is motivated by the search for the weakest assumptions needed to ensure the existence of a polynomial-time algorithm when the connection costs take arbitrary 0/1 values.

Let us first focus on CNDP on a tree with 0/1 connection costs. Let \(G=(V,E)\) be a tree with n nodes and \(\ell \) leaves. Given \(u,v\in V\), we denote by [u, v] the node set of the unique path joining u and v in G. Given \(a\in V\) and \(S\subseteq V\), we define the boundary of S with respect to a, and denote it by \(B_a(S)\), as follows:

$$\begin{aligned}B_a(S)=\{v\in S: [a,v]\cap S=\{v\}\}.\end{aligned}$$

Clearly, \(|B_a(S)|\le \ell \).

We will calculate the following values:

  • \(f_a(k,B)\) for all integers k such that \(0\le k\le n(n-1)/2\) and every \(B\subseteq V(G_a)\) such that \(|B|\le \ell \): \(f_a(k,B)\) is the minimum total weight of a subset of nodes \(S\subseteq V(G_a)\) such that \(c(G_a-S)=k\) and \(B_a(S)=B\);

  • \(g_{a,i}(k,B)\) for all integers k such that \(0\le k\le n(n-1)/2\) and every \(B\subseteq V(G_{a,i})\) such that \(|B|\le \ell \): \(g_{a,i}(k,B)\) is the minimum total weight of a subset of nodes \(S\subseteq V(G_{a,i})\) such that \(c(G_{a,i}-S)=k\) and \(B_a(S)=B\).

As in the previous algorithms, these values are assumed to be infinite whenever the conditions cannot be satisfied. This happens, in particular, whenever B is not a set of the type \(B_a(S)\) for any \(S\subseteq V(G_a)\) (or \(S\subseteq V(G_{a,i})\)), for instance (but not only) when B is larger than the number of leaves of the subtree. (Indeed, we could use the number of leaves of \(G_a\) or \(G_{a,i}\) as a bound for |B|, but this would slightly complicate the description of the algorithm.) It is also convenient to set the above values to infinity when \(k<0\).

If a is a leaf, we have

$$\begin{aligned} f_a(k,B)= {\left\{ \begin{array}{ll} w_a&{}\hbox {if } k=0 \hbox { and } B=\{a\},\\ 0&{}\hbox {if } k=0 \hbox { and } B=\emptyset ,\\ \infty &{}\text{ otherwise }, \end{array}\right. } \end{aligned}$$
(11)

while if a is a non-leaf node the formula is

$$\begin{aligned} f_a(k,B)=g_{a,1}(k,B). \end{aligned}$$
(12)

For a non-leaf node a we also have

$$\begin{aligned} g_{a,s}(k,B)= {\left\{ \begin{array}{ll} w_a+\min \{f_{a_s}(k,B'):B'\subseteq V(G_{a_s}),\,|B'|\le \ell \}&{}\hbox { if}\ B=\{a\},\\ f_{a_s}\big (k-\sum \{c_{av}:v\in V(G_{a_s}),\,[a,v]\cap B=\emptyset \},B\big )&{}\hbox { if}\ a\notin B,\\ \infty &{}\text{ otherwise }, \end{array}\right. }\nonumber \\ \end{aligned}$$
(13)

and, for \(i<s\),

$$\begin{aligned} g_{a,i}(k,B)\\ \quad ={\left\{ \begin{array}{ll} \min \{f_{a_i}(p,B')+g_{a,i+1}(k-p,\{a\}): 0\le p\le k,\,B'\subseteq V(G_{a_i}),\,|B'|\le \ell \}&{}\hbox { if}\ B=\{a\},\\ \min \{f_{a_i}(p,B\cap V(G_{a_i}))+g_{a,i+1}(k-p-\sigma (a,i,B),B\cap V(G_{a,i+1})):\\ \qquad \quad 0\le p\le k\}&{}\hbox { if}\ a\notin B,\\ \infty &{}\text{ otherwise }, \end{array}\right. } \end{aligned}$$
(14)

where \(\sigma (a,i,B)=\sum \{c_{uv}:u\in V(G_{a_i}),\,v\in V(G_{a,i+1}),\,[u,v]\cap B=\emptyset \}\). The optimal value is

$$\begin{aligned}\min \{k:f_r(k,B)\le W,\,0\le k\le n(n-1)/2,\,B\subseteq V,\,|B|\le \ell \}.\end{aligned}$$

The correctness of (11) and (12) is easy to check.

In formula (13), the first and third cases express the fact that if \(a\in B\) and B is a set of the form \(B_a(S)\) for some \(S\subseteq V(G_a)\), then necessarily \(B=S=\{a\}\). In this case, a is removed from \(G_a\) and we are left with the subproblem on \(G_{a_s}\). (In this subproblem the boundary set \(B'\) is arbitrary, as it does not affect the fact that \(B=\{a\}\).) On the other hand, if \(a\notin B\) and \(B=B_a(S)\) for some \(S\subseteq V(G_a)\), then \(S\subseteq V(G_{a_s})\) and \(B=B_{a_s}(S)\). We then obtain the second case of the formula, where the term \(\sum \{c_{av}:v\in V(G_{a_s}),\,[a,v]\cap B=\emptyset \}\) counts the number of nodes connected to a in \(G_{a_s}-S\).

Formula (14) is based on a similar argument. We only remark some points. When \(B=S=\{a\}\), two subproblems on \(G_{a_i}\) and \(G_{a,i+1}\) are created. Since a is removed from \(G_{a,i}\), the boundary set of the first subproblem is an arbitrary \(B'\) (as this does not affect the fact that \(B=\{a\}\)), while in the second subproblem the boundary set must be \(\{a\}\) (as a is the root of \(G_{a,i+1}\)). When \(a\notin B\), we use the fact that if \(B=B_a(S)\) for some \(S\subseteq V(G_{a,i})\), then \(B_a(S\cap V(G_{a_i}))=B\cap V(G_{a_i})\) and \(B_a(S\cap V(G_{a,i+1}))=B\cap V(G_{a,i+1})\). The term \(\sigma (a,i,B)\) count the number of surviving connections between the two subtrees.

We obtain the following result.

Proposition 4

CNDP, CEDP, and CNEDP-1 can be solved in polynomial time when the underlying graph is a tree whose number of leaves is bounded by a constant and the connection costs are 0/1.

Proof

For CNDP the polynomiality follows from the above algorithm, after observing that the number of boundary sets B to consider is \(O(n^\ell )\), which is polynomial when \(\ell \) is constant. To derive a polynomial-time dynamic programming algorithm for CNEDP-1, one can use the subdivision approach described in the proof of Lemma 1. (We omit the details.) The polynomiality of CEDP then follows because, as already observed, this problem is a special case of CNEDP-1.\(\square \)

For CNEDP-2, we need to restrict to unit weights.

Proposition 5

CNEDP-2 can be solved in polynomial time when the underlying graph is a tree whose number of leaves is bounded by a constant, the node and edge weights are unitary, and the connection costs are 0/1.

Proof

A polynomial-time dynamic programming algorithm can be obtained by combining the approach described in this section with that developed in Sect. 2.3. The basic idea is to define \(f_a(k_V,k_E,B)\) as the minimum cardinality of a subset \(S\subseteq V(G_a)\cup E(G_a)\) such that \(|S\cap V|\le k_V\), \(|S\cap E|\le k_E\), and \(B_a(S)=B\), and similarly for \(g_{a,i}(k_V,k_E,B)\). We omit the details.\(\square \)

We remark that what makes the algorithm polynomial is the constant bound of \(\ell \) on the cardinality of the boundary sets. Requiring that G has at most \(\ell \) leaves is a stronger hypothesis, but it does not seem easy to find weaker reasonable assumptions on G that ensure this property.

4 Concluding remarks

We conclude the paper with a couple of possible directions for future research.

One natural question is whether one can devise polynomial-time algorithms for other classes of critical node/edge detection problems. This paper deals with variants of some of the most studied versions of the problem, but is limited to trees. As mentioned in the introduction, to the best of our knowledge the literature offers only few polynomiality results for problems of this type, which are limited to graphs with simple structure. It seems that some different ideas are needed to go beyond the basic cases.

In Sect. 3 we provided a polynomial-time algorithm for our problems under the assumption that the number of leaves is bounded by a given constant \(\ell \). Since the number of iterations required by the algorithm contains a term of the form \(n^\ell \), this algorithm does not imply that the problem is fixed-parameter tractable (FPT). It would be interesting to understand whether the problem is indeed FPT.