1 Introduction

Classical scheduling problems deal with situations in which a set of tasks has to be processed on some processing resource or machine and a certain performance indicator has to be optimized. In multi-agent scheduling problems there are k disjoint sets of tasks, each set belonging to one agent, and each agent is interested in optimizing a performance index depending only its own set of tasks. Although these problems can be viewed as a special case of multicriteria scheduling problems (T’Kindt and Billaut 2006), their specific properties and applications have motivated a considerable amount of research since the seminal work by Agnetis et al. (2004) and Baker and Smith (2003). For a detailed and exhaustive view on multiagent scheduling problems, one can refer to the recent book (Agnetis et al. 2014).

There are two main streams of research in the recent literature on multi-agent scheduling problems. One stream deals with the problem in a multi-objective optimization perspective (see, for example, Leung et al. 2010; Zhao and Lu 2013); the other is from the algorithmic game theory point of view. In the latter context, for instance, mechanism design has received considerable attention in the recent literature (see, e.g. Angel et al. 2006; Immorlica et al. 2009; Nisan and Ronen 1999). The goal is to design system-wide rules which, given the selfish decisions of the users, maximize the total social welfare. The degree to which these rules approximate the social welfare in a worst-case equilibrium is known as the price of anarchy of the mechanism.

In this work we address a multi-agent generalization of a two-agent scheduling problem introduced in Agnetis et al. (2003) and later thoroughly analyzed in Nicosia et al. (2015). Here, we consider k agents, each owning a set of nonpreemptive tasks (or jobs), that require a single, jointly used, machine to process their tasks. Each agent pursues the minimization of a given objective function, such as makespan, sum of completion times or sum of weighted completion times. Additionally, an external coordination mechanism, aiming at reaching a high throughput, or number of processed tasks per time unit, regulates access of agents’ tasks to the machine as follows. Each agent submits one unscheduled task, if available, for possible processing. The shortest among the submitted tasks is selected by the coordinator and scheduled at the end of the current schedule, which is initially empty. In the following we refer to the above steps as rounds.

Since no information about future tasks is given, this selection of the shortest submitted task in each round is the only reasonable rule for improving the overall performance of the machine, e.g. the average work-in-process. Moreover, this decision rule gives no incentive to the agents for exaggerating the length of their tasks since this would worsen their chances for speedy processing. In this sense, it contributes to truthfulness of the agents.

Analogous situations where several involved parties (companies, departments, etc.) share a (manufacturing) resource and compete for its use can be found in many industrial settings. An independent coordinator employs a decision rule to manage the usage of the resource and thus determines the respective schedules on the shared system. Often such a situation follows a global objective function which a central authority explicitly pursues, as far as possible under the actions of the agents. These kinds of scenarios have been considered in (Cohen et al. 2011; Huynh Tuong et al. 2012) where an indicator independent of the objectives of the agents, e.g., the overall performance of a workshop or the global revenue of a company, has to be optimized. However, in our setting no global objective function is manifestly taken into account.

We look at the problem in two different settings. In a centralized perspective we aim at characterizing the set of Pareto optimal schedules in terms of size and computational complexity, as in a multicriteria optimization problem. Such an approach has been used also in Agnetis et al. (2004) and Perez-Gonzalez and Framinan (2014) and is given broad attention in the recent monograph (Agnetis et al. 2014). In a single agent perspective we search for an algorithm, i.e. a decision mechanism that suggests to the agent which task to submit in each round. This algorithm strives to minimize the agent’s objective function and may take the outcome of previous rounds into account. For such an algorithm we are interested in its performance as it is studied for on-line algorithms. In this context we study the effectiveness of two algorithms implied by natural and well known priority rules, i.e. when the agent submits its tasks in SPT (shortest processing time first) or WSPT (weighted shortest processing time first) order. Our analysis exhibits surprisingly high worst case performance ratios for these sequencing rules which are optimal in the corresponding off-line single-agent problems.

This twofold approach has been also adopted in Agnetis et al. (2003, 2015), Marini et al. (2013) and Nicosia et al. (2011, 2015). In particular, in Agnetis et al. (2003) the authors introduce a class of two-agent scheduling problems in which the decision process is organized in rounds and provide some preliminary results for different shop configurations. A detailed analysis of the so-called linear conveyor shop configuration is carried out in Agnetis et al. (2015), where a number of properties and solution algorithms are presented taking into account both centralized and single-agent perspectives. The shop configuration of Agnetis et al. (2015) refers to a manufacturing application in which two linear conveyor belts, one for each agent, transport parts to the machine. So, each agent sequences the parts on the conveyor, implying that at each round one of the two candidate tasks has been unsuccessfully submitted in the preceding round. In other words, each task is submitted for possible processing, in the given order, until it is scheduled. In Nicosia et al. (2015) consider a more general configuration in which there are no queues at the machine and at each round any part from the two agents’ buffers can be picked up and submitted for possible processing. Hence, in this case, the agents are free to choose any available task for submission at each round, independently from the outcome of the previous round. This is also the setting considered in the current paper which extends and generalizes the results in Nicosia et al. (2015) from the special case of 2 agents to the scenario of k agents.

The paper is organized as follows. In Sect. 2 we formally introduce the problem, present the notation, and summarize all the results of the paper in two tables. Sections 3 and 4 address the problem of characterizing the set of Pareto optimal (PO) solutions for various objective functions. In particular, we investigate the complexity of finding PO solutions and determine their number. In Sect. 5 we consider a single agent perspective. We provide results on the worst-case performance of SPT and WSPT algorithms for different objectives. Finally, in Sect. 6 some conclusions are drawn and open questions are pointed out.

2 Notation and summary of results

Let k be the number of agents. Each agent \(i=1,\ldots , k\) owns a set of n nonpreemptive tasksFootnote 1 with nonnegative integer processing times \(p_j^i\,\), \(j=1,\ldots ,n\). For convenience we assume that \(p_1^i \le p_2^i \le \cdots \le p_n^i\) for all i. Moreover, we assume that the agents are sorted by their longest task length such that \(p_n^i \le p_n^{i+1}\). We will frequently refer to tasks by their processing times. All tasks have to be performed on a single machine which can process only one task at a time.

Sometimes each task also has a weight indicating its importance. We will only need explicit weight values for one particular agent h and thus only introduce a nonnegative weight \(w_j\) for a task \(p_j^h\), \(j=1,\ldots ,n\). All data are known by all agents and all tasks are available at time 0.

Each agent i wants to optimize its own objective function, which only depends on the completion times of its tasks: \(f^i = f^i (C^i_1, \ldots , C^i_n)\), where \(C^i_j\) is the completion time of task j of agent i, \(i = 1, \ldots , k\). In this paper we consider for an agent i the minimization of

  1. 1.

    Makespan: \(f^i = \max \{C^i_1, \ldots , C^i_n\}\)

  2. 2.

    Sum of completion times: \(f^i = \sum _{j=1}^n\, C^i_j\)

  3. 3.

    Sum of weighted completion times for \(i=h\): \(f^h = \sum _{j=1}^n\, w_j C^h_j\).

As in Agnetis et al. (2015), we denote the problem resulting from a k-tuple of objective functions as Problem \((f^1,\ldots , f^k)\).

The decision process is divided into rounds each of them consisting of the following two steps.

  1. 1.

    Each agent submits one of its unscheduled tasks (if there is still one available).

  2. 2.

    The shortest among the (at most) k submitted tasks is selected and scheduled at the end of the current schedule. Ties are broken lexicographically, i.e. agent i wins against agent h for \(1\le i < h \le k\).

In the following, we say that an agent or task wins a round, if it is selected to be scheduled on the machine, otherwise it loses. Note that the decision of an agent on which task to submit in any round may take the submissions and outcomes of previous rounds into account but is not restricted by these past events. This corresponds to the flexible processing setting described in Agnetis et al. (2003) and treated extensively in Nicosia et al. (2015) for the special case of \(k=2\) agents.

Clearly not all sequences of tasks can be the output of the process described above. A schedule with task \(p_j^h\) of agent h scheduled in round \(\ell \) is feasible if there is no agent \(i\ne h\) which at round \(\ell \) has all its unscheduled tasks with processing time smaller than \(p_j^h\).

The decision version of the above problem is defined as the following Recognition problem \(REC(f^1,\ldots , f^k)\):

Given k nonnegative values \(Q^i\), \(i=1,\ldots ,k\), does there exist a feasible solution \(\sigma \) of Problem \((f^1,\ldots , f^k)\) such that \(f^i(\sigma ) \le Q^i\) for all \(i=1,\ldots ,k\)?

The following tables summarize the results of this paper. Table 1 shows the results concerning the centralized perspective: in the second column (Size of PO set) we report, for each addressed problem, an estimate on the number of Pareto optima. In the third column (Complexity of recognition problem) we indicate the complexity of the corresponding decision problem \({ REC}\).

Table 1 Summary of results for the centralized perspective (Sects. 3, 4)
Full size table

Table 2 presents the worst-case performance ratios of SPT and WSPT algorithms when used by one agent h against any combination of algorithms followed by the other \(k-1\) agents.

Table 2 Performance ratios for standard sequencing rules H for one agent h (Sect. 5)
Full size table

3 Centralized perspective: minimizing makespan

In this paper the centralized perspective is always restricted to feasible solutions, i.e. solutions that can be generated by the rounds of the submission process.

For problem \(\left( C_{\max }^1, \ldots , C_{\max }^k\right) \), where all agents want to minimize their makespan, we observe that the largest task can never win against any opponent’s task. So, the owner of the largest task, i.e. agent k, will always have a makespan of \(\sum _{i=1}^k \sum _{j=1}^n p_j^i \). Hence, in any Pareto optimal solution all tasks of agent k are scheduled consecutively at the end of the schedule from time \(\sum _{i=1}^{k-1} \sum _{j=1}^n p_j^i \) to time \(\sum _{i=1}^k \sum _{j=1}^n p_j^i \) (this can be achieved by letting agent k submit task \(p_n^k\) first). The same argument can now be applied to agent \(k-1\), \(k-2\), down to agent 1. So, the tasks of any agent h are scheduled consecutively between \(\sum _{i=1}^{h-1} \sum _{j=1}^n p_j^i \) and \(\sum _{i=1}^{h} \sum _{j=1}^n p_j^i \). Hence, we have the following statement.

Proposition 1

For problem \(\left( C_{\max }^1, \ldots , C_{\max }^k\right) \) there is only one Pareto optimal schedule.

In particular, this single Pareto optimum is obtained when agent h with \(1 \le h \le k\) wins rounds \((h-1)n+1, \ldots , hn\), against \(k-h\) submissions of the other remaining agents.

4 Centralized perspective: mixing makespan and sum of completion times

The most interesting aspect of this section concerns the case in which one agent \(h \in \{1,\ldots ,k\}\) wants to minimize its sum of completion times, while all other \(k-1\) agents minimize their makespan, i.e.

$$\begin{aligned} \text{ Problem }\quad \left( C_{\max }^1, \ldots , C_{\max }^{h-1}, \sum C_j^h, C_{\max }^{h+1}, \ldots , C_{\max }^{k}\right) . \end{aligned}$$

We can state immediately that it suffices to consider the case \(h=k\). Since \(p_n^i \le p_n^{i+1}\) for all \(i=1, \ldots k-1\), in any feasible solution it must be \(C_{\max }^{h} < C_{\max }^{i}\) for \(i=h+1,\ldots , k\). Hence, in any PO solution the agents \({h+1}, \ldots , {k}\) process their tasks in blocks placed after the completion of the last task of agent h, as described in Sect. 3. Therefore, the above problem is equivalent to considering only the subproblem consisting of agents \(1,\ldots , h\). Hence, we now address the problem \(\left( C_{\max }^1, \ldots , C_{\max }^{k-1}, \sum _j C_j^k\right) \).

Using standard arguments and those of Sect. 3 we observe that in any PO solution the following three conditions must hold:

(F1)::

Each agent i, with \(i= 1, \ldots , k-1\), schedules its tasks consecutively in one block, i.e. knowing the maximum completion time \(C_{\max }^{i}\) the tasks must be scheduled in time interval \(\left[ C_{\max }^{i}- \sum _{j=1}^n p_j^i , C_{\max }^{i}\right] \);

(F2)::

\(C_{\max }^{i} < C_{\max }^{i+1}\) for all \(i= 1, \ldots , k-1\);

(F3)::

The tasks of agent k appear in the schedule in SPT order, i.e. \(C_j^k< C_{j+1}^k\).

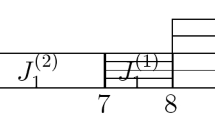
This implies that any PO solution consists of \(k-1\) uninterrupted blocks of tasks, one for each agent \(i= 1, \ldots , k-1\), possibly interleaved by tasks of agent k. The uninterrupted blocks are sequenced from 1 to \(k-1\), while the tasks of agent k are in SPT order, see Fig. 1 for a pictorial representation of the structure of a PO solution.

Fig. 1
figure 1

Problem \(\left( C_{\max }^1, \ldots , C_{\max }^{k-1}, \sum _j C_j^k\right) \): structure of a Pareto optimal solution

Full size image

We now consider the number \(\beta \) of Pareto optima resulting from the above structure. In order to compute an upper bound on \(\beta \), we observe that, in the worst case, each block of tasks of the first \(k-1\) agents can be placed in one of at most \(n-1\) “slots” between two tasks \(p^k_{j-1}\) and \(p^k_{j}\), of agent k, \(j=2,\ldots ,n\), or before \(p^k_1\). Therefore, recalling that the blocks are sequenced in order from 1 to \(k-1\) and since two or more blocks may be placed in the same slot, we have that \(\beta \) cannot exceed the number of \((k-1)\)-combinations with repetitions from a set of size n, that is

$$\begin{aligned} \beta \le \left( {n\atopwithdelims ()k - 1}\right) = {n+k-2 \atopwithdelims ()k-1}. \end{aligned}$$
(1)

To show that the upper bound of Eq. (1) can in fact be reached, we consider an instance where \(p^i_n > p^k_{n-1}\), for all agents \(i=1,\ldots , k-1\), so that each block of tasks of the first \(k-1\) agents may be placed in any of the n slots implied by the tasks of agent k. Otherwise, any block of tasks of an agent violating this condition could not be placed, e.g. between \(p^k_{n-1}\) and \(p^k_{n}\).

Now we introduce the following instance I of \(\left( C_{\max }^1, \ldots , C_{\max }^{k-1}, \sum _j C_j^k\right) \) such that the tasks of the first \(k-1\) agents have the following processing times

$$\begin{aligned} \begin{array}{ll} p^i_j = \left\{ \begin{array}{l@{\quad }l} 1 &{} \text{ for }\quad j=1,\ldots ,n-1; \\ M - k + i &{} \text{ for }\quad j=n \end{array} \right.&\qquad i = 1, \ldots , k-1 \end{array} \end{aligned}$$

while the last agent k has

$$\begin{aligned} p^k_j = \left\{ \begin{array}{l@{\quad }l} j\ &{} \text{ for }\quad j=1,\ldots ,n-1;\\ M\ &{} \text{ for }\quad j=n \end{array} \right. \end{aligned}$$

where M is a large enough integer (so that \(p^1_n = M - k + 1 > n - 1 = p^k_{n-1}\)).

For this instance a schedule is feasible and nondominated (cf. above) if conditions (F1–F3) hold. In particular, to meet condition (F1), it is enough for each agent i to play task \(p^i_n\) first. As soon as its longest task is scheduled, agent i can continue submitting its \(n-1\) tasks of length 1. Moreover, since \(p^i_n = M - k + i < p^{i+1}_n = M - k + i+1 \) then \(C^i_{\max } < C^{i+1}_{\max }\) holds and condition (F2) is guaranteed, for all \(i= 1, \ldots , k-1\). Finally, we only consider schedules such that tasks of agent k are scheduled in SPT order.

This means that every Pareto efficient solution consists of two subsequences of tasks: One containing all tasks of agents \(1,\ldots , k-1\) in consecutive blocks for each agent and sorted by increasing \(p^i_n\), i.e. in increasing order of agent index, and another one containing all tasks of agent k in increasing order of processing times. Any way of merging these two fixed subsequences is feasibleFootnote 2 and gives rise to a distinct Pareto efficient solution.

Since there are \(\left( {n\atopwithdelims ()k - 1}\right) \) ways to place the \(k-1\) blocks corresponding to the tasks of agents \(1, \ldots , k-1\), in the n slots implied by the tasks of agent k, we may obtain exactly \({n+k-2 \atopwithdelims ()k-1}\) distinct nondominated schedules.

In conclusion, the above arguments prove the following result:

Theorem 1

For problem \(\left( C_{\max }^1, \ldots , C_{\max }^{k-1},\sum _j C_j^k \right) \) the number of Pareto optimal solutions is \(\varTheta (n^k)\).

Observe that if k is a fixed constant we have a polynomial number of Pareto optima, whereas if k is considered as part of the input, the number of PO solutions is in fact exponential. However, note that, also in this latter case, the corresponding recognition problem \({ REC}\) can be solved in polynomial time by the following Algorithm 1. This means that an exponential number of PO solutions does not necessarily imply the \({\mathcal {NP}}\)-completeness of \({ REC}\). This is a notable exception since in all results on the central perspective in Agnetis et al. (2015) and Nicosia et al. (2015), an exponential size of the PO solution set always coincided with \({\mathcal {NP}}\)-completeness of the associated recognition problem.

figure a

The algorithm basically assigns blocks of tasks for agents \(1,\ldots ,k-1\) as late as possible and then inserts the tasks of agent k in SPT order, moving the reserved blocks to an earlier starting time if nonpreemption would cause idle times. Note that each job j of agent k, with \(j\ge t(i)\) can only be scheduled after block \(B_i\). Clearly, the resolution of preemption in line 14 does not change the sum of completion times for agent k, while the maximum completion times of the other agents may decrease.

It is easy to see that given the ordering of the processing times Algorithm 1 can be executed in linear time.

Theorem 2

Problem \(REC\left( C_{\max }^1, \ldots , C_{\max }^{k-1},\sum _j C_j^k \right) \) can be decided in O(nk) time after sorting.

If more than one agent wants to minimize its sum of completion times, while the others’ objectives are makespan minimization, e.g. the two agents h and \(\ell \) in

$$\begin{aligned} \text{ Problem }\quad \left( C_{\max }^1, \ldots , \sum C_j^h, C_{\max }^{h+1}, \ldots , \sum C_j^{\ell }, C_{\max }^{\ell +1},\ldots , C_{\max }^{k}\right) , \end{aligned}$$

then this problem is a generalization of the two agent problem \(\left( \sum C_j^1,\sum C_j^2\right) \). It was shown in Nicosia et al. (2015, Theorem 5) that there are exponentially many PO solutions for this problem, which holds a fortiori for the above k-agent problem. Moreover it was shown in Nicosia et al. (2015, Theorem 6) that it is \({\mathcal {NP}}\)-complete to answer the corresponding recognition problem.

Finally, we consider the case in which one agent h with weights \(w_j\) wants to minimize its sum of weighted completion times while the objective of all the others is makespan minimization, i.e.

$$\begin{aligned} \text{ Problem } \quad \left( C_{\max }^1, \ldots , C_{\max }^{h-1}, \sum w_j\, C_j^h, C_{\max }^{h+1}, \ldots , C_{\max }^{k}\right) . \end{aligned}$$

It suffices to refer to Proposition 3 in Nicosia et al. (2015), where it was shown that even problem \((C_{\max }^1,\sum w_j\,C_j^2)\) has exponentially many solutions and its decision version is \({\mathcal {NP}}\)-complete. Thus, the same negative results hold if one or more agents minimize their sum of weighted completion times while the other agents minimize their makespan.

5 Perspective of a single agent against \(k-1\) opponents

Considering the behavior of one particular agent, say \(h \in \{1,\ldots ,k\}\), we analyze the outcome of its objective function if agent h follows the classical heuristics SPT and WSPT, which are known to yield optimal schedules for the corresponding single agent scheduling problems. Moreover, SPT is a natural strategy for the given decision rule in each round.

We proceed to perform a worst-case analysis for the objective function of the schedule an agent h attains, when its tasks are submitted by a certain standard, single-agent heuristic algorithm H. Of course, the schedule obtained by H depends heavily on the behavior of the other \(k-1\) agents. More formally, we impose that each agent i follows a certain deterministic algorithm which outputs in each round the next task for submission. The algorithm may use as input in each round the submissions and outcomes of all previous rounds.Footnote 3 From a worst-case perspective a heuristic H of agent h should perform well against any combination of algorithms applied by the other agents. Therefore, we consider for each \((k-1)\)-tuple of algorithms pursued by the other \(k-1\) agents the loss incurred for agent h by following H instead of a best possible response against this \((k-1)\)-tuple. Then we consider the maximum of such a loss over all possible combinations of algorithms chosen by the other agents. Such an analysis is closely related to the performance ratio studied for on-line algorithms.

Let \({\mathcal {A}}^i\) be the set of all possible algorithms for agent i. For every k-tuple of algorithms \((a^1, \ldots , a^k) \in {\mathcal {A}}^1 \times \cdots \times {\mathcal {A}}^k\) followed by the agents, let \(\sigma (a^1, \ldots , a^k)\) denote the resulting schedule. In the following we analyze the value of the performance ratio (representing the loss) of a certain heuristic algorithm \(H\in {\mathcal {A}}^h\) applied by agent h with an objective function \(f^h\):

$$\begin{aligned} \rho (H) \le {\mathop {\mathop {\max }\limits _{a^i\in {\mathcal {A}}^i}}\limits _{i\ne h}} \left\{ \frac{f^h\left( \sigma \left( a^1, \ldots , a^{h-1},H, a^{h+1},\ldots , a^k\right) \right) }{\min _{a^h\in {\mathcal {A}}^h}\left\{ f^h\left( \sigma \left( a^1, \ldots , a^h, \ldots , a^k\right) \right) \right\} } \right\} \end{aligned}$$
(2)

Note that the maximum in (2) is taken over all \((k-1)\)-tuples of algorithms for the competitors of h and the expression to be maximized is the loss, i.e. the ratio between the outcome for agent h produced by algorithm H and the outcome reached by the best response of h, which is the minimum objective over all algorithms \(a^h\) for h against the same \((k-1)\)-tuple of competing algorithms.

As usual, we call a performance bound \(\rho (H)\) tight, if no larger value than \(\rho (H)\) exists which fulfills (2). In this section we mainly provide bounds for \(\rho (SPT)\) and also extend them for \(\rho ({ WSPT})\). For the special case \(k=2\) the derived bounds of Theorems 3–5 coincide with the corresponding results of Nicosia et al. (2015, Sect. 4).

For each task \(p_j^h\) of agent h we define an agent \(h_j\) such that \(h_j := \max \{i \mid p_n^i \le p_j^h, i=1,\ldots ,h-1\}\), i.e. all tasks of agents \(1,\ldots , h_j\) are smaller than or equal to \(p_j^h\) and thus win against \(p_j^h\) in any case. Now we state a fairly rough but sufficient bound on the completion times obtained from the SPT heuristic.

Lemma 1

Against any combination of algorithms employed by \(k-1\) agents the SPT algorithm of agent h attains a completion time for task \(p_j^h\)

$$\begin{aligned} \tilde{C}_j^h \le \sum _{r=1}^j p_r^h + \sum _{i=1}^{h_j} \sum _{r=1}^n p_r^i + (k-1)(n-1) p_j^h. \end{aligned}$$

Proof

In a worst-case scenario for the SPT algorithm of agent h, every task \(p_j^h\) might be preceded by all tasks with length at most \(p_j^h\), since tasks with length greater than \(p_j^h\) cannot be scheduled before \(p_j^h\) by the SPT rule. This means that task \(p_j^h\) might be preceded by all tasks of agents \(1, \ldots , h_j\) and by the at most \(n-1\) tasks of length at most \(p_j^h\) of all other agents. These can be \(k-1\) agents in the worst case, i.e. when \(h_j=0\). \(\square \)

Theorem 3

For \(f^h=C_{\max }^h\) the SPT algorithm for agent h has the performance ratio

$$\begin{aligned} \rho (SPT) = n (k-1) -k+2. \end{aligned}$$

Proof

A simple lower bound on the objective function value of h is given by

$$\begin{aligned} z^h \ge \sum _{r=1}^n p_r^h + \sum _{i=1}^{h_n} \sum _{r=1}^{n} p_r^i \end{aligned}$$
(3)

since all tasks of agent h have to be processed and no algorithm of h can avoid that all tasks of agents 1 to \(h_n\) precede task \(p_n^h\). In the worst case we might have by Lemma 1:

$$\begin{aligned} z^h_{SPT} = \tilde{C}_n^h\le & {} \sum _{r=1}^{n-1} p_r^h + p_n^h + \sum _{i=1}^{h_n} \sum _{r=1}^n p_r^i + (k-1)(n-1) p_n^h \\= & {} \sum _{r=1}^{n-1} p_r^h + ((k-1)n - k +2 )\, p_n^h + \sum _{i=1}^{h_n} \sum _{r=1}^n p_r^i\\\le & {} ((k-1)n - k +2 ) z^h \end{aligned}$$

To show that this bound is tight we use the following instance with \(h=1\), for some large value M:

$$\begin{aligned} p_j^1 = \left\{ \begin{array}{l@{\quad }l} 1 &{}\ j=1\\ 2&{}\ j=2,\ldots ,n-1\\ M&{}\ j=n\end{array}\right. \quad p_j^i = \left\{ \begin{array}{l@{\quad }l} M-1&{}\ j=1,\ldots ,n-1\\ M+1&{}\ j=n\end{array}\right. \ i =2, \ldots , k \end{aligned}$$

We define the following algorithm \(\tilde{a}\) executed by all agents \(i=2, \ldots , k\). Submit the shortest task in the first round. In the second round the following (arguable quite strange) decision takes place: If the winner of the first round won with its smallest task, then proceed by submitting the shortest remaining task in all subsequent rounds (SPT). If the winner of the first round won with any other tasks, then proceed by submitting the longest remaining task in all subsequent rounds (LPT). Of course, \(\tilde{a}\) is not a very attractive algorithm but serves only for showing the tightness of the bound.

The instance is now processed as follows: The SPT algorithm of agent 1 submits \(p_1^1\) in the first round and wins. As a reaction algorithm \(\tilde{a}\) decides for all agents \(i=2, \ldots , k\) to perform SPT as well. Thus, agent 1 wins also the next rounds and schedules its tasks 2 to \(n-1\). Then agents \(i=2, \ldots , k\) win with all their tasks of length \(M-1\). Finally, agent 1 wins with \(p_n^1\) against all \(p_n^i\). This yields the following completion time \(\tilde{C}_n^1\) for the last task of agent 1:

$$\begin{aligned} \tilde{C}_n^1 = 1+(n-2)2+(k-1)(n-1)(M-1) + M \approx (n(k-1) -k +2)M + o(M) \end{aligned}$$

A best response algorithm of agent 1 against \(\tilde{a}\) would submit \(p_2^1\) in the first round and win against all \(p_1^i\). This causes \(\tilde{a}\) to change to LPT. Thus, all agents \(2, \ldots , k\) submit their task n with \(p_n^i=M+1\) in the following rounds allowing agent 1 to win and schedule all its tasks (by any algorithm) which yields

$$\begin{aligned} C_n^1 = 2 +1 + (n-3)2 + M \approx M + o(M), \end{aligned}$$

while all \(C_j^1\) are of order o(M) for \(j<n\). Thus, we obtain the desired bound for \(M\rightarrow \infty \) for the minimization of \(C^1_{\max }\). \(\square \)

Theorem 4

For \(f^h=\sum _j C^h_{j}\) the SPT algorithm for agent h has the performance ratio

$$\begin{aligned} \rho (SPT) = n (k-1) -k+2. \end{aligned}$$

Proof

As a lower bound for the objective function value we use

$$\begin{aligned} z^h \ge \sum _{j=1}^n \sum _{r=1}^j p_r^h + \sum _{j=1}^n \sum _{i=1}^{h_j} \sum _{r=1}^n p_r^i =\sum _{j=1}^n \left( \underbrace{\sum _{r=1}^{j-1} p_r^h + \sum _{i=1}^{h_j} \sum _{r=1}^n p_r^i + p_j^h}_{=:\,D_j^h}\right) , \end{aligned}$$
(4)

where the first term is the optimal solution derived from the SPT heuristic considering only tasks of agent h. The second term captures the fact that all tasks of agents \(1, \ldots , h_j\) will precede task \(p_j^h\) in any solution.

With Lemma 1 we can compare the completion time of each task \(p_j^h\) obtained by the SPT heuristic to \(D_j^h\):

$$\begin{aligned} \tilde{C}_j^h\le & {} \sum _{r=1}^j p_r^h + \sum _{i=1}^{h_j} \sum _{r=1}^n p_r^i + (k-1)(n-1) p_j^h\nonumber \\\le & {} \sum _{r=1}^{j-1} p_r^h + \sum _{i=1}^{h_j} \sum _{r=1}^n p_r^i + ((k-1)(n-1)+1) p_j^h\nonumber \\\le & {} ((k-1)(n-1)+1) D_j^h \end{aligned}$$
(5)

Together with (4) this proves the performance bound since \(z^h_{SPT} = \sum _{j=1}^n \tilde{C}_j^h\).

The tightness of the bound follows from exactly the same instance and the same algorithm \(\tilde{a}\) as given in the proof of Theorem 3. \(\square \)

Theorem 5

For \(f^h=\sum _j w_j\, C^h_{j}\) the SPT algorithm for agent h has the performance ratio

$$\begin{aligned} \rho (SPT) = (n-1 )k +1. \end{aligned}$$

Proof

By a similar argument as used in (4) we can give a rough bound on the completion time \(C_j^h\) of a task \(p_j^h\) in any schedule resulting from the considered decision scenario:

$$\begin{aligned} C_j^h \ge p_j^h + \sum _{i=1}^{h_j} \sum _{r=1}^n p_r^i\,. \end{aligned}$$
(6)

Again with Lemma 1 we can bound the completion time \(\tilde{C}_j^h\) of any task \(p_j^h\) in the solution derived from the SPT algorithm:

$$\begin{aligned} \tilde{C}_j^h\le & {} \sum _{r=1}^{j} p_r^h + \sum _{i=1}^{h_j} \sum _{r=1}^n p_r^i + (k-1)(n-1) p_j^h \\\le & {} (j + (k-1)(n-1)) p_j^h +\sum _{i=1}^{h_j} \sum _{r=1}^n p_r^i \\\le & {} (k(n-1) +1) C_j^h \end{aligned}$$

Plugging in this estimate for every \(C_j^h\) yields the stated performance ratio.

For showing the tightness of the bound we use the following instance with \(h=1\) for large M and a small constant \(\varepsilon >0\):

$$\begin{aligned} p_j^1 = \left\{ \begin{array}{l@{\quad }l} M\;&{} j=1,\ldots ,n-1\\ M+1\;&{} j=n\end{array}\right. \quad p_j^i = \left\{ \begin{array}{l@{\quad }l} M-1\;&{} j=1,\ldots ,n-1\\ M+2\;&{} j=n\end{array}\right. \ i =2, \ldots , k \end{aligned}$$

For agent 1 we also have weights \(w_j=\varepsilon \) for \(j=1,\ldots ,n-1\) and \(w_n=M\).

All agents \(i=2, \ldots , k\) execute algorithm \(\tilde{a}'\) which is a minor modification of \(\tilde{a}\) described in the proof of Theorem 3. Algorithm \(\tilde{a}'\) starts by submitting the longest task in the first round. Then it proceeds exactly as \(\tilde{a}\) with the same decision between SPT or LPT.

Processing the above instance the SPT algorithm of agent 1 submits \(p_1^1\) in the first round and wins against the \(p_n^i\) tasks. Now algorithm \(\tilde{a}'\) decides for all agents \(i=2, \ldots , k\) to perform SPT. Thus, agent 1 loses with its task \(p_2^1\) against all tasks of length \(M-1\) and can schedule its tasks only before the tasks \(p_n^i\). Since \(\varepsilon \) can be chosen arbitrarily small, the objective of agent 1 only depends on \(\tilde{C}_n^1\) which can be calculated as

$$\begin{aligned} \tilde{C}_n^1= & {} M + (k-1)(n-1)(M-1) + (n-2)M + M+1 \\\approx & {} (k(n-1)+1)M + o(M). \end{aligned}$$

A best response algorithm of agent 1 against \(\tilde{a}'\) would submit \(p_n^1\) in the first round and win against all \(p_n^i\), \(i\ge 2\), yielding \(C_n^1 = M+1\). This settles the case and proves the lower bound since the remaining schedule is irrelevant because of the given weights. \(\square \)

Theorem 6

For \(f^h=\sum _j w_j\, C^h_{j}\) the WSPT algorithm for agent h has the performance ratio

$$\begin{aligned} \rho ({ WSPT}) \le n (k-1) -k+2. \end{aligned}$$

Proof

It is easy to see that also after sorting the tasks of agent h by the WSPT rule and renumbering them accordingly while leaving the tasks of the other agents in the given nondecreasing order, the completion times produced by the WSPT heuristic can still be bounded by the same expression as given in Lemma 1.

Now it suffices to repeat the arguments of the proof of Theorem 4. The lower bound (4) holds verbatim for the objective function value of minimizing \(\sum _j w_j C_j\) after renumbering the tasks of agent h according to the WSPT rule. Since the bounds on the completion times derived in (5) work exactly as before we immediately reach the same performance ratio as above.

The lower bound example can be taken from the proof of Theorem 3 by simply setting \(w_j=1\) for all j. By this choice SPT and WSPT coincide and also the objective function values remain unchanged. \(\square \)

6 Conclusions

In this paper we studied a multi-agent scheduling problem where the operator of a single machine iteratively selects the next task to be processed from a set of tasks submitted by the agents. This work adopts the same setting considered in Nicosia et al. (2015) for the two agents case, generalizing its results to any number k of agents.

The situation described in this paper could also be viewed in a game-theoretic setting, in which the algorithms induce strategies for the agents and each solution of the problem determines the corresponding agents’ payoffs. Thus, we could also apply the concepts of extensive games with a decision tree. Note that in our case, the special form with simultaneous moves would apply (see e.g. Osborne 2004, Sect. 7.1) since all the k agents submit their tasks in parallel. In this framework, determining an optimal strategy of a single agent, assuming that also the other agents may follow a selfish optimal strategy, can be done by backward induction, but it requires exponential time in general. This situation was studied for other combinatorial optimization problems and two agents, e.g. in Darmann et al. (2016). When dealing with k-agent scheduling, it would be interesting to identify polynomially solvable special cases, either by restricting the scheduling environment or the agents’ strategies.