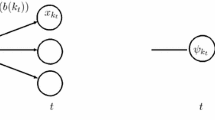Decomposition methods for multi-horizon stochastic programming

Abstract

Multi-horizon stochastic programming includes short-term and long-term uncertainty in investment planning problems more efficiently than traditional multi-stage stochastic programming. In this paper, we exploit the block separable structure of multi-horizon stochastic linear programming, and establish that it can be decomposed by Benders decomposition and Lagrangean decomposition. In addition, we propose parallel Lagrangean decomposition with primal reduction that, (1) solves the scenario subproblems in parallel, (2) reduces the primal problem by keeping one copy for each scenario group at each stage, and (3) solves the reduced primal problem in parallel. We apply the parallel Lagrangean decomposition with primal reduction, Lagrangean decomposition and Benders decomposition to solve a stochastic energy system investment planning problem. The computational results show that: (a) the Lagrangean type decomposition algorithms have better convergence at the first iterations to Benders decomposition, and (b) parallel Lagrangean decomposition with primal reduction is very efficient for solving multi-horizon stochastic programming problems. Based on the computational results, the choice of algorithms for multi-horizon stochastic programming is discussed.

1 Introduction

Multi-horizon stochastic programming (MHSP) is a powerful modelling approach that can include long-term and short-term uncertainty for long-term investment planning problems with much smaller model size than traditional multi-stage stochastic programming (Kaut et al. 2014). MHSP was further formalised in Escudero and Monge (2018). In addition, the bounds and formulation of MHSP have been studied (Maggioni et al. 2020). The literature on MHSP is much more sparse compared with multi-stage stochastic programming. Existing literature mainly centres around the application of MHSP for long-term investment planning problems, especially in energy system planning (Zhang et al. 2022; Backe et al. 2022). The applications show that although MHSP reduces the problem size, the monolithic model can still be hard to solve. Therefore, in this paper, we extend the literature by proposing and comparing decomposition algorithms for MHSP.

Fewer decomposition methods for MHSP have been proposed. Mazzi et al. (2021) proposed adaptive Benders decomposition to solve large-scale optimisation problems with column bounded block-diagonal structure, where subproblems differ in right-hand side and cost coefficients. MHSP belongs to this class of optimisation problems if it is formulated using a node formulation and the operational scenarios are identical in all nodes. They apply the adaptive Benders decomposition to solve a stochastic investment planning problem, and show that the computational time reduces significantly. The limitation of Mazzi et al. (2021) is that adaptive Benders cannot solve problems where operational scenarios are different in each node. Zhang et al. (2022) proposed stabilised adaptive Benders decomposition to solve MHSP, and apply it to solve a large-scale power system planning problem. Furthermore, Zhang et al. (2023) proposed centre point stabilised adaptive Benders decomposition for solving large scale problem with integer variables. The existing literature only has focused on developing Benders type decomposition utilising the node formulation of MHSP. Decomposition algorithms that utilise the scenario formulation of MHSP are missing in the literature.

In this paper, we propose Parallel Lagrangean decomposition with Primal Reduction (PLPR) to solve linear programming based MHSP with a scenario formulation. In addition, we show that scenario based MHSP can be decomposed by Lagrangean decomposition. Compared with Lagrangean decomposition, the PLPR solves the scenario subproblem in parallel, and reduces the primal problem by keeping one copy in each scenario group at each stage, and solves the primal problem in parallel. The choice of Lagrangean type decomposition and Benders type decomposition is not clear for MHSP. Therefore, we apply Lagrangean decomposition, Benders decomposition and PLPR to solve MHSP problem instances to provide some computational insights.

The following assumptions are made in this paper: (1) each operational problem can be solved using commercial linear programming solvers, (2) the operational problem in each strategic node has several scenarios but not a multi-stage stochastic programming problem itself, and (3) the problem has relatively complete recourse at every stage.

We apply the proposed algorithms to solve the REORIENT model (Zhang et al. 2023). The REORIENT model is an MHSP proposed for integrated energy system planning considering investment, retrofit and abandonment. In this paper, we turn off the retrofit and abandonment options. Therefore, the problem instances only have continuous variables.

The contributions of this paper are the following: (1) it is the first paper formalising and proposing decomposition methods based on node formulation and scenario formulation of MHSP, (2) PLPR is proposed to utilise the special structure of MHSP to potentially reduce computational time significantly, and (3) the performance of Benders decomposition and Lagrangean decomposition is compared and analysed.

The outline of the paper is as follows: Sect. 2 provides definition of MHSP and highlight the differences between MHSP and traditional multi-stage stochastic programming. Section 3 first introduces a node formulation of MHSP and formalises that it can be decomposed by Benders type algorithms. Section 4 provides a scenario formulation of MHSP, and shows that MHSP can be decomposed by Lagrangean decomposition. Section 5 proposes the PLPR algorithm. Section 6 presents the stochastic investment planning model used in the case study. Section 7 reports the computational results and numerical analysis. Section 8 discusses the implications of the method and results and summarises the limitations of the research. Section 9 concludes the paper and suggests further research.

2 MHSP and multi-stage stochastic programming

MHSP is a modelling approach for stochastic programming with short-term and long-term uncertainty. The spirit of MHSP is to branch only based on long-term uncertainty between the long-term stages. The operational nodes can be seen as embedded into their respective long-term nodes. This is based on the assumption that long-term decisions typically do not depend directly on any particular short-term scenario but rather on the overall short-term problem during the time since the previous long-term decisions. In this way, the short-term nodes that are embedded in a long-term node can be treated as a block. Therefore, MHSP has a block separable property that can be exploited for efficient decomposition algorithms.

On the contrary, in traditional multi-stage stochastic programming, the scenario tree is branched based on both long-term and short-term uncertainty. This leads to a larger scenario tree. Also, nested Benders decomposition is needed to decompose traditional multi-stage stochastic programming under short-term and long-term uncertainty (Birge 1985). A comparison between the MHSP and traditional multi-stage stochastic programming is presented in Fig. 1. Note that here, the short-term uncertainty embedded in the long-term node is revealed only once. However, the short-term problem can be a multi-stage stochastic programming itself. In this paper, we consider the case where the short-term uncertainty reveals only once in its embedded long-term node.

Fig. 1

Comparison between a multi-stage stochastic programming and b MHSP. (blue circles: strategic nodes, red squares: operational periods)

3 Benders decomposition

In this section, we first describe a general node formulation of MHSP, and show that it can be decomposed using Benders decomposition. An illustration of the node formulation of MHSP is presented in Fig. 1b, the blue circles represent strategic nodes and red squares represent operational nodes. We then explain that due to the special structure of MHSP, Benders can be directly applied for solving multi-stage stochastic programming. Traditionally, multi-stage stochastic programming is usually solved using nested Benders decomposition (Birge 1985).

When formulating MHSP using a node formulation, the non-anticipativity constraints are not expressed explicitly. Instead, indices are used to denote the ancestor node of a node in the scenario tree. We denote the strategic decision nodes by $i \in {\mathcal {I}}$, and the set of strategic decision nodes k that are ancestors to a decision node i by ${\mathcal {I}}_{i}$. The ${\mathcal {S}}_i$ denotes the set of operational scenarios that are embedded in strategic node i. The set of operational stages is represented by ${\mathcal {T}}_i$. The superscripts indicate the type of nodes that vectors and matrices belong to. The subscripts are the indices. The $x_i$ are the strategic decision variables, and $y_{its}$ are the operational variables. The deterministic equivalent of the linear programming MHSP is defined as a full master problem given by Eqs. (1).

$$\begin{aligned}&\min _{x_{i}, y_{its}}{} & {} \sum _{i \in {\mathcal {I}}} \pi _{i}\left( c_{i}^{\top }x_{i} + \sum _{s \in {\mathcal {S}}_i}\omega _{is} \sum _{t \in {\mathcal {T}}_i}q_{its}^{\top }Q_{its}y_{its}\right) \end{aligned}$$

(1a)

$$\begin{aligned}&\text {s.t.}{} & {} T^{I}_{k}x_{k} + W^{I}_i x_i \le h^{I}_i,&\quad i \in {\mathcal {I}} \setminus \{1\}, k \in {\mathcal {I}}_i, \end{aligned}$$

(1b)

$$\begin{aligned}&\quad{} & {} T^{0} x_i \le h^{0},&\quad i =1, \end{aligned}$$

(1c)

$$\begin{aligned}&\quad{} & {} T^O_{its} x_i + W^O_{its} y_{its} \le h^{O}_{its},&\quad i \in {\mathcal {I}}, t=1, s \in {\mathcal {S}}_i, \end{aligned}$$

(1d)

$$\begin{aligned}&\quad{} & {} T^O_{its} y_{i(t-1)s} + W^O_{its} y_{its} \le h^{O}_{its},& \quad i \in {\mathcal {I}}, t \in {\mathcal {T}}_i \setminus \{1\}, s \in {\mathcal {S}}_i, \end{aligned}$$

(1e)

$$\begin{aligned}&\quad{} & {} x \ge 0, y \ge 0,&\end{aligned}$$

(1f)

where x and y include all variables $x_i$ and $y_{its}$, and where $\pi _i$ is the probability of strategic node i, sum of $\pi _i$ in each strategic stage is equal to 1, $c_i \in {\mathbb {R}}^{n_i}$, $h^I_i \in {\mathbb {R}}^{m_i}$, $W^I_i \in {\mathbb {R}}^{m_i \times n_i}$, are vectors and matrices at strategic node $i \in {\mathcal {I}}$, and $T^I_k \in {\mathbb {R}}^{m_i \times n_k}$ is the matrix for its ancestor nodes $k \in {\mathcal {I}}_i$. We assume that if $i=1$, then $T^I_k=T^0$, $W^I_i=0$, and $h^I_i=h^0$. The probability of operational scenario s that is embedded in strategic node i is denoted by $\omega _{is}$, and $\sum _{s \in {\mathcal {S}}_{i}} \omega _{is}=1$. Operational vectors and matrices at operational node i, in operational scenario s, operational stage t are given by $T^O_{its} \in {\mathbb {R}}^{m_{it} \times n_{it}}$, $W^O_{its} \in {\mathbb {R}}^{m_{it} \times n_{it}}$, $q_{its} \in {\mathbb {R}}^{n_{it}}$, $h^{O}_{its} \in {\mathbb {R}}^{n_{it}}$. For operational stage $t=1$, we have $T^{O}_{i1s} \in {\mathbb {R}}^{m_{i1} \times n_{i}}$. Equations (1) provide a general mathematical formulation for MHSP.

By fixing the complicating variable $x_i$, we can decompose the full size problem using Benders decomposition. The Benders reduced master problem is as follows,

$$\begin{aligned}&\min _{x_i}{} & {} \sum _{i \in {\mathcal {I}}} \pi _{i}\left( c_{i}^{\top }x_{i} + \beta _i\right) \end{aligned}$$

(2a)

$$\begin{aligned}&\text {s.t.}{} & {} T^{I}_{k}x_{k} + W^{I}_i x_i \le h^{I}_i,&\quad i \in {\mathcal {I}} \setminus \{1\}, k \in {\mathcal {I}}_i, \end{aligned}$$

(2b)

$$\begin{aligned}&\quad{} & {} T^{0} x_i \le h^{0},&\quad i =1, \end{aligned}$$

(2c)

$$\begin{aligned}&\quad{} & {} \beta _{i} \ge \theta + \lambda ^{\top }(x_{i}-x),&\quad (x,\theta ,\lambda ) \in {\mathcal {F}}_{i(j-1)}, i \in {\mathcal {I}}, \end{aligned}$$

(2d)

$$\begin{aligned}&\quad{} & {} x \ge 0,&\end{aligned}$$

(2e)

where Constraint (2d) are the projected cuts added to the Benders reduced master problem until iteration $j-1$, $\beta _i$ is a variable for the approximated cost of the operational problem that is embedded in strategic node i. The set of cutting planes associated with subproblem i built up to iteration $j-1$ is denoted by ${\mathcal {F}}_{i(j-1)}$. The $\theta$ collects the optimal objective value of each subproblem i until iteration $j-1$. The subgradient w.r.t. $x_{ij}$ until iteration $j-1$ is collected by $\lambda$. The sampled points until iteration $j-1$ are denoted by x.

For a given node i, the Benders subproblem is formulated as

$$\begin{aligned}&\min _{y_{its }}{} & {} \pi _{i}\sum _{s \in {\mathcal {S}}_i}\omega _{is}q_{its}^{\top }Q_{its}y_{its} \end{aligned}$$

(3a)

$$\begin{aligned}&\text {s.t.}{} & {} T^O_{its} x_i + W^O_{its} y_{its} \le h^{O}_{its},& \quad i \in {\mathcal {I}}, t=1, s \in {\mathcal {S}}_i, \end{aligned}$$

(3b)

$$\begin{aligned}&\quad{} & {} T^O_{its} y_{i(t-1)s} + W^O_{its} y_{its} \le h^{O}_{its},& \quad i \in {\mathcal {I}}, t \in {\mathcal {T}}_i \setminus \{1\}, s \in {\mathcal {S}}_i, \end{aligned}$$

(3c)

$$\begin{aligned}&\quad{} & {} y \ge 0,&\end{aligned}$$

(3d)

and the Benders subproblems can be solved in parallel.

Traditionally, a stochastic linear program with multiple stages is formulated as a multi-stage stochastic program (Birge and Louveaux 2011), and then such a problem can be decomposed and solved using nested Benders decomposition. Here we show that by exploiting the special structure of MHSP, we can decompose the problem using classic Benders decomposition (Benders 1962) to solve multi-stage stochastic programs. In the Benders reduced master problem, we solve for all strategic nodes, and the operational problems are the Benders subproblems. In addition, if $W^{O}_{ist}$ is the same in all nodes, and the operational problem has certain properties, one can improve Benders decomposition by avoiding solving all operational problems at each iteration, such as the adaptive Benders decomposition (Mazzi et al. 2021; Zhang et al. 2022). These approaches also utilise the property of MHSP that Benders subproblems are independent.

The Benders decomposition is presented in Algorithm 1.

Remark 1

The block separable structure of MHSP enables the application of two-stage Benders to solve a multi-stage stochastic programming problem.

Proof

MHSP is block separable due to the fact that the blocks of short-term nodes (red squares in Fig. 1b) are independent from each other.

Following the proposition in Louveaux (1986), MHSP with short-term and long-term uncertainty is equivalent to a two-stage stochastic program where the first stage is the long-term problem involves only the long-term decisions and the value function of the second stage is the probability weighted sum of the short-term recourse function.

Therefore, a two-stage Benders decomposition can be applied to solve MHSP, where the master problem includes all the long-term nodes, and the blocks of short-term nodes are independent subproblems. $\square$

4 Lagrangean decomposition

MHSP can also be formulated in a scenario based formulation. It can then be decomposed by Lagrangean decomposition. When the problem is large, Benders decomposition may have a larger and more ill-conditioned master problem and be hard to converge. In such a case, Lagrangean decomposition may be preferred.

4.1 Scenario formulation for MHSP

Here, we present a scenario formulation for MHSP. We denote the set of strategic stages by $h \in {\mathcal {H}}$, and the set of strategic scenarios by $v \in {\mathcal {S}}^{I}$. The set of operational scenarios is denoted by $s \in {\mathcal {S}}^{O}_{hv}$, and the set of operational stages is denoted by $t \in {\mathcal {T}}^{O}_{hv}$. We define set ${\mathcal {J}}:=\{(h,v,v^{\prime }): h \in {\mathcal {H}}, v, v^{\prime } \in {\mathcal {S}}^{I}, v \text { and } v^{\prime } \text { are indistinguishable in strategic stage}\, h\}$ for formulating the Non-Anticipativity Constraint (NAC). Variables $x_{hv}$ and $y_{hvts}$ are the investment and operational variables respectively. The mathematical formulation of the full size problem is given as follows,

$$\begin{aligned}&\min _{x_{hv}, y_{hvts}}{} & {} {\sum _{v \in {\mathcal {S}}^{I}} \pi _{v}\left( \sum _{h \in {\mathcal {H}}}\left( c_{hv}^{\top }x_{hv} + \sum _{s \in {\mathcal {S}}^{O}_{hv}}\omega _{hvs} \sum _{t \in {\mathcal {T}}^{O}_{hv}}q_{hvts}^{\top }Q_{hvts}y_{hvts}\right) \right) }&\end{aligned}$$

(4a)

$$\begin{aligned}&\text {s.t.}{} & {} T^{I}_{(h-1)v}x_{(h-1)v} + W^{I}_{hv} x_{hv} \le h^{I}_{hv},& \quad h \in {\mathcal {H}} \setminus \{1\}, \quad v \in {\mathcal {S}}^{I}, \end{aligned}$$

(4b)

$$\begin{aligned}&\quad{} & {} T^{0} x_{hv} \le h^{0},&\quad h =1, \quad v \in {\mathcal {S}}^{I}, \end{aligned}$$

(4c)

$$\begin{aligned}&\quad{} & {} T^O_{hvts} x_{hv} + W^O_{hvts} y_{hvts} \le h^{O}_{hvts},&\quad h \in {\mathcal {H}}, \quad v \in {\mathcal {S}}^{I}, \quad t=1, s \in {\mathcal {S}}^{O}_{hv}, \end{aligned}$$

(4d)

$$\begin{aligned}&\quad{} & {} T^O_{hvts} y_{hv(t-1)s} + W^O_{hvts} y_{hvts} \le h^{O}_{hvts},&h \in {\mathcal {H}}, \quad v \in {\mathcal {S}}^{I}, t \in {\mathcal {T}}^{O}_{hv} \setminus \{1\}, s \in {\mathcal {S}}^{O}_{hv}, \end{aligned}$$

(4e)

$$\begin{aligned}&\quad{} & {} x_{hv}=x_{hv^{\prime }},&\quad (h, v, v^{\prime }) \in {\mathcal {J}}, \end{aligned}$$

(4f)

$$\begin{aligned}&\quad{} & {} x \ge 0, y \ge 0,&\end{aligned}$$

(4g)

where x and y include all variables $x_{hv}$ and $y_{hvts}$, and where $\pi _{v}$ is the probability of strategic scenario v, sum of $\pi _v$ is equal to 1, $c_{hv} \in {\mathbb {R}}^{n_{hv}}$, $h^I_{hv} \in {\mathbb {R}}^{m_{hv}}$, $W^I_v \in {\mathbb {R}}^{m_{hv} \times n_{hv}}$, are vectors and matrices for strategic stage $h \in {\mathcal {H}}$, scenario $v \in {\mathcal {S}}^{I}$, and $T^I_{(h-1)v} \in {\mathbb {R}}^{m_{hv} \times n_{hv}}$ is the matrix for its previous stage. We assume that if $h=1$, $T^I_{hv}=T^0$, $W^I_{hv}=0$, and $h^I_{hv}=h^0$. The probability of operational scenario s is denoted by $\omega _{hvs}$, and $\sum _{s \in {\mathcal {S}}^{O}_{hv}} \omega _{hvs}=1$. Operational vectors and matrices in strategic stage h, strategic scenario v, operational stage t, operational scenario s, are given by $T^O_{hvts} \in {\mathbb {R}}^{m_{vt} \times n_{vt}}$, $W^O_{hvts} \in {\mathbb {R}}^{m_{hvts} \times n_{vt}}$, $q_{hvts} \in {\mathbb {R}}^{n_{vt}}$, $h^{O}_{hvts} \in {\mathbb {R}}^{n_{vt}}$. For operational stage $t=1$, we have $T^{O}_{hv1s} \in {\mathbb {R}}^{m_{v1} \times n_{v}}$. Equations (4) correspond to a general scenario based mathematical formulation for MHSP. Equation (4f) is the NAC. Note that due to the properties of the MHSP, operational decisions are independent of future strategic scenarios, and the operational decision variables are embedded in the strategic node. Therefore, NAC is not needed for operational decisions. We denote the full size scenario based formulation, Eqs. (4), by Lagrangean master problem. The NACs, Eq. (4f), are the complicating constraints that link the scenarios. An illustration of the scenario formulation for MHSP is presented in Fig. 2.

Fig. 2

Illustration of scenario formulation for MHSP (blue circles: strategic nodes, red squares: operational periods). The blue dashed lines represent the NAC

By relaxing Eq. (4f), one can obtain the Lagrangean dual. The problem, given by the Eqs. (4), is then decomposed by scenarios. The Lagrangean dual is as follows,

$$\begin{aligned}&\min _{x_{hv}, y_{hvts}}{} & {} {\sum _{v \in {\mathcal {S}}^{I}} \pi _{v}\left( \sum _{h \in {\mathcal {H}}}\left( c_{hv}^{\top }x_{hv} + \sum _{s \in {\mathcal {S}}^{O}_{hv}}\omega _{hvs} \sum _{t \in {\mathcal {T}}^{O}_{hv}}q_{hvts}^{\top }Q_{hvts}y_{hvts})\right) \right) } -&\nonumber \\&\quad{} & {} {\sum _{(h,v,v^{\prime })\in {\mathcal {J}}}\lambda ^{\top }_{hvv^{\prime }}(x_{hv}-x_{hv^{\prime }})}&\end{aligned}$$

(5a)

$$\begin{aligned}&\text {s.t.}{} & {} T^{I}_{(h-1)v}x_{(h-1)v} + W^{I}_{hv} x_{hv} \le h^{I}_{hv},&\quad h \in {\mathcal {H}} \setminus \{1\}, v \in {\mathcal {S}}^{I}, \end{aligned}$$

(5b)

$$\begin{aligned}&\quad{} & {} T^{0} x_{hv} \le h^{0},&\quad h =1, v \in {\mathcal {S}}^{I}, \end{aligned}$$

(5c)

$$\begin{aligned}&\quad{} & {} T^O_{hvts} x_{hv} + W^O_{hvts} y_{hvts} \le h^{O}_{hvts},&\quad h \in {\mathcal {H}}, \quad v \in {\mathcal {S}}^{I}, \quad t=1, \quad s \in {\mathcal {S}}^{O}_{hv}, \end{aligned}$$

(5d)

$$\begin{aligned}&\quad{} & {} T^O_{hvst} y_{hv(t-1)s} + W^O_{hvts} y_{hvts} \le h^{O}_{hvts},&\quad h \in {\mathcal {H}}, v \in {\mathcal {S}}^{I}, \quad t \in {\mathcal {T}}^{O}_{hv} \setminus \{1\}, \quad s \in {\mathcal {S}}^{O}_{hv}, \end{aligned}$$

(5e)

$$\begin{aligned}&\quad{} & {} x \ge 0, \quad y \ge 0,&\end{aligned}$$

(5f)

where $\lambda _{hvv^{\prime }}$ is the Lagrangean multiplier. The Lagrangean dual can be solved per scenario $v \in {\mathcal {S}}^{I}$ in parallel. We use the subgradient method to update the Lagrangean multiplier. The Lagrangean decomposition algorithm is presented in Algorithm 2. A bottleneck strategy is used to construct a feasible solution from the relaxed solutions. When restoring the NAC constraint for a group of scenarios, the decision variable $x_{hv}$ in all scenarios are forced to take the relaxed solution from the scenario with the largest uncertain cost coefficients and the smallest absolute uncertain right hand side parameters element wise. This is because this scenario can be regarded as potentially most sensitive to the dual Lagrangean function. If the solution is feasible for this scenario, it is feasible for the other scenarios. For simplifying the notation, we denote the objective value of each Lagrangean subproblem v at iteration j as $\theta _{vj}$.

5 PLPR

This section proposes PLPR. In PLPR, the subproblems are solved in parallel, and a primal reduction is proposed to potentially speed up the algorithm.

The primal reduction step is to reduce the size of Eqs. (4) and parallelise the solution process. In Lagrangean decomposition, to obtain an upper bound, one needs to construct a feasible solution from the relaxed solution and solve the original problem, meaning solving Eqs. (4) with a fixed investment solution $x_{hv}$. When the original problem is large, the full size problem may still be hard to solve after fixing some variables.

Assuming a feasible strategic solution $x_{hvj}$ is given as parameters, the investment-related costs can be directly calculated. Also, the primal problem becomes a group of independent operational problems and parallelisable. In addition, not all operational problems need to be solved because once the NAC is restored, some operational problems become exactly equivalent to each other. In fact, the number of operational problems that need to be solved is theoretically reduced to $|{\mathcal {I}}|$, where ${\mathcal {I}}$ is the set of long-term nodes in the node formulation. This is achieved by solving only one of the short-term problems for the scenarios that are governed by the same NAC constraint. This is because for the scenarios governed by the same NAC constraints, the short-term problems are simply copy of each other and are exactly equivalent to each other. Each operational problem is indexed by strategic stage $h \in {\mathcal {H}}$ and strategic scenario $v \in {\mathcal {S}}^{RI}$, where ${\mathcal {S}}^{RI}$ is the reduced set of scenarios. For a given problem $h \in {\mathcal {H}}, v \in {\mathcal {S}}^{RI}$, we define the corresponding subproblem as a node subproblem. The formulation of the node subproblem is given as follows,

$$\begin{aligned}&\min _{y_{hvts} \in {\mathcal {Y}}}{} & {} {\pi _v\left( c_{hv}^{\top }x_{hv} + \sum _{s \in {\mathcal {S}}^{O}_{hv}}\omega _{hvs} \sum _{t \in {\mathcal {T}}^{O}_{hv}}q_{hvts}^{\top }Q_{hvts}y_{hvts}\right) }&\end{aligned}$$

(6a)

$$\begin{aligned}&\text {s.t.}{} & {} T^O_{hvts} x_{hv} + W^O_{hvts} y_{hvts} \le h^{O}_{hvts},& \quad h \in {\mathcal {H}},\quad v \in {\mathcal {S}}^{I},\quad t=1,\quad s \in {\mathcal {S}}^{O}_{hv}, \end{aligned}$$

(6b)

$$\begin{aligned}&\quad{} & {} T^O_{hvts} y_{hv(t-1)s} + W^O_{hvts} y_{hvts} \le h^{O}_{hvts},&\quad h \in {\mathcal {H}}, \quad v \in {\mathcal {S}}^{I}, \quad t \in {\mathcal {T}}^{O}_{hv} \setminus \{1\}, \quad s \in {\mathcal {S}}^{O}_{hv}, \end{aligned}$$

(6c)

$$\begin{aligned}&\quad{} & {} y \ge 0.&\end{aligned}$$

(6d)

A Lagrangean upper bound can be obtained after solving all the node subproblems. Here, $c_{hv}^{\top }x_{hv}$ becomes a constant in the objective function. This reduction can produce an exact upper bound because the structure of MHSP makes the operational problem only depend on its investment decisions. The computational time can be significantly reduced by reducing the size of the primal problem and parallelising the solving process. The PLPR is presented in Algorithm 3. To simplify the notation, we denote the probability weighted operational cost, $\pi _v\sum _{s \in {\mathcal {S}}^{O}_{hv}}\omega _{hvs} \sum _{t \in {\mathcal {T}}^{O}_{hv}}q_{hvts}^{\top }Q_{hvts}y_{hvts}$, as $\theta ^{NSP}_{hv}$.

Remark 2

There is no dedicated NAC constraint for operational decision variables in MHSP because the operational decision variables are embedded in the investment node. This leads to fewer Lagrangean multipliers and a simpler search for a feasible solution.

6 Mathematical model

This section presents an MHSP model for a power system investment and operational planning problem adapted from Zhang et al. (2022, 2023). The model is to choose the cost optimal investment strategy and operational scheduling for a power system to achieve emission targets.

The problem under consideration aims to make optimal investment and operational decisions for a power system that satisfies the emission reduction goals under: (a) short-term uncertainty, including renewable energy availability and power demand; and (b) long-term uncertainty, including CO$_2$ budget, CO$_2$ tax, and long-term power demand.

We consider teachnologies including: (a) thermal generators (Coal-fired plant, OCGT, CCGT, Diesel, and nuclear plants); (b) generators with Carbon Capture and Storage (CCS) (Coal- fired plant with CCS); (c) renewable generators (offshore wind, onshore wind and solar PV); and (d) electric storage (PHES and lithium). The capital expenditures and fixed operational costs are assumed to be known. The problem is to determine: (a) the capacities of technologies and (b) operational strategies that include scheduling of generators, storage to meet the power demand with minimum overall investment, operational and environmental costs.

Here, we focus on how the proposed algorithms fit the mathematical model. We use the conventions that calligraphic capitalised Roman letters denote sets, upper case Roman and lower case Greek letters denote parameters, and lower case Roman letters denote variables. The indices are subscripts, and name extensions are superscripts. The names of variables, parameters, sets and indices are single symbols.

6.1 Nomenclature

Investment planning model sets

${\mathcal {H}}$:

Set of investment stages, h

${\mathcal {H}}_h$:

Set of all earlier investment stages of stage h ($h \in {\mathcal {H}}$), h

${\mathcal {I}}$:

Set of operational nodes, i

${\mathcal {I}}_{0}$:

Set of investment nodes, $i_{0}$

${\mathcal {I}}_{i}$:

Set of investment nodes $i_0$ $(i_0 \in {\mathcal {I}}_{0})$ ancestor to operational node i $(i \in {\mathcal {I}})$

${\mathcal {P}}$:

Set of technologies, p, (${\mathcal {P}}={\mathcal {G}}\cup {\mathcal {R}}\cup {\mathcal {S}})$

${\mathcal {S}}^I$:

Set of investment scenarios, v

Investment planning model variables

$c^{INV}$:

Total expected investment cost (€)

$c^{OPE}_i$:

Estimated operational cost in operational node i ($i \in {\mathcal {I}}$) (€)

$x_{pi/phv}^{Acc}$:

Accumulated capacity of device p in operational node i/ in stage h scenario v ($p \in {\mathcal {P}}, i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^{I}$) [MW]

$x_{pi/phv}^{Inst}$:

Newly invested capacity of device p in investment node $i_{0}$/ in stage h scenario v ($p \in {\mathcal {P}}, i \in {\mathcal {I}}_{0}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^{I}$) [MW]

Operational model parameters

$C_g^G/C_s^{SE}$:

Total operational cost of a generator g/ a storage facility s ($g \in {\mathcal {G}}$/ $s \in {\mathcal {S}}$) [€/MW]

$E^{G}_g$:

Emission factor of gas turbine g $(g \in {\mathcal {G}})$ [tonne/MWh]

$H_t$:

Number of hour(s) in one operational period t ($t \in {\mathcal {T}}$)

$W_{t}$:

Probability multiplied weight of operation period t ($t \in {\mathcal {T}}$)

$\alpha ^{G}_{g}$:

Maximum ramp rate of gas turbines ($g \in {\mathcal {G}}$) [MW/MW]

$\eta _{s}^{SE}$:

Efficiency of electricity storage s ($s \in {\mathcal {S}}$)

Operational model sets

${\mathcal {G}}$:

Set of thermal generators, g

${\mathcal {N}}$:

Set of time slices, n

${\mathcal {R}}$:

Set of renewable generations, r

${\mathcal {S}}$:

Set of electricity storage, s

${\mathcal {T}}$:

Set of hours in all time slices, t

${\mathcal {T}}_n$:

Set of hours in time slice, n

Operational model variables

$p_{git/ghvt}^{G}$:

Power generation of gas turbine g in operational node i in period t/ in stage h scenario v period t ($g \in {\mathcal {G}}, i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^{I}, t \in {\mathcal {T}}$) [MW]

$p_{it/hvt}^{GShedP}$:

Generation shed in operational node i/ in stage h scenario v period t ($i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^{I}, t \in {\mathcal {T}}$) [MW]

$p_{it/hvt}^{ShedP}$:

Load shed in operational node i/ in stage h scenario v in period t ($i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^{I}, t \in {\mathcal {T}}$) [MW]

$p_{sit/shvt}^{SE+}$:

Charge power of electricity storage s in operational node i/ in stage h scenario v period t ($s \in {\mathcal {S}}, i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^{I}, t \in {\mathcal {T}}$) [MW]

$p_{sit/shvt}^{SE-}$:

Discharge power of electricity storage s in operational node i/ stage h scenario v in period t($s \in {\mathcal {S}}, i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^{I}, t \in {\mathcal {T}}$) [MW]

$q_{sit/shvt}^{SE}$:

Energy level of electricity storage s in operational node i/ in stage h scenario v at the start of period t ($s \in {\mathcal {S}}, i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^I, t \in {\mathcal {T}}$) [MWh]

Uncertain parameters

$\mu ^{E}_{i/hv}$:

Carbon emission budget in operational node i/ in stage h scenario v ($i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^I$) [tonne]

$\mu ^{DP}_{i/hv}$:

Long-term demand scaling in operational node i/ in stage h scenario v ($i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^I$)

$C^{CO_2}_{i/hv}$:

CO$_2$ cost in operational node i/ in stage h scenario v ($i \in {\mathcal {I}}, h \in {\mathcal {H}}, v \in {\mathcal {S}}^I$) [€/tonne]

$P^{DP}_{t}$:

Power demand in period t $(t \in {\mathcal {T}})$ [MW]

$R_{rt}^{R}$:

Capacity factor of renewable unit r in period t ($r \in {\mathcal {R}}, t \in {\mathcal {T}}$)

6.2 Investment planning model (Benders master problem)

In this section, we present the investment planning problem Eqs. (7) that follows the general formulation of the Benders reduced master problem given by Eqs. (2).

$$\begin{aligned}&\min{} & {} {c^{INV}+\kappa \sum _{i \in {\mathcal {I}}}\pi ^{I}_{i}c_i^{OPE}}&\end{aligned}$$

(7a)

$$\begin{aligned}&\text {s.t.}{} & {} {c^{INV}= \sum _{i\in {\mathcal {I}}_{0}}\delta ^{I_{0}}_{i}\pi ^{I_{0}}_{i}\sum _{p \in {\mathcal {P}}} C^{Inv}_{pi}x^{Inst}_{pi}+\kappa \sum _{i \in {\mathcal {I}}}\delta ^{I}_{i}\pi ^{I}_{i}\sum _{p \in {\mathcal {P}}}C^{Fix}_{pi}x^{Acc}_{pi}}&\end{aligned}$$

(7b)

$$\begin{aligned}{} & {} {}&x^{Acc}_{pi}=X^{Hist}_{pi}+\sum _{i_0 \in {\mathcal {I}}_{i}|\kappa \left( I^{L}_{i}-I^{L}_{i_{0}}\right) \le H^{P}_{p}}x_{pi}^{Inst},& \quad p \in {\mathcal {P}}, \quad i \in {\mathcal {I}}, \end{aligned}$$

(7c)

$$\begin{aligned}{} & {} {}&x^{Acc}_{pi} \le X^{Max}_{p},& \quad p \in {\mathcal {P}}, \quad i \in {\mathcal {I}}, \end{aligned}$$

(7d)

$$\begin{aligned}{} & {} {}&c^{OPE}_i \ge \theta + \lambda ^{\top }(x_i-x)&(x, \theta , \lambda ) \in {\mathcal {F}}_{i(j-1)}, \quad i \in {\mathcal {I}}, \end{aligned}$$

(7e)

$$\begin{aligned}{} & {} {}&{x^{Inst}_{pi}, \quad x^{Acc}_{pi} \in {\mathbb {R}}^{+}_{0}.} \end{aligned}$$

(7f)

The total cost for investment planning, Eq. (7a), consists of actual discounted investment costs and discounted fixed operating and maintenance costs $c^{INV}$, as well as the expected operational cost of the system over the time horizon $\kappa \sum _{i \in {\mathcal {I}}}\pi ^{I}_{i}c^{OPE}$. Here, $\kappa$ is a scaling factor that depends on the time step between two successive investment nodes. Constraint (7c) states that the accumulated capacity of a technology $x^{Acc}_{pi}$ in an operational node equals the sum of the historical capacity $X^{Hist}_{p}$ and newly invested capacities $x^{Inst}_{pi}$ in its ancestor investment nodes ${\mathcal {I}}_{i}$. The parameter $X^{Max}_{p}$ denotes the maximum accumulated capacity of technologies. We define $x_i=\left( \{x^{Acc}_{pi}, p \in {\mathcal {P}}\}, \mu ^{DP}_{i}, \mu ^{E}_{i}\right) , i \in {\mathcal {I}}$ that collects all right hand side coefficients, and will be fixed in the Benders subproblem Eqs. (8) through vector $x_i$. Also, $c_i=\left( C^{CO_2}_{i}\right) ,i \in {\mathcal {I}}$ collects all the cost coefficients into vector $c_i$.

6.3 Operational model (Benders subproblem)

We now compute the operational cost $c^{OPE}(x_i,c_i)$ at one operational node $i \in {\mathcal {I}}$ by solving Benders subproblem Eqs. (8) given the decisions $x_i$ and $c_i$ determined in the master problem Eqs. (7).

$$\begin{aligned}&\min \quad{} & {} {\sum _{t \in {\mathcal {T}}}W_{t}H_{t}\left( \sum _{g \in {\mathcal {G}}}C^{G}_{g}p^{G}_{git}+ \sum _{s \in {\mathcal {S}}}C^{SE}_{s}p^{SE+}_{sit} + C^{ShedP}p^{ShedP}_{it} \right) }&\end{aligned}$$

(8a)

$$\begin{aligned}&\text {s.t.}{} & {} p^{G}_{git} \le x^{Acc}_{gi},& \quad g \in {\mathcal {G}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(8b)

$$\begin{aligned}&\quad{} & {} p_{sit}^{SE+} \le x_{si}^{Acc},& \quad s \in {\mathcal {S}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(8c)

$$\begin{aligned}&\quad{} & {} p_{sit}^{SE-} \le x_{si}^{Acc},& \quad s \in {\mathcal {S}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(8d)

$$\begin{aligned}&\quad{} & {} q_{sit}^{SE} \le \gamma ^{SE}_{s}x_{si}^{Acc},& \quad s \in {\mathcal {S}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(8e)

$$\begin{aligned}&\quad{} & {} -\alpha ^{G}_{g}x_{gi}^{Acc} \le p_{git}^{G}-p_{gi(t-1)}^{G} \le \alpha ^{G}_{g}x_{gi}^{Acc},& \quad g \in {\mathcal {G}}, \quad n \in {\mathcal {N}}, \quad t \in {\mathcal {T}}_{n}, \end{aligned}$$

(8f)

$$\begin{aligned}&\quad{} & {} {\sum _{g \in {\mathcal {G}}}p_{git}^{G}+\sum _{s \in {\mathcal {S}}}p_{sit}^{SE-}+\sum _{r \in {\mathcal {R}}}R^{R}_{rt}x_{ri}^{Acc}+ p_{it}^{ShedP}}&\nonumber \\&\quad{} & {} = \mu ^{DP}_{i}P^{DP}_{t}+\sum _{s \in {\mathcal {S}}}p_{sit}^{SE+}+p_{it}^{GShedP},& \quad t \in {\mathcal {T}}, \end{aligned}$$

(8g)

$$\begin{aligned}&\quad{} & {} q_{si(t+1)}^{SE}=q_{sit}^{SE}+H_{t}\left( \eta _{s}^{SE}p_{sit}^{SE+}-p_{sit}^{SE-}\right) ,& \quad s \in {\mathcal {S}}, \quad n \in {\mathcal {N}}, \quad t \in {\mathcal {T}}_{n}, \end{aligned}$$

(8h)

$$\begin{aligned}&\quad{} & {} \sum _{t \in {\mathcal {T}}}\sum _{g \in {\mathcal {G}}} W_{t}H_{t}E^{G}_{g}p^{G}_{git}\le \mu ^{E}_i,&\end{aligned}$$

(8i)

$$\begin{aligned}{} & {} {}&{p^{G}_{git}, p^{ShedP}_{it}, p^{SE+}_{sit}, p^{SE-}_{sit}, q^{SE}_{sit}, p^{GShedP}_{it} \in {\mathbb {R}}_{0}^{+}.} \end{aligned}$$

(8j)

The operational subproblem corresponds to Benders subproblem Eqs. (3). The operational cost includes total operating costs of all generators and storage facilities $C^{G}_{g}p^{G}_{gt}+C^{S}_{s}p^{SE+}_{sit}$ and load shedding costs $C^{ShedP}p^{ShedP}_{it}$. The parameters $C^{G}_{g}$ and $C^{SE}_{s}$ include the variable operational cost of generators and storage. For thermal generators, $C^{G}_{g}$ also includes the fuel cost and the CO$_2$ tax charged for the emissions of generators. Constraint (8f) captures how fast thermal generators can ramp up or down their power output, respectively. The parameter $\alpha ^{G}_{g}$ is the maximum ramp rate of thermal generators. The power balance, Constraint (8g), ensures that in one operational period t, the sum of total power generation of thermal generators $p^{G}_{git}$, power discharged from all the electricity storage $p^{SE-}_{sit}$, renewable generation $R^{R}_{t}x^{Acc}_{ri}$, and load shed $p^{ShedP}_{it}$ equals the sum of power demand $\mu ^{DP}_{i}P^{DP}_{t}$, and power generation shed $p^{GShedP}_{it}$. The parameter $R^{R}_{rt}$ is the capacity factor of a renewable unit that is a fraction of the nameplate capacity $x^{Acc}_{ri}$. Constraint (8h) states that the state of charge $q^{SE}_{sit}$ in period $t+1$ depends on the previous state of charge $q^{SE}_{sit}$, the charged power $p^{SE+}_{sit}$ and discharged power $p^{SE-}_{sit}$. The parameter $\eta ^{SE}_{s}$ represent the charging efficiency. Constraint (8i) limits the total emission. The parameter $H_t$ is the length of the period t. The symbol $E^{G}_{g}$ is the emission factor per unit of power generated. The capacities $x^{Acc}_{pi}$, scaling factor of demand $\mu ^{DP}_i$ and CO$_2$ budget $\mu ^E_i$ are passed from the master problem Eqs. (7) via vector $x_i$ and CO$_2$ tax that is included in cost coefficient $C^{G}_g$ is passed from master problem Eqs. (7) via vector $c_i$.

6.4 Lagrangean subproblem

In Lagrangean decomposition, the subproblem corresponds to each scenario without the NAC constraint. Unlike Benders decomposition, which projects the operational decision onto the investment space, the Lagrangean subproblem keeps a copy of a part of the original problem. The Lagrangean subproblem for scenario $v \in {\mathcal {S}}^{I}$ is as follows:

$$\begin{aligned}&\min{} & {} {\sum _{h \in {\mathcal {H}}}\delta ^{H}_{h}\pi ^{SI}_{v}\left( \sum _{p \in {\mathcal {P}}} \left( C^{Inv}_{phv}x^{Inst}_{pv}+\kappa C^{Fix}_{phv}x^{Acc}_{phv}\right) \right. }&\nonumber \\{} & {} {}&{+ \kappa \sum _{t \in {\mathcal {T}}}W_{t}H_{t}\left. \left( \sum _{g \in {\mathcal {G}}}C^{G}_{g}p^{G}_{ghvt}+ \sum _{s \in {\mathcal {S}}}C^{SE}_{s}p^{SE+}_{shvt} +C^{ShedP}p^{ShedP}_{hvt} \right) \right) +\sum _{p \in {\mathcal {P}}}\sum _{h \in {\mathcal {H}}}\lambda _{phv}x^{Inst}_{phv}}&\end{aligned}$$

(9a)

$$\begin{aligned}&\text {s.t.}{} & {} x^{Acc}_{phv}=X^{Hist}_{phv}+\sum _{h_0 \in {\mathcal {H}}_{h}|\kappa (h-h_0)\le H^{P}_{p}}x_{phv}^{Inst},&\quad p \in {\mathcal {P}}, \quad h \in {\mathcal {H}}, \end{aligned}$$

(9b)

$$\begin{aligned}{} & {} {}&x^{Acc}_{phv} \le X^{Max}_{p},&\quad p \in {\mathcal {P}}, \quad h \in {\mathcal {H}}, \end{aligned}$$

(9c)

$$\begin{aligned}{} & {} {}&p^{G}_{ghvt} \le x^{Acc}_{ghv},&\quad g \in {\mathcal {G}}, \quad h \in {\mathcal {H}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(9d)

$$\begin{aligned}&\quad{} & {} p_{shvt}^{SE+} \le x_{shv}^{Acc},&\quad s \in {\mathcal {S}}, \quad h \in {\mathcal {H}},\quad t \in {\mathcal {T}}, \end{aligned}$$

(9e)

$$\begin{aligned}&\quad{} & {} p_{shvt}^{SE-} \le x_{shv}^{Acc},&\quad s \in {\mathcal {S}}, \quad h \in {\mathcal {H}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(9f)

$$\begin{aligned}&\quad{} & {} q_{shvt}^{SE} \le \gamma ^{SE}_{s}x_{shv}^{Acc},&\quad s \in {\mathcal {S}},\quad h \in {\mathcal {H}},\quad t \in {\mathcal {T}}, \end{aligned}$$

(9g)

$$\begin{aligned}{} & {} {}&-\alpha ^{G}_{g}p_{ghv}^{AccG} \le p_{ghvt}^{G}-p_{ghv(t-1)}^{G} \le \alpha ^{G}_{g}p_{ghv}^{AccG},&\quad g \in {\mathcal {G}}, \quad h \in {\mathcal {H}}, \quad n \in {\mathcal {N}},\quad t \in {\mathcal {T}}_{n}, \end{aligned}$$

(9h)

$$\begin{aligned}&\quad{} & {} {\sum _{g \in {\mathcal {G}}}p_{ghvt}^{G}+\sum _{s \in {\mathcal {S}}}p_{shvt}^{SE-}+\sum _{r \in {\mathcal {R}}}R^{R}_{rt}x_{rhv}^{Acc}+ p_{hvt}^{ShedP}}=&\nonumber \\&\quad{} & {} \mu ^{DP}_{hv}P^{DP}_{t}+\sum _{s \in {\mathcal {S}}}p_{shvt}^{SE+}+p_{hvt}^{GShedP},&\quad h \in {\mathcal {H}},\quad t \in {\mathcal {T}}, \end{aligned}$$

(9i)

$$\begin{aligned}&\quad{} & {} q_{shv(t+1)}^{SE}=q_{shvt}^{SE}+H_{t}\left( \eta _{s}^{SE}p_{shvt}^{SE+}-p_{shvt}^{SE-}\right) ,&\quad s \in {\mathcal {S}}, \quad h \in {\mathcal {H}}, \quad n \in {\mathcal {N}}, \quad t \in {\mathcal {T}}_{n}, \end{aligned}$$

(9j)

$$\begin{aligned}&\quad{} & {} \sum _{t \in {\mathcal {T}}}\sum _{g \in {\mathcal {G}}} W_{t}H_{t}E^{G}_{g}p^{G}_{ghvt}\le \mu ^{E}_{hv},&\quad h \in {\mathcal {H}}, \end{aligned}$$

(9k)

$$\begin{aligned}{} & {} {}&{x^{Inst}_{phtv}, x^{Acc}_{phv}, p^{G}_{ghvt}, p^{ShedP}_{hvt}, p^{SE+}_{shvt}, p^{SE-}_{shvt}, q^{SE}_{shvt}, p^{GShedP}_{hvt} \in {\mathbb {R}}_{0}^{+}.} \end{aligned}$$

(9l)

Equations (9) correspond to the Lagrangean dual Eqs. (5). The objective function of the Lagrangean subproblem consists of the total investment and operational costs in all stages in scenario v, and the penalty term $\sum _{p \in {\mathcal {P}}}\sum _{h \in {\mathcal {H}}}\lambda _{phv}x^{Inst}_{phv}$ for the deviation from the NAC constraint, where $\lambda _{phv}$ are the Lagrangean multipliers. The investment-related constraints Eqs. (9b) and (9c) are similar to Eqs. (7c) and (7d) in the Benders reduced master problem. Also, the operational constraints Eqs. (9d)–(9k) are similar to Eqs. (8b)–(8i) in the Benders subproblem. Therefore, we omit to explain all the constraints here.

The Lagrangean master problem in Lagrangean decomposition is simply the original full size problem Eqs. (4) with fixed investment decisions $x_{hv}$.

6.5 Lagrangean node subproblem

In this section, we present the Lagrangean node subproblem for stage $h \in {\mathcal {H}}$, scenario $v \in {\mathcal {S}}^{RI}$ given by Eqs. (10).

$$\begin{aligned}&\min{} & {} {\kappa \sum _{t \in {\mathcal {T}}} {W_{t}H_{t}\left( \sum _{g \in {\mathcal {G}}}C^{G}_{g}p^{G}_{ghvt}+ \sum _{s \in {\mathcal {S}}}C^{SE}_{s}p^{SE+}_{shvt} + C^{ShedP}p^{ShedP}_{hvt} \right) }} \end{aligned}$$

(10a)

$$\begin{aligned}&\text {s.t.}{} & {} p^{G}_{ghvt} \le x^{Acc}_{ghv},&\quad g \in {\mathcal {G}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(10b)

$$\begin{aligned}&\quad{} & {} p_{shvt}^{SE+} \le x_{shv}^{Acc},&\quad s \in {\mathcal {S}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(10c)

$$\begin{aligned}&\quad{} & {} p_{shvt}^{SE-} \le x_{shv}^{Acc},&\quad s \in {\mathcal {S}}, \quad t \in {\mathcal {T}}, \end{aligned}$$

(10d)

$$\begin{aligned}&\quad{} & {} q_{shvt}^{SE} \le \gamma ^{SE}_{s}x_{shv}^{Acc},&\quad s \in {\mathcal {S}},\quad t \in {\mathcal {T}}, \end{aligned}$$

(10e)

$$\begin{aligned}{} & {} {}&-\alpha ^{G}_{g}x_{ghv}^{Acc} \le p_{ghvt}^{G}-p_{ghv(t-1)}^{G} \le \alpha ^{G}_{g}x_{ghv}^{Acc},&\quad g \in {\mathcal {G}}, \quad \in {\mathcal {N}},\quad t \in {\mathcal {T}}_{n}, \end{aligned}$$

(10f)

$$\begin{aligned}&\quad{} & {} {\sum _{g \in {\mathcal {G}}}p_{ghvt}^{G}+\sum _{s \in {\mathcal {S}}}p_{shvt}^{SE-}+\sum _{r \in {\mathcal {R}}}R^{R}_{rt}x_{rhv}^{Acc}+ p_{hvt}^{ShedP}} =&\nonumber \\&\quad{} & {}\mu ^{DP}_{hv}P^{DP}_{t}+\sum _{s \in {\mathcal {S}}}p_{shvt}^{SE+}+p_{hvt}^{GShedP},&\quad t \in {\mathcal {T}}, \end{aligned}$$

(10g)

$$\begin{aligned}&\quad{} & {} q_{shv(t+1)}^{SE}=q_{shvt}^{SE}+H_{t}\left( \eta _{s}^{SE}p_{shvt}^{SE+}-p_{shvt}^{SE-}\right) ,&\quad s \in {\mathcal {S}}, \quad n \in {\mathcal {N}}, \quad t \in {\mathcal {T}}_{n}, \end{aligned}$$

(10h)

$$\begin{aligned}&\quad{} & {} \sum _{t \in {\mathcal {T}}}\sum _{g \in {\mathcal {G}}} W_{t}H_{t}E^{G}_{g}p^{G}_{ghvt}\le \mu ^{E}_{hv},&\end{aligned}$$

(10i)

$$\begin{aligned}{} & {} {}&{x^{Acc}_{phv}, p^{G}_{ghvt}, p^{ShedP}_{hvt}, p^{SE+}_{shvt}, p^{SE-}_{shvt}, q^{SE}_{shvt}, p^{GShedP}_{hvt} \in {\mathbb {R}}_{0}^{+}.} \end{aligned}$$

(10j)

The Lagrangean node subproblem corresponds to the node subproblem Eqs. (6) in the general formulation of the PLPR. The Lagrangean node subproblem is similar to the Benders subproblem. Once a feasible investment solution is obtained, the investment-related costs can be directly calculated. Then the subproblems need to be solved to obtain the operational costs. Here, we use the primal reduction by solving only one operational problem for the scenarios that are governed by the same NAC constraint at each stage. These Lagrangean node subproblems are solved in parallel. Eventually, an upper bound can be calculated.

7 Results

In this section, we provide the case study and the computational results. We use the REORIENT model (Zhang et al. 2023) to solve a single region investment planning problem, and apply Benders, Lagrangean and PLPR to solve the problem instances. The performance of the methods is compared.

7.1 Case study

In the case study, we use the model to solve a UK power system expansion problem. The data can be found in Zhang et al. (2022, 2023). We implemented the algorithms and model in Julia 1.8.2 using JuMP (Dunning et al. 2017), and solved with the barrier solver in Gurobi 10.0 (Gurobi Optimization, LLC 2022). We ran the code on a computer cluster (25 computer nodes) with a 2x 3.6GHz 8 core Intel Xeon Gold 6244 CPU and 384 GB of RAM, running on CentOS Linux 7.9.2009. The cluster was shared by other users and had no resource allocation and queuing systems. Therefore, solution times may have been affected by interfering traffic during program executions.

7.1.1 Computational results

An overview of the case study tested in this paper is presented in Table 1. The different cases vary in the number of investment stages, long-term uncertainty, operational scenarios, and representative hours in the operational problem. For the test instances, we use a 1% convergence tolerance and 3600 s as stopping criteria.

Parameter tuning is important for the Lagrangean decomposition and PLPR decomposition. In the computational study, $\delta _0=0.01, \underline{\gamma }=0.8, \gamma _0=0.99, \overline{\gamma }=1.4$. Please note that for a different problem, the parameters can vary significantly based on the numerical scales of the problem. Therefore, the parameters used in this study may not guarantee a good performance for different problems.

Table 1 Overview of the cases used in the computational study

Table 2 Comparative results for Benders and Lagrangean decomposition

Table 3 Computational results for PLPR

The computational results of Benders decomposition and Lagrangean decomposition are reported in Table 2. Benders decomposition performs well and in some cases outperforms the full space problem with Gurobi. We can see that Lagrangean decomposition is much worse than Benders decomposition. This is because, in Lagrangean decomposition, both the Lagrangean subproblems and the Lagrangean master problem are solved in series. In addition, the original full size problem after fixing investment decisions is still large to solve. A full size problem is solved at each iteration, which leads to poor performance. This suggests that for MHSP, Lagrangean decomposition without parallel computing is not a suitable approach. Also, a drawback of Lagrangean decomposition is that their convergence is highly dependent on the adjustment of step sizes. Extensive tests have been conducted to find suitable parameters for the adjustment. In contrast, Benders decomposition requires no effort in choosing parameters, which makes it more robust.

The gaps in Benders iterations are presented in Fig. 3. We can see that the initial gaps in Benders decomposition are large. This is because Benders decomposition requires a sufficiently large number of cutting planes to approximate accurately the objective function.

Fig. 3

Bounds in Cases 4, 5, and 8 using Benders decomposition. (UB: upper bound, LB: lower bound)

The computational results of PLPR are reported in Table 3. The proposed PLPR yields very good performance across all test instances. This is because the Lagrangean subproblem is solved in parallel, so the computational time almost does not increase with the number of scenarios given enough computer nodes. The value of PLPR is more significant for larger instances.

We note that PLPR can obtain small initial gaps in the first iterations, as illustrated in Fig. 4. This is because like other Lagrangean type decomposition, PLPR only needs to find the optimal multipliers. This would suggest that Lagrangean type decomposition methods may be preferred if the underlying problem does not have to be solved to a very tight tolerance. This may be the case when dealing with huge investment planning problems where a very tight convergence tolerance is not meaningful.

Fig. 4

Bounds in Cases 4, 5, and 8 using PLPR (UB: upper bound, LB: lower bound)

An analysis of computational times is presented in Table 4. We can see that as the number of scenarios increases, the time spent on solving scenario subproblems increases significantly in Lagrangean decomposition compared with PLPR. In addition, due to the primal reduction in PLPR and parallel computing, the time spent on solving the primal problem is much less in PLPR than in Lagrangean decomposition.

Table 4 Comparative analysis of the computational time (in seconds) of Lagrangean and PLPR

7.1.2 Power system investment decisions

This section presents the optimal investment decisions in the first stage for Cases 1–8. We can see from Table 5 that by including operational uncertainty, the investment decisions are considerably different. The differences in long-term and short-term uncertainty in Cases 1–8 are presented in Table 1. Cases 1–4 only differ in operational uncertainty, we can see from Table 5 that the investments in CoalCCS and OnWind are significantly different. It is the same case for Cases 5–8. Cases 1 and 5 differ only in long-term uncertainty, we can see that the investment in OnWind in Case 1 is 79.83 GW compared with 76.63 GW in Case 5. The difference can also be observed by comparing Cases 2 and 6, Cases 3 and 7, and Cases 4 and 8. From this, we can see that both long-term and short-term uncertainty can affect investment decisions significantly. This shows the value of including short-term and long-term uncertainty in a long-term stochastic investment planning problem.

Table 5 Investment decisions in the first stage in the cases

8 Discussion

In this paper, we have proposed the PLPR (Parallel Lagrangean decomposition with Primal Reduction) algorithm, and formalised Benders decomposition and Lagrangean decomposition for MHSP. We tested the proposed methods on a UK power system expansion problem using the REORIENT model.

Through computational tests, we found that PLPR is a very efficient decomposition method for MHSP that utilises the scenario structure of the MHSP. The computational time does not scale much as the problem instance grows due to the use of parallel computing. Despite parallel computing and primal reduction, PLPR inherits the advantages and the disadvantages of Lagrangean decomposition.

We found that Lagrangean type decomposition can obtain a good convergence gap in the initial iterations. However, one limitation of Lagrangean type decomposition is that it is sensitive to parameter tuning. Although MHSP reduces the number of multipliers, finding good ones can still be hard. In addition, we notice that Lagrangean decomposition requires substantially more memory than Benders decomposition. Lagrangean decomposition duplicates the variables, which leads to a larger model size. However, Lagrangean decomposition can solve more classes of problems such as the ones with integer operational variables, which were not addressed in this paper. Benders decomposition can only solve linear programming or mixed-integer linear programming with integer variables in the reduced master problem.

Benders decomposition is more robust than Lagrangean decomposition because its convergence does not depend on parameter tuning. However, the drawback of Benders decomposition is that once the scenario tree is large, the master problem may become harder to solve. This is because a two-stage Benders solves a multi-stage stochastic program. Therefore, the reduced master problem includes all investment nodes. Once there are a number of investment nodes, or there are integer variables in the reduced master problem, the speed of Benders decomposition may be affected significantly.

For very large problems, combining Lagrangean decomposition with Benders decomposition may be beneficial. For example, use Benders decomposition to solve the Lagrangean subproblem. It is also possible to utilise adaptive oracles (Mazzi et al. 2021) in Lagrangean decomposition.

9 Conclusions and future work

In this paper, we first proposed, formalised and compared decomposition algorithms for linear programming MHSP. We formalised the node and scenario based formulations of MHSP. Decomposition methods including Benders, Lagrangean and PLPR were proposed based on the special structure of MHSP. Some properties based on the structure of MHSP were presented. From the computational study, we found that: (1) PLPR is a very efficient decomposition algorithm that utilises the structure of MHSP; (2) Lagrangean is not an efficient method for MHSP; (3) Benders decomposition is more robust in terms of parameter tuning. The choice of algorithms for MHSP was discussed based on the computational tests.

This is the first paper that has systematically studied decomposition methods for MHSP. Future work may include (1) developing algorithms that further exploit the special structure of MHSP, such as Benders decomposition with cut sharing or combined Lagrangean decomposition and Benders decomposition algorithm, (2) extending the algorithm to solve mixed integer linear programming MHSP, and (3) benchmarking the performance of PLPR with enhanced Benders decomposition and scenario based decomposition methods.