1 Introduction

Sustainability is a concept that stems from the anxiety of all segments of society about the damaging effects that human activities have on the environment and, consequently, on the economy and society in general. In particular, the recent environmental, social, and financial crises have inevitably led regulators, practitioners, and scholars to strengthen sustainability research to investigate the various mechanisms of the companies’ behavior w.r.t. their sustainability initiatives and financial performance from different perspectives. In this regard, over the past recent decades, many investors have turned their attention to the so-called Socially Responsible Investment (SRI), also called “ethical funds”. Even though there is no unique definition of SRI due to its heterogeneity (see, e.g., Sandberg et al. 2009), it is usually viewed as a class of investments that integrates into the decision-making process, along with appropriate features in terms of gain and risk (see Markowitz 1952, 1959), also non-strictly financial features, such as environmental, social, and ethical aspects. The idea of socially sustainable investment first appeared in the late 1980 s (see the seminal Bruyn 1991). Then, mainly in the last two decades, interest in SRIs has significantly grown (according to, e.g., Sparkes and Cowton 2004), and, as of 2020, global sustainable investments in five of the largest markets (United States, Canada, Europe, Japan, and Australasia) amounted to 35.3 trillion dollars, representing more than one-third of the total value of the assets traded in the same markets (see Global Sustainable Investment Alliance 2020).

As mentioned above, the development of SRI has its roots in various historical happenings that have led policymakers and financial practitioners to address the issue of socially responsible investing. The three main pillars of SRI are Environmental, Social, and corporate Governance (ESG). The integration of these criteria into the evaluation process of companies and investments is a topic that is widely discussed by practitioners and academics (see, e.g., Widyawati 2020; Billio et al. 2021; Chatterji et al. 2016; Berg et al. 2022; Li et al. 2021).

ESG was first mentioned in the “Who Cares Wins 2005 Conference Report” ([42]), where institutional investors and regulators stressed the relevance of ESG factors in asset management and sustainable finance research. Accordingly, several scholars have attempted to examine the impact of ESG factors on the portfolio selection process to achieve sustainability goals (Utz et al. 2014, 2015; Van Duuren et al. 2016; Bermejo et al. 2021; Cesarone et al. 2022; Steuer and Utz 2022). Furthermore, a large literature has fed into the debate over the years on the relationship between ESG ratings and financial performance (see Brunet 2019; Derwall et al. 2005; Nofsinger and Varma 2014; Brooks and Oikonomou 2018; Giese and Lee 2019; Friede et al. 2015).

Following this global trend, the strategic plans of many companies focus not only on economic sustainability but also on environmental and social sustainability. In fact, companies have invested in the sustainability of the decision-making processes to meet stakeholders’ demands and regulatory requirements.

In this context, the Sustainable Finance Conflict of interest Regulation (European Union 2019), the Taxonomy Regulation (European Union 2020), and the Low Carbon Benchmark Regulation (European Union 2019) represent a new set of rules introduced by the 2018 Sustainable Finance Action Plan (European Union 2019), with the aim of better identifying the ESG profile of financial products, improving market transparency, and promoting sustainable investments. This new set of standards allows all market participants to pursue their sustainability goals using a common regulatory framework established by government authorities.

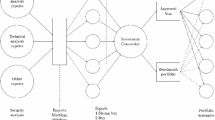
Thus, companies’ asset management, while being classically interested in meeting each individual client’s expectations, to comply with the above mentioned stakeholders’ demands and regulatory requirements, also seeks to optimize the company’s overall (social) ESG impact that in turn depends on the aggregated trades from all the clients’ accounts they manage. We propose to rely on bilevel programming to model this complicated problem: at the so-called upper-level, the firm sets the best incentives to be given to the account’s holders so that its overall ESG impact, i.e. the ESG score from all the managed accounts, is maximized; at the lower-level, given such incentives, each individual account’s owner’s utility is guaranteed to be maximized, given the other accounts’ trades. In fact, since in practice multiple accounts from different clients are accommodated simultaneously and the related trades are pooled for common execution, the transaction costs for each portfolio depend on the trades from all the managed accounts and, in turn, at the lower-level, the multiple portfolios are coupled to each other by the market impact of their transactions (see Lampariello et al. 2021; O’Cinneide et al. 2006; Yang et al. 2013). Hence, in the same spirit of the analysis in Lampariello et al. (2021), to model the lower-level interplay of the multiple portfolios, once the upper-level incentives are fixed, we adopt the (parametric) Nash Equilibrium Problem (NEP) formulation given by the collection of the accounts-related (parametric) problems à la Markowitz where, apart from the classical portfolio expected return and risk terms, also transaction costs and portfolio ESG score are considered. Given the upper-level incentives, the trades of each client’s account are guaranteed to be in a Nash equilibrium: for no account, given the other accounts’ trades, the objective function can be decreased by modifying unilaterally the trades to any other feasible solution. Clearly, we assume the following standard conditions to hold (see Nash 1951; Tirole 1988): accounts are managed rationally and optimized simultaneously, and each account’s information is shared with the others. For more details, also concerning algorithmic developments, about Nash games, we refer the reader to Aussel and Sagratella (2017); Dreves et al. (2011); Facchinei and Sagratella (2011); Facchinei and Lampariello (2011); Sagratella (2016, 2017a, b, 2019).

Summing up, in line with the regulatory requirements described above,

  • We rely on a novel bilevel approach to ESG-oriented multi-portfolio selection. We remark that, as a major departure from conceptually simpler models where the lower-level problem does not depend (parametrically) on upper-level design variables (see, e.g., Bigi et al. 2021; Dempe et al. 2010; Facchinei et al. 2014; Lampariello et al. 2021; Scutari et al. 2012; Shehu et al. 2019) and, in the context of multi-portfolio selection, Lampariello et al. 2021), in this work, we consider more general “genuine” bilevel structures;

  • We provide a theoretical analysis of the resulting complicated single-leader multi-follower framework, identifying viable sufficient conditions that make it numerically tractable;

  • We devise a provably (subsequentially) convergent novel algorithm that borrows from the sequential convex approximation paradigm (see Facchinei et al. 2020, 2020, 2022, 2021 for some recent developments);

  • Based on real financial datasets, we equip our study with some numerical experiments that show that our problem model is solvable for considerable problem sizes.

The rest of the paper is organized as follows. In Sect. 2, starting from the single-leader multi-follower framework we consider, we introduce our bilevel approach to model the ESG multi-portfolio selection, along with some theoretrical properties. The core Sect. 3 contains the presentation of some mild sufficient conditions that make our bilevel program numerically tractable by means of a sequential convex approximation-like method that is specifically tailored to deal with our problem model. In Sect. 4, we present and discuss the computational results of the numerical testing of our approach, based on real-world data. Finally, in Sect. 5, we give some concluding remarks and we outline possible future developments.

2 Problem model

2.1 A single-leader multi-follower framework

We considers K assets of a market and N accounts. Each asset \(k=1, \ldots , K\) has its own return, relative to a single-period investment, that is denoted by the random variable \(r_k\). For each account \(\nu \in \left\{ 1,\ldots ,N\right\}\), the aim is to choose the fractions \(y^\nu \in {\mathbb {R}}^K\) of a given budget \(b^\nu \in {\mathbb {R}}_+\) to be invested in K assets with the aim of optimizing multiple objectives; since we consider different budgets for different accounts, referring to amounts to be invested rather than relying on shares (with unitary budgets) seems a natural choice in a multi-portfolio context (see the discussion in Lampariello et al. 2021, Sect. 2). Classical criteria to be considered are portfolio’s income, given by budget times portfolio’s expected return,

$$\begin{aligned} I_\nu (y^\nu ) \triangleq b^\nu (\mu ^\nu )^Ty^\nu , \end{aligned}$$

where \(\mu ^\nu = \mathbb {E^\nu }(r) \in {\mathbb {R}}^K\) are expectations of the assets’ returns, and portfolio’s risk

$$\begin{aligned} R_\nu (y^\nu ) \triangleq \frac{1}{2} (b^\nu )^2 (y^\nu )^T\Sigma ^\nu y^\nu , \end{aligned}$$

for which we rely on portfolio’s return variance \((y^\nu )^T\Sigma ^\nu y^\nu\), where

$$\begin{aligned} \Sigma ^\nu \triangleq {\mathbb {E}}^\nu ((r-\mu ^\nu )(r-\mu ^\nu )^T) \end{aligned}$$

is the symmetric and positive semidefinite assets’ returns covariance matrix. Since, unless expectations are assumed homogeneous, the evaluation of investments is account dependent (see also the description in Lampariello et al. 2021, Section Sect. 2), we consider, for both the theoretical developments and the experimental study (see Sect. 4.1), assets’ returns expectations and covariance matrix that are related to each single account \(\nu\).

As a main departure from standard choices à la Markowitz, we include in our analysis the transaction costs term

$$\begin{aligned} TC_\nu (y^1, \ldots , y^N) \triangleq b^\nu (y^\nu -v^\nu )^T\Omega \sum _{\lambda =1}^N b^\lambda (y^\lambda -v^\lambda ), \end{aligned}$$

where \(v^\nu \in {\mathbb {R}}^K\) denotes the current positions and \(\Omega \in {\mathbb {R}}^{K \times K}\) is the (common to all accounts) symmetric and positive semidefinite market impact matrix whose entry at position (i, j) gives the impact of the liquidity of asset i on the liquidity of asset j (for further information about \(\Omega\), see Lampariello et al. (2021) and Yang et al. (2013). In fact, we focus on liquidity as the main driver of transaction costs: when trades from different accounts are pooled for common execution, individual accounts can suffer the market impact caused, e.g., by liquidity shortages because the joint demand of assets might be much larger than the individual one. We adopt, for each account, the linear market impact unitary cost function \(\Omega \sum _{\lambda =1}^N b^\lambda (y^\lambda -v^\lambda )\) that depends on the invested capital of the aggregated trades from all accounts.

Finally, we introduce a novel sustainability-oriented criterion given by the linear portfolio’s ESG score:

$$\begin{aligned} S_\nu (y^\nu ) \triangleq b^\nu ESG^T y^\nu , \end{aligned}$$

where \(ESG \in {\mathbb {R}}^K\) are the assets’ ESG scores.

For each account, the objective function to be minimized \(\theta _\nu : {\mathbb {R}}^{NK+1} \rightarrow {\mathbb {R}}\), where all the criteria above are included in a weighted sum fashion, clearly depends on variables \(y^\nu\), as well as on the variables from all the other accounts (via the coupling transaction costs term), which we collect in vector \(y^{-\nu }\):

$$\begin{aligned} y^{-\nu } \triangleq \begin{pmatrix} y^1\\ \vdots \\ y^{\nu -1}\\ y^{\nu +1}\\ \vdots \\ y^N \end{pmatrix} \in {\mathbb {R}}^{(N-1)K}. \end{aligned}$$
(1)

We also indicate with \(y \in {\mathbb {R}}^{NK}\) the vector formed by all the accounts’ decision variables and, to emphasize the account \(\nu\)’s decision variables within y, we sometimes write \((y^\nu ,y^{-\nu })\) instead of y, still indicating the vector \(y = (y^1,\ldots ,y^\nu ,\ldots ,y^N)\).

Also, the positive parameter \(\tau ^\nu\) that weights the impact of the ESG-oriented objective on the account \(\nu\)’s trades plays a key role, as detailed next:

$$\begin{aligned} \begin{array}{rl} \theta _\nu (\tau ^\nu , y^\nu ,y^{-\nu }) \triangleq &{} -I_\nu (y^\nu ) + \rho ^\nu R_\nu (y^\nu ) + TC_\nu (y^1, \ldots , y^N) - \tau ^\nu S_\nu (y^\nu )\\ = &{} -b^\nu (\mu ^\nu )^Ty^\nu + \rho ^\nu \frac{1}{2}(b^\nu )^2(y^\nu )^T\Sigma ^\nu y^\nu \\ &{} + b^\nu (y^\nu -v^\nu )^T\Omega {{[b^\nu (y^\nu -v^\nu ) + \sum _{\lambda \ne \nu } b^\lambda (y^\lambda -v^\lambda )]}}\\ &{} - \tau ^\nu b^\nu ESG^T y^\nu , \end{array} \end{aligned}$$

where \(\rho ^\nu \in {\mathbb {R}}_+\) is the risk aversion parameter. Note that the term \(b^\nu \tau ^\nu\) can be intended to represent a (monetary) incentive to be given to the account holder in order to invest in ESG-oriented portfolios.

We observe that, for every \(\nu ,\) given \(\tau ^\nu\), \(\theta _\nu\) is continuously differentiable, quadratic and convex with respect to \(y^\nu\). Hence, for each account \(\nu\), given \(\tau ^\nu\) and \(y^{-\nu }\), the following convex problem is addressed:

$$\begin{aligned} \text {minimize}_{y^{\nu }}\theta _{\nu }(\tau ^\nu ,y^\nu ,y^{-\nu }) \quad \text {s.t.} \quad y^\nu \in Y_\nu , \end{aligned}$$
(2)

where \(Y_\nu \subseteq {\mathbb {R}}^K\) is the nonempty, convex and compact set of feasible portfolios.

In the same spirit of the analysis in Lampariello et al. (2021), to model the resulting multiple portfolios selection, once \(\tau ^\nu\)s are fixed, we adopt the (parametric in \(\tau ^\nu\), \(\nu =1, \ldots , N\)) NEP formulation given by the collection of the N accounts-related parametric problems (2). The NEP we rely on is the problem to

$$\begin{aligned} \text {find} \; y \in Y: \; \theta _{\nu }(\tau ^\nu ,y^\nu ,y^{-\nu }) \le \theta _{\nu }(\tau ^\nu ,w^\nu ,y^{-\nu }) \quad \forall w^\nu \in Y_\nu , \quad \nu = 1, \ldots , N, \end{aligned}$$
(3)

where \(Y \triangleq Y_1 \times \ldots \times Y_N\). Any such point is termed equilibrium or solution of the NEP. Accordingly, the (parametric in \(\tau ^\nu\), \(\nu =1, \ldots , N\)) set of equilibria is denoted by

$$\begin{aligned} SOL(\tau ) \triangleq \left\{ y \in Y :\; \theta _{\nu }(\tau ^\nu ,y^\nu ,y^{-\nu }) \le \theta _{\nu }(\tau ^\nu ,w^\nu ,y^{-\nu }) \quad \forall w^\nu \in Y_\nu , \, \nu = 1, \ldots , N \right\} . \end{aligned}$$
(4)

At a lower-level, given \(\tau ^\nu\)s, a non cooperative setting seems to fit well within the demands of the accounts’ owners who just pursue their own interest. Their preferences are clearly satisfied when an equilibrium is reached: in this case, for no account, given the other accounts’ trades, the objective function can be decreased by modifying unilaterally the trades to any other feasible solution.

At an upper-level, properly setting the weights \(\tau ^\nu\) (for the portfolios’ ESG scores-related term) allows the firm to influence the choices of the accounts’ holders so that the overall ESG originating from the ESG scores of the managed portfolios is optimized, having the accounts’ owners’ still satisfied. We propose to rely on a novel (standard optimistic) bilevel approach, where, at the upper-level, the firm’s problem consists in choosing the best values for \(\tau\), with

$$\begin{aligned} \tau \triangleq \begin{pmatrix} \tau ^1\\ \vdots \\ \tau ^N \end{pmatrix} \in {\mathbb {R}}^N_+, \end{aligned}$$

and, thus, for the monetary incentives \([\tau ^\nu b^\nu ]_{\nu =1}^N\) to be given to the accounts’ holders so that the firm’s overall “social” ESG impact, i.e. the ESG score from all the managed accounts, is maximized in agreement with the clients, while, at the lower-level, the accounts are still guaranteed to be in a non cooperative equilibrium:

$$\begin{aligned} \begin{array}{rl} \text{ minimize}_{\tau ,y} &{} F(y) \triangleq -ESG^T\left( \sum _{\nu =1}^{N}b^\nu y^\nu \right) \\ \text {s.t.} &{} \tau \in T,\ y\in SOL(\tau ), \end{array} \end{aligned}$$
(5)

where \(T \subseteq {\mathbb {R}}^N_+\) is a nonempty, convex and compact set.

2.2 A bilevel formulation

NEP (3) is easily seen to be a potential game (see, e.g., Sagratella 2017a and Lampariello et al. 2021; Yang et al. 2013), so that equilibria of (3) coincide with stationary solutions of the following convex optimization problem:

$$\begin{aligned} \text{ minimize}_y \; p(\tau , y) \triangleq \frac{1}{2} y^T Q y+d^Ty + \tau ^TCy \; \text {s.t.} \; y \in Y, \end{aligned}$$
(6)

where p is a potential function.

To derive the explicit expression of \(Q \in {\mathbb {R}}^{NK \times NK}\), \(d \in {\mathbb {R}}^{NK}\) and \(C \in {\mathbb {R}}^{N \times NK}\), we preliminarily compute the gradient of \(\theta _\nu (\tau ^\nu , \bullet , y^{-\nu })\) at \(y^\nu\):

$$\begin{aligned}\begin{array}{rcl} \nabla _{y^\nu }\theta _\nu (\tau ^\nu ,y^\nu ,y^{-\nu }) &{} = &{}-\left( b^\nu \mu ^\nu +2 (b^\nu )^2 \Omega v^\nu +b^\nu \Omega \sum _{\lambda \ne \nu }b^\lambda v^\lambda + \tau ^\nu b^\nu ESG\right) \\ &{} &{}+(b^\nu )^2\left( \rho ^\nu \Sigma ^\nu + 2\Omega \right) y^\nu + b^\nu \Omega \sum _{\lambda \ne \nu }b^\lambda y^\lambda . \end{array}\end{aligned}$$

Hence, the Jaco-Hessian Q, is given by

$$\begin{aligned} \begin{array}{c} Q \triangleq \begin{pmatrix} \nabla ^\top _{y^1}(\nabla _{y^1} \theta _1(\tau ,y)) &{} \cdots &{} \nabla ^\top _{y^N}(\nabla _{y^1} \theta _1(\tau ,y))\\ \vdots &{} \ddots &{} \vdots \\ \nabla ^\top _{y^1}(\nabla _{y^N} \theta _N(\tau ,y)) &{} \cdots &{} \nabla ^\top _{y^N}(\nabla _{y^N} \theta _N(\tau ,y))\\ \end{pmatrix}\\ = \begin{pmatrix} (b^1)^2[\rho ^1\Sigma ^1+2\Omega ] &{} b^1 b^2\Omega &{} \cdots &{} b^1 b^N\Omega \\ b^2 b^1\Omega &{} (b^2)^2[\rho ^2\Sigma ^2+2 \Omega ] &{} &{} b^2 b^N\Omega \\ \vdots &{} &{} \ddots &{}\\ b^N b^1\Omega &{} b^N b^2 \Omega &{} &{} (b^N)^2[\rho ^N\Sigma ^N+2 \Omega ] \end{pmatrix}, \end{array} \end{aligned}$$

which turns out to be symmetric and positive semidefinite because \(\Omega\) and every covariance matrix \(\Sigma ^\nu\) are symmetric and positive semidefinite.

Vector d and matrix C in the expression of p are obtained according to the following formula:

$$\begin{aligned} \begin{array}{rcl} \begin{pmatrix} \nabla _{y^1} \theta _1(\tau ,0)\\ \vdots \\ \nabla _{y^N} \theta _N(\tau ,0) \end{pmatrix} &{} = &{} \begin{pmatrix} -[b^1 (\mu ^1+\Omega \sum _{\lambda \ne 1}b^\lambda v^\lambda + \tau ^1ESG)+ 2(b^1)^2\Omega v^1]\\ \vdots \\ -[b^N (\mu ^N+\Omega \sum _{\lambda \ne N}b^\lambda v^\lambda + \tau ^NESG)+ 2(b^N)^2\Omega v^1] \end{pmatrix}\\ &{} = &{} \underbrace{\begin{pmatrix} -[b^1 (\mu ^1+\Omega \sum _{\lambda \ne 1}b^\lambda v^\lambda )+ 2(b^1)^2\Omega v^1]\\ \vdots \\ -[b^N (\mu ^N+\Omega \sum _{\lambda \ne N}b^\lambda v^\lambda )+ 2(b^N)^2\Omega v^1] \end{pmatrix}}_{{d}}\\ &{} &{} + \underbrace{\begin{pmatrix} -b^1ESG &{} 0 &{} \cdots &{} 0\\ 0 &{} -b^2ESG &{} &{} 0\\ \vdots &{} &{} \ddots &{}\\ 0 &{} 0 &{} &{} -b^NESG \end{pmatrix}}_{{C^\top }} \tau . \end{array} \end{aligned}$$

Thanks to the equivalent formulation of NEP (3) as the convex optimization problem (6), we have

$$\begin{aligned} SOL(\tau ) = \arg \min _y \{p(\tau , y): \; y \in Y\} = \{y \in Y: p(\tau , y) \le \min _{v}\{p(\tau ,v): v \in Y \}\}. \end{aligned}$$

In turn, as commonly done in the literature, leveraging the value-function equivalent formulation of the implicitly defined constraint in (5), and introducing a reasonable positive tolerance \(\epsilon\) on the optimal value of the lower-level problem (see, e.g., Lignola and Morgan 2019), the references therein, and Lin et al. (2014) where justifications for this choice are provided both from a theoretical point of view and from a more practical, model-related one), we tackle (5) via the following (non convex) mathematical program:

$$\begin{aligned} \begin{array}{rl} \text{ minimize}_{\tau ,y} &{} F(y)\\ \text {s.t.} &{} \tau \in T,\ y\in Y \\ &{} p(\tau ,y) \le \min _{v}\{p(\tau ,v): v \in Y \}+\epsilon .\\ \end{array} \end{aligned}$$
(7)

3 How to treat the problem numerically

We wish to rely on a sequential convex approximation (SCA)-like algorithm that is specifically tailored to deal with problem (7), and essentially consists in the alternate solution of the lower level problem (once the value of \(\tau\) is iteratively fixed) and of a suitable (local) convex “approximating” version of (7), which is constructed based on the previous step. A sufficient condition for the procedure to achieve convergence to a stationary solution of (7) is the convexity of p (with respect to both \(\tau\) and y): such a requirement, while apparently restrictive, is shown to be satisfied, for the problem at hand, under standard assumptions. In particular, we rely on the following set of conditions which are assumed to hold throughout the rest of the paper.

Assumption A

$$\begin{aligned} \sigma ^{M_\nu }_m \ge \sigma > 0, \qquad b_\nu ^2 \Vert ESG \Vert ^2 \le \Gamma , \quad \nu =1,\ldots ,N, \end{aligned}$$
(8)

where \(\sigma ^M_m\) stands for the minimum eigenvalue of a square matrix M, \(M_\nu \triangleq (b^\nu )^2\ [\Omega +\rho ^\nu \Sigma ^\nu ]\) and \(\Gamma\) is a nonnegative scalar.

We note that, for example, the positive definiteness of \(\Omega\) is sufficient for the first relation in (8) to hold. Also, the latter inequality yields the following consequence.

Proposition 3.1

Matrix Q is positive definite and, in turn, SOL(\(\tau\)) is a singleton for every \(\tau\).

Proof

To prove the claim, suffice it to observe that

$$\begin{aligned} Q = \begin{pmatrix} (b^1)^2[\rho ^1\Sigma ^1+\Omega ] &{} 0 &{} \cdots &{} 0\\ 0 &{} (b^2)^2[\rho ^2\Sigma ^2+ \Omega ] &{} &{} 0\\ \vdots &{} &{} \ddots &{}\\ 0 &{} 0 &{} &{} (b^N)^2[\rho ^N\Sigma ^N+ \Omega ] \end{pmatrix} + b b^\top \otimes \Omega , \end{aligned}$$

where \(b = \begin{pmatrix} b^1&b^2&\cdots&b^N \end{pmatrix}^\top\) with \(\sigma _m^{bb^\top } = 0\), and recalling that the Kronecker product \(\otimes\) of positive semidefinite matrices is positive semidefinite. \(\square\)

Following the same line of reasoning in Lampariello and Sagratella (2020), adding to p a sufficiently large quadratic term (in \(\tau\)), the resulting modified function

$$\begin{aligned} p_\beta (\tau ,y)\triangleq p(\tau , y) + \frac{\beta }{2} \Vert \tau \Vert ^2 \end{aligned}$$

turns out to be convex in view of Assumption A.

Proposition 3.2

If

$$\begin{aligned} \beta \ge \frac{\Gamma }{\sigma }, \end{aligned}$$
(9)

then \(p_\beta\) is convex.

Proof

For every \(z \in {\mathbb {R}}^N\), we have,

$$\begin{aligned} 0&\le \left( \beta -\frac{\Gamma }{\sigma }\right) \Vert z \Vert ^2 \\&\le \beta \Vert z\Vert ^2 - \frac{\Vert C\Vert ^2}{\sigma ^{Q}_m}\Vert z \Vert ^2 \\&\le \beta \Vert z\Vert ^2 - \frac{1}{\sigma ^{Q}_m}\Vert C z\Vert ^2 \\&\le z^T(\beta I)z - z^T C^TQ^{-1}Cz \\&= z^T(\beta I -C^TQ^{-1}C)z, \end{aligned}$$

that is \((\beta I -C^TQ^{-1}C)\succeq 0\). Therefore, by the Schur Complement Theorem,

$$\begin{aligned}\nabla ^2 p_\beta (\tau ,y) = \begin{pmatrix} \beta I &{} C\\ C^T &{} Q\\ \end{pmatrix} \succeq 0\end{aligned}$$

and in turn \(p_\beta\) is convex. \(\square\)

We remark that replacing p with \(p_\beta\) in (6) and in (7) does not modify the problems. On the one hand, since, in \(p_\beta\), the quadratic term depending on \(\tau\) is constant with respect to y, problem

$$\begin{aligned} \text{ minimize}_y \ p_\beta (\tau ,y) \quad \text {s.t.} \quad y \in Y \end{aligned}$$
(10)

is equivalent to (6). On the other hand, problem (7), by adding \(\frac{\beta }{2} \Vert \tau \Vert ^2\) to both sides of the functional constraint, is equivalent to

$$\begin{aligned} \begin{array}{rl} \text{ minimize}_{\tau ,y} &{} F(y)\\ \text {s.t.} &{} \tau \in T,\ y\in Y \\ &{} p_\beta (\tau ,y) \le \phi _\beta (\tau )+\epsilon , \end{array} \end{aligned}$$
(P)

where

$$\begin{aligned}\phi _\beta (\tau )\triangleq \min _{y}\{p_\beta (\tau ,y): y \in Y \} = \min _{y}\{p(\tau ,y): y \in Y \} + \frac{\beta }{2} \tau ^\top \tau .\end{aligned}$$

Also, the straightforward relation \(SOL(\tau ) = \arg \min _v \{p_\beta (v, \tau ): v \in Y\}\) is freely invoked in the following developments.

Problem (P) enjoys some useful properties that make it numerically tractable. Specifically, standard constraint qualifications hold for it (see (i) in Remark 3.2), function \(\phi _\beta\), while still implicitly defined, is continuously differentiable and convex (see Proposition 3.3), and, in turn, relation \(p_\beta (\tau ,y)-\phi _\beta (\tau ) \le \epsilon\) turns out to be a DC (difference of convex functions) constraint.

Proposition 3.3

Function \(\phi _\beta\) is convex and continuously differentiable. Moreover, for every \(\tau\) and \(w = SOL (\tau ),\)

$$\begin{aligned}\nabla \phi _\beta (\tau ) = Cw+\beta \tau . \end{aligned}$$

Proof

By Proposition 3, \(p_\beta\) is convex, and then \(\nabla \phi _\beta (\tau )= \nabla _{\tau } p_\beta (\tau ,w) = Cw+\beta \tau\) due to (Lampariello and Sagratella 2020, Proposition 1). \(\square\)

From now on, we freely invoke some mathematical properties and tools from variational analysis. For example, we denote by \(N_S(z)\) the classical normal cone (to the convex set \(S \subseteq {\mathbb {R}}^n\) at \(z \in S\)) of convex analysis. As for the definitions of continuity properties for set-valued mappings, we refer the reader to Rockafellar and Wets (1998).

Remark 3.1

Bilevel problems (7) and (P) share the same standard optimistic point of view. Actually, for the specific problem at hand, they turn out to be equivalent, both in a global and in a local sense, to their original optimistic counterparts (see Lampariello and Sagratella (2017); Zemkoho (2016) for further details about the two different versions of optimistic bilevel problems). More precisely, the original optimistic version of (P) reads as follows:

$$\begin{aligned} \begin{array}{rl} minimize _{\tau } &{} \min _y \left\{ F(y) : \, y\in Y, \, p_\beta (\tau ,y) \le \min _{v}\{p_\beta (\tau ,v): v \in Y \}+\epsilon \right\} \\ s.t. &{} \tau \in T. \end{array} \end{aligned}$$
(11)

While, in general, there is a perfect correspondence between global optima of the original version and the ones of the standard optimistic bilevel problem, this is no more true for local solutions: local minima of the standard optimistic problem might not lead to corresponding local minima for the original optimistic counterpart (see Dempe et al. 2012; Zemkoho 2016). But, this is not the case for (P) and (11): following the same line of reasoning in (Lampariello et al. 2019, (ii,a) in Proposition 4.2), suffice it to observe that the set-valued mapping \(\{y \,: \, p_\beta (\bullet , y) - \phi _\beta (\bullet ) - \epsilon \le 0\} \cap Y\) is continuous on T in view of the continuity of \(p_\beta (\bullet , \bullet ) - \phi _\beta (\bullet )\) and the convexity of \(p_\beta (\tau , \bullet )\), and since the Slater’s constraint qualification is verified for every \(\tau \in T\) (see Bank et al. 1982, Theorems 3.1.1, 3.1.6). Similarly, the claim can be shown to hold also for (7) and its corresponding original optimistic version.

In the light of all the properties above, one can rely on the following novel algorithmic scheme to obtain (subsequential) convergence to stationary points of the nonconvex problem (P) and, thus, equivalently, (7).

Starting from \(\tau ^0 \in T\), \(y^0 \in Y\), for every \(k = 0,\ 1,\ \ldots\):

  • Step 1 compute \(w^k = SOL (\tau ^k)\)

  • Step 2 compute a solution (\(\tau ^{k+1}, y^{k+1}\)) of the following subproblem:

    $$\begin{aligned} \begin{array}{ll} \text{ minimize}_{\tau ,y} &\quad {} F(y)\\ \text {s.t.} &\quad {} \tau \in T,\ y\in Y \\ &\quad {} p_\beta (\tau ,y) \le p_\beta (\tau ^k,w^k)+\nabla _{\tau } p_\beta (\tau ^k,w^k)^T\left( \tau -\tau ^k\right) +\epsilon . \quad \quad P(\tau ^k,w^k) \end{array} \end{aligned}$$

Subproblem (P\((\tau ^k,w^k)\)) is a convex surrogate for (P), where, at each iteration \((\tau ^k, w^k)\), the concave part in the DC constraint is replaced by its local (at the base point \((\tau ^k, w^k)\)) linear approximation. We also observe that the Slater’s condition is easily seen to hold for (P\((\tau ^k,w^k)\)) at every iteration, as recalled in Remark 3.2, where we collect some well-known results (see, e.g., Lampariello and Sagratella 2020) that are instrumental to prove convergence.

Remark 3.2

The following properties hold:

  1. (i)

    the Mangasarian--Fromovitz constraint qualification (MFCQ) is satisfied everywhere on the feasible set of (P), i.e. the following condition is satisfied for every \((\tau , y)\) that is feasible for (P):

    $$\begin{aligned} \begin{array}{rcl} \Bigg \{\lambda \in {\mathbb {R}} &{}: &{} \lambda \in N_{{\mathbb {R}}_-}(p_\beta (\tau , y) - \phi _\beta (\tau ) - \epsilon ),\\ &{} &{} 0 \in \begin{pmatrix} \nabla _\tau p_\beta (\tau , y) - \nabla \phi _\beta (\tau )\\ \nabla _y p_\beta (\tau , y) \end{pmatrix} \lambda + N_T(\tau ) \times N_Y(y)\Bigg \} = \{0\} \end{array} \end{aligned}$$
  2. (ii)

    the Slater’s constraint qualification, i.e.

    $$\begin{aligned} \left\{ ({{\widehat{\tau }}}, {{\widehat{y}}}) \in T \times Y: \, p_\beta ({{\widehat{\tau }}}, {{\widehat{y}}})- p_\beta (\tau , w) - \nabla _\tau p_\beta (\tau , w)^\top ({{\widehat{\tau }}} - \tau ) - \epsilon < 0\right\} \ne \emptyset , \end{aligned}$$

    (and thus, equivalently, the MFCQ) is verified on the convex feasible set of (P\((\tau ,w))\), for every \((\tau ,w) \in T \times Y\).

While the idea to rely on a convex (inner) approximation of the bilevel problem feasible set can be traced back to the SCA paradigm and, in particular, to Lampariello and Sagratella (2020), the procedure laid down above differs from classical SCA approaches in that no proximal regularization is present in the objective of subproblems (P\((\tau ^k,w^k)\)). As a result, one has to resort to a different proof technique.

Theorem 3.4

Every limit point \(({\overline{\tau }},{\overline{y}},{\overline{w}})\) of the sequence generated by the algorithm is such that \(({\overline{\tau }},{\overline{y}})\) is a KKT solution for problem (P), i.e.

$$\begin{aligned} 0 \in \begin{pmatrix} 0 \\ \nabla F({\overline{y}}) \end{pmatrix} + \begin{pmatrix} \nabla _{\tau } p_\beta ({\overline{\tau }},{\overline{y}})- \nabla _{\tau } \phi _\beta ({\overline{\tau }})\\ \nabla _{y} p_\beta ({\overline{\tau }},{\overline{y}}) \end{pmatrix} {\overline{\lambda }}+ [N_T({\overline{\tau }})\times N_Y({\overline{y}})], \end{aligned}$$
(12)

for some \({\overline{\lambda }} \in N_{{\mathbb {R}}_-} (p_\beta ({\overline{\tau }},{\overline{y}})- \phi _\beta ({\overline{\tau }})-\epsilon )\).

Proof

We first observe that, for every k,

$$\begin{aligned} \begin{array}{rcl} (\tau ^k,y^k) \in FEAS^s(\tau ^k,w^k) \triangleq \big \{(\rho , v) \in T \times Y \, &{}: &{} p_\beta (\rho , v) \le p_\beta (\tau ^k,w^k)\\ &{} &{} +\nabla _{\tau } p_\beta (\tau ^k,w^k)^\top \left( \rho -\tau ^k\right) +\epsilon \big \}, \end{array} \end{aligned}$$
(13)
$$\begin{aligned} (\tau ^{k+1},y^{k+1})\in SOL^s(\tau ^k,w^k) \triangleq \arg \min _{\rho , v} \left\{ F(v): \, (\rho , v) \in FEAS^s(\tau ^k,w^k)\right\} , \end{aligned}$$
(14)

where (13) is shown to be valid reasoning similarly to the proof of (Lampariello and Sagratella 2020, Theorem 4.1), while (14) follows from the definition in step 2 of the algorithm.

As a consequence of (13), for every k, we have

$$\begin{aligned} F(y^{k+1}) \le F(y^k). \end{aligned}$$
(15)

Thus, \(\{F(y^k)\}\) is a non increasing, bounded from below, and thus convergent sequence.

Relations (13)–(15) are the building blocks of the proof of convergence: in order to prove the claim, we first establish some continuity properties of problem (P\((\bullet ,\bullet ))\) feasible and solution set-valued mappings. In fact, since the Slater’s constraint qualification holds on \(FEAS^s(\tau ,w)\) for every \((\tau , w) \in T \times Y\) (see (ii) in Remark 3.2), the set-valued mapping \(FEAS^s\) is continuous relative to \(T \times Y\) at any point in \(T \times Y\) (see Bank et al. 1982, Theorems 3.1.1 and 3.1.6). In turn, the value function

$$\begin{aligned}\psi (\tau ,w) \triangleq \min _{\rho , v} \left\{ F(v): \, (\rho , v) \in FEAS^s(\tau ,w)\right\} \end{aligned}$$

is continuous on \(T \times Y\), due to (Bank et al. 1982, Theorem 4.3.3), and finally, the set-valued mapping \(SOL^s(\bullet , \bullet ) = \left\{ (\rho , v): F(v) \le \psi (\bullet , \bullet )\right\} \cap FEAS^s(\bullet ,\bullet )\) is outer semicontinuous relative to \(T \times Y\) at any point in \(T \times Y\) (again, by Bank et al. 1982, Theorem 3.1.1). Following the same line of reasoning, but here in a simplified framework, it is standard to show that the single valued mapping \(SOL^l\) is continuous over T (see Rockafellar and Wets 1998, Corollary 5.20).

All the properties above yield the convergence result: suffice it to observe that, in view of the compactness of T and Y, subsequencing, we can write, without loss of generality, \((\tau ^k,y^k,w^k) \rightarrow ({\overline{\tau }},{\overline{y}},{\overline{w}})\), \((\tau ^{k+1},y^{k+1}) \rightarrow ({\widetilde{\tau }},{\widetilde{y}})\), and taking the limit in (13), by the continuity of \(FEAS^s\) on \(T \times Y\), we get

$$\begin{aligned} ({\overline{\tau }},{\overline{y}}) \in FEAS^s({\overline{\tau }},{\overline{w}}), \end{aligned}$$
(16)

where \({\overline{w}} \in SOL^l({\overline{\tau }})\), in view of step 1. Also, by (14), thanks to the outer semicontinuity of \(SOL^s\) over \(T \times Y\),

$$\begin{aligned} ({\widetilde{\tau }},{\widetilde{y}}) \in SOL^s({\overline{\tau }},{\overline{w}}). \end{aligned}$$
(17)

Finally, taking into account (15),

$$\begin{aligned} F({\overline{y}})=F({\widetilde{y}}). \end{aligned}$$
(18)

From (16), \(({\overline{\tau }},{\overline{y}})\) is feasible, and, in view of (17) and (18), also optimal for (P\(({\overline{\tau }},{\overline{w}}))\). Since the latter problem is convex and the Slater’s condition is satisfied (see point (ii) in Remark 3.2), this is equivalent to the existence of a multiplier \({\overline{\lambda }} \in N_{{\mathbb {R}}_-} (p_\beta ({\overline{\tau }},{\overline{y}})- p_\beta ({\overline{\tau }},{\overline{w}})-\epsilon )\) so that

$$\begin{aligned} 0 \in \begin{pmatrix} 0 \\ \nabla F({\overline{y}}) \end{pmatrix} + \begin{pmatrix} \nabla _{\tau } p_\beta ({\overline{\tau }},{\overline{y}})- \nabla _{\tau } p_\beta ({\overline{\tau }},{\overline{w}})\\ \nabla _{y} p_\beta ({\overline{\tau }},{\overline{y}}) \end{pmatrix} {\overline{\lambda }}+ [N_T({\overline{\tau }})\times N_Y({\overline{y}})], \end{aligned}$$
(19)

with \({\overline{w}} = SOL^l({\overline{\tau }})\). Observing that \(p_\beta ({\overline{\tau }},{\overline{w}}) = \phi _\beta ({\overline{\tau }})\) and \(\nabla _{\tau } p_\beta ({\overline{\tau }},{\overline{w}}) = \nabla \phi _\beta ({\overline{\tau }})\), the claim follows because (19) turns out to be equivalent to (12). \(\square\)

Clearly, equipping the objective in (P\((\tau ^k,w^k)\)) with the additional prox term \(\alpha /2 \Vert (\tau - \tau ^k, y - y^k)\Vert ^2\), for some positive \(\alpha\), convergence can be guaranteed a fortiori (see Lampariello and Sagratella 2020). In this case, the (now single-valued) solution set mapping of the modified subproblems turns out to be continuous (rather than just outer semicontinuous, as shown in Theorem 3.4); but this at the price of a reduced ability to possibly “move away” from the current iterate \((\tau ^k, y^k)\).

4 Experimental Study

In this section, we test the bilevel model (P) on two real-world datasets. More in detail, we compare the performances of our approach with the case where the upper-level decision variables \(\tau\) are fixed to 0; we do so to evaluate the impact of the upper-level decisions on the followers’ different objectives, i.e., portfolio expected return, risk, transaction costs and ESG. In Sect. 4.1, we describe the experimental setup, i.e., the dataset and the performance measures used in this work. In Sect. 4.2, we discuss some algorithm-related choices. Finally, in Sect. 4.3, we report the results of the empirical analysis. All the experiments are implemented on MATLAB R2022b using the built-in functions quadprog and fmincon, on a PC with Intel(R) Core(TM) i7-11800 H 2.30GHz, with 16 GB of RAM.

4.1 Problem data

We consider two datasets consisting in daily prices, adjusted for dividends and stock splits, daily traded volumes and daily ESG scores (from 01/01/2019 to 31/12/2020) downloaded from Thomson Reuters Datastream. Specifically, we consider the Dow Jones Industrial Average (DJIA), composed of \(K=28\) assets, and the NASDAQ 100 (NDX), composed of \(K=91\) assets. In both cases, we set the number of accounts \(N=5\), thus leading to a problem with \(N\times K\) variables, i.e., 140 for the DJIA dataset and 455 for the NDX dataset. We deal with discrete random returns drawn from historical data. Therefore, let \(T+1\) be the length of the time series of the prices, where \(p_{k,t}\) denotes the price of asset k at time t; given the prices, we compute the (linear) returns \(r_{k,t}=\frac{p_{k,t}-p_{k,t-1}}{p_{k,t-1}}\), with \(k=1,\ldots , K\) and \(t=1\ldots ,T\). Besides, we assume equally likely scenarios, so that every scenario has an equal probability of occurrence \(\frac{1}{T}\). Consequently, we compute \({\overline{\mu }}_{k}=\frac{1}{T}\sum _{t=1}^{T}r_{k,t}\) and \({\overline{\sigma }}_{kj}=\frac{1}{T}\sum _{t=1}^{T}(r_{k,t}-{\overline{\mu }}_{k})(r_{j,t}-{\overline{\mu }}_{j})\) which denote, respectively, the expected return of asset k and the covariance between assets k and j. The values \(\mu ^{\nu }\in [1,1.2]{\overline{\mu }}\) and \(\Sigma ^{\nu }\in [1,1.2]{\overline{\Sigma }}\) are uniformly randomly generated. As for the transaction costs, let \(vol_{k,t}\) be the traded volume of asset k at time t; then, we compute the correlation matrix of the traded volumes, in order to capture the effect of trades between different assets, where the interrelation of the traded volume between asset k and asset j is expressed as follows (see Lampariello et al. 2021):

$$\begin{aligned} \omega _{kj}=\frac{\sum _{t=1}^{T}(vol_{k,t}-{\overline{vol}}_{k})(vol_{j,t}-{\overline{vol}}_{j})}{\sqrt{\sum _{t=1}^{T}(vol_{k,t}-{\overline{vol}}_{k})^{2}}\sqrt{\sum _{t=1}^{T}(vol_{k,t}-{\overline{vol}}_{k})^{2}}}, \end{aligned}$$

with \({\overline{vol}}_{k}=\frac{1}{T}\sum _{t=1}^{T}vol_{k,t}\). We obtain the matrix \(\Omega =(\omega _{kj})^{K}_{k,j=1}\). Given the ESG score of the asset k at time t \(ESG_{k,t}\), we simply compute the arithmetic mean of such scores, i.e., \({\overline{ESG}}_{k}=\frac{1}{T}\sum _{t=1}^{T}ESG_{k,t}\). Furthermore, we uniformly randomly generate each value \(b^{\nu }\) and \(\rho ^{\nu }\), such that \(b^{\nu }\in [0, B]\) and \(\rho ^{\nu }\in [0,1]\frac{4\cdot 100}{B}\), with \(B=200\). Finally, we set the current positions \(v^{\nu }=0\), for \(\nu =1\ldots ,N\).

We consider the case of long-only portfolios: thus, for each \(\nu\), \(Y_{\nu }=\{y^{\nu }\in {\mathbb {R}}^{K}:e^{T}y^{\nu }=1,y^{\nu }\ge 0\}\), where e is the all ones vector; also, we take \(T=\{\tau \in \mathbb R^{N}:\tau \ge 0\}\).

4.2 Algorithmic choices

Concerning numerical computation, the lower-level optimization problem is solved using the built-in MATLAB solver quadprog, while the upper-level problem is solved using fmincon’s interior point method, where the gradient of the objective function and constraint are supplied to the solver. Default tolerances are adopted and, at iteration \(k+1\), \((y^k,\tau ^k)\) is employed as the starting point for the upper-level optimization. The parameter \(\beta\) is computed following (9) and then rescaled assuring the convexity of \(p_\beta\). Finally, the tolerance \(\epsilon\) is set to \(10^{-2}\).

Fig. 1
figure 1

Upper-level objective function for DJIA and NDX datasets

Full size image

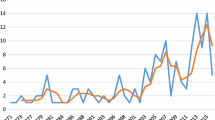
In Fig. 1, we show the value of the upper-level objective function through 10000 iterations for both datasets considered. Note that the monotonic decrease (i.e. relation 15) holds in both instances.

4.3 Results

We compare the performances of our model lower-level problems with the case where the accounts’ holders have no monetary incentive to construct an ESG-oriented portfolio. Therefore, in the latter case, the upper-level design variables \(\tau\) are taken equal to 0, which leads to the following single level optimization problem:

$$\begin{aligned} \text{ minimize}_y \; p(0, y) = \frac{1}{2} y^T Q y+d^Ty \quad \text {s.t.} \; y \in Y. \end{aligned}$$
(20)

We consider the following measures:

  • Income: it consists in the portfolio expected return \((\mu ^{\nu })^Ty^{\nu }\);

  • Risk: it is represented by the portfolio variance \((y^{\nu })^T\Sigma ^{\nu }y^{\nu }\);

  • TC: it is defined as the transactions costs of the portfolio \(y^\nu \Omega \sum _{\lambda \ne \nu } y^\lambda\);

  • ESG: it consists in the portfolio expected ESG score \({\overline{ESG}}^Ty^{\nu }\);

The main results are reported in Tables 1 (DJIA) and 2 (NDX). We display the values of Income, Risk, TC and ESG for each account \(\nu\). Besides, for each measure, we show the performances both in the case where \(\tau =0\) and where \(\tau\) is suitably optimized according to (P) (\(\tau =\tau ^{*}\)); for each reported measure, we also give the difference of the value that is obtained when \(\tau =\tau ^{*}\) and the value that is achieved if \(\tau =0\). As shown in Table 1, regarding DJIA, in two out of five accounts Income increases taking \(\tau =\tau ^{*}\); on the other hand, both Risk and TC increase, but the same happens to the remaining accounts. As it is expected, every account experiences an increase in ESG, as well. For each \(\nu\) a considerable fraction of the budget (more than 15%) is invested in the Microsoft stock, which yields the highest ESG score and the second highest expected return; the only exception is the third account (approximately 1% of the budget is invested in the Microsoft stock), which also faces the highest drop in Income. However, when compared to the others, such account also experiences lower increase in Risk (probably due to the high risk aversion, as well), TC and ESG. Interestingly enough, for all the accounts a fraction of the budget that ranges from 10% to 26% is invested in the stocks 3 M and Walgreens Boots Alliance, which have among the highest ESG scores and lowest expected return. The most diversified portfolio is the one held by the third account’s owner: this is the account experiencing the highest loss of Income, and the least increase of Risk, TC, and ESG; conversely, the least diversified portfolio is the one held by fourth account’s owner: this is the account where only the two assets with the highest ESG scores, i.e., Microsoft and 3 M, are included in the portfolio (leading to the largest increase in the ESG among all the accounts). As for NDX, as displayed in Table 2, whenever \(\tau\) is suitably optimized according to (P), we observe a loss of Income, and increase in Risk (with the only exception of the fourth account), TC and ESG. For all the accounts, a fraction of their budget comprised between 15% and 48% is invested in the Astrazeneca stock, which yields the highest ESG score, and one of the lowest expected return among all the assets. It is worth noting that, in the case that \(\tau =\tau ^{*}\), the fourth account’s owner, which is the one with the lowest risk aversion, experiences the largest reduction in Income and the smallest increase in Risk and TC. Like for DJIA, this account holder is the one with the least diversified investments since they only invest in the two assets with the largest ESG score (Microsoft and Astrazeneca); again, such account experiences the greatest increment in the ESG term.

Finally, for the sake of completeness, we report in Tables 3 and 4, for DIJA and NDX datasets, parameters and objectives values for the lower-level account-related problems. In Table 5, we indicate the optimal upper-level decision variables \(\tau\).

Summarizing, taking a bilevel point of view leads to a clear overall improvement in the ESG performances of the computed multiple portfolios (see Tables 1 and 2) and of the firm (see Fig. 1).

Table 1 Influence of the upper-level incentives on the lower-level objectives for DIJA dataset
Full size table
Table 2 Influence of the upper-level incentives on the lower-level objectives for NDX dataset
Full size table
Table 3 Parameters and objective function value for every \(\nu\) for DIJA dataset
Full size table
Table 4 Parameters and objective function value for every \(\nu\) for NDX dataset
Full size table
Table 5 Optimal upper-level decision variables \(\tau ^\nu\)
Full size table

5 Conclusions

We deal with ESG-oriented multiple portfolios selection. This complicated problem arises naturally when financial service providers decide to adopt SRI policies to comply with stakeholders’ demands and regulatory requirements. We rely on a novel bilevel approach where, at the upper-level, incentives are properly set to encourage the account’s holders, who play à la Nash at the lower-level, to make ESG-friendly investments, so that the overall ESG impact of the firm is optimized. Differently from conceptually simpler approaches in the literature, where the lower-level problem does not depend (parametrically) on upper-level design variables, we consider more general “genuine” bilevel structures. We establish practical sufficient conditions that make our model numerically tractable by means of a novel SCA-like algorithmic approach, whose convergence properties are investigated. This, together with an experimental study involving real-world data, show the viability of the approach we have developed.

We leave the investigation of even more general problem structures, where, e.g., assumptions yielding a lower-level (parametric) potential game with a unique solution are relaxed, and more complicated upper-level objectives are considered, to future research.