A criterion space decomposition approach to generalized tri-objective tactical resource allocation

Abstract

We present a tri-objective mixed-integer linear programming model of the tactical resource allocation problem with inventories, called the generalized tactical resource allocation problem (GTRAP). We propose a specialized criterion space decomposition strategy, in which the projected two-dimensional criterion space is partitioned and the corresponding sub-problems are solved in parallel by application of the quadrant shrinking method (QSM) (Boland in Eur J Oper Res 260(3):873–885, 2017) for identifying non-dominated points. To obtain an efficient implementation of the parallel variant of the QSM we suggest some modifications to reduce redundancies. Our approach is tailored for the GTRAP and is shown to have superior computational performance as compared to using the QSM without parallelization when applied to industrial instances.

1 Introduction

We present the generalized tactical resource allocation problem (GTRAP), which is a generalization of a previously introduced tactical resource allocation problem (TRAP); (Fotedar et al. 2022). The TRAP is a bi-objective multi-item capacitated production planning problem with a medium–to–long-term planning horizon defined for a large tier-1 aerospace engine system manufacturer. The bi-objective mixed-integer linear programming (MILP) model defined for the TRAP identifies routes that a product/part may take through the factory over a long planning horizon. There is a tendency (in our case company GKN Aerospace)¹ to utilize a few capable machines (w.r.t. tolerances, speed, and functionality) to a higher extent than other machines. This results in a resource loading imbalance in the production system which may further result in production delays. To relieve loading imbalance we consider qualifying alternative machines for a given type of task/job of the TRAP. Consequently, in the TRAP tasks/jobs are allocated to machines with the bi-objective goal to minimize both qualification costs and resource loading imbalance, while demand in each time period and various other side constraints are satisfied. The GTRAP, on the other hand, allows building some inventories between time periods and defines a third objective function, thus resulting in a tri-objective MILP. This work facilitates an understanding of the trade-off between the three objectives as well as the effect on the two previously defined objectives for the TRAP.

When facing real-world decision problems, decision-makers want to be mindful of the trade-off between different objectives/goals of the stakeholders, which are often in conflict. Therefore, various such problems are modeled as multi-objective optimization problems (MOOPs), which yield a set of so-called efficient solutions (corresponding objective vectors are called non-dominated points (NDPs)). This set contains solutions such that none of the objective functions’ values can be improved (reduced in a minimization problem) without degrading (increasing for a minimization problem) one or several objective functions’ value(s). A common method to solve MOOPs is the criterion/objective space search method.² Different criterion space search methods have varying effects on the computational performance depending on the problem properties and the instances. In this work, we present an approach to enhance the computational performance of the Quadrant shrinking method (QSM) (Boland et al. 2017) by means of parallelization.

1.1 Contribution

Our contribution is two-fold. Firstly, we modify the previously defined TRAP (Fotedar et al. 2022) to include inventories of both semi-finished and finished products/parts. We refer to this model as the GTRAP. We provide a mathematical formulation of the problem at hand. Secondly, we present a few propositions for our problem which are utilized in the development of a tailored approach to partition the criterion space. The resulting sub-problems are solved in parallel using the criterion space Quadrant shrinking method (QSM) by Boland et al. (2017). The choice of the QSM is due to its utilization of the so-called concept of projection onto the two-dimensional criterion space, which can easily be parallelized due to the properties of the GTRAP. This, along with some modifications to reduce redundancies while computing NDPs, results in an improved computational performance as compared to simply using the QSM without parallelization. Computational experiments are performed for numerical instances provided by GKN Aerospace.

1.2 Outline

In Sect. 2, we discuss literature concerning both tactical production planning models and multi-objective optimization methods. A mathematical model for the GTRAP is defined in Sect. 3. In Sect. 4, we present an approach to decompose the projected two-dimensional criterion space (see Def. 2) and define sub-problems solved in parallel. We also present modifications necessary for the effective implementation of the parallel variant of the QSM, the P-QSM. In Sect. 5, we test our approach on fifteen industrial instances and compare the computational performance of the QSM to that of our proposed parallel variant, the P-QSM. We perform sensitivity analyses to assess the performance of P-QSM and QSM by varying the loading threshold (an input parameter in our model). We assess the quality of resulting representations of the Pareto front using cardinality and coverage gap values.

2 Literature, scope, and the quadrant shrinking method (QSM)

We next present key aspects of tactical planning models, define the scope of the GTRAP, and provide some classical results for multi-objective (integer) linear optimization methods (criterion space search methods in particular).

2.1 Tactical planning literature and model scope

Tactical production planning determines material flows, inventory levels, and resource utilization; it is usually done 1–4 years in advance (in the Aerospace industry) and acts as an input to operational models, such as machine scheduling. There are five main characteristics of tactical planning problems (Díaz-Madroñero et al. 2014): (a) number of products/items and structure of bill–of–materials/levels (e.g. series, assembly, general, arborescence) (Pochet and Wolsey 2006, Chapter 13); (b) uncertainty in demand/processing times/costs; (c) time discretization; (d) capacity constraints; (e) types of objective functions. In any modern production system, multiple products are produced, each requiring at least one part/component. Several articles model uncertainty using stochastic programming (Lan et al. 2011; Nourelfath 2011), less commonly using fuzzy sets (Chen and Huang 2010; Lan et al. 2011), and sometimes by robust approaches (Wei et al. 2011; Genin et al. 2008). Mainly two types of time discretizations are considered: short time buckets, with enough time to manufacture only one part/item; long time buckets, in which multiple parts or an entire product is produced. Most companies employ a so-called rolling horizon and prepare a production schedule only when a customer order has been created in their planning system which is generally a few hours/days/weeks (varying between companies) before the delivery time/date is fixed. Hence, simultaneous scheduling and tactical allocation are not that useful in an industrial setting. Generally, tactical planning models have long time buckets which vary between months and quarters of a year, depending on the lead times of products. The capacity constraints in tactical models are on machines (hours available), man-hours, fixtures, tools, and inventory levels. The most common type of objective function minimizes cost/time (processing time, set-up time, and fixture cost (Bradley and Glynn 2002; Mieghem 2003)).

The GTRAP is a multi-item, multi-level (series assembly) tactical production planning model. The series product structure is due to each product requiring a sequence of (machining) operations such as milling, turning, and grinding. The raw material undergoes a series of operations to result in a product. The capacity limitation is on the number of raw materials available, machine capacity (time limitations), availability of technical staff to verify whether an operation can be performed in a machine, and an upper limit on the total inventory. The demand is considered deterministic due to long-term contracts and the availability of an accurate forecast (over a long time bucket). We consider three objective functions: (a) minimizing the maximum resource (machine) loading above a given threshold, (b) minimizing the qualification cost required to verify that a task can be performed in a machine, and (c) minimizing the total inventory (mathematical details in Sect. 3).

2.2 Multi-objective optimization literature

The two key computational challenges in the effective implementation of a criterion space search method (for discrete MOOPs)³ are the number/type of scalarized problems solved to identify all the NDPs, and efficiently update the search region (required to identify the region containing yet-unknown NDPs). For the latter Dächert et al. (2017) and Klamroth et al. (2015) provide efficient approaches based on updating local upper bounds, but neither of them discusses what type of scalarization to use. This work focuses on the former since for the GTRAP most of the computational effort is spent on solving the scalarized problems. Laumanns et al. (2006) provide a theoretical bound of $(|F_\mathrm{ndp}|+1)^{k-1}$ scalarized problems required to find all NDPs of a discrete MOOP, k and $|F_\mathrm{ndp} |$ being the number of objectives and NDPs, respectively. Dächert and Klamroth (2014) are (to the best of our knowledge) the first to provide linear bounds $2 |F_\mathrm{ndp} |-1$ on the number of scalarized problems required to identify all the NDPs of a tri-objective integer linear programming (TOILP) problem using the split criterion space search method. Another method specially designed for TOILP problems is the so-called L-shaped method (LSM); the number of scalarizations solved by LSM is, however, bounded between $2|F_\mathrm{ndp} |+ 1$ and $|F_\mathrm{ndp} |^{2} + |F_\mathrm{ndp} |+ 1$ (Boland et al. 2015, Theorem. 14). Theoretically, the split method of Dächert and Klamroth (2014) is superior to LSM. There is, however, a trade-off between solving fewer scalarized problems (Dächert and Klamroth 2014) with increasing difficulty (as more disjunctive constraints are added) and solving more scalarized problems of manageable sizes (Boland et al. 2015). One of the benefits of LSM is that it produces high-quality approximate efficient frontiers faster than the split method in (Dächert and Klamroth 2014). The computational benefits of LSM are demonstrated by numerical tests on numerous publicly available instances; see (Boland et al. 2015).

The main idea behind the split method by Dächert and Klamroth (2014) is the following: at an iteration $t\ge 2$, the algorithm searches for a NDP, $\mathbf{f}^{t} \not \in \{ \mathbf{f}^{1}, \ldots , \mathbf{f}^{t-1} \}$. This is done by adding $t-1$ binary variables that impose $\mathcal {O}(t-1)$ disjunctive constraints, to remove the dominated points from the search space. Consequently, with an increasing number of iterations, the scalarized problems grow larger and become much harder to solve to (near-)optimality. To avoid adding too many disjunctive constraints and binary variables, various methods suggest a decomposition of the criterion space using projections onto a two-dimensional criterion space. One such method is the recursive method (Özlen et al. 2013) which searches the projected two-dimensional criterion space by restricting the value of the third objective function. The projected two-dimensional criterion space can be explored using the well-known $\varepsilon$-constraint method. The LSM (Boland et al. 2015, Sect. 4.2) uses both rectangular as well as L-shapes in the projected two-dimensional criterion space. To reduce the number of single-objective scalarized problems required to identify all the NDPs, the authors developed the so-called quadrant shrinking method (QSM) (Boland et al. 2017, Algorithm 1) which requires at most $3|F_\mathrm{ndp}|+1$ single-objective ILPs to be solved as opposed to $|F_\mathrm{ndp}|^{2} + |F_\mathrm{ndp}|+1$ in the LSM. Boland et al. (2017) showed that the QSM has a better computational performance than both the LSM and the split method, as well as the enhanced recursive algorithm by Özlen et al. (2013) on various publicly available instances.

Parallel methods for discrete MOOPs. Each scalarization of a discrete MOOP is generally $\mathcal{N}\mathcal{P}$-hard; hence, industry-size instances may require long computing times, which may discourage end-users from utilizing a decision support tool relying on the solution of multiple scalarized problems to near-optimality. On the other hand, the rapid growth of technology concerning processors (multi-core), networks, and architecture have led to parallelization becoming a subject of interest within the optimization community. Already, there has been an extensive parallelization of the branch–and–bound method, which is utilized in all commercial MILP solvers such as Gurobi and CPLEX; (Bixby et al. 1999). There are some frameworks presented for the parallelization of metaheuristics used to solve MOOPs (summary in (Talbi et al. 2008, Ch. 13.2)). Such general frameworks do, however, rarely exist for exact criterion space search methods, one reason being that most exact criterion space search methods are sequential and require a solution to the previous scalarized problem to adjust the current one appropriately. A few articles parallelize parts of a given criterion space search method. For instance, Dhaenens et al. (2006) solve a bi-objective flow-shop problem by parallelizing the weighted sum method using so-called dichotomic search, which initiates two new parallel searches once a solution is found. Hence, several processors are idle in the first phase of the approach. Lemesre et al. (2007) present a parallel approach to solving the bi-objective flow-shop problem in which the two-phase method in (Ulungu and Teghem 1994) is parallelized. To the best of our knowledge, discrete MOOPs with more than two objectives have not been considered for parallelization in the literature.

2.3 Preliminaries, and the QSM

To enable parallel computing, we must first identify an appropriate criterion space search method. We choose the QSM (Boland et al. 2017) due to two reasons: (a) as indicated in the previous subsection it has a superior computational performance (for several benchmarking instances); (b) most importantly, it works on the projected two-dimensional criterion space, thus facilitating an efficient decomposition of the criterion space (discussed in Sect. 4). The QSM is briefly presented, starting with some important notations and definitions.

Let $k \ge 2$ (we use the notations only for comparing vectors, for scalars regular notations are used). For any two vectors $\textbf{u}, \textbf{w} \in \mathbb {R}^{k}$ it holds that

$$\begin{aligned}&\textbf{u} \leqq \textbf{w}{} & {} \iff{} & {} w_i \in [u_i, \infty ) \quad \forall i \in \{1,\ldots ,k\}; \end{aligned}$$

(1a)

$$\begin{aligned}&\textbf{u} \le \textbf{w}{} & {} \iff{} & {} w_i \in [u_i, \infty ) \quad \forall i \in \{1,\ldots ,k\} \;\; \mathrm{and} \;\; \textbf{u} \ne \textbf{w}; \end{aligned}$$

(1b)

$$\begin{aligned} \qquad&\textbf{u} < \textbf{w}{} & {} \iff{} & {} w_i \in (u_i, \infty ) \quad \forall i \in \{1,\ldots ,k\}. \end{aligned}$$

(1c)

Definition 1

(Efficient solutions) Given a TOILP problem

$$\begin{aligned} \min _{\textbf{x} \in X} \; \big \{f_{1}(\textbf{x}), f_{2}(\textbf{x}), f_{3}(\textbf{x}) \big \}, \end{aligned}$$

(2)

where the feasible set $X \subset \mathbb {Z}_{+}^{n}$ is defined by a set of affine constraints in the decision space, and the objective functions $f_{1}, f_{2}, f_{3}: \mathbb {Z}^n_+ \mapsto \mathbb {R}_{+}$ are linear and non-negative on the feasible set. The image F of X, defined as $F{:}{=} \textbf{f}(X) {:}{=} \{ \, \textbf{f} \in \mathbb {R}_{+}^{3} \, |\, \textbf{f} = \textbf{f}(\textbf{x}) \text { for some } \textbf{x} \in X \, \}$, represents the feasible set in the criterion space.

A solution $\textbf{x}^{*} \in X$ is called weakly efficient in (2) if there exists no feasible solution $\textbf{x} \in X$ such that $\textbf{f}(\textbf{x}) < \textbf{f}(\textbf{x}^{*})$.

A solution $\textbf{x}^{*} \in X$ to (2) is called efficient if there exists no feasible solution $\textbf{x} \in X$ such that $\textbf{f}(\textbf{x}) \le \textbf{f}(\textbf{x}^{*})$. The corresponding point in the criterion space $\textbf{f}(\textbf{x}^{*})$ is called a non-dominated point (NDP). A set of efficient solutions is denoted as $X_{\mathrm{eff}}$.

Any two points $\textbf{u}^{1}, \textbf{u}^{2} \in \mathbb {R}_{+}^{2}$ such that $\textbf{u}^{1} \le \textbf{u}^{2}$ define a rectangle (or a line segment if either $u^{1}_{1}= u^{2}_{1}$ or $u^{1}_{2}= u^{2}_{2}$ ) $R(\textbf{u}^{1}, \textbf{u}^{2}){:}{=} \{\textbf{u} \in \mathbb {R}_{+}^{2} \, |\, u_{1}^{1} \le u_{1} \le u_{1}^{2}, u_{2}^{1}\le u_{2} \le u_{2}^{2}\}$. The next definition is used in the QSM and several other methods employing the projection of NDPs onto lower-dimensional subspaces.

Definition 2

(Projection onto two-dimensional criterion space) We denote the projection of a point $\textbf{f} {:}{=} (f_{1}, f_{2}, f_{3})^{\top } \in \mathbb {R}_{+}^{3}$ onto the two-dimensional criterion space of the two first dimensions as $\hat{\textbf{f}} {:}{=} (f_{1}, f_{2})^{\top } \in \mathbb {R}_{+}^{2}$. Subsequently, a projected two-dimensional criterion space is defined as the space that contains the points obtained by projecting each objective point corresponding to a feasible solution onto the two-dimensional criterion space.

The QSM works in a projected two-dimensional criterion space (w.l.o.g. we consider projection onto the first two objective functions). Given an upper bound (on the first two objectives) $\textbf{u} \in \mathbb {R}_{+}^{2}$, the main operation is to find yet-unknown NDPs in $R(\textbf{0},\textbf{u})$ (also referred to as a quadrant with upper bound $\textbf{u}$). Consider a NDP $\textbf{f}^{*} = \textbf{f}(\textbf{x}^{*})$ possessing the property that its projection $\hat{\textbf{f}}^{*} \in \mathbb {R}_{+}^{2}$ satisfies $\hat{\textbf{f}}^{*} \leqq \textbf{u}$ for a given $\textbf{u}$ in the two-dimensional projected criterion space and that can be found by solving two integer programming problems (see Def. 3). The results are formally described in a general setting as follows.

Definition 3

(Two-stage scalarization; (Kirlik and Sayın 2014)) For $\textbf{u}\in \mathbb {R}_{+}^{2}$, $\textbf{f}: \mathbb {Z}^{n}_{+}\rightarrow \mathbb {R}_{+}^{3}$ (linear and non-negative functions), $X\subset \mathbb {Z}_{+}^{n}$ and $k \in \{ 1, 2, 3 \}$ the set $X^{k}(\textbf{u})$ of optimal solutions to the two-stage scalarization of (2) is defined as

$$\begin{aligned}{} & {} X^{k}(\textbf{u}) {:}{=}{} & {} {{\,\mathrm{arg\,min}\,}}_{\textbf{x} \in X} \;\; \sum _{j=1}^{3}f_{j}(\textbf{x}), \end{aligned}$$

(3a)

$$\begin{aligned}{} & {} {} & {} \text {s.t.} \quad \qquad f_{j}(\textbf{x})&\le u_{j},{} & {} j \in \{1,2,3\} \setminus \{ k \},{} & {} {} & {} {} & {} \end{aligned}$$

(3b)

$$\begin{aligned}{} & {} {} & {} f_{k}(\textbf{x})&= \bar{f}_{k}(\textbf{u}), \end{aligned}$$

(3c)

where

$$\begin{aligned}{} & {} \bar{f}_{k}(\textbf{u}) {:}{=}{} & {} \min _{\textbf{x} \in X} \;\; f_{k}(\textbf{x}), \end{aligned}$$

(4a)

$$\begin{aligned}{} & {} {} & {} \text {s.t.} \quad f_{j}(\textbf{x})&\le u_{j},{} & {} j \in \{ 1, 2 ,3 \} \setminus \{ k \}.{} & {} {} & {} {} & {} \end{aligned}$$

(4b)

Theorem 4

(Kirlik and Sayın 2014, Theorem 1) Let $k \in \{ 1, 2, 3 \}$. For any $\textbf{u} \in \mathbb {R}_{+}^{2}$ any optimal solution $\textbf{x}^{k}(\textbf{u}) \in X^{k}(\textbf{u})$ to the two-stage scalarization Eqs. (3)–(4) is efficient for the TOILP problem (2).

Theorem 5

(Kirlik and Sayın 2014, Theorem 2) For any efficient solution $\bar{\textbf{x}}$ of a TOILP (2), there exists an $\textbf{u} \in \mathbb {R}_{+}^{2}$ such that for some $k \in \{ 1, 2, 3 \}$, $\bar{\textbf{x}} \in X^{k}(\textbf{u})$ holds, i.e. $\bar{\textbf{x}}$ is optimal in the two-stage scalarization (3)–(4).

To give a brief overview of the QSM we provide an example (for more details, see (Boland et al. 2017, Algorithm 1, pp. 875–877)). Let $F_\mathrm{ndp}$ be the set of NDPs identified and U be the set of upper bounds of quadrants that may contain projections onto the $(g_{1}, g_{2})$-criterion space of unidentified NDPs. The set U is initialized with the pre-defined upper bounds $\mathbf{u}^{1} \in \mathbb {R}_{+}^{2}$ on the first two objectives, as depicted in Fig. 1a. We apply the two-stage scalarization (see Def. 3) for the vector $\mathbf{u}^{1}$. The resulting solution $\mathbf{x}^{1} \in X^{3}(\mathbf{u}^{1})$ corresponds to the NDP $\mathbf{f}^{1} \in \mathbb {R}_{+}^{3}$, which is such it has the least value for the third objective. Consequently, the set $F_\mathrm{ndp}=\{\mathbf{f}^{1}\}$. The projection $\hat{\mathbf{f}}^{1}= (f^{1}_{1}, f^{1}_{2})^{\top }$ is illustrated in Fig. 1b. From (Boland et al. 2017, Prop. 6) follows that the search region $\{ \, \hat{\mathbf{f}} \in \mathbb {R}^{2} \, |\, \hat{\mathbf{f}} \ge \hat{\mathbf{f}}^{1} \, \}$ contains projections of points that are dominated by the point $\mathbf{f}^{1} \in \mathbb {R}_{+}^{3}$. Hence, the dark grey-shaded region does not contain projections of NDPs. Subsequently, the set U of upper bounds is updated with the inclusion of $\mathbf{u}^{2}$ and $\mathbf{u}^{3}$, and the removal of $\mathbf{u}^{1}$. To avoid recomputing $\mathbf{f}^{1}$, the upper bounds are defined as $\mathbf{u}^{2} = (u_{1}^{1}, \hat{f}^{1}_{2} - \delta _{2})^\top$, where $\delta _{2}>0$ is an appropriate discretization of $f_{2}$ ($\delta _{2}$ can equal 1 if $f_{2}$ is integer-valued). Analogously, the usage of a discretization parameter $\delta _{1} > 0$ results in $\mathbf{u}^{3} = ( \hat{f}_{1}^{1}-\delta _{1}, u^{1}_{2} )^\top$. In the next iteration, the quadrant $R(\textbf{0}, \mathbf{u}^{2})$ is searched for NDPs; the NDP $\mathbf{f}^{2}$ is found (its projection $\hat{\mathbf{f}}^{2}$ is illustrated in Fig. 1c). The set $F_\mathrm{ndp}$ is updated by the inclusion of $\mathbf{f}^{2}$, and U by the removal of $\mathbf{u}^{2}$ and the inclusion of $\mathbf{u}^{4}$ and $\mathbf{u}^{5}$. In the next iteration, $R(\textbf{0}, \mathbf{u}^{4})$ is searched for NDPs, resulting in an infeasible model (4); hence, no objective vector is projected onto this region (light grey-shaded in Fig. 1d). A reasoning about the order of removal and inclusion of elements from/into the set U is given in (Boland et al. 2017, Lemma 11).

Fig. 1

In each sub-figure the set $F_\mathrm{ndp}$ (circles) contains projections of some of the NDPs onto the two-dimensional criterion space, while the set U (triangles) contains upper bounds on the quadrants used to search for NDPs (the upper bound of the explored quadrant is underlined). Shaded areas indicate regions without any projection of NDPs (dark) and with no feasible projection (light)

3 Description of the GTRAP

Definition 6

(Generalized Tactical Resource Allocation Problem (GTRAP)) Given a set $\mathcal {L}$ of part/product types, for each part/product $\ell \in \mathcal {L}$ an ordered sequence $\mathcal {J}_{\ell } {:}{=} \{1, \ldots , J_{\ell }\}$ of manufacturing operations are performed, starting from raw material and ending with a finished part, when all operations in $\mathcal {J}_{\ell }$ are performed. In each time period $t\in \mathcal {T}$, orders of task $(j,\ell ) \in \mathcal {M}$, must be assigned to one or several machines from the set $\mathcal {K}$. Let $p^{\ell }_{jk}$ be the processing time (including set-up time) of task $(j,\ell )$ when performed in a compatible machine $k \in \mathcal {K}^{\ell }_{j} \subseteq \mathcal {K}$. Each machine $k \in \mathcal {K}$ has the capacity $C_{kt}$ (time units) in time period $t \in \mathcal {T}$ and a (relative) loading threshold $\zeta \in [0, 1]$. The demand $a^{\ell }_{t}$ of part $\ell \in \mathcal {L}$ in time period $t \in \mathcal {T}$ must be met. The number of machines allocated to the same task in each time period may not exceed the value of the parameter $\tau \in \mathbb {Z}_{+}$. Any task–to–machine assignment $(j,\ell ,k)$ such that $k \in \mathcal {N}^{\ell }_j \subseteq \mathcal {K}^{\ell }_{j}$ requires a so-called qualification (or verification), which generates the additional one-time cost $\beta ^{\ell }_{jk}$, $j \in \mathcal {J}_{\ell }$, $\ell \in \mathcal {L}$. For (pre-qualified) machines $k \in \mathcal {K}^{\ell }_j \setminus \mathcal {N}^{\ell }_{j}$ the assignment $(j,\ell ,k)$ does not require a qualification. Since inventories of semi-finished or finished parts⁴ can be stored between time periods, the production in each time period may exceed or fall short of the demand. The total number of qualifications performed per time period t may not exceed the value of the parameter $\gamma \in \mathbb {Z}_{+}$. Upper limits $\bar{r}^{\ell }_{jt}$, $j \in \widetilde{\!\!\mathcal {J}}_{\ell }{:}{=} \mathcal {J}_{\ell } \cup \{0\}$, $t \in \mathcal {T}$, $\ell \in \mathcal {L}$ (0 referring to the raw material) are set on the inventories. The total amount of raw material for $\ell \in \mathcal {L}$ ordered in each time period t may not exceed $d\,a^{\ell }_{t}$, where $d> 0$ is a user-defined limiting factor and $a^{\ell }_{t}$ is the demand of part type $\ell$ in time period t. $\square$

The three objectives considered are the following: (i) minimize the sum (over time periods) of the maximum excess resource loading above the given threshold $\zeta$; (ii) minimize the total qualification cost; (iii) minimize the total inventory. Since the objectives are measured in different units they cannot be combined in a single objective function, neither they obey any clear priority order but are considered equally important. The notations are summarized in Table 1.

Table 1 Notations for the GTRAP

3.1 Network formulation

Fig. 2

Network illustration for a given $\ell \in \mathcal {L}$, where $J_{\ell } = 2$ (the upper index $\ell$ being omitted in the figure notations). The node labels denote for $j \in \widetilde{\!\!\mathcal {J}}_\ell$ and $t \in \mathcal {T}$

Fig. 2 illustrates the underlying network structure of the GTRAP for a single part $\ell \in \mathcal {L}$. The three horizontal levels (from top to bottom) correspond to $\widetilde{\!\!\mathcal {J}}_{\ell } = \{0,1,2\}$, while the three vertical levels (from left to right) represent $\mathcal {T}=\{1,2,3\}$. Each node corresponds to a 2-tuple (j, t), where $j \in \widetilde{\!\!\mathcal {J}}_{\ell }$ and $t \in \mathcal {T}$. The network should fulfill a balanced flow according to the following. Each node labelled (j, t) receives a flow of semi-finished ($0<j<J_{\ell }$) or finished ($j=J_{\ell }$) parts, or raw materials ($j=0$) either from the inventory (the variable $r^{\ell }_{j,t-1}$; horizontal incoming arcs) or after operation j is performed in a compatible machine in the set $\mathcal {K}^{\ell }_{j}$ in time period t (vertical incoming arcs) or raw materials (the variable $m^{\ell }_{t}$). The flow out of node (j, t) either (if $j<J_{\ell }$) undergoes operation $j+1$ in one of the compatible machines in $\mathcal {K}^{\ell }_{j+1}$ (vertical outgoing arcs), or (if $j=J_{\ell }$) it is used to meet the demand $a^{\ell }_{t}$ or results in the inventory $r^{\ell }_{jt}$ (horizontal outgoing arcs). The amount of raw material ordered in each time period is represented by $m^{\ell }_{t}$.

We next present a mathematical model defining the set of feasible solutions to the GTRAP. The constraints (5a) model the flow balance of the raw materials for each part. The constraints (5b) model the flow balance for all semi-finished parts (when the raw material has gone through operations $j \in \mathcal {J}_{\ell } \setminus {\{J_{\ell }\}}$), for which there is no external demand. The constraints (5c) model the flow balance for $(J_{\ell },\ell , t)$, i.e. for the final operation to obtain a part $\ell \in \mathcal {L}$. The constraints (5d) set the initial inventory of semi-finished/finished parts to their respective input values. The constraints (5e) set the variables $s^{\ell }_{jkt}$ to one if $x^{\ell }_{jkt}>0$; see Table 1 for the coefficients $M^{\ell }_{jkt}$. The constraints (5f) restrict the number of machines for a given type of task in each time period to a user-defined value $\tau$. The constraints (5g) set the upper limit on the total number of hours available in a given machine in each time period, and establish the variables $n_{t}$, $t \in \mathcal {T}$, used in the first objective function. The constraints (5h) set the value of the variable $z^{\ell }_{jkt}$ to 1 if a task $(j,\ell )$ is to be qualified for a machine $k \in \mathcal {N}^{\ell }_{j}$ in time period t. These constraints imply that if $s^{\ell }_{jkq}=1$, where $k\in \mathcal {N}^{\ell }_{j}$, $q\in \mathcal {T}$, then a qualification of machine k for task $(j,\ell )$ must be done once during the time periods $\{ 1, \ldots , q \}$. The constraints (5i) define an upper limit on the total number of qualifications performed during each time period, due to a limited availability of technical staff. The constraints (5j) set upper limits for the inventories. Similarly, (5k) sets an upper limit on the maximum amount of raw materials ordered in each time period, which is due to the reluctance of the manufacturer to increase the tied-up working capital. The constraints (5l)–(5q) state that the variables $\textbf{s}$ and $\textbf{z}$ are binary, $\textbf{r}$, $\textbf{x}$, and $\textbf{m}$ are non-negative integers, and $\textbf{n} \ge \textbf{0}$ are continuous.

$$\begin{aligned} m^{\ell }_{t} + r^{\ell }_{0,t-1}&= r^{\ell }_{0t} + \sum _{k \in \mathcal {K}^{\ell }_{1}}x^{\ell }_{1kt},{} & {} \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5a)

$$\begin{aligned} \sum _{k \in \mathcal {K}^{\ell }_{j}} x^{\ell }_{jkt} + r^{\ell }_{j,t-1}&= r^{\ell }_{jt} + \!\! \sum _{k \in \mathcal {K}^{\ell }_{j+1}} \!\!\! x^{\ell }_{j+1,k,t} ,{} &\!\! {} j \in \mathcal {J}_{\ell }\setminus {J_{\ell }}, \, \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5b)

$$\begin{aligned} \!\!\!\! \sum _{k \in \mathcal {K}^{\ell }_{J_{\ell }}} x^{\ell }_{J_{\ell }kt} + r^{\ell }_{J_{\ell }, t-1}&= r^{\ell }_{J_{\ell }t} + a^{\ell }_{t},{} & {} \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5c)

$$\begin{aligned} r^{\ell }_{j0}&= \bar{r}^{\ell }_{j0},{} & {} j \in \widetilde{\!\!\mathcal {J}}_{\ell }, \, \ell \in \mathcal {L}, \end{aligned}$$

(5d)

$$\begin{aligned} x^{\ell }_{jkt}&\le M_{jkt}^{\ell } s^{\ell }_{jkt},{} & {} k \in \mathcal {K}^{\ell }_{j}, \, j \in \mathcal {J}_{\ell }, \, \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5e)

$$\begin{aligned} \sum _{k\in \mathcal {K}^{\ell }_j} s^{\ell }_{jkt}&\le \tau ,{} & {} j \in \mathcal {J}_{\ell }, \, \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5f)

$$\begin{aligned} \!\!\!\!\!\!\!\! \frac{1}{C_{kt}}\sum _{\ell \in \mathcal {L}}\sum _{j \in \mathcal {J}_{\ell }} p^{\ell }_{jk} x^{\ell }_{jkt}&\le n_{t} + \zeta \le 1{}, & {} k \in \mathcal {K}, \, t \in \mathcal {T}, \end{aligned}$$

(5g)

$$\begin{aligned} \sum _{t \in \mathcal {T}: t \le q} z^{\ell }_{jkt}&\ge s^{\ell }_{jkq},{} & {} k \in \mathcal {N}^{\ell }_{j}, j \in \mathcal {J}_{\ell }, \ell \in \mathcal {L}, q \in \mathcal {T}, \end{aligned}$$

(5h)

$$\begin{aligned} \sum _{\ell \in \mathcal {L}}\sum _{j \in \mathcal {J}} \sum _{k \in \mathcal {N}^{\ell }_j} z^{\ell }_{jkt}&\le \gamma ,{} & {} t \in \mathcal {T}, \end{aligned}$$

(5i)

$$\begin{aligned} r^{\ell }_{jt}&\le \bar{r}^{\ell }_{jt},{} & {} j \in \widetilde{\!\!\mathcal {J}}_{\ell }, \, \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5j)

$$\begin{aligned} m^{\ell }_{t}&\le d \cdot a^{\ell }_{t},{} & {} \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5k)

$$\begin{aligned} x^{\ell }_{jkt}&\in \mathbb {Z}_{+},{} & {} k \in \mathcal {K}^{\ell }_{j}, \, j \in \mathcal {J}_{\ell }, \, \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5l)

$$\begin{aligned} s^{\ell }_{jkt}&\in \mathbb {B},{} & {} k \in \mathcal {K}^{\ell }_{j}, j \in \mathcal {J}_{\ell }, \ell \in \mathcal {L}, t \in \mathcal {T}, \end{aligned}$$

(5m)

$$\begin{aligned} z^{\ell }_{jkt}&\in \mathbb {B},{} & {} k \in \mathcal {N}^{\ell }_{j}, \, j \in \mathcal {J}_{\ell }, \ell \in \mathcal {L}, t \in \mathcal {T}, \end{aligned}$$

(5n)

$$\begin{aligned} m^{\ell }_{t}&\in \mathbb {Z}_{+},{} & {} \ell \in \mathcal {L}, \, t \in \mathcal {T}, \end{aligned}$$

(5o)

$$\begin{aligned} n_{t}&\ge 0,{} & {} t \in \mathcal {T}, \end{aligned}$$

(5p)

$$\begin{aligned} r^{\ell }_{jt}&\in \mathbb {Z}_{+},{} & {} j \in \widetilde{\!\!\mathcal {J}}_{\ell }, \, \ell \in \mathcal {L}, \, t \in \mathcal {T}\cup \{0\}. \end{aligned}$$

(5q)

We consider three objective functions possessing equal priority, namely the excess resource loading, defined as $g_{1} {:}{=} \sum _{t \in \mathcal {T}} n_{t}$, the sum of all qualification costs $g_{2} {:}{=} {\sum }_{t \in \mathcal {T}} {\sum }_{\ell \in \mathcal {L}} {\sum }_{j \in \mathcal {J}_{\ell }} {\sum }_{k \in \mathcal {N}^{\ell }_{j}} \beta ^{\ell }_{jk} z^{\ell }_{jkt}$, and the total inventory,⁵ expressed as $g_{3} {:}{=} {\sum }_{t \in \mathcal {T}} {\sum }_{\ell \in \mathcal {L}} {\sum }_{j \in \widetilde{\!\!\mathcal {J}}_{\ell }} r^{\ell }_{jt}$. The feasible set for the GTRAP is $B{:}{=}\{(\textbf{y},\textbf{r}) \ |\ (\textbf{y},\textbf{r}) \text { satisfy }(5)\}$, where ${\mathbf{y}}: = ({\mathbf{x}},{\mathbf{s}},{\mathbf{z}},{\mathbf{n}},{\mathbf{m}})$ and $\textbf{r}$ are vectors of variables. The objective functions are defined as $g_{1}:{\mathrm{proj}}_{y}(B) \mapsto \mathbb {R}_{+}$, $g_{2}:{\mathrm{proj}}_{y}(B)\mapsto \mathbb {Z}_{+}$, and $g_{3}:{\mathrm{proj}}_{r}(B) \mapsto \mathbb {Z}_{+}$. All the variables except $\textbf{n}$ take integer/binary values; hence, $\textbf{n}$ will take only discrete values. Consequently, the GTRAP is a (discrete) tri-objective optimization problem such that it has a finite number of NDPs. The projection of each NDP onto the $(g_{1}, g_{2})$-criterion space must be in $R(\textbf{0}, \hat{\textbf{g}}^{\mathrm{ub}})$, where $\hat{\textbf{g}}^{\mathrm{ub}}\in \mathbb {R}_{+}^{2}$ is a vector of upper bounds on $g_{1}$ and $g_{2}$ over the feasible set B. The set of efficient solutions to the GTRAP is denoted as $B_\mathrm{eff}$ and the corresponding NDPs are denoted as $\textbf{g}(B_\mathrm{eff})$.

4 Decomposing the projected two-dimensional criterion space

The QSM as well as several other discrete tri-objective criterion space search methods include solving a sequence of single-objective (i.e. scalarized) optimization problems. One way to reduce the solution time is to solve these single-objective sub-problems simultaneously on separate computers in a cluster. However, all criterion space search methods (including the QSM) generate NDPs sequentially and they are non-trivial to parallelize. We exploit the structure of the GTRAP to enable a parallel computing approach. The following definitions and propositions are used when presenting our proposed approach.

Definition 7

(Orthogonal projection) The orthogonal projection of a set $S\subset \mathbb {R}^{n+m}$ onto the linear space $\mathbb {R}^{n} \times \{0\}^{m}$ is ${\mathrm{proj}}_{y}(S){:}{=} \{\textbf{y} \in \mathbb {R}^{n} : \exists \, \textbf{z} \in \mathbb {R}^{m} \text { s.t. } (\textbf{y},\textbf{z}) \in S\}$.

Definition 8

($\varepsilon$-constrained subset of S w.r.t. $\textbf{g}$ and $\varvec{\varepsilon }$) Let $k>0$, $S \subset \mathbb {R}^{n+m}$, the function $\textbf{g}: S \mapsto \mathbb {R}^{k}_{+}$, and $\varvec{\varepsilon } \in \mathbb {R}_{+}^{k}$. An $\varepsilon$-constrained subset of S w.r.t. $\textbf{g}$ and $\varvec{\varepsilon }$ is defined as $S^{\textbf{g}}(\varvec{\varepsilon }){:}{=} \{(\textbf{y},\textbf{z}) \in S \, |\, \textbf{g}(\textbf{y,z}) \le \varvec{\varepsilon }\} \subseteq S$, where $\textbf{y} \in \mathbb {R}^{n}$ and $\textbf{z} \in \mathbb {R}^{m}.$

We observe that if $B^{g_{3}}_\mathrm{eff}(0) = \{ \, (\textbf{y,r}) \in B_\mathrm{eff} \, |\, g_{3}(\textbf{r}) \le 0 \, \} \ne \emptyset$ holds (cf. Def. 8 with $S {:}{=} B_\mathrm{eff}$, $k{:}{=}1$, $\textbf{g}{:}{=}g_{3}$, and $\varepsilon {:}{=}0$). Then, since $g_{3}$ equals the sum of inventories, the constraints $\textbf{r}=\textbf{0}$ (no inventory) must hold. Consequently, it results in a bi-objective optimization model (with the objectives $g_{1}$ and $g_{2}$). A point $(g_{1}^{*}, g_{2}^{*}) \in \mathbb {R}_{+}^{2}$ is a NDP in the resulting bi-objective optimization problem exactly when $( g_{1}^{*}, g_{2}^{*}, 0)$ is a NDP corresponding to the tri-objective GTRAP. Next, we formally prove this in a more general setting.

Proposition 9

Consider a discrete tri-objective optimization problem with a feasible set $S \subset \mathbb {R}_{+}^{n_{1}}\times \mathbb {Z}^{n_2}_{+} \times \mathbb {Z}^{m}_{+}$, being a mixed-integer polyhedral set of the variables $\textbf{y} \in \mathbb {R}_{+}^{n_1} \times \mathbb {Z}_{+}^{n_2}$ and $\textbf{z} \in \mathbb {Z}_{+}^{m}$, where $n_1+n_2=n \ge 2$ and $m\ge 2$. The objective functions are $g_{1}: {\mathrm{proj}}_{y}(S) \mapsto \mathbb {R}_{+}$, $g_{2}: {\mathrm{proj}}_{y}(S) \mapsto \mathbb {R}_{+}$, and $g_{3}: {\mathrm{proj}}_{z}(S) \mapsto \mathbb {R}_{+}$, where $g_i(\textbf{y}) = \textbf{c}_i^\top \textbf{y}$, $i=1,2$, $g_3(\textbf{z}) = \textbf{c}_3^\top \textbf{z}$, and $\textbf{c}_{i} \ge \textbf{0}$, $i=1,2,3$. Let $\mathcal {D}$ and $\widehat{\mathcal {D}}$ denote the non-empty and finite sets of NDPs of the MOOPs ${\min }_{\textbf{y,z}} \{ ( g_{1}(\textbf{y}), g_{2}(\textbf{y}), g_{3}(\textbf{z}) ) : (\textbf{y} , \textbf{z} ) \in S^{g_{3}}(0) \}$ and ${\min }_{\textbf{y}} \{ ( g_{1}(\textbf{y}), g_{2}(\textbf{y}) ) : \textbf{y} \in {\mathrm{proj}}_{y}(S^{g_{3}}(0)) \}$, respectively. Then, it holds that $\mathcal {D} = \{ (\textbf{u}, 0) \,|\, \textbf{u} \in \widehat{\mathcal {D}} \, \}$.

Proof

Since $\mathcal {D}\ne \emptyset$, it holds that $S^{g_{3}}(0) \ne \emptyset$. Let $( \textbf{y},\textbf{z}) \in S^{g_{3}}(0)$; then $g_{3}(\textbf{z}) \le 0$. Further, since $\textbf{c}_{3} \ge \textbf{0}^{m}$ and $\textbf{z} \in \mathbb {Z}^{m}_{+}$, it holds that $g_{3}(\textbf{z}) \ge 0$. It follows that $g_{3}(\textbf{z})=0$ and $\textbf{z}=\textbf{0}^{m}$.

We first show that the inclusion $\{ ( \textbf{u} ,0 ) \,|\, \textbf{u} \in \widehat{\mathcal {D}} \,\} \subseteq \mathcal {D}$ holds; then that the inclusion $\mathcal {D} \subseteq \{(\textbf{u}, 0) \,|\, \textbf{u} \in \widehat{\mathcal {D}} \,\}$ holds.

Consider a NDP $\textbf{u}^{\mathrm{b}} {:}{=} (g_{1}(\textbf{y}^{\mathrm{b}}), g_{2}(\textbf{y}^{\mathrm{b}}))^{\top } \in \widehat{\mathcal {D}}$ (i.e. for the bi-objective MOOP) and assume the contradiction, that $(\textbf{u}^{\mathrm{b}},0) \not \in \mathcal {D}$. This implies there exists a NDP $(\textbf{u}^{*}, 0) \in \mathcal {D}$ (with corresponding solution $(\textbf{y}^{*},\textbf{0}) \in S^{g_{3}}(0)$) such that $(\textbf{u}^{*}, 0) \le (\textbf{u}^{\mathrm{b}}, 0)$ (see (1) for vector comparison) which implies that $u_1^{*} \le {u}^{\mathrm{b}}_1$, $u_2^{*} \le {u}^{\mathrm{b}}_2$, and $\textbf{u}^{*} \not = \textbf{u}^{\mathrm{b}}$. Hence, it holds that $g_{i}(\textbf{y}^{*}) \le g_{i}(\textbf{y}^{{\mathrm{b}}})$, for $i=1,2$, and $(g_{1}(\textbf{y}^{*}),g_{2}(\textbf{y}^{*})) \not = (g_{1}(\textbf{y}^{{\mathrm{b}}}), g_{2}(\textbf{y}^{{\mathrm{b}}}))$. We know that if $(\textbf{y}^{*},\textbf{0}) \in S^{g_{3}}(0)$, by Def. 7

the inclusion $\textbf{y}^{*} \in {\mathrm{proj}}_{y}(S^{g_{3}}(0))$ holds. Hence, $\textbf{y}^{{\mathrm{b}}}$ is not an efficient solution in the bi-objective MOOP, which is a contradiction. The inclusion follows.

Now, consider $(\textbf{u}^{\mathrm{t}},0) \in \mathcal {D}$, where $u^{\mathrm{t}}_{i}=g_{i}(\textbf{y}^{t}), i=1,2$, and $g_{3}(\varvec{0}^{m})=0$. Assume that $\textbf{u}^{\mathrm{t}} \not \in \widehat{\mathcal {D}}$; then $\exists$ a NDP $\textbf{u}^{*}\in \widehat{\mathcal {D}}$ such that $u_1^{*} \le {u}^{\mathrm{t}}_1$, $u_2^{*} \le {u}^{\mathrm{t}}_2$, and $\textbf{u}^{*} \not = \textbf{u}^{\mathrm{t}}$. The corresponding solution fulfills $\textbf{y}^{*} \in {\mathrm{proj}}_{y}(S^{g_{3}}(0))$ (Def. 7); hence, $(\textbf{y}^{*},\textbf{0}) \in S^{g_{3}}(0)$ holds, which implies $(\textbf{u}^{\mathrm{t}},0) \not \in \mathcal {D}$, i.e. a contradiction. The proposition follows. $\square$

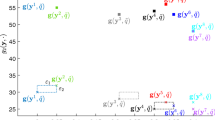
Note that if $\textbf{g}^{*} \in \mathbb {R}_{+}^{3}$ is a NDP of the GTRAP, the projection of $\textbf{g}^{*}$ onto the ($g_{1}, g_{2}$)-criterion space is not dominated by the projection of any NDP satisfying $g_{3}=0$. Fig. 3 illustrates this for the upper bounds $g^\mathrm{ub}_{1}=2.5$ and $g^\mathrm{ub}_{2}=70$, along with the projections of the four elements in the set $\textbf{g}(B^{g_{3}}_\mathrm{eff}(0)) {:}{=}\{\textbf{g}(\textbf{y}, \textbf{r}) \,|\, (\textbf{y}, \textbf{r}) \in B^{g_{3}}_{\mathrm{eff}}(0) \} = \{\textbf{g}^{1}, \textbf{g}^{2}, \textbf{g}^{3}, \textbf{g}^{4}\}$. The dark grey-shaded region contains no projections of NDPs onto the $(g_{1}, g_{2})$-criterion space.

Fig. 3

The region of the projected two-dimensional criterion space that does not contain projections of NDPs is shaded in dark grey

We next show this formally.

Proposition 10

Consider a discrete tri-objective optimization problem with objective functions $g_{1}: {\mathrm{proj}}_{y}(S) \mapsto \mathbb {R}_{+}$, $g_{2}: {\mathrm{proj}}_{y}(S) \mapsto \mathbb {R}_{+}$, and $g_{3}: {\mathrm{proj}}_{z}(S) \mapsto \mathbb {R}_{+}$, where $S\subset \mathbb {R}_{+}^{n_{1}} \times \mathbb {Z}^{n_{2}}_{+} \times \mathbb {Z}^{m}_{+}$ is a mixed-integer polyhedral set of the variable vectors $\textbf{y}\in \mathbb {R}_{+}^{n_{1}} \times \mathbb {Z}^{n_{2}}_{+}$ and $\textbf{z} \in \mathbb {Z}_{+}^{m}$, i.e. $(\textbf{y}, \textbf{z} ) \in S$. Further, $g_i(\textbf{y}) = \textbf{c}_i^\top \textbf{y}$, $i=1,2$, $g_3(\textbf{z}) = \textbf{c}_3^\top \textbf{z}$, $\textbf{c}_{i} \ge \textbf{0}$, $i=1,2,3$ ($n_{1}+n_{2}\ge 2$, $m\ge 2$ ). We denote the set of efficient solutions by $S_\mathrm{eff}$. Then, the projections of the (finite number of) NDPs onto the two-dimensional ${(g_{1},g_{2})}$-criterion space are in the set (see the white region in Fig. 3):

$$\begin{aligned} N(S^{g_{3}}_\mathrm{eff}(0)) {:}{=} \bigg \{ \begin{pmatrix} g_{1} \\ g_{2} \end{pmatrix} \in \mathbb {R}_{+}^{2} \,\bigg |\, g_{i} \le g^\mathrm{ub}_{i}, i=1,2 ; \, \begin{pmatrix} g_{1} \\ g_{2} \end{pmatrix} \not \ge \begin{pmatrix} g'_{1} \\ g'_{2} \end{pmatrix}, \forall \textbf{g}' \in \textbf{g}(S^{g_{3}}_\mathrm{eff}(0))\bigg \}, \end{aligned}$$

where $g_{1}^\mathrm{ub}$ and $g_{2}^\mathrm{ub}$ denote the upper bounds on the values of the objective functions $g_{1}$ and $g_{2}$, respectively, $S_\mathrm{eff}^{g_{3}}(0){:}{=}\{(\textbf{y}; \textbf{z}) \in S_{\mathrm{eff}}\, |\, g_{3}(\textbf{z}) \le 0\}$) (see Def. 8), and the corresponding NDPs are denoted as $\textbf{g}(S_\mathrm{eff}^{g_{3}}(0)) \subset \mathbb {R}_{+}^{3}$.

Proof

Let $\textbf{g}^{*} \in \textbf{g}(S_{\mathrm{eff}})$ be a NDP of the given tri-objective problem. We will show that $(g^{*}_{1},g^{*}_{2}) \in N(S^{g_{3}}_\mathrm{eff}(0))$ by considering the two cases $S_\mathrm{eff}^{g_{3}}(0)= \emptyset$ and $S_\mathrm{eff}^{g_{3}}(0) \not = \emptyset$.

Suppose $S_\mathrm{eff}^{g_{3}}(0)= \emptyset$. Then, $\textbf{g}(S^{g_{3}}_{\mathrm{eff}}(0))=\emptyset$ and $N(S^{g_{3}}_\mathrm{eff}(0)) = \{ (g_1,g_2) \in \mathbb {R}^{2}_{+} |g_{i} \le g^\mathrm{ub}_{i}, i=1,2\}$. It is obvious that if $\textbf{g}^{*}$ is a NDP (i.e. it has a corresponding feasible solution) then $(g^{*}_{1},g^{*}_{2}) \leqq (g^{\mathrm{ub}}_{1}, g^{\mathrm{ub}}_{2})$; hence, $(g^{*}_{1}, g^{*}_{2}) \in N(S^{g_{3}}_{\mathrm{eff}}(0))$.

Suppose the opposite, i.e. $S^{g_{3}}_\mathrm{eff}(0) \ne \emptyset$. We assume contradictory that $\textbf{g}^{*} \in \textbf{g}(S_\mathrm{eff})$ is such that $(g_{1}^{*}, g^{*}_{2}) \not \in N(S^{g_{3}}_\mathrm{eff}(0))$. Since $\textbf{g}^{*} \in \mathbb {R}^{3}_{+}$ is a feasible objective vector, the inequalities $g^{*}_{i} \le g_{i}^{\mathrm{ub}}$, $i=1,2$, hold. Consequently, there exists a point $\textbf{g}' \in \textbf{g}(S^{g_{3}}_\mathrm{eff}(0))$ fulfilling the inequality $(g_{1}^{*}, g^{*}_{2}) \ge (g'_{1}, g'_{2})$. Since the least value of the third function is 0 and $g'_{3}=0$, we have that $(g^{*}_{1}, g^{*}_{2}, g^{*}_{3}) \ge (g'_{1}, g'_{2}, 0)$. Since $\textbf{g}^{*}$ is dominated (at least weakly) by $\textbf{g}'$, it is not a NDP. Hence, the assumption that $\textbf{g}^{*} \in \textbf{g}(S_\mathrm{eff})$ cannot hold. The proposition follows. $\square$

We summarize some of the set notations presented hitherto in Table 2.

Table 2 Summary of set notations

4.1 Outline of the Algorithm

Consider $B^{g_{3}}_{\mathrm{eff}}(0)\ne \emptyset$. We need to compute the NDPs of the tri-objective problem $\min \, \{ ( g_{1} ({\mathbf{y}}),g_{2} ({\mathbf{y}}),g_{3} ({\mathbf{r}}) ) : ({\mathbf{y}},{\mathbf{r}})\in B^{{g_{3}}} (0) \}$. These NDPs can be obtained by solving a corresponding discrete bi-objective optimization problem (cf. Prop. 9):

$$\begin{aligned}\underset{\textbf{y} \in {\mathrm{proj}}_{y}(B^{g_{3}}(0))}{\min }\{g_{1}(\textbf{y}), g_{2}(\textbf{y})\}.\end{aligned}$$

We use the solution approach proposed by Fotedar et al. (2022) to solve the above bi-objective optimization problem (also known as the TRAP).

4.2 Defining the sub-problems

Once we identify the set $B^{g_{3}}_{\mathrm{eff}}(0)\ne \emptyset$, the search region $N(B^{g_{3}}_\mathrm{eff}(0))\subset \mathbb {R}^{2}$ (as defined in Prop. 10, replacing S by B)⁶ can be split into smaller regions such that their union covers the total search region. Let us consider $U(B^{g_{3}}_\mathrm{eff}(0))\subset \mathbb {R}_{+}^{2}$ as the set of upper bounds corresponding to the NDPs $\textbf{g}(B^{g_{3}}_\mathrm{eff}(0))\subset \mathbb {R}^{3}_{+}$. The following two conditions must hold for a set of upper bounds;⁷

• 1. The inclusion $N(B^{g_{3}}_\mathrm{eff}(0)) \, \subseteq \underset{\textbf{u} \in U(B^{g_{3}}_\mathrm{eff}(0))}{\bigcup } R(\textbf{0}, \textbf{u})$ holds;

• 2. For any two $\textbf{u}^{1}, \textbf{u}^{2} \in U(B^{g_{3}}_\mathrm{eff}(0))$ it holds that $R(\textbf{0}, \textbf{u}^{1}) \not \subset R(\textbf{0}, \textbf{u}^{2})$.

The first condition ensures that the region $N(B^{g_{3}}_\mathrm{eff}(0))$ is covered by the rectangles while the second ensures that none of the rectangles strictly contains other rectangles as that would lead to redundancies. Consequently, a sub-problem is defined for each quadrant $R(\textbf{0},\textbf{u})$, with upper bounds $\textbf{u} \in U(B^{g_{3}}_\mathrm{eff}(0))$. Now, consider $K = |B^{g_{3}}_\mathrm{eff}(0)|$ and define $K+1$ sub-problems. The set of objective vectors $H^{k}\subset \mathbb {R}^{3}_{+}$ are obtained after solving the $k^\text {th}$ sub-problem using the QSM method on the set $B^{\widehat{\textbf{g}}}(\textbf{u}^{k}){:}{=}\{(\textbf{y}, \textbf{r})\in B \,|\, g_{i}(\textbf{y})\le u^{k}_{i}, i=1,2 \}$. Then, the equality $\bigcup _{k=1}^{K+1} H^{k} = \textbf{g}(B_\mathrm{eff})$ will be satisfied, as stated in Prop. 11, below.

We create an ordered list of the NDPs corresponding to $\textbf{g}(B^{g_{3}}_\mathrm{eff}(0))$ such that they are sorted in an increasing order of the first objective function’s value.⁸ We define a local upper bound $\textbf{u}^{k}$ as

$$\begin{aligned} \textbf{u}^{k}{:}{=} {\left\{ \begin{array}{ll} (g^{1}_{1}, g^\mathrm{ub}_{2}), &{} \hbox { if}\ k=1,\\ (g^{k}_{1}, g^{k-1}_{2}), &{} \hbox { if}\ 2\le k\le K, \\ \left( g^\mathrm{ub}_{1}, g^{K}_{2}\right) , &{} \hbox { if}\ k= K+1, \end{array}\right. } \end{aligned}$$

(6)

where $(g_{1}^\mathrm{ub}, g_{2}^\mathrm{ub})$ are upper bounds on the first two objective functions. Fig. 4 illustrates an example with $|B^{g_{3}}_\mathrm{eff}(0)|=4$ satisfying the aforementioned conditions. The following proposition ensures that all the NDPs of the GTRAP are identified (see (Appendix) for a proof of the following proposition).

Proposition 11

Let $\textbf{u}^{k}$ be defined by (6) and let $H^{k}$ be the set of objective vectors obtained by applying the QSM to the GTRAP (5) with the additional constraints $g_{1}(\textbf{y})\le u_{1}^{k}$ and $g_{2}(\textbf{y}) \le u_{2}^{k}$. If $B_{\mathrm{eff}}^{g_{3}}(0)\ne \emptyset$, then the equality $\bigcup _{k=1}^{K+1}H^{k}=\textbf{g}(B_\mathrm{eff})$ holds, where $K=|B^{g_{3}}_{\mathrm{eff}}(0)|$.

Fig. 4

Decomposing the projected $(g_{1}, g_{2})$-criterion space. Circles represent projections of NDPs corresponding to $B^{g_{3}}_\mathrm{eff}(0)$ onto this space; triangles represent upper bounds for the five sub-problems

4.3 Parallel QSM

We next present a brief overview of our approach, referred to as the Parallel QSM (P-QSM) and outlined in Algorithm 1. The first step initializes an empty set of efficient solutions to the GTRAP, i.e. $B_\mathrm{eff}$. The discretization parameters $\delta _{1}$ and $\delta _{2}$ are used.⁹ Next, the set $B^{g_{3}}_\mathrm{eff}(0)$ is computed by first solving a bi-objective optimization model called the TRAP (without the variables $\textbf{r}$) and applying Prop. 9. The algorithm includes three modifications to avoid several redundancies.

4.3.1 Modifications

First modification. As the sub-problems are solved simultaneously, it is possible that some of the NDPs corresponding to $B^{g_{3}}_\mathrm{eff}(0)$ are recomputed. For instance, in Fig. 4 while solving the third sub-problem we apply the QSM on $B^{\widehat{\textbf{g}}}(\textbf{u}^{3})$. It is obvious that we will recompute both $\textbf{g}^{2}$ and $\textbf{g}^{3}$. Note that both of these NDPs are also recomputed while solving the second, and the fourth sub-problems, respectively. To avoid this redundancy we simply modify the values of the upper bounds for each sub-problem.

Since the second objective function $g_{2}$ is integer-valued we define a new (adjusted) upper bound¹⁰$\tilde{u}_{1}^{k}{:}{=} u_{1}^{k}$, $\tilde{u}^{k}_{2}{:}{=} u^{k}_{2}-1$, for $k=2, \ldots , |B^{g_{3}}_\mathrm{eff}(0)|+1$ and $\tilde{\textbf{u}}^{1}= \textbf{u}^{1}$. Consequently, each quadrant $R(\textbf{0}, \mathbf {\tilde{u}}^{k})$, for $k=1, \ldots , |B^{g_{3}}_\mathrm{eff}(0)|+1$ contains the projection of at most one NDP from the set $\textbf{g}(B^{g_{3}}_\mathrm{eff}(0))$. In the example in Fig. 5 each adjusted quadrant $R(\textbf{0}, \tilde{\textbf{u}}^{k})$ is shown and the positions of the upper bounds are adjusted. We need to show that $\bigcup _{k=1}^{K+1}R(\textbf{0}, \tilde{\textbf{u}}^{k})$, where $K=|B^{g_{3}}_\mathrm{eff}(0)|$, contains projections of all the NDPs of the GTRAP onto the two-dimensional $(g_1,g_2)$-criterion space. It is formally stated as follows (see Sec. 1 (appendix) for the proof):

Proposition 12

If $B_{\mathrm{eff}}^{g_{3}}(0)\ne \emptyset$ then the projection of a NDP onto the $(g_{1}, g_{2})$-criterion space of the GTRAP is contained in the set $\bigcup _{k=1}^{K+1}R(\textbf{0}, \tilde{\textbf{u}}^{k})$, where $K=|B^{g_{3}}_\mathrm{eff}(0)|$.

Fig. 5

First modification. Circles represent projections of NDPs corresponding to $B^{g_{3}}_\mathrm{eff}(0)$ onto the $(g_{1}, g_{2})$-criterion space; triangles represent modified upper bounds for each sub-problem

Second modification. A NDP $\textbf{g}^{k} \in \textbf{g}(B^{g_{3}}_\mathrm{eff}(0))$ is pre-computed for each sub-problem $k=1, \ldots , |B^{g_{3}}_\mathrm{eff}(0)|$, and by construction $g_{3}^{k}=0$ holds. We will again generate $\textbf{g}^{k}$ first while applying the QSM for $B^{\widehat{\textbf{g}}}(\textbf{u}^{k})$ (see Table 2), i.e. the $k^{\text {th}}$ sub-problem. Consequently, each sub-problem $k=1,\ldots ,|B^{g_{3}}_\mathrm{eff}(0)|$ is initialized with the two upper bounds $(\tilde{u}^{k}_{1}, g^{k}_{2}-1)$ and $(g_{1}^{k}-\delta _{1},\tilde{u}_{2}^{k})$ instead of the pre-defined upper bound $\tilde{\textbf{u}}^{k}$ used in the QSM. This avoids recomputing $\textbf{g}^{k}, k=1, \ldots , |B^{g_{3}}_\mathrm{eff}(0)|$. For instance, in Fig. 5 for the second sub-problem, instead of exploring the quadrant $R(\textbf{0}, \tilde{\textbf{u}}^{2})$, we search $R(\textbf{0}, (\tilde{u}^{2}_{1}, g^{2}_{2}-1))$ and $R(\textbf{0}, (g_{1}^{2}-\delta _{1},\tilde{u}_{2}^{2}))$ (see line 15 in Algorithm 1).

Third modification. Let $K{:}{=}|B^{g_{3}}_{\mathrm{eff}}(0)|$. If $g^{K}_{1}=g^{\mathrm{ub}}_{1}$, then $\textbf{u}^{K}{:}{=}(g^{\mathrm{ub}}_{1}, g^{K-1}_{2})$ follows from (6), and the modified upper bound is $\tilde{\textbf{u}}^{K}=(g^{\mathrm{ub}}_{1},g^{K-1}_{2}-1 )$. By construction, $u^{K}_{2}=g^{K-1}_{2}>g^{K}_{2}=u^{K+1}_{2}$ (see (6)), and in this case $u^{K}_{1}=g_{1}^{\mathrm{ub}}=u^{K+1}_{1}$. Consequently, $R(\textbf{0}, \tilde{\textbf{u}}^{K+1}) \subset R(\textbf{0}, \tilde{\textbf{u}}^{K})$ holds. Hence, the $(K+1)$’th sub-problem needs not be solved (lines 4–5 in Algorithm 1). Similarly, if $g^{1}_{1}=0$ (which is common in our instances) then $\textbf{u}^{1} = (g^{1}_{1}, g^{\mathrm{ub}}_{2})$ (see (6)), which implies $\textbf{u}^{1} = \tilde{\textbf{u}}^{1} = (g^{1}_{1}, g^{\mathrm{ub}}_{2})$, and $g^{1}_{1}=0$, which implies $\tilde{\textbf{u}}^{1}=(0, g^{\mathrm{ub}}_{2})$. Now $R(\textbf{0}, \tilde{\textbf{u}}^{1})$ is actually a line segment between $\tilde{\textbf{u}}^{1}$ and the origin. Hence, the only region that may contain projections of NDPs not identified by solving the second sub-problem is $\{\hat{\textbf{g}}\in \mathbb {R}_{+}^{2} \, |\, g^{1}_{2} \le \hat{g}_{2} \le g^{\mathrm{ub}}_{2}, \hat{g}_{1}=0 \}$. Any point with projection on this line segment is, however, at least weakly dominated by $\textbf{g}^{1}$. Consequently, there is no need to solve the first sub-problem (lines 9–11 in Algorithm 1).

5 Computational experiments, and conclusion

This section provides an overview of the input data, the computational set-up, and the experiment design. We present the different performance indicators used to benchmark P-QSM with QSM. Further, we investigate the sensitivity of the performance of algorithms by varying the discretization parameter $\delta _{1}$ and the threshold value $\zeta \in \{0.70,0.75,0.8\}$.

All algorithms are written using Spyder IDE for Windows system(s) with a 1.70 GHz processor, 16 GB RAM, and 4 cores. We use Python 3.7 as the interpreter and Gurobi 9 as the solver. The sub-problems are simulated and solved on parallel identical computers in a cluster. Each computer solves a sub-problem and its full processor capacity and all CPU cores are available to Gurobi when solving a sub-problem. For each scalarized problem we use two stopping criteria: (a) MIP duality gap of $10^{-4}$; (b) a time limit of 1500 seconds (for sensitivity analyses it is increased to 2500 seconds); hence, the solutions found are approximately efficient. Further, the discretization parameter $\delta _{1}$ is selected as either 0.1 or 0.05, while $\delta _{2}=1$, yielding two different representations of the Pareto front for each algorithm.

5.1 Industrial instances

We use data provided by GKN Aerospace for most of the parameters and sets indicated in Table 1. However, the processing times $p^{\ell }_{jk}$ and qualification cost parameters $\beta _{{jk}}^{\ell }$ for product type $\ell \in \mathcal {L}$, operation $j\in \mathcal {J}_{\ell }$ in machine $k\in \mathcal {N}^{\ell }_{j}$ (qualification required) were not available. We have uploaded fifteen public instances along with details about the distributions used to generate each instance at https://bit.ly/3B4uLes. The demand is from quarterly forecasts provided by GKN Aerospace in January 2015 for the period 2016–2017. There are $L=85$ part types, $|\mathcal {M} |= 517$ tasks, and $|\mathcal {K} |= 125$ machines. The minimum, maximum, and median values of the demand are 1, 149, and 12, respectively (we consider only non-zero values for the calculation of minimum, maximum, and median). For the processing times $p^{\ell }_{jk}$, $k \in \mathcal {K}^{\ell }_{j}$, $j \in \mathcal {J}_{\ell }$, $\ell \in \mathcal {L}$ the minimum, maximum, and median are 0.1, 80, and 5.0 hours, respectively. Each machine has a yearly capacity of 5000 hours which can be equally divided among four quarters in a year. The planning period of two years with quarterly time buckets yields $T=8$ time periods. The parameter values $\tau =3$, $\gamma =4$, and $\zeta = 0.70$ (although for sensitivity analyses we also investigate for $\zeta \in \{ 0.75, 0.80 \}$) apply to all fifteen instances. The limiting factor for ordering raw materials is $d =1.5$. The initial values and upper limits on inventories are $\bar{r}^{\ell }_{j0}=0$ and $\bar{r}^{\ell }_{jt}=\lceil 0.5\,a^{t}_{\ell }\rceil$, $t \in \mathcal {T}$, respectively, $j \in \mathcal {J}_{\ell }$, $\ell \in \mathcal {L}$.

5.2 Design of experiments

To assess the performance of the two algorithms QSM and P-QSM we use solution times¹¹ and two different representation measures. Due to the discretization of $g_{1}$ and the limited solution time set for the scalarized problems, only a subset of the set of (approximately) efficient solutions is known, and the exact Pareto front is not available. Therefore, we need to investigate the quality of representation of the Pareto front obtained by each of the two methods. We denote by $B_{\mathrm{eff}}^{i}$ the set of efficient solutions to the $i^\mathrm{th}$ instance, while the representative set of approximately efficient solutions to the $i^\mathrm{th}$ instance obtained by an algorithm $j \in \mathcal {A} {:}{=} \{ \mathrm{QSM}, \mathrm {P\text {-}QSM} \}$ is denoted as $B_{\widetilde{\mathrm{eff}}}^{i}(j)$. We then denote by $B_{\widetilde{\mathrm{eff}}}^{i}(\mathcal {A})$ the set of solutions that are efficient¹² with respect to the set ${\bigcup _{j \in \mathcal {A}}} B_{\widetilde{\mathrm{eff}}}^{i}(j)$. Then, for the $i^\mathrm{th}$ instance and algorithm $j \in \mathcal {A}$, we define the cardinality (of NDPs) ratio measure¹³$\mu ^{i}(j) {:}{=} {\big |B_{\widetilde{\mathrm{eff}}}^{i}(\mathcal {A}) \bigcap B_{\widetilde{\mathrm{eff}}}^{i}(j) \big |} / {\big |B_{\widetilde{\mathrm{eff}}}^{i}(\mathcal {A}) \big |}$.

5.3 Results

In Table 3 the columns $\#$NDPs refer to ${\big |B_{\widetilde{\mathrm{eff}}}^{i}(\mathcal {A}) \bigcap B_{\widetilde{\mathrm{eff}}}^{i}(j) \big |}$ for the respective instance i and algorithm j. With the discretization $\delta _{1}=0.1$, P-QSM found all the NDPs in $B_{\widetilde{\mathrm{eff}}}^{i}(\mathcal {A})$ for nine out of the fifteen instances, i.e. $\mu ^{i}({\mathrm{P\text {-}QSM}})=1$; for the other six instances, it found more (or equal) NDPs than QSM, i.e. $\mu ^{i}({\mathrm{P\text {-}QSM}}) \ge \mu ^{i}(\mathrm{QSM})$. For thirteen out of the fifteen instances P-QSM had a significantly shorter computing time than QSM; only for instances 7 and 12 the solution time of P-QSM was longer than that of QSM, but then P-QSM identified two and seven additional NDPs, respectively. With $\delta _{1}=0.05$ we obtained, as expected, more NDPs. Fourteen out of the fifteen instances (i.e. all for except instance 10) satisfy $\mu ^{i}(\mathrm{P\text {-}QSM}) \ge \mu ^{i}(\mathrm{QSM})$. For twelve out of the fifteen instances, the solution time of P-QSM was shorter than that of QSM.

Table 3 Comparison of QSM and P-QSM for $\zeta =0.70$ and two discretizations. The time $t^{i}(j)$ is in seconds

Visualization. Pareto fronts of TOILP problems are much more complicated to visualize than for BOILP problems. A scatter plot matrix is a simple technique adept at representing a pair-wise relationship of objectives. The drawback is, however, that one has to study three separate plots. Heatmap plots (as shown in Fig. 6) represent objective values by different shades of grey. In a heatmap each column corresponds to a NDP (there are 19 NDPs in Fig. 6), and each row corresponds to an objective function to which an intensity of greyness is assigned that reflects its value. The lighter the grey-shade, the higher the value. To define the color gradient we normalized each objective function’s values. From the heatmap the decision makers can identify some interesting NDPs, for instance, the NDPs 4 and 5 have (almost) the same values for the first (second) objective function, but for the third objective function the former is significantly better, by 299 units.

Fig. 6

Heatmap for the instance $i=14$, algorithm $j=\text {P-QSM}$, $\delta _{1}=0.1$, $\delta _{2}=1$, and #NDPs $= 19$

5.4 Sensitivity analysis

We perform sensitivity analyses to investigate the effect of varying the threshold ($\zeta$) and discretization ($\delta _{1}$) parameters on the solution times and representation measures, such as cardinality and coverage gap (Ceyhan et al. 2019, Def. 6) for P-QSM and QSM. In these experiments, we increase the time limit to 2500 seconds per scalarized problem.

In Fig. 7a and b we employ the discretization $\delta _{1}=0.05$. Figure 7a presents the distribution (over all fifteen instances i) of percentage increase in the cardinality ratio measure using P-QSM as opposed to QSM, i.e. $\bar{\mu }^{i}({\mathrm{P}\text {-}\mathrm{QSM}}) {:}{=} \frac{\mu ^{i}({\mathrm{P}\text {-}\mathrm{QSM}}) - \mu ^{i}({\mathrm{QSM}})}{ \mu ^{i}({\mathrm{QSM}})}\cdot 100\%$; for the three values of the loading threshold for machines ($\zeta$), there is an increased cardinality ratio (values above $0\%$) using P-QSM. For $\zeta =0.70$ ($\zeta =0.75, \zeta = 0.8$) the median is $4.49\%$ ($10.38\%, 27\%$). Figure 7b illustrates the effect on solution time of using P-QSM. For the threshold, $\zeta =0.70$ all the instances require less time when P-QSM is applied (values $<1$). For $\zeta =0.8$, P-QSM requires more computational time than QSM for several instances. It should be noted that–-as indicated in Fig. 7a—P-QSM identifies more NDPs than QSM for $\zeta =0.8$. For $\zeta =0.75$ the ratio of the solution time is $<1$ for most of the instances. For $\zeta =0.70$ ($\zeta =0.75, \zeta =0.8$) the median values of the ratio of solution time of P-QSM to QSM is 0.75 (0.625, 1.15). Figure 8a illustrates the difference of solution times for QSM and P-QSM; the median value of the difference is 1410 ($1351,-207$) seconds for the threshold 0.70 (0.75, 0.8).

Figures 7c and 7d employ the discretization $\delta _{1}=0.1$, $\delta _{2}=1$. For $\zeta =0.70$ ($\zeta =0.75, \zeta =0.80$) the median value of the ratio of solution time of P-QSM to QSM is 0.787 (1.02, 1.408). However, as indicated in Fig. 7c, with an increasing threshold, the number of NDPs found by P-QSM is significantly larger than by the QSM. For $\zeta =0.70$ ($\zeta =0.75, \zeta =0.80$) the median value of the cardinality ratio is $0\%$ ($17\%, 66.66\%$). The median values for the difference (in seconds) of computing times of QSM and P-QSM (see Fig. 8b) are $650,-33$, and $-360$ seconds for thresholds 0.70, 0.75, and 0.8, respectively.

Fig. 7

Sensitivity plots: distributions of two performance indicators over the fifteen instances, separated for two levels of the discretization parameter $\delta _{1}$, and grouped by three values of the threshold $\zeta$. A red plus sign denotes an outlier outside 1.5 times the inter-quartile range

Fig. 8

Difference of solution time for QSM and P-QSM [s] for threshold values $\zeta \in \{ 0.70, 0.75, 0.80 \}$

It is known (Ceyhan et al. 2019) that finding more NDPs does not always result in the corresponding representation becoming significantly better. Hence, coverage gap values can be used. We adjust (Ceyhan et al. 2019, Def. 6) for minimization problems and normalize the three objectives, as they have different dimensions, to calculate the coverage gap values. The coverage gap, $\alpha ^{i}(j)$, of algorithm j for instance i, measures the distance to the worst represented point in the set $B_{\widetilde{\mathrm{eff}}}^{i}(\mathcal {A})$ (i.e. the best known representation of the efficient set $B_{\mathrm{eff}}^{i}$) from the obtained representative set of approximately efficient solutions, i.e. $B_{\widetilde{\mathrm{eff}}}^{i}(j)$. Figures 9a–9b present on the right axis the ratio of the difference of the coverage gap values of QSM and P-QSM to the coverage gap value of QSM (i.e. $\bar{\alpha }^{i}({\text {P-QSM}}){:}{=} \frac{\alpha ^{i}({\text {QSM}}) - \alpha ^{i}({\text {P-QSM}})}{\alpha ^{i}({\text {QSM}})}$), referred to as coverage gap ratio. As it is desired to have a lower coverage gap value; for P-QSM to outperform QSM, the ratio needs to be greater than zero. Table 4 summarizes the results from the fifteen instances and over all three threshold values. Hence, there are 45 values reported for both $\delta _{1}=0.05$ and $\delta _{1}=0.1$. For $\delta _{1}=0.1$, there are 30 occurrences when both the cardinality ratio and coverage gap ratio are positive. In only one occurrence both of them are less than or equal to zero. The results for $\delta _{1}=0.05$ are analogously presented. There is no occurrence where both coverage and cardinality ratios are less than or equal to zero.

Fig. 9

Sensitivity plots. Left axis: grey-bars with corresponding cardinality ratio. Right axis: black-rhombuses representing coverage gap ratios. Each group of three bars corresponds to the threshold values 0.7, 0.75, and 0.8

Table 4 Summary of sensitivity analyses

Discussion: The reduction in solution time can be attributed to the parallelization used in P-QSM, although there is a significant improvement in the coverage gap that is not due to the parallelization. In most of our computations, the time limit of 2500 seconds per scalarized problem is not reached, but still, the approximation of the Pareto front provided by QSM is much inferior to that of P-QSM in almost all of the instances (over variation of threshold and discretization parameters). As an explanation, consider the following example, which is illustrated in Fig. 10. Assume there are four NDPs and three of them, $\textbf{g}^{1}, \textbf{g}^{2}$, and $\textbf{g}^{3}$, correspond to the efficient solutions in $B^{g_{3}}_\mathrm{eff}(0)$, i.e. $g^1_3 = g^2_3 = g^3_3 = 0$. In P-QSM, four sub-problems are initialized corresponding to the upper bounds $\tilde{\textbf{u}}^{1}, \tilde{\textbf{u}}^{2}, \tilde{\textbf{u}}^{3}$, and $\tilde{\textbf{u}}^{4}$. QSM, however, starts with the upper bound $\tilde{\textbf{l}}^{1}$. The first application of the two-stage scalarizations will result in one of the NDPs corresponding to $B^{g_{3}}_\mathrm{eff}(0)$, w.l.o.g. assume the NDP $\textbf{g}^{3}$ is identified.¹⁴ For $\delta _{1}=0.5$, the subsequent upper bounds will be $\tilde{\textbf{l}}^{2}$ and $\tilde{\textbf{l}}^{3}$. Due to the discretization, the NDPs $\textbf{g}^{2}$ and $\textbf{g}^{4}$ will be overlooked by the QSM, but not by the P-QSM as both points are identified while solving the second sub-problem, i.e. for $R(\textbf{0}, \tilde{\textbf{u}}^{2})$. Hence, both the parallelization and the solving of the bi-objective TRAP first give P-QSM a computational advantage over QSM.

Fig. 10

Illustration of the reason for P-QSM yielding a better representation. For QSM and P-QSM the upper bounds used are $\{\tilde{\textbf{l}}^{1}, \tilde{\textbf{l}}^{2}, \tilde{\textbf{l}}^{3}\}$ and $\{\tilde{\textbf{u}}^{1}, \tilde{\textbf{u}}^{2},\tilde{\textbf{u}}^{3}, \tilde{\textbf{u}}^{4}\}$, respectively

5.5 Conclusion

We present a modified version, P-QSM, of the quadrant shrinking method (QSM) for identifying a representative set of approximately efficient solutions to a generalized tri-objective tactical resource allocation problem. The computational benefits of the P-QSM are due to solving sub-problems in parallel/simultaneously on different computers and to initiating the algorithm with a subset of the NDPs. For most of the instances, the P-QSM identifies more NDPs than the QSM; it also results in a smaller coverage gap. Future work may consider providing tighter formulations of the scalarization of the sub-problems in P-QSM.

Appendix

Proof of Proposition 11

We will first show that $\textbf{g}(B_{\mathrm{eff}}) \subseteq \bigcup _{k=1}^{K+1}H^{k}$. Consider an efficient solution $(\textbf{y}^{*}, \textbf{r}^{*}) \in B_{\mathrm{eff}}$ and the corresponding objective vector $\textbf{g}(\textbf{y}^{*}, \textbf{r}^{*}) \in \textbf{g}(B_{\mathrm{eff}})$. Assume the contradiction, that $\textbf{g}(\textbf{y}^{*}, \textbf{r}^{*}) \not \in \bigcup _{k=1}^{|B^{g_{3}}_{\mathrm{eff}}(0)|+1}H^{k}$. We know from Prop. 10 that the projection of any NDP onto the $(g_{1}, g_{2})$-criterion space lies in $N(B^{g_{3}}_\mathrm{{eff}}(0))$, and by the construction of upper bounds, it holds that $N(B^{g_{3}}_\mathrm{{eff}}(0)) \subseteq \bigcup _{k=1}^{|B^{g_{3}}_\mathrm{{eff}}(0)|+1}R(\textbf{0}, \textbf{u}^{k})$. This implies $\textbf{g}(\textbf{y}^{*}, \textbf{r}^{*})$ has a projection $\widehat{\textbf{g}}(\textbf{y}^{*},\textbf{r}^{*} )=(g_{1}(\textbf{y}^{*}),g_{2}(\textbf{y}^{*}))^{\top } \in R(\textbf{0}, \textbf{u}^{k})$ for at least one sub-problem k. Note that $\textbf{g}(\textbf{y}^{*}, \textbf{r}^{*})$ is a NDP corresponding to a feasible set B, which implies that it must be a NDP for any (feasible) subset $B^{\widehat{\textbf{g}}}(\textbf{u}^{k}){:}{=} \{\, (\textbf{y}, \textbf{r}) \in B \,|\, g_{1}(\textbf{y}) \le u_{1}^{k},\, g_{2}(\textbf{y}) \le u_{2}^{k} \,\} \subseteq B$. Since applying the QSM algorithm to the feasible set $B^{\widehat{\textbf{g}}}(\textbf{u}^{k})$ results in all the NDPs (denoted as $H^{k}$), it must identify $\textbf{g}(\textbf{y}^{*},\textbf{r}^{*} )$ as well. Hence, we have a contradiction, i.e. $\textbf{g}(\textbf{y}^{*}, \textbf{r}^{*}) \in \bigcup _{k=1}^{|B^{g_{3}}_\mathrm{{eff}}(0)|+1}H^{k}$ .

Next, we show that $\bigcup _{k=1}^{K+1}H^{k} \subseteq \textbf{g}(B_\mathrm{{eff}})$. We assume the converse, i.e. $\textbf{g}^{*} \notin \textbf{g}(B_\mathrm{{eff}})$ and $\textbf{g}^{*} \in H^{k}$ (for one of the sub-problems k). Consequently, $\exists \,\bar{\textbf{g}} \in \textbf{g}(B_\mathrm{{eff}})$ such that $\bar{\textbf{g}} \le \textbf{g}^{*}$. However, by the property of the QSM we know $\textbf{g}^{*}$ is a NDP of the GTRAP with additional constraints $g_{i}(\textbf{y}) \le u_{i}^{k}$, $i=1,2$. Hence, at least one of the constraints $\bar{g}_{1} > u^{k}_{1}$ and $\bar{g}_{2} > u^{k}_{2}$ must hold. Consequently, at least one of the constraints $g_{1}^{*} \le u^{k}_{1} < \bar{g}_{1}$ and $g_{2}^{*} \le u^{k}_{2} <\bar{g}_{2}$ holds, which implies that $\bar{\textbf{g}}$ does not dominate $\textbf{g}^{*}$. The proposition follows by contradiction.

Proof of Proposition 12

Let $K {:}{=} |B^{g_{3}}_\mathrm{eff}(0)|$. The projections onto the two-dimensional criterion space of all the NDPs are in the set $\bigcup _{k=1}^{K+1}R(\textbf{0}, \textbf{u}^{k})$ (as stated in Prop. 11). If we prove $A{:}{=}\big \{ \bigcup _{k=1}^{K+1}R(\textbf{0}, \textbf{u}^{k}) \setminus \bigcup _{k=1}^{K+1}R(\textbf{0}, \tilde{\textbf{u}}^{k}) \big \} \bigcap \, \widehat{\textbf{g}}(B_\mathrm{eff}) = \emptyset$ (see Table 2 for notations) then the proposition follows. Let us assume a feasible solution $(\bar{\textbf{y}}, \bar{\textbf{r}}) \in B_\mathrm{{eff}}$ and $(g_{1}(\bar{\textbf{y}}), g_{2}(\bar{\textbf{y}}) ) \in A$. This implies the inequalities $\tilde{u}^{k}_{2}<g_{2}(\bar{\textbf{y}}) \le u^{k}_{2}$ for at least one $k \in \{ 2, \ldots , K+1 \}$ ($k=1$ is not included since $\textbf{u}^{1}=\tilde{\textbf{u}}^{1}$). Since $g_{2}$ is integer-valued function and $\tilde{u}^{k}_{2}= u^{k}_{2}-1$, it follows that $g_{2}(\bar{\textbf{y}}) = u^{k}_{2}$. Moreover, the inequalities $0 \le g_{1}(\bar{\textbf{y}}) \le u^{k}_{1}$ hold. Let us first consider the case when $0 \le g_{1}(\bar{\textbf{y}}) < u^{k-1}_{1}$. This implies that $g_{2}(\bar{\textbf{y}}) = u^{k}_{2} < u^{k-1}_{2}$ (the latter strict inequality follows from (6)). This can be equivalently stated as $g_{2}(\bar{\textbf{y}}) < \tilde{u}^{k-1}_{2}+1 \iff g_{2}(\bar{\textbf{y}}) \le \tilde{u}^{k-1}_{2}$. Hence, it holds that $(g_{1}(\bar{\textbf{y}} ), g_{2}(\bar{\textbf{y}})) \in R(\textbf{0}, \tilde{\textbf{u}}^{k-1})$ which, from the assumption that $(g_{1}(\bar{\textbf{y}} ), g_{2}(\bar{\textbf{y}} )) \in A$, is obviously a contradiction.

Hence, we consider the case when $g_{1}(\bar{\textbf{y}} ) \in [u^{k-1}_{1}, u^{k}_{1}]$. From (6) we know that $u^{k}_{2}=g^{k-1}_{2}$, $k=2, \ldots , K+1$, such that $g_{2}(\bar{\textbf{y}} ) = u^{k}_{2} = g_{2}^{k-1}$ holds. Subsequently, from (6) we know that $u^{k}_{1}=g^{k}_{1}$, $k = 2, \ldots , K$, such that $u^{k-1}_{1}=g^{k-1}_{1}$ holds. Thus, we have that the inequalities $g_{1}^{k-1}\le g_{1}(\bar{\textbf{y}}) \le u^{k}_{1}$ hold. Therefore, it holds that $g_{1}^{k-1}\le g_{1}(\bar{\textbf{y}})$, $g_{2}^{k-1}= g_{2}(\bar{\textbf{y}})$, and by definition $g^{k-1}_{3}=0$. Moreover, since $(g_{1}^{k-1}, g_{2}^{k-1}) \in R(\textbf{0}, \tilde{\textbf{u}}^{k-1})$ we have that $\textbf{g}^{k-1} \ne \textbf{g}(\bar{\textbf{y}})$, because $\textbf{g}(\bar{\textbf{y}}) \in A$. Consequently, $\textbf{g}^{k-1}$ must dominate $\textbf{g}(\bar{\textbf{y}})$, which is a contradiction as the latter is assumed to be a NDP. $\square$