American options and stochastic interest rates

Abstract

We study finite-maturity American equity options in a stochastic mean-reverting diffusive interest rate framework. We allow for a non-zero correlation between the innovations driving the equity price and the interest rate. Importantly, we also allow for the interest rate to assume negative values, which is the case for some investment grade government bonds in Europe in recent years. In this setting we focus on American equity call and put options and characterize analytically their two-dimensional free boundary, i.e. the underlying equity and the interest rate values that trigger the optimal exercise of the option before maturity. We show that non-standard double continuation regions may appear, extending the findings documented in the literature in a constant interest rate framework. Moreover, we contribute by developing a bivariate discretization of the equity price and interest rate processes that converges in distribution as the time step shrinks. This discretization, described by a recombining quadrinomial tree, allows us to compute American equity options’ prices and to analyze their free boundaries with respect to time and current interest rate. Finally, we document the existence of non-standard optimal exercise policies for American call options on a non-dividend-paying equity.

1 Introduction

In an arbitrage-free financial market the role of the short-term interest rate is twofold: on one hand it represents the rate at which the equity price appreciates under the risk neutral measure; on the other hand it drives the locally risk-free asset and the related discount rate. Therefore, neglecting the variability of short-term interest rates may induce significant mispricing on both interest rates and equity derivatives. This issue is particularly relevant for American equity options, due to the optionality of their exercise policy. In fact, the holder of an American option has to timely chose when to cash in by exercising the option, balancing the effects from the discount rate and from the expected rate of return of the underlying asset. When both of these effects depend on a stochastic process, the valuation of the option becomes tricky.

Our paper develops an extensive analysis of American call and put options written on equity with constant volatility in a stochastic interest rate framework of Vasicek type¹ (see Vasicek (1977)). We employ the Vasicek mean-reverting model for the interest rate, because it allows for mildly negative interest rate values, as the ones documented nowadays in the Eurozone. The feasibility of negative interest rates within the Vasicek model, once a source of major criticism, has very recently become the reason of renewed interest in the model itself because of the aforementioned market circumstances. We also allow for a non-zero constant correlation between the Brownian innovations of the interest rate and the equity price processes. A positive (resp. negative) correlation between the interest rate and the equity price corresponds to a negative (resp. positive) correlation between the bond and the equity prices². The literature on American equity options³ has so far focused on alternative stochastic interest rates models, such as the CIR one, based on the seminal work of Cox et al. (1885) (see Medvedev and Scaillet (2010), Boyarchenko and Levendorskiǐ (2013) and Wei et al. (2013), among others). Our paper is, to our knowledge, the first that addresses the valuation of American equity options in a stochastic interest rate framework of Vasicek type, allowing for the possibility of negative interest rates.⁴

We contribute to the literature by offering an intuitive and effective lattice method to compute the price, the optimal exercise policies and the related free boundaries of American equity options in the presence of market and interest rate risks. In the spirit of Cox et al. (1979), building on Nelson and Ramaswamy (1990), who provide a tree approximation for an univariate process, we construct a discrete joint approximation for the both the equity price and the interest rate processes⁵. We provide an extensive investigation of American equity call and put options and their free boundaries. Our findings contribute to the literature on American options with stochastic interest rates, that usually restricts to non-negative interest rates. In particular, we unveil two novel significant features of the free boundary that appear when the stochastic interest rate may take mildly negative values.

First, we show that for American put (resp. call) options the early exercise region is not always downward (resp. upward) connected. The early exercise region is downward (resp. upward) connected if optimal exercise at t of the put (resp. call) option for some underlying equity price implies optimal exercise at t for all lower (resp. greater) values of the underlying equity price. In a stochastic interest rate framework Detemple and Tian (2002) and Detemple (2014) retrieve the free boundary by a discretization of an integral equation for the early exercise premium decomposition. However, this method requires an a priori knowledge of the geometry of the early exercise/continuation region(s). On the contrary, our quadrinomial tree allows us to obtain an “automatic” accurate description of the free boundary(ies), regardless the structure of the derivative’s payoff. For American call options Detemple (2014) argues that the exercise region is connected in the upward direction. Our results show that this property holds true if interest rates are always non-negative, but may fail if the interest rates’ positivity assumption is not satisfied. In this case, we document the existence of a non standard double continuation region first described by Battauz et al. (2015) in a constant interest rate framework. In particular, a non-standard additional continuation region appears where the option is most deeply in the money and the underlying pays a negative dividend. A negative dividend can be interpreted as a storage cost for commodities (e.g. gold or silver) or as the result of the interplay of domestic and foreign interest rates when evaluating options on foreign equities (see Battauz et al. (2019)). Under these circumstances a mildly negative interest rate may lead to optimal postponment of the deeply in the money option as the holder is confident the option will still be in the money later and prefers to delay the cash-in.

Second, we show that early exercise may be optimal for an American call option even if the underlying equity does not pay any dividend. This happens when a mildly negative initial interest rate causes the underlying equity’s drift to be negative as well, pushing the underlying equity towards the out of the money region. In this case, immediate exercise turns out to be optimal as soon as the option is sufficiently in the money. Moreover, for the American call option, we show that the critical equity price that triggers optimal early exercise is increasing with respect to the interest rate value, as the higher the interest rate, the higher the underlying equity drift, the lower the risk of ending up in the out of the money region for the call option, and thus the higher has to be the immediate payoff to be optimally exercised before maturity.

The remainder of the paper is organized as follows: in Sect. 2 we introduce the financial market and develop its lattice-based discretization, that we call quadrinomial tree. In Sect. 3 we deal with American put and call equity options in our stochastic interest rate environment, characterizing their optimal exercise policies and the main analytical features of their free boundaries. We also provide numerical pricing results for the discretized market via our quadrinomial tree, showing the pricing differences from the standard constant interest rate case. We provide a graphical characterization of the free boundaries that confirm their analytical features in the continuous-time setting. Section 4 concludes. All proofs are in the Appendix.

2 The market and the quadrinomial tree

2.1 The assets in the market

Consider a stylized financial market in a continuous time framework with investment horizon $T >0$. A risky security S(t) is traded. Following the seminal work of Vasicek (1977), we assume a mean-reverting stochastic process for the prevailing short term interest rate on the market r(t). We allow for a non zero correlation between the innovations of S and r. We assume that a continuum of zero coupon bonds with maturities in [0, T] is traded in the market. A market player can invest in the short-term interest rate, which is locally risk-free, through the money market account⁶B(t), which is exploited as a numéraire.

The dynamics of the risky equity price, of the short-term interest rate and of the money market account under the risk-neutral⁷ measure ${\mathbb {Q}}$ are:

$$\begin{aligned} \left\{ \begin{array}{rl} \displaystyle \frac{\mathrm {d} S(t)}{S(t)} &{} = (r(t)-q)\mathrm {d}t + \sigma _S \mathrm {d}W_S^{{\mathbb {Q}}}(t) \\ \mathrm {d} r(t) &{} = \kappa \left( \theta - r(t) \right) \mathrm {d} t + \sigma _r \mathrm {d} W_r^{{\mathbb {Q}}}(t) \\ \mathrm {d} B(t) &{} = r(t)B(t)\mathrm {d} t \end{array} \right. \end{aligned}$$

(1)

with $\langle \mathrm {d} W_S^{{\mathbb {Q}}} (t), \mathrm {d} W_r^{{\mathbb {Q}}} (t) \rangle = \rho \mathrm {d} t$ and given some initial conditions $S(0) = S_0$, $r(0) = r_0$ and $B(0)=1$. The parameter q is the constant annual dividend rate of the equity, $\sigma _S > 0$ the volatility of the equity price, $\kappa$ the speed of mean-reversion of the short-term interest rate, $\theta$ its long-run mean, $\sigma _r > 0$ the volatility of the short-term interest rate and $\rho \in [-1,1]$ the correlation between the Brownian shocks on S and r.

The explicit solution to the System (1) is

$$\begin{aligned} \left\{ \begin{array}{rl} S(t) &{} = S_0 \exp \left[ \displaystyle \int _{0}^{t} r(s) \mathrm {d} s -\left( q + \displaystyle \frac{\sigma _S^2}{2} \right) t + \sigma _S W^{\mathbb {Q}}_S(t) \right] \\ r(t) &{} = r_0 e^{-\kappa t} + \theta (1-e^{-\kappa t}) + \sigma _r \displaystyle \int _{0}^t e^{-\kappa (t-s)} \mathrm {d} W^{\mathbb {Q}}_r(s) \\ B(t) &{} = \exp \left[ \displaystyle \int _{0}^{t} r(s) \mathrm {d} s \right] \end{array} \right. \end{aligned}$$

(2)

It is well known that r(t) is normally distributed,

$$\begin{aligned} r(t) \sim {\mathcal {N}} \left( r_0 e^{-\kappa t} + \theta (1-e^{-\kappa t}) , \frac{\sigma _r^2}{2 \kappa } (1 - e^{-2\kappa t}) \right) . \end{aligned}$$

As a consequence, the support of r(t) is unbounded, which allows for negative interest rates and is one of the main novelty of our paper. Notice that, while mildly negative interest rates are observable nowadays, too negative rates are clearly not plausible. However, with the same model parameters of the main numerical examples of Sec. 3.1, it turns out that very negative values of r have a negligible risk-neutral probability⁸.

The zero-coupon bond with maturity T pays 1 at its holder at T and its price at $t \in (0,T)$ is labelled with p(t, T). By no arbitrage valuation, we have

$$\begin{aligned} p(t,T) = {\mathbb {E}}^{{\mathbb {Q}}} \left[ \left. \frac{1}{B(T)} \right| {\mathcal {F}}_t \right] = e^{A(t,T)-B(t,T)r(t)}, \end{aligned}$$

(3)

where the deterministic functions A(t, T) and B(t, T) are defined in Section 3.2.1 of Brigo and Mercurio (2007).

In this fairly general pricing framework, the price of European options on S can be derived in closed formulae by applying the change of numéraire as described⁹ in Geman et al. (1995). Full computations of the prices of European calls and puts can be found in Abudy and Izhakian (2013) or in Appendix 2 of Brigo and Mercurio (2007). We recall here these formulae as they are used in the next section.

Proposition 1

(Value of the European put/call equity option) In the financial market specified in (1), the price at $t\in [0,T]$ of an European put option on S with strike K is equal to

$$\begin{aligned} \pi _{E}^{put}(t,S(t),r(t)) = K p(t,T) N(-\tilde{d_2}) -S(t) e^{-q(T-t)} N(-\tilde{d_1}) \end{aligned}$$

(4)

with¹⁰:

$$\begin{aligned} \tilde{d_1} =\, & {} \displaystyle \frac{1}{\sqrt{\Sigma _{t,T}^2}}\left( \ln \displaystyle \frac{S(t)}{Kp(t,T)} + \displaystyle \frac{1}{2} \Sigma _{t,T}^2 - q(T-t) \right) , \quad \tilde{d_2} = \tilde{d_1} - \sqrt{\Sigma _{t,T}^2} \\ \Sigma _{t,T}^2 =\, & {} \sigma _S^2 (T-t) +2\sigma _S\sigma _r\rho \left( \frac{ -1+e^{-\kappa (T-t)} + \kappa (T-t)}{\kappa ^2} \right) + \\&- \sigma _r^2 \left( \frac{ 3+e^{-2\kappa (T-t)} - 4e^{- \kappa (T-t)} -2\kappa (T-t) }{2 \kappa ^3} \right) . \end{aligned}$$

The price at $t\in [0,T]$ of an European call option on S with strike K is equal to

$$\begin{aligned} \pi _{E}^{call}(t,S(t),r(t)) = S(t) e^{-q(T-t)} N(\tilde{d_1}) -K p(t,T) N(\tilde{d_2}). \end{aligned}$$

(5)

2.2 The quadrinomial tree

In their seminal work, Cox et al. (1979) show how to discretize the lognormal process of the price of a risky security and how to easily exploit such a binomial discretization in order to evaluate derivatives written on the primary asset (more recently, see also Zanette and Gaudenzi (2017)). Embedding this geometric Brownian motion case into a more general class of diffusion processes, Nelson and Ramaswamy (1990) propose a one-dimensional scheme to properly define a binomial process that approximates a one-dimensional diffusion process. They do so by matching the diffusion’s instantaneous drift and its variance and imposing a recombining structure to their discretized process.

We propose here a quadrinomial tree to jointly model a mean-reverting process for the short term interest rate as suggested first by Vasicek (1977) and the process for the risky equity’s price with constant volatility and the drift that embeds the stochastic interest rate as in Eq. (1).

Let $X(t)=(Y(t),r(t))$, where $Y(t)=\ln S(t)$ and r(t) are defined in (1), and consider the discrete uniform partition $\left\{ i \frac{T}{n}, i=1, \dots , n \right\}$ of the time interval [0, T] and define $\Delta t := \frac{T}{n}$. For each n we construct the approximating bivariate stochastic process $\{ X_n \}$ on [0, T] as follows. Given n,  consider the generic i-th step of the bivariate discrete process $X_i = (Y_i,r_i)$. At the following step $i+1$ the process $X_{i+1}$ assumes one of the following four values:

$$\begin{aligned} X_{i+1}=(Y_{i+1},r_{i+1}) = \left\{ \begin{array}{ll} (Y_i + \Delta Y^+, r_i + \Delta r^+) &{} \text { with probability } q_{uu} \\ (Y_i + \Delta Y^+, r_i + \Delta r^-) &{} \text { with probability } q_{ud} \\ (Y_i + \Delta Y^-, r_i + \Delta r^+) &{} \text { with probability } q_{du} \\ (Y_i + \Delta Y^-, r_i + \Delta r^-) &{} \text { with probability } q_{dd} \\ \end{array} \right. \end{aligned}$$

(6)

where $\Delta Y^\pm , \Delta r^\pm$ are the jumping increments and the four transition probabilities are both time-dependent and state-contingent, defined as follows:

$$\begin{aligned}&\begin{array}{rl} \Delta Y^+ &{} = \sigma _S\sqrt{\Delta t} = - \Delta Y^- := \Delta Y \\ \Delta r^+ &{} = \sigma _r\sqrt{\Delta t} = - \Delta r^- := \Delta r \end{array} \end{aligned}$$

(7)

$$\begin{aligned}&\begin{array}{rl} q_{uu} &{} = \displaystyle \frac{\mu _Y \mu _r \Delta t + \mu _Y \Delta r +\mu _r \Delta Y +(1+\rho )\sigma _r \sigma _S}{4 \sigma _r \sigma _S} \\ q_{ud} &{} = \displaystyle \frac{-\mu _Y \mu _r \Delta t+\mu _Y \Delta r -\mu _r \Delta Y +(1-\rho )\sigma _r \sigma _S}{4 \sigma _r \sigma _S} \\ q_{du} &{} = \displaystyle \frac{-\mu _Y \mu _r \Delta t-\mu _Y \Delta r +\mu _r \Delta Y +(1-\rho )\sigma _r \sigma _S}{4 \sigma _r \sigma _S} \\ q_{dd} &{} = \displaystyle \frac{\mu _Y \mu _r \Delta t-\mu _Y \Delta r -\mu _r \Delta Y +(1+\rho )\sigma _r \sigma _S}{4 \sigma _r \sigma _S}. \end{array} \end{aligned}$$

(8)

with $\mu _Y := \left( r(t) - q - \displaystyle \frac{\sigma _S^2}{2} \right)$ and $\mu _r := \kappa (\theta - r(t))$ (Fig. 1). The parameters defined in the Eqs. (7) and (8) allow the bivariate process X to match the first two moments of (Y, r) (see the first section of the Appendix for the details). Moreover, the four transition probabilities sum up to one and the quadrinomial tree has a recombining structure.¹¹ The number of different outcomes of our discretization grows quadratically (and not exponentially) in the number of steps¹². Figure 2 provides a graphical intuition of this trick: starting from $(Y_0,r_0)$, after two steps the bivariate binomial process may assume nine possible values, namely all the possible ordered couples of $\{ Y_0 - 2\Delta Y, Y_0, Y_0+2\Delta Y \}$ and of $\{ r_0 - 2\Delta r, r_0, r_0+2\Delta r \}$. Thus, for a generic number of time steps n, the final possible outcomes of the discretization are $(n+1)^2$ rather than $2^{n+1}$, the number of possible outcomes along a non recombining tree.

Fig. 1

One step of the bivariate binomial discretization

Fig. 2

Two steps of the bivariate binomial discretization

Exploiting convergence results of Section 11.3 of Stroock and Varadhan (1997) we can prove that

Theorem 2

(Convergence of the quadrinomial tree) The bivariate discrete process $(X_i)_i$ defined in (6) with the parameters in (7) and (8) converges in distribution to the process $X=(Y,r)$.

Proof

See Appendix 3. $\square$

3 American options

In this section we focus on American equity put (resp. call) options, whose final payoff is $\varphi (S):=(K-S)^+$ (resp. $\varphi (S):=(S-K)^+$). The value at $t\le T$ of the American equity option with maturity T is:

$$\begin{aligned} V(t)&= ess \sup _{t \le \tau \le T} {\mathbb {E}}^{{\mathbb {Q}}} \left[ \left. \frac{B(t)}{B(\tau )}\varphi ( S(\tau ) ) \right| {\mathcal {F}}_t \right] \nonumber \\&= ess \sup _{t \le \tau \le T} {\mathbb {E}}^{{\mathbb {Q}}} \left[ \left. e^{-\int _{t}^{\tau } r(s) \mathrm {d} s} \varphi ( S(\tau ) ) \right| {\mathcal {F}}_t \right] \end{aligned}$$

(9)

where $\tau$ ranges among all possible stopping times of the natural filtration of $(W_S^{\mathbb {Q}},W_r^{\mathbb {Q}})$ with values in [t, T] (see for instance Chapter 28 in Björk (2019)).

In the following proposition we show that the value of the American option defined in Eq. (9) is a deterministic function of time t (or, equivalently, of time to maturity $T-t$) and of the current value of both the underlying asset $S=S(t)$ and the short term interest rate $r=r(t)$. This deterministic function inherits the same monotonicity properties with respect to t and S as in the constant interest rate environment. We also prove that the American equity put option is decreasing with respect to the current value of the interest rate r, whereas the American equity call option is increasing with respect to r. Intuitively, in the constant interest rate framework, an increase in r has a direct effect on American equity options via the discounting of future cashflows, that becomes more severe. It has also an indirect effect, channelled through the equity drift, that increases if r increases. For an American equity put option this implies that the likelihood of lower payoffs increases. Thus an increase in r diminishes the value of an American equity put option. On the contrary, for an American equity call option, the drift increase determined by the increase of r pushes the underlying equity towards higher payoffs’ regions, thus potentially increasing the call option value. This positive effect prevails over the negative effect of the increased discounting, and the American call option is actually increasing with respect to r. In Proposition 3 we show that these monotonicity properties are satisfied even in our stochastic interest rate framework.

Proposition 3

(The American option value function) In the market described by (1), the value of an American call (resp. put) option on S in Eq. (9) is of the form:

$$\begin{aligned} V (t) = F(t,S(t),r(t)) \end{aligned}$$

with $F:[0,T]\times {\mathbb {R}}^+ \times {\mathbb {R}} \mapsto {\mathbb {R}}^+$ given by:

$$\begin{aligned} F(t,S,r)= & {} \sup _{0 \le \eta \le T-t} {\mathbb {E}}^{{\mathbb {Q}}} \left[ \exp \left( - \int _{0}^{\eta } r(s) \mathrm {d}s \right) \cdot \right. \nonumber \\&\left. \cdot \varphi \left( S\exp \left( \int _{0}^{\eta } r(s) \mathrm {d}s - \left( q + \frac{1}{2} \sigma _S^2 \right) \eta + \sigma _S W^{\mathbb {Q}}_S(\eta )\right) \right) \right] \end{aligned}$$

(10)

where $r(0)=r$, $\varphi (x)=(x-K)^+$ (resp. $\varphi (x)=(K-x)^+$) and $\eta$ is a stopping time of the natural filtration of $(W_S^{\mathbb {Q}},W_r^{\mathbb {Q}})$ with values in $[0,T-t]$.

The function F is decreasing with respect to time t, convex with respect to S and increasing (resp. decreasing) in the call (resp. put) case. Moreover, F is increasing (resp. decreasing) in the call (resp. put) case with respect to r. Moreover $F(t,S,r) \ge \varphi (S)$ on the whole domain (value dominance).

Proof

See Appendix 3. $\square$

As the American equity option value is a deterministic function of (t, S, r), at each $t\in [0,T]$, the plane $(S,r) \in {\mathbb {R}}^+ \times {\mathbb {R}}$ can be divided into two complementary regions:

• the continuation region $CR(t) = \left\{ (S,r) \in {\mathbb {R}}^+ \times {\mathbb {R}} : F(t,S,r) > \varphi (S) \right\}$, the set of couples (S, r) where it is optimal to continue the option at t; the r-section of the continuation region at t is $CR_r (t) = \left\{ S\in {\mathbb {R}}^+: F(t,S,r) > \varphi (S) \right\}$;

• the early exercise region $EER(t) = \left\{ (S,r) \in {\mathbb {R}}^+ \times {\mathbb {R}} : F(t,S,r) = \varphi (S) \right\}$, the set of couples (S, r) where it is optimal to exercise the option at t; the r-section of the early exercise region at t is $EER_r (t) = \left\{ S\in {\mathbb {R}}^+: F(t,S,r) = \varphi (S) \right\}$.

The boundary separating the continuation region and the early exercise region as t varies in [0, T] is a surface called free boundary in the three-dimensional space (t, S, r). In Theorem 5 we describe the main features of the free boundary surface, that can be single (the standard case) or double. In Battauz et al. (2015) it is shown that in the constant positive (resp. negative) interest rate environment, the early exercise region, if any, is separated from the continuation region by a single (resp. double) one-dimensional free boundary separating the single (resp. double) continuation region. In particular, the exercise region for the American put option with negative interest rates fails to be downward connected. This happens when $F(t,0,r)>K$. Equation (10) implies $F(t,0,r) = \sup _{0 \le \eta \le T-t} {\mathbb {E}}^{{\mathbb {Q}}} \left[ \exp \left( - \int _{0}^{\eta } r(s) \mathrm {d}s \right) \cdot K \right] =K \sup _{0 \le \eta \le T-t} p(0,\eta ).$ If $p(0,\eta ) \le 1$ for all $\eta ,$ then $F(t,0,r)=K$ and convexity and value dominance of F imply that the early exercise region of the American put option (if any) is downward connected with respect to S, since (0, r) belongs to the early exercise region at t. On the contrary assume that there exists some deterministic $\eta$ such that $p(0, \eta )>1$. Then $F(t,0,r) \ge K \cdot p(0, \eta ) >K.$ In this case, if early exercise is optimal at t, r for some value of S, then the early exercise region will be bounded from below by a strictly positive equity value. A non-standard continuation region at t including (0, r) appears when the put is most deeply in the money. Proposition 4 formalizes this intuition for both American put and call options and provides local necessary conditions for the existence of optimal early exercise opportunities when the current interest rate value determines the existence of a zero-coupon-bond price greater than 1. This is very likely to occur when the current interest rate value is non-positive. Theorem 5 offers then a thorough description of the free boundary surface.

Proposition 4

(Asymptotic necessary conditions for the existence of optimal early exercise opportunities) In the market described by (1), at any point in time t and given the current value of the interest rate $r(t) = r$, suppose that

• [NC0] $r\alpha -\theta (\alpha +(T-t) )> 0$ with $\alpha =\frac{e^{-\kappa (T-t)}-1}{\kappa }\le 0$

Then the following are jointly necessary conditions for the existence of optimal exercise opportunities at t,  for sufficiently small $T-t$:

• [NC1] the dividend yield is non positive, $q \le 0$;

• [NC2] for some S, $\pi _{E}(t,S,r) = \varphi (S)$, where $\pi _{E}(t,S,r)$ is the value of the European put (resp. call) option defined in Proposition 1.

Proof

See Appendix 3. $\square$

Condition [NC0] is very likely satisfied when $r<0$, as the long-run mean of the interest rate $\theta$ is commonly assumed to be positive. [NC1] ensures that the discounted price of the risky security is not a supermartingale. If this was the case, we show in the proof that, under condition [NC0], this would lead automatically to optimal exercise of the American put option at maturity only. For the American put option, if early exercise is optimal under condition [NC0], then $EER_r,$ the early exercise region section at r,  is bounded by below by a strictly positive (non standard) lower boundary. A similar reasoning works for American equity call options. We remark that our results cannot be obtained from standard symmetry results for American options (see Battauz et al. (2015) and the references therein) due to the stochasticity of our interest rates. In the standard Black-Scholes case, the American put-call symmetry swaps the constant interest rate with the constant dividend yield. Being our interest rate stochastic and our dividend yield constant, such symmetry result is not viable.

Under [NC0], [NC2] ensures that the price of the European option $\pi _{E}(t,S,r)$ does not dominate the immediate payoff value. If this was the case, the American option would dominate the immediate payoff value as well, thus preventing the existence of immediate optimal early exercise opportunities. Although the formal proof of the necessary conditions in Proposition 4 requires the time to maturity to be small enough, we show in the following section that actually those conditions correctly identify nodes on the tree in which a double continuation region appears along the whole lifetime of the option (see Fig. 5).

In the following theorem we describe the main properties of the free boundary surface under the assumption that the early exercise region is non-empty. We distinguish between the standard case of a non-negative interest rate and the case of a negative interest rate, when unusual optimal continuation policies may appear. For an analysis of the smoothness of the free boundary with stochastic interest rates reflected at zero see Cai et al. (2021).

Theorem 5

(The free-boundary surface)

• 1. Suppose $r\ge 0$ and assume that $EER_r( {\overline{t}})$ is non-empty for some ${\overline{t}} \in (0,T)$. For the American put option

  $$\begin{aligned} {\overline{S}}^*(t,r) =\sup \left\{ S\ge 0: F(t,S,r) = \varphi (S) \right\} \end{aligned}$$

  (11)

  defines the (standard upper) free boundary and early exercise is optimal at any $t\ge {\overline{t}}$ for S(t) and $r(t)=r$ if $S(t) \le {\overline{S}}^*(t,r)$. The free boundary ${\overline{S}}^*(t,r)$ is increasing with respect to $t\ge {\overline{t}}$ and $r\ge 0$.

  For the American call option

  $$\begin{aligned} {\underline{S}}^*(t,r) =\inf \left\{ S\ge 0: F(t,S,r) = \varphi (S) \right\} \end{aligned}$$

  (12)

  defines the (standard lower) free boundary and early exercise is optimal at any $t\ge {\overline{t}}$ for S(t) and $r(t)=r$ if $S(t) \ge {\underline{S}}^*(t,r)$. The free boundary ${\underline{S}}^*(t,r)$ is decreasing with respect to $t\ge {\overline{t}}$ and increasing with respect to $r\ge 0$.

• 2. Suppose $r<0$ and that the necessary conditions of Propositions 4 are satisfied with $q<0$ and assume that $EER_r( {\overline{t}})$ is non-empty. Then the segment with extremes $[{\underline{S}}^*(t,r),{\overline{S}}^*(t,r)]$ (see Eqs. (11), (12)) is non-empty for any $t\in \left[ {\overline{t}},T\right] .$ The option is optimally exercised at any $t\ge {\overline{t}}$ for S(t) and $r(t)=r$ whenever $S(t) \in \left[ {\underline{S}}^*(t,r) ,{\overline{S}}^*(t,r) \right] .$ The lower free boundary, ${\underline{S}}^*(t,r),$ is decreasing with respect to t and the upper free boundary ${\overline{S}}^*(t,r)$ is increasing with respect to t for any $t\ge {\overline{t}}$.

  When $r/q \le 1$, for the American put it holds

  $$\begin{aligned} \frac{rK}{q} \le {\underline{S}}^*(t,r) < {\overline{S}}^*(t,r) \le K. \end{aligned}$$

  Their limits at maturity are $\lim _{ t \rightarrow T}{\overline{S}}^*(t,r) =K ={\overline{S}}^*(T,r)$ and ${\underline{S}}^*(T^-,r)= \lim _{ t \rightarrow T} {\underline{S}}^*(t,r) = \frac{rK}{q}> {\underline{S}}^*(T,r)=0.$ The lower free boundary, ${\underline{S}}^*(t,r),$ is decreasing with respect to r and the upper free boundary ${\overline{S}}^*(t,r)$ is increasing with respect to r.

  When $r/q \ge 1$, for the American call it holds

  $$\begin{aligned} K\le {\underline{S}}^*(t,r) < {\overline{S}}^*(t,r) \le \frac{rK}{q}. \end{aligned}$$

  Their limits at maturity are $\lim _{ t \rightarrow T}{\underline{S}}^*(t,r) =K ={\underline{S}}^*(T,r)$ and ${\overline{S}}^*(T^-,r)= \lim _{ t \rightarrow T} {\overline{S}}^*(t,r) = \frac{rK}{q}< {\overline{S}}^*(T,r)=+\infty .$ The lower free boundary, ${\underline{S}}^*(t,r),$ is increasing with respect to r and the upper free boundary ${\overline{S}}^*(t,r)$ is decreasing with respect to r.

• 3. Suppose $r<0$ and $q=0$. Then the early exercise region for the American put option at t is empty.

  For the American call, suppose $EER_r( {\overline{t}})$ is non-empty for some ${\overline{t}} \in (0,T)$. Then early exercise is optimal at any $t\ge {\overline{t}}$ for S(t) and $r(t)=r$ if $S(t) \ge {\underline{S}}^*(t,r)$ (see Equation (12)). The free boundary ${\underline{S}}^*(t,r)$ is decreasing with respect to $t\ge {\overline{t}}$ and increasing with respect to $r\ge 0$

Proof

See Appendix 3. $\square$

3.1 Numerical examples

We now present and describe three illustrative numerical examples that show the optimal exercise strategies and the possible characterizations of the continuation region for the American put and call options in the market described by (1), highlighting the free boundary’s features derived in Theorem 5.

We exploit our quadrinomial tree to evaluate American options by backward induction. Once the whole quadrinomial tree, namely all the couples (S, r) and the related transition probabilities, have been generated, we start from the values of the state variables S and r at maturity T. At maturity, the American option is exercised in all the nodes in which it is in the money; the resulting payoff is the value of the American option at T. At any other generic instant $t \in \{ 0, \Delta t, 2\Delta t, \dots , T-\Delta t \}$, and for any couple (S(t), r(t)), we compute the immediate payoff $\varphi (S)$ and we compare it to the continuation value of the option. The continuation value is obtained as the discounted (by the current realization of r(t)) expected value (according the transition probabilities computed at (S(t), r(t))) of the four values of the American option at $t + \Delta t$ connected on the tree to the current node. From the comparison between the immediate exercise and the continuation value, we get the value of the American option in the node (S(t), r(t)). Going backward, we finally get the price of the American option at $t=0$.

Theorem 2 showed that the quadrinomial tree we proposed converges in distribution to the bivariate process that solves (1), as the time step shrinks. Mulinacci and Pratelli (1998) prove that the convergence in distribution of the lattice-based approximation of the underlying state variables implies that the price of the American option evaluated according to the backward procedure described above converges to its theoretical value given by (9). In the following proposition we show that also the free boundaries recovered along our quadrinomial tree converge pointwise to their continuous-time counterparts defined in (11) and (12).

Proposition 6

(Convergence of the free boundaries) Let $t \in (0,T)$ and $V_d(t)=F_d(t,S,r)$ be the value of the American option along the quadrinomial tree built with n time steps. Define the discretized free boundaries as

$$\begin{aligned}&{\overline{S}}_d^*(t,r) =\sup \left\{ S\ge 0: V_d(t)=F_d(t,S,r) = \varphi (S) \right\} \\&{\underline{S}}_d^*(t,r) =\inf \left\{ S\ge 0: V_d(t)=F_d(t,S,r) = \varphi (S) \right\} . \end{aligned}$$

Then, ${\overline{S}}_d^*(t,r) \underset{n \rightarrow + \infty }{\longrightarrow } {\overline{S}}^*(t,r)$ and ${\underline{S}}_d^*(t,r) \underset{n \rightarrow + \infty }{\longrightarrow } {\underline{S}}^*(t,r)$.

Proof

See Appendix 3. $\square$

In all of the three following examples the parameters are: $T=2$, $n=125$, $S_0=K=1$, $\sigma _S=0.15$, $r_0=0$, $\theta = 0.02$, $\kappa = 0.5$, $\sigma _r = 0.01$ and $\rho = 0.5$. The dividend yield q of the equity is the only parameter that varies across the examples: in the first one we set $q=0$, in the second $q=0.02$ and $q=-0.02$ in the last one.

For each example we:

• Compute the value at inception of the European counterpart $\pi _{E}$ obtained both with the formula of Proposition 1 and along the quadrinomial tree (the values obtained in the two ways are indistinguishable);

• Compute the value at inception of the American option $\pi _{A}$ along the quadrinomial tree¹³;

• Compute the price of the American option, $\pi _{A}^{r_0}$, evaluated along the standard binomial tree of Cox et al. (1979) with a deterministic interest rate $r=r_0=0$¹⁴. Our aim is to quantify the error that an “unsophisticated” investor would make by evaluating American options within a flat term structure framework rather than within a fluctuating one;

• Graphically show how the single, or double (if any), free boundaries look like in the tSr-space. These graphs characterize the optimal exercise policy: at any t, the investor should look at the current values of (S(t), r(t));

• Graphically highlight the nodes of the quadrinomial tree where the necessary conditions of Proposition 4 are satisfied.

We first show the numerical results for the American put option that are summed up in Table 1.

Table 1 Results from the three numerical examples for the American put option

Fig. 3

First example, American put: $q=0\%$

Fig. 4

Second example, American put: $q=2\%$

Fig. 5

Third example, American put: $q=-2\%$. Green points in the bottom panels show the nodes of the quadrinomial tree in which necessary conditions [NC0], [NC1] and [NC2] of Proposition 4 for a double continuation region hold simultaneously. In the bottom-right panel, which is a view from above of the 3D plot in the bottom-left one, we brought to the foreground the red points of the lower boundary

Fig. 6

$r-$sections of free boundaries for the American put option. Left panel $r=2\%$ and $q=0\%$. Right panel $r=-1\%$ and $q=-2\%$

First example: $q=0\%$. If the underlying pays no dividend and its volatility is reasonably small, the expected drift of S basically coincides with $r(t)=r$. This splits the domain of r in two complementary regions according to the sign of r, as can be seen in the right panel of Fig. 3 (that displays the free boundary section at $t = \frac{T}{2}$). In the left region where r and $\mu =r-q-\frac{\sigma _S^2}{2}$ are both negative, the investor is willing to wait and postpone the exercise as much as possible in order to gain from both the negative discount rate and the implied expected depreciation of S. In the right region, on the contrary, where r and $\mu$ are both positive, we have the standard tradeoff between a positive discount rate (that makes the investor willing to exercise the option as soon as possible) and a negative expected drift of S (that makes the investor willing to wait for a larger payoff). This generates the standard upper boundary shown in the left panel of Fig. 3. We notice that the standard upper boundary is increasing with respect to r. Indeed, early exercise is more profitable when r increases and S is likely to appreciate.

The investor who believes that the term structure is flat and evaluates the American put option with a constant discount rate equal to our $r_0$ makes a relative error equal to 5.32%. This figure is economically significant as it is greater than the maximal error due to suboptimal exercise delay of the option as estimated¹⁵ in Chockalingam and Feng (2015).

Second example: $q=2\%$. If the underlying pays (positive) dividends, the drift of S is equal to r plus a negative quantity ($-q-\frac{\sigma _S^2}{2} <0$). This splits the domain of r into three complementary regions. The first one in which r and $\mu$ are both negative, the one in which r is positive but small so that $\mu$ is still negative, the last one in which r and $\mu$ are both positive. In the first one, the option is optimally exercised at maturity, as before. In the middle region there is a new tradeoff: the investor would like to cash in as soon as possible due to $r>0$ but the value of S is expected to decrease as $\mu <0$. This allows for a standard upper boundary. The critical price below which the investor will exercise, though, becomes smaller as r approaches 0: as r decreases the threat of the positive discount rate weakens and, therefore, the investor would postpone the exercise unless the underlying reaches a very low level. In other words, if the discount is not that strong, the investor prefers to gain the relative high dividend yield keeping the asset as long as possible. In the last region, we find the standard behaviour already outlined in the first example.

The investor who believes that the term structure is flat and evaluates the American option with a constant interest rate makes here an even higher relative error than before ($6.73\%$).

Third example: $q=-2\%$. In the case of negative dividends¹⁶, the drift of S is equal to r plus a quantity which is now positive ($-q-\frac{\sigma _S^2}{2} >0$). As a result, $\mu$ may be positive also when r is mildly negative. This splits again the domain of r into three complementary regions, as shown in the top-right panel of Fig. 4: the one in which r and $\mu$ are both negative, the one in which r is negative but $\mu$ is positive and the last one in which r and $\mu$ are both positive. In the first region, the option is again optimally exercised at maturity as in the previous examples. In the middle section a double continuation region appears: this is the case in which the necessary conditions in Proposition 4 are satisfied as documented in the bottom panels of Fig. 4. To the best of our knowledge, this is the first paper that documents the existence of a non standard double free boundary in a stochastic interest rates framework, generalizing the result obtained in the constant interest rates setting by Battauz et al. (2015). In the last region where both r and $\mu$ are positive, we find the standard behaviour already outlined in the first two examples.

We conclude our analysis of the American put option’s free boundaries, by displaying in Fig. 6 their time-dependence structure. In particular, we show that, for fixed values of r, the upper critical price of the American put is increasing with respect to time t whereas the lower critical price (if any) is decreasing, as already proved in Theorem 5 and documented in the constant interest rate framework by Battauz et al. (2015).

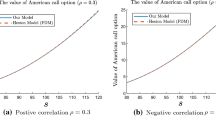
In Appendix 4 we also document the impact of the correlation on the American equity options’ prices.

We now turn to the American call options. Numerical pricing results for the American call option in the same scenarios analysed above for the American put option are summed up in Table 2. We notice that in all cases the investor who believes that the term structure is flat and evaluates the American call option with a constant discount rate equal to our $r_0$ makes a non-negligible relative error between 7% and 9.5%.

It is well known that American call options on non-dividend paying assets do not display any early exercise premium. This is true under usual market circumstances, i.e. when interest rates are non negative. In fact, in this case, the zero-coupon bonds of any maturity have initial prices that are smaller than one, i.e. $p(0,\tau )<1$ for any $\tau \in [0,T]$. Indeed, Jensen’s inequality implies that

$$\begin{aligned} {\mathbb {E}}^{\mathbb {Q}} \left[ \left( S(\tau ) - K \right) ^+e^{ -\int _{0}^{\tau } r(s) \mathrm {d}s } \right]&\ge \left( S(0) - K p(0,\tau ) \right) ^+ > \left( S(0) - K \right) ^+. \end{aligned}$$

The same holds true if S pays a negative dividend yield as ${\mathbb {E}}^{\mathbb {Q}} \left[ S(\tau ) e^{ -\int _{0}^{\tau } r(s) \mathrm {d}s } \right] = S(0)e^{-q\tau } > S(0)$.

Within our framework, interest rates are not always positive and zero-coupon bonds may have initial prices larger than one. Thus, early exercise may be optimal under some circumstances as one can indeed see in the following first example.

Table 2 Results from the three numerical examples for the American call option

Fig. 7

First example, American call: $q=0\%$

Fig. 8

Second example, American call: $q=2\%$

Fig. 9

Third example, American call: $q=-2\%$. Green points in the bottom panels show the nodes of the quadrinomial tree in which necessary conditions [NC0], [NC1] and [NC2] of Proposition 4 for a double continuation region hold simultaneously. In the bottom-right panel, which is a view from above of the 3D plot in the bottom-left one, we brought to the foreground the blue points of the upper boundary

Fig. 10

$r-$sections of free boundaries for the American call option. Left panel $r=-2\%$ and $q=0\%$. Right panel $r=-5\%$ and $q=-2\%$

First example: $q=0\%$. As explained above, early exercise may be optimal in this case only if zero-coupon bonds display initial prices larger than one for some maturity. This is the case portrayed in Fig. 7, where a (standard lower) free boundary for the American call option is documented for initial interest rates values smaller than $-1\%$. To our knowledge, this is the first paper that shows the existence of optimal early exercise opportunities for an American call option when the dividend yield is zero. We notice that the critical price, and thus the continuation region, is increasing in r, as the increasing drift $\mu$ of S pushes the option towards the in the money region. The impact of these optimal early exercise opportunities on the price of the option, however, is negligible because the risk-neutral probability of the equity price entering the early exercise region is quite small, as one can see from the first row of Table 2.

Second example: $q=2\%$. When the dividend yield is positive, early exercises of the American call option become profitable. In Fig. 8 we document the existence of a (lower standard) free boundary that is again increasing in r. Interestingly, the slope of the free boundary becomes steeper when $\mu$, the drift of S, turns positive, and the continuation region increases substantially as S is expected to appreciate. Consequently, early exercise in this case is optimal only if S is very deeply in the money.

Third example: $q=-2\%$. As already discussed for the American put option example, when the dividend yield is negative, the instantaneous drift of S, $\mu$, is always positive but for very negative values of r. As a result, early exercise for the American call option is never optimal unless r is very negative. In this case, for negative values of r, a non standard early exercise region appears surrounded by two continuation regions (see the top panels of Fig. 9). However, as in the first example with $q=0\%$, the early exercise premium does not significantly contribute to the price of the American call option because the equity price enters the early exercise region with a very small risk-neutral probability, as one can see from the third row of Table 2. The green dots in the bottom panels of Fig. 9 mark the region where our necessary conditions for non standard early exercise of Proposition 4 are satisfied. We notice that this region overlaps very accurately with the area where early exercise is optimal as portrait in the top-left panel of Fig. 9. We conclude our analysis of the American call option’s free boundaries, by portraying in Fig. 10 their time-dependence structure. In particular, we see that for American call options the upper critical price (if any) is increasing with respect to time t whereas the lower critical price is decreasing (see Fig. 10), thus confirming the results of Theorem 5 and of (Battauz et al. 2015) in a constant interest rate framework.

4 Conclusions

In this paper we have studied American equity options in a correlated stochastic interest rate framework of Vasicek (1977) type. We have introduced a tractable lattice-based discretization of the equity price and interest rate processes by means of a quadrinomial tree. Our quadrinomial tree matches the joint discretized moments of the equity price and the stochastic interest rate and converges in distribution to the continuous time original processes. This allowed us to employ our quadrinomial tree to characterize the two-dimensional free boundary for American equity put and call options, that consists of the underlying asset and the interest rate values that trigger the optimal exercise of the option. Our results are in line with the existing literature when interest rates lie in the positive realm. In particular, for the American put options, the higher the dividend yield, the higher the benefits from deferring the option exercise. Moreover, in this case, the exercise region is downward connected with respect to the underlying asset value. On the contrary, when interest rate are likely to assume even mildly negative values, optimal exercise policies change, depending on the tradeoff between the interest rate and the expected rate of return on the equity price. If such expected rate of return is negative, optimal exercise occurs at maturity only as the option goes (on average) deeper in the money as time goes by and the negative interest rates make the investor willing to cash in as late as possible. If the expected rate of return on the equity asset is positive, the option is expected to move towards the out of the money region. This effect is compensated by the preference to postponement due to negative interest rates. The tradeoff results in a non-standard double continuation region that violates the aforementioned downward connectedness of the exercise region for American put option.

We quantified the pricing error that an investor would make assuming a constant interest rate and therefore neglecting the variability (and the related risk) of the term structure. Finally, we documented similar non standard optimal exercise policies also for American call options. In particular, we find that early exercise of the American call option might be optimal even when the equity does not pay any dividend. These results numerically confirm the analytical features of the free boundaries retrieved in Theorem 5 for the continuous-time framework.

Appendices

Appendix 1: Construction of the quadrinomial tree

The stochastic differential equations (SDEs) of System (1) can be rewritten equivalently in the following vectorial specification:

$$\begin{aligned} \left\{ \begin{array}{rl} \displaystyle \frac{\mathrm {d} S(t)}{S(t)} &{} = \mu _S\mathrm {d}t +\nu _S \cdot \mathrm {d}W^{{\mathbb {Q}}}(t) \\ \mathrm {d} r(t) &{} = \mu _r\mathrm {d} t + \nu _r \cdot \mathrm {d} W^{{\mathbb {Q}} }(t) \end{array} \right. \end{aligned}$$

(13)

where $\mu _S = (r(t)-q)$, $\mu _r = \kappa (\theta - r(t))$, $\nu _S = [\sigma _S \quad 0]$, $\nu _r = [\sigma _r \rho \quad \sigma _r \sqrt{1-\rho ^2} ]$, $W^{{\mathbb {Q}}}(t) = \left[ W_1^{{\mathbb {Q}}}(t) \quad W_2^{{\mathbb {Q}}}(t) \right] ^{\prime }$ is a standard two-dimensional Brownian motion and $\cdot$ is the matrix product.

To show that our process $X_n$ defined via Eqs. (6), (7) and (8) converges to $X=(lnS,r)$ we refer to the general technique of Section 11.3 of Stroock and Varadhan (1997) exploiting the very convenient notation introduced in Section 3.2.1 of Prigent (2003). For the ease of the reader we recall here their template. Consider the following bivariate SDE:

$$\begin{aligned} \mathrm {d} X(t) = \mu (x,t) \mathrm {d}t + \sigma (x,t) \cdot \mathrm {d} W(t) \end{aligned}$$

(14)

where $X(t)_{t \ge 0} = (Y(t),r(t))_{t \ge 0}$, W(t) is a standard two-dimensional Brownian motion, $\mu (x,t) : ({\mathbb {R}} \times {\mathbb {R}} ^+) \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}^2$, $\sigma (x,t) : ({\mathbb {R}} \times {\mathbb {R}}^+) \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}^{2 \times 2}$ and an initial condition $X(0) = (x_0,r_0)$ is given.

To determine the parameters defined in the Eqs. (7) and (8) we match the first two (discretized) moments of Y(t) and r(t) as well as their cross variation. We neglect the $\Delta t$-second order terms, impose the proper constraint on the probabilities and a recombining tree condition as explained in Sect. 2. This leads to the following system of eight equations in eight unknowns:

$$\begin{aligned} \left\{ \begin{array}{rrl} {\mathbb {E}}_t[\Delta Y] = &{} (q_{uu}+q_{ud}) \Delta Y^+ + (q_{du}+q_{dd}) \Delta Y^- &{} \overset{!}{=} \mu _Y \Delta t \\ {\mathbb {E}}_t[\Delta r] = &{} (q_{uu}+q_{du}) \Delta r^+ + (q_{ud}+q_{dd}) \Delta r^- &{} \overset{!}{=} \mu _r \Delta t \\ {\mathbb {E}}_t[\Delta Y^2] = &{} (q_{uu}+q_{ud}) (\Delta Y^+)^2 + (q_{du}+q_{dd}) (\Delta Y^-)^2 &{} \overset{!}{=} \sigma _S^2 \Delta t \\ {\mathbb {E}}_t[\Delta r^2] = &{} (q_{uu}+q_{du}) (\Delta r^+)^2 + (q_{ud}+q_{dd}) (\Delta r^-)^2 &{} \overset{!}{=} \sigma _r^2 \Delta t \\ {\mathbb {E}}_t[\Delta Y \Delta r] = &{} q_{uu}\Delta Y^+\Delta r^+ + q_{ud}\Delta Y^+\Delta r^- + \qquad \qquad \qquad \qquad &{} \\ &{} + q_{du}\Delta Y^-\Delta r^+ + q_{dd}\Delta Y^-\Delta r^- &{} \overset{!}{=} \rho \sigma _S \sigma _r \Delta t \\ &{} \qquad \qquad \qquad \qquad \qquad q_{uu} + q_{ud} + q_{du} + q_{dd} &{} \overset{!}{=} 1 \\ &{} \Delta Y^+ &{} \overset{!}{=} -\Delta Y^- \\ &{} \Delta r^+ &{} \overset{!}{=} -\Delta r^- \end{array} \right. \end{aligned}$$

As noted in Nelson and Ramaswamy (1990), the four transition probabilities are not necessarily positive. In the limit, namely as $\Delta t \rightarrow 0$, we have $\Delta Y, \Delta r \rightarrow 0$ and, therefore, $q_{uu}, q_{dd} \rightarrow \frac{(1+\rho )}{4} > 0$ and $q_{ud}, q_{du} \rightarrow \frac{(1-\rho )}{4} > 0$. For $\Delta t > 0$, due to the discretization, some of the four probabilities in (8) may become non-positive. This may happen for extreme values of (Y, r) as described in Appendix 2. It is possible to correct for non-positive probabilities using a modification of the four transition probabilities (as proposed in Appendix 2). However, fixing this discretization error, namely correcting for possibly negative probabilities, does not have any detectable impact on option pricing. Therefore, all the numerical results in Sect. 3.1 are computed via the original algorithm, using the probabilities in (8).

Appendix 2: Bounds of the probabilities in the quadrinomial tree

Recall that at each t the four probabilities of an upward/downward movement of r/Y on the tree are:

$$\begin{aligned} \begin{array}{rl} q_{uu} &{} = \displaystyle \frac{\mu _Y \mu _r \Delta t + \mu _Y \Delta r^+ +\mu _r \Delta Y^+ +(1+\rho )\sigma _r \sigma _S}{4 \sigma _r \sigma _S} \\ q_{ud} &{} = \displaystyle \frac{-\mu _Y \mu _r \Delta t+\mu _Y \Delta r^+ -\mu _r \Delta Y^+ +(1-\rho )\sigma _r \sigma _S}{4 \sigma _r \sigma _S} \\ q_{du} &{} = \displaystyle \frac{-\mu _Y \mu _r \Delta t-\mu _Y \Delta r^+ +\mu _r \Delta Y^+ +(1-\rho )\sigma _r \sigma _S}{4 \sigma _r \sigma _S} \\ q_{dd} &{} = \displaystyle \frac{\mu _Y \mu _r \Delta t-\mu _Y \Delta r^+ -\mu _r \Delta Y^+ +(1+\rho )\sigma _r \sigma _S}{4 \sigma _r \sigma _S} \end{array} \end{aligned}$$

(15)

with $\Delta r^+ = \sigma _r \sqrt{\Delta t}$, $\Delta Y^+ = \sigma _S \sqrt{ \Delta t}$, $\mu _Y = r(t) - q - \frac{\sigma _S^2}{2}$ and $\mu _r = \kappa ( \theta -r(t))$. From now on we light the notation writing r instead of r(t). Nevertheless, it is crucial to remember that these probabilities are different for each node of the quadrinomial tree.

As already pointed out, the four probabilities sum up to one by construction. Unfortunately, they do not necessarily lie in (0,1). As a first control, we investigate what happens as the length of the time step goes to zero, namely, as $\Delta t \rightarrow 0$. We have

$$\begin{aligned}&\lim _{\Delta t \rightarrow 0} q_{uu} = \lim _{\Delta t \rightarrow 0} q_{dd} = \frac{1+\rho }{4}, \\&\lim _{\Delta t \rightarrow 0} q_{ud} = \lim _{\Delta t \rightarrow 0} q_{du} = \frac{1-\rho }{4} \end{aligned}$$

which are all positive quantities (at least as $\rho \in (-1,1)$). Therefore, the problem of having possibly negative probabilities is only due to the discretization procedure.

For instance, with $n=250$ steps and $T=1$ (that corresponds to $\Delta t = 0.004$), we need to impose the positivity constraint on all the four numerators in (15).

Imposing $q_{uu}\ge 0$ and solving with respect to r leads to:

$$\begin{aligned} A_{uu} r^2 + B_{uu} r + C_{uu} \le 0 \end{aligned}$$

(16)

where:

$$\begin{aligned} A_{uu}&= \kappa \\ B_{uu}&= -\kappa \left( \theta + q + \frac{\sigma _S^2}{2} - \frac{ \sigma _S}{\sqrt{\Delta t}} \right) - \frac{\sigma _r}{\sqrt{\Delta t}} \\ C_{uu}&= -\kappa \theta \left( -q - \frac{\sigma _S^2}{2} + \frac{ \sigma _S}{\sqrt{\Delta t}} \right) - \frac{\sigma _r }{\sqrt{\Delta t}} \left( - q - \frac{\sigma _S^2}{2} \right) - \frac{(1+\rho )\sigma _r \sigma _S}{ \Delta t}. \end{aligned}$$

Provided that the discriminant of Eq. (16) is positive, which surely holds true as $\Delta t \rightarrow 0$, the solution is ${\underline{r}}_{uu} \le r \le {\overline{r}}_{uu}$, where, of course,

$$\begin{aligned} {\underline{r}}_{uu} = \frac{-B_{uu}-\sqrt{B_{uu}^2-4A_{uu}C_{uu}}}{2A_{uu}} \quad \mathrm {and} \quad {\overline{r}}_{uu} = \frac{-B_{uu}+\sqrt{ B_{uu}^2-4A_{uu}C_{uu}}}{2A_{uu}}. \end{aligned}$$

Similarly, we can work out all of the other probabilities.

Imposing $q_{ud} \ge 0$ leads to:

$$\begin{aligned} A_{ud}r^2 + B_{ud}r + C_{ud} \ge 0 \end{aligned}$$

where:

$$\begin{aligned} A_{ud}&= \kappa \\ B_{ud}&= -\kappa \left( \theta + q + \frac{\sigma _S^2}{2} - \frac{ \sigma _S}{\sqrt{\Delta t}} \right) + \frac{\sigma _r}{\sqrt{\Delta t}} \\ C_{ud}&= -\kappa \theta \left( -q - \frac{\sigma _S^2}{2} + \frac{ \sigma _S}{\sqrt{\Delta t}} \right) - \frac{\sigma _r }{\sqrt{\Delta t}}\left( q + \frac{\sigma _S^2}{2} \right) + \frac{(1-\rho )\sigma _r \sigma _S}{\Delta t} , \end{aligned}$$

that is solved by $r \le {\underline{r}}_{ud}$ or $r \ge {\overline{r}}_{ud}$.

Imposing $q_{du} \ge 0$ leads to:

$$\begin{aligned} A_{du} r^2 + B_{du} r + C_{du} \ge 0 \end{aligned}$$

where:

$$\begin{aligned} A_{du}&= \kappa \\ B_{du}&= -\kappa \left( \theta + q + \frac{\sigma _S^2}{2} + \frac{ \sigma _S}{\sqrt{\Delta t}} \right) - \frac{\sigma _r}{\sqrt{\Delta t}} \\ C_{du}&= -\kappa \theta \left( - q - \frac{\sigma _S^2}{2} - \frac{ \sigma _S}{\sqrt{\Delta t}} \right) + \frac{\sigma _r }{\sqrt{\Delta t}}\left( q + \frac{\sigma _S^2}{2} \right) + \frac{(1-\rho )\sigma _r \sigma _S}{\Delta t} , \end{aligned}$$

that is solved by $r \le {\underline{r}}_{du}$ or $r \ge {\overline{r}}_{du}$.

Finally, imposing $q_{dd} \ge 0$ leads to:

$$\begin{aligned} A_{dd} r^2 + B_{dd} r + C_{dd} \le 0 \end{aligned}$$

where:

$$\begin{aligned} A_{dd}&= \kappa \\ B_{dd}&= -\kappa \left( \theta + q + \frac{\sigma _S^2}{2} + \frac{ \sigma _S}{\sqrt{\Delta t}} \right) + \frac{\sigma _r}{\sqrt{\Delta t}} \\ C_{dd}&= -\kappa \theta \left( -q - \frac{\sigma _S^2}{2} - \frac{ \sigma _S}{\sqrt{\Delta t}} \right) + \frac{\sigma _r }{\sqrt{\Delta t}}\left( - q - \frac{\sigma _S^2}{2} \right) - \frac{(1+\rho )\sigma _r \sigma _S}{\Delta t}. \end{aligned}$$

that is solved by ${\underline{r}}_{dd} \le r \le {\overline{r}}_{dd}$.

Summing up, probabilities in (15) stay positive as long as r satisfies:

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{r}}_{uu} \le r \le {\overline{r}}_{uu} \\ r \le {\underline{r}}_{ud} \text { or } r \ge {\overline{r}}_{ud} \\ r \le {\underline{r}}_{du} \text { or } r \ge {\overline{r}}_{du} \\ {\underline{r}}_{dd} \le r \le {\overline{r}}_{dd} \end{array} \right. \end{aligned}$$

The solution to the previous system of inequalities depends on the sign of the correlation $\rho$. Given the sign of $\rho$, the eight extremes values ${\underline{r}}_{uu}, {\underline{r}}_{ud}, \dots , {\overline{r}}_{du}, \overline{r }_{dd}$ always satisfy the same chain of inequalities. Furthermore, notice that these eight values depend only on the parameters of the model and not on t.

When $\rho \in (0,1]$, the only interval on which all of the inequalities hold true is ${\overline{r}}_{ud} \le r \le {\underline{r}}_{du}$ as it can be conveniently seen in Fig. 11.

Fig. 11

Graphical solution to the system of inequalities when $\rho \in (0,1]$

The intuition here is that when r and S move together and the discretization of r reaches values far away from its long run mean $\theta$ , a further movement of r away from $\theta$ and in the opposite direction of S is extremely unlikely and, eventually, happens “with a negative probability”.

If, for example, $r(0) = 0$, $\theta = 0.02$, $\sigma _r = 0.01$, $\kappa = 0.7$, $S(0) = 1$, $\sigma _S = 0.15$, $q = 0$, $\rho = 0.5$, $T=1$ and $n = 125$, after $m = 100$ steps, namely at $t = m \cdot \Delta t = m \cdot \frac{ T}{n} = 0.8$, r(t) spans the interval [−0.0885,    0.0885] and Y(t) the interval [−1.3282,    1.3282], both of them assuming $m = 101$ different values. Hence, at $t=0.8$ there are $101^2 = 10201$ possible nodes on tree. As an instance, at the node $\left( S(t), r(t) \right) _{t = 0.8} = (0.5847,-0.0751)$ the four probabilities are:

$$\begin{aligned} q_{uu}&= 0.4885 \\ q_{ud}&= -0.0143 \\ q_{du}&= 0.2780 \\ q_{dd}&= 0.2478. \end{aligned}$$

Indeed, with the given parameters, probabilities are all positive as long as ${\overline{r}}_{ud} = -0.0660 \le r(t) \le 0.0861 = {\underline{r}}_{du}$, which is not our case. As r(t) is extremely far away from its long-run mean and since $\rho > 0$ implies that r and S are likely to move together in the same direction, $q_{ud}$, namely the probability that r deviates even further from its long-run mean and also against S, becomes negative. Notice that $q_{ud} > q_{dd}$, meaning that the force that drives r towards its long-run mean prevails on the positive correlation between the two processes.

When such a scenario happens, one can adjust the probabilities by setting the negative one to 0 and normalizing to 1 the others. From the example above one would then get:

$$\begin{aligned} q_{uu}&= 0.4816 \\ q_{ud}&= 0 \\ q_{du}&= 0.2741 \\ q_{dd}&= 0.2443. \end{aligned}$$

A very similar situation happens when $\rho \in [-1,0)$ and the four probabilities stay positive as long as ${\underline{r}}_{dd} \le r \le {\overline{r}}_{uu}$. Figure 12 shows the solution to the system of inequalities in this case. Now $q_{uu}$ or $q_{dd}$ might become negative. This is due to the negative correlation: as r and S are likely to move in the opposite direction, when r is far away from its long-run mean, moving even further in the same direction of S may result in a negative probability. Again, one can correct for such a phenomenon with the normalization described above.

Fig. 12

Graphical solution to the system of inequalities when $\rho \in [-1,0)$

For sake of completeness, we briefly discuss also the limit of zero correlation between r and S. When $\rho = 0$, ${\underline{r}}_{uu} = {\underline{r}}_{ud}$, ${\overline{r}}_{ud} = {\underline{r}}_{dd}$, ${\overline{r}} _{uu} = {\underline{r}}_{du}$ and ${\overline{r}}_{du} = {\overline{r}}_{dd}$. Hence, the two intervals we found for the two previous cases, ${\overline{r}} _{ud} \le r \le {\underline{r}}_{du}$ when $\rho \in (0,-1]$ and $\underline{ r}_{dd} \le r \le {\overline{r}}_{uu}$ when $\rho \in [-1,0)$, coincide. When $\rho = 0$, probabilities stay positive as long as r belong to that interval.

Since the support of the discretization of r(t) is known at each t, we can retrieve the maximum t before which no normalization of the probabilities is needed.

Given the two thresholds ${\underline{r}}$ and ${\overline{r}}$ (where ${\underline{r}}={\overline{r}}_{ud}$, ${\overline{r}}={\underline{r}}_{du}$ if $\rho > 0$ and ${\underline{r}}={\underline{r}}_{dd}$, ${\overline{r}}={\overline{r}}_{uu}$ if $\rho < 0$) we can set ${\underline{t}}$ and ${\overline{t}}$ as:

$$\begin{aligned} {\underline{t}} := \min _{ s \in \{ 0, \Delta t, 2\Delta t, \dots , T \} } \left\{ r(s) \ge {\underline{r}} \right\} \quad \mathrm {and} \quad \overline{t } := \max _{ s \in \{ 0, \Delta t, 2\Delta t, \dots , T \} } \left\{ r(s) \le {\overline{r}} \right\} . \end{aligned}$$

Given the binomial structure of the discretization, after m steps we have:

$$\begin{aligned} r(0)-m\Delta r^- = r(0)-m\sigma _r\Delta t \le r(t) \le r(0)+m\sigma _r\Delta t = r(0)+m\Delta r^+ \end{aligned}$$

and, therefore, from

$$\begin{aligned} \begin{array}{l} r(0)-{\underline{m}} \sigma _r \Delta t \ge {\underline{r}} \\ r(0)+{\overline{m}} \sigma _r \Delta t \le {\overline{r}} \end{array} \end{aligned}$$

(17)

we can explicitly compute:

$$\begin{aligned} {\underline{t}}= & {} {\underline{m}} \Delta t = \frac{r(0)-{\underline{r}}}{\sigma _r \sqrt{\Delta t}} \Delta t = \frac{r(0)-{\underline{r}}}{\sigma _r } \sqrt{ \Delta t} \\ {\overline{t}}= & {} {\overline{m}} \Delta t = \frac{{\overline{r}}-r(0)}{\sigma _r \sqrt{\Delta t}} \Delta t = \frac{{\overline{r}}-r(0)}{\sigma _r } \sqrt{\Delta t}. \end{aligned}$$

Of course, neither ${\underline{r}}$, ${\overline{r}}$ nor ${\underline{t}}$, ${\overline{t}}$ are likely to correspond to any node of the discretized process r(t) or to the discretized time line $\{ 0, \Delta t, 2\Delta t, \dots , T \}$. In this case, we set ${\underline{r}}$, ${\overline{r}}$ and ${\underline{t}}$, ${\overline{t}}$ equal to the smallest values on the grid of r(t) and t that satisfy the constraints in (17). Going back to the numerical example above, we have that ${\underline{t}} = 0.5840$ and ${\overline{t}} = 0.7680$. A section of the quarinomial tree in this case is displayed in Fig. 13.

Remark

Numerical examples show that the probabilities’ modification previously suggested has no visible impact on option prices. More precisely, the magnitude of the absolute difference of the prices in Tables 1 and 2, when computed with and without the correction, is of order $10^{-16}$ or lower. This is due to the fact that the tree regions where probabilities are modified are very unlikely, i.e. occur with very small probability.

Fig. 13

Section of the quadrinomial tree for $S = 0$. Red points indicate nodes at which one transition probability becomes negative. Parameters: $r(0) = 0$, $\theta = 0.02$, $\sigma _r = 0.01$, $\kappa = 0.7$, $S(0) = 1$, $\sigma _S = 0.15$, $q = 0$, $\rho = 0.5$, $T=1$, $n = 125$

Appendix 3: Proofs of the claims

Proof of Theorem 2

(Convergence of the quadrinomial tree.)  We now need to show that the bivariate discrete process $(X_i)_i$ defined in (6) with the parameters in (7) and (8) converges in distribution to $X(t)=(Y(t),r(t))$ defined via Eq. (13). With the notation of the general case in (14) and exploiting the result of Section 11.3 of Stroock and Varadhan (1997), the desired result holds true if the following four conditions are met:

• (A1) the functions $\mu (x,t)$ and $\sigma (x,t)$ are continuous and $\sigma (x,t)$ is positive definite valued;

• (A2) with probability 1 a solution $(X_t)_t$ to the SDE:

  $$\begin{aligned} X_t = X_0 + \int _{0}^{t} \mu (X_s,s) \mathrm {d} s + \int _{0}^{t} \sigma (X_s, s) \cdot \mathrm {d} W(s) \end{aligned}$$

  exists for $0<t<+\infty$ and it is unique in law;

• (A3) for all $\delta , T > 0$

  $$\begin{aligned} \lim _{ n \rightarrow +\infty } \sup _{||x||\le \delta , 0 \le t \le T} |\Delta Y^{\pm } | = 0 \end{aligned}$$
  $$\begin{aligned} \lim _{ n \rightarrow +\infty } \sup _{||x||\le \delta , 0 \le t \le T} |\Delta r^{\pm } | = 0; \end{aligned}$$

• (A4) let $X_{i,j}$ indicate the j-th entry of $X_i$ and let ${\mathcal {F}}_i = \sigma (X_1, \dots , X_i)$ be the filtration generated by the discrete bivariate process $(X_i)$. Define:

  $$\begin{aligned} \mu _i(x,t) := \left[ \begin{array}{c} \mu _{i,1}(x,t) \\ \mu _{i,2}(x,t) \end{array} \right] \text { and } \sigma _i^2(x,t) := \left[ \begin{array}{c} \sigma _{i,1}^2(x,t) \\ \sigma _{i,2}^2(x,t) \end{array} \right] \end{aligned}$$

  where $\mu _{i,j}(x,t) = \displaystyle \frac{{\mathbb {E}}^{{\mathbb {Q}}} [X_{i+1,j}-X_{i,j} | {\mathcal {F}}_i]}{\frac{T}{n}}$ and $\sigma _{i,j}^2(x,t) = \displaystyle \frac{{\mathbb {E}}^{{\mathbb {Q}}} [(X_{i+1,j}-X_{i,j})^2 | {\mathcal {F}}_i]}{\frac{T}{n}}$ for $j=1,2$. Let $\rho _{i}(x,t) = \displaystyle \frac{{\mathbb {E}}^{{\mathbb {Q}}} [(X_{i+1,1}-X_{i,1})(X_{i+1,2}-X_{i,2}) | {\mathcal {F}}_i]}{\frac{T}{n}}$ and $\rho (x,t) = \sigma _1(x,t) \cdot \sigma _2(x,t)^{\prime }$ where $\sigma _j(x,t)$ is the j-th row of $\sigma (x,t)$. Then, for all $\delta , T > 0$,

  $$\begin{aligned}&\lim _{ n \rightarrow +\infty } \sup _{||x||\le \delta , 0 \le t \le T} || \mu _i(x,t) - \mu (x,t) || = 0\\&\lim _{ n \rightarrow +\infty } \sup _{||x||\le \delta , 0 \le t \le T} || \sigma ^2_i(x,t) - \sigma ^2(x,t) \cdot {\mathbf {I}}_{2} || = 0\\&\lim _{ n \rightarrow +\infty } \sup _{||x||\le \delta , 0 \le t \le T} | \rho _i(x,t) - \rho (x,t) | = 0 \end{aligned}$$

  where ${\mathbf {I}}_{n}$ is the column vector with all of the n entries equal to one.

For our quadrinomial tree we have $X_t = [Y(t), \quad r(t)]'$,

$$\begin{aligned} \mu (X_t,t) = \left[ \begin{array}{c} \left( r(t) - q -\frac{\sigma _S^2}{2} \right) \\ \kappa (\theta -r(t)) \end{array} \right] \quad \text { and } \quad \sigma (X_t,t) = \left[ \begin{array}{cc} \sigma _S &{}\quad 0 \\ \sigma _r \rho &{} \quad \sigma _r \sqrt{1 - \rho ^2} \end{array} \right] . \end{aligned}$$

Assumption (A1) holds true as $\sigma _S >0$ and $\det \sigma (X_t,t) >0$, that implies that the matrix $\sigma (X_t,t)$ is positive definite valued.

Assumption (A2) holds true if the standard conditions for the existence and the uniqueness of the solution to an SDE are met. According, e.g., to Proposition 5.1 in Björk (2019), it is sufficient to show that there exists a constant K such that the following are satisfied for all $x_i=[y_i, \quad r_i]'$, $i=1,2$ and t:

$$\begin{aligned} || \mu (x_1,t) - \mu (x_2,t) ||&\le K ||x_1-x_2||,\\ || \sigma (x_1,t) - \sigma (x_2,t) ||&\le K ||x_1-x_2||,\\ || \mu (x_1,t) || + || \sigma (x_1,t) ||&\le K \left( 1 + ||x_1|| \right) . \end{aligned}$$

Notice that the second and the third conditions involve the operator norm of a matrix $A \in {\mathbb {R}}^n$ defined as $||A||:=\sup _{||x||=1} \{ ||A\cdot x|| : x \in {\mathbb {R}}^n \}.$

As $|| \mu (x_1,t) - \mu (x_2,t) || = \sqrt{1 + \kappa ^2} |r_1-r_2|$ and $(r_1-r_2)^2 \le ||x_1-x_2||^2$, the first condition is surely satisfied for any $K \ge \sqrt{1 + \kappa ^2}$. As $\sigma (x_i,t)$ is actually constant and independent of $x_i$ and t, $|| \sigma (x_1,t) - \sigma (x_2,t) || = 0$ and the second condition is surely satisfied for any $K \ge 0$. Finally, as

$$\begin{aligned} ||\sigma (x_1,t)|| = \sigma _S^2 + \rho ^2 \frac{\sigma _r^2}{2} + |\rho | \frac{\sigma _r}{2} \sqrt{4\sigma _s^2 + \sigma _r^2} \end{aligned}$$

is constant and as

$$\begin{aligned} ||\mu (x_1,t)|| = \sqrt{\left( r_1-q-\frac{\sigma _S^2}{2} \right) ^2+\kappa ^2 (\theta - r_1)^2} \end{aligned}$$

can be bounded from above by $\sqrt{2(1+\kappa ^2)r_1^2}$, we have

$$\begin{aligned} || \mu (x_1,t) || + || \sigma (x_1,t) || \le \sqrt{2(1+\kappa ^2)}||x_1||+|| \sigma (x_1,t) || \le K(1+||x_1||) \end{aligned}$$

for any $K \ge \max \{ \sqrt{2(1+\kappa ^2)}, || \sigma (x_1,t) || \}$. As the three conditions hold true simultaneously for any $K \ge \max \{ \sqrt{2(1+\kappa ^2)}, || \sigma (x_1,t) || \}$, assumption (A2) is satisfied.

As the increments of the bivariate discrete process $\Delta Y^\pm = \pm \sigma _S \sqrt{\Delta t} = \pm \sigma _S \sqrt{\frac{T}{n}}$, $\Delta r^\pm = \pm \sigma _r \sqrt{\Delta t} = \pm \sigma _r \sqrt{\frac{T}{n}}$ are constant and do not depend neither on $x_i$, $i=1,2$, nor on t,

$$\begin{aligned}&\sup _{||x||\le \delta , 0 \le t \le T}|\Delta Y^{\pm } | = |\Delta Y^{\pm } | = \sigma _S \sqrt{\frac{T}{n}}, \\&\sup _{||x||\le \delta , 0 \le t \le T}|\Delta r^{\pm } | = |\Delta r^{\pm } | = \sigma _r \sqrt{\frac{T}{n}}. \end{aligned}$$

As both of the sups are infinitesimal with respect to n, (A3) holds true as well.

As the parameters in (7) and (8) of the bivariate discretization $X_i = (Y_i,r_i)$ are chosen in order to match the first two moments and the cross-variation of $X(t)=(Y(t),r(t))$, we have $\mu _i(x,t) = \mu (x,t)$, $\sigma _i^2(x,t) = \sigma ^2(x,t)\cdot {\mathbf {I}}_2$ and $\rho _i(x,t) = \rho (x,t)$. Hence, assumption (A4) is satisfied by construction.

Theorem 11.3.3 of Stroock and Varadhan (1997) allows us to conclude. $\square$

Proof of Proposition 3

(The American option value function.)  The bivariate process (S, r) defined in (1) is a time-homogeneous strong Markov diffusion (see Chapter 7 in Øksendal (1998)). Hence, for all stopping times $\tau$ of the natural filtration of $(W_S^{\mathbb {Q}},W_r^{\mathbb {Q}})$ with values in [t, T]

$$\begin{aligned} \left. \left( \int _{t}^{\tau }r(s)\mathrm {d}s,S(\tau )\right) \right| _{r(t)=x,S(t)=y}\overset{d}{\sim }\left. \left( \int _{0}^{\tau -t}r(s) \mathrm {d}s,S(\tau -t)\right) \right| _{r(0)=x,S(0)=y}. \end{aligned}$$

As in Lemma 3.9 of Jaillet et al. (1990), since $\{ (W_S^{\mathbb {Q}}(t+a)-W_S^{\mathbb {Q}}(t),W_r^{\mathbb {Q}}(t+a)-W_r^{\mathbb {Q}}(t) )\}_{a \ge 0}$ and $\{ (W_S^{\mathbb {Q}}(a),W_r^{\mathbb {Q}}(a) )\}_{a \ge 0}$ have the same law, we have indeed that

$$\begin{aligned}&{\mathbb {E}}^{{\mathbb {Q}}} \left[ \left. \exp \left( - \int _{t}^{\tau } r(s) \mathrm {d}s \right) \cdot \varphi \left( S(\tau ) \right) \right| {\mathcal {F}}_t \right] \\&\quad = {\mathbb {E}}^{{\mathbb {Q}}} \left[ \exp \left( - \int _{0}^{\tau -t} r(s) \mathrm {d}s \right) \cdot \varphi \left( y\exp \left( \int _{0}^{\tau -t} r(s) \mathrm {d}s - \left( q + \frac{1}{2} \sigma _S^2 \right) (\tau -t ) \right. \right. \right. \\&\qquad \left. \left. \left. + \sigma _S W^{\mathbb {Q}}_S(\tau -t) \right) \right) \right] \end{aligned}$$

with $r(0)=x$ and $y=S(0)$. Therefore, the value of the American option on S defined in (9) reduces to a deterministic function of the current values of the state variables as follows

$$\begin{aligned} V(t) = F(t,S(t),r(t)) \end{aligned}$$

with

$$\begin{aligned} F(t,S,r)= & {} \sup _{0 \le \eta \le T-t} {\mathbb {E}}^{{\mathbb {Q}}} \left[ \exp \left( - \int _{0}^{\eta } r(s) \mathrm {d}s \right) \cdot \right. \\&\left. \cdot \varphi \left( S\exp \left( \int _{0}^{\eta } r(s) \mathrm {d}s - \left( q + \frac{1}{2} \sigma _S^2 \right) \eta + \sigma _S W_S(\eta )\right) \right) \right] . \end{aligned}$$

where t enters only the upper bound of $\eta = \tau - t$, namely the time to maturity of the option and $r(0) = r$. From this last expression it is immediate to see that F enjoys the same monotonicity properties of $\varphi$ w.r.t. S, that it is decreasing w.r.t. t, and convex w.r.t. S. For the put option we show now that F is decreasing in r. To this aim we rewrite

$$\begin{aligned} F(t,S,r) = \sup _{0 \le \eta \le T-t} {\mathbb {E}}^{{\mathbb {Q}}} \left[ e^{- \int _{0}^{\eta } r(s) \mathrm {d}s} \left( K-S e^{ \int _{0}^{\eta } r(s) \mathrm {d}s - \left( q + \frac{1}{2} \sigma _S^2 \right) \eta + \sigma _S W_S(\eta )} \right) ^+\right] \end{aligned}$$

(18)

where $r=r(0)$.

The explicit strong solution of r in (2) can be written as

$$\begin{aligned} r(t)|_{r_0=x} = x e^{-\kappa t} + \theta (1-e^{-\kappa t}) + \sigma _r \displaystyle \int _{0}^t e^{-\kappa (t-s)} \mathrm {d} W^{\mathbb {Q}}_r(s). \end{aligned}$$

Thus, with a small abuse of notation, $r(t)|_{r_0=x} = xe^{-\kappa t} + r(t)|_{r_0=0}.$ Therefore, for any $r'>r$,

$$\begin{aligned} r(t)|_{r_0=r'} = r'e^{-\kappa t} + r(t)|_{r_0=0} > re^{-\kappa t} + r(t)|_{r_0=0} = r(t)|_{r_0=r} \end{aligned}$$

and $\int _{0}^{\eta } r(s) \mathrm {d}s$ started at $r(0)=r'>r$ is larger than $\int _{0}^{\eta } r(s) \mathrm {d}s$ started at $r(0)=r$. As the object of the expectation in (18) is a decreasing function of $\int _{0}^{\eta } r(s) \mathrm {d}s$, we conclude that F(t, S, r) is decreasing in r. Therefore, if $r'>r$, then $F(t,S,r')\le F(t,S,r)$.

To show that the American call option is increasing with respect to r, we apply a change of numéraire to isolate the effect of the interest rate in the underlying drift only (as under the original risk neutral measure an increase in r has opposite effects in the discount factor and in the call’s payoff).

$$\begin{aligned} {\mathbb {E}}^{\mathbb {Q}} \left[ \left( S(\tau ) - K \right) ^+e^{ -\int _{0}^{\tau } r(s) \mathrm {d}s } \right]&= {\mathbb {E}}^{\mathbb {Q}} \left[ \frac{S(\tau )e^{q \tau }}{S(0)B(\tau )} \left( \frac{1}{K} - \frac{1}{S(\tau )} \right) ^+ K e^{ -q\tau } S(0) \right] \\&= {\mathbb {E}}^{\mathbb {Q}} \left[ L^S(\tau ) \left( \frac{1}{K} - \frac{1}{S(\tau )} \right) ^+ K e^{ -q\tau } S(0) \right] \end{aligned}$$

where $L^S(\tau )$ is the Radon-Nikodym derivative of ${\mathbb {Q}}^S$, the equivalent martingale measure linked to the numéraire $\left\{ \frac{S(t)e^{q t}}{S(0)} \right\} _t$, with respect to ${\mathbb {Q}}$, defined as

$$\begin{aligned} \frac{\mathrm {d} {\mathbb {Q}}^S}{\mathrm {d} {\mathbb {Q}}} = L^S(t) = \frac{S(t)e^{qt}}{S(0)B(t)} \text { on } {\mathcal {F}}_t, 0 \le t \le T. \end{aligned}$$

(19)

Thus the call option is a put option under the new measure on KS(0)/S, starting at $t=0$ at the level K, with strike S(0) and interest rate q

$$\begin{aligned} {\mathbb {E}}^{\mathbb {Q}} \left[ \left( S(\tau ) - K \right) ^+e^{ -\int _{0}^{\tau } r(s) \mathrm {d}s } \right] = {\mathbb {E}}^{{\mathbb {Q}}^S} \left[ \left( S(0)- \frac{K S(0)}{S(\tau )} \right) ^+ e^{ -q\tau } \right] \end{aligned}$$

Recalling the dynamics of the equity price and of the interest rate under ${\mathbb {Q}}$,

$$\begin{aligned} \left\{ \begin{array}{rl} \displaystyle \frac{\mathrm {d} S(t)}{S(t)} &{} = (r(t)-q)\mathrm {d}t +[\sigma _S \quad 0] \cdot \mathrm {d}W^{{\mathbb {Q}}}(t) \\ \mathrm {d} r(t) &{} = \kappa (\theta - r(t))\mathrm {d} t + [\sigma _r \rho \quad \sigma _r \sqrt{1-\rho ^2} ] \cdot \mathrm {d} W^{{\mathbb {Q}}}(t) \end{array} \right. \end{aligned}$$

(20)

Girsanov’s theorem implies that $\mathrm {d}W^{\mathbb {Q}}(t) = \mathrm {d}W^{{\mathbb {Q}}^S} (t) + [\sigma _S \quad 0]' \mathrm {d} t$ and, therefore, (20) becomes

$$\begin{aligned} \left\{ \begin{array}{rl} \displaystyle \frac{\mathrm {d} S(t)}{S(t)} &{} = (r(t)-q+\sigma _S^2)\mathrm {d}t +[\sigma _S \quad 0] \cdot \mathrm {d}W^{{\mathbb {Q}}^S}(t) \\ \mathrm {d} r(t) &{} = \kappa (\theta - r(t) +\frac{\rho \sigma _S \sigma _r}{\kappa })\mathrm {d} t + [\sigma _r \rho \quad \sigma _r \sqrt{1-\rho ^2} ] \cdot \mathrm {d}W^{{\mathbb {Q}}^S}(t) \end{array} \right. \end{aligned}$$

(21)

Ito’s formula implies that

$$\begin{aligned} \mathrm {d} \left( \frac{1}{S(t)} \right) = \frac{1}{S(t)} \left( (q-r(t))\mathrm {d}t - [\sigma _S \quad 0] \cdot \mathrm {d}W^{{\mathbb {Q}}^S}(t) \right) \end{aligned}$$

and therfore the new underlying

$$\begin{aligned} \mathrm {d} \left( \frac{K}{S(t)} \right) = \frac{K}{S(t)} \left( (q-r(t))\mathrm {d}t - [\sigma _S \quad 0] \cdot \mathrm {d}W^{{\mathbb {Q}}^S}(t) \right) \end{aligned}$$

has drift $q-r(t)$. Thus the call option is a put option whose underlying under the new measure is

$$\begin{aligned} \frac{K}{S(t)} =\frac{K}{S(0)} e^{ \int _{0}^{\eta } (q- r(s)) \mathrm {d}s - \frac{1}{2} \sigma _S^2 \eta - \sigma _S W_1^{{\mathbb {Q}}^S}( \eta ) } \end{aligned}$$

Thus, as pointed out when dealing with the monotonicity of the American put option, $r(t)|_{r_0=r'} > r(t)|_{r_0=r}$ implies that the factor $\int _{0}^{\eta } (q-r(s)) \mathrm {d}s$ started at $r(0)=r'$ is smaller than the one started at $r(0)=r$. Therefore, the put’s payoff is larger, and the value of the corresponding American option is larger as well. This shows that for the American call option $r'>r$ implies $F(t,S,r')>F(t,S,r)$. $\square$

Proof of Proposition 4

(Asymptotic necessary conditions for the existence of a double continuation region). As discussed in the comments before Proposition 4, a necessary condition for the existence of a non-standard double continuation region is the existence of some deterministic $\eta$ such that $p(0, \eta )>1$, then $F(t,0,r) \ge K \cdot p(0, \eta ) >K$. We now deduce [NC0] by imposing $p(0, \eta ) >1$ for some $\eta \in [0,T-t].$ Exploiting Jensen’s inequality and the uniform integrability of r(s), we get:

$$\begin{aligned} {\mathbb {E}}^{{\mathbb {Q}}} \left[ \exp \left( - \int _{0}^{\eta } r(s) \mathrm {d}s \right) \right] \ge \exp \left( - {\mathbb {E}}^{\mathbb {Q}} \left[ \int _{0}^{\eta } r(s) \mathrm {d}s \right] \right) = \exp \left( - \int _{0}^{\eta } {\mathbb {E}}^{\mathbb {Q}} \left[ r(s) \right] \mathrm {d}s \right) . \end{aligned}$$

As before, thanks to (2), we have:

$$\begin{aligned}&{\mathbb {E}}^{{\mathbb {Q}}} \left[ \exp \left( - \int _{0}^{\eta } r(s) \mathrm {d}s \right) \right] \ge \exp \left( - \int _{0}^{\eta } re^{-\kappa s} + \theta (1-e^{-\kappa s}) \mathrm {d}s \right) \\&\quad = \exp \left( r\alpha -\theta (\alpha + \eta ) \right) \end{aligned}$$

where we set $\alpha := \displaystyle \frac{e^{-\kappa \eta } -1}{\kappa }$. Notice that $\alpha \le 0$ for any $\kappa$ and $\eta \in [0,T-t]$.

If $r\alpha -\theta (\alpha + \eta ) >0$, then $F(t,0,r) > K$.

For the American put option, under [NC0], if [NC1] is not satisfied, i.e. $q>0$, than the discounted risky security ${\tilde{S}}$ is driven by

$$\begin{aligned} \mathrm {d}{\tilde{S}}(t) = -q\mathrm {d} t + \sigma _S \mathrm {d} W^{{\mathbb {Q}}}_S(t), \end{aligned}$$

and ${\tilde{S}}$ is a supermartingale. Thus, for any $t<\tau <T$,

$$\begin{aligned} {\mathbb {E}}^{\mathbb {Q}} \left[ \left. S(\tau )e^{ -\int _{t}^{\tau } r(s) \mathrm {d}s } \right| {\mathcal {F}}_t \right] \le S(t) \end{aligned}$$

and, by Jensen’s inequality,

$$\begin{aligned} {\mathbb {E}}^{\mathbb {Q}} \left[ \left. \left( K-S(\tau ) \right) ^+e^{ -\int _{t}^{\tau } r(s) \mathrm {d}s } \right| {\mathcal {F}}_t \right]&\ge \left( K{\mathbb {E}}^{{\mathbb {Q}}} \left[ \left. e^{ -\int _{t}^{\tau } r(s) \mathrm {d}s } \right| {\mathcal {F}}_t \right] - S(t)e^{-q(\tau -t)} \right) ^+ \\&\ge (K-S(t))^+, \end{aligned}$$

where the last inequalities holds under $[NC0]$. This shows that, for the American put option, under $[NC0]$, if $[NC1]$ is violated, early exercise is never optimal at t.

We deal now with the American call option. For $0< \tau < T$, we have by Jensen’s inequality,

$$\begin{aligned} {\mathbb {E}}^{\mathbb {Q}} \left[ \left. \left( S(\tau ) - K \right) ^+e^{ -\int _{t}^{\tau } r(s) \mathrm {d}s } \right| {\mathcal {F}}_t \right]&\ge \left( S(t)e^{-q(\tau -t)}- K{\mathbb {E}}^{{\mathbb {Q}}} \left[ \left. e^{ -\int _{t}^{\tau } r(s) \mathrm {d}s } \right| {\mathcal {F}}_t \right] \right) ^+ \\&= \left( S(t)e^{-q(\tau -t)}- K p(t, \tau ) \right) ^+ \\&\ge (S(t)-K)^+, \end{aligned}$$

if $q \le 0$ and $p(t, \tau )\le 1.$ Therefore, to ensure the existence of optimal early exercise opportunities for the American call option, we must assume that $q > 0,$ or $q \le 0$ and $p(t, \tau ) > 1$ for some $\tau$. Under $[NC0]$, if $[NC2]$ is not satisfied, then $\pi _{A}(t,S,r) \ge \pi _{E}(t,S,r)>(K-S)^+$, that means that early exercise is never optimal at t. $\square$

Proof of Theorem 5

(The free-boundary surface.) The case $r \ge 0$ is standard (see Detemple 2014), and therefore we focus on $r<0$. The continuity, the monotonicity of the r-sections of the put option’s free boundaries with respect to t and S and their limits as $t\rightarrow T^-$ follow by adapting the proof of Theorem 2.3 in Battauz et al. (2015) where now the operator ${\mathcal {L}}$ becomes

$$\begin{aligned} {\mathcal {L}}F= \frac{\partial F}{\partial S} S(r-q) + \frac{\partial F}{\partial r} \kappa (\theta -r) +\frac{1}{2} \frac{\partial ^2 F}{\partial S^2} \sigma ^2_S S^2 +\frac{1}{2} \frac{\partial ^2 F}{\partial r^2} \sigma ^2_r +\frac{\partial ^2 F}{\partial r\partial S } \rho \sigma _r \sigma _S . \end{aligned}$$

The monotonicity properties of the free boundaries with respect to r follow from the monotonicity properties of F. In fact, let $r'>r$, and assume $S \in EER_r.$ Then $(K-S)^+ \le F(t,S,r') \le F(t,S,r) =(K-S)^+$, where the first inequality follows from value dominance and the second one from the fact that F is decreasing in r. Thus if $S \in EER_r,$ then $S \in EER_{r'},$ and $EER_{r'}\supseteq EER_r.$ By passing to the infimum (resp. supremum) we conclude that the lower (resp. upper) free boundary is decreasing (resp. increasing) with respect to r. The derivation of the upper and lower bounds of the free boundaries follows from Theorem 2.3 in Battauz et al. (2015) noticing that, in the early exercise region, the new operator ${\mathcal {L}}$ coincides with the constant interest rate one as $F(t,S,r)=(K-S)^+$ does not depend on r.

For the call option, we start from the monotonicity properties of the free boundaries with respect to r. As the call option is increasing in r, we have that if $r'>r$ and $S \in EER{r'}$ then $(S-K)^+ \le F(t,S,r) \le F(t,S,r') =(K-S)^+$, where the first inequality follows from value dominance and the second one from the fact that F is increasing in r. This means that $EER{r'}\subseteq EER_r.$ By passing to the infimum (resp. supremum) we conclude that the lower (resp. upper) free boundary is increasing (resp. decreasing) with respect to r.

For the other call option’s properties, we cannot simply adapt the proof of Theorem 3.3 in Battauz et al. (2015), as it relies on a symmetry result in a constant interest rate environment that fails to be applicable to our setting. The monotonicity properties of ${\underline{S}}^*$ and ${\overline{S}}^*$ with respect to t follow from the fact that F is decreasing with respect to t, similarly to the put case. We then prove the inequalities satisfied by the free boundaries. In the EER the function F satisfies

$$\begin{aligned} \frac{\partial F}{\partial t}+{\mathcal {L}} F \le r F \end{aligned}$$

(22)

On the EER in the call case $F(t,S,r)=S-K$ and therefore Eq. (22) simplifies to $1 \cdot S(r-q) \le r(S-K).$ Thus $-Sq \le -rK$ for all $S \in EER_r$, i.e. $S \le \frac{r}{q}K$ for all $S \in EER_r,$ as $q<0$. By passing to the supremum we get $K\le {\underline{S}}^*(t,r) < {\overline{S}}^*(t,r) \le \frac{rK}{q}.$

At maturity ${\underline{S}}^*\left( T,r \right) =K$ and ${\overline{S}}^*\left( T,r \right) =+\infty$, as the option is exercised at T whenever $S(T) \ge K.$

We now show that ${\underline{S}}^* \left( T^{-},r\right) =K$ and ${\overline{S}}^* \left( T^{-},r \right) =\frac{r K}{q}$. By construction ${\underline{S}}^* \left( t,r\right) \ge K$ for all $t\in \left( {\overline{t}};T\right) ,$ and hence ${\underline{S}}^*\left( T^{-},r \right) \ge K.$ Suppose by contradiction that ${\underline{S}}^*\left( T^{-},r \right) >K.$ The set $\left( {\overline{t}};T\right) \times \left( K ; {\underline{S}}^*\left( T^{-},r \right) \right) \subset CR_r$ and therefore $\left( {\mathcal {L}}-r \right) F=-\frac{\partial }{\partial t}F\ge 0$, as F is decreasing w.r.t. t. As $t\uparrow T$ we have $\left( {\mathcal {L}}-r \right) F \rightarrow$ $\left( {\mathcal {L}}-r \right) \left( S-K\right) =$ $-qS+rK$ for $S \in \left( K ; {\underline{S}}^*\left( T^{-},r \right) \right) .$ This implies $-qS+rK \ge 0$ for $S \in \left( K ; {\underline{S}}^*\left( T^{-},r \right) \right)$ and passing to the supremum over $S \in \left( K ; {\underline{S}}^*\left( T^{-},r \right) \right)$ this delivers ${\underline{S}}^* \left( T^{-},r \right) \ge \frac{r K}{q}$ which is a contradiction. We deal now with the upper free boundary limit. Suppose (by contradiction) that ${\overline{S}}^*\left( T^{-},r \right) < \frac{r K}{q}.$ But then the set $\left( {\overline{t}};T\right) \times \left( {\overline{S}}^*\left( T^{-},r \right) ; \frac{r K}{q}\right) \subset CR_r$ and $\left( {\mathcal {L}}-r \right) F=$ $-\frac{\partial }{\partial t}F\ge 0$ for $S\in \left( {\overline{S}}^*\left( T^{-},r \right) ; \frac{r K}{q}\right)$. As $t\uparrow T$ we have $\left( {\mathcal {L}}-r \right) F \rightarrow$ $\left( {\mathcal {L}}-r \right) \left( S-K \right) =-qS+rK$ for $S\in \left( {\overline{S}}^*\left( T^{-},r \right) ; \frac{r K}{q}\right)$ (here the limits are in distribution). Then $-qS+rK \ge 0$ for all $S\in \left( {\overline{S}}^*\left( T^{-},r \right) ; \frac{r K}{q}\right)$ and therefore also for the infimum $-q{\overline{S}}^*\left( T^{-},r \right) +rK \ge 0$ that implies the contradiction ${\overline{S}}^*\left( T^{-},r \right) \ge \frac{r K}{q}.$ $\square$

Proof of Proposition 6

(Convergence of the free boundaries.) According to Mulinacci and Pratelli (1998), $V_d(t)=F_d(t,S,r) \underset{n \rightarrow + \infty }{\longrightarrow } V(t) = F(t,S,r)$.

Consider the American put option first. The convergence of the discretized standard upper boundary can be proved by adapting the arguments in Lamberton (1993). We prove here the convergence of the non standard lower free boundary. Fix t and assume that ${\underline{S}}_d^*(t,r) \rightarrow {\underline{S}}^*(t,r) + \varepsilon$ with $\varepsilon \in {\mathbb {R}}$ and suppress t and r for sake of readability. By definition,

$$\begin{aligned} K-{\underline{S}}^*_d = V_d({\underline{S}}^*_d) = V_d({\underline{S}}^* + \varepsilon ). \end{aligned}$$

(23)

As $n \rightarrow +\infty$, $K-{\underline{S}}_d^* \rightarrow K-({\underline{S}}^*+\varepsilon )$ and $V_d({\underline{S}}^* + \varepsilon ) \rightarrow V({\underline{S}}^* + \varepsilon )$. Therefore, as $n \rightarrow +\infty$, (23) delivers

$$\begin{aligned} K - ({\underline{S}}^*+\varepsilon ) = V({\underline{S}}^*+\varepsilon ). \end{aligned}$$

Therefore, given r, ${\underline{S}}^* + \varepsilon$ belongs to the early exercise region for the continuous-time option and, as a consequence, $0<\varepsilon <{\overline{S}}^*-{\underline{S}}^*$. As ${\underline{S}}^* + \varepsilon$ belongs to the early exercise region, F in ${\underline{S}}^* + \varepsilon$ is a local strict supermartingale and, as a consequence, it satisfies

$$\begin{aligned} \frac{\partial }{\partial t} F(t,S,r) + \frac{1}{2} \sigma ^2 S^2 \frac{\partial ^2}{\partial S^2} F(t,S,r) + (r-q)S \frac{\partial }{\partial S} F(t,S,r) > rF(t,S,r) \end{aligned}$$

(24)

where $S = {\underline{S}}^* + \varepsilon$. As in the early exercise region $F(t,S,r) = K -S$, for $S = {\underline{S}}^* + \varepsilon$ (24) delivers

$$\begin{aligned} -(r-q)({\underline{S}}^*+\varepsilon )&> r(K-{\underline{S}}^*-\varepsilon ) \\ -r{\underline{S}}^* +q{\underline{S}}^* -r\varepsilon + q\varepsilon&> rK -r{\underline{S}}^* -r\varepsilon \\ q({\underline{S}}^* + \varepsilon )&> rK. \end{aligned}$$

As $q<0$, the last inequality is equivalent to

$$\begin{aligned} {\underline{S}}^* < \frac{rK}{q} - \varepsilon . \end{aligned}$$

But Theorem 5 ensures that

$$\begin{aligned} {\underline{S}}^* \ge \frac{rK}{q} \end{aligned}$$

and since $\varepsilon \ge 0$, it must be $\varepsilon = 0$ and, consequently, the thesis holds true.

The proof for the upper boundary of the American call option follows by a similar argument. $\square$

Appendix 4: Additional numerical analysis

1.1 4.1 The impact of correlation

In this subsection we assess the impact of the correlation between the two risk factors (the equity and the interest rate ones) on the price of American options. In order to do so, we expand Tables 1 and 2 by adding the cases $\rho =0$ and $\rho = -50\%$. European option prices are increasing with respect to correlation between the two risk factors as their sensitivity to rho is always positive. It is so also for American options as one can see in Tables 1 and 2. It is interesting to notice how, at least for put options, the correlation impacts more European options than American ones. For call options instead, the impact is approximatively the same as the early exercise premium is always quite small (Tables 3 and 4).

Table 3 Results from the three numerical examples for the American put option

Table 4 Results from the three numerical examples for the American call option

1.2 4.2 The comparison to Longstaff and Schwartz (2001)

In this subsection we compare the numerical results we obtain through our quadrinomial tree to the ones we obtained using the Least Square Methods for the value of American options proposed by Longstaff and Schwartz (2001). Tables 5 and 6 extend Tables 1 and 2 including also $\pi _A^{LSM}$, the initial price of the American options computed by the LSM algorithm with 100’000 paths and the radius of the related 95% confidence interval. The prices obtained via the two different algorithms do not differ significantly.

Table 5 Results from the three numerical examples for the American put option

Table 6 Results from the three numerical examples for the American call option