Forecasting Value-at-Risk in turbulent stock markets via the local regularity of the price process

Abstract

A new computational approach based on the pointwise regularity exponent of the price time series is proposed to estimate Value at Risk. The forecasts obtained are compared with those of two largely used methodologies: the variance-covariance method and the exponentially weighted moving average method. Our findings show that in two very turbulent periods of financial markets the forecasts obtained using our algorithm decidedly outperform the two benchmarks, providing more accurate estimates in terms of both unconditional coverage and independence and magnitude of losses.

1 Introduction

Since its adoption by the Basel Committee on Banking Supervision in 1996, Value at Risk—roughly defined as the maximum loss that can be expected over a given interval of time, once a certain level of confidence is fixed—has gained an increasing consensus as market-risk measurement tool in the banking sector. Despite the fact that it is not a coherent measure of risk Philippe et al. (1999), the success of VaR is largely due to its conceptual simplicity and immediacy. The coarse definition recalled above reveals that VaR is inherently dictated from the distribution of returns of the portfolio whose risk is being assessed. Many approaches have been proposed to estimate the VaR quantile, and—even though no method can be considered the best since each has its limitations Lechner and Ovaert (2010)—one common assumption is that daily portfolio returns are normally distributed. This is for example the premise of the parametric variance-covariance approach, that calculates VaR as the $\alpha$-quantile of the estimated distribution. The assumption of normality on the one hand greatly simplifies calculations, particularly when one deals with multi-asset portfolios and/or multi-horizons, but on the other hand it often underestimates VaR, since the unconditional distributions of financial returns tend to display fat tails and left skewness hard to be modeled. This is mainly due to volatility and kurtosis clustering: in fact, it is well known Engle (1982) that if, conditional on the variance, returns are normally distributed, then the resulting unconditional distribution will be fat-tailed with respect to the normal distribution. Even when this effect is accounted for using models such as the Exponentially Weighted Moving Average (EWMA) or the Generalised Autoregressive Conditional Heteroscedasticity (GARCH), empirical evidence suggests that also the conditional kurtosis of the returns is not constant. As noted by Guermat and Harris (2002), the time-varying degree of persistence of volatility clustering—captured by both EWMA and GARCH models—can be a potential cause of kurtosis clustering. This has relevant consequences for risk assessment, and for VaR in particular. In fact, unlike the variance (concerned mainly with the central mass of distribution), kurtosis affects specifically tail probabilities, which represent precisely the focus of VaR.

Several attempts to modeling time-varying kurtosis have been made: Hansen (1994) extends Engle’s ARCH model to permit parametric specifications for conditional dependence and finds evidence of time-varying kurtosis; Engle and Manganelli (2004) introduce the Conditional Autoregressive Value at Risk (CAViaR), which estimates conditional quantiles in dynamic settings using an autoregressive process and, assuming independence in the probability of exceeding the VaR, they test the adequacy of the model; CAViaR is extended into Multi-Quantile CAViaR by White et al. (2008), who apply their method to estimate the conditional skewness and kurtosis of the S&P500 daily variations; Wilhelmsson (2009) proposes a model with time varying variance, skewness and kurtosis based on the Normal Inverse Gaussian (NIG) distribution and finds that NIG models outperform Gaussian GARCH models; jointly modeling long memory in volatility and time variation in the third and fourth moments, Dark (2010) generalizes the Hyperbolic Asymmetric Power ARCH (HYAPARCH) model to allow for time varying skewness and kurtosis in the conditional distribution and finds that, when forecasting VaR, skewness and leptokurtosis in the unconditional return distribution is generally better captured via an asymmetric conditional variance model with Gaussian innovations; Gabrielsen et al. (2015) propose an exponential weighted moving average (EWMA) model that jointly estimates volatility, skewness and kurtosis over time using a modified form of the Gram-Charlier density and describe VaR as a function of the time-varying higher moments, by applying the Cornish-Fisher expansion series of the first four moments. Despite the refinements introduced, the authors find that the results from the validation process are inconclusive in favour of their model; similarly, Marcucci (2005) and Alizadeh and Gabrielsen (2013) could not find a uniformly accurate model. Authors in Gabrielsen et al. (2015) ascribe this to the selection of the back-testing period, coinciding with the credit crisis. To some extent, this would support the provocative and a bit simplistic idea that prompted hedge fund manager David Einhorn to refer to VaR as to “an airbag that works all the time, except when there is a crash".

The need to put a special emphasis on the response of risk assessment models during times of crisis emerged dramatically with the last global financial crisis and was incorporated in the most recent directions formulated by the Basel Committee on Banking Supervision. The Basel III document states:

“11. One of the key lessons of the crisis has been the need to strengthen the risk coverage of the capital framework. Failure to capture major on- and off-balance sheet risks, as well as derivative related exposures, was a key destabilising factor during the crisis.

12. In response to these shortcomings, the Committee in July 2009 completed a number of critical reforms to the Basel II framework. These reforms will raise capital requirements for the trading book and complex securitisation exposures, a major source of losses for many internationally active banks. The enhanced treatment introduces a stressed value-at-risk (VaR) capital requirement based on a continuous 12-month period of significant financial stress.[...]” [68], paragraph 2 (Enhancing risk coverage)

To provide a framework for the purpose highlighted in bold in the previous quotation is precisely the main motivation of this work. In order to evaluate and improve the response of VaR estimates in periods of significant financial stress, we model the price dynamics as a (discretized) Multifractional Process with Random Exponent (MPRE) Ayache and Taqqu (2005) whose pointwise regularity index (or pointwise Hurst parameter) is provided by an autoregressive process estimated on real data. The idea takes its cue from the encouraging findings of Frezza (2018), where empirical evidence is provided that even using simple AR(1) or AR(2) processes to model the pointwise regularity exponent of a MPRE generates marginal distributions that fit the actual ones. Even if more recent and refined approaches (see, e.g. Garcin (2020)) use fractional dynamics to characterize the pointwise regularity parameter, the common idea is to build from data an appropriate dynamics of the time-changing regularity exponents in order to obtain more realistic models of the price dynamics which can replicate the stylized facts of financial time series. In our approach, the AR process is used to generate the dynamics of the pointwise regularity exponents needed to simulate the trajectories of the MPRE. We then use this model to simulate the conditional distributions and to forecast the conditional VaR quantiles for three main stock indices (S&P500, Eurostoxx and Nikkei 225) during two financial crises: the 2000–2002 downturn, which affected primarily the United States stock market with a variation of about $-39.5\%$ of the S&P500 between January 3rd, 2000 and December 31st, 2002); and the 2007–2008 global financial crisis ($-36.2\%$ of the S&P500 between January 3rd, 2007 and December 31st, 2008). One of the advantages in modeling financial data through the MPRE lies in the generalization of the so called $t^\frac{1}{2}$ rule, widely used in financial practice to scale risks and distributions over different time horizons. In this respect, we find that the recommendations of the Basel Committee can be reformulated to improve the forecasts of VaR estimates over longer time horizons.

In this work, the analysis is restricted to the stock market because our main target is to test VaR forecasts faced with the occurrence of unexpected crises which typically affect stocks with more emphasis with respect to other large and global markets, such as e.g. the exchange rates. These display some peculiarities; for example, the rates series are generally reputed stationary and the classical Brownian motion model is there transformed by the Ornstein-Uhlenbeck approach or the Lamperti transform; samely, fractional Brownian motion is made stationary using similar techniques (see, e.g., Cheridito Kawaguchi and Maejima (2003), Chronopoulou and Viens (2012), Flandrin et al. (2003), Garcin (2019)). In addition to these standard approaches, it is worthwhile to quote the recent work by Garcin (2020), who - stressing the analogue with the evolution of the volatility models and by using a Fisher-like transformation - defines the Multifractional Process with Fractional Exponent (MPFE). Remarkably, the new process, which is characterized by the fact that its pointwise regularity exponent is itself a fractional sequence, is self-similar and with stationary increments.

Finally, it should be noticed that in recent years a substantial literature dealt with the Value-at-Risk in a multifractal context. For example, using simulation based on the Markov switching bivariate multifractal model, Calvet et al. (2006) computed VaR in the US bond market and the exchange market for USD-AUD; using the multifractal random walk (MRW) and multifractal model of asset retruns (MMAR) respectively, Bacry et al. (2008) and Batten et al. (2014) measured VaR in exchange market; Bogachev and Bunde (2009) introduced a historical VaR estimation method considering multifractal property of data; Dominique et al. (2011) find that the SP-500 Index is characterized by a high long-term Hurst exponent and construct a frequency-variation relationship that can be used as a practical guide to assess the Value-at-Risk; Lee et al. (2016) introduce a VaR consistent with the multifractality of financial time series using the Multifractal Model of Asset Returns (MMAR); Brandi and Matteo (2021) propose a multiscaling consistent VaR using a Monte Carlo MRW simulation calibrated to the data. Anyway, the majority of such contributions follows the multifractal approach, which influences the regularity of the trajectories by acting on a proper time-change instead of calibrating the pointwise regularity itself. This second approach is the one we analyze in this work.

The paper is organized as follows. In Sect. 2 VaR methodology is shortly recalled and the variance-covariance and the EWMA approaches, that we use as benchmarks, are discussed. Section 3 describes the model we adopt to estimate VaR and discusses several technical issues. The empirical analysis is developed in Sect. 4, where also the results are discussed. Finally, Sect. 5 concludes.

2 Value at risk

With reference to the sample space $\varOmega \equiv \mathbb {R}$ of the rates of return r on a given investment or portfolio W (expressed in domestic currency units), let $r_\tau$ be the rate of return of W over the time horizon $\tau$. Let us denote by $F_\tau :\varOmega \rightarrow [0,1]$ the distribution function of $r_\tau$, i.e. $F_\tau (x):=P(r_\tau \le x)=\int _{-\infty }^x p(r_\tau )dr_\tau$, where p is the probability density of $r_\tau$. Let $\tilde{\varOmega } \equiv \mathbb {R}$ be the sample space of currency-valued returns, defined as $R_\tau =r_\tau W$. Let us denote by $L_\tau$ the (potential) loss resulting from holding the portfolio over a time horizon $\tau$; it is defined as the negative difference between the return and its mean value $\mu$, that is $L_\tau :=-(R_\tau -\mu W)=\mu W - R_\tau =(\mu -r_\tau )W$. The distribution function of the loss $\tilde{F_\tau }: \tilde{\varOmega } \rightarrow [0,1]$ is therefore (see e.g. De Vries (2006), Hult and Lindskog (2007))

$$\begin{aligned} \tilde{F_\tau }(l)=P(L_\tau \le l) =1-F_\tau \left( \mu -l/W\right) \end{aligned}$$

(1)

With the notation above, we can give the following

Definition 1

Given the loss $L_\tau$ and the confidence level $\alpha \in (0,1)$, $VaR_\alpha (L_\tau )$ is the smallest number l such that the probability that the loss $L_\tau$ exceeds l is no larger than $1-\alpha$, i.e.

$$\begin{aligned} VaR_\alpha (L_\tau )&=\inf \{l \in \mathbb {R}: P(L_\tau >l)\le 1-\alpha \} \\&=\inf \{l \in \mathbb {R}: P(r_\tau \le \mu -l/W)\le 1- \alpha \} \end{aligned}$$

Definition 2

Given a nondecreasing function $F: \mathbb {R} \rightarrow \mathbb {R}$, the generalized inverse of F is given by

$$\begin{aligned} F^\leftarrow (y) = \inf \{x\in \mathbb {R}: F(x)\ge y\} \end{aligned}$$

(2)

with the convention $\inf \emptyset =\infty$.

Remark 1

If F is strictly increasing the $F^\leftarrow = F^{-1}$, that is the usual inverse.

Using the generalized inverse, for the distribution function of loss $L_\tau$, by (2) the $\alpha$-quantile of $\tilde{F_\tau }$ is

$$\begin{aligned} q_\alpha (\tilde{F_\tau })=\tilde{F_\tau }^\leftarrow (\alpha )=\inf \{l\in \mathbb {R}:\tilde{F_\tau }(l)\ge \alpha \}, \quad \alpha \in (0,1). \end{aligned}$$

(3)

Thus, with the notation above, it readily follows

$$\begin{aligned} VaR_\alpha (L_\tau )=q_\alpha (\tilde{F_\tau }) \end{aligned}$$

(4)

According to the Basel III framework, the basis of the calculation is the one-day VaR ($\tau =1$) computed at the 99th percentile using the one-tailed confidence interval and at least one year of data as past sample. The one-day VaR is then scaled, because “an instantaneous price shock equivalent to a 10 day movement in prices is to be used, i.e. the minimum “holding period” will be ten trading days. Banks may use value-at-risk numbers calculated according to shorter holding periods scaled up to ten days by, for example, the square root of time (...)” [68]. Thus, the rule $VaR_\alpha (L_{t+10,\tau })=10^{1/2}VaR_\alpha (L_{t,\tau })$ is used to settle the minimum requirement in terms of risk assessment. This rule of thumb rests on the prevalent, but not necessarily well specified, assumption of independence of the price variations, which in its turn is justified by the assumption that the market would be informationally efficient. From a topological point of view (see Sect. 3), this means to assume that the pointwise regularity of the price process is everywhere constant and equal to $\frac{1}{2}$.

The different approaches that can be followed to estimate VaR can be grouped into four categories: the Variance-Covariance (VC) or parametric method, the historical simulation, the Monte Carlo simulation and the Extreme Value approach. Despite the proliferation of alternative methodologies, which span from GARCH models with various specifications, aimed to capture the “volatility on volatility” Corsi et al. (2008), to fractionally autoregressive moving average (ARFIMA) models Andersen et al. (2001), that directly capture the volatility dynamics in terms of conditional mean, more than $70\%$ of banks among 60 U.S., Canadian and large international banks over 1996–2005 have reported that their VaR methodology used was historical simulation, followed by the Monte Carlo (MC) simulation as the second most popular method Pérignon and Smith (2010).

For this reason, we will refer in the following to the two popular benchmarks introduced in Riskmetrics of J.P. Morgan (Morgan 1996): the Variance-Covariance and the Exponential Weighted Moving Average (EWMA). We will omit the results obtained using historical simulation, since they are very close to those provided by VC. Both VC and EWMA are shortly recalled in the next two paragraphs.

2.1 Variance-covariance (V-C)

Among the different approaches to market risk measurement, the variance-covariance method, also known as parametric approach or linear VaR, or even delta normal VaR, is maybe one of the most widespread among financial institutions. This is due to historical (it was developed first, exploits results from the modern portfolio theory, and its usage quickly spread among US banks), technical (it is conceptually and computationally simple) and practical reasons (the Riskmetrics database is based on this approach and a large number of professional software use it).

The VC method assumes that the daily change in the price is linearly related to the daily returns from market variables, which in turn are assumed to be normally distributed. This implies that volatility can be described in terms of standard deviation and that only the first two moments (the mean $\mu$ and the standard deviation $\sigma$) fully describe the whole distribution. The method uses therefore covariances (volatilities and correlations) of the risk factors and the sensitivities of the portfolio with respect to these risk factors in order to determine directly the value at risk of the portfolio. With the assumption above, the Z-score (that is the number of standard deviations from the mean value of the reference population) of $X \overset{d}{=} N(\mu , \sigma )$ is simply calculated as $Z=\frac{X-\mu }{\sigma }$ and, unless the mean value, VaR can be calculated as multiple of standard deviation; for example, $\varPhi _Z(-2.326)\approx 0.01$ or $1\%$, indicating that this is the probability to extract a standard normal random variable whose value is lower than $-2,326$. In terms of VaR, the probability for losses larger than $x=z_\alpha \sigma +\mu$ is associated to the area under the normal curve, left of X and equal to $1-\alpha$. For $\alpha =99\%$, $z_\alpha =-2.326$, and the area is $1\%$ of total area under the normal distribution, so there is confidence of $99\%$ that losses will not exceed $-2,326\sigma +\mu$. Thus, referring to an initial value $W_{t,\tau }$ (where t denotes the timeline in, e.g., days, and $\tau$ the time horizon) subject a normally distributed changes with mean 0 and standard deviation $\sigma$, the one-day VaR in currency-valued terms, is calculated as (recall that $z_\alpha <0$)

$$\begin{aligned} VaR_{\alpha }(W_{t+1,\tau }) =-z_\alpha \sigma W_{t,\tau }. \end{aligned}$$

(5)

The VaR of a portfolio $\varPi$ is usually calculated as:

$$\begin{aligned} VaR_{\alpha }(\varPi _{t+1, \tau }) = (VCV^T)^\frac{1}{2} \end{aligned}$$

(6)

where V is the row vector of VaRs of the individual positions, C is the correlation matrix, and $V^T$ denotes as usual the transpose of V.

2.2 Exponentially weighted moving average (EWMA)

The Exponentially Weighted Moving Average (EWMA) approach has been introduced to reconcile the observed market heteroskedasticity with the unrealistic assumption that past returns have all the same weight on the latest observations. The method, which consists in weighting more the recent data, can be obtained as a special case of the GARCH(1,1) model, according to which

$$\begin{aligned} r_{t+1}=\mu + \sigma _t \epsilon _{t+1} \end{aligned}$$

and

$$\begin{aligned} \sigma _t^2 = \omega + \beta \sigma ^2_{t-1}+\alpha \sigma _{t-1}^2\epsilon _t^2, \end{aligned}$$

where $\omega \ge 0$, $\beta \ge 0$ and $\alpha \ge 0$ ensure positive variances, and $\epsilon _t$ is assumed to follow some probability distribution with zero mean and unit variance, such as the standard Gaussian distribution. Setting $\mu =\omega = 0$, $\beta =\lambda$ and $\alpha =1-\lambda$, with $\lambda$ called decay factor, the return return variance conditional on information accumulated up to time t reads as

$$\begin{aligned} \sigma _t^2 = \lambda \sigma _{t-1}^2 + (1-\lambda ) r^2_t. \end{aligned}$$

The decay factor $\lambda$ is generally set equal to 0.94 for daily data (see, e.g. Riskmetrics).

Using EWMA approach, the one-day VaR is calculated as in (6), that is

$$\begin{aligned} VaR_{\alpha }(W_{t+1})=-z_\alpha \sigma _{t+1} W \end{aligned}$$

(7)

where $\sigma _{t+1}$ is the standard deviation of the portfolio’s return, $r_{t+1}$, conditional on the information accumulated up to time t, and $z_\alpha$ is the $\alpha$-quantile of the standard normal distribution.

3 Path regularity and value at risk

In this Section we will introduce a VaR estimate based on the pointwise regularity of a sample path. The idea is that volatility affects the smoothness of the graph describing the dynamics of financial price changes. In order to deduce such an estimate, we first recall the notion of pointwise regularity.

Consider the stochastic process $X(t,\omega )$ with a.s. continuous and not differentiable trajectories over the real line $\mathbb {R}$. The local Hölder regularity of the trajectory $t \mapsto X(t,\omega )$ with respect to some t can be measured through its pointwise Hölder exponent, defined as (see Ayache (2013))

$$\begin{aligned} \small {\alpha _X(t,\omega )=\sup \left\{ \alpha \ge 0: \limsup _{h \rightarrow 0} \frac{|X(t+h,\omega )-X(t,\omega )|}{|h|^\alpha }=0\right\} .} \end{aligned}$$

(8)

Fig. 1

Hölder regularity of the graph of a random function

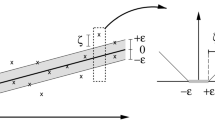
The geometrical intuition of (8) is provided by Fig. 1: function X has exponent $\alpha$ at $t_0$ if, for any positive $\epsilon$, there exists a neighborhood of $t_0$, $I(t_0)$, such that, for $t\in I(t_0)$, the graph of X is included in the envelope defined by $t \mapsto X(t_0) - c|t-t_0|^{\alpha -\epsilon }$ and $t \mapsto X(t_0)+c|t-t_0|^{\alpha +\epsilon }$ (see Lévy Véhel and Barriére (2008)). For certain classes of stochastic processes, remarkably for Gaussian processes, by virtue of zero-one law, there exists a non random quantity $a_X(t)$ such that $\mathbb {P}(a_X(t)=\alpha _X(t,\omega ))=1$ ( Ayache (2013)). In addition, when $X(t,\omega )$ is a semimartingale (e.g. Brownian motion), $\alpha _X=\frac{1}{2}$; values different from $\frac{1}{2}$ describe non-Markovian processes, whose smoothness is too high (low volatility), when $\alpha _X \in \left( \frac{1}{2},1\right)$, or too low (high volatility), when $\alpha _X \in \left( 0,\frac{1}{2}\right)$, to satisfy the martingale property. In particular, the quadratic variation of the process can be proven to be zero, if $\alpha _X>\frac{1}{2}$ and infinite, if $\alpha _X<\frac{1}{2}$.

Examples of stochastic processes that can be characterized by the Hölder pointwise regularity are:

• the fractional Brownian motion (fBm) of parameter H, for which $\alpha (t,\omega )=H$ a.s., and, as a special case, the standard Brownian motion ($\alpha (t,\omega )=1/2$ a.s.). Recall that, up to a multiplicative constant and for all $t \in \mathbb {R}$, the fBm has the following harmonizable representation

  $$\begin{aligned} \tilde{B}_H(t) = \int _\mathbb {R} \frac{e^{it\xi }-1}{|\xi |^{H+\frac{1}{2}}}d\hat{W}(\xi ) \end{aligned}$$

  (9)

  where dW is the usual Brownian measure and $d\hat{W}$ is the unique complex-valued stochastic measure satisfying $\int _\mathbb {R} f(x)dW(x) = \int _\mathbb {R} \hat{f}(x)d\hat{W}(x)$ for all $f \in L^2(\mathbb {R})$. A different representation of fBm involves the stochastic integral with respect to the Wiener process on the real line $\{W(s), -\infty<s<\infty \}$

  $$\begin{aligned} B_{H}(t)= & {} \frac{1}{\varGamma \left( H+1/2\right) }\left\{ \int _{-\infty }^0\left[ \left( t-s\right) ^{H-1/2} -\left( -s\right) ^{H-1/2}\right] dW(s)\right. \nonumber \\&\left. +\int _0^t\left( t-s\right) ^{H-1/2}dW(s)\right\} \end{aligned}$$

  (10)

  Up to an equality in probability, (10) is the only Gaussian process such that: (a) $B_H(0)=0$, and (b) there exists $K>0$ such that for any $t \ge 0$ and $h>0$, $B_H(t+h)-B_H(t)$ distributes as $N\left( 0,K^{2H}h^{2H}\right)$, where K is a scale factor;

• the multifractional Brownian motion (mBm) with functional parameter H(t), for which $\alpha (t,\omega )=H(t)$ a.s.;

• the Multifractional Processes with Random Exponents (MPRE) of parameter $H(t,\omega )$, for which—under some technical conditions (see Theorem 3.1 in Ayache and Taqqu (2005))—it is again $\alpha (t,\omega )=H(t,\omega )$ a.s.;

• the symmetric $\alpha$-stable Lévy motion ($0 < \alpha \le 2$), for which $H=1/\alpha$ a.s.;

• the fractional Lévy motion, of parameter $H-\frac{1}{2}+\frac{1}{\alpha }$ a.s.

All these fractal processes have been considered to some extent as potential models of the financial dynamics Tapiero et al. (2016); in particular, the mBm and the MPRE seem to account for many stylized facts (Bouchaud 2005), primarily the log-return heteroskedasticity, which constitutes one of the main challenges for VaR assessment. For this reason, following Costa and Vasconcelos (2003), Frezza (2012), Bianchi and Pianese (2014), Corlay et al. (2014), Garcin (2017), Bertrand et al. (2018)), we will assume the log-price process to be modeled as an MPRE with random parameter $H(t):=H(t,\omega )$. This process can be represented as an extension of the harmonizable fBm (9) as

$$\begin{aligned} Z(t) = \int _\mathbb {R} \frac{e^{it\xi }-1}{|\xi |^{H(t)+\frac{1}{2}}}d\hat{W}(\xi ). \end{aligned}$$

(11)

If H(t) is independent on $d\hat{W}$, the stochastic integral is well-defined ( Papanicolaou and Sølna (2002), Ayache and Taqqu (2005)) and the main results stated for the mBm can be extended to the MPRE. In particular, assuming the paths of the process $\left\{ H(t)\right\} _{t \in \mathbb {R}}$ to be almost surely Hölder functions of order $\beta =\beta (T)>\max _{t \in T}H(t)$ on each compact $T \subset \mathbb {R}$, the pointwise Hölder regularity of the graph of Z(t) equals the stochastic parameter H(t) almost surely (see Ayache et al. 2007).

3.1 Estimation of H(t)

Two main directions have been followed in literature to estimate H(t): the generalized quadratic variations (Istas and Lang 1997; Benassi et al. 1998) and the absolute moments of a Gaussian random variable (Péltier and Lévy Véhel 1994; Bianchi 2005; Bianchi et al. 2013). The properties and the accuracy of these estimators have been widely discussed (see, e.g., Istas and Lang 1997; Bianchi 2005; Ayache and Peng 2012; Storer et al. 2014), and in consideration of the results exhibited in Benassi et al. (2000), Coeurjolly (2001), Coeurjolly (2005), Gaci and Zaourar (2010), Gaci et al. (2010), Bianchi et al. (2013), Frezza (2018)), we have chosen to adopt the estimation procedure provided by Pianese et al. (2018). The advantage is that it efficiently combines both the approaches and produces fast and unbiased estimates of the function H(t). In the following, we will summarize the estimation technique.

Let us consider a discrete version $\varvec{X}=\left( X(i/n)\right) _{i=1,..,n}$ of $\{Z(t), t\in [0,1]\}$, with H(t) independent on $d\hat{W}$ and Hölder continuous. As mentioned above, both these assumptions legitimize the use of the estimator that will be described. Coeurjolly Coeurjolly (2005) introduces a local version of the k-th order variations statistics that fits the case of a Hölderian function $H: t\in [0,1] \rightarrow H(t)$ of order $0< \alpha \le 1$ and such that $\sup _tH(t)<\min (1,\alpha )$. Since the variance of the estimator is minimal for $k=2$, in the following the discussion will be referred only to the case $k=2$. Given the two integers $\ell$ and p, a filter $\varvec{a}:=(a_0,...,a_{\ell })$ of length $\ell +1$ and order $p \ge 1$ is built with the following properties:

$$\begin{aligned} \sum _{q=0}^\ell a_q q^r =0, \text { for } r = 0,\cdots ,p-1 \text { and } \sum _{q=0}^\ell a_q q^p \ne 0. \end{aligned}$$

The filter is a discrete differencing operator; for example, $\varvec{a}=(1,-1)$ returns the discrete differences of order 1 of $\varvec{X}$; $\varvec{a}=(1,-2,1)$ returns the second order differences, and so on. The filter, which defines the new time series

$$\begin{aligned} V^{\varvec{a}} \left( \frac{j}{n} \right) =\sum _{q=0}^\ell a_q X \left( \frac{j-q}{n} \right) \text { for } j=\ell +1,...,n-1, \end{aligned}$$

acts to make the sequence locally stationary and to weaken the dependence between the observations sampled in $\varvec{X}$.

Given the neighborhood of t, $\mathcal {V}_{n,\varepsilon _n}(t):=\{j=\ell +1, \cdots , n: |j/n-t| \le \varepsilon _n\}$ for some $\varepsilon _n > 0$ such that $n\varepsilon _n \rightarrow 0$ as $n \rightarrow \infty$ and denoted by $\nu :=\nu _n(t)$ the number of observations in $\mathcal {V}_{n,\varepsilon _n}(t)$, the quadratic variations statistics associated to the filter $\varvec{a}$ is defined as

$$\begin{aligned} V_{n,\varepsilon _n}(t,\varvec{a})=\frac{1}{\nu } \sum _{j \in \mathcal {V}_{n,\varepsilon _n}(t)}\left\{ \frac{V^{\varvec{a}}(j/n)^2}{\mathbb {E}(V^{\varvec{a}}(j/n)^2)}-1\right\} . \end{aligned}$$

(12)

Under these assumptions, it can be proved that $V_{n,\varepsilon _n}(t,\varvec{a}) \rightarrow 0$ as $n \rightarrow \infty$ and this asymptotic behavior allows to define estimators of H(t) by acting into two directions:

• (a) as the filter $\varvec{a}$ is dilated m times, exploiting the local H(t)-self similarity of $\varvec{X}$, the linear regression of $\log \mathbb {E}\left( \frac{1}{\nu } \sum _{j \in \mathcal {V}_{n,\varepsilon _n}(t)}V^{\varvec{a^m}}(j/n)^2\right)$ versus $\log m$ for $m=1,...,M$, defines the class of unbiased estimators $\hat{H}_{n,\varepsilon _n}(t, \varvec{a},M)$ whose variance is $\mathcal {O}((n\varepsilon _n)^{-1})$. In particular, Coeurjolly Coeurjolly (2005) proves that a filter of order $p \ge 2$ ensures asymptotic normality for any value of H(t), whereas if $\varvec{a}=(1,-1)$, the convergence holds if and only if $0< \sup _t H(t) < \frac{3}{4}$. In this case, by taking $\varepsilon _n=\kappa n^{-\alpha }\ln (n)^\beta$ with $\kappa >0$, $0<\alpha <1$ and $\beta \in \mathbb {R}$, it follows that $Var(\hat{H}_{n,\varepsilon _n}(t, \varvec{a},M))=\mathcal {O}\left( \frac{1}{\kappa n^{1-\alpha } \ln (n)^\beta }\right)$;

• (b) by setting $p=1$ and $a=(1,-1)$, for $j=t-\nu ,\cdots ,t-1$ and $t=\nu +1,\ldots ,n$, Eq. (12) becomes

  $$\begin{aligned} V_{n,\varepsilon _n}(t,\varvec{a})=\frac{\frac{1}{\nu }\sum _{j}|X_{j+1}-X_{j}|^2}{K^2\left( n-1\right) ^{-2H(t)}}-1. \end{aligned}$$

  (13)

  From this, Bianchi (2005), Bianchi et al. (2013), Bianchi and Pianese (2014) and Bensoussan et al. (2015) define the estimator

  $$\begin{aligned} \hat{H}_{\nu ,n,K}(t) = -\frac{\ln \left( \frac{1}{\nu }\sum _{j}|X_{j+1}-X_{j}|^2\right) }{2\ln (n-1)}+\frac{\ln K}{\ln (n-1)} \quad (j=t-\nu ,\dots ,t-1),\nonumber \\ \end{aligned}$$

  (14)

  whose rate of convergence is $\mathcal {O}(\nu ^{-\frac{1}{2}}(\ln n)^{-1})$, enough to ensure accuracy even for small estimation windows $\nu$. When actual data are considered, the scale factor K is generally unknown and—as it is evident from (14)—a misleading value produces estimates which are shifted with respect to the true ones. In addition, since the logarithm is slowly varying at infinity, the shift can be significant even for large n. Therefore, estimating H(t) by using in (14) an arbitrary running parameter $K^*$, will lead to the bias given by the second term of the right-hand side of

  $$\begin{aligned} H(t) = \hat{H}_{\nu ,n,K^*}(t)+\frac{\ln (K/K^*)}{\ln (n-1)}. \end{aligned}$$

  (15)

One way to get rid of the parameter K (see e.g. Istas and Lang (1997), Benassi et al. (1998), Garcin (2017)) is to calculate the numerator of (13) using different resolutions. For example, by halving the points into the estimation window, for $a=(1,-1)$ one has¹

$$\begin{aligned} M_2(t,a)=\frac{1}{\nu }\sum _{j=0}^{\nu -1}|X_{j+1}-X_{j}|^2, \quad \text {and} \quad M_2'(t,a)=\frac{2}{\nu }\sum _{j=0}^{\nu /2-1}|X_{2(j+1)}-X_{2j}|^2; \end{aligned}$$

since as n tends to $\infty$, $M_2(t,a)$ and $M_2'(t,a)$ tend to $K^2(n-1)^{-2H(t)}$ and $K^2\left( \frac{n-1}{2}\right) ^{-2H(t)}$, respectively, their ratio tends to $2^{2H(t)}$, from which an estimate of the Hurst exponent which converges almost surely to H(t) is

$$\begin{aligned} \hat{H}_{\nu ,n}(t,a)=\frac{1}{2}\log _2 \left( \frac{M_2'(t,a)}{M_2(t,a)}\right) \end{aligned}$$

(16)

Given the rate of convergence discussed in (a), this technique leads to erratic estimates, to the point that recently Garcin Garcin (2017) has proposed a non-parametric smoothing technique to reduce the noise. Thus, estimator (16) is unbiased, but affected by a large variance, whereas estimator (14) exhibits low variance and a bias (due to the unknown K) that requires a computationally intensive correction (see e.g. Bianchi and Pianese (2008) or Bianchi et al. (2013)). The solution, recently proposed by Pianese et al. (2018), is to combine the two estimators into one, as follows. Denoted by $\xi$ a zero-mean random variable, one can write

$$\begin{aligned} \hat{H}_{\nu ,n}(t,a) = H(t) + \xi (t). \end{aligned}$$

(17)

On the other side, from (15) it is also

$$\begin{aligned} \hat{H}_{\nu ,n,K^*}(t) = H(t) - \frac{\ln (K/K^*)}{\ln (n-1)}. \end{aligned}$$

(18)

Therefore,

$$\begin{aligned} \frac{\ln (K/K^*)}{\ln (n-1)} = \hat{H}_{\nu ,n}(t,a) -\xi (t) -\hat{H}_{\nu ,n,K^*}(t), \end{aligned}$$

from which, by averaging with respect to t, it immediately follows

$$\begin{aligned} h:= \frac{\ln (K/K^*)}{\ln (n-1)} = \frac{1}{n} \sum _{t=1}^{n}\left( \hat{H}_{\nu ,n}(t,a) - \hat{H}_{\nu ,n,K^*}(t)\right) . \end{aligned}$$

Notice that, since $K^*$ is chosen arbitrarily, the corrected estimate

$$\begin{aligned} \hat{\mathbb {H}}_{\nu ,n}(t,a) = \hat{H}_{\nu ,n,K^*}(t) + h \end{aligned}$$

(19)

does not depend on K any longer.

3.2 VaR forecast through $\hat{\mathbb {H}}_{\nu ,n}(t,a)$

Since the Basel III framework gives the banks the freedom to choose among models based on variance-covariance matrices, historical simulations or Monte Carlo simulations, value at risk can be calculated starting from the pointwise regularity of the log-prices estimated by (19). This is particularly useful when prices display high volatility, subject to abrupt changes even in very short time spans. Indeed, this is the case in which standard models generally do not work efficiently, despite the fact that VaR is conceived precisely to face stress circumstances.

The procedure that we suggest can be described through the following steps:

• following Frezza (2018), given the daily log-prices and denoted by n the sample size, for each $t=\nu ,\ldots ,n$ the last d estimates $\hat{\mathbb {H}}_{\nu ,n}(t,a)$ are used to simulate N paths of d regularity exponents $(\tilde{H}^{(i)}(t+k)), i=1,\ldots ,N; k=1,\ldots ,d$, as autoregressive processes of order $\lambda _t$, namely

  $$\begin{aligned} \tilde{H}^{(i)}(t+k)=\sum _{j=1}^{\lambda _t} \theta _j \tilde{H}^{(i)}(t+k-j)+\epsilon _{t+k} \end{aligned}$$

  where the innovations $\epsilon _{t+k}$ are white noise.

  As far as the knowledge of the authors, there are few studies documenting the distribution of H(t) estimates; nevertheless, the vast majority of the literature about dynamic estimates of the regularity exponents (or Hurst parameter) for financial series indicates values in the range 0.2–0.7. Even if some preliminary results seem to credit that a Gaussian distribution could be enough to describe the dynamics of H(t) (see e.g. Lillo and Doyne Farmer (2004), Cajueiro and Tabak (2004), Bianchi and Pantanella (2011), Bianchi et al. (2015)), the choice to consider an autoregressive model with Gaussian innovations as a first approximation is clearly arbitrary (see Garcin (2020) for a discussion of what happens when considering non-Gaussian extensions in the case of FX markets). Although aware of this limit, in this paper we restrict ourselves to this dynamic for consistency with what we assumed about the distribution of H(t) in order to apply the estimator (14).

  The optimal $\lambda _t$ is chosen by exploiting the Bayesian Information Criterion (BIC) for lags varying from 1 to $\nu$. This technique—also known as Schwartz criterion Schwarz (1978) and related to the Akaike Information Criterion (AIC)—is based on the log-likelihood function and constitutes a standard procedure in model selection. The model with the lowest BIC is preferred. Notice that the standard procedure requiring at least one year of past prices to calculate the one-day VaR rests on the premise that data belonging to this window be homogeneous. This is a crucial weakness, because precisely in turbulent periods data homogeneity usually deteriorates very quickly. To overcome this limit, in the application we will choose a smaller time horizon.

• the simulated $\tilde{H}^{(i)}(t+k)$ constitute the input to generate N sample paths of MPRE, $\tilde{Z}^{(i)}(t+k)$.² The 1-day log-return $\ln \frac{\tilde{Z}^{(i)}(t+1)}{\tilde{Z}^{(i)}(t)}$ is then used to build the 1-day distribution and to calculate the corresponding $\alpha$-quantile ($VaR_\alpha$);

• as discussed above, regulators suggest to forecast the h-days VaR by applying the $t^{1/2}$-rule, namely $VaR_\alpha (L_{t+h})\simeq h^{1/2}VaR_\alpha (L_{t})$. Since our results show that H(t) actually changes through time and can stay far from $\frac{1}{2}$ even for not negligible periods, opposite to the standard approach, the h-days log-returns are calculated by replacing the $t^{1/2}$ rule by the following scaling law

  $$\begin{aligned} \tilde{R}^{(i)}(t+h)=h^{\tilde{H}^{(i)}(t+h)}R(t), \quad 2 \le h \le d; i=1,\ldots ,N \end{aligned}$$

  (20)

  which accounts for the sequence of time-changing regularity exponents from time t to time $t+h$. Finally, the values $R^{(i)}(t+h)$ are used to build the h-days distribution and, by this, to compute the h-days VaR.

3.3 Evaluation of results

The assessment of the three VaR forecasting models (V-C, EWMA, MPRE) was performed by using three backtesting statistics justified by the arguments shortly discussed hereafter.

• (a) As a fundamental requirement (see the Basel’s directives), the model should generate a violation rate (proportion of times that VaR forecast is exceeded) “close” to the nominal value, that is the model should provide correct unconditional coverage. Thus, the number of exceptions should be neither too large (risk underestimation) nor too small (risk overestimation) and ideally, the violation rate should converge to the VaR quantile $\alpha$ as the sample size increases. The setup to test this is the Bernoulli trials framework. Under the null hypothesis that the model is correctly calibrated, the number of violations V over a sample N follows the binomial probability distribution $f(V)=\left( {\begin{array}{c}N\\ V\end{array}}\right) \alpha ^x(1-\alpha )^{N-V}$, with $\mathbb {E}(V)=\alpha N$ and $Var(V)=\alpha (1-\alpha )N$. As N increases, the central limit theorem ensures that the binomial distribution converges to the normal distribution. Therefore, the statistic which can test the unconditional coverage is (see, e.g., Guermat and Harris 2002; Jorion 2006, pp.143–146)

  $$\begin{aligned} t_{U}= \frac{V-\alpha N}{\sqrt{V\left( 1-\frac{V}{N}\right) }} \rightarrow N(0,1), \text {for large } N \end{aligned}$$

  (21)

• (b) A more demanding requirement is that a VaR model should also account for the “unpredictability” of exceptions, that is the model should provide conditional coverage independence. This was tested through the $LR_{C}$-statistic proposed by Christoffersen (1998):

  $$\begin{aligned} LR_{C}=2\left( \ln L_{A}-\ln L_{0}\right) , \end{aligned}$$

  (22)

  where $L_{A}=\left( 1-\pi _{01}\right) ^{T_{00}} \cdot \pi ^{T_{01}}_{01}\cdot \left( 1-\pi _{11}\right) ^{T_{10}}\cdot \pi ^{T_{11}}_{11},$ $\pi _{ij}=\frac{T_{ij}}{T_{i0}+T_{i1}}$, $L_{0}=( 1-\pi )^{T_{00}+T_{10}} \cdot \pi ^{T_{01}+T_{11}}$ and $\pi =\left( T_{01}+T_{11}\right) /\left( T_{00}+T_{01}+T_{10}+T_{11}\right)$, $T_{ij}$ being the number of times that state i is followed by state j. State 0 and state 1 indicate, respectively, the time in which actual portfolio loss is less than the estimated VaR and viceversa. It is worthwhile to highlight that we tested separately the unconditional and conditional coverage independence, because— as observed by Campbell et al. Campbell (2005)—in some cases the model can pass the joint test while still failing either the independence test or the unconditional one;

• (c) since the magnitude as well as the number of violations constitute two fundamental parameters to assess the quality of a VaR forecast model, the performances of the three approaches were evaluated also through the regulators’ loss-function proposed by Sarma et al. (2003) Sarma et al. (2003). By modifying the loss-function of Lopez (1998) Lopez (1998), the measure assigns the score $S_{i}, \text { } i=1,\ldots ,N$, to each candidate model as follows:

  $$\begin{aligned} S_{i} = \bigg \{ \begin{array}{ll} (L_{i}-V_{i})^2 &{} \text { if } L_{i} > V{_i} \\ 0 &{} \text { otherwise} \\ \end{array} \end{aligned}$$

  (23)

  where $V_{i}$ is the estimated VaR and $L_{i}$ is the observed loss at time i. Following the regulator’s directions, Sarma measure $S=\sum ^{n}_{i=1}S _{i}$ penalizes the model displaying more violations and—as a consequence—the model with lower value should be preferred.

Finally, as prescribed by the regulators, a 250-day window was used for the V-C and EWMA methods (Basel III requires at least one year of observations to calculate VaR). However, the difference in width between the window considered for the MPRE (32 trading days) and for the standard estimates (V-C and EWMA) does not impact on the results of the VaR estimates because the EWMA method calculated with a window of only 32 trading days virtually produces the same results as that calculated with a window of 250 trading days, since the weight attributed to less recent observations decreases exponentially. This effect is described in Fig. 2 for the years 2003–2005. We observe the convergence of the V-C method to the EWMA and the absence of differences between the EWMA calculated at 250 days and at 32 days. For this reason, when evaluating the performance of the VaR estimates calculated with the mBm compared with those calculated with the two standard methods, reference will mostly be made to the benchmark represented by the EWMA, which - for the reason explained above—tends to coincide with the V-C at 32 days.

Fig. 2

Comparison of VaR forecasts for Euro STOXX 50 Index (SX5E). Notice the convergence of the V-C method to the EWMA and the substantial absence of differences between the EWMA calculated at 250 days and at 32 days

Table 1 Basic statistics of the autoregressive fitting

4 Application

4.1 Data and parameters

The VaR forecast methodology described in Sect. 3.2 was applied to three stock indices: the Standard&Poor’s 500 (S&P500), the Nikkei 225 (N225) and the Euro STOXX 50 (SX5E), representative of the three main financial areas U.S., Asia and Europe. Table 2 summarizes the basic statistics of the daily log-changes of the three indices. The analysis was focused on two periods of special relevance in terms of market turbulence and high volatility: the stock market downturn of 2000-2002, that can be viewed as part of the correction—triggered also by shocks as 9/11 and the dot com bubble—that began in 2000 after a decade-long rising market; and the global financial crisis of 2007–2008, which is considered to have been one of the worst financial crises since the Great Depression.

Table 2 Basic statistics of log-changes of the three samples, $^{(*)} \times 10^{-4}$

Fig. 3

Percentage of violations (left) and $t_U$ statistic (right) for the three stock indices and the three levels of confidence. The left panels show that the MPRE outperforms both V-C and EWMA in terms of unconditional coverage; in all cases, the number of violations of MPRE forecasts is in line with the nominal ones. As h increases, the number of violations for V-C (worst case) and EWMA systematically exceeds the nominal values. This pattern suggests that the usage of the $t^{1/2}$ rule leads to underestimate the risk in turbulent periods. The right panels show the $t_{U}$-statistics for the V-C, the EWMA and the MPRE, along with the confidence intervals of the statistic: for any h and $\alpha$, the MPRE generally lie within the confidence interval, whereas the V-C is always outside and the EWMA diverges from the confidence interval as the number of days ahead increases

Estimator (19) was implemented on the series of the daily closing indices with parameters $a=(-1,1)$ (i.e. first differences were considered) and $\nu =21$, set to match about one trading month. To ensure the statistical significance of the sample and to simulate efficiently the MPRE, minimizing the computational time, we chose to set $d=32$. To save the integrity of the time series, H(t) was estimated also before the starting date reported in Table 2; in fact, since the forecasted VaR starts on January 2nd, 2000 and on January 2nd, 2007, respectively, the first d estimates of H(t) used to simulate the first $AR(\lambda _t)$ belong to the last d days of 1999 or 2006, respectively.

For each examined index and each period, Table 1 summarizes the basic statistics of the autoregressive fitting. We report the values only for the first-order autoregressive term since the optimal $\lambda _t$ chosen by the Schwarts criterion is 1 in over $95\%$ of cases.

4.2 Results and discussion

Figure 3 displays the proportion of violations and the corresponding $t_{U}$-statistic for the three indices and different days ahead h, in the period of $2007-2008$, while Table 3 summarizes the $LR_{C}$-statistic for the same period. Tables 4, 5 and 6 report—for each index—the $t_{U}$-statistic (top) and $LR_{C}$-statistic (bottom) in the period $2000-2002$ (to streamline the presentation of the results, we omitted the corresponding graphs). Finally, Fig. 4 displays the S-Sarma measure for all indices in both periods.

Figure 3 shows that MPRE outperforms both V-C and EWMA in terms of unconditional coverage. For the three confidence levels, the number of violations of MPRE forecasts is in line with the nominal ones; as h increases, the number of violations for V-C (worst case) and EWMA systematically exceeds the nominal values. This pattern—which is particularly evident for the S&P500 between 2000 and 2002 at $\alpha =0.01$ (see the last three columns of Table 4)—suggests that in turbulent periods using the $t^{1/2}$ rule leads to underestimate the risk: this is evident for the EWMA, which is close to the nominal value for one- or two-days forecasts, but increasingly biased as h increases; V-C forecasts instead are generally biased starting from the very one-day estimate. The graphs summarizing the $t_{U}$-statistics (see Fig. 3, right panels) fully agree with this conclusion: for any h and for any $\alpha$, MPRE forecast lie within the confidence interval of the statistic, whereas—as expected—V-C forecasts are always outside and EWMA forecasts diverge from the confidence interval as the number of days ahead increases.

Similar results hold also in the time interval 2000–2002 for MPRE forecasts (see Tables 4, 5 and 6), which in all cases belong or are closer (with respect to the other models) to the confidence intervals. However, in this period, both V-C and EWMA forecasts are generally better with respect to those of 2007–2008. A possible explanation for this behavior is the different nature of the turbu lence which affected markets in the two periods: while the period 2000–2002 was characterized by a slow dowturn with very rare sudden downward variations, the period 2007–2008 was on the contrary marked out from unexpected and violent crashes (one for all, the Lehman Brothers bankruptcy), witnessed by a distribution of log-price variations which displays much fatter left tail with respect to 2000–2002. This implies faster changes in the volatility, which both V-C and EWMA forecasts don’t fully succeed to capture.

Table 3 The table reports the $LR_{C}$-Christoffersen statistic for years 2007–2008, to test the null hypothesis of correct conditional coverage independence, that is VaR model should also account for the “unpredictability” of exceptions. To test this the $LR_{C}$-statistic can be used. It is defined as $LR_{C}=2\left( \ln L_{A}-\ln L_{0}\right)$, where $L_{A}=\left( 1-\pi _{01}\right) ^{T_{00}} \cdot \pi ^{T_{01}}_{01}\cdot \left( 1-\pi _{11}\right) ^{T_{10}}\cdot \pi ^{T_{11}}_{11},$ $\pi _{ij}=\frac{T_{ij}}{T_{i0}+T_{i1}}$, $L_{0}=( 1-\pi )^{T_{00}+T_{10}} \cdot \pi ^{T_{01}+T_{11}}$ and $\pi =\left( T_{01}+T_{11}\right) /\left( T_{00}+T_{01}+T_{10}+T_{11}\right)$, $T_{ij}$ being the number of times that state i is followed by state j. State 0 and state 1 indicate, respectively, the time in which actual portfolio loss is less than the estimated VaR and viceversa. The $5\%$, $2.5\%$ and $1\%$ critical values are, respectively, 3.84, 5.02 and 6.63. The independence in the number of violations is generally preserved only when $h = 1$ for almost all methods, except for some cases displaying independence up to two days (for example, MPRE and EWMA for S&P500 when $\alpha =0.025$ or $\alpha =0.01$)

Table 4 $t_{U}$-statistic (top) and $LR_{C}$-statistic (bottom) for S&P500 in period 2000–2002. The respective $5\%$, $2.5\%$ and $1\%$ critical values for the $LR_{C}$ are 3.84, 5.02 and 6.63 while the acceptance region for the $t_{U}$-statistic are $(-1.65,1.65)$, $(-1.96,1.96)$ and $(-2.33,2.33)$, respectively

Table 5 $t_{U}$-statistic (top) and $LR_{C}$-statistic (bottom) for N225 in period 2000-2002. The respective $5\%$, $2.5\%$ and $1\%$ critical values for the $LR_{C}$ are 3.84, 5.02 and 6.63 while the acceptance region for the $t_{U}$-statistic are $(-1.65,1.65)$, $(-1.96,1.96)$ and $(-2.33,2.33)$, respectively

Table 6 $t_{U}$-statistic (top) and $LR_{C}$-statistic (bottom) for SX5E in period 2000–2002. The respective $5\%$, $2.5\%$ and $1\%$ critical values for the $LR_{C}$ are 3.84, 5.02 and 6.63 while the acceptance region for the $t_{U}$-statistic are $(-1.65,1.65)$, $(-1.96,1.96)$ and $(-2.33,2.33)$, respectively

The $LR_{C}$-statistics (Table 3) indicate that, with the exception of EWMA at $95\%$, the independence cannot be rejected only for $h=1$. As the forecasting horizon increases, all methods display dependence in the number of violations, even if for the MPRE the $LR_{C}$-statistic is generally smaller than the corresponding values calculated for both V-C and EWMA.

Figure 4 summarizes the Sarma’s measure, sensitive not only to the number but also to the magnitude of the violations. In all cases but the S&P500 in 2007–2008, MPRE forecasts provides losses significantly lower than both V-C and EWMA. Interestingly, the behavior of the Sarma’s index is consistent with the argument discussed above regarding the diverse nature of the turbulence in the two examined periods. For the period 2007–2008 the measure is one order magnitude larger than in period 2000–2002; this is clearly attributable to the huge unforeseen downward movements which impacted on the size of the losses, for all the methods.

To complete the analysis, we have also compared the results provided by the MPRE-based VaR estimator during the calm period 2003–2005 with respect to those calculated using the EWMA approach. Figure 5 summarizes the comparison in terms of percentage of violations and $t_U$ statistic for the three stock indices and the three levels of confidence. In all cases, both the estimates seem virtually superimposed and there no significant difference in the two forecasts. This would suggest that the new method, while performing better than the standard ones in turbulent periods, does not lose its forecast capability in stable periods.

Of interest is also the response of VaR estimators to flash crashes, particularly of those occurred when circuit breakers were not regulated yet³. As an example, for the Black Monday of 1987 we have recorded the following VaR estimates, respectively for the 95, 97.5 and $99\%$: EWMA ($-3.11\%$, $-3.71\%$, $-4.41\%$), MPRE ($-5.65\%$, $-6.43\%$, $-7.54\%$). Even if still far from the sudden variation recordered in the market (the S&P500 dropped 57.86 points, about $-20.47\%$ in a single day), the VaR estimates obtained by the MPRE for the S&P500 are almost twice those achieved by EWMA (from 1.71 to 1.82). Conversely, as all fat-tails models, the MPRE is slower in the after-crash phase, the is it takes more time than EWMA to restore the spike towards more reduced values. This is clearly due to how the estimator is designed; while the EWMA gives more weight to the most recent observations, the MPRE equally weighs the observations in the estimation window.

5 Conclusion

Risk assessment is one of the most relevant issues for individual firms, banks and regulators. One of the dimensions with respect to whom it is estimated is the market risk, that is the possibility that an investor suffers losses due to factors that affect the overall performance of the financial markets. Value at Risk is probably the most known and widely used tool to assess the exposure to market risk of an individual asset or a portfolio. Classical approaches are known to perform poorly during periods of high volatility, owing to the inertia originated by the large amount of past data used to build the forecasting distributions. The limitations of the standard models have become dramatically evident during the last global financial crisis, when losses have been underestimated to such an extent to induce a deep revision of the directions given by regulators.

In this paper we propose an alternative model to estimate value at risk and provide evidence that it produces better forecasts with respect to the variance-covariance method and to the exponentially weighted moving average method. Our approach rests on the estimation of the pointwise regularity exponent of the price process, which succeeds to capture the changes of volatility timely. Our forecasts are based on a Monte Carlo methods: past data (which serve as training period) are used to build autoregressive processes which are used as inputs to simulate paths of Multifractional Processes with Random Exponents (by Monte Carlo simulation). Our findings, related to two long turbulent market periods (2000–2002 and 2007–2008) and to three main stock indices (Standard & Poor’s 500, Nikkei 225 and Eurostoxx), show that the forecasts obtained by this methodology outperform those achieved using the other two methods, in terms of unconditional coverage and independence and of (minimal) magnitude of extra-losses (defined as Sarma’s measure).

Fig. 4

Sarma measures. The performances of the three approaches are evaluated also through the regulators’ loss-function proposed by Sarma et al. (2003). The measure assigns a score to each candidate model which penalizes the model displaying more violations and—as a consequence – the model with lower value should be preferred

Fig. 5

Percentage of violations (left) and $t_U$ statistic (right) for the three stock indices and the three levels of confidence. To complete the analysis, the MPRE-based VaR estimator is compared with the EWMA approach during a calm period (2003–2005). In all cases, both the estimates seem virtually superimposed and there no significant difference in the two forecasts. This would suggest that the new method, while performing better than the standard ones in turbulent periods, does not lose its forecast capability in stable periods

Our research could be extended in several ways. A refinement of the estimation procedure could come from considering a time-changing training period, which could depend on the level of local volatility (of pointwise regularity) in such a way to integrate in our estimator the capability shown by the Exponentially Weighted Moving Average. A further extension, supported by the results obtained for quiet market periods, could be to define a switching model to properly assess market risk, depending on the local volatility level. Finally, our study only considered indices because more emphasis was placed on the novelty of the estimation procedure rather than on the number of the samples. Since the new standard for capital requirements for market risk calls for backtesting at both the individual financial assets and the aggregate levels, it could be of interest to analyze also the case of single assets and portfolios.