1 Introduction

Since Markowitz (1952) posed the allocation problem of portfolio theory a large number of extensions have been introduced (see, e.g., Fastrich et al. 2015; Kawas and Thiele 2017; Bauder et al. 2021). In Markowitz (1952) a portfolio which provided the smallest risk given an expected return was proposed. Here the variance of the portfolio was used as a risk measure. The use of variance as a risk measure has been criticized by practitioners and researchers in finance. One of the critiques is that when an asset return is large the variance scales accordingly. An asset with higher return does not need to be riskier. The variance also depends on the whole loss distribution which might not be desirable. This has led to one of many extensions to Markowitz portfolio theory, the change of risk measure. One generalisation is that the variance has been replaced by a quantile-based risk measure (see, e.g., Linsmeier and Pearson 2000; Rockafellar and Uryasev 2002; Bonaccolto et al. 2018). The two most commonly used are value-at-risk (VaR) and conditional value-at-risk (CVaR) which is a consequence of the solvency 2 and basel 3 requirements. In solvency 2 restrictions on insurance companies are imposed by using the VaR as a risk measure while the recent Basel requirements enforce financial institutions to transition from VaR to CVaR for measuring risk.

Albeit a quantile-based measure for risk has generally been accepted by academics and practitioners, the expected return is most commonly taken as a default for the measure of profit. More recent advancements in portfolio theory such as Yu et al. (2014) or Jiang et al. (2016), make use of the portfolio mean as a portfolio profit measure. For the motivation of the applications of other measures of portfolio profit, an investor is considered who delivers a certain capital or portfolio benchmark, such as a monthly percentage return. In this case, a large loss (though rare) will heavily distort the result. This does not imply that the portfolio is not probable to deliver upon the requirements. It is merely a result from the portfolio return measure, since it depends on all losses as well as returns. To our knowledge, most practitioners seldom communicate requirements in terms of average or percentage return but rather w.r.t. realised returns in relation to benchmarks. From this perspective it is more natural to communicate aims and targets in terms of probabilities to achieve a certain profit over some specified time horizon. With this argument the portfolio mean is essentially replaced by a return measure that is based on quantiles, which is the primary motivation for the problem at hand. Ideas such as these have been considered in continuous time, e.g., He and Zhou (2011), but to our knowledge no portfolios in a static single-period setting have been investigated. A second motivation to quantile-based return measures is when the portfolio distribution is complicated, such as a skew or a mixture of distributions, which has recently gained attention. References such as Adcock (2010) or Eling (2014) amongst others investigate these phenomenas and find that skewness seems to be present in return distributions, especially for data in higher frequencies. If skewness should be accounted for or not is of course for the investor to decide and can easily be accounted for in the framework proposed in the paper.

Moreover, since the parameters of the data-generating model are usually not known when a portfolio is to be constructed, one must use their estimates to realise the positions. As an estimate, the sample mean is known to be poor in terms of stability and convergence when compared to the quantities used for constructing risk measures, such as the covariance matrix (see, e.g., Merton 1980; Best and Grauer 1991; Chan et al. 1999; Bodnar et al. 2017, 2018b, 2019a). Although the investor can use an improved estimator for the mean vector (cf., Bodnar et al. 2019b), it will still take two tails of the portfolio return distribution into account and will not answer question why not to include another return measure in the portfolio selection problem.

Portfolios using quantile-based risk measures in a single-period setting together with the mean as a return measure have been studied in Alexander and Baptista (2002), Alexander and Baptista (2004) and Yao et al. (2013) to name a few. Alexander and Baptista (2002) investigated a mean-VaR portfolio selection problem under Gaussian returns. The authors used the mean as a return measure while minimizing the risk, measured by VaR. Alexander and Baptista (2004) then extended their work from 2002 by considering the mean-CVaR portfolio under Gaussian returns. Huang et al. (2010) considered a robust version of the portfolio selection problem, placing bounds on the unknown parameters of interest while considering the mean-CVaR portfolio selection problem. Since Rockafellar and Uryasev (2002) showed that the CVaR has the property of being coherent (convex) under weak conditions imposed on the asset return distribution, a number of optimal mean-CVaR portfolios have been suggested in the literature which do not rely on the precise definition of the portfolio return distribution in their construction. In particular, the unknown distribution function of the portfolio return is replaced by the empirical distribution function which depends on the historical data on asset returns only. Yao et al. (2013) thereafter considered another nonparametric mean-CVaR portfolio by using kernel density estimators to approximate the true density of portfolio return.

We introduce the conditional value of return (CVoR) portfolio which is solely constructed from quantile-based measures. The mean is replaced by a quantile-based measure which depends on the positive part of the portfolio return distribution. The risk is constrained by using a quantile-based risk measure. By doing so both tails of the portfolio return distribution are taken into account. To our knowledge, no such portfolio selection problem exists in the literature for a single-period setting. The aim is to show the applicability and flexibility of such a portfolio for investors who are interested in maximizing their profit while constraining their risk. This is in accordance with the modern portfolio theory of Markowitz (1952).

The CVoR portfolio will also be connected to the work of Merton (1972) who proved that the Markowitz portfolio lies on the efficient frontier, a parabola in the mean-variance space. Merton also showed that the parabola is completely determined by a set of three parameters (see, e.g., Bodnar and Schmid 2009; Font 2016; Bodnar et al. 2018a). One of which determines the shape of the parabola and the other two specify the location of the parabola vertex. The properties of the parameters that constitute the efficient frontier have been widely investigated under different assumptions. Bodnar and Gupta (2009) derived the parametric form of the efficient frontier under elliptically distributed asset returns which will be connected to the CVoR portfolio obtained under the same distributional assumption.

The remainder of the paper is outlined as follows. In Sect. 2 the CVoR portfolio is presented in its most general form. Here, the implications of using such a portfolio is discussed. In Sect. 3 a special case of the CVoR portfolio is presented when assuming that the asset returns follow an elliptically contoured distribution. Under this assumption one can connect the CVoR portfolio to the efficient frontier in the mean-variance space and give a closed-form solution to the portfolio weights and its characteristics. A numerical illustration is given in Sect. 4 and the paper ends with a number of closing remarks in Sect. 5.

2 The conditional value of return portfolio

In this section the conditional value of return is defined and the corresponding portfolio selection problem is introduced, which extends the class of quantile-based portfolio choice problems discussed in Alexander and Baptista (2002), Alexander and Baptista (2004) and Huang et al. (2010). Let \(\mathbf {x}\) be p-dimensional vector consisting of the asset returns with absolutely continuous cumulative distribution function and let \(\mathbf {w}\) be the p-dimensional vector of portfolio weights. The portfolio return is defined as a random variable \(X=X(\mathbf {w}) := \mathbf {w}^\top \mathbf {x}\) for a given set of weights \(\mathbf {w}\). Note that X is affine in \(\mathbf {w}\), which can of course be extended to a function \(f(\mathbf {w}, \mathbf {x})\). The affine structure is commonly used in practice and we will therefore continue using it. Let \(Y = Y(\mathbf {w}):= -X\) be a random variable representing the loss of X. If \(F_Z(\cdot )\) denotes the cumulative distribution function for the random variable Z, then the Value-at-Risk (VaR) is defined as \({\text {VaR}}_{\beta }(Y(\mathbf {w})):= \inf _y \{F_Y(y)\ge \beta \}\), \(\beta \in (0,1)\). Another most commonly used quantile-based risk functional is the Conditional Value-at-Risk (CVaR). For a continuous random variable the CVaR is defined by

$$\begin{aligned} {\text {{CVaR}}}_\beta (Y(\mathbf {w}))={\text {E}}[Y(\mathbf {w}) | Y(\mathbf {w}) \ge {\text {VaR}}_{\beta }(Y(\mathbf {w}))]. \end{aligned}$$
(1)

The definition is a special case of (Proposition 6, Rockafellar and Uryasev 2002) where the authors showed that the the CVaR is a coherent functional for a general loss distribution (see, e.g., Artzner et al. 1999) and investigated its properties as a function of the portfolio weights \(\mathbf {w}\).

Note that there is nothing in their proofs limiting the interpretation of the random variable \(Y(\mathbf {w})\) as a return/profit instead of a loss. If one does so, then all consecutive results of Rockafellar and Uryasev (2002) will hold. As a result, one can define the functional (1) as a return/profit measure instead of a risk. Formally, the Conditional Value-of-Return (CVoR) is defined by

Definition 1

Let \(\alpha \in (0,1)\) and define \({\text {VoR}}_{\alpha }(X(\mathbf {w})):= \inf _y \{F_{X(\mathbf {w})}(y)\ge \alpha \}\) as the Value-of-Return. The Conditional Value-of-Return (CVoR) is defined as

$$\begin{aligned} {\text {CVoR}}_\alpha (X(\mathbf {w})) = E[X(\mathbf {w}) | X(\mathbf {w}) \ge {\text {VoR}}_{\alpha }(X(\mathbf {w}))] \end{aligned}$$
(2)

From (2) one can see that the ordinary portfolio return \({\text {E}}[X(\mathbf {w})]\) is a special case of the CVoR. This follows by taking the limit \(\lim _{\alpha \rightarrow 0} {\text {CVoR}}_\alpha (X(\mathbf {w})) = {\text {E}}[X(\mathbf {w})]\) (which is an analogy with letting \(\beta \rightarrow 1\) for CVaR). The intuition is the same as in the case of quantile-based risk measures. It excludes information about extreme negative values in the measure of return since they have been already accounted for in the risk measure. The confidence level \(\alpha \) connects to what the investor can deliver at what probability but also how much of the distribution that should be excluded. It can be seen as a hyperparameter of the portfolio selection problem.

Let \(\rho _{\alpha _2}(X(\mathbf {w}))\) denote a quantile-based risk measure at the significance level \(\alpha _2\) constructed for the loss distribution of \(X(\mathbf {w})\). There may be distributions or quantile-based risk measures which are independent of the value of \(\alpha _2\), which are included in this notation. In the context of quantile-based risk measures, the significance level \(\alpha _2\) can informally represent a connection to the probability of losses. The interpretation is simpler in the context of portfolio selection. Consider the following optimization problem

$$\begin{aligned} \begin{aligned} \max _{ \mathbf {w} \in \mathcal {W} } \;&{\text {CVoR}}_{\alpha _1}(X(\mathbf {w})) \\&\rho _{\alpha _2}(X(\mathbf {w})) \le v_0, \end{aligned} \end{aligned}$$
(3)

where \(\alpha _1,\alpha _2 \in (0,1)\) and \(v_0\) is the largest loss the investor is willing to place under risk. The risk constraint reflects the investors behaviour towards risk. The value of \(\alpha _2\) would indicate that a loss, which happens with probability \(\alpha _2\), should not exceed a certain amount, here denoted \(v_0\). The constraint set \(\mathcal {W} := \{\mathbf {w}: h_i(\mathbf {w}) = 0,\; i=1,...,m,\; \mathbf {w} \in \mathbb {R}^p\}\) includes all possible vectors of portfolio weights \(\mathbf {w}\) which fulfill m constraints \(h_i(\mathbf {w}) = 0\), \(i=1,...,m\), which might be imposed on the portfolio structure. One of such constraints which is usually present in portfolio theory is that the sum of the weights is equal to one \(\mathbf {w}^\top \mathbf {1}-1=0\), i.e., the whole investor’s wealth is shared between the selected assets. Other examples of constraints \(h_i(\mathbf {w}) = 0\) might include position restrictions, cost models or the specification that the weights should be normalized appropriately. The optimization problem (3) and its optimal solution will henceforth be called the CVoR portfolio. The CVoR portfolio can be seen as an extension of the mean-variance portfolio but with quantile-based measures for both portfolio return and portfolio risk. By optimizing towards \({\text {CVoR}}_{\alpha _1}(X(\mathbf {w}))\) and constraining the risk in terms of \(\rho _{\alpha _2}(X(\mathbf {w}))\), both tails of the portfolio return distribution are accounted for.

The main idea behind the approach is to separate the influence of the right and left tails of the portfolio return distribution in the investment decision process. One of the classical criticism of the variance as a risk measure is that it takes both tails of the asset return distribution into account, while large positive values of portfolio return should not be treated as a risk. Since the left tail of the portfolio return distribution has been used for the determination of the risk, the idea behind the CVoR portfolio is to use the right tail of the portfolio return distribution to compute the portfolio profit.

It is expected that the CVoR portfolio will have a higher risk than the portfolio with the smallest VaR (CVaR), which is in line with the modern portfolio theory of Markowitz where optimal portfolios are determined by maximizing the return for the given value of variance or my minimizing the variance for the given level of expected return. A special case of Markowitz’s optimal portfolios is the global minimum variance portfolio, i.e. the optimal portfolio with the smallest possible variance. Similarly, the idea behind the CVoR portfolio is to maximize the level of the return under the constraint imposed on the risk. In the special case, when the investor is fully risk averse, he/she will choose to invest into the portfolio with the smallest risk measure presented as the VaR or CVaR. To this end it is noted that if \(\alpha _1,\alpha _2 \rightarrow 1\) and CVaR is chosen as a risk measure in (3), then the optimization problem (3) coincides with the Markowitz problem.

Throughout this paper the following assumptions on \(\mathcal {W}\) and the risk functional \(\rho \) are made to ensure the existence and the uniqueness of the solution of the optimization problem (3). This places some restrictions on the investor, who needs to verify that the constraints they use are practically viable.

Assumption 1

The set \(\mathcal {W} \cup \{\mathbf {w}: \rho _{\alpha _2}(X(\mathbf {w})) \le v_0\} \ne \emptyset \).

Assumption 2

The functions \(h_i(\mathbf {w})\), \(i=1,...,m\) that constitute \(\mathcal {W}\) are convex and differentiable.

Assumption 3

If there exists a gradient of \(\rho _{\alpha _2}(X(\mathbf {w}))\) then it, together with the gradients of \(h_i(\mathbf {w})\), \(i=1,...,m\) are linearly indpendent at any local optimum of (3).

From the results of Rockafellar and Uryasev (2002) necessary and sufficient conditions for the existence of the CVoR portfolio are retrieved when \(\rho _{\alpha _2}(X(\mathbf {w}))\) is chosen to be the CVaR. These are summarized in Theorem 1, whose proof follows immediately from the proof of the Karush–Kuhn–Tucker (KKT) conditions presented in Theorems 4.3.7 and 4.3.8 of Bazaraa et al. (2013).

Theorem 1

Let \(\rho _{\alpha _2}(X(\mathbf {w}))={\text {CVaR}}_{\alpha _2}(-X(\mathbf {w}))\) as defined in (1). A portfolio \(\mathbf {w}^*\) is a global solution to (3) if and only if there exists scalars \(\lambda _i\), \(i=1,2,...,m+1\) such that

$$\begin{aligned}&\nabla {\text {CVoR}}_{\alpha _1}(X(\mathbf {w}^*)) + \lambda _1 \nabla \rho _{\alpha _2}(X(\mathbf {w}^*)) + \sum _{k=2}^{m+1} \lambda _k \nabla h_i(\mathbf {w}) = \mathbf {0} \end{aligned}$$
(4)
$$\begin{aligned}&\lambda _1 \left( \rho _{\alpha _2}(X(\mathbf {w}^*)) - v_0 \right) = 0 \nonumber \\&\quad \lambda _1 \ge 0 \end{aligned}$$
(5)

By construction, the CVoR portfolio inherits sufficient and necessary conditions under a general continuous return distribution. Not only does it imply an extreme flexibility in terms of modelling in the context of the CVoR portfolio, but it also gives great comfort in terms of its economical applicability. If an investor needs to work in the context of the new Basel requirements, then he/she will choose the CVaR as a risk measure. The investor can then be sure that the solution and optimum of (3) is the unique maximum. He/she cannot do any better. This result also gives some indication to what set of equations should be solved to obtain such a portfolio.

The result of Theorem 1 is not limited to the use of CVaR as a risk measure. However, the practical relevance of the CVoR portfolio is then lost (to some extent) because of the Basel requirements. As long as the investors can limit themselves to a certain class of risk measures, the results of Theorem 1 still apply:

Remark 1

The results of Theorem 1 holds if \(\rho _{\alpha _2}(X(\mathbf {w}))\) is a coherent risk measure.

An example of risk measures that are coherent is the class of spectral risk measures. For a more thorough introduction to spectral risk measures, see e.g. Acerbi (2002) or Adam et al. (2008).

In an insurance context, European insurers have to follow the Solvency 2 regulation. The risk measure is now chosen to be the Value-at-Risk (VaR). All quantile-based risk measures are not obviously coherent (convex), see, e.g., Rockafellar and Uryasev (2000) and one such example is the VaR. This poses several difficulties for the construction of the CVoR portfolio under a general return distribution when \(\rho _{\alpha _2}(X(\mathbf {w}))={\text {VaR}}_{\alpha _2}(-X( \mathbf {w}))\) in (3), since the distribution function \(F_{X(\mathbf {w})}(x)\) may contain atoms. However, by imposing regularity conditions one may provide somewhat weaker conditions in comparison to Theorem 1. Under these assumptions, a verification type theorem is presented for the CVoR portfolio using the VaR as a risk measure.

Theorem 2

Let \(\mathcal {X}\) denote the class of random variables which are absolutely continuous, have support on \(\mathbb {R}^p\) and whose cumulative distribution function is quasiconcaveFootnote 1. Let \(\rho _{\alpha _2}(X(\mathbf {w}))={\text {VaR}}_{\alpha _2}(-X(\mathbf {w}))\) and assume that the return distribution of \(\mathbf {x}\) belongs to \(\mathcal {X}\). A portfolio \(\mathbf {w}^*\) which fulfills the Karush–Kuhn–Tucker conditions of (3) is a global optimum.

Proof

By absolute continuity, the constraint in the optimization problem (3) can be rewritten as \(1-\alpha _2 \le F_{X(\mathbf {w})}(v_0)\). By Theorem 4.39 of Shapiro et al. (2009) the constraint is a quasiconcave function of \(\mathbf {w}\) and continuous on its whole domain. The rest of the proof follows from the proof of Theorem 4.3.8 of Bazaraa et al. (2013). \(\square \)

The sufficient conditions give us some comfort in the applicability of the CVoR portfolio under Solvency 2. The class of absolutely continuous distributions is large. Distributions of complicated forms, such as skew, fat tailed or mixture of distributions are covered. Note that the assumption that the cumulative distribution function of asset returns is quasiconcave in turn implies that the cumulative distribution function of the portfolio return is also quasiconcave. An example of quasiconcave distribution functions is the family of log-concave distribution functions, such as the log-normal or log-t distribution.

One specific class of distributions that has been widely considered in financial applications is the elliptically contoured distribution, which is quasiconcave. Some examples of applications and reviews of the topic are Owen and Rabinovitch (1983), Hamada and Valdez (2008) and Gupta et al. (2013). In the next section, an analytical solution to (3) under this flexible class of probability distributions is derived.

3 The CVoR Portfolio for elliptically contoured distribution

3.1 Elliptically contoured distributions

If a random vector \(\mathbf {y}\) has the following characteristic function

$$\begin{aligned} {\text {E}}[\exp (i\mathbf {t}^\top \mathbf {y})] = \exp \{ i \varvec{\mu }^\top \mathbf {t}\} \phi (\mathbf {t}^\top \mathbf {D}\mathbf {t}), \text { for } \mathbf {t} \in \mathbb {R}^p, \end{aligned}$$

it is said to have a p-dimensional elliptically contoured distribution with location parameter \(\varvec{\mu }\), dispersion matrix \(\mathbf {D}\) and the function \(\phi (\cdot )\) determines a specific family of elliptical distributions. In the following this general class of multivariate distributions is denoted by \({\text {ECD}}_p({\varvec{\mu }}, \mathbf {D}, \phi (\cdot ))\). If the second moments of \(\mathbf {y}\) exist, then \(\varvec{\mu }={\text {E}}[\mathbf {y}]\) and \({\varvec{\Sigma }}={\text {Var}}[\mathbf {y}]=\gamma ^2\mathbf {D}\) with \(\gamma =\sqrt{-\phi '(0)/2}\). Moreover, assuming that \(\mathbf {y}\) has a density \(f_{\mathbf {y}}(\cdot )\), then

$$\begin{aligned} f_{\mathbf {y}}(\mathbf {z})= |\mathbf {D}|^{-1/2} g((\mathbf {z}-{\varvec{\mu }})^\top \mathbf {D}^{-1}(\mathbf {z}-{\varvec{\mu }})). \end{aligned}$$
(6)

where \(g(\cdot )\) is the density generator. For the interested reader, the technical conditions when \(\mathbf {y}\) actually has a density can be found in Fang and Zhang (1990). In the following it is assumed that the density exists.

Elliptically contoured distributions constitute a large class of multivariate (and also matrix-variate) distributions. Some examples of these are the multivariate normal distribution, the t-distribution and the multivariate Laplace distribution [see, e.g., Fang and Zhang (1990)]. Elliptically contoured distributions have many desirable properties. One of interest is the following: If \(Y = (\mathbf {m}^\top \mathbf {y} -\mathbf {m}^\top {\varvec{\mu }})/\sqrt{\mathbf {m}^\top \mathbf {D}\mathbf {m}}\), then the distribution of Y is independent of the vector of \(\mathbf {m}\) [see, Theorem 2.6.3 of Fang and Zhang 1990]. It only depends on the specific family of elliptical distributions \(\mathbf {y}\) belongs to. The canonical example of this property is the multivariate normal distribution.

In the next section the closed form solution of the CVoR portfolio choice problems is derived when the asset returns follow an elliptically contoured distribution.

3.2 Closed form solution

In this section we will consider the class of elliptically contoured distributions which are absolutely continuous and for which the second moments exist.

The expected return of the portfolio with weights \(\mathbf {w}\) is given by \({\text {E}}[X(\mathbf {w})]=\mathbf {w}^\top {\varvec{\mu }}\) and its variance by \({\text {Var}}(X(\mathbf {w}))=\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w}\). Let \(d_{\alpha _1}\) be the \(\alpha _1\)-percentile of the standardized portfolio return \(X\overset{d}{=}(\mathbf {w}^\top \mathbf {x} -\mathbf {w}^\top {\varvec{\mu }})/\sqrt{\mathbf {w}^\top \mathbf {D}\mathbf {w}}\) (which is independent of \(\mathbf {w}\)) and \(f_X(\cdot )\) together with \(F_X(\cdot )\) denote the density and cumulative distribution function of X, respectively. Throughout this section assume that \(\mathcal {W}=\{\mathbf {w}: \mathbf {w}^\top \mathbf {1}= 1\}\). When using CVaR as a risk measure the optimization problem in (3) can be rewritten as

$$\begin{aligned} \begin{aligned}&\max _{\mathbf {w}} \mathbf {w}^\top {\varvec{\mu }} + k_{\alpha _1}\sqrt{ \mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} } \\ s.t.&\text { } \mathbf {w}^\top \mathbf {1}= 1 \\&- \mathbf {w}^\top {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} } \le v_0 \end{aligned} \end{aligned}$$
(7)

where

$$\begin{aligned} k_{\alpha } = \frac{\int _{d_{\alpha }} ^{\infty }xf_{X}(x)dx }{(1-\alpha )\gamma }, \;\; d_{\alpha }=F^{-1}_{X}(\alpha ). \end{aligned}$$

The risk measure CVaR can easily be changed to VaR in this setting. This is simply done by replacing the constant \(k_{1-\alpha _2}\) with \(d_{1-\alpha _2}\) in the risk-constraint. For this reason, the theoretical results are derived when CVaR is used as a risk measure and it is noted that they hold true with minor modification when VaR is used as a risk measure.

Since the risk constraint is a convex function of \(\mathbf {w}\), there exists a global optimum. A question is whether or not the risk constraint results in equality. It holds that

Lemma 1

Let \(\mathbf {w}_{CVoR}\) denote the global optimum of (7). Then it holds that

$$\begin{aligned} - \mathbf {w}_{CVoR}^\top {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}_{CVoR}^\top {\varvec{\Sigma }}\mathbf {w}_{CVoR} } = v_0, \end{aligned}$$

the risk constraint of (7) results in equality, i.e., the constraint is active.

Proof

Let \(\mathcal {W}=\{\mathbf {w}:\mathbf {w}^\top \mathbf {1}= 1,- \mathbf {w}^\top {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} } \le v_0\}\), i.e. the set of weights which fulfills the constraints of (7) and let \(\mathcal {W}_{v_0}=\{\mathbf {w}:\mathbf {w}^\top \mathbf {1}= 1,- \mathbf {w}^\top {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} }= v_0\}\) denote its boundary. It holds that

$$\begin{aligned} \mathbf {w}_{CVoR}= & {} \arg \max _{\mathbf {w}\in \mathcal {W}} \left\{ \mathbf {w}^\top {\varvec{\mu }} + k_{\alpha _1}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} }\right\} \\= & {} \arg \max _{\mathbf {w}\in \mathcal {W}} \left\{ \left( 1-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}\right) \mathbf {w}^\top {\varvec{\mu }} - \frac{k_{\alpha _1}}{k_{1-\alpha _2}} \left( -k_{1-\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} }- \mathbf {w}^T {\varvec{\mu }}\right) \right\} \end{aligned}$$

where \(-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}>0\) since \(\alpha _1, \alpha _2 \in (1/2,1)\).

Assume that the statement of the lemma does not hold, i.e. there exists \(v_1<v_0\) such that for the solution \(\mathbf {w}^*_{CVoR}\) of the optimization problem

$$\begin{aligned} \mathbf {w}^*_{CVoR}= & {} \arg \max _{\mathbf {w}\in \mathcal {W} \backslash \mathcal {W}_{v_0}} \left\{ \mathbf {w}^\top {\varvec{\mu }} + k_{\alpha _1}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} }\right\} , \end{aligned}$$

it holds that

$$\begin{aligned} - \mathbf {w}_{CVoR}^{* ~\top } {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}_{CVoR}^{*~\top } {\varvec{\Sigma }}\mathbf {w}_{CVoR}^* } = v_1. \end{aligned}$$

Then, the application of \(-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}>0\) yields

$$\begin{aligned}&\left( 1-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}\right) \mathbf {w}_{CVoR}^{*~\top } {\varvec{\mu }} - \frac{k_{\alpha _1}}{k_{1-\alpha _2}} \left( -k_{1-\alpha _2}\sqrt{\mathbf {w}_{CVoR}^{*~\top } {\varvec{\Sigma }}\mathbf {w}^*_{CVoR} }- \mathbf {w}_{CVoR}^{*~\top } {\varvec{\mu }}\right) \\&\quad = \left( 1-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}\right) \mathbf {w}_{CVoR}^{*~\top } {\varvec{\mu }} - \frac{k_{\alpha _1}}{k_{1-\alpha _2}} v_1 <\left( 1-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}\right) \mathbf {w}_{CVoR}^{*~\top } {\varvec{\mu }} - \frac{k_{\alpha _1}}{k_{1-\alpha _2}} v_0\\&\quad \le \max _{\mathbf {w}\in W} \left\{ \left( 1-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}\right) \mathbf {w}^\top {\varvec{\mu }} - \frac{k_{\alpha _1}}{k_{1-\alpha _2}} v_0 \right\} =\left( 1-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}\right) \max _{\mathbf {w}\in W} \left\{ \mathbf {w}^\top {\varvec{\mu }}\right\} - \frac{k_{\alpha _1}}{k_{1-\alpha _2}} v_0. \end{aligned}$$

Since \(\mathbf {w}^\top {\varvec{\mu }}\) is a linear function and \(\mathcal {W}\) is a bounded set, then \(\max _{\mathbf {w}\in \mathcal {W}} \left\{ \mathbf {w}^\top {\varvec{\mu }}\right\} \) is attained at the boundary of \(\mathcal {W}\), that is in \(\mathcal {W}_{v_0}\). Consequently, the solution of \(\max _{\mathbf {w}\in \mathcal {W}} \left\{ \mathbf {w}^\top {\varvec{\mu }}\right\} \) satisfies the constraint \(- \mathbf {w}^\top {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} } = v_0\) and

$$\begin{aligned} \max _{\mathbf {w}\in \mathcal {W} \backslash \mathcal {W}_{v_0}} \left\{ \mathbf {w}^\top {\varvec{\mu }} + k_{\alpha _1}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} }\right\} < \max _{\mathbf {w}\in \mathcal {W}} \left\{ \mathbf {w}^\top {\varvec{\mu }} + k_{\alpha _1}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} }\right\} \end{aligned}$$

The last inequality contradicts that the solution of (7) is an interior point of \(\mathcal {W}\). \(\square \)

By Lemma 1 one may impose an equality on the risk constraint in the CVoR portfolio, which is done throughout the remainder of this section. A consequence of the equality constraint is that the CVoR portfolio can be attained by considering an easier optimization problem. Let \(\mathcal {W}\) denote the constraint set of (7). Then

$$\begin{aligned} \mathbf {w}_{CVoR}= & {} \arg \max _{\mathbf {w}\in \mathcal {W}} \left\{ \mathbf {w}^\top {\varvec{\mu }} + k_{\alpha _1}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} }\right\} \\= & {} \arg \max _{\mathbf {w}\in \mathcal {W}} \left\{ \left( 1-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}\right) \mathbf {w}^\top {\varvec{\mu }} - \frac{k_{\alpha _1}}{k_{1-\alpha _2}} v_0\right\} =\arg \max _{\mathbf {w}\in \mathcal {W}}\left\{ \mathbf {w}^\top {\varvec{\mu }}\right\} , \end{aligned}$$

where it is used that \(-\frac{k_{\alpha _1}}{k_{1-\alpha _2}}>0\) since \(\alpha _1, \alpha _2 \in (1/2,1)\). Hence, the CVoR portfolio retrieved from (7) does not depend on \(k_{\alpha _1}\), which can be explained by the symmetry of the distribution of \(\mathbf {x}\). Therefore, if a solution exists to (7) then the same solution can be obtained by solving

$$\begin{aligned} \begin{aligned}&\max _{\mathbf {w}} \mathbf {w}^\top {\varvec{\mu }} \\ s.t.&\text { } \mathbf {w}^\top \mathbf {1}= 1 \\&\text { } - \mathbf {w}^\top {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} } = v_0. \end{aligned} \end{aligned}$$
(8)

The above problem is closely related to the portfolio discussed in Alexander and Baptista (2002) and Alexander and Baptista (2004). Here, the authors introduced the mean-VaR and mean-CVaR efficient frontier in the context of an equivalent optimization problem to (8) under the assumptions of normality. The authors considered minimizing the portfolio CVaR (VaR) with a constraint on the expected return. Under the assumption of Gaussian returns they showed that the portfolio is mean-variance efficient. To show that the same holds for the CVoR portfolio, let

$$\begin{aligned} \mathbf {w}_{\text {GMV}}=\frac{{\varvec{\Sigma }}^{-1}\mathbf {1}}{\mathbf {1}^\top {\varvec{\Sigma }}^{-1}\mathbf {1}}, \;\;R_{GMV}= \frac{{\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1}\mathbf {1}}{\mathbf {1}^\top {\varvec{\Sigma }}^{-1}\mathbf {1}}, \;\; V_{GMV}=\frac{1}{\mathbf {1}^\top {\varvec{\Sigma }}^{-1}\mathbf {1}} \end{aligned}$$

be the weight, the expected return and the variance of the global minimum variance (GMV) portfolio. For each point \((R,V) \in \mathbb {R} \times \mathbb {R}_+\), the efficient frontier in its parametric form, is defined as

$$\begin{aligned} (R_{GMV}- R)^2 =s\left( V-V_{GMV}\right) \end{aligned}$$
(9)

where \(s={\varvec{\mu }}^\top \mathbf {Q} {\varvec{\mu }}\) and \(\mathbf {Q} = {\varvec{\Sigma }}^{-1} - ({\varvec{\Sigma }}^{-1}\mathbf {1}\mathbf {1}^\top {\varvec{\Sigma }}^{-1})/\mathbf {1}^\top {\varvec{\Sigma }}^{-1}\mathbf {1}\) is the slope parameter of the efficient frontier. Note that for the mean-variance efficient frontier to exist it should hold that \({\varvec{\mu }}\) is not proportional to \(\mathbf {1}\) which is included in Assumption 3. For all practical purposes this poses no issue, it is merely technical. If the assumption is false, then the efficient frontier would collapse and become a line in the mean variance space. The only optimal portfolio is then the GMV portfolio.

In the next step to derive a closed-form solution it is shown that the CVoR portfolio is mean-variance efficient under elliptically distributed returns.

Theorem 3

Assume that \(\mathbf {x}\sim {\text {ECD}}_p({\varvec{\mu }}, {\varvec{\Sigma }}, \phi (\cdot ))\), where \({\text {rank}}({\varvec{\Sigma }})=p\) and let \(\mathbf {w}_{\text {CVoR}}\) denote the CVoR portfolio. If \(\mathbf {w}_{\text {CVoR}}^\top {\varvec{\mu }} > R_{GMV}\) and \(k_{1-\alpha _2}^2 > s\), then the CVoR portfolio is mean-variance efficient.

Proof

The Lagrangian of (8) is defined as

$$\begin{aligned} \mathcal {L}(\mathbf {w}, \lambda _1, \lambda _2) = \mathbf {w}^\top {\varvec{\mu }} + \lambda _1 \left( - \mathbf {w}^\top {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} } - v_0\right) +\lambda _2(\mathbf {w}^\top \mathbf {1}- 1).\qquad \end{aligned}$$
(10)

Computing the gradient and setting it to the zero vector yields the following system of equations

$$\begin{aligned} {\left\{ \begin{array}{ll} {\varvec{\mu }} - \lambda _1 \left( {\varvec{\mu }} - k_{\alpha _2} \frac{{\varvec{\Sigma }}\mathbf {w}}{\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w}}} \right) +\lambda _2\mathbf {1}= 0 \\ - \mathbf {w}^\top {\varvec{\mu }} -k_{1-\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w} } - v_0 = 0 \\ \mathbf {w}^\top \mathbf {1}- 1 = 0. \end{array}\right. } \end{aligned}$$
(11)

Since the Lagrange parameters are arbitrary, let

$$\begin{aligned} {\tilde{\lambda }}_1:=\frac{\lambda _1-1}{\lambda _1 k_{\alpha _2}}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w}} \quad \text {and} \quad {\tilde{\lambda }}_2:=-\frac{\lambda _2\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w}}}{\lambda _1 k_{\alpha _2}}, \end{aligned}$$

where \(k_{\alpha _2}=-k_{1-\alpha _2}\) since the distribution of \(\mathbf {w}^\top {\varvec{x}}\) is symmetric around \(\mathbf {w}^\top {\varvec{\mu }}\). Then the first equation in (11) becomes

$$\begin{aligned} \mathbf {w}={\tilde{\lambda }}_2 {\varvec{\Sigma }}^{-1} \mathbf {1}+ {\tilde{\lambda }}_1 {\varvec{\Sigma }}^{-1} {\varvec{\mu }} \end{aligned}$$
(12)

and by using the second and third equations of (11), Eq. (12) can be rewritten as

$$\begin{aligned} {\tilde{\lambda }}_2 \mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}+ {\tilde{\lambda }}_1 \mathbf {1}^\top {\varvec{\Sigma }}^{-1} {\varvec{\mu }}&= 1 , \end{aligned}$$
(13)
$$\begin{aligned} {\tilde{\lambda }}_2 {\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}+ {\tilde{\lambda }}_1 {\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} {\varvec{\mu }}&= k_{\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w}} - v_0. \end{aligned}$$
(14)

Let \( \mu _0=\mathbf {w}^\top {\varvec{\mu }}\). Since \(\mu _0=k_{\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w}} - v_0\), (13) and (14) yield

$$\begin{aligned} \begin{pmatrix} {\tilde{\lambda }}_2 \\ {\tilde{\lambda }}_1 \end{pmatrix}&= \begin{pmatrix} \mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}&{} \quad \mathbf {1}^\top {\varvec{\Sigma }}^{-1} {\varvec{\mu }} \\ {\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}&{} \quad {\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} {\varvec{\mu }} \end{pmatrix}^{-1} \begin{pmatrix} 1 \\ k_{\alpha _2}\sqrt{\mathbf {w}^\top {\varvec{\Sigma }}\mathbf {w}} - v_0\end{pmatrix} \nonumber \\&=\frac{1}{s} \begin{pmatrix} \frac{{\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} {\varvec{\mu }}}{\mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}} - \mu _0 R_{GMV}\\ \mu _0 -R_{GMV}\end{pmatrix}, \end{aligned}$$
(15)

and

$$\begin{aligned} \frac{{\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} {\varvec{\mu }}}{\mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}}&= \frac{{\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} {\varvec{\mu }}}{\mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}} - \left( \frac{{\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}}{\mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}}\right) ^2 +\left( \frac{{\varvec{\mu }}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}}{\mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}}\right) ^2 = V_{GMV}s+R_{GMV}^2. \end{aligned}$$

Hence,

$$\begin{aligned} \begin{pmatrix} {\tilde{\lambda }}_2 \\ {\tilde{\lambda }}_1 \end{pmatrix} = \frac{1}{s} \begin{pmatrix}V_{GMV}s + R_{GMV}^2 - \mu _0 R_{GMV}\\ \mu _0-R_{GMV}\end{pmatrix} \end{aligned}$$

which implies

$$\begin{aligned} \mathbf {w}&= \mathbf {w}_{\text {GMV}}+ \left( ({\tilde{\lambda }}_2-V_{GMV}){\varvec{\Sigma }}^{-1} \mathbf {1}+ {\tilde{\lambda }}_1 {\varvec{\Sigma }}^{-1} {\varvec{\mu }} \right) \\&= \mathbf {w}_{\text {GMV}}+ \frac{\mu _0-R_{GMV}}{s} {\varvec{\Sigma }}^{-1} {\varvec{\mu }}- \frac{ \mu _0- R_{GMV}}{s}R_{GMV}{\varvec{\Sigma }}^{-1} \mathbf {1}. \end{aligned}$$

Since \({\varvec{\Sigma }}^{-1} \mathbf {1}R_{GMV}= {\varvec{\Sigma }}^{-1} \mathbf {1}\mathbf {1}^\top {\varvec{\Sigma }}^{-1} {\varvec{\mu }}/\mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}\) it can be further simplified to

$$\begin{aligned} \mathbf {w}_{CVoR}= \mathbf {w}_{\text {GMV}}+ \frac{\mu _0-R_{GMV}}{s} \mathbf {Q} {\varvec{\mu }}, \end{aligned}$$

where \(\mathbf {Q}={\varvec{\Sigma }}^{-1}- {\varvec{\Sigma }}^{-1} \mathbf {1}\mathbf {1}^\top {\varvec{\Sigma }}^{-1}/\mathbf {1}^\top {\varvec{\Sigma }}^{-1} \mathbf {1}\). Given that \(\mu _0 > R_{GMV}\), the portfolio \(\mathbf {w}_{CVoR}\) is mean-variance efficient. \(\square \)

The constraints \(\mathbf {w}_{CVoR}^\top {\varvec{\mu }}>R_{GMV}\) and \(k_{1-\alpha _2}^2 > s\) in the statement of Theorem 3 guarantee that the CVoR portfolio lies on the efficient frontier, not only on the mean-variance parabola. The following theorem provides the closed-form solution to the CVoR portfolio.

Theorem 4

Assume that \(\mathbf {x}\sim {\text {ECD}}_p({\varvec{\mu }}, {\varvec{\Sigma }}, \phi (\cdot ))\), where \({\text {rank}}({\varvec{\Sigma }})=p\). Also, assume that \(\mathbf {w}_{{\text {CVoR}}}^\top {\varvec{\mu }} > R_{GMV}\), \(\alpha _2 \in (1/2,1)\), \(k_{1-\alpha _2}^2 > s\) and \(v_0\ge {\text {CVaR}}_{\alpha _2}(X(\mathbf {w}_{gmv}))\), then the CVoR portfolio exists and it has the following weights and characteristics

$$\begin{aligned} \mathbf {w}_{{\text {CVoR}}}&= \mathbf {w}_{\text {GMW}} + \frac{\eta }{s} \mathbf {Q}{\varvec{\mu }}, \end{aligned}$$
(16)
$$\begin{aligned} R_{\text {CVoR}}&= {\text {E}}[X_{\mathbf {w}}] = R_{GMV}+ \eta , \end{aligned}$$
(17)
$$\begin{aligned} V_{\text {CVoR}}&= {\text {Var}}[X_{\mathbf {w}}] = \mathbf {w}_{\text {CVoR}}^\top {\varvec{\Sigma }}\mathbf {w}_{\text {CVoR}}=\left( V_{GMV}+\frac{\eta ^2}{s}\right) \end{aligned}$$
(18)
$$\begin{aligned} {\text {E}}[X_{\mathbf {w}} | X_{\mathbf {w}} > q_{\alpha _1}]&= R_{GMV}+ \eta + k_{\alpha _1}\sqrt{\left( V_{GMV}+\frac{\eta ^2}{s}\right) }, \end{aligned}$$
(19)

where \(R_{\text {CVoR}}, V_{\text {CVoR}}\) is the portfolio return and variance respectively, and

$$\begin{aligned} \eta = \frac{(R_{GMV}+v_0)s + \left( k_{1-\alpha _2}^2 s\left( (R_{GMV}+v_0)^2+(s-k_{1-\alpha _2}^2) V_{GMV}\right) \right) ^{1/2}}{k_{1-\alpha _2}^2- s} \nonumber \\ \end{aligned}$$
(20)

Proof

By Theorem 3 it holds that

$$\begin{aligned} \mathbf {w}_{\text {CVoR}} = \mathbf {w}_{\text {GMV}} +\frac{\mu _0-R_{GMV}}{s}\mathbf {Q}{\varvec{\mu }}. \end{aligned}$$
(21)

The portfolio \(\mathbf {w}_{\text {CVoR}}\) satisfies the CVaR constraint given by (8) and, hence,

$$\begin{aligned}&-\mu _0 - k_{1-\alpha _2}\sqrt{\mathbf {w}_{\text {CVoR}}^\top {\varvec{\Sigma }}\mathbf {w}_{\text {CVoR}}} = v_0 \Leftrightarrow \;\;\;\;&\mathbf {w}_{\text {CVoR}}^\top {\varvec{\Sigma }}\mathbf {w}_{\text {CVoR}} = \left( \frac{v_0 + \mu _0}{k_{1-\alpha _2}} \right) ^2. \end{aligned}$$
(22)

Since \(\mathbf {w}_{\text {GMV}} {\varvec{\Sigma }}\mathbf {Q} {\varvec{\mu }}=\mathbf {0}\) and \({\varvec{\mu }}^\top \mathbf {Q} {\varvec{\Sigma }}\mathbf {Q} {\varvec{\mu }}=s\), Eq.  (22) can be further simplified to

$$\begin{aligned} \left( V_{GMV}+ \frac{(\mu _0-R_{GMV})^2}{s}\right) = \left( \frac{v_0 + \mu _0}{k_{1-\alpha _2}} \right) ^2. \end{aligned}$$
(23)

To solve (23) for \(\mu _0\), we need to solve a second degree polynom expressed as

$$\begin{aligned} a_1\mu _0^2-2a_2\mu _0+ a_3= 0 \end{aligned}$$
(24)

where

$$\begin{aligned} a_1= k_{1-\alpha _2}^2-s, \, a_2=R_{GMV}k_{1-\alpha _2}^2+s v_0 \, \text {and}\, a_3=V_{GMV}k_{1-\alpha _2}^2 s + R_{GMV}^2k_{1-\alpha _2}^2-v_0^2 s . \end{aligned}$$

Assuming that \(k_{1-\alpha _2}^2 > s\), the solution to (24) is given by \(\mu _0=(a_2\pm \sqrt{a_2^2-a_3a_1})/a_1\) where

$$\begin{aligned} a_2^2-a_3a_1&=2k_{1-\alpha _2}^2R_{GMV}v_0 s - V_{GMV}k_{1-\alpha _2}^4 s + v_0^2 s k_{1-\alpha _2}^2\\&\quad + V_{GMV}k_{1-\alpha _2}^2 s^2+R_{GMV}^2 k_{1-\alpha _2}^2 s \\&=k_{1-\alpha _2}^2 s \left( (R_{GMV}+ v_0)^2 + (s-k_{1-\alpha _2}^2)V_{GMV}\right) . \end{aligned}$$

Therefore the roots are equal to

$$\begin{aligned} \mu _0 = \frac{k_{1-\alpha _2}^2 R_{GMV}+s v_0 \pm \left( k_{1-\alpha _2}^2 s\left( (R_{GMV}+v_0)^2+(s-k_{1-\alpha _2}^2) V_{GMV}\right) \right) ^{1/2}}{k_{1-\alpha _2}^2- s}.\nonumber \\ \end{aligned}$$
(25)

Since the aim is to maximize the expected return of the portfolio, the first root is optimal. Also if \(\mu _0 \in \mathbb {R}\), then the following needs to hold

$$\begin{aligned} k_{1-\alpha _2}^2 s\left( (R_{GMV}+v_0)^2+(s-k_{1-\alpha _2}^2) V_{GMV}\right) \ge 0. \end{aligned}$$

The condition is equivalent to

$$\begin{aligned} v_0 \ge -R_{GMV}+\sqrt{(k_{1-\alpha _2}^2-s)} \sqrt{V_{GMV}}, \end{aligned}$$
(26)

and since \(\sqrt{(k_{1-\alpha _2}^2-s)} \le \sqrt{k_{1-\alpha _2}^2}=-k_{1-\alpha _2}\), the inequality \(v_0 \ge {\text {CVaR}}_{\alpha _2}(X_ {\mathbf {w}_{GMV}})\) holds if (26) does. The characteristics \(R_{CVoR}, V_{CVoR}\) can be easily calculated by using the closed-form expression of the portfolio derived CVoR portfolio weights. \(\square \)

From Theorems 3 and 4 two especially interesting facts arise. When using CVaR as a risk measure, the CVoR portfolio exists only if \(k_{1-\alpha _2}^2 > s\), and analogously VaR exists if \(d_{1-\alpha _2}^2 > s\). The same inequality is presented in Bodnar et al. (2012) to ensure the existence of the minimum CVaR portfolio. Alexander and Baptista (2002) showed that the inequality \(d_{1-\alpha _2}^2 > s\) is the criteria for existence of the minimum VaR portfolio. Also, the CVoR portfolio puts a constraint on the constant \(v_0\) in order for it to exist. This has many interesting economical interpretations. The investor is never limited to small confidence levels \(\alpha _2\), but he/she is limited in the choice of \(v_0\) given that confidence level. This is intuitively appealing. If an investor wants to pick a large confidence level, then he or she must be committed to place more capital at risk, i.e., a larger \(v_0\). The following proposition explains the behaviour of \(\eta \) through the choice of \(v_0\) and \(\alpha _2\).

Proposition 1

Assume that \(R_{\text {CVoR}} > R_{GMV}\), \(v_0\ge {\text {CVaR}}_{\alpha _2}(X(\mathbf {w}_{GMV}))\), \(\alpha _2 \in (1/2,1)\), and \(k_{1-\alpha _2}^2 > s\). Then \(\eta \) is increasing in \(v_0\). If additionally \(k_{1-\alpha _2}^2 > \max \{s,2\}\), then \(\eta \) is decreasing in \(\alpha _2\).

Proof

First, it is noted that \(\eta \) is a composite function of the quantile function \(k_{1-\alpha _2}^2=k^2_{\alpha _2}\) which is increasing in \(\alpha _2\). Further, \(\eta \) can be seen as a function of \(k=k_{1-\alpha _2}^2\) where k has support \(\{k> \max \{s,2\}\}\) and the support of v is \(\{v\ge -R_{GMV}+ \sqrt{kV_{GMV}}\}\) given by

$$\begin{aligned} \eta (k,v) = \frac{g_1(v) + \sqrt{g_2(k,v)}}{g_3(k)}, \end{aligned}$$

where \(g_1(v) = (R_{GMV}+v)s \ge \sqrt{kV_{GMV}} \ge 0\), \(g_2(k,v)=ks((R_{GMV}+v)^2-(k-s)V_{GMV}) \ge 0\) and \(g_3(k)=k-s \ge 0\) for all k and v from their supports.

It holds that \(\eta \) is increasing in v, since both \(g_1(v)\) and \(g_2(k,v)\) are increasing in v. Moreover, it holds that \(g'_3(k)=1\),

$$\begin{aligned} \frac{\partial g_2(k,v)}{\partial k}=s((R_{GMV}+v)^2-(k-s)V_{GMV})-ks V_{GMV}\le 0 \end{aligned}$$

and, hence,

$$\begin{aligned} \frac{\partial \eta (k,v) }{\partial k} = -\frac{g'_3(k)}{(g_3(k))^2}\left( g_1(v) + \sqrt{g_2(k,v)}\right) + \frac{1}{2 g_3(k)\sqrt{g_2(k,v)}}\frac{\partial g_2(k,v)}{\partial k}<0, \end{aligned}$$

which proves the proposition. \(\square \)

Note that the constraint \(k_{1-\alpha _2}^2 > \max \{s,2\}\) is equally conservative as \(k_{1-\alpha _2}^2 >s\) for all practical purposes. Since \(k_{1-\alpha _2}^2 \ge d_{1-\alpha _2}^2\) and if the normal distribution is assumed, then as long as \(\alpha _2\ge 0.95\) then \(d_{1-\alpha _2}^2 \ge (1.96)^2>2\). This proposition implies that the characteristics of the CVoR portfolio are strictly increasing functions of \(v_0\) through their dependence of \(\eta \). An investor will accept more return and risk by increasing the value of \(v_0\). In the context of the CVoR portfolio, a risk-averse investor might choose \(v_0\) to be equal to the CVaR (or VaR) for the GMV portfolio for a given \(\alpha _2\). He/she might even be interested in placing less money at risk, thus decreasing their \(v_0\). The constraint on the constant \(v_0\) in Theorem 4 can be replaced by a more tight one. The investor can choose smaller values of \(v_0\) and still have that the CVoR portfolio exists. This is displayed in the remark below.

Remark 2

Assume that \(\mathbf {x}\sim ECD_p({\varvec{\mu }}, {\varvec{\Sigma }}, \phi (\cdot ))\), where \(rank({\varvec{\Sigma }})=p\), and assume that \(\mathbf {w}_{CVoR}^\top {\varvec{\mu }} > R_{GMV}\) together with \(\alpha _2 \in (1/2, 1)\) such that \(k_{1-\alpha _2}^2>s\). If

$$\begin{aligned} v_0\ge -R_{GMV}+\sqrt{(k_{1-\alpha _2}^2-s)}\sqrt{V_{GMV}} \end{aligned}$$
(27)

then the CVoR portfolio exists.

The inequality follows immediately from the proof of Theorem 4. The CVoR portfolio exists under a tighter constraint on \(v_0\), but the economical implications are somewhat lost. There is a possibility to choose less capital at risk when constructing the CVoR portfolio. Note that the constraint \(k_{1-\alpha _2}^2> s\) appears once again. One can now show that if equality holds in (27) then under this assumption, the constant \(\eta \) takes on the explicit form of \(\sqrt{V_{GMV}/(k_{1-\alpha _2}^2- s)}s\) and the weights and the characteristics of the CVoR portfolio change thereafter. Under this assumption, increasing the confidence level \(\alpha _2\) towards one implies that the CVoR portfolio tends towards the GMV portfolio for both CVaR and VaR as a risk measure.

4 Numerical illustration

In this section the performance of the CVoR portfolio is investigated under different circumstances and assumptions. Since the parameters of the data-generating process are unknown quantities in practical applications, they have to be first estimated before the CVoR portfolio is constructed. This will introduce an additional uncertainty into the considered optimal portfolio choice problem, so-called estimation error. Although the incorporation of the estimation error into the optimization problem when an optimal portfolio is constructed is itself an important topic of research, it is neglected in the discussed numerical illustration and is left for future research. Throughout this section, the only restriction imposed on the portfolio weights is that their sum is equal to one, i.e., \(\mathcal {W}=\{\mathbf {w}: \mathbf {w}^\top \mathbf {1}= 1\}\).

By convexity, the optimality of the CVoR portfolio choice problem is easily attained under weak assumptions imposed on the return distribution by standard optimization algorithms. In the context of the Basel requirements, the optimization problem can be solved for any distribution function. As discussed in Rockafellar and Uryasev (2002), if one believes that the true distribution function of the portfolio return can be accurately approximated by its sample counterpart, namely by the empirical cumulative distribution function (ECDF), then the portfolio allocation problem (3) becomes a linear programming problem. Moreover, it is also possible to show a similar results for the CVoR portfolio using the CVaR as a risk measure and approximating the unknown distribution function of the portfolio return by the corresponding ECDF which is constructed by employing a sample \(\mathbf {x}_1, \mathbf {x}_2,...,\mathbf {x}_n\) of asset return vectors. Then, the application of Theorem 10 in Rockafellar and Uryasev (2002) leads to

$$\begin{aligned} {\text {CVoR}}_{\alpha }(X_1(\mathbf {w}), X_2(\mathbf {w}), ..., X_n(\mathbf {w})) = \min _q \left\{ q + \frac{1}{(1-\alpha )n} \sum _{k=1}^n [X_k(\mathbf {w})-q]^+ \right\} .\nonumber \\ \end{aligned}$$
(28)

The risk measure (or our return measure) now depends on the sample \(X_i(\mathbf {w})=\mathbf {x}_1^\top \mathbf {w}\), \(i=1,...,n\) only. By using (28) one can rewrite (3) and arrive at a linear programming problem, whose result is presented in Lemma 2 given in the appendix.

By Theorem 2 there is still a guarantee on the optimality of the CVoR portfolio under Solvency 2, using the VaR as a risk measure. The regularity conditions constrain the random variables to absolutely continuous return distributions, implying that their densities exist. An optimal portfolio \(\mathbf {w}\) may then be found using algorithms such as gradient ascent or Newton’s method (ch. 8.2, Bazaraa et al. 2013) from the Lagrangian. However, this relies on the fact that a large number of integrals can be evaluated, since the portfolio return distribution is determined by a (potentially large) convolution of the asset return distributions. The evaluation of the objective function may be costly and time-consuming. A great deal of attention has been devoted to these types of problems which are usually referred to as chance-constrained problems in the literature (with their corresponding sample counterpart). Since these problems rely on a very different set of algorithms, outside of the scope of this paper, the readers are referred to, e.g., Jünger et al. (2009), Boukouvala et al. (2016) or Xie and Ahmed (2018) for recent advancements and an overview of how to solve these types of problems.

The data used in this empirical illustration consist of monthly returns from 80 randomly chosen stocks from an incomplete S&P500 asset universe of size 394. The range of data is from the 1st of January, 2000 to the 1st of January, 2021. The universe is incomplete due to the fact that not all 500 stocks were included in the S&P500 index during the last 20 years.

Fig. 1
figure 1

Boxplot of the monthly log-returns

Full size image
Fig. 2
figure 2

Histogram containing moments for each univariate asset return series

Full size image

In Fig. 1 a boxplot of the monthly log-returns on each stock is displayed. Although it is hard to asses the univariate distribution of the asset returns visually, they seem to be roughly symmetric. There are some very large losses as well as returns in the stocks CCL and MGN. However, there is no reason to doubt these values and they will not be removed from the sample. The first four sample moments of each asset return, namely the sample mean, sample variance, sample skewness and sample (excess) kurtosis are computed and shown in Fig. 2. A large portion of the means are positive, so one could expect the portfolios to make a profit over the considered period of 20 years. Most of the variances are small, as it is usually observed for asset returns in empirical studies. One very rarely see movements larger than a few percent in monthly returns unless there has been a structural break. In the second row the skewness for the univariate asset returns is displayed whose values are concentrated in the interval from \(-1\) to 0 showing the presence of small negative skewness in the univariate distribution of asset returns. This is in line with finance theory, namely with the observation that loses tend to be larger than gains, since loses tend to be more “unexpected”. We also observe that the computed kurtosis coefficients belong to the interval from 0 to 5 indicating the presence of heavy tails in the univariate distributions of the asset returns. In order to test the symmetry of the multivariate distribution, Mardia’s test statistic for multivariate skewness and kurtosis is computed. Both tests result in p-values close to 0 and as such they reject the hypotheses that the skewness and the (excess) kurtosis in the multivariate distribution are zero.

Fig. 3
figure 3

Location of the CVoR portfolio together with the benchmark portfolios on the efficient frontier

Full size image

The performance of the suggested CVoR portfolio will be computed for different risk measures (VaR, CVaR) at significance level \(\alpha _2=0.99\) and compared to a number of benchmark portfolios. These portfolios are the equally weighted (EW) portfolio, global minimum variance (GMV) portfolio, maximum Sharpe ratio (SR) portfolio and minimum VaR/CVaR (minVaR/minCVaR) portfolios computed at significance level \(\alpha _2=0.99\). Since all portfolios depend on different parameters, the absence of dependency on a parameter is denoted by “-” in the table and figures.

The portfolios are constructed using a moving window approach. That is, the portfolio weights are estimated using the past 180 observation and held for the next period (month). The out-of-sample portfolio return is thereafter computed and then the new portfolio weights are estimated, excluding the first observation in our time window but including the latest one. Following this setup we compute 61 out-of-sample returns of each portfolio considered in the study.

In Fig. 3 the efficient frontier is displayed for the randomly chosen 80 stocks based on the first 180 observations. Since the number of portfolios is large, they are grouped by “Portfolio” and “Type” in the legend of the figure. Three considered portfolios lie below the efficient frontier. These portfolios are the EW portfolio and the CVoR portfolios obtained following the nonparametric approach without imposing any assumptions on the distribution of the asset returns. These findings are not surprising since there is no theoretical justification for either of these portfolios to be mean-variance efficient. Moreover, the portfolios derived by minimizing risk measures are located close to the vertex of the efficient frontier which is the GMV portfolio. In the figure, the influence of the assumption of a parametric distribution imposed on the asset returns is documented as well. The t-distribution with five degrees of freedom leads to mean-variance optimal portfolios with the largest expected return and variance.

Fig. 4
figure 4

Development of the investor wealth for the considered optimal portfolios. The significance level used in the computation of VaR is set to \(\alpha _2=0.99\)

Full size image

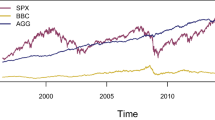
In Fig. 4 the development of investment wealth obtained after selecting the described portfolio strategies is presented. The results in the figure are grouped by their objective (e.g., minimum risk) and the distributional assumption imposed on the asset return distribution. The best portfolio with the best performance during the considered time period should result in the largest wealth at its end. From the beginning of 2016 to the middle of 2018, all considered benchmark portfolios seem to outperform the CVoR portfolios. However, starting from the middle of 2018, the CVoR portfolios take off and consistently outperform the benchmark portfolios. The only exception seems to be the SR portfolio which shows the second best result at the end of the investment period slightly outperforming the CVoR portfolio constructed under the assumption of the Laplace distribution.

Due to the presence of negative skewness in the univariate distributions of the asset returns documented in Fig.  2, one might expect that the two nonparametric CVoR portfolios which does not impose any distributional assumption on the asset returns might be most profitable in terms of wealth out of the CVoR portfolios. However, as it is shown in Fig. 4, this portfolio is ranked on the fourth place being worse than the CVoR portfolios constructed under the assumption that the asset returns are multivariate t-distributed with five degrees of freedom and under the assumption that the asset returns follow a multivariate Laplace distribution.

In Table 1 several performance measures of the considered portfolios are displayed. The list of portfolios is more exhaustive since the figure is already crowded. These metrics are calculated according to their respective sample counterparts. The out-of-sample CVoR is calculated using \(\alpha _1=0.5\).

As it can be seen in Table 1, the variances of the constructed portfolios are smaller than those presented in Fig. 2 which is explained by the effect of diversification [see, Markowitz 1952]. It is interesting that the optimal portfolio that maximizes the Sharpe ratio does not show the best performance with respect to the criteria based on the maximization of the out-of-sample Sharpe ratio. This finding is explained by extreme impreciseness present in the estimated weights of the SR portfolio (cf., Schmid and Zabolotskyy 2008). From the figure describing the wealth, it is noted that holding of the CVoR portfolio with \(v_0=0.08\) computed under the assumption of the t-distribution results in the highest wealth at the end of the investment period. That is not the case when comparison of portfolios is performed in terms of the Sharpe ratio. In this case the minimum CVaR portfolio computed under the assumption of the t-distribution shows the best performance. This should not be surprising since the large cumulation of wealth in Fig. 4 implies a larger variance which reduces the Sharpe ratio. Furthermore, the larger variance is a consequence of the fact that the CVoR portfolio assumes that the investor has a larger risk appetite.

Table 1 Performance measures of different portfolios over a 61 months period
Full size table

An important quantity, which Fig. 4 does not convey, is the turnover defined by [see, e.g., Golosnoy et al. 2019]

$$\begin{aligned} \text {Turnover}= \sum _{t=t_0+1}^{t_1} \sum _{i=1}^p |w_{i;t}^{Port}-w_{i;t-1}^{Port}|, \end{aligned}$$

where \(t_0\) and \(t_1\) are the initial and the last time of the rolling window estimation and the abbreviation ”Port” is one the portfolios specified in the first column of Table 1 where the results are displayed. The CVoR portfolios obtained without imposing assumption on the asset return distribution demonstrate the highest turnover. Any profit or return obtained by these portfolios would have been completely consumed by the turnover. The portfolio with the third highest turnover is the portfolio which shows the best performance in terms of the investor wealth in Fig. 4. This is one explanation to why the portfolio can possess such a good performance in terms of wealth. It reacts rapidly to market movements, but does not cope with the fact that reacting to such movements is costly. This is of course not surprising since the transaction costs are not included in the optimization problem. The portfolio with the smallest turnover is the equally weighted, since it is never reweighted, while the GMV portfolio is ranked on the second place with respect to this performance measure.

5 Summary

In this paper an entirely quantile-based optimal portfolio choice problem is introduced. It takes both tails of the return distribution into account. The resulting optimal portfolios are obtained under general distributional assumptions on the asset returns. Both sufficient and necessary conditions for the existence of the optimal portfolio, called the CvoR portfolio, are provided under different risk measures. A special emphasis is placed on the use of risk measures which are demanded by current Basel and Solvency regulations. For instance, the insurance companies have to follow the Solvency 2 regulations and restrictions, and because of that they might prefer to use quantile-based return measures, like the CVoR, as a complement to quantile-based risk measures. In such a way, non-overlapping information presented in the portfolio return distribution is used to specify the risk and the profit of the portfolio. The resulting CVoR portfolio is shown to be very flexible and it provides good theoretical results as well as a straightforward implementation of numerical procedures. The empirical illustration also demonstrates a good performance of the CVoR portfolio in comparison to the considered benchmark portfolios based on several performance measures.

The results of the empirical application relies on the true underlying return distribution which is not known. The model parameters in the data-generating process are estimated by their sample counterparts, which are then used instead of unknown population quantities. In doing so, estimation error is introduced in the decision process which is, however, not accounted for in the derived theoretical results. Also, the investigation of temporal independence in the underlying data-generating process has been neglected in the empirical application. This was done in order to avoid that the numerical illustration would loose its focus on the main results of the current paper.

The introduced quantile-based portfolio selection problem is not restricted to the usage of the CVoR but other quantile-based return measures could be used. The topic is not treated in the paper and it is left for future research. As the CVoR is a modification of the CVaR and the CVaR is a special case of spectral risk measures, one can incorporate a modification of spectral risk measures into the portfolio selection problem. The use of these would imply a great deal of flexibility for investors which can then also rely on nice theoretical properties of the optimization problem.