Constructing banking networks under decreasing costs of link formation

Abstract

The structure of networks plays a central role in the behavior of financial systems and their response to policy. Real-world networks, however, are rarely directly observable: banks’ assets and liabilities are typically known, but not who is lending how much and to whom. This paper adds to the existing literature in two ways. First, it shows how to simulate realistic networks that are based on balance-sheet information. To do so, we introduce a model where links cause fixed-costs, independent of contract size; but the costs per link decrease the more connected a bank is (scale economies). Second, to approach the optimization problem, we develop a new algorithm inspired by the transportation planning literature and research in stochastic search heuristics. Computational experiments find that the resulting networks are not only consistent with the balance sheets, but also resemble real-world financial networks in their density (which is sparse but not minimally dense) and in their core-periphery and disassortative structure.

1 Introduction

It is well known that the structure of financial networks is important in assessing systemic risk (Allen and Gale 2000; Freixas et al. 2000; Lux 2017), but is also important in other areas, such as market efficiency or payments processing (see Glassermann and Young 2015 for a review). In spite of its importance, the analysis of networks is made difficult by a lack of data for essential markets. For many crucial financial networks, a researcher only has the assets and liabilities of individual agents in a financial network, while the bilateral arrangements between individuals are missing.

One strategy for dealing with the lack of network data is to use balance sheet information. The assets and liabilities are reported at an aggregate level, and the absence of granular information prohibits the reconstruction of actual links or contract sizes. Based on simplifying or plausibility assumptions, several methods exist to create or simulate networks that reflect at least the available information; however, the results reproduce stylized facts only to a varying degree.

In this paper, we suggest an alternative approach to reconstruct networks from only balance sheet information; the resulting networks, however, better capture some real-world properties. We assume that establishing and maintaining a network is costly, and that the parties involved have incentives to arrange themselves in relationships that are cost-efficient.

We start from a basic fixed cost of a link, which is consistent with the observation that interbank activity is based on relationships (see Anand et al. 2015; Cocco et al. 2009). Establishment and maintenance of a lending-borrowing relationship (that is, a link) is expensive. The monitoring costs associated with this link are incurred by the borrower, the lender, or both. Independent of contract size, our model assigns to each bank a fixed cost for its first link but decreases for every additional link formed by a bank. The interpretation of this is that, as a bank develops risk controls within its institution, these controls are subject to increasing returns to scale.

In other words, additional links are expensive due to information processing, risk management and credit-worthiness checks, but such costs decrease as the bank establishes more links and its infrastructure grows. Establishing more links is helpful where it might not be possible to find a single counterparty to satisfy all liquidity or borrowing needs. Moreover, our model allows us to distinguish costs that are born by the lender, the borrower, or by both.

The model determines the optimal network configuration, where optimality is defined with respect to geometrically decreasing cost of link formation (i.e., decreasing fixed-costs). The optimization problem is NP-hard and the search space has frictions and multiple local and global optima. To solve it, borrowing from operations research literature for transportation problems, we introduce the permuted North-West-Corner-Rule (pNWCR) in combination with Simulated Annealing, a stochastic optimization technique, which allows reliable solutions to be found within reasonable time. pNWCR provides a solution to an aggregate and static cost minimization problem, which is then a solution from the viewpoint of a social planner and not necessarily equivalent to the optimal solution emerging from a disaggregated search of individual contractors in the interbank market.

Our numerical experiments show that the proposed approach reproduces several stylized facts of interbank networks: sparsity, core-periphery and disassortative structures. By starting from a realistic marginal distribution of assets and liabilities, the core-periphery of Craig and von Peter (2014) emerges as a natural property of the system, and the distribution of contract sizes exhibits a smaller right tail than left tail. This indicates the less extreme lender-borrower relationships that we generally observe. Due to its simplicity, we can further explore what happens when the borrowers or the lenders pay the cost of a link, and we consider a shared-cost version.

The problem of constructing a network that satisfies a given set of assets and liabilities of the individual banks has prompted a stream of research (see Squartinia et al. 2018; Gao et al. 2018; Hueser 2015 for reviews on these methods applied to financial networks). Upper and Worms (2004) suggested employing maximum entropy methods as they are easy to compute. However, maximum entropy, while satisfying the balance sheet constraint, does not replicate characteristics such as sparsity and a core-periphery structure that are observed in real-world networks where more complete data are available. In such a structure core members are strongly connected to each other, whereas periphery members establish just a few links with core members but none with other periphery members (Borgatti and Everett 2000).

Alternative methods based on copulas, bootstrap and iterative algorithms have been subsequently developed and compared. Among these alternatives, Anand et al. (2018) consider 25 different financial markets spread out among 13 regulatory jurisdictions where the complete network data are available. The fixed cost model developed by Anand et al. (2015) tends to simulate networks that outperform all other simulations with respect to the Hamming distance and accuracy score between the simulated and actual networks. This model constructed a sparse network which managed to avoid the inclusion of links that are not present in the actual network. The simulations very rarely exhibited a core-periphery structure, and used an algorithm that performed slowly, often converging to a local optimum (see Fig. 1 in Anand et al. (2015)).

Where bilateral data exist, a few works so far have focused on different financial markets. These include (Boss et al. 2004) for the Austrian interbank market, Li et al. (2018) for the Chinese loan network with core-periphery structure, Silva et al. (2016) for the Brazilian core-periphery market structure, Finger et al. (2013) for the e-MID overnight money market, Iori et al. (2015), Temizsoy et al. (2015) for the e-MID Interbank market and Van Lelyveld and In’T Veld (2012) for the core-periphery structure in Netherlands. These empirical investigations establish a few stylized facts of interbank lending, such as a typical core-periphery structure, network sparsity, and disassortativeness.

The agent-based modeling literature has focused on replicating some of these characteristics as in the work of Gurgone et al. (2018) and Liu et al. (2018) and within dynamic modeling frameworks, as in Zhang et al. (2018), Guleva et al. (2017), Xu et al. (2016), and Capponi and Chen (2015). Lux (2015) introduces a simple dynamic agent-based model that, starting from a heterogeneous bank size distribution and relying on a reinforcement learning algorithm based on trust, allows the system to naturally evolve toward a core-periphery structure where core banks assume the role of mediators between the liquidity needs of many smaller banks. Blasques et al. (2018) propose a dynamic network model of interbank lending for the Dutch interbank market, pointing out that credit-risk uncertainty and peer monitoring are driving factors for the sparse core-periphery structure.

The paper is structured as follows. Section 2 discusses state-of-the-art methods and our proposed model with decreasing costs of link formation. Section 3 focuses on the optimization model and introduces the new pNWCR obtained by combining heuristics, such as simulated annealing, with the classical NWCR from transportation theory. Section 4 describes the properties of networks under decreasing costs of link formation. Finally, Sect. 5 draws the main conclusions and the outlook for further research.

2 Constructing networks

2.1 Existing methods

The problem of constructing banking networks based on limited information has attracted some attention in the literature, in particular for the case where, for N banks, their (total) assets, $A_i$, and liabilities, $L_j$, with $i,j = 1, \ldots , N$ are known, but not who is lending to whom, let alone the exact amounts, $z_{ij}$. All we do know is that the volumes are not negative and that budget constraints must hold; and, if the banks’ identities are known (and indices i and j match), where self-lending is excluded:

$$\begin{aligned} \sum _{j=1}^{N} z_{ij} = A_i, \quad \sum _{i=1}^{N} z_{ij} = L_j, \quad z_{ij} \ge 0, \quad (z_{ii} = 0) ~~. \end{aligned}$$

(1)

The basic problem in this situation is that there are (potentially infinitely) many networks ${\mathbb {Z}} = [z_{ij}]$ that meet these criteria. Network construction methods can therefore not assume that there is a unique solution but require additional assumptions. These can simplify or aggravate the computational requirements, and they often lead to different network properties more or less close to stylized facts for real networks.¹

A popular group of such construction methods is based on the maximum entropy (ME) principle. In simple terms, the idea is to create a fully connected network (with or without the constraint $z_{ii}=0$) where the contract size $z_{ij}$ between lender i and borrower j is proportional to the size of $A_i$ and $L_j$ relative to their market shares. Initiated by Upper and Worms (2004), this method is simple and fast, but cannot replicate important stylized facts of real-world networks. Among other things, real banking networks are far from fully connected, and contract sizes are not deliberately chosen to be proportional to the lenders’ and borrowers’ market shares. Subsequent methods try to incorporate this: Drehmann and Tarashev (2013), for example, suggest re-scaling ME networks based on stochastic principles while retaining 100% density.

Other approaches explicitly control for the density: Cimini et al. (2015), e.g., incorporate a density parameter in their fitness model, while Musmeci et al. (2013) combine the density-driven link selection with ME. Hałaj and Kok (2013), on the other hand, suggest an iterative sampling technique. They start with an empty network, $z_{ij}^{(0)}=0$. In each iteration, t, a random pair (i, j) of a lender i and a borrower j is drawn and their contract size is increased according to $z_{ij}^{(t)} = z_{ij}^{(t-1)}+ u \cdot \min \left( A_i^{(t-1)}, L_j^{(t-1)} \right)$. Here, u is a uniform random number and $A_i^{(t-1)}$ and $L_j^{(t-1)}$ are not yet allocated assets and liabilities of i and j, respectively. This is repeated until all banks’ assets and liabilities are assigned. In addition, a probability map can be imposed that reflects the likelihood that two banks do business; if that probability is $p_{ij}<1$, then the chosen pair is rejected with a likelihood of $1-p_{ij}$ with no (additional) contract, and $z_{ij}^{(t)} = z_{ij}^{(t-1)}$. This probability map can be used to model preferences for certain banks, e.g., to model a domestic bias. The resulting network typically exhibits low density, but not necessarily a core-periphery structure (unless imposed via the probability map).

Anand et al. (2015) consider sparsity as an explicit objective: links are costly and banks therefore have an inherent motive to keep the number of links as low as possible. They argue that any active link causes fixed-costs irrespective of the actual contract size. Their approach claims to identify the most probable links and loads them with the largest possible exposure consistent with the total lending and borrowing observed for each bank. Banks do not spread their borrowing or lending across the entire system, since the costs in terms of information processing, risk management and creditworthiness checks might be prohibitive for all but the large banks. Additional or avoidable fixed-costs should then be avoided, and keeping the number of links at a minimum is advantageous. Constructing a network can therefore be considered a minimization problem for the overall cost of the network, $F({\mathbb {Z}})$:

$$\begin{aligned} \min _{{\mathbb {Z}}} F({\mathbb {Z}}) \end{aligned}$$

(2)

where

$$\begin{aligned} F({\mathbb {Z}})= & {} c \cdot \sum _{i=1}^{N} \sum _{j=1}^{N} {\mathbbm {1}}_{ij} \end{aligned}$$

(3)

$$\begin{aligned} {\mathbbm {1}}_{ij}= & {} {\left\{ \begin{array}{ll} 1 &{} \text {if } z_{ij}>0\\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(4)

under budget and non-negativity constraints (1). c are the constant fixed-costs per link, and ${\mathbbm {1}}_{ij}$ is a binary indicator as to whether or not bank i lends to bank j. This is equivalent to finding the network with the lowest average degree, i.e., the lowest number of edges, under given constraints.

Since this is a directed network with edges (links) running from lenders (assets) to borrowers (liabilities), the out-degree, $d_i^{A}$, of bank i is the number of banks i is lending to, while j’s in-degree, $d_j^{L}$, is the number of banks j is borrowing from:

$$\begin{aligned} d_i^{A} = \sum _{j=1}^{N} {\mathbbm {1}}_{ij}, \quad d_j^{L} = \sum _{i=1}^{N} {\mathbbm {1}}_{ij}. \end{aligned}$$

The cost function can be rewritten as a function of the banks’ (and, ultimately, the network’s) degrees—from the lenders’ perspective as

or, from the borrowers’ perspective as

$$\begin{aligned} F({\mathbb {Z}}) = c \cdot \sum _{j=1}^{N} d_j^{L}, \end{aligned}$$

or, if costs are incurred by either side and $c = c_A + c_L = c\cdot \alpha + c \cdot (1-\alpha )$ with $0 \le \alpha \le 1$, then

The total number of links in the minimum density (MD) network ${\mathbb {Z}}_{MD}$ is $\sum _{i,j} {\mathbbm {1}}_{ij} = \sum _i d_i^{A} = \sum _j d_j^{L}$ and can be considered the lower bound for the actual number of links in the real (unobserved) network. From an optimization point of view, c is just a scalar, and solving optimization problem (2) produces a minimum density network with the lowest possible degree. Anand et al. (2018) find that networks constructed using such methods compare favorably with those using other popular methods along many dimensions. Nonetheless, there are still aspects that can be improved. For one, real-world networks are usually less sparse than the MD solution, and MD networks do not have a pronounced core-periphery structure. Also, it might be a strong assumption that any link causes the same fixed-costs. Therefore, we suggest an extended model to address these issues.

2.2 A model with decreasing costs of link formation

If the fixed-costs of a link are caused by establishing and maintaining a link between two banks, then it seems reasonable to assume a learning curve: an already well-connected bank with risk management processes and creditworthiness checks in place can draw from experience and can spread its overhead over more contracts, and any additional link will incur lower costs than the previous (or first) one. Assuming a geometric decay in the costs of the bank’s additional links and parametrized by $\gamma$ with $0\le \gamma \le 1$, the first link’s costs are expressed as c, the second link’s cost as $c \cdot \gamma$, the third as $c \cdot \gamma ^2$ and so on until the last with $c \cdot \gamma ^{d-1}$ where d is the bank’s degree, i.e., its number of links. In total, the bank’s costs add up to

$$\begin{aligned} C(d,\gamma )= & {} c \cdot \left( 1+ \gamma + \cdots + \gamma ^{d-1}\right) = c \cdot \sum _{k=0}^{d-1} \gamma ^k\nonumber \\= & {} c \cdot {\left\{ \begin{array}{ll} d &{} \text {for } \gamma = 1\\ \frac{1-\gamma ^{d}}{1-\gamma }< d&{} \text {for } 0 \le \gamma < 1 \end{array}\right. } . \end{aligned}$$

(5)

Assume that, akin to (3*), all costs are from the lenders’ perspective so that the new cost function is then

$$\begin{aligned} F_A^*({\mathbb {Z}}) = c \cdot \sum _{i=1}^{N} C(d_i^A, \gamma _A). \end{aligned}$$

In this extended model, the costs of the network still depend on the degree, but no longer in a linear fashion when the marginal costs are shrinking, $\gamma _A<1$. If there is no decay in fixed-costs, $\gamma _A=1$, then this model is identical to the minimum density (MD) model.

In the MD model, it makes no difference whether costs are incurred by lenders, borrowers, or both, and the solution for cost function (3**) is not affected by the choice of $\alpha$. When costs for additional links are decreasing, however, things change: lenders and borrowers can have different (distributions of) degrees, and they might face different learning curves with separate $\gamma _A$ and $\gamma _L$.

The new optimization model with decreasing fixed-costs or decreasing costs of link formation can then be summarized as follows:

$$\begin{aligned} \min _{{\mathbb {Z}}} F^*({\mathbb {Z}}) = c \cdot \alpha \cdot \sum _{i=1}^{N} C(d_i^A, \gamma _A) + c \cdot (1-\alpha ) \cdot \sum _{j=1}^{N} C(d_i^L, \gamma _L) \end{aligned}$$

(6)

with banks’ cost function (5) and with constraints (1) on budget, non-negative volumes, and, where applicable, self-lending. The parameter $\alpha$ controls who incurs the costs: for $\alpha =1$, it is exclusively the lenders, for $\alpha =0$, it is the borrowers, and for values between these extremes, it is a combination. Note that linearly scaling c to change the level of the costs for the first link has no impact on optimality; for simplicity, it will therefore be fixed to $c=1$. What can make a difference, though, is whether one type of bank has higher cost than the other type (expressed via $\alpha$), and how their respective costs decrease due to economics of scale (expressed via the $\gamma _A$ and $\gamma _L$). The model is then flexible enough to capture different potential set-ups for the interbank network, depending also on the availability of other information, which could then better specify if the borrowers or lenders bear the main costs and the rate of decrease in the fixed costs. In fact, we can set different values of $\gamma _A$ and $\gamma _L$ to consider the fact that the lender costs might be driven by the monitoring of the clients’ creditworthiness, while the borrower costs might be related to the management processes of liquidity provision. Moreover, the parameter $\alpha$ allows to allocate costs between the borrowers and the lenders.

3 Finding cost-optimized networks

3.1 The optimization problem

Both the minimum density and the decreasing costs of link formation models present challenging optimization problems: there are no closed-form analytical solutions, and numerically they are hard to tackle. They are discrete and non-convex with local optima, rendering hill-climbing methods unreliable. Non-deterministic methods might be suitable to overcome those local optima. For example, Anand et al. (2015) employ a Markov-Chain Monte-Carlo (MCMC) approach and find sparse solutions to their test problems. However, a closer look reveals that convergence is rather slow, and that even for their small test problem with just six lenders and five borrowers, their reported solution turns out to be suboptimal. Interestingly, they also point out that their problem is equivalent to the Fixed-Cost Transportation Problem (FCTP), a popular archetypal problem in logistics. There, the situation is that suppliers $i=1,\ldots ,M$ can produce goods that are sold in outlets $j=1,\ldots ,N$. The assignment problem then is to find the quantities $x_{ij}$ that are shipped from producers i to outlets j such that the outlets’ demands are met ($\sum _i x_{ij}=D_j$) without exceeding the suppliers’ capacities ($\sum _j x_{ij} \le S_i$) while minimizing the overall costs, $\sum _i \sum _j x_{ij} \cdot v_{ij} + \sum _i \sum _j {\mathbbm {1}}_{ij} \cdot f$, where $v_{ij}$ are proportional costs per unit of goods (e.g., costs per truck transporting one unit of goods over the distance between i and j) and f is the fixed-costs for this active link (e.g., the set-up costs for the cooperation between i and j). Quantities must not be negative ($x_{ij}\ge 0$), and ${\mathbbm {1}}_{ij}=1$ indicates an active link (if $x_{ij}>0$; ${\mathbbm {1}}_{ij}=0$ otherwise). For the special case of $\sum _i S_i = \sum _jD_j$, the problem is also known as Balanced FCTP.

In the banking network problem, the lenders correspond to the suppliers, the borrowers to the outlets, and contract sizes to the shipped quantities. $v_{ij}$ could be seen as the interest rate; if this is the same for all combinations ($v_{ij}= v$ $\forall (i,j)$, e.g., in the absence of risk premia, time spreads, etc.), the variable part of the cost function can be dropped as it always adds up to the same value, leaving only the part with the fixed-costs to be relevant. And it is exactly this part that makes it a challenging optimization problem: for a relatively small number of producers and outlets (or, here, banks), optimal solutions cannot be found in a reasonable time frame. In a market with N banks, there are up to $N^2$ potential links each of which could be active or inactive; this amounts to as many as $2^{N^2}$ combinations even before considering how to distribute the quantities. With the constraint $z_{ii}=0$ active (a situation hardly relevant in the traditional FCTP), these numbers are lowered to $N (N-1) = N^2-N$ and $2^{N^2-N}$, respectively; either way, the search space is vast, even for very small markets: for just $N=10$ banks, there would be $2^{100} > 1.26e{+30}$ and $2^{90} > 1.23e{+27}$ alternatives, respectively, just for setting the links, before assigning actual quantities $z_{ij}$. This is why a number of initialization methods have been developed to create solutions that are at least feasible and valid with respect to the constraints.

One such method is the North-West-Corner-Rule (NWCR; see, e.g., Hillier and Liebermann (2010)) which we enhance to approach our cost-minimization problem for network construction.

3.2 The permuted North-West-Corner-Rule

The original North-West-Corner-Rule uses a tableau where the rows are the suppliers (here: lenders) and the columns are the outlets (here: borrowers) and where quantities are iteratively assigned. Using the notation from our problem, it is initialized by considering all assets and liabilities to be unassigned ($A_i^{(0)} = A_i$, $L_j^{(0)}=L_j$) and all links to be inactive ($z_{ij}^{(0)}=0$). Then follows an iterative procedure where in each iteration, t, one pair of a lender i and a borrower j is selected. In the first iteration, it is the combination of the top-left corner (“north-west” corner, hence the name) of the tableau with $(i=1,j=1)$. Next, one checks how much of i’s supply is still unassigned, and how much open demand j has left. The lower of the two is the maximum contract size between the two and chosen for $z_{ij}$, while i’s available supply and j’s open demands are lowered accordingly: $z_{ij}^{(t)} = \min \left( A_i^{(t-1)}, L_j^{(t-1)}\right)$, $A_i^{(t)} = A_i^{(t-1)} - z_{ij}$, and $L_j^{(t)} = L_j^{(t-1)} - z_{ij}$. If i’s assets are now exhausted ($A_i^{(t)}=0$), one moves on to the next supplier ($i := i+1$; move south in the tableau); if j has no further demand for liabilities ($L_j^{(t)}=0$), one moves to the next borrower ($j:=j+1$; move east in the tableau). This finishes iteration t and starts iteration $t+1$. These iteration steps are then repeated until no available assets and no demand for liabilities are left, and the south-east corner has been reached. The network ${\mathbb {Z}}_{MD}$ in Table 1b has been created in exactly that fashion.²

The NWCR does produce a feasible solution as it is based on the constraints. However, it does not guarantee an optimal solution for two reasons: (a) costs, fixed and variable alike, are ignored in the construction process, and (b) the sequence in which the banks are listed drives the assignments. At the same time, it tends to produce very sparse networks, which, here, keeps the aggregate fixed-costs low. The second aspect concerning the sequence is usually considered a downside, as the sorting and the resulting pairs (i, j) are often arbitrary. For the problem at hand, we suggest to turn this into a crucial feature of the optimization: we restate the search process as finding permutations of the lenders and borrowers, respectively, that minimizes the costs of a resulting pNWCR network. This turns the optimization problem into a sorting problem similar to the traveling salesman problem (TSP)—which is NP hard (i.e., with no known algorithm where the required computation time is no worse than polynomial in the number of instances), but for which non-deterministic search methods have been found to have favorable convergence properties. For the problem at hand, we adopt a Simulated Annealing algorithm, originally suggested by Kirkpatrick et al. (1983), and fit it to our problem: starting with a random solution, each iteration produces one new solution (here: a slightly different permutation of lenders and borrowers) by mutating the current one. Simple ways of achieving this include switching two or more randomly chosen elements (e.g, aBcdEf becomes aEcdBf), or by choosing a random segment of the sequence and reversing its order (e.g., abCDEf becomes abEDCf). If the mutant solution is better than the current one, it replaces it; but also a (slightly) worse solution can be accepted, with a certain probability, to overcome local optima: the larger the downhill step (and the longer the search process has been going on), the lower that probability. After its final iteration, the algorithm reports the best of all tested candidates. Appendix B provides pseudo-algorithms for the Simulated Annealing algorithm and the Permuted North-West Corner Rule.

Mimicking the real-world crystallization and annealing process, a “temperature” parameter gears the search process: if the temperature is too generous (high), any mutant is accepted and the search turns into a random walk; if it is converging to zero (i.e., even the slightest deterioration is unlikely to be accepted), then it turns into a hill-climber. With a well-chosen temperature and cooling plan, however, the process creates a trajectory through the search domain that can overcome local optima (thanks to accepting some of the downhill steps) yet with a tendency to converge to the optimum (thanks to ignoring very damaging steps, but with a dominating preference for uphill steps). Typically, the temperature parameter is therefore set to a reasonably high value in the beginning, but gradually lowered towards zero, to shift the search process from an explorative to an exploitative behavior.³

4 Properties of networks under decreasing costs of link formation

4.1 A simple illustrative example

Assume there are six banks that are all lenders with assets $[A_i] = [50, 15, 12, 11, 8, 4]$ and another six banks that are all borrowers with liabilities $[L_j] = [51, 14, 13, 10, 9, 3]$. No bank is both lender and borrower; the self-lending constraint can be ignored. Banks are sorted by size in descending order to facilitate interpretation. Table 1 shows three different networks all of which satisfy the budget and non-negativity constraints and produce the required assets and liabilities. The scalar c is assumed to be 1 here and in all subsequent experiments.

The network ${\mathbb {Z}}_{ME}$ in Table 1a has been created with the maximum entropy (ME) approach. Note that all columns (portfolios of borrowers) are proportional to each other, reflecting the relative size of the banks’ liabilities; the same is true for all rows (portfolios of lenders): bank E is twice the size of F, $z_{Ej} = 2 \cdot z_{Fj} \,\, \forall j=1,\ldots ,N$. By construction, this is a fully connected network with 36 (out of a possible 36) active links, resulting in a density of 100%, and where each lender is linked to any borrower and vice versa. Any bank, lender and borrower, therefore, has a degree of 6. With fixed constant costs of 1 per link, this adds up to total network costs of 36. If costs are incurred by lenders and their decay factor is $\gamma _A=0.7$, the costs for additional links go down, and each lender’s costs are reduced from 36 to 2.94, causing overall network costs of 17.65 (imprecision due to rounding).

Table 1 Constructed networks for a simple example with six lenders (A–F) and six borrowers (K–P), respectively. $d_i^A$ is the (out) degree of lender i, $C_i^A$ are i’s total costs, depending on decay factor $\gamma _A$. Costs are incurred by lenders only ($\alpha =1$)

Network ${\mathbb {Z}}_{MD}$ in Table 1b is one possible solution when the network is being constructed under minimum density (MD).⁴ Any bank i with positive assets needs to have at least one link. If there is another bank j with liabilities $L_j = A_i$, then both can do with just this one link, otherwise, either i or j needs at least one additional link, depending on whose position is larger. In this example, (at least) three of these additional links are required. It can be seen that a density of 25% (9 active out of 36 possible links) suffices to generate a valid solution. In this particular solution, lenders can do with just one or at most two links, reducing their respective costs to 1 and 2 when there are constant fixed-costs, adding up to overall costs of 9, which is optimal under constant fixed-costs: for this market, there exists no solution with fewer than nine links.

When additional fixed-costs decrease with $\gamma _A=0.7$, the lender’s costs are 1 (when $d_i^A=1$) and 1+0.7 = 1.7 (when $d_i^A=2$), respectively. In this case, the overall costs for the MD network are now just 8.1—which is no longer optimal: there exist solutions that have more links, yet lower overall costs, thanks to exploiting reduced costs for additional links. Simply speaking, if there is a need for one extra link, it is cheaper to have it not as a second link, but to ride the learning curve and have this extra link with a lender who already has several links. In fact, one second link (additional costs: 0.7) can be more expensive than a fourth and fifth link combined ($0.7^3 + 0.7^4 = 0.58$). Hence, a slightly higher density is not necessarily more expensive if links are well chosen.

The optimal network under decreasing costs of link formation for additional links (DC), ${\mathbb {Z}}_{DC}$ in Table 1c, exhibits exactly that. It has a total of 11 links, but they are more unevenly distributed among the lenders: while most have just one link, the first (and largest) lender has six. With $\gamma _A=0.7$, this lender’s first contract comes with unit cost, the second one costs 0.7, the third just 0.49 and so on, down to less than 0.17 for the sixth. These five extra links cost a total of 1.94. In ${\mathbb {Z}}_{MD}$, on the other hand, there were three lenders (B, C, and F) who all had one extra link; each of these cost them 0.7, totaling 2.1 and exceeding A’s five additional links. In other words, the lenders now have out-degrees either at the bare minimum with just one link, or they are the provider(s) of as many of the required extra links as possible. Overall, parsimonious networks are still highly desirable; however, concentration can make additional links acceptable.

The consequences of decreasing cost of link formation manifest themselves in the distribution of the lenders’ degrees. Revisiting the ME network, the Herfindahl index, H, and, for easier comparison, its normalized version, $H^*$, for the out-degrees are

$$\begin{aligned} H({\mathbb {Z}}_{ME}) = \frac{\sum _i d_i^2}{(\sum _i d_i)^2} = 0.167 = \frac{1}{6} = \frac{1}{N} \quad H^*({\mathbb {Z}}_{ME}) = \frac{H({\mathbb {Z}}_{ME})-\frac{1}{N}}{1-\frac{1}{N}} = 0.0. \end{aligned}$$

which shows perfect evenness. For the MD network, $H = 0.185$ ($H^* = 0.02$), indicating that the out-degrees are still quite even. For the DC network, however, $H=0.339$ ($H^*=0.21$), highlighting the strong unevenness in the lenders’ number of links.

Another way of looking at ${\mathbb {Z}}_{DC}$ is that there are many banks (both lenders and borrowers) with few links (and, in particular, no links between them), and one bank on either side with many links (with links between these two and all the other ones). This is typical for core-periphery networks where a small group of banks (core) have many links to any other banks, while the large group of all other banks (periphery) are typically linked to some of the cores, but with hardly any links to other periphery banks.

Note that $\gamma _A<1$ will lower the average costs per contract: a lender with just one link faces costs of 1.0; the lender with 6 links, on the other hand, faces average costs of just $2.94/6 = 0.49$. If lenders pass their costs on to the borrowers, then a core lender can offer more attractive conditions than one from the periphery. However, in this model, we only consider where the costs originate and not how they are re-distributed within the system, and we are refraining from additional interpretations of this aspect.

In short, ${\mathbb {Z}}_{DC}$, found under the decreasing costs of link formation, is quite sparse, but not at its absolute minimum, and it resembles a core-periphery structure. To test whether this is a typical outcome, a large scale computational experiment with artificial data was performed, described in the following sections.

4.2 Experimental setup for artificial markets and preliminary tests

For the computational experiments, numerous artificial markets were generated. The main experiments reported in this paper are based on 100 markets, each consisting of $N=100$ banks where assets and liabilities follow a log-normal distribution. Also, it is assumed that self-links can be identified when $i=j$ and the constraint $z_{ii} = 0$ is enforced. The parameter for shifting the costs between assets and liabilities was chosen from $\alpha \in \{1, 0.5, 0\}$; the decay factors were selected from $\gamma _A, \gamma _L \in \{0.5, 0.55, ..., 0.85, 0.90, 0.925, 0.95, 0.975, 1.0\}$, including the combinations when both sides incur costs (i.e., $\alpha =0.5$).

In addition, markets with $N \in \{25, 50, 100, 200\}$ banks have been simulated, where assets and liabilities were drawn from parametric distributions such as the log-normal, Pareto, chi-squared, and uniform, and also by bootstrapping from anonymized empirical data. We found that the main findings can be observed in all of these markets, yet to various degrees: reactions to changes in the decay parameter(s) were more abrupt in smaller, and smoother in larger, markets, but with the latter requiring substantial CPU time in the optimization process and, perhaps, leaving more room for convergence. Similar variations could be found when the distributions of assets and liabilities were more or less skewed.

Stochastic optimization methods are not guaranteed to find the global optimum, but they have an increased chance of finding the optimum or a solution close to it when granting more iterations and when allowing for restarts and reporting only the best of repeated attempts. This is why all problems for the main experiments have undergone numerous (typically hundreds of) restarts with random initial solutions, but also with initial solutions that were found to be optimal in previous runs (and with the renewed threshold sequence allowing for more than just a refined local search) as well as optimal solutions for similar problems (identical market, but different settings of $\gamma _A$, $\gamma _L$, and $\alpha$).

Also, it should be noted that the suggested procedure of constructing a network by searching a permutation of banks and mapping it via the pNWCR into a network does not guarantee that the reported result is the global optimum. Numerous preliminary experiments, however, suggest that it is more efficient than other methods in the sense that it finds solutions that are at least as good, but in substantially less time, in particular for larger problems. It can therefore be assumed that the reported results typically are close enough to the actual optima to reflect important properties. Nonetheless, results will be interpreted cautiously, also because in these problems, global optima are not necessarily unique, and even while they share the same minimum costs, their other characteristics might differ.

All implementations and experiments were done in Matlab version 2018b. For comparison, Appendix C provides results for networks created with alternative methods, such as Maximum Entropy (ME) by Upper and Worms (2004) and methods inspired by Hałaj and Kok (2013).

4.3 Findings for artificial markets

The toy example in Table 1 illustrated that overall costs are lower when fixed-costs for links are subject to decay: taking the minimum density solution already lowers costs whenever there are banks that require more than one link. They benefit from the reduced costs, and it might be beneficial to have more links with a highly connected bank than two links with a bank that has only a few connections. This means that, on a macro level, the overall number of links and the density of the network will go up. On a micro level, poorly connected banks will have even fewer links (perhaps just one) and become (even more) peripheral, while the highly connected ones (typically also those with large balance sheets) will have even more links.

Fig. 1

Aggregate results for 100 markets consisting of $N=100$ banks each with log-normally distributed assets and liabilities when all costs are incurred by lenders ($\alpha =1$)

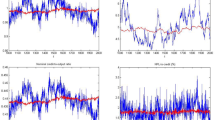
These effects are confirmed by the experiments with the 100 artificial markets with $N=100$ banks each. Figure 1 looks at the overall effects when costs are incurred by the lenders ($\alpha =1$). As can be seen from Fig. 1a, the stronger the decay in marginal costs (i.e., the lower $\gamma _A$), the lower the overall cost of the network; this is particularly noticeable when compared to the minimum density network (i.e., when $\gamma _A=1$). Note that, for lower $\gamma _A$, the costs converge to 100: the market consists of $N=100$ banks, and every bank needs to have at least one link. The first link has unit costs of $c=1$, while the additional ones will be (substantially) cheaper; their contribution to the overall network costs become less noticeable. By construction, every bank has a positive budget and therefore requires at least one link. At the same time, optimal networks tend to have overall more links, which is equivalent to a higher density; cf. Panel 1(b).

Larger markets allow a more subtle analysis of the results. Panel 1(c) shows that lenders differ more in how many links they have (i.e., the lenders’ out-degree), but for the same reason as in the small example: larger banks with many links already in place are the preferred partners for borrowers’ additional (or even first) links, as this lowers the additional costs. Borrowers’ numbers of links are also slightly more uneven, but the effect is much less pronounced than on the lenders’ side (or in the toy example where alternatives were very limited). The additional lenders tend to be large ones with many outlinks. Note that very strong decay might soften that effect somewhat: when $\gamma _A$ is (very) low and the number of links is high already, the marginal costs will be virtually negligible, as will be the marginal decrease in the absolute (dollar) values. Hence, the second most connected lender is effectively as favorable as the lender with the highest degree, and lenders with slightly lower assets also can gain core status. This is underlined by two additional statistics: comparing the active links and the rank (with respect to size) of the lender and borrower involved, it is generally true that larger lenders cooperate with smaller borrowers and vice versa. The larger the decay in marginal costs, the more obvious this pattern becomes, and the negative rank correlations become substantially more pronounced; see panel 1(e). At the same time, more banks can be considered core (Panel 1(f)).

When costs are entirely incurred by borrowers, $\alpha =0$, then sides are swapped, and they encounter all the effects just seen for lenders, and vice versa.

Fig. 2

Aggregate results for 100 markets consisting of $N=100$ banks each with log-normally distributed assets and liabilities when both lenders and borrowers contribute to the network costs ($\alpha =0.5$)

Fig. 3

Adjacency matrices and network structures for one of the artificial markets under different cost regimes

When both sides contribute to the network costs, with $\alpha = 0.5$, and fixed-costs for a lender’s and a borrower’s first link on either side are $\alpha c = (1-\alpha )c = \frac{1}{2} c$, respectively, effects are combined, largely influenced by the respective decay factors. Figure 2 summarizes the main results, which confirm what already observed in Fig. 1. In fact, from subplots (a) and (b) we notice that as expected, when $\gamma _A$ (x-axis) and $\gamma _L$ (y-axis) increase and tend to 1, the average overall costs increase, while the average network density decreases as banks pay a higher price than for smaller $\gamma$ values for establishing additional links and therefore only few large banks can afford it. This is also confirmed by looking at subplot (g), which shows that the larger the values for $\gamma _A$ and $\gamma _L$ , the smaller the core sizes as fewer banks have many links. The smaller the $\gamma _A$ and $\gamma _L$ are, the stronger and the more negative the Pearson symmetry (subplot (h)) as larger lenders will cooperate with smaller borrower. Subplots (c) and (d) report the normalized Herfindahl index of lenders’ and borrowers’ degrees, respectively and subplot (e) and (f) are almost mirror image as they report the borrowers’ and lenders’ depth. Notice that the highest lenders’ depth (subplot e) is for low values of $\gamma _L$ and values of $\gamma _A$ between 0.5 and 0.9, when the borrowers bear very similar costs to add additional links while there is still only a small number of large lenders, highly concentrated (see subplot (c)) as costs are decreasing at a lower rate. The larger the $\gamma _L$, the smaller the depth for lenders as it becomes more expensive for lenders to establish more links. The mirror analysis applies then also for subplot (d) and (f) as for values of $\gamma _L$ between 0.6 and 0.9 and $\gamma _A$ smaller than 0.5, we have largest depth for borrowers (subplot (f)) as well the highest concentration (see subplot (d)), as few borrowers have an incentive to establish links. As $\gamma _A$ increases, the marginal costs for lenders increases and it is more difficult for borrowers to find partners.

Figure 3 provides the adjacency matrices and network structures for one of the sample markets. Lenders are along the vertical axis (sorted by size; largest on top), borrowers along the horizontal axis (also sorted by size, largest on the left). A dot indicates an existing link ($z_{ij}>0$, ${\mathbbm {1}}_{ij}=1$). The top left network is for the minimum density case; top right and bottom left are for the case where costs decay with a factor of $\gamma _A=\gamma _L=0.7$ and are incurred by lenders ($\alpha =1$) and borrowers ($\alpha =0$) only, respectively; bottom right is the case where both incur costs ($\alpha =0.5$). A core-periphery structure emerges in particular in the last of these cases: large banks (low indices) tend to be highly linked, while small banks have few links, which are mostly to large banks.

5 Conclusion

This paper contributes to the existing literature in two ways, a novel model to network creation and an optimization algorithm. The proposed model introduces decreasing costs of link formation for additional links in order to construct banking networks with realistic characteristics. We argue that establishing a link between a borrower and a lender is costly, yet with decreasing costs: banks face a learning curve which might depend on information costs, risk management processes and creditworthiness checks, and the process for setting up an additional link is cheaper than establishing the first link. This makes large banks attractive partners: A single large lender has sufficient assets to be the sole partner for many small borrowers, and a single large borrower can provide assets for many small lenders. In either case, the decreasing costs on one side is beneficial for the overall costs. The larger partner therefore is well-linked and benefits from scale economies. The model is stated as an optimization problem for the social planner, not as a result of equilibrium game theoretic behavior of individual banks. The problem is both numerically and theoretically challenging and beyond the scope of this paper. To approach the optimization problem for the social planner, we introduce a new algorithm, the Permuted North-West-Corner-Rule, pNWCR.

The proposed model rests on strong assumptions, most notably that there are no other benefits or costs that drive network formation apart from fixed costs when establishing links, and that the network is static and ignores dynamic changes and adaptions. Nonetheless, numerical experiments for artificial markets show that the resulting networks exhibit some typical stylized facts observed in real-world banking networks: they are quite, but not too, sparse with densities similar to those observed in real-world networks. A core-periphery structure emerges where a few (large) banks constitute the core and are connected to many other banks, while (small) periphery banks have very few links, which are mostly to core banks. The model is flexible enough to consider different rates of cost decrease for borrowers or lenders and also an allocation of costs only to the borrowers or to the lenders or both. Our algorithm has many potential applications that can be extended to agent-based modeling and empirical structural estimation. The fact that our focus has been on a cost structure facing the system assists in this extension, with some important caveats.

First, the cost structure is aggregated so that it is unclear whether the algorithm can be used to solve problems where the banks or agents are individually optimizing over their cost structure. Work needs to be done on our model where the social planner’s problem is related to that of the equilibrium achieved by the optimizing behavior of the separate agents. Second, while the costs of a link are important, they are not the only costs associated with financial networks. Beside costs, banks might want to take into account solvency and liquidity constraints as well the the credit worthiness of its counterparty (see e.g., Hałaj and Kok (2015)). Future research will extend our model and algorithm to incorporate aspects such as diversification, explicit limits on contract sizes (e.g., to reflect regulatory requirements), different interest rates, and possibly even the spatial dimension (see, e.g., Bradde et al. (2010)). Third, the current model is static and provides no information on the possible existence of credit relationships lasting over different consecutive time periods, which might play a relevant role in defining the network structure. High on the agenda is to incorporate dynamic aspects, such as multiperiod network formation and adaptation. Finally, so far our empirical investigation is based on simulated data, which we benchmark to stylized facts regarding interbank networks reported in the literature. Having access to a real-world dataset is a priority, as it could provide further insights both on formation as well as the evolution of networks through time.

Appendices

A Multiple global optima

Both under the minimum density model and the model with decreasing costs of link formation, solutions are not unique. Typically, there exist several or even many solutions all of which exhibit the same (globally optimal) network costs and distribution of lenders’ and borrowers’ degree, yet have different adjacency matrices. Building on the small illustrative example in Sect. 4.1, Table 2 illustrates this for the minimum density model, and Table 3 for the minimum cost model under decreasing costs of link formation for additional links as proposed in this paper. It is important to note that descriptive statistics for the network structure (and adjacency matrix) can therefore vary.

Table 2 Some of the globally optimal solutions, alternative to the solution reported in Table 1b, under minimum density for the illustrative example in Sect. 4.1 with $[A_i] = [50, 15, 12, 11, 8, 4]$ and $[L_j] =[51,14,13,10,9,3]$; more exist. All have a degree of 9, i.e., a density of $\frac{9}{36} = 25\%$

Table 3 Some of the globally optimal solutions under decreasing fixed-costs with $\gamma _A=0.7$ and $\alpha =1$, alternative to the solution reported in Table 1(c), for the illustrative example in Sect. 4.1; more exist. In all of these cases, the first lender has 6 links, all other lenders just 1, amounting to overall network costs of 7.94

B The search and optimization algorithms

C Results for related models

Table 4 summarizes key statistics for alternative methods for network construction for the artificial markets used in the main study of this paper, and with 1000 runs per market to lower Monte Carlo noise in methods with stochastic components.

Table 4 Statistics for alternative network-creation models, averaged over the 100 artificial markets and 1000 runs per market. normHerf is the normalized Herfindahl index of banks’ degrees;

Column “random NWCR” (column 2) uses the pNWCR allocation algorithm, but with random sequences of asset and liability banks. The resulting networks can be considered typical starting solutions for the proposed search algorithm, yet without (or prior to) optimizing for costs.

Column “ME” (column 3) refers to the Maximum Entropy method by Upper and Worms (2004) as presented in Sect. 2.1.

Columns 4-6 refer to approaches inspired by Hałaj and Kok (2013) along with this model’s presentation in Anand et al. (2018): Starting with an empty network, random pairs (i, j) of asset and liability banks are picked and their exposure is increased by $\lceil \varDelta x_{ij}\rceil$ until all assets and liabilities are allocated. More specifically,

$$\begin{aligned} x_{ij}^{(t)} = x_{ij}^{(t-1)} + \left\lceil \varDelta x_{ij}^{(t)}\right\rceil , \quad A_i^{(t)} = A_i^{(t-1)} - \left\lceil \varDelta x_{ij}^{(t)}\right\rceil , \quad L_j^{(t)} = L_j^{(t-1)} - \left\lceil \varDelta x_{ij}^{(t)}\right\rceil \end{aligned}$$

where

$$\begin{aligned} \varDelta x_{ij}^{(t)} = {\left\{ \begin{array}{ll} u^{(t)} \cdot \min \{A_i^{(t-1)}, L_j^{(t-1)}\} &{} \text {HK1}\\ \min \left\{ A_i^{(t-1)}, L_j^{(t-1)}, ~u^{(t)} \cdot \min \{A_i, L_j\}\right\} &{} \text {HK2}\\ \min \{A_i^{(t-1)}, L_j^{(t-1)}\} &{} \text {HK3} \end{array}\right. } \end{aligned}$$

$A_i$, $L_j$ are the banks’ total assets and liabilities; $A_i^{(t)}$, $L_j^{(t)}$ the yet-unmatched remainders after t iterations; $u^{(t)}$ a uniform random value between zero and one; and initial values $A_i^{(0)}=A_i$, $L_j^{(0)}=L_j$, and $x_{ij}^{(0)} = 0$; the ceiling operator $\lceil \cdot \rceil$ rounds up to the nearest integer. HK1 therefore takes a fraction of the yet-unmatched quantities (rounding up ensures that all quantities are ultimately assigned); HK2 of the total quantities; and HK3 as much of the yet-unmatched quantity as possible. On average, ME, HK1 and HK2 converge to networks with a larger number of links as well as higher cost, density and core size than random NWCR, while achieving lower Herfindal and depth, and positive symmetry. Instead, by construction, HK3 is closest to the (unoptimized) NWCR, “random NWCR”, in terms of number of links, cost, density lending and borrowing depth and core size. Note also, that despite reaching a much smaller value of Pearson symmetry (i.e. $-0.029$), it is the only model, except random NWCR, with a negative value. Still, the Herfindal diversification for assets and liabilities tend to be smaller than in random NWCR.