1 Introduction

The von Neumann–Morgenstern expected utility theory (see, von Neumann and Morgenstern (1944)) is often used to find the optimal portfolio weights. These weights represent the optimal fractions of wealth allocated to individual assets and lead to the maximum expected utility of future wealth. The future wealth or portfolio return is random implying that the expected utility depends on the parameters of the distribution used to model the data generating process of the underlying assets. An issue, which has to be addressed by the investor, is the choice of the functional form of the utility function. Typically, the analysis is constrained to the quadratic or exponential utilities [c.f., Tobin (1958), Bodnar et al. (2015)], which allow for explicit solutions of the portfolio problem. Other functions, like the power utility, require numerical techniques. Usually, most of the utility functions depend on an additional parameter referred to as a risk aversion coefficient. This parameter quantifies the investor’s attitude towards risk. Its choice is subjective and can be hardly justified by economic reasoning. In this paper, we argue that the risk aversion coefficient can be linked to the distribution used as a model for the data generating process and to the level of the value-at-risk (VaR) in which the investor is interested in or is required to report.

The quadratic utility function is commonly applied in portfolio theory because of its nice mathematical properties. First, an analytic solution is easy to obtain for the quadratic utility function. Second, Tobin (1958) showed that the Bernoulli principle is satisfied for the mean-variance solution only if one of the following two conditions is valid: the asset returns are normally distributed or the utility function is quadratic. Moreover, the quadratic utility presents a good approximation of other utility functions [see, e.g., Kroll et al. (1984), Brandt and Santa-Clara (2006), Levy and Levy (2014), Markowitz (2014)]. Levy and Markowitz (1979) considered the expected utility function in terms of the portfolio return and showed that it can be well approximated by a function of the mean and the variance of the portfolio return. For a portfolio with the weights \(\mathbf {w}=(w_1,\ldots ,w_k)^\prime \) such that \(\mathbf {w}^\prime \mathbf {1}=1\) where \(\mathbf {1}\) denotes the k-dimensional vector of ones, the quadratic utility is given by

$$\begin{aligned} U_{quad}(R_{\mathbf {w}})=R_{\mathbf {w}}-\frac{\gamma _{quad}}{2}R^2_{\mathbf {w}}=\mathbf {X}^\prime \mathbf {w}-\frac{\gamma _{quad}}{2}(\mathbf {X}^\prime \mathbf {w})^2, \end{aligned}$$
(1)

where \(\mathbf {X}=(X_{1},\ldots ,X_{k})^\prime \) is the k-dimensional vector of asset returns and \(R_{\mathbf {w}}\) denotes the return of the portfolio with the weights \(\mathbf {w}\). The symbol \(\gamma _{quad}>0\) stands for the risk aversion coefficient.

The second utility function considered in the paper is the exponential utility given by

$$\begin{aligned} U_{exp}(R_{\mathbf {w}})=1-e^{-\gamma _{exp}R_{\mathbf {w}}}, \end{aligned}$$
(2)

where \(\gamma _{exp}>0\) is the corresponding risk aversion coefficient. If the asset returns are multivariate normally distributed then the maximization of \(E(U_{exp}(R_{\mathbf {w}}))\) is equivalent to the so-called mean-variance utility function expressed as [cf. Ingersoll (1987), Okhrin and Schmid (2006, 2008)]

$$\begin{aligned} \varvec{\mu }^\prime \mathbf {w}-\frac{\gamma _{mv}}{2} \mathbf {w}^\prime \varvec{\Sigma }\mathbf {w}\longrightarrow \max ~~ \text {w.r.t.}~~\mathbf {w},\quad \text {subject to}\quad \mathbf {w}^\prime \mathbf {1}=1, \end{aligned}$$
(3)

where \(\varvec{\mu }=E(\mathbf {X})\) and \(\varvec{\Sigma }=Var(\mathbf {X})\). Bodnar et al. (2013) compared the solutions resulting from maximizing \(E(U_{quad}(R_{\mathbf {w}}))\), \(E(U_{exp}(R_{\mathbf {w}}))\), and (3) and found that although they are mathematically equivalent, their stochastic properties appear to be different.

Note that the choice of the values for both \(\gamma _{quad}\) and \(\gamma _{exp}\) in practice is unclear. There are a few papers dealing with the estimation of the risk aversion coefficient from market data. For instance, Jackwerth (2000) derives the implied absolute risk aversion coefficient by estimating the risk-neutral and historical probabilities from option prices, while estimators relying on the realized volatility were suggested by Bollerslev et al. (2011). It is important to note, that the corresponding risk aversions characterize an aggregate and not an individual investor. The usual values of \(\gamma \)’s considered in empirical applications lie between 1 and 50 (for the quadratic utility) and the choice of the risk aversion coefficient is, usually, performed heuristically. In contrast, our approach is motivated by the financial interpretation of the solutions of the expected utility maximization problems based on the utilities (1) and (2).

The VaR-based regulation of the financial sector makes the VaR one of the central risk measures not only for funds but also for other investors [see, e.g., Bonaccolto et al. (2017)]. As a result the minimum-VaR portfolio of Alexander and Baptista (2002, 2004) became an appealing alternative to the classical mean-variance portfolio selection strategies. This is additionally supported by the good out-of-sample performance of these portfolios as documented by Alexander et al. (2009) and Durand et al. (2011). The authors show that using VaR as an additional constraint within a mean-variance portfolio strategy clearly reduce the impact of estimation risk in the parameters of asset returns. Furthermore, the resulting portfolios are more efficient compared to the portfolios without this constraint.

The idea of linking the risk aversion coefficient to the VaR level is not new and was recently popularized in Das et al. (2010) and Alexander and Baptista (2011). Generally it appears that the attitude towards risk can be easier specified by using the confidence level of VaR than by fixing abstract risk aversion coefficients. Das et al. (2010) impose a VaR constraint on the portfolio return and determine the implied risk aversion coefficient which leads to the targeted VaR of the portfolio. Alexander and Baptista (2011) derived an explicit expression for the implied risk aversion coefficient as a function of the VaR confidence level. This framework allows to incorporate the mental accounts and objectives of investors. Note that in both papers the authors assume Gaussian asset returns and the quadratic utility function.

In this paper, we extend the above mentioned paper by considering two different utility functions and elliptically distributed asset returns. More precisely we link the optimal portfolio obtained from a particular utility function to the minimum VaR optimal portfolio. The latter portfolio is determined by the significance level \(\alpha \), which can be fixed relying on the regulatory recommendations. This allows us to derive analytic expressions for \(\gamma _{quad}(.)\) and \(\gamma _{exp}(.)\) as functions of the VaR level. Thus, we quantify the investor’s attitude towards risk for different utilities and under different and more realistic distributional assumptions. The results of the empirical study justify the values of the risk aversion coefficients which are usually used in practice.

The rest of the paper is organized as follows. In Sect. 2, we present the main results of the paper. Here, the analytical expressions for \(\gamma _{quad}\) and \(\gamma _{exp}\) are presented under the assumption that the asset returns are multivariate normally distributed. In Sect. 3, these findings are extended to non-normal distributions. The influence of the parameter uncertainty is analyzed in Sect. 4, while the results of the empirical study are shown in Sect. 5. Concluding remarks are presented in Sect. 6. The “Appendix” contains the proofs of theoretical results.

2 Risk aversion for Gaussian returns

The results of this section are derived assuming that the asset returns are multivariate normally distributed, i.e. \(\mathbf {X}\sim \mathcal {N}_k(\varvec{\mu },\varvec{\Sigma })\), whereas the findings under a more general class of distributions are presented in the next section.

We consider two investors who aim to maximize the expected quadratic utility function given by

$$\begin{aligned} E(U_{quad}(R_{\mathbf {w}})) \rightarrow \; \max \quad \text { w.r.t. }\mathbf {w}, \text { subject to} \quad \mathbf {w}^\prime \mathbf {1}=1 \end{aligned}$$
(4)

and the expected exponential utility function expressed as

$$\begin{aligned} E(U_{exp}(R_{\mathbf {w}})) \rightarrow \; \max \quad \text { w.r.t. }\mathbf {w}, \text { subject to} \quad \mathbf {w}^\prime \mathbf {1}=1, \end{aligned}$$
(5)

respectively.

Merton (1969) proved that if the asset returns are multivariate normally distributed then the maximization of the expected exponential utility function is equivalent to the maximization of the mean-variance utility (3). The solution of (3) coincides with the Markowitz efficient frontier which is a parabola in the mean-variance space (Merton 1972) uniquely determined by the three parameters [cf. Bodnar and Schmid (2008b, 2009)), Font (2016)]

$$\begin{aligned}&R_{\textit{GMV}}=\frac{\mathbf {1}^\prime \varvec{\Sigma }^{-1} \varvec{\mu }}{\mathbf {1}^\prime \varvec{\Sigma }^{-1} \mathbf {1}},\quad V_{\textit{GMV}}=\frac{1}{\mathbf {1}^\prime \varvec{\Sigma }^{-1} \mathbf {1}}, \quad \text {and} \nonumber \\&s=\varvec{\mu }^\prime \mathbf {R}\varvec{\mu }~~ \text {with}~~\mathbf {R}=\varvec{\Sigma }^{-1}-\frac{\varvec{\Sigma }^{-1}\mathbf {1}\mathbf {1}^\prime \varvec{\Sigma }^{-1}}{\mathbf {1}^\prime \varvec{\Sigma }^{-1}\mathbf {1}}. \end{aligned}$$
(6)

The quantities \(R_{\textit{GMV}}\) and \(V_{\textit{GMV}}\) are the expected return and the variance of the global minimum variance (GMV) portfolio [cf., Bodnar et al. (2017)] that determine the location of the parabola’s vertex in the mean-variance space, while s is the slope parameter of the parabola.

The maximization of the exponential utility function, i.e. (5), leads to the optimal portfolio with the weights

$$\begin{aligned} \mathbf {w}_{EU}=\frac{\varvec{\Sigma }^{-1}\mathbf {1}}{\mathbf {1}^\prime \varvec{\Sigma }^{-1}\mathbf {1}}+\gamma _{exp}^{-1}\mathbf {R}\varvec{\mu }. \end{aligned}$$
(7)

Similarly, the solution of (4) is given by

$$\begin{aligned} \mathbf {w}_{QU}=\frac{\mathbf {A}^{-1}\mathbf {1}}{\mathbf {1}^\prime \mathbf {A}^{-1}\mathbf {1}}+\gamma _{quad}^{-1}\mathbf {R}_{\mathbf {A}} \varvec{\mu }, \end{aligned}$$
(8)

where \(\mathbf {A}=E(\mathbf {X}\mathbf {X}^\prime )\) and \(\mathbf {R}_{\mathbf {A}}=\mathbf {A}^{-1}-\frac{\mathbf {A}^{-1}\mathbf {1}\mathbf {1}^\prime \mathbf {A}^{-1}}{\mathbf {1}^\prime \mathbf {A}^{-1}\mathbf {1}}\). Bodnar et al. (2012) derived another expression for the weights of the optimal portfolio in the sense of maximizing the expected quadratic utility function expressed as

$$\begin{aligned} \mathbf {w}_{QU}=\frac{\varvec{\Sigma }^{-1}\mathbf {1}}{\mathbf {1}^\prime \varvec{\Sigma }^{-1}\mathbf {1}}+\tilde{\gamma }_{quad}^{-1}\mathbf {R}\varvec{\mu }, \end{aligned}$$
(9)

with [see, Bodnar et al. (2012, Theorem 1)]

$$\begin{aligned} \tilde{\gamma }_{quad}=\frac{1+s}{\gamma _{quad}^{-1}-1-R_{\textit{GMV}}} \end{aligned}$$
(10)

In the next step we use another way of constructing an optimal portfolio on the efficient frontier which characterizes the investor’s attitude towards risk in a more natural way. A suitable candidate is the minimum VaR portfolio suggested by Alexander and Baptista (2002, 2004). The VaR at the confidence level \(\alpha \in (0.5,1)\) (\({\textit{VaR}}_\alpha \)) is defined as a portfolio loss satisfying

$$\begin{aligned} P\{\mathbf {X}^\prime \mathbf {w}<-\textit{VaR}_\alpha \}=1-\alpha . \end{aligned}$$

If \(\mathbf {X}\) is multivariate normally distributed then \(\textit{VaR}_\alpha \) is calculated implicitly and it is given by

$$\begin{aligned} \textit{VaR}_\alpha =-\mathbf {w}^\prime \varvec{\mu }-z_{1-\alpha } \sqrt{\mathbf {w}^\prime \varvec{\Sigma }\mathbf {w}}, \end{aligned}$$

where \(z_{\beta }=\Phi ^{-1}(\beta )\) is the \(\beta \)-quantile of the standard normal distribution. In practice, the values of \(\alpha \) are usually taken from the interval [0.95, 1). The VaR is a standard method of risk monitoring suggested by the Basel Committee on Banking Supervision. Alexander and Baptista (2002) went beyond taking of VaR for monitoring purposes, but use the VaR as a risk proxy in portfolio management. The optimization problem is given by

$$\begin{aligned} \textit{VaR}_{\alpha }=-\mathbf {w}^\prime \varvec{\mu }-z_{1-\alpha } \sqrt{\mathbf {w}^\prime \varvec{\Sigma }\mathbf {w}} \rightarrow \min \quad \text { w.r.t. }\mathbf {w}, \text { subject to } \mathbf {1}^{\prime }\mathbf {w}=1. \end{aligned}$$
(11)

Alexander and Baptista (2002) proved that the solution of (11) lies on the efficient frontier and presented the expression for the weights of this portfolio. Additionally to a very concise and intuitive mathematical formulation of the problem, the minimum-VaR portfolios show a good out-of-sample performance as noted by Alexander et al. (2009) and Durand et al. (2011). The portfolios diminish the damaging impact of estimation risk and appear to be more efficient than the classical benchmarks.

Bodnar et al. (2012) restated the formula for the weights of the minimum VaR portfolio using the structure of (7):

$$\begin{aligned} \mathbf {w}_{\textit{VaR};\alpha }=\mathbf {w}_{\textit{GMV}}+\frac{\sqrt{V_{\textit{GMV}}}}{\sqrt{z_{1-\alpha }^2-s}}\mathbf {R}\varvec{\mu }. \end{aligned}$$
(12)

The last expression implies that the VaR confidence level should be sufficiently high to guarantee that \(z_{1-\alpha }^2> s\) as was also originally identified in Alexander and Baptista (2002).

The above results can be summarized as follows:

  • It is important to note that all three solutions of the maximization problems in (4), (5) and (11) [cf. Bodnar et al. (2012)] lie on the Markowitz efficient frontier.

  • Equations (7), (9) and (12) show that all optimal portfolios have the same structure. Moreover, from (10) we conclude that the maximization of the expected quadratic utility function with the risk aversion coefficient \(\gamma _{quad}\) leads to the same portfolio as the maximization of the expected exponential utility function with the risk aversion coefficient \(\gamma _{exp}=\tilde{\gamma }_{quad}\) where the latter is given in (10).

The risk aversion coefficients \(\gamma _{quad}\), \(\gamma _{exp}\) and the \(\alpha \) value of VaR are related as obviously follows from (7), (9) and (12). Previously this idea was already exploited in Alexander and Baptista (2011) and Das et al. (2010) for Gaussian returns and quadratic utility function. From financial perspective the linkage is reasonable too, since investors can assess their attitude to risk using the confidence level of VaR in a more precise way, than by relying on an abstract risk aversion coefficient. This is additionally justified by the popularity of the VaR as a risk measure in the current regulatory laws.

The explicit relation depends on the parameters of the efficient frontier, \(R_{\textit{GMV}}\), s and \(V_{\textit{GMV}}\) only. Using (12) we are able to specify the closed-form expressions for risk aversion coefficients \(\gamma _{quad}\) and \(\gamma _{exp}\) used in (1) and (2), respectively, such that the corresponding portfolios coincide with the minimum VaR portfolio. Our results are summarized in the following theorem.

Theorem 1

Let \(\mathbf {X}\sim \mathcal {N}_k(\varvec{\mu },\varvec{\Sigma })\) and \(z_{1-\alpha }^2>s\). Then the implied risk aversion coefficients for the exponential and quadratic utility functions can be given in terms of the characteristics of the mean-variance efficient frontier and the confidence level of the VaR as follows:

$$\begin{aligned} \gamma _{exp}= & {} \frac{\sqrt{z_{1-\alpha }^2-s}}{\sqrt{V_{\textit{GMV}}}}, \end{aligned}$$
(13)
$$\begin{aligned} \gamma _{quad}= & {} \left( 1+R_{\textit{GMV}}+\frac{1+s}{\gamma _{exp}}\right) ^{-1}= \left( 1+R_{\textit{GMV}}+\frac{(1+s)\sqrt{V_{\textit{GMV}}}}{\sqrt{z_{1-\alpha }^2-s}}\right) ^{-1}. \end{aligned}$$
(14)

The proof of Theorem 1 follows directly from the expressions for the weights given in (7), (9), and (12). Note that the expression in (14) coincides with equation (34) of Alexander and Baptista (2011), if the boundary for the portfolio return is appropriately selected. A semi-analytic expression for the implied risk aversion can also be found in Das et al. (2010) within a slightly different setup. For a given level of \(\alpha \) the investor attempts to minimize the most negative \(\alpha \dot{1}00\%\) of losses. Thus, \(\alpha \) reflects the risk attitude of the investor. If \(\alpha \) is large, then (s)he minimizes the extreme losses and, hence, the investor is very risk averse. If \(\alpha \) is small, then the investor cares about losses in general without paying particular attention to large losses. This implies that his risk aversion is moderate. In general it holds that both risk aversions are monotonously increasing in \(\alpha \).

At first sight, the dependence of the risk aversion on the characteristics of the efficient frontier appears to be surprising. However, this evidence is natural since the investor is averse to a particular amount of loss or of risk, implying non-constant \(\gamma \)’s. For a very risky portfolio the investor is more risk averse, than for a portfolio with a moderate risk. Moreover, the maximization of the expected quadratic utility function as well as of the expected exponential utility function leads to the portfolios which lie on the efficient frontier. As a result, the investor’s attitude towards risk depends on the position of the efficient frontier in the mean-variance space, which is fully determined by three parameters: \(R_{\textit{GMV}}\), \(V_{\textit{GMV}}\), and s.

3 Determination of the risk aversion coefficients for elliptically contoured distributed asset returns

We now extend the results of Sect. 2 to elliptically contoured (EC) distributions. This is a large class of multivariate distributions which includes the multivariate normal, Laplace and t distributions as special cases. This class has been already widely discussed in financial literature. For instance, Owen and Rabinovitch (1983) extended Tobin’s separation theorem, Bawa’s rules of ordering certain prospects to EC distributions. While Chamberlain (1983) showed that elliptical distributions imply the mean-variance utility functions, Berk (1997) argued that one of the necessary conditions for the validity of the capital asset pricing model (CAPM) is an elliptical distribution for the asset returns. Furthermore, Zhou (1993) extended findings of Gibbons et al. (1989) by applying their test to EC distributed returns. A further test for the CAPM under elliptical assumptions was proposed by Hodgson et al. (2002). The application of matrix variate elliptically contoured distributions in portfolio theory was initiated by Bodnar and Schmid (2008a) and Bodnar and Gupta (2009).

In this section, we restrict the discussion to the class of EC distributions for which the density function exists. The vector of asset returns \(\mathbf {X}\) is said to be elliptically contoured distributed if its density function is given by

$$\begin{aligned} f_{\mathbf {X}}(\mathbf {x})=c_k g((\mathbf {x}-\varvec{\mu })^\prime \mathbf {D}^{-1}(\mathbf {x}-\varvec{\mu })), \end{aligned}$$
(15)

where \(c_k>0\) is a constant which depends on the specific type of elliptically contoured distribution, i.e. on the function g(.) and the dimension of the vector \(\mathbf {X}\) only. Hereafter we use the shorthand notation \(\mathbf {X}\sim E_k(\varvec{\mu },\mathbf {D},g)\). The symbol \(\varvec{\mu }\) is the location vector, while \(\mathbf {D}\) denotes the dispersion matrix. If the second moment of \(\mathbf {X}\) exists then

$$\begin{aligned} \varvec{\mu }=E(\mathbf {X}) \quad \text {and} \quad \varvec{\Sigma }=Cov(\mathbf {X})=\omega \mathbf {D}, \end{aligned}$$

i.e. \(\varvec{\mu }\) is the mean vector and the covariance matrix is proportional to \(\mathbf {D}\) with \(\omega =E(r^2)\) (see 16). The stochastic representation of the random vector \(\mathbf {X}\) is a convenient tool for simulation purposes. If the density function exists for all \(k \ge 1\) then the stochastic representation of \(\mathbf {X}\) is given by [cf. Fang and Zhang (1990)]

$$\begin{aligned} \mathbf {X}{\mathop {=}\limits ^{d}}\varvec{\mu }+ r \mathbf {D}^{1/2} \mathbf {Z}, \end{aligned}$$
(16)

where \(\mathbf {Z}\sim \mathcal {N}_k(\mathbf {0}_k,\mathbf {I}_k)\) is independent of the scalar nonnegative random variable r. The symbol \(\mathbf {0}_k\) denotes the k-dimensional zero vector, while \(\mathbf {I}_k\) stands for the identity matrix of order k. Moreover, from (16) it holds that r fully determines the type of elliptical contoured distribution.

Using (16) we can calculate the expected quadratic utility and the expected exponential utility under the assumption that the asset returns follow an EC distribution. For the quadratic utility function it holds that

$$\begin{aligned} E(U_{quad}(R_{\mathbf {w}}))= & {} E(\mathbf {X})^\prime \mathbf {w}-\frac{\gamma _{quad}}{2}E\left( (\mathbf {X}^\prime \mathbf {w})^2\right) \nonumber \\= & {} \varvec{\mu }^\prime \mathbf {w}-\frac{\gamma _{quad}}{2}\mathbf {w}^\prime \mathbf {A}\mathbf {w}. \end{aligned}$$
(17)

Consequently, the optimization problem based on (17) subject to \(\mathbf {1}^\prime \mathbf {w}=1\) is the same as the one in the case of the multivariate normally distributed asset returns. As a result, its solution is given by (9).

Similarly, using that \(R_{\mathbf {w}}|r \sim N(\varvec{\mu }^\prime \mathbf {w},r^2 \mathbf {w}^\prime \mathbf {D}\mathbf {w})\) for the exponential utility function we get

$$\begin{aligned} E(U_{exp}(R_{\mathbf {w}}))= & {} 1-E\left( e^{-\gamma _{exp}R_{\mathbf {w}}}\right) \nonumber \\= & {} 1-E\left( E\left( e^{-\gamma _{exp}R_{\mathbf {w}}}|r\right) \right) \nonumber \\= & {} 1-E\left( e^{-\gamma _{exp}\varvec{\mu }^\prime \mathbf {w}+ \frac{\gamma _{exp}^2 \mathbf {w}^\prime \mathbf {D}\mathbf {w}}{2}r^2}\right) , \end{aligned}$$

where the last identity is obtained observing that the conditional expectation is the moment generating function of the univariate normal distribution at point \(-\gamma _{exp}\). Hence,

$$\begin{aligned} E(U_{exp}(R_{\mathbf {w}}))= & {} 1-e^{-\gamma _{exp}\varvec{\mu }^\prime \mathbf {w}}E\left( e^{\frac{\gamma _{exp}^2 \mathbf {w}^\prime \mathbf {D}\mathbf {w}}{2}r^2}\right) \nonumber \\= & {} 1-e^{-\gamma _{exp}\varvec{\mu }^\prime \mathbf {w}}m_{r^2}\left( \frac{\gamma _{exp}^2 \mathbf {w}^\prime \mathbf {D}\mathbf {w}}{2}\right) \nonumber \\= & {} 1-e^{-\gamma _{exp}\varvec{\mu }^\prime \mathbf {w}}m_{r^2}\left( \frac{\gamma _{exp}^2 \mathbf {w}^\prime \varvec{\Sigma }\mathbf {w}}{2E(r^2)}\right) , \end{aligned}$$
(18)

where \(m_{r^2}(t)=E\left( e^{t r^2}\right) \) is the moment generating function of \(r^2\). As a result, the maximization of the expected exponential utility function is equivalent to

$$\begin{aligned} \varvec{\mu }^\prime \mathbf {w}-\frac{1}{\gamma _{exp}}\log \left( m_{r^2}\left( \frac{\gamma _{exp}^2 \mathbf {w}^\prime \varvec{\Sigma }\mathbf {w}}{2E(r^2)}\right) \right) \rightarrow \, \max \quad \text { w.r.t. }\mathbf {w}, \text { subject to} \quad \mathbf {1}^\prime \mathbf {w}=1. \end{aligned}$$
(19)

Lemma 1

Let \(\mathbf {X}\sim E_k(\varvec{\mu },\mathbf {D},g)\) with the moment generating function of \(r^2\) given by \(m_{r^2}(.)\). Then the solution of the optimization problem (19) is given by

$$\begin{aligned} \mathbf {w}_{EU}=\frac{\varvec{\Sigma }^{-1}\mathbf {1}}{\mathbf {1}^\prime \varvec{\Sigma }^{-1}\mathbf {1}}+\tilde{\gamma }_{exp}^{-1}\mathbf {R}\varvec{\mu }, \end{aligned}$$
(20)

where \(\tilde{\gamma }_{exp}\) is the solution with respect to \(\kappa \) of

$$\begin{aligned} \kappa \psi ^\prime \left( \frac{\gamma _{exp}^2 (V_{\textit{GMV}}+\kappa ^2 s)}{2E(r^2)}\right) =\frac{E(r^2)}{\gamma _{exp}} \end{aligned}$$
(21)

with \(\psi (x)=\log \left( m_{r^2}(x)\right) \).

The results of Lemma 1 are appealing from a practical perspective. Although the maximization of the expected exponential utility function results in a challenging non-linear multivariate optimization problem, it can be simplified to an univariate one, for which the solution is determined by solving (21) with respect to \(\kappa \). This result continues to be true independently how large is the dimension of the constructed portfolio. Finally, we note that if the asset returns are multivariate normally distributed then \(r=1\) and, consequently, \(E(r^2)=1\), \(m_{r^2}(x)=e^x\), and \(\psi ^\prime (x)=1\). It follows from (21) that \(\kappa =\gamma _{exp}^{-1}\).

Next, we compare the solution of the maximization problems (4) and (5) under the assumption of elliptically distributed asset returns with the one obtained by minimizing the VaR at the confidence level \(\alpha \). In the case of elliptically contoured distribution, the VaR of the portfolio with weights \(\mathbf {w}\) is given by

$$\begin{aligned} \textit{VaR}_\alpha =-\mathbf {w}^\prime \varvec{\mu }-d_{1-\alpha } \sqrt{\mathbf {w}^\prime \mathbf {D}\mathbf {w}}=-\mathbf {w}^\prime \varvec{\mu }-\frac{d_{1-\alpha }}{\sqrt{E(r^2)}} \sqrt{\mathbf {w}^\prime \varvec{\Sigma }\mathbf {w}}, \end{aligned}$$

where \(d_{1-\alpha }\) depends on k and g(.) only and it is independent of \(\mathbf {w}\). Minimizing \(\textit{VaR}_\alpha \) with respect to \(\mathbf {w}\) leads to the following expression for the weights

$$\begin{aligned} \mathbf {w}_{\textit{VaR};\alpha }=\mathbf {w}_{\textit{GMV}}+\frac{\sqrt{V_{\textit{GMV}}}}{\sqrt{d_{1-\alpha }^2/E(r^2)-s}}\mathbf {R}\varvec{\mu }. \end{aligned}$$
(22)

Using (22) we are able to specify the closed-form expressions for the risk aversion coefficients \(\gamma _{quad}\) and \(\gamma _{exp}\). It holds that

Theorem 2

Let \(\mathbf {X}\sim E_k(\varvec{\mu },\mathbf {D},g)\) with the moment generating function of \(r^2\) given by \(m_{r^2}(.)\) and let \(d_{1-\alpha }^2/E(r^2)>s\). Then

$$\begin{aligned} \gamma _{quad}= & {} \left( 1+R_{\textit{GMV}}+\frac{(1+s)\sqrt{V_{\textit{GMV}}}}{\sqrt{d_{1-\alpha }^2/E(r^2)-s}}\right) ^{-1}. \end{aligned}$$

Additionally, \(\gamma _{exp}\) is the solution of

$$\begin{aligned} \gamma _{exp} \psi ^\prime \left( \frac{\gamma _{exp}^2 (V_{\textit{GMV}}+\kappa ^2 s)}{2E(r^2)}\right) = \frac{E(r^2)}{\kappa } , \end{aligned}$$

with \(\kappa =\frac{\sqrt{V_{\textit{GMV}}}}{\sqrt{d_{1-\alpha }^2/E(r^2)-s}}\).

The expression for the quadratic utility resembles the result under the Gaussian assumption, but for the exponential case the results appear to be more involved.

4 Estimation and inference procedure

In this section we deal with the problem of parameter uncertainty which has become a popular topic in finance recently [see, e.g., Kawas and Thiele (2017)]. The parameters of asset returns, i.e. \(\varvec{\mu }\) and \(\varvec{\Sigma }\), are unknown and have to be estimated from a sample. Replacing the population parameters with their sample counterparts in the above equations for the risk aversion coefficients we obtain their sample counterparts. In order to access the statistical properties of estimators we derive their stochastic representations.

Let \(\mathbf {X}_1,\ldots ,\mathbf {X}_n\) be a sample of asset returns used to estimate the parameters \(\varvec{\mu }\) and \(\varvec{\Sigma }\) by

$$\begin{aligned} \hat{\varvec{\mu }}=\frac{1}{n}\sum \limits _{j=1}^n\mathbf {X}_j\quad \text {and}\quad \hat{\varvec{\Sigma }}=\frac{1}{n-1}\sum \limits _{j=1}^n(\mathbf {X}_j-\hat{\varvec{\mu }})(\mathbf {X}_j-\hat{\varvec{\mu }})^\prime . \end{aligned}$$
(23)

Substituting \(\hat{\varvec{\mu }}\) and \(\hat{\varvec{\Sigma }}\) from (23) in (6), the estimators for the three parameters of the efficient frontier \(R_{\textit{GMV}}\), \(V_{\textit{GMV}}\), and s are obtained, namely,

$$\begin{aligned} \hat{R}_{\textit{GMV}}=\frac{\mathbf {1}^\prime \hat{\varvec{\Sigma }}^{-1}\hat{\varvec{\mu }}}{\mathbf {1}^\prime \hat{\varvec{\Sigma }}^{-1}\mathbf {1}},\quad \hat{V}_{\textit{GMV}}=\frac{1}{\mathbf {1}^\prime \hat{\varvec{\Sigma }}^{-1}\mathbf {1}},\quad \hat{s}=\hat{\varvec{\mu }}^\prime \hat{\mathbf {R}}\hat{\varvec{\mu }}\quad \text {with}\quad \hat{\mathbf {R}}=\hat{\varvec{\Sigma }}^{-1}-\frac{\hat{\varvec{\Sigma }}^{-1}\mathbf {1}\mathbf {1}^\prime \hat{\varvec{\Sigma }}^{-1}}{\mathbf {1}^\prime \hat{\varvec{\Sigma }}^{-1}\mathbf {1}}. \end{aligned}$$
(24)

Because \(\hat{\varvec{\mu }}\) and \(\hat{\varvec{\Sigma }}\) are random quantities, the estimated characteristics in (24) are random too. Assuming that the asset returns are iid and normal, Bodnar and Schmid (2008b, 2009) derived the exact distributions of \(\hat{R}_{\textit{GMV}}\), \(\hat{V}_{\textit{GMV}}\), and \(\hat{s}\). Let \(\phi (\cdot )\) be the density function of the standard normal distribution. By \(f_{\chi ^2_n}(\cdot )\) we denote the density of the \(\chi ^2\)-distribution with n degrees of freedom, while \(f_{F_{n_1,n_2,\lambda }}(\cdot )\) stands for the density of the non-central F-distribution with \(n_1\) and \(n_2\) degrees of freedom and the non-centrality parameter \(\lambda \). The symbol \(f_{N(\mu ,\sigma ^2)}(.)\) is used for the density function of the normal distribution with mean \(\mu \) and variance \(\sigma ^2\).

In the following lemma we summarize some results of Bodnar and Schmid (2008b, 2009). Particularly, we provide the exact joint and marginal distributions of \(\hat{R}_{\textit{GMV}}\), \(\hat{V}_{\textit{GMV}}\), and \(\hat{s}\).

Lemma 2

Let \(\mathbf {X}_1,\ldots ,\mathbf {X}_n\) be a random sample of independent vectors such that \(\mathbf {X}_i\sim \mathcal {N}_k(\varvec{\mu },\varvec{\Sigma })\) for \(i=1,\ldots ,n\) and \(n > k\). Let \(\varvec{\Sigma }\) be positive definite. Then it holds that

  1. (a)

    \(\hat{V}_{\textit{GMV}}\) is independent of \((\hat{R}_{\textit{GMV}},\hat{s})\).

  2. (b)

    \((n-1){\hat{V}_{\textit{GMV}}}/{V_{\textit{GMV}}} \sim \chi ^2_{n-k}\).

  3. (c)

    \(\frac{n(n-k+1)}{(n-1)(k-1)} \hat{s}\sim F_{k-1,n-k+1,n\,s}\).

  4. (d)

    \(\hat{R}_{\textit{GMV}}| \hat{s}=y \sim \mathcal {N}\left( R_{\textit{GMV}},\frac{1+\frac{n}{n-1}y}{n}V_{\textit{GMV}}\right) \).

  5. (e)

    The joint density function of \(\hat{R}_{\textit{GMV}}\), \(\hat{V}_{\textit{GMV}}\), and \(\hat{s}\) is given by

    $$\begin{aligned} f_{\hat{R}_{\textit{GMV}},\hat{V}_{\textit{GMV}},\hat{s}}(x,y,z)&=\frac{n(n-k+1)}{(k-1)V_{\textit{GMV}}} f_{\chi ^2_{n-k}}\left( \frac{n-1}{V_{\textit{GMV}}}z\right) \\&\times f_{N(R_{\textit{GMV}},\frac{1+\frac{n}{n-1}y}{n}V_{\textit{GMV}})}(x)\\&f_{F_{k-1,n-k+1,n\,s}}\left( \frac{n(n-k+1)}{(n-1)(k-1)}y\right) . \end{aligned}$$

The application of the closed-form expressions for the risk aversion coefficients derived in Theorem 1 leads to the following estimators of these quantities given by

$$\begin{aligned} \hat{\gamma }_{exp}= & {} \frac{\sqrt{z_{1-\alpha }^2-\hat{s}}}{\sqrt{\hat{V}_{\textit{GMV}}}}, \end{aligned}$$
(25)
$$\begin{aligned} \hat{\gamma }_{quad}= & {} \left( 1+\hat{R}_{\textit{GMV}}+\frac{(1+\hat{s})\sqrt{\hat{V}_{\textit{GMV}}}}{\sqrt{z_{1-\alpha }^2-\hat{s}}}\right) ^{-1}. \end{aligned}$$
(26)

The formulas (25) and (26) show that the risk aversion coefficients can be estimated only if \(\hat{s}<z^2_{1-\alpha }\). Moreover, the corresponding population quantities can be interpreted if \(s<z^2_{1-\alpha }\) only. These two observations show that we are not able to derive the unconditional distributions of \(\hat{\gamma }_{exp}\) and \(\hat{\gamma }_{exp}\) but only the corresponding conditional distributions provided that \(\hat{s}<z_{1-\alpha }^2\). Following the approach of Bodnar et al. (2012) we first establish the conditional distributions of \(\hat{\gamma }_{quad}\) and \(\hat{\gamma }_{exp}\) given \(\hat{s}=s^*\) and generalize the results thereafter.

From Lemma 2 we obtain the following stochastic representations of \(\hat{R}_{\textit{GMV}}\) and \(\hat{V}_{\textit{GMV}}\) given \(\hat{s}=s^*\), denoted by \(\hat{R}_{\textit{GMV}}^*\) and \(\hat{V}_{\textit{GMV}}^*\). They are expressed as

$$\begin{aligned} \hat{R}_{\textit{GMV}}^*{\mathop {=}\limits ^{d}}R_{\textit{GMV}} + \sqrt{\frac{1}{n}+\frac{s^*}{n-1}}\sqrt{V_{\textit{GMV}}}\xi _1, \quad \hat{V}_{\textit{GMV}}^*{\mathop {=}\limits ^{d}}\frac{V_{\textit{GMV}}}{n-1}\xi _2, \end{aligned}$$
(27)

where \(\xi _1 \sim N(0,1)\) and \(\xi _2 \sim \chi ^2_{n-k}\) are independently distributed. In Theorem 3 we establish the stochastic representations of \(\hat{\gamma }_{exp}\) and \(\hat{\gamma }_{quad}\) conditional on \(s^*=\hat{s}\). These quantities are denoted by \(\hat{\gamma }_{exp}^*\) and \(\hat{\gamma }_{quad}^*\).

Theorem 3

Let \(\mathbf {X}_1,\ldots ,\mathbf {X}_n\) be a random sample of independent vectors such that \(\mathbf {X}_i\sim \mathcal {N}_k(\varvec{\mu },\varvec{\Sigma })\) for \(i=1,\ldots ,n\) and \(n > k\). Let \(\varvec{\Sigma }\) be positive definite. Then it holds that

$$\begin{aligned} \hat{\gamma }_{exp}^*&{\mathop {=}\limits ^{d}}&\frac{\sqrt{z_{1-\alpha }^2-s^*}\sqrt{n-1}}{\sqrt{V_{\textit{GMV}}}\sqrt{\xi _2}}, \end{aligned}$$
(28)
$$\begin{aligned} \hat{\gamma }_{quad}^*&{\mathop {=}\limits ^{d}}&\left( 1+R_{\textit{GMV}}+\sqrt{\frac{1}{n}+\frac{s^*}{n-1}}\sqrt{V_{\textit{GMV}}}\xi _1 +\frac{(1+s^*)\sqrt{V_{\textit{GMV}}}\sqrt{\xi _2}}{\sqrt{n-1}\sqrt{z_{1-\alpha }^2-s^*}}\right) ^{-1}. \end{aligned}$$
(29)

The results of Theorem 3 possess several interesting applications. First, for simulating \(\hat{\gamma }_{exp}^*\) and \(\hat{\gamma }_{quad}^*\) it is not necessary to generate n independent k-variate normally distributed random vectors. It is sufficient to simulate two independent random variables \(\xi _1\) and \(\xi _2\) from the well-known univariate distributions and then to apply the expressions of Theorem 3. Second, Theorem 3 is useful if one wants to derive the the densities of \(\hat{\gamma }_{exp}^*\) and \(\hat{\gamma }_{quad}^*\).

5 Extension to robust portfolio selection

Our results can be extended to the case where the investor solves

$$\begin{aligned} \max E(u(\mathbf {X}^\prime \mathbf {w})) \; \text { w.r.t. } \mathbf {w}, \text { subject to } \mathbf {w}^\prime \mathbf {1}=1, \end{aligned}$$
(30)

where u(.) is a utility function. If the distribution of asset returns is partially known then the portfolio selection problem (30) can be reformulated with robust optimization technique as follows [cf. Fabozzi et al. (2010)]

$$\begin{aligned} \max _{\mathbf {w}} \; \min _{\mathbf {X}\sim (\varvec{\mu },\varvec{\Sigma })} E(u(\mathbf {X}^\prime \mathbf {w})) \; \quad \text {subject to} \quad \mathbf {w}^\prime \mathbf {1}=1 , \end{aligned}$$
(31)

where the notation \(\mathbf {X}\sim (\varvec{\mu },\varvec{\Sigma })\) indicates that the distribution of \(\mathbf {X}\) belongs to the class of k-dimensional distributions with the mean vector \(\varvec{\mu }\) and the covariance matrix \(\varvec{\Sigma }\).

Let

$$\begin{aligned} V(\mathbf {w}) = \min _{\mathbf {X}\sim (\varvec{\mu },\varvec{\Sigma })} E(u(\mathbf {X}^\prime \mathbf {w})) \end{aligned}$$
(32)

denote the value of the inner minimization problem for given weights \(\mathbf {w}\). Popescu (2007) proved that (32) is equivalent to an optimization problem with univariate distributions with a given mean and variance, i.e.

$$\begin{aligned} V(\mathbf {w}) = \min _{R_{\mathbf {w}} \sim (\mu _{\mathbf {w}},\sigma ^2_{\mathbf {w}})} E(u(R_{\mathbf {w}})) . \end{aligned}$$
(33)

Moreover, if \(V(\mathbf {w})\) is continuous, non-decreasing in \(\mu _{\mathbf {w}}\), non-increasing in \(\sigma ^2_{\mathbf {w}}\), and quasi-concave, then (31) is equivalent to the following quadratic optimization problem [cf. Popescu (2007)]

$$\begin{aligned} \max _{\mathbf {w}} \; \gamma \varvec{\mu }^\prime \mathbf {w}- (1-\gamma ) \mathbf {w}^\prime \varvec{\Sigma }\mathbf {w}\quad \text {subject to} \quad \mathbf {w}^\prime \mathbf {1}=1, \end{aligned}$$
(34)

where \(\gamma \in [0,1]\). Moreover, if \(\mathbf {w}(\gamma )\) is the solution of (34) then \(V(\mathbf {w}(\gamma ))\) is continuous and unimodal in \(\gamma \).

Next we fix a portfolio \(\mathbf {w}\) and a confidence level \(\alpha \in (1/2,1]\). Fabozzi et al. (2010) argue that a robust version of VaR, denoted by RVaR, is given by

$$\begin{aligned} \textit{RVaR}_{\alpha }=\max _{R_{\mathbf {w}} \sim (\mu _{\mathbf {w}},\sigma ^2_{\mathbf {w}})}{} \textit{VaR}_{\alpha }. \end{aligned}$$
(35)

The application of Chebyshev’s inequality leads to [see Alexander and Baptista (2002, Section 3.2)]

$$\begin{aligned} \textit{RVaR}_{\alpha }=-\mathbf {w}^\prime \varvec{\mu }+d_{1-\alpha }(\mathbf {w}) \sqrt{\mathbf {w}^\prime \varvec{\Sigma }\mathbf {w}}, \end{aligned}$$
(36)

where \(d_{1-\alpha }=d_{1-\alpha }(\mathbf {w})=1/\sqrt{1-\alpha }\). The solutions of the optimization problem (34) and

$$\begin{aligned} \textit{RVaR}_{\alpha } \rightarrow \; \min \text { w.r.t. }\mathbf {w}, \text { subject to } \mathbf {w}^\prime \mathbf {1}=1 \end{aligned}$$

provide us the probabilistic interpretation of \(\gamma \). Following the proof of Theorem 1 we obtain

$$\begin{aligned} \gamma =\left( 1+\frac{\sqrt{d_{1-\alpha }^2-s}}{2\sqrt{V_{\textit{GMV}}}}\right) ^{-1}. \end{aligned}$$
(37)

6 Empirical illustration

For illustration purposes we use monthly data for the MSCI Developed Markets Indexes (Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Hongkong, Ireland, Israel, Italy, Japan, Netherlands, New Zealand, Norway, Portugal, Singapore, Spain, Sweden, Switzerland, the UK, the US) and for the MSCI Emerging Markets Indexes (Brazil, Chile, China, Colombia, Czech Republic, Egypt, Greece, Hungary, India, Indonesia, South Korea, Malaysia, Mexico, Peru, Philippines, Poland, Russia, South Africa, Taiwan, Thailand, Turkey). The markets cover 23 and 21 countries respectively and the time span from June 2004 till March 2014, resulting in 117 observations. To assess the impact of the dimension we consider portfolios consisting of \(k = 2, 5, 10, 15, 21\) (or 23) assets. For simplicity we select the assets for the first part of the study in alphabetic order, e.g., when \(k=2\), the countries are Australia and Austria for developed markets and Brazil and Chile for emerging. The characteristics of the frontier are summarized in Table 1. As expected the variance of the GMV portfolio \(V_{\textit{GMV}}\) decreases with increasing k, but the return \(R_{\textit{GMV}}\) and the slope s increase. Furthermore, the return and variance of the global minimum variance portfolio are lower for the developed markets, compared to the emerging markets, which is consistent with our expectations.

Table 1 Characteristics of the mean-variance frontier for the first k developed markets (left) and emerging markets (right) for the period from June 2004 to March 2014
Full size table

6.1 Gaussian returns

The risk aversion coefficients \(\gamma _{quad}\) and \(\gamma _{exp}\) for Gaussian returns as functions of \(\alpha \) are shown in Fig. 1. In accordance with Theorem 1, note that these coefficients are monotonously increasing in \(\alpha \). Additionally, the coefficients are also increasing in k (the number of assets). Hence, if the size of the portfolio increases, then the minimum-VaR portfolio corresponds to a higher risk aversion coefficient. The same is observed by comparing the results for developed and emerging markets, where for the latter the implied risk aversion is lower despite of higher volatility. In general, for \(\alpha >0.95\) the risk aversion is high and the portfolio is close to the GMV portfolio. Even for small values of \(\alpha \) the risk aversion is much higher than the frequently used values from 1 to 10 for \(\gamma _{exp}\). This implies that if the investors are interested in the commonly used VaR at the 99% confidence level, then they are much more risk averse than typically assumed in empirical work.

Fig. 1
figure 1

The risk aversion coefficients \(\gamma _{quad}\) (top) and \(\gamma _{exp}\) (bottom) as functions of \(\alpha \) for portfolios consisting of the first k developed markets (left) and emerging markets (right)

Full size image

In order to make the study robust to the choice of the indices we fix \(\alpha \) at 99% and sample 200 portfolios of different sizes from both pools of indexes. For each portfolio we compute the corresponding risk aversion coefficients and plot their histograms in Fig. 2. The result that the risk aversion coefficients increase in the number of assets still holds. Hence, this result is robust to using different sets of assets. Furthermore, small portfolios lead to systematically lower risk aversions compared to larger portfolios.

Fig. 2
figure 2

Histograms of risk aversion coefficients \(\gamma _{quad}\) (top) and \(\gamma _{exp}\) (bottom) for \(\alpha =0.99\) and portfolios consisting of \(k=2\) (left), \(k=5\) (middle) and \(k=15\) (right) randomly sampled emerging markets

Full size image

6.2 Elliptical returns

To illustrate the theoretical results for elliptical distributions we concentrate on the multivariate Laplace distribution. This distribution is obtained assuming that \(r^2\) follows exponential distribution with intensity equal to 1. In a univariate framework the resulting distribution of \(X_i\) is the Laplace distribution with the density \(\frac{1}{2} \sqrt{\frac{2}{\lambda }} exp\left\{ -\sqrt{\frac{2}{\lambda }} |x_i-\mu _i|\right\} \). The \(1-\alpha \) quantile of this distribution is used as the \(d_{1-\alpha }\)-quantile in Theorem 2. Technical details on the multivariate Laplace distribution can be found in Eltoft et al. (2006), whereas Kotz et al. (2001) discuss the application of the multivariate Laplace distribution in portfolio theory. Alternatively, one may consider the multivariate t-distribution, which is very frequently applied in portfolio selection.

The Laplace distribution has heavier tails compared to the normal and thus is a reasonable alternative in financial applications. An explicit application of this distribution is technically demanding due to complex expressions for the density (see Eltoft et al. 2006). In our case, however, the stochastic representation allows us to work with r only. The corresponding risk aversion coefficients \(\gamma _{quad}\) and \(\gamma _{exp}\) as functions of \(\alpha \) are shown in Fig. 3. Similarly to the normal distribution, the risk aversion attains very high values even for modest levels of \(\alpha \). However, it is important to note that the values of the coefficients are lower than for the normal distribution. This implies that if we switch from the normal to a more heavy-tailed distribution the uncertainty about the future portfolio returns is partly captured by the new distribution. Particularly this is crucial for the minimum VaR portfolio, where we attempt to reduce the chances of large losses. Since the losses are partly taken into account by the new model, the investor becomes less risk averse within the new framework.

Fig. 3
figure 3

The risk aversion coefficients \(\gamma _{quad}\) (top) and \(\gamma _{exp}\) (bottom) as functions of \(\alpha \) for portfolios consisting of the first k developed markets (left) and emerging markets (right) assuming multivariate Laplace distribution for the returns

Full size image

6.3 Estimation risk

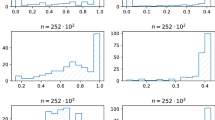
With the next example we illustrate the simulated density functions of the sample risk aversions \(\hat{\gamma }_{quad}^*\) and \(\hat{\gamma }_{exp}^*\) by relying on Theorem 3. We use the same data as in the above examples and condition on \(s^*=\hat{s}\), where \(\hat{s}\) is obtained individually for each portfolio. We observe that the precision of the estimators is relatively high. Note that the number of assets has an opposite impact on the precision for the two risk aversions. While for the exponential utility the densities are narrower for small portfolios, they become wider for the quadratic utility (Fig. 4).

Fig. 4
figure 4

The conditional densities of \(\gamma _{quad}^*\) (top) and \(\gamma _{exp}^*\) (bottom) given \(s^*\) for portfolios consisting of the first k developed markets (left) and emerging markets (right) assuming multivariate normal distribution for the returns

Full size image

7 Summary

In the paper we consider the exponential and quadratic utility functions which are frequently applied in portfolio management. Since the VaR plays a key role in monitoring risk, many investors follow the minimum VaR portfolio strategies. We link both approaches to obtain a functional relationships between the risk aversions and the level of VaR. The results are obtained assuming that the vector of asset returns is multivariate normally distributed and they are generalized to the class of elliptically contoured distributions. The latter is particularly important due to well known heavy-taildness of asset returns. Finally, we take the parameter uncertainty into account and give conditional stochastic representation of the empirical risk aversion coefficients. The theoretical results are validated in an empirical study.