Abstract
We derive bounds on the expectation of a class of periodic functions using the total variations of higher-order derivatives of the underlying probability density function. These bounds are a strict improvement over those of Romeijnders et al. (Math Program 157:3–46, 2016b), and we use them to derive error bounds for convex approximations of simple integer recourse models. In fact, we obtain a hierarchy of error bounds that become tighter if the total variations of additional higher-order derivatives are taken into account. Moreover, each error bound decreases if these total variations become smaller. The improved bounds may be used to derive tighter error bounds for convex approximations of more general recourse models involving integer decision variables.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Consider the two-stage recourse model with random right-hand side
where the recourse function Q is defined for the tender variables \(z \in {\mathbb {R}}^m\) as
and the value function v is defined for \(s \in {\mathbb {R}}^m\) as
This model describes a two-stage decision problem under uncertainty. The uncertainty arises from the random vector \(\omega \) of which the distribution is known. In the first stage, a decision x has to be made while the realization of \(\omega \) is not yet available, whereas in the second stage, the realization of \(\omega \) is known and recourse actions y can be taken to repair infeasibilities of the random constraints \(Tx \ge \omega \). The model is called an integer recourse model if \(Y = {\mathbb {Z}}^{n_2}_+\). If in addition \(W = I_m\), then the model is referred to as a simple integer recourse (SIR) model. More general formulations of (1) exist, with uncertainty in the technology matrix T and cost parameters q, see e.g. the textbooks (Birge and Louveaux 1997; Shapiro et al. 2009).
Throughout this paper, we make the following assumptions, which guarantee that Q is finite everywhere.
-
(i)
The recourse is complete: for all \(s \in {\mathbb {R}}^m\), there exists a \(y \in Y\) such that \(Wy \ge s\), so that \(v(s) < \infty \).
-
(ii)
The recourse is sufficiently expensive: \(v(s) > -\infty \) for all \(s \in {\mathbb {R}}^m\).
-
(iii)
\({\mathbb {E}}[|\omega _i|]\) is finite for all \(i=1,\ldots ,m\).
Recourse models are highly relevant in practice, as demonstrated by numerous applications in problems where uncertainty plays a role. Areas of application include energy, telecommunication, production planning, and environmental control; see e.g. Gassmann and Ziemba (2013) and Wallace and Ziemba (2005). Furthermore, integrality restrictions on the recourse actions arise naturally when modelling real-life situations, for example to capture on/off decisions or batch size restrictions.
Unfortunately, solving integer recourse problems is generally time-consuming and practically impossible, because the recourse function Q is in general non-convex (Rinnooy Kan and Stougie 1988). Traditional solution methods typically combine ideas from deterministic mixed-integer programming and stochastic continuous programming, see e.g. Laporte and Louveaux (1993), Schultz et al. (1998), Carøe and Schultz (1999), Ahmed et al. (2004), Sen and Higle (2005), Ntaimo (2013), Zhang and Küçükyavuz (2014) and Gade et al. (2014), and the survey papers by Schultz (2003), Sen (2005) and Romeijnders et al. (2014).
However, in this paper we focus on an alternative solution methodology introduced by van der Vlerk (1995). His approach is to approximate the non-convex recourse function Q by a convex approximation \(\hat{Q}\), obtaining an approximating model for (1). The advantage is that the approximating model can be solved efficiently using known convex optimization techniques to obtain an approximate solution \(({\hat{x}}, {\hat{z}})\) for (1).
In the literature, convex approximations are typically derived by simultaneously modifying the underlying recourse structure (Y, q, W) and the distribution of the random vector \(\omega \). For example, Klein Haneveld et al. (2006) propose the so-called \(\alpha \)-approximations for SIR models, van der Vlerk (2004) studies a class of convex approximations for the general integer case, and Romeijnders et al. (2016b) propose a convex approximation, the shifted LP-relaxation, for integer recourse problems with a totally unimodular (TU) recourse matrix W. The latter approximation is generalized to the general mixed-integer recourse case by Romeijnders et al. (2016a).
To guarantee the performance of the approximating solution \((\hat{x},\hat{z})\) in the original model (1), Romeijnders et al. (2015) show that for every approximation \(\hat{Q}\),
That is, the absolute optimality gap of \((\hat{x},\hat{z})\) is at most \(2\Vert \hat{Q} - Q\Vert _{\infty }\). For this reason, bounds on \(\Vert \hat{Q} - Q\Vert _{\infty }\) are used to guarantee the quality of the approximating solution \((\hat{x},\hat{z})\). Such error bounds are derived by Klein Haneveld et al. (2006) and by Romeijnders et al. (2015) for various types of convex approximations. They are expressed in terms of the total variations of the marginal probability density functions (pdf) of the random right-hand side vector \(\omega \). For general mixed-integer and TU integer recourse models, Romeijnders et al. (2016a, b), respectively, derive similar error bounds by making use of periodicity in the difference of the underlying value functions of the recourse function Q and its convex approximation \(\hat{Q}\). In this way, bounds on \(\Vert \hat{Q}-Q\Vert _{\infty }\) are obtained by deriving total variation bounds on the expectation of periodic functions. Since we also exploit this relationship between expectations of periodic functions and the difference between \(\hat{Q}\) and Q, we explain this relationship in more detail in Sect. 2.
Romeijnders et al. (2016b) use worst-case analysis to prove that their error bounds are tight for certain piecewise constant pdf. For other pdf, there may be a considerable difference between the error bound and the actual error as shown by numerical experiments on a fleet allocation and routing problem and on an investment problem in stochastic activity networks (Romeijnders et al. 2017). Motivated by these observations, we improve the error bounds of Romeijnders et al. (2016b) by using information on the higher-order derivatives of the underlying pdf of the random variables in the model. To be specific, we use that the total variation of the higher-order derivatives of the underlying pdf can be used to improve the error bound. The intuition behind our approach is that by imposing restrictions on the higher-order derivatives of the underlying pdf we are able to exclude the piecewise constant pdf, which have jump discontinuities.
To obtain these error bounds we improve the existing bounds on the expectation of periodic functions by Romeijnders et al. (2016b) using higher-order total variations, i.e. total variations of the higher-order derivatives of the underlying marginal pdfs. This is the main contribution of this paper since these bounds may be used to improve error bounds of convex approximations for mixed-integer recourse models in general. We illustrate their potential by improving error bounds for the shifted LP-relaxation approximation of SIR models by Romeijnders et al. (2016b). The improved error bounds decrease with the total variations of the underlying pdf and its higher-order derivatives.
The remainder of this paper is organized as follows. Section 2 describes in more detail the relationship between error bounds for the shifted LP-relaxation of integer recourse models and bounds on the expectation of periodic functions. In Sect. 3, we improve bounds on the expectation of a class of periodically monotone functions, and in Sect. 4 we illustrate how these results can be applied in the setting of SIR models. In Sect. 5 we conclude and summarize our results.
2 Total variation error bounds
In this section, we describe parts of the procedure employed by Romeijnders et al. (2016b) to derive an error bound for the so-called shifted LP-relaxation approximation \({\hat{Q}}\) of Q for TU integer recourse models. The idea behind this approximation is to simultaneously relax the integrality restrictions in the model and to perturb the random right-hand side vector \(\omega \).
Definition 1
The shifted LP-relaxation \({\hat{Q}}\) of the mixed-integer recourse function Q is defined as
where \(e_m\) is the m-dimensional all-one vector.
The shifted LP-relaxation is a special case of the convex approximation for general two-stage mixed-integer recourse models by Romeijnders et al. (2016a). Here, we focus on the one-dimensional SIR case. Partly this is for simplicity, but we are also inspired by the fact that Romeijnders et al. (2016b) derive an error bound for the TU integer recourse case using one-dimensional results. Setting \(q = 1\) and \(W = 1\), the integer recourse function Q reduces to
where \(\lceil \cdot \rceil \) denotes the round-up function and \(\lceil s \rceil ^+ := \max \{0,\lceil s \rceil \} \), \(s \in {\mathbb {R}}\). The shifted LP-relaxation then becomes
Since \(||{\hat{Q}} - Q||_{\infty }\) is the quantity of interest, consider
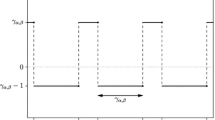
with underlying difference function \(\psi (t):= (t)^+- \left\lceil t - 1/2\right\rceil ^+\), see Fig. 1.
The difference function \(\psi \) defined in (3)
If we ignore the positive part operators and define
then \(\varphi \) is a real-valued periodic function with period \(p = 1\) and mean value \(\nu = p^{-1}\int _0^p \varphi (t)dt = 0.\) The function \(\psi \), however, is only half-periodic, that is
Romeijnders et al. (2016b) use this property to derive error bounds for the shifted LP-relaxation. Similarly, Romeijnders et al. (2016a) make use of asymptotic periodicity results for mixed-integer programs to find error error bounds for the general mixed-integer recourse case.
The error bounds are based on a worst-case approach with respect to the total variation \(|{\varDelta }| f\) of the underlying pdf f of \(\omega \), since the expectation in (2) is intractable in general. The following definition of total variation is taken directly from Romeijnders et al. (2016b).
Definition 2
Let \(f: {\mathbb {R}}\rightarrow {\mathbb {R}}\) be a real-valued function, and let \(I \subset {\mathbb {R}}\) be an interval. Let \({\varPi }(I)\) denote the set of all finite ordered sets \(P = \{x_1,\ldots ,x_{N+1}\}\) with \(x_{1}< \cdots < x_{N + 1}\) in I. Then, the total variation of f on I, denoted \(|{\varDelta }|f(I)\), is defined as
where
Write \(|{\varDelta }|f := |{\varDelta }|f({\mathbb {R}})\). A function f is said to be of bounded variation if \(|{\varDelta }|f\) is finite.
The worst-case approach adopted by Romeijnders et al. (2016b) is to derive a bound, for any bounded periodic function \(\varphi \) and \(B \in {\mathbb {R}}\) with \(B > 0\), on
where \({\mathcal {F}}\) denotes the set of all continuous pdf of bounded variation. This bound is used to derive an error bound on \(\Vert \hat{Q} - Q\Vert _{\infty }\) in (2), presented in Theorem 1 below. We will improve the bounds on the expectation of periodic and half-periodic functions, which directly leads to an improved error bound for SIR models.
Theorem 1
Consider the simple integer recourse function Q defined as
and its shifted LP-relaxation approximation \({\hat{Q}}\), defined as
where \(\omega \) is a continuous random variable with pdf f of bounded variation. Then
where
Proof
See Romeijnders et al. (2016b). \(\square \)
Romeijnders et al. (2016b) show that there exist piecewise constant pdf for which the error bound in Theorem 1 is tight. For example, for \(B \ge 4\), the pdf \({\hat{f}} :{\mathbb {R}}\rightarrow {\mathbb {R}}\) defined as
satisfies \(|{\varDelta }|{\hat{f}} = B\) and
Remark 1
Observe that \(\hat{f}\) can be interpreted as a pdf with \(|{\varDelta }|\hat{f}' = +\infty \).
In the next sections we will assume that f is continuously differentiable and that its derivative \(f'\) is of bounded variation. In this way, we exclude piecewise constant densities such as \(\hat{f}\). By using the higher-order total variations of f we are able to derive tighter bounds.
3 Improving bounds on the expectation of periodic functions
In this section, we improve the bounds on the expectation of periodic functions derived by Romeijnders et al. (2016b) for the class of point-symmetric periodic functions (see Definition 7). Next to that, we improve bounds on the expectation of half-periodic functions \(\psi :{\mathbb {R}} \rightarrow {\mathbb {R}}\), which are of the form
where \(\varphi \) is a point-symmetric periodic function.
The organization of this section is as follows. In Sect. 3.1, we consider packed densities, a concept introduced by Romeijnders et al. (2016b) which we generalize to higher-order derivatives. Next, in Sect. 3.2, we introduce point-symmetric periodic functions, the class of periodic functions for which we are able to derive results. In Sect. 3.3 we use the concept of bound propagation to derive a hierarchy of total variation bounds. In Sect. 3.4, we present bounds on the expectation of periodic and half-periodic functions.
3.1 Higher-order derivatives of packed densities
The main contribution of this paper is to generalize the results by Romeijnders et al. (2016b) to higher-order derivatives. The key insight here is that including information on the total variation and the maximum norm of higher-order derivatives of the underlying pdf leads to improved expectation bounds. We generalize several definitions by Romeijnders et al. (2016b) to allow for these elements to be included in our analysis. They consider the set \({\mathcal {F}}\) containing all one-dimensional pdf of bounded variation. In Definition 3, we introduce the sets \({\mathcal {F}}_n\), \(n \in {\mathbb {N}}\), which satisfy the relationship \({\mathcal {F}}\supset {\mathcal {F}}_0 \supset {\mathcal {F}}_1 \supset \cdots \).
Definition 3
Let \({\mathcal {F}}_n\) denote the set of one-dimensional pdf f, such that the first n derivatives of f exist, are continuous, and are of bounded variation. Denote the k-th derivative of f by \(f^{(k)}\) and write \(f = f^{(0)}\).
Definition 4
For all bounded integrable functions \(\varphi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) and positive constants \( B := (B_0,\ldots ,B_n)\) and \( C := (C_0,\ldots ,C_n)\) define \(M_n\) as
where \(||\cdot ||_{\infty }\) denotes the maximum norm defined as
Remark 2
In Definition 4, we could have suppressed the constants \(C_0,\ldots ,C_n\), since an upper bound \(B_k\) on \(|{\varDelta }|f^{(k)}\) directly implies an upper bound \(\frac{B_k}{2}\) on \(||f^{(k)}||_{\infty }\). However, these bounds may be larger than \(C_k\) so that by including these constants we may obtain tighter bounds.
The main goal of this section is to derive a bound on \(M_n(\varphi ,B,C)\). This is useful, because such a bound can be used to derive performance guarantees for convex approximations of mixed-integer recourse functions. We derive such bounds for periodic and half-periodic functions \(\varphi \). The key objects of our analysis are packed densities, introduced by Romeijnders et al. (2016b), which are functions defined on [0, p] such that for either periodic of half-periodic functions \(\varphi \) with period p,
For periodic functions \(\varphi \), Romeijnders et al. (2016b) define this packed density as
Intuitively, \(f_p(x)\) represents the sum of the densities corresponding to \(\varphi (x)\) and \(\varphi (x + pk)\) for every \(k \in {\mathbb {Z}}{\setminus }\{0\}\). For half-periodic functions \(\varphi \), however, we require an alternative packed density, which we call the half-packed density. This packed density does not include the values of \(f(x + pk)\) for \(k < 0\), since \(\varphi \) is only half-periodic and thus \(\varphi (x + pk) = 0\) for \(k < 0\). Definition 5 below contains the definitions of both the original and the new packed density.
Definition 5
For all \(f \in {\mathcal {F}}_0\) and \(p \in {\mathbb {R}}\) with \(p>0\), define the classical packed density \(f_p :[0,p] \rightarrow {\mathbb {R}}\) as
Further, define the half-packed density \(\hat{f}_p:[0,p] \rightarrow {\mathbb {R}}\) as
Remark 3
Note that the half-packed density does not integrate to one in general, as opposed to the classical packed density. As a result, the half-packed density cannot be interpreted as a pdf.
Remark 4
We define the (higher-order) derivatives of the classical packed density and the half-packed density at the endpoints of the closed interval [0, p] by their one-sided derivatives, provided that they exist.
Romeijnders et al. (2016b) show that the total variation of f can be used to bound the total variation of \(f_p\) on [0, p]. Interestingly, similar bounds can be derived for the total variation of half-packed densities \(\hat{f}_p\) on [0, p]. Moreover, similar bounds also hold for higher-order derivatives \(f^{(k)}, k=1,\ldots ,n\), of f.
Lemma 1
Let \(n \in {\mathbb {N}}\) be given and let \(f \in {\mathcal {F}}_n\). Consider its corresponding classical packed density \(f_p\) and half-packed density \({\hat{f}}_p\), as in Definition 5. Then, for \(k = 0,\ldots ,n\),
-
(i)
\(f_p^{(k)}\) and \({\hat{f}}_p^{(k)}\) exist and are continuous on [0, p],
-
(ii)
\(f_p^{(k)}(0)= f_p^{(k)}(p)\) and \({\hat{f}}_p^{(k)}(0)= {\hat{f}}_p^{(k)}(p) + f^{(k)}(0)\), and
-
(iii)
\(|{\varDelta }| f_p^{(k)}([0,p]) \le |{\varDelta }| f^{(k)}\) and \(|{\varDelta }|{\hat{f}}_p^{(k)}([0,p]) \le |{\varDelta }|f^{(k)} - |f^{(k)}(0)|\). Moreover, for all bounded integrable periodic functions \(\varphi \) with period p, and half-periodic functions \(\psi \) of the form
$$\begin{aligned} \psi (x) = \left\{ \begin{array}{ll}0 ,&{} x < 0 ,\\ \varphi (x),&{} x \ge 0,\end{array}\right. \end{aligned}$$ -
(iv)
\({\mathbb {E}}_{f}[\varphi (\omega )] = \int _0^p\varphi (x) f_p(x)dx\) and \({\mathbb {E}}_{f}[\psi (\omega )] = \int _0^p\varphi (x){\hat{f}}_p(x)dx\).
Proof
We refer to the proof of corresponding properties involving packed densities in Romeijnders et al. (2016b). \(\square \)
Observe that the properties involving the classical packed density generalize readily to higher-order derivatives. With respect to the half-packed density, notice the additional terms \(f^{(k)}(0)\) and \(-|f^{(k)}(0)|\) in properties (ii) and (iii), respectively. These terms result from the fact that the half-packed density only sums over the non-negative integers.
In our analysis in the next sections, we will initially not make a distinction between the classical packed density and the half-packed density. This is possible because they belong to the broader class of packed densities, which we introduce in Definition 6.
Definition 6
For a given \(n \in {\mathbb {N}}\) and \(p \in {\mathbb {R}}\) with \(p >0\), let \(g:[0,p]\rightarrow {\mathbb {R}}\) be an n times continuously differentiable function such that its first n derivatives are of bounded variation on the interval [0, p]. Assume \(\gamma _k := g^{(k)}(p) - g^{(k)}(0)\) is bounded for \(k = 0,\ldots ,n\). Then g is referred to as a packed density with discontinuities \( \gamma = (\gamma _0,\ldots ,\gamma _n)\).
Indeed, from Lemma 1 it follows directly that both the classical and the half-packed density are packed densities with discontinuities \(\gamma =(0,\ldots ,0)\) and \((f^{(0)}(0),\ldots ,f^{(n)}(0))\), respectively. Considering property (iv) in Lemma 1, we are interested in the quantity
for a periodic function \(\varphi \) and a packed density g of Definition 6. It equals the expectation of a periodic function if g is a classical packed density, in which case the discontinuities corresponding to g are \( \gamma = (0,\ldots ,0)\). Furthermore, for \(\varphi \) defined as in (3), the quantity \(D(\varphi ,g)\) is equal to the approximation error of the shifted-LP relaxation of a simple integer recourse model if g is a half-packed density, \(\hat{f}_p\) of Definition 5, with \( \gamma = (f^{(0)}(0),\ldots , f^{(n)}(0))\).
3.2 Point-symmetric periodic functions
We restrict our attention to point-symmetric periodic functions, a concept we introduce in Definition 7, since the underlying periodic function that arises when studying the shifted LP-relaxation for TU integer recourse models is point-symmetric periodic with period \(p=1\). However, our results apply to all point-symmetric periodic functions \(\varphi \) with period \(p >0\).
Definition 7
A periodic function \(\varphi :{\mathbb {R}} \rightarrow {\mathbb {R}}\) with period p satisfying
or equivalently
for all \(x \in [0,p]\) is said to be point-symmetric periodic, or a PSP(p) function.
For a packed density g of Definition 6 and a PSP(p) function \(\varphi \), we are able to derive an upper bound on \(D(\varphi ,g)\). The first step we take in obtaining such a bound is to prove in Lemma 2 that there exists a function \(g_p\) that is symmetric in the same sense as \(\varphi \) and carries all relevant information of g for computing \(D(\varphi ,g)\). Moreover, the total variation of \(g_p\) on [0, p] does not exceed that of g on [0, p]. Next, in Lemma 3, we obtain bounds on higher-order derivatives of \(g_p\) by combining the symmetry of \(g_p\) with the mean-value theorem. In Sect. 3.3, we translate these bounds into a single bound on \(g_p\), a process we refer to as bound propagation.
Lemma 2
Let \(n \in {\mathbb {N}}\) and \(p \in {\mathbb {R}}\) with \(p >0\) be given. Let \(\varphi : {\mathbb {R}} \rightarrow {\mathbb {R}}\) be a PSP(p) function. For a packed density g of Definition 6, define \(g_p:[0,p] \rightarrow {\mathbb {R}}\) as
Then,
and for all integers k satisfying \(0\le k \le n\),
Proof
For property (i), note that it follows from a substitution that
where the latter equality holds since \(\varphi \) is a PSP(p) function. Using (iv) in Lemma 1 we have
and thus the first equality in (i) holds. To prove the second equality in (i), note that
where the second term on the right-hand side can be rewritten as
To prove (ii) we make use of standard properties of the total variation of functions. Define \(l :{\mathbb {R}}\rightarrow {\mathbb {R}}\) as \(l(x) := g(p - x)\). We have
where the second equality holds since \(|{\varDelta }|(\alpha f)(I) = |\alpha | |{\varDelta }|f(I)\), for every closed interval \(I \subset {\mathbb {R}}\), scalar \(\alpha \) and f of bounded variation, and where the inequality follows from \(|{\varDelta }|(f + g)(I) \le |{\varDelta }|f(I) + |{\varDelta }|g(I)\) for f and g of bounded variation. \(\square \)
We now state and prove a number of properties of \(g_p\) that we will use to prove the results in Sects. 3.3 and 3.4. We make a distinction between odd and even-order derivatives of \(g_p\), because they share different properties.
Lemma 3
For a given \(n \in {\mathbb {N}}\) and \(p \in {\mathbb {R}}\) with \(p >0\), let \(g:[0,p]\rightarrow {\mathbb {R}}\) be a packed density with discontinuities \(\gamma _k := g^{(k)}(0) - g^{(k)}(p)\), \(k = 0,\ldots ,n\). Define \(g_p:[0,p] \rightarrow {\mathbb {R}}\) as \(g_p(x):= \frac{1}{2}(g(x) - g(p - x))\). Then, for all even k, \(0 \le k \le n\),
Furthermore, for all odd k, \(1 \le k \le n\),
Proof
Note that from the definition of \(g_p\),
so that,
Properties (i) and (ii) then follow directly.
To prove property (iv) we make use of the mean-value theorem and property (ii). Together they imply that there exists a \(c_k \in (0,p)\) such that
The existence of \(x_k \in \left( 0,p/2\right] \) as in property (iv) then follows from the symmetry of odd-order derivatives, see (8).
We will prove (iii) by contradiction using property (ii) in Lemma 2. Fix an even k and assume for contradiction that \(\left| g_p^{(k)}(t^*)\right| > w_k\) for some \(t^* \in \left[ 0,p/2\right) \). This implies that
because, as a consequence of (ii), \(|{\varDelta }|g^{(k)}([0,p]) \ge |\gamma _k|\).
Consider the partition \(P = \left\{ 0,t^*,p - t^*,p \right\} \). Following the notation introduced in Definition 2, we have for this partition,
where the equality is due to equation (8) and property (ii). We thus find a contradiction with Lemma 2, property (ii).
Property (v) follows in a similar fashion, since by combining (iv) with (8) it is possible to arrive at a contradiction with property (ii) in Lemma 2 if (v) does not hold. \(\square \)
3.3 Bound propagation
In this section, we use the bounds on \(g_p^{(k)}, k =0,\ldots ,n\), in Lemma 3 to derive a single tighter bound on \(g_p\) as defined in (7) for a given packed density g with known discontinuities \((\gamma _0,\ldots ,\gamma _n)\). We use information on the total variation of g and its higher-order derivatives to bound \(g_p\). Clearly, we obtain tighter bounds if we include information on more higher-order derivatives of g.
For illustration, suppose that information is available on g and \(g^{(1)}\). Given a bound on \(|{\varDelta }|g\), property (iii) in Lemma 3 directly yields a uniform bound on \(|g_p(x)|\) for \(x \in [0,p]\), denoted \(w_0\). An additional bound on \(|{\varDelta }|g^{(1)}\) yields a bound on \(|g_p^{(1)}(x)|\), denoted \(w_1\), using property (v) in Lemma 3. The latter bound can be used to improve the bound on \(|g_p(x)|\) itself, using the concept of bound propagation, which we will now demonstrate.
Let q(x) be such that \(\left| g_p^{(1)}(x)\right| \le q(x)\) for \(x \in \left[ 0,p/2\right] \). Using that \(g_p\left( p/2\right) = 0\) according to property (i) in Lemma 3, and that
we obtain an upper bound on \(|g_p(x)|\). Similarly we can extrapolate around \(x = 0\) and use the fact that \(g_p(0) = \frac{\gamma _0}{2}\) to obtain
This means that we can transform an upper bound q(x) on \(|g_p^{(1)}(x)|\) for all \(x \in [0,p/2]\) into an upper bound on \(|g_p(x)|\) for every \(x \in [0,p/2]\). We formalize this transformation by defining an operator T that maps the upper bound q on \(|g_p^{(1)}|\) into an upper bound Tq on \(|g_p|\). This operator is defined as,
and includes the uniform upper bound \(w_0\) on \(|g_p|\) as defined in Lemma 3 (iii). From the analysis above it follows that \(|g_p(x)| \le (Tq)(x)\) for \(x \in \left[ 0,p/2 \right] \). Note that (Tq)(x) provides a tighter bound than the bound based on \(|{\varDelta }|g\) alone, which is given by \(w_0\).
We generalize this idea to higher-order derivatives by introducing appropriate operators in Definition 8. The idea is that a bound q on \(|g_p^n|\) may be propogated in dynamic programming fashion to obtain a bound \(T \cdots Tq\) on \(|g_p|\). In our case, however, we have to define two operators \(T^1\) and \(T^2\) since the process of bound propagation is different for odd and even higher-order derivatives. In Definition 9, we use these operators to define functions \(q_0^n\), \(n \in {\mathbb {N}}\), which represent a bound on \(\left| g_p(x)\right| \) based on information on the first n derivatives of g. Intuitively, including more derivatives should lead to sharper bounds. This intuition is confirmed in Corollary 1.
Definition 8
For a given \(p >0\), a function \(q:\left[ 0,p/2\right] \rightarrow {\mathbb {R}}\), and parameters \(w >0\) and \(\gamma \in {\mathbb {R}}\), define the operators \(T_{w,\gamma }^1\) and \(T_{w,\gamma }^2\) by
and
Definition 9
Let \(n \in {\mathbb {N}}\) and \(p >0\) be given. Let \(w_k > 0\) and \(\gamma _k \in {\mathbb {R}}\), \(k =0,\ldots ,n\), be given constants. Define \(q_n^n:\left[ 0,p/2\right] \rightarrow {\mathbb {R}}\) as \(q_n^n(x):= w_n\). For \(k < n\), define \(q_k^n:\left[ 0,p/2\right] \rightarrow {\mathbb {R}}\) using backward recursion as
Before we are ready to prove that \(q_0^n\) yields a bound on \(|g_p|\), we need some elementary properties of the operators introduced in Definition 8. In Lemma 4, we prove that \(T^j\), \(j = 1,2\), are non-negative and monotone operators.
Lemma 4
Let \(p > 0\) be given. Let \(q, \tilde{q}:\left[ 0,p/2\right] \rightarrow {\mathbb {R}}\) be non-negative functions such that \({\bar{q}} \ge q\). Then for all \(w >0\) and \(\gamma \in {\mathbb {R}}\),
-
(i)
\(T^j_{w,\gamma }q\) is a non-negative function, \(j = 1,2\), and
-
(ii)
\(T^j_{w,\gamma }{\bar{q}} \ge T^i_{w,\gamma }q\), \(j = 1,2\).
Proof
Property (i) follows directly from the non-negativity of q. Property (ii) is a direct consequence of \({\bar{q}} \ge q\). \(\square \)
Proposition 1
Let \(n \in {\mathbb {N}}\) and \(p > 0\) be given. Let \(g:[0,p] \rightarrow {\mathbb {R}}\) be a packed density with discontinuities \((\gamma _0,\ldots ,\gamma _n)\). Define \(g_p:[0,p] \rightarrow {\mathbb {R}}\) as \(g_p(x):= \frac{1}{2}(g(x) - g(p - x))\). For \(k = 0,\ldots ,n\), define
so that \(w_k\) denotes a uniform bound on \(\left| g_p^{(k)}\right| \). Define \(q_k^n\), \(k = 0,\ldots ,n\), as in Definition 9. Then,
Proof
The non-negativity of \(T^j\), \(j=1,2\), implies that \(q_k^n\), \(k = 0,\ldots ,n\), are non-negative functions. We prove the stronger claim
for all \(x \in \left[ 0,p/2\right] \), for \(k = 0,\ldots ,n\) using backward induction.
For \(k = n\), the inequality in (9) follows directly from property (iii) and (iv) in Lemma 3. For the induction step, assume (9) holds for \(k = m + 1\), with \(0 \le m < n\). We consider odd and even m separately. For even m, we have to show that
Since
it suffices to show that for all \(x \in [0,p/2]\),
and
The induction step for even m then follows by combining (10), (11), and (12).
The inequality in (10) is due to property (iii) in Lemma 3. To prove (11), we use that
by the triangle inequality. Using the induction hypothesis and the fact that \(q^n_{m+1}\) is a non-negative function, we obtain
Then, (11) follows by inserting \(g_p^{(m)}(0) = \frac{\gamma _m}{2}\) by Lemma 3 (ii), and rearranging terms. The inequality in (12) can be proved in a similar manner as (11) by applying the triangle inequality to \(\left| g_p^{(m)}\left( p/2\right) -g_p^{(m)}(x)\right| \). We conclude that the induction step holds for even m.
For odd m, we have to show that
By definition, \((T^1_{w_m,\gamma _{m-1}}q_{m+1}^n)(x)\) equals
so that it suffices to show for all \(x \in [0,p/2]\) that
and
The inequality in (13) follows directly from property (v) in Lemma 3. To prove (14) we make use of in Lemma 3 (iv), which states that there exists \(x_m \in \left( 0,p/2\right] \) such that \(g_p^{(m)}(x_m) = - \frac{\gamma _{m - 1}}{p}\). By the triangle inequality,
Together with the induction hypothesis, this yields
To arrive at (14), we make the following observation
where the inequality holds since \(x_m \in \left( 0,p/2\right] \) and \(q^n_{m+1}\) is non-negative. This completes the induction step for odd m, and the proof of (9). \(\square \)
We now present a corollary of Lemma 4, which states the intuitive result that the bounds on \(g_p\) become sharper if more higher-order derivatives are included.
Corollary 1
Let \(n \in {\mathbb {N}}\) and \(p > 0\) be given. Let \(\gamma _k\) and \(w_k > 0 \), \(k = 0,\ldots ,n\), be given constants. Define \(q_0^l\), \(l = 0,\ldots ,n\), as in Definition 9. Then,
Proof
Fix an \(l \in \{1,\ldots ,n\}\). We will use backward induction to prove that \(q_k^{l-1} \ge q_k^{l}\) for \(k = 0,\ldots ,l-1\). The claim then follows by setting \(k= 0\).
It follows directly from the definition of \(q_k^n\) that \(q_{l-1}^{l-1} \ge q_{l-1}^{l}\). For the induction step, suppose that \(q_k^{l-1} \ge q_k^{l}\) for some k, \(0<k\le l - 1\). It follows from the monotonicity of \(T^j\), \(j = 1,2\), that \(q_{k-1}^{l-1} \ge q_{k-1}^{l}\), completing the proof. \(\square \)
3.4 Error bounds
We are now ready to state the main results of this section. In Theorem 2, we formulate an improved bound on the expectation of PSP(p) functions and Theorem 3 states the bound on the expectation of half-periodic functions where the underlying periodic function is PSP(p).
Theorem 2
Let \(n \in {\mathbb {N}}\) and \(p > 0\) be given. Let \(\varphi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a PSP(p) function and let \( B = (B_0,\ldots ,B_n)\) and \( C = (C_0,\ldots ,C_n)\) be positive constants. Then, for \(M_n\) defined as
there holds
where \(q_0^n\) is defined as in Definition 9, with \(\gamma _k = 0\), \(k = 0,\ldots ,n\), and
Proof
For a given PSP(p) function \(\varphi \) and pdf \(f \in {\mathcal {F}}_n\), we know from Lemma 1 that
where \(f_p\) denotes the classical packed density corresponding to f. The function \(f_p\) is a packed density with discontinuities \(\gamma = (0,\ldots ,0)\). Lemma 2 informs us that
where \(g_p(x)=\frac{1}{2}(f_p(x) - f_p(p - x))\). This implies
By Lemma 1, property (iii), we know that \(B_k\) is an upper bound on \(|{\varDelta }|f_p^k([0,p])\), \(k = 0,\ldots ,n\). Combining Proposition 1 with the monotonicity of the operators \(T^j\), \(j = 1,2\), yields that \(q_0^n\) is an upper bound on \(|g_p|\), completing the proof. \(\square \)
Remark 5
Note that the bound presented in Theorem 2 is independent of C. This is because the discontinuities of the classical packed density are zero.
Theorem 3
Let \(n \in {\mathbb {N}}\) and \(p > 0\) be given. Let \(\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a half-periodic function defined as
where \(\varphi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) is a PSP(p) function. Let \(B = (B_0,\ldots ,B_n)\) and \( C = (C_0,\ldots ,C_n)\) be positive constants. Then, for \(M_n\) defined as
there holds
where \(q_0^n\) is defined as in Definition 9, with \(\gamma _k = C_k\), \(k = 0,\ldots ,n\), and
Proof
For a given half-periodic function \(\psi \) with underlying PSP(p) function \(\varphi \) and pdf \(f \in {\mathcal {F}}_n\), we know from Lemma 1 that
where \({\hat{f}}_p\) denotes the half-packed density corresponding to f. The function \({\hat{f}}_p\) is a packed density with discontinuities \(\gamma = (f^{(0)}(0),\ldots ,f^{(n)}(0))\). Lemma 2 informs us that
where \(g_p(x)=\frac{1}{2}({\hat{f}}_p(x) - {\hat{f}}_p(p - x))\). This implies
By Lemma 1, property (iii), we know that \(B_k - |f^{(k)}(0)|\) is an upper bound on \(|{\varDelta }|{\hat{f}}_p^k([0,p])\), \(k = 0,\ldots ,n\). Furthermore, \(|\gamma _k| = |f^{(k)}(0)| \le C_k\). Combining Proposition 1 with the monotonicity of the operators \(T^j\), \(j = 1,2\), yields that \(q_0^n\) is an upper bound on \(|g_p|\), and the result follows. \(\square \)
4 Applications and examples
In this section, we apply the results in Sect. 3 to specific functions. As in Sect. 3, we make a distinction between periodic and half-periodic functions. First, we apply Theorem 2 to a particular PSP(p) function. Second, we derive an improved error bound for the shifted LP-relaxation approximation of one-dimensional SIR models. Since the underlying difference function is half-periodic, we can use Theorem 3 to derive such a bound. This error bound can be generalized to higher-dimensional SIR models. Finally, we conduct numerical experiments to compare the performance of the error bound by Romeijnders et al. (2016b) and the improved bound derived in this section.
4.1 Point symmetric periodic functions
Here, we derive a bound on the expectation of the underlying periodic function \(\varphi \) for the shifted LP-relaxation for SIR models, defined as \(\varphi (x):= x - \lceil x - \frac{1}{2}\rceil \). Note that \(\varphi \) is a PSP(1) function and that \(|\varphi (x)| = x\) for \(x \in [0,\frac{1}{2}]\). In the notation of Theorem 2, take \(n = 1\), which is to say that we make use of the total variation of the underlying pdf and its first derivative. Furthermore, \(q^1_1(x) = \frac{B_1}{2}\) and
Applying Theorem 2 yields
Using this, we find that for any \(f \in {\mathcal {F}}_1\)
Since this bound holds for all \(f\in {\mathcal {F}}_1\), it follows that if \(\omega \) has pdf \(f \in {\mathcal {F}}_1\), then
This result is an improvement of the bound by Romeijnders et al. (2016b), who showed that
Note that the improvement is large if \(|{\varDelta }|f'\) is small relative to \(|{\varDelta }|f\). We now apply this result to a range of specific pdf’s.
Example 1
Let f denote the pdf of a normally distributed random variable \(\omega \) with variance \(\sigma ^2\). Then,
Observe that the ratio
increases linearly in \(\sigma \). This implies that the improvement over the original total variation bound is unbounded and increases with \(\sigma \). We have
Figure 2 shows the true value of \(\sup _{z\in {\mathbb {R}}}\{{\mathbb {E}}_{\omega }[\varphi (\omega - z)]\}\), the upper bound \(\frac{1}{2}h(|{\varDelta }|f)\) derived by Romeijnders et al. (2016b), and the upper bound \(k(|{\varDelta }|f,|{\varDelta }|f')\) based on \(M_1\). Moreover, we include the upper bound based on \(M_2\). The latter bound is tractable, but an analytical expression is cumbersome and does not yield further insights and is therefore omitted. Note that the bounds based on \(M_1\) and \(M_2\) provide a tighter bound compared to \(\frac{1}{2}h(|{\varDelta }|f)\) for large values of \(\sigma \). \(\lozenge \)
The true value of \(\sup _{z\in {\mathbb {R}}}\{{\mathbb {E}}_{\omega }[\varphi (\omega - z)]\}\) (solid), and the upper bounds based on Romeijnders et al. (2016b) (dotted), \(M_1\) (dashed), and \(M_2\) (dash-dotted) as a function of \(\sigma \), where \(\omega \) follows a normal distribution with variance \(\sigma ^2\)
Note that our results only apply to continuously differentiable pdf, nevertheless, for continuous pdf f that are not continuously differentiable we can still apply our results by considering the right derivative of f, denoted \(f'_+\), instead of the derivative of f. The reason for this lies in the fact that there exists a continuously differentiable approximation \({\tilde{f}}\) of f such that \(|{\varDelta }|f = |{\varDelta }|{\tilde{f}}\), \(|{\varDelta }|f'_+ = |{\varDelta }|\tilde{f}'\), and \({\mathbb {E}}_f[\varphi (\omega - z)]\) is arbitrarily close to \({\mathbb {E}}_{{\tilde{f}}}[\varphi (\omega - z)]\). We illustrate this in the next example.
Example 2
Suppose that \(\omega \) follows a triangular distribution with support [a, b] and mode m, \(a< m < b\). See Fig. 3 for illustration.
Denote the pdf of \(\omega \) by f. Write \(d := b -a\) and note that \(f(m) = \frac{2}{d}\), so that,
furthermore,
This leads to
Note that \(|{\varDelta }|f\) is independent of the mode m, however, changing m does affect \(|{\varDelta }|f'_+\). In fact, for given a and b, \(|{\varDelta }| f'_+\) is minimized by \(m = \frac{1}{2}(a + b)\). Hence, as the mode is closer to the midpoint of the support of \(\omega \), \(|{\varDelta }|f'_+\) is smaller and we obtain tighter bounds. \(\lozenge \)
4.2 Error bound shifted-LP relaxation
In this section, we consider the underlying difference function \(\psi \), defined in (4), for the shifted LP-relaxation for SIR models. Recall that bounds on the expectation of \(\psi \) can be used directly to derive error bounds for the shifted LP-relaxation for SIR models.
We apply Theorem 3 with \(n = 1\) to derive a such a bound. We have \(\varphi (x) = x- \left\lceil x - \frac{1}{2}\right\rceil \). Like in Sect. 4.1, \(|\varphi (x)| = x\) for all \(x \in [0,\frac{1}{2}]\). Note that \( q^1_1(x) = C_0 + \frac{B_1}{2} =: D\) and that
Hence, by Theorem 3,
where \(D = 2C_0 + B_1\). Note that for any pdf f,
where equality holds if f is unimodal. For this reason, we take \(C_0 = \frac{B_0}{2}\), so that the resulting bound holds for all pdf \(f \in {\mathcal {F}}_1\). For unimodal pdf’s the resulting bound is the tightest bound we can provide, whereas tighter bounds can be derived for non-unimodal pdf. Simple computations yield
where
for positive x and y. We thus have that for any \(f \in {\mathcal {F}}_1\),
The original bound by Romeijnders et al. (2016b) is given by \(\frac{|{\varDelta }|f}{16}\), so \(S(|{\varDelta }|f,|{\varDelta }|f')\) represents the improvement over their results. Note that \(S(|{\varDelta }|f,|{\varDelta }|f') \rightarrow \frac{1}{3}\) as \(\frac{|{\varDelta }|f'}{|{\varDelta }|f} \rightarrow 0\), which is to say that the improvement factor converges to three. We return to this fact in the following example, where we apply our results to a normally distributed random variable.
Example 3
We numerically evaluate \(||{\hat{Q}} - Q||_{\infty }\) in the one-dimensional SIR case, where \({\hat{Q}}\) denotes the shifted-LP relaxation by Romeijnders et al. (2016b) as in Definition 1 and where \(\omega \) follows a normal distribution with arbitrary mean and variance \(\sigma ^2\), for \(\sigma \in [0.2,4]\). We compare the actual error to the error bound based on Romeijnders et al. (2016b) and the improved error bounds based on \(M_1\) and \(M_2\). We omit the analytical expression for the bound based on \(M_2\), which is tractable but cumbersome.
Denote the pdf of \(\omega \) by f. To compute the (improved) error bounds, we make use of the expressions for \(|{\varDelta }|f\) and \( |{\varDelta }|f'\) found in Example 1. It follows from these expressions that
as \(\sigma \rightarrow \infty \), which implies that the improvement factor over the original total variation bound converges to three for large values of \(\sigma \). Figure 4 shows the results of this numerical experiment. Note that the improvement over the original error bound increases with \(\sigma \). \(\lozenge \)
The true value of \(||{\hat{Q}} - Q||_{\infty }\) (solid), and the upper bounds based on Romeijnders et al. (2016b) (dotted), \(M_1\) (dashed), and \(M_2\) (dash-dotted) in the one-dimensional SIR case as a function of \(\sigma \), where \(\omega \) follows a normal distribution with variance \(\sigma ^2\)
5 Conclusion
We consider existing convex approximations for two-stage mixed-integer recourse models. We construct a hierarchy of bounds on the expectation of periodic and half-periodic functions using total variations of higher-order derivatives of the underlying probability density function. We use these results to derive improved error bounds for the shifted LP-relaxation of simple integer recourse models. Moreover, the results presented here may be used to improve error bounds of convex approximations for general mixed-integer recourse model approximations.
There are multiple directions for future research. One extension is to generalize our results to a to a higher-dimensional setting. A first step in this direction may be to consider totally unimodular integer recourse models. Another avenue is to apply the results to a particular application of integer recourse models. Finally, our results may be extended to a larger class of periodic functions, which may be useful for other types of convex approximations.
References
Ahmed S, Tawarmalani M, Sahinidis NV (2004) A finite branch-and-bound algorithm for two-stage stochastic integer programs. Math Program 100:355–377
Birge JR, Louveaux F (1997) Introduction to stochastic programming. Springer, New York
Carøe CC, Schultz R (1999) Dual decomposition in stochastic integer programming. Oper Res Lett 24:37–45
Gade D, Küçükyavuz S, Sen S (2014) Decomposition algorithms with parametric gomory cuts for two-stage stochastic integer programs. Math Program 144:39–64
Gassmann HI, Ziemba WT (eds) (2013) Stochastic programming: applications in finance, energy, planning and logistics, volume 4 of World Scientific Series in finance. World Scientific, Singapore
Klein Haneveld WK, Stougie L, van der Vlerk MH (2006) Simple integer recourse models. Math. Program 108:435–473
Laporte G, Louveaux FV (1993) The integer L-shaped method for stochastic integer programs with complete recourse. Oper Res Lett 13:133–142
Ntaimo L (2013) Fenchel decomposition for stochastic mixed-integer programming. J Glob Optim 55:141–163
Rinnooy Kan AHG, Stougie L (1988) Stochastic integer programming. In: Ermoliev Y, Wets RJ-B (eds) Numerical techniques for stochastic optimization, volume 10 of Springer series in computational mathematics. Springer, Berlin, pp 201–213
Romeijnders W, Stougie L, van der Vlerk MH (2014) Approximation in two-stage stochastic integer programming. Surv Oper Res Manag Sci 19:17–33
Romeijnders W, van der Vlerk MH, Klein Haneveld WK (2015) Convex approximations of totally unimodular integer recourse models: a uniform error bound. SIAM J Optim 25:130–158
Romeijnders W, Schultz R, van der Vlerk MH, Klein Haneveld WK (2016a) A convex approximation for two-stage mixed-integer recourse models with a uniform error bound. SIAM J Optim 26:426–447
Romeijnders W, van der Vlerk MH, Klein Haneveld WK (2016b) Total variation bounds on the expectation of periodic functions with applications to recourse approximations. Math Program 157:3–46
Romeijnders W, Morton D, van der Vlerk MH (2017) Assessing the quality of convex approximations for two-stage totally unimodular integer recourse models. INFORMS J Comput 29:211–231
Schultz R (2003) Stochastic programming with integer variables. Math Program 97:285–309
Schultz R, Stougie L, van der Vlerk MH (1998) Solving stochastic programs with integer recourse by enumeration: a framework using Gröbner basis reductions. Math Program 83:229–252
Sen S (2005) Algorithms for stochastic mixed-integer programming models. Handb Oper Res Manag Sci 12:515–558
Sen S, Higle JL (2005) The \(C^3\) theorem and a \(D^2\) algorithm for large scale stochastic mixed-integer programming: set convexification. Math Program 104:1–20
Shapiro A, Dentcheva D, Ruszczyński A (2009) Lectures on stochastic programming: modeling and theory. SIAM, Philadelphia
van der Vlerk MH (1995) Stochastic programming with integer recourse. Ph.D. thesis, University of Groningen, The Netherlands
van der Vlerk MH (2004) Convex approximations for complete integer recourse models. Math Program 99:297–310
Wallace SW, Ziemba WT (eds) (2005) Applications of stochastic programming. MPS-SIAM series on optimization, SIAM, Philadelphia
Zhang M, Küçükyavuz S (2014) Finitely convergent decomposition algorithms for two-stage stochastic pure integer programs. SIAM J Optim 24:1933–1951
Acknowledgements
We are grateful to Wim Klein Haneveld for his constructive comments on a preliminary version of our manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
van der Laan, N., Romeijnders, W. & van der Vlerk, M.H. Higher-order total variation bounds for expectations of periodic functions and simple integer recourse approximations. Comput Manag Sci 15, 325–349 (2018). https://doi.org/10.1007/s10287-018-0315-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10287-018-0315-z