Abstract
In production-inventory problems customer demand is often subject to uncertainty. Therefore, it is challenging to design production plans that satisfy both demand and a set of constraints on e.g. production capacity and required inventory levels. Adjustable robust optimization (ARO) is a technique to solve these dynamic (multistage) production-inventory problems. In ARO, the decision in each stage is a function of the data on the realizations of the uncertain demand gathered from the previous periods. These data, however, are often inaccurate; there is much evidence in the information management literature that data quality in inventory systems is often poor. Reliance on data “as is” may then lead to poor performance of “data-driven” methods such as ARO. In this paper, we remedy this weakness of ARO by introducing a model that treats past data itself as an uncertain model parameter. We show that computational tractability of the robust counterparts associated with this extension of ARO is still maintained. The benefits of the new model are demonstrated by a numerical test case of a well-studied production-inventory problem. Our approach is also applicable to other ARO models outside the realm of production-inventory planning.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With the uprise of Big Data, most of the currently available (theoretical or practical) methods for controlling a multi-stage production-inventory system, are using a “data-driven” approach. At each period t data in the future is treated as uncertain, while data from the past is considered known (certain). The affinely adjustable robust counterpart (AARC) method (Ben-Tal et al. 2004), which is the focus of this paper, needs exact past demands to derive a decision, by inserting them in a linear decision rule. In reality, however, there is a strong evidence (see below) that even past data is far from being exact. For example, in inventory/production systems what is usually reported as a surrogate for the demand are sales, which then ignores lost sales due to excess demand.
In general, even when it seems that the full data on the uncertain demand is available at some stage, one cannot rely blindly on this information. Arguably, many developments in information technology have enabled firms to collect real-time data. However, despite these enormous developments in our Big Data era, poor data quality is still a big issue. In DeHoratius and Raman (2008) results of an empirical study are reported; they found that 65 % of the inventory records were inaccurate, and “the value of the inventory reflected by these inaccurate records amounted to 28 % of the total value of the expected on-hand inventory”. In Redman (1998) it is estimated that 1–5 % of data fields are erred, which led to a costs increase of 8–12 % of revenue in some carefully studied cases, and to a consumption of 40–60 % of the expenditure in service organizations. Haug et al. (2011) summarize the literature that deal with the big impact of poor data quality: “Less than 50 % of companies claim to be very confident in the quality of their data”, “75 % of organizations have identified costs stemming from dirty data”. See also Soffer (2010) for a general exploration of data inaccuracy in business processes. One paper that develops a method to handle inaccurate inventory records is by Kök and Shang (2007). Their approach assumes that the distribution of the errors (describing the inaccuracy) is known and that inspections can be made at certain costs to exactly observe these errors.
In this paper we extend the AARC method to a method named adjustable robust counterpart with decision rules based on inexact data (ARCID) that incorporate past data uncertainty while keeping the resulting (deterministic) robust counterpart tractable. This is our main contribution, and it is achieved using results and techniques from the current robust optimization arsenal.
We illustrate the benefits of the ARCID model by revisiting the inventory problem that was used in the first paper on ARO (Ben-Tal et al. 2004). Numerical results for this production-inventory problem show that if one neglects the inexact nature of the revealed data, then the resulting solution might violate the constraints in many scenarios. For our numerical example, violations occurred for up to \(80\,\%\) of the simulated demand trajectories. The ARCID model is able to avoid this severe infeasibility and produce more reliable solutions.
Although the focus of this paper is on production-inventory problems, there are various other areas where our ARCID model could be used to solve uncertain multistage problems. For example, ARO techniques were used in facility location planning (Baron et al. 2011), flexible commitment models (Ben-Tal et al. 2005), portfolio optimization (Calafiore 2008, 2009; Rocha and Kuhn 2012), capacity expansion planning (Ordóñez and Zhao 2007) and management of power systems (Guigues and Sagastizábal 2012; Ng and Sy 2014) among others. A more elaborate list of examples up to 2011 can be found in the aforementioned survey by Bertsimas et al. (2011a). We emphasize that our proposed ARCID framework remains applicable for multistage problems outside the realm of production-inventory planning.
The remainder of this paper is organized as follows. In Sect. 2 we describe the adjustable robust models used in the literature. Section 3 then introduces the new ARCID models with inexact revealed data in the decision rules and derive tractable representations of the resulting optimization problems. Section 4 presents our production-inventory model and the corresponding ARCID model. The numerical results are given and analyzed in Sect. 5. Conclusions are presented in Sect. 6. Throughout this paper we use bold lower-case and upper-case letters for vectors and matrices, respectively, while scalars are printed in regular font.
2 Adjustable robust models
In the nonadjustable RC model all decisions are chosen prior to knowing the realization of the uncertain parameter. This can be very conservative in a dynamic setting where part of the variables can be chosen at a later stage when some information on the uncertain parameters is revealed. Suppose that \(\mathbf x \in \mathbb {R}^n\) is a here-and-now decision and that we have an additional wait-and-see decision \(\mathbf y \in \mathbb {R}^m\). This means that \(\mathbf x \) has to be chosen prior to knowing any of the information on the uncertain parameters and \(\mathbf y \) has to be chosen after some information is revealed. We start with the assumption that \(\mathbf y \) is chosen after perfectly accurate information on \(\varvec{\zeta }\) has been revealed. The model with this underlying assumption is called the adjustable robust optimization model (ARO), where the variables \(\mathbf y \) can adjust themselves to the revealed information. This model was introduced in Ben-Tal et al. (2004):

where J is the number of constraints, \(\mathbf{a _i},\mathbf c \in R^n\), \(\mathbf A _i\in \mathbb {R}^{n\times L}\), \(\mathbf b _i\in \mathbb {R}^m\), and \(d_i \in \mathbb {R}\). The uncertainty in our model is driven by the parameter \(\varvec{\zeta }\), which resides in a closed convex set \(\mathcal {Z}\subset \mathbb {R}^L\). The parameter \(\mathbf{a _i}\) is called the nominal value of the coefficients for \(\mathbf x \) in the i-th constraint. This model can be readily extended to the case where \(d_i\) also depends on \(\varvec{\zeta }\). We can see \(\mathbf y \) as a function, or decision rule, on the uncertain parameters since we have to assign a feasible value for each realization \(\varvec{\zeta }\). However, finding the optimal decision rule would involve optimizing over the class of all functions, which is in general intractable (in fact NP-hard as shown in Guslitzer 2002). We restrict the functional dependence to linear decision rules for the wait-and-see decision:
where \(\mathbf u \in \mathbb {R}^m\) and \(\mathbf V \in \mathbb {R}^{m \times L}\) are new (here-and-now) decision variables that determine the affine dependence on the revealed value of the parameter \(\varvec{\zeta }\). Although the restriction from ‘any’ function to a linear decision rule might seem very severe, these linear decision rules appear to perform quite well in practice (Ben-Tal et al. 2004, 2005) and are even provably optimal in some cases (Bertsimas et al. 2011b; Bertsimas and Goyal 2012; Iancu et al. 2013). With this new so-called linear decision rule, the problem (ARO) can be written as

This problem is now again a standard robust optimization problem. We may, without loss of generality, consider the uncertainty constraint-wise, see Ben-Tal et al. (2009), in order to derive the tractable affinely adjustable robust counterpart (AARC) for each constraint i:
which is equivalent to
or
where \(\delta ^*(\varvec{\nu }\ | \ \mathcal {Z}) = \max _{\varvec{\zeta }\in \mathcal {Z}}\{\varvec{\zeta }^\top \varvec{\nu }\}\) is the so-called support function of the set \(\mathcal {Z}\). The notation \(\delta ^*\) is the conjugate function of the indicator function
For many different closed convex sets \(\mathcal {Z}\) the support function can be explicitly constructed. Some examples are given in Table 1 and many more can be found in (Ben-Tal et al. 2015, pp. 275).
3 The new adjustable robust model based on inexact data
This section introduces our model that extends the ARC model to the case where revealed data is inexact. We stress that the models described here are more general and not limited to production-inventory problems. They could be used for any ARO problem within operations management where the revealed data is inexact.
The ARO model with decision rules based on exact data assumes that there is one moment in time where the data \(\varvec{\zeta }\in \mathcal {Z}\), used to decide upon the variable \(\mathbf y \), is known exactly. However, in many practical applications only an estimate \({\widehat{\varvec{\zeta }}}\in \mathcal {Z}\) of the true value \(\varvec{\zeta }\) can be obtained. In that case we have inexact data and \({\widehat{\varvec{\zeta }}}\) is not exactly equal to \(\varvec{\zeta }\), but we may assume that the estimation error \({\widehat{\varvec{\zeta }}} - \varvec{\zeta }\) resides in another closed convex set \({\widehat{\mathcal {Z}}}\), which we call the estimation uncertainty. We also denote this as \(\varvec{\zeta }\in \{{\widehat{\varvec{\zeta }}}\} + {\widehat{\mathcal {Z}}}\), the Minkowski sum of a singleton and a set. Note that estimation errors of different components of \({\widehat{\varvec{\zeta }}} - \varvec{\zeta }\) can be correlated. The decision rule for the wait-and-see variable is only allowed to use the estimate \({\widehat{\varvec{\zeta }}}\) (and not the unobserved \(\varvec{\zeta }\)):
where (here-and-now) decision variables \(\mathbf u \) and \(\mathbf V \) determine the affine dependence of \(\mathbf y \) on estimate \({\widehat{\varvec{\zeta }}}\). We call the robust counterpart in this new setting the (affine) adjustable robust counterpart with decision rules based on inexact data, or ARCID:

where
provides us with a new uncertainty set that describes in a general way the uncertain parameter \(\varvec{\zeta }\), its estimate \({\widehat{\varvec{\zeta }}}\) and the relation between these two uncertain vectors. Note that the set \(~\mathcal {U}\) is closed and convex whenever the sets \(\mathcal {Z}\) and \({\widehat{\mathcal {Z}}}\) are closed and convex. The relation between the RC, the new ARCID and the classical ARC uncertainty sets in terms of the inexactness in the revealed data, is depicted in Fig. 1. In the RC none of the revealed information is used, so it assumes that the parameter can still take any value in the uncertainty set when deciding upon \(\mathbf y \). The ARCID uses the revealed information and takes into account that the data used in the decision rule is inexact and therefore is still uncertain to some extent. The ARC model also uses the revealed information, but does however assume that these data are exact. The implications of this assumption, when in reality the observed information is inexact, shall become clear in our numerical example in Sect. 4. Note that in the uncertainty described in (3) both the true parameter and its estimate are in the set \(\mathcal {Z}\). Another modelling choice could be to leave out any further condition on the estimate and just have \(({\widehat{\varvec{\zeta }}} - \varvec{\zeta }) \in {\widehat{\mathcal {Z}}}\). Omitting this condition \({\widehat{\varvec{\zeta }}} \in \mathcal {Z}\), however, leads to an increase of the size of the uncertainty set for the estimate. In that case, the decision rule should be valid on a larger uncertainty set which might lead to more conservative solutions. Furthermore, some values for the estimates can be naturally omitted. For example, demand is nonnegative and any negative estimates can be rounded up to zero.
As in the previous ARC setting we consider, without loss of generality, constraint-wise uncertainty. Hence, we only have to determine the tractable formulation of the i-th constraint
which follows from the next theorem.
Theorem 1
Let \(\mathcal {U}\) be a closed set with nonempty relative interior as given in (3). Then \((\mathbf x ,\mathbf u ,\mathbf V )\) satisfies constraint (4) if and only if there exists a \(\varvec{w}_i\in \mathbb {R}^L\) that satisfies
Proof
We can replace the semi-infinite constraint (4) by constraints involving maximization over the uncertainty and obtain the following constraint:
or, by using the definition of support functions,
Hence, all we need to do is to find an expression for the support function of \(\mathcal {U}\). To do so, note that for the indicator function we have \(\delta \left( \begin{pmatrix}{}\varvec{\zeta }\\ {\widehat{\varvec{\zeta }}} \end{pmatrix} |\ \mathcal {U}\right) = \delta (\varvec{\zeta }\ |\ \mathcal {Z}) + \delta ({\widehat{\varvec{\zeta }}}\ |\ \mathcal {Z}) + \delta (({\widehat{\varvec{\zeta }}} - \varvec{\zeta }) \ |\ {\widehat{\mathcal {Z}}})\). If we define the function \(h(\varvec{\zeta }, {\widehat{\varvec{\zeta }}}) = \delta \left( ({\widehat{\varvec{\zeta }}} - \varvec{\zeta }) \ |\ {\widehat{\mathcal {Z}}}\right) \), then by using the definition of conjugate functions as in Rockafellar (1997), we can obtain its conjugate function:
Using this conjugate function, and the fact that \(\mathcal {U}\) has nonempty relative interior, we can now find the expression for the support function in (5) using the conjugate of a sum of functions (see Rockafellar 1997, Chapter 16):
Substituting this result in (5) yields that (4) is feasible if and only if there exist \(\varvec{w}_i,{\varvec{\widetilde{w}}_i},\varvec{z}_i,{\varvec{\widetilde{z}}_i}\in \mathbb {R}^L\) that satisfy
The result then follows by elimination of the variables \({\varvec{\widetilde{w}}_i}\), \(\varvec{z}_i\) and \({\varvec{\widetilde{z}}_i}\). \(\square \)
The two assumptions on the uncertainty set (closedness and nonempty relative interior of \(\mathcal {U}\)) used in Theorem 1 are satisfied for all closed sets \(\mathcal {Z}\) and \({\widehat{\mathcal {Z}}}\) with nonempty relative interior and 0 being an element of the relative interior of \({\widehat{\mathcal {Z}}}\). A few common choices for uncertainty sets, that satisfy these conditions, have been given in Table 1. Below we give two examples of constraints with different choices for the estimation uncertainty. In the first example (Box-Box) we have both box uncertainty for the parameter \(\varvec{\zeta }\) and a box for the estimation error (independent estimation errors). In the second example (Box-Ball) the estimation errors reside in a ball.
Example 1
If \(\mathcal {Z}= \{\varvec{\zeta }: ||\varvec{\zeta }||_\infty \le \theta \}\) and \({\widehat{\mathcal {Z}}} = \{\varvec{\xi }: ||\varvec{\xi }||_\infty \le \rho \}\) for some scalar uncertainty levels \(\theta ,\rho \ge 0\) then, according to Theorem 1, \((\mathbf x ,\mathbf u ,\mathbf V )\) satisfies constraint (4) if and only if there exists a \(\varvec{w}_i\in \mathbb {R}^L\) such that
where the expressions for the support functions with these choices for the uncertainty sets are found using Table 1. This constraint can be represented by a set of linear constraints.
Example 2
If \(\mathcal {Z}= \{\varvec{\zeta }: ||\varvec{\zeta }||_\infty \le \theta \}\) and \({\widehat{\mathcal {Z}}} = \{\varvec{\xi }: ||\varvec{\xi }||_2 \le \rho \}\) for some scalar uncertainty levels \(\theta ,\rho \ge 0\) then, according to Theorem 1, \((\mathbf x ,\mathbf u ,\mathbf V )\) satisfies constraint (4) if and only if there exists a \(\varvec{w}_i\in \mathbb {R}^L\) such that
where the expressions for the support functions with these choices for the uncertainty sets are again found using Table 1. This constraint can be represented by a set of linear constraints and a conic quadratic constraint.
Theorem 1 can also be used to argue that the new ARCID model bridges the gap between models that do not use information at all in the second stage (RC) and those that rely on fully accurate revealed information in the decision rules (ARC). Namely, if the estimation uncertainty is large (i.e. \({\widehat{\mathcal {Z}}}\) is large), then there is no value in the revealed inexact data. In that case the optimal value of the nonadjustable version is equal to the optimal value of (ARCID). More formally, consider the situation where there exists a realisation \({\bar{\varvec{\zeta }}} \in \mathcal {Z}\) such that \(\mathcal {Z}\subset {\bar{ \varvec{\zeta }}} + {\widehat{\mathcal {Z}}}\). Then, if (P:ARCID) is feasible, it follows directly that there must also exist a decision rule with \(\mathbf V = 0\), i.e., a nonadjustable decision. For Example 1 and 2 we have that the ARCID model is equivalent to the nonadjustable model when \(\rho \ge \theta \) for the first example (Box-Box) and \(\rho \ge \sqrt{L}\theta \) for the second example (Box-Ball). In case there is no estimation error (\({\widehat{\mathcal {Z}}} = \{0\}\)), the ARC and the ARCID are equivalent in the sense that they have the same feasible region and the same optimal objective value.
So far, we have focussed on the two period case for illustrative purposes. However, often we have multiple periods \(1,2,\ldots ,T\), in which we consecutively have to make decisions \(\mathbf y ^1,\mathbf y ^2,\ldots ,\mathbf y ^T\). In period t we can make decisions based on estimates available in that period: estimate \({\widehat{\varvec{\zeta }}}^{t}\). So, we have in period t a linear decision rule \(\mathbf y ^t = \mathbf u ^t + \mathbf V ^t\varvec{R}^t{\widehat{\varvec{\zeta }}}^{t}\), with variables \(\mathbf u ^t \in \mathbb {R}^m\) and \(\mathbf V ^t \in \mathbb {R}^{m \times L}\). The matrix \(\varvec{R}^t \in \mathbb {R}^{L\times L}\) is the (fixed) diagonal information matrix with entries 0 everywhere but on the diagonal. The entries on the diagonal are either 0 (if no data is revealed) or 1 if the estimate is available at time t. For the standard case in the literature, with decision rules based on exact data \(\varvec{\zeta }\), we have
Note that the true parameter has the same (unknown) value over all periods \(t=1,\ldots ,T\), only the information matrix might change. If we now take into account the inexact nature of our estimates, i.e., basing decision in period t on the observed estimate \({\widehat{\varvec{\zeta }}}^{t}\), this constraint becomes
which is the multistage equivalent of constraint (4) with uncertainty set
where \({\widehat{\mathcal {Z}}}_{t}\) describes the estimation uncertainty for \({\widehat{\varvec{\zeta }}}^{t}\), which is the estimate of \(\varvec{\zeta }\) in period t. We can readily extend Theorem 1 to these types of constraints in multistage problems. The proof is similar to the proof for the two period case and can be found in Appendix 1.
Theorem 2
Let \(\mathcal {Z},\ {\widehat{\mathcal {Z}}}_{1}, \ldots ,\ {\widehat{\mathcal {Z}}}_{T}\) be closed sets with nonempty interior as given in (7). Then \((\mathbf x \), \(\mathbf u ^1\), \(\ldots ,\mathbf u ^T\), \(\mathbf V ^1,\ldots ,\mathbf V ^T)\) satisfies (6) if and only if there exist \(\varvec{w}_{i1},\ldots ,\varvec{w}_{iT} \in \mathbb {R}^L\) that satisfy
In Theorem 1 we only consider constraints that are linear. This theorem can be readily extended to the case where the constraint is convex (but not necessarily linear) in the here-and-now variables \(\mathbf x \). To do so, we can use Fenchel duality as has been done for nonadjustable robust models in Ben-Tal et al. (2015).
The construction of the standard uncertainty set and the estimation uncertainty set can be done in different ways. Our model based on inexact revealed data has additional uncertainty in the estimates described by the uncertainty sets \({\hat{\mathcal {Z}}}\) or \({\widehat{\mathcal {Z}}}_{1},\ldots ,{\widehat{\mathcal {Z}}}_{T}\) in the multiperiod case. We have to construct another uncertainty set that captures all estimation errors for which we want to be protected in our future planning periods. For constructing the estimation uncertainty set we can use the same techniques as for the static case (see e.g. Bertsimas et al. 2013). We can for instance use historical data on the errors, \(\varvec{\zeta }- {\widehat{\varvec{\zeta }}}^{t}\), obtained from previous planning horizons. If there is insufficient historical data, one can still define uncertainty sets with realistic a priori reasoning. In retail stores, and especially with the growing share of online retail, customers often return a product if it does not meet their requirements. Sales figures then give an indication of the total demand, but it is known that in each period between, for example, 5 and \(10\,\%\) of all products are returned. The bandwidth of this percentage can then be used to construct the estimation uncertainty around the demand estimate obtained via sales figures. Another situation of estimation uncertainty arises when the demand estimate is obtained via accumulation of (correlated) demand from different stores. If we know that different stores need different amounts of time to come up with accurate data (e.g., sales reports), then there is still some uncertainty on the total demand if, for example, only 9 out of 10 stores have reported their sales. In both of these described situations more information will be revealed in later periods and estimates are likely to become more accurate over time. An example of this type of uncertainty set where estimates become more accurate over time is used in the production-inventory problem in the next section.
4 Production-inventory problem
In this section we apply the ARCID approach to the production-inventory problem that was introduced in Ben-Tal et al. (2004), the seminal paper on adjustable robust optimization.
4.1 The nominal model
We consider a single product inventory system, which is comprised of a warehouse and I factories. A planning horizon of T periods is used. In the model we use the following parameters and variables, using the same notation as in Ben-Tal et al. (2004):
4.2 Parameters
- \(d_t\) :
-
Demand for the product in period t;
- \(P_i(t)\) :
-
Production capacity of factory i in period t;
- \(c_i(t)\) :
-
Costs of producing one product unit at factory i in period t;
- \(V_{\text {min}}\) :
-
Minimal allowed level of inventory at the warehouse;
- \(V_{\text {max}}\) :
-
Storage capacity of the warehouse;
- \(Q_i\) :
-
Cumulative production capacity of the i-th factory throughout the planning horizon.
4.3 Variables
- \(p_i(t)\) :
-
The amount of the product to be produced in factory i in period t;
- v(t):
-
Inventory level at the beginning of period t (v(1) is given).
We try to minimize the total production costs over all factories and the whole planning horizon. The restriction is that all demand in period t must be satisfied by units in stock in the warehouse or by the production in period t. If all the demand, and all other parameters, are certain in all periods \(1,\ldots ,T\), then the problem is modeled by the following linear program (Ben-Tal et al. 2004, Sect. 5):

4.4 The affinely adjustable robust model based on inexact data
We assume that we can make decisions based on estimates of the realized demand scenario \(\mathbf d = (d_1,\ldots ,d_T)\). We should specify our production policies for the factories before the planning periods starts, at period 0. When we specify these policies, we only know that demand in consecutive periods are independent and reside in a certain box region,
with given \(0<\theta \le 1\), the level of uncertainty, and nominal demand \(d_t^*\) in period t. So far the model is exactly the same as in Ben-Tal et al. (2004) if we assume that we can estimate the demand \(d_t\) exactly in periods \(r\in I_t\), where \(I_t\) is a given subset of \(\{1,\ldots ,T\}\). In Ben-Tal et al. (2004) different sets for \(I_t\) are used:
-
\(I_t = \{1,\ldots ,t\}\), the information basis where demand from the past and the present is known exactly, for the future no extra information is known;
-
\(I_t = \{1,\ldots ,t-1\}\), the information basis where all demand from the past is known exactly, there is no information about the present;
-
\(I_t = \{1,\ldots ,t-4\}\), the information about the past is received with a four day delay. For other periods in the past (\(t-3,t-2\) and \(t-1\)) there is no extra information at all.
Now we assume the decisions in period t are based on estimates \({\widehat{d}}_{r,t}\), made in period t, for the actual demand \(d_r\) in the period \(r\in \{1,\ldots ,t\}\). We assume that these estimates can, in principle, take any value that the demand \(d_r\) can take, so \({\widehat{d}}_{r,t} \in \mathcal {Z}_r\) and that the estimation error \({\widehat{d}}_{r,t} - d_r\) lies in a box region:
where the parameter \(\rho _{r,t}\) indicates the fraction of initial uncertainty level \(\theta \) for the estimate \({\widehat{d}}_{r,t}\).
Note that if we have exact information for periods in the information basis, i.e., \({\widehat{d}}_{r,t} = d_t\) for all \(r \in I_t\) and no extra information (besides \({\widehat{d}}_{r,t} \in \mathcal {Z}_t\)) for all periods outside the information basis, then we end up in the case of exact revealed information as considered by Ben-Tal et al. (2004). This situation can be can be modeled as a special case of our model by using the following values for \(\rho _{r,t}\)
which means that the estimation error equals zero for estimates on demand in periods that lie in the information set and it is \(\theta \) (so very large) for periods outside this information basis.
The general situation with inexact data lies in between the two extreme scenarios where one either knows the demand exact, or not at all. For this we specify the information set in a more general way:
This definition of \(\hat{I}_t\) is indeed a more general description. For large estimation errors (\(\rho _{r,t} \ge 1\)) we could just as well decide on the variables beforehand, i.e., we have no extra useful information on the actual realizations compared to the information at time \(t=0\). We can therefore safely exclude all periods where the estimates are too noisy (the periods for which \(r\not \in \hat{I}_t\)). Since we apply the ARCID method based on inexact data, we take affine decision rules based on inexact estimates:
where the coefficients \(\pi _{i,t}^r\) are the new nonadjustable variables in the model. For notational convenience we write the vector \({\widehat{\mathbf{d }}}_{t}\) as the vector containing all the estimates \({\widehat{d}}_{r,t}\) for all \(r\in \hat{I}_t\), \(t=1,\ldots ,T\). The uncertainty set can now be written as:
with \(\mathcal {Z}_t\) and \({\widehat{\mathcal {Z}}}_{r,t}\) as specified in respectively (8) and (9). The linear problem (P:Nominal) becomes (after elimination of the v-variables) a semi-infinite LP if we use linear decision rule (10):

The resulting tractable robust counterpart can be found using Theorem 2 and is given in Appendix 2.
4.5 Data set from Ben-Tal et al. (2004)
We take the same data set as in the illustrative example by Ben-Tal et al. (2004, p. 370–371): “There are \(I=3\) factories producing a seasonal product, and one warehouse. The decisions concerning production are made every two weeks, and we are planning production for 48 weeks, thus the time horizon is \(T=24\) periods. The nominal demand \(d^*\) is seasonal, reaching its maximum in winter, specifically,
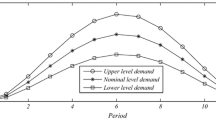
We assume that the uncertainty level \(\theta \) is \(20\,\%\), i.e., \(d_t \in [0.8d_t^*,1.2d_t^*]\), as shown on Fig. 2.
The production costs per unit of the product depend on the factory and on time and follow the same seasonal pattern as the demand, i.e., rise in winter and fall in summer. The production costs for a factory i at a period t is given by (Fig. 3):
The maximal production capacity of each one of the factories at each two-weeks period is \(P_i(t) = 567\) U, and the integral production capacity of each one of the factories for a year is \(Q_i=13{,}600\). The inventory at the warehouse should be no less than 500 units, and cannot exceed 2000 U”.
The initial inventory level v(1) was not stated in Ben-Tal et al. (2004), but this value is equal to the lower bound of the inventory level at the warehouse, namely 500. Note that the initial inventory level could also be chosen uncertain if the initial state is unkown. For new products, where no past demand has occured, it is realistic to assume no uncertainty on the stock as the inventory level is set by the manager itself. Here we also assume that the initial inventory level is known, as in Ben-Tal et al. (2004).
5 Numerical results
Ben-Tal et al. (2004) conduct two series of experiments based on the data given in Sect. 4.3. In the first series of experiments they modify the parameter \(\theta \) to analyze the influence of demand uncertainty on the total production cost. In the second series of experiments they change the information basis \(I_t\), the (exact) information that is used in the decision rule. Note that Ben-Tal et al. (2004) deal with the case where in period t all demand from the periods in the information set \(I_t\) is known exactly. For instance, if the information set is equal to \(I_t = \{1,\ldots ,t-1\}\), then in period t we can base our production decision rule on the exact values of the demand realizations in periods \(1,\ldots ,t-1\), and use no information on the demand in periods after \(t-1\). We extend these experiments to include inexact data in some periods to show the benefits of the ARCID model over the ARC model.
Just as in Ben-Tal et al. (2004), we test the management policies by simulating 100 demand trajectories, \(d = (d_1,\ldots ,d_T)\). For every simulation the demand trajectory is randomly generated with \(d_t\) uniformly distributed in \([(1-\theta )d_t^*,(1+\theta )d_t^*]\), where \(20\,\%\) (\(\theta = 0.2\)) is the chosen uncertainty level. The uncertainty level of the demand is set to \(20\,\%\) in all experiments, as this seems to be the most restrictive level of uncertainty and is the same level that has been used by Ben-Tal et al. (2004). For higher uncertainty levels like \(30\,\%\), even the model without uncertainty (P:Nominal) is no longer feasible for the maximal demand pattern with \(d_t = (1+\theta )d_t^*\) (without uncertainty) because of the bounds on production imposed by \(P_i(t)\) and \(Q_i\). In line with the experiments performed by Ben-Tal et al. (2004), we compute the average costs for our solutions by assuming an uniform distrutibution for the estimated demand. In Ben-Tal et al. (2004) they have used 100 simulated demand trajectories to approximate the mean costs. However, since the costs are linear in the estimated demand parameter, this can be found by substituting the expected (nominal) demand in the objective function. All solutions are obtained by the commercial solver (Gurobi Optimization 2015) programmed in the YALMIP language (Löfberg 2004) in MATLAB.
5.1 Experiments with decision rules using inexact data on demand
Similar to Ben-Tal et al. (2004), we saved the demand trajectories to compute the so-called costs of the ideal setting, the utopian world where the entire demand trajectory is known beforehand. The ideal setting is used to benchmark the performance of the ARCID solution. In the ideal setting one sets the policy only for one sample demand realization, so the solution does not have to be feasible for all possible demand trajectories. Hence, the costs in the ideal setting are obviously a lower bound of the costs for the ARCID solutions. For the ideal setting the worst case is the demand trajectory with the highest demand: \(d_t = (1+\theta )d_t^*\) for all t. The worst case costs in the ideal setting can be easily solved and turns out to be 44, 199. The mean costs in the ideal case are approximated by averaging the ideal costs for the 100 simulated demand trajectories and equals 33, 729.
In our model, the demand from the past periods is not known exactly, but we assume to have inexact estimates for some past and present periods. Several cases are investigated, for instance those where the delay for receiving the exact demand information is even more than 2 periods, i.e., the exact demand is known after 3, 4 or more periods. These cases are infeasible in the ARC model, see Ben-Tal et al. (2004).
In the experiments, the influence of the estimation error \(\rho _{r,t}\) on the total production costs is tested. An estimation error of \(0\,\%\) for the demand in period \(t-1\) means that \(\rho _{t-1,t} = 0\) (exact information). An estimation uncertainty of \(10\,\%\) for the demand in period \(t-4\) means that \(\rho _{t-4,t} = 0.1\) and so forth. We have considered various estimation uncertainties for the estimates on past realizations, as depicted in Table 2. Note that in all cases the estimates become more accurate over time. In other words, the estimation error decreases over time: \(\rho _{t-r,t} \le \rho _{t-s,t}\) for all \(r \le s\) and all periods t. In Table 2 one notices this by seeing that the values for the estimation errors are decreasing right-to-left. Therefore, estimates on demand values from longer ago in the past are more accurate than estimates on recent demand realizations.
The cases in Table 2 can be explained as follows:
-
For Cases 1 and 2 we assume that all demand from the past is known exactly. For the present period we have a good estimate on the demand that gives extra information compared to the information known at the start of the planning period (\(t=0\)).
-
The Cases 3–6 assume to have no additional knowledge about the present. Furthermore, the exact demand from previous periods is received with a certain delay, but there are already estimates on the demand available before this information is received.
-
Case 4 is equivalent to the uncertainty set from (Ben-Tal et al. 2004) with exact revealed information and the information sets being \(\{1,\ldots ,t-2\}\).
To compare the solutions in different cases we have to take into account that there could be multiple optimal solutions. These solutions all give the same worst case costs, but could perform differently on individual demand trajectories and therefore also result in different mean costs. To overcome this problem, we used the two step approach that has been given in Iancu and Trichakis (2013) and de Ruiter et al. (2016). In this two step approach, one first minimizes the worst case costs as usual in robust optimization. To choose one solution among the set of robustly optimal solutions that performs good on average, a second step is introduced. In this second step, we add a constraint that the worst case costs do not exceed the optimal worst case costs and we replace the objective by the costs attained for the nominal demand. If in the second step the costs are minimized for the nominal demand, then one obtains the costs that are best for the mean.
The mean costs in Table 2 show a strange pattern among the different cases at first sight. For instance, Case 5 produces higher mean costs than Case 6, but the estimation error is much less. This phenomenon can be explained in the following way. In the two step approach, we first search for a solution with minimal worst case costs \(F^*\) and then we search among all solutions with worst case costs \(F^*\) for the solution that minimizes the nominal demand trajectory. Hence, the information in Case 2 is used to decrease the worst case costs, possibly at the costs of the average behavior.
5.2 Comparison with affinely adjustable robust model based on exact data
For each case we compare the WC costs and feasibility of the ARCID to the costs and feasibility resulting from the AARC approach, where one is only allowed to use the estimates that are exact (estimates with an estimation error of \(0\,\%\)). Hence, for the AARC solutions we only included the exact estimates, those corresponding with \(\rho _{r,s} = 0\), in the decision rule. The results are given in Table 3.
Case 4 only deals with exact estimates. The ARCID and the AARC are equivalent in those cases because there is no estimation uncertainty. There are other situations, namely in Case 5 and 6, where the ARCID use the extra inexact data to produce feasible solutions whereas the AARC is infeasible.
For the cases where both the AARC and the ARCID model are feasible, we notice that there is only a minor improvement in the worst case costs. For those cases, the question might rise whether we can neglect the estimation error and just apply the AARC model from (Ben-Tal et al. 2004). In contrast to the AARC that we used to obtain the results in Table 3, we now take the information set for the AARC that includes all (estimated) demands that have an estimation error less than \(100\,\%\). Hence, all estimation errors strictly between 0 and \(100\,\%\) are neglected and the corresponding demand estimates are used as if they were exact. To empirically see how many violations occur if the inexact nature is neglected in the AARC model, we also have to draw the demand estimates in each of the 100 demand trajectories. We draw the estimates on demand from a uniform distribution as well, using the same simulated actual demand trajectories across all cases. In every period t we know for the estimate \({\widehat{d}}_{r,t}\) on the simulated demand in period r that \({\widehat{d}}_{r,t} - d_r \in [-\rho _{r,t}\theta d_r^*,\rho _{r,t}\theta d_r^*]\), where the value \(d_r\) is taken from the earlier simulated demand patterns. Furthermore, \({\widehat{d}}_{r,t}\) resides in the box region \([(1-\theta )d_r^*,(1+\theta )d_r^*]\). The estimates are therefore uniformly drawn from the region:
For each case we check for how many demand trajectories, out of the 100 simulated realizations, the inventory level is lower than the minimimum inventory level \(V_{\text {min}}\) of 500 or higher than the maximum inventory level \(V_{{\text {max}}}\) at some point in the planning period. The results are given in Table 4.
In Case 4 there are no violations, since this one is equivalent to the AARC based on exact information as we argued in Sect. 5.1. Table 4 also shows that constraints are violated more often when the estimation uncertainty is in the recent periods t and \(t-1\). For example, the solution in Case 1, which has only \(10\,\%\) estimation uncertainty in period t, violates the minimum required inventory level 64 out of 100 times and for 55 simulated demand trajectories the stock level exceeded maximum allowed inventory level. The inventory levels for three arbitrary trajectories of Case 4 are depicted in Fig. 4 for both the ARCID and the AARC that neglects the estimation errors.
6 Conclusions
In this study we consider uncertain multistage inventory systems where the observed data on demand obtained in each period is inexact. We extend the adjustable robust counterpart (ARC) method for production-inventory problems to the (ARCID) model in which the decision rules are based on inexact revealed data. Our numerical results demonstrate that ARCID outperforms ARC, which can only rely on exact revealed demand data. Two cases that are infeasible for the ARC solution, are feasible for the ARCID model. It is evident that neglecting the inexact nature of the revealed data may have severe consequences. For example, the inventory level dropped below the allowed minimum in up to \(80\,\%\) of the simulated demand trajectories.
The use of the ARCID method is thus well justified, in particular so since the resulting optimization problem that need to be solved maintain a comparable tractability status to that of the ARC method. Furthermore, there exist several software packages, such as YALMIP (Löfberg 2012), ROME (Goh and Sim 2011) and (AIMMS 4.19 2016), that can do reformulation of adjustable robust optimization problems which can be readily extended to the ARCID model. Finally, we emphasize that the ARCID model set up in this paper can also be applied to other ARC models where revealed data in each stage is inexact in various areas of operations management, such as facility location planning, flexible commitment models, capacity expansion planning, portfolio optimization and management of power systems.
References
AIMMS 4.19 (2016) AIMMS B.V., Haarlem, The Netherlands, software available at http://www.aimms.com/
Baron O, Milner J, Naseraldin H (2011) Facility location: a robust optimization approach. Prod Oper Manag 20(5):772–785
Ben-Tal A, Goryashko A, Guslitzer E, Nemirovski A (2004) Adjustable robust solutions of uncertain linear programs. Math Program 99(2):351–376
Ben-Tal A, Golany B, Nemirovski A, Vial JPh (2005) Retailer-supplier flexible commitments contracts: a robust optimization approach. Manuf Serv Oper Manag 7(3):248–271
Ben-Tal A, El Ghaoui L, Nemirovski A (2009) Robust optimization. Princeton series in applied mathematics. Princeton University Press, Princeton
Ben-Tal A, den Hertog D, Vial JPh (2015) Deriving robust counterparts of nonlinear uncertain inequalities. Math Program 149(1–2):265–299
Bertsimas D, Goyal V (2012) On the power and limitations of affine policies in two-stage adaptive optimization. Math Program 134(2):491–531
Bertsimas D, Brown DB, Caramanis C (2011a) Theory and applications of robust optimization. SIAM Rev 53(3):464–501
Bertsimas D, Iancu DA, Parrilo PA (2011b) A hierarchy of near-optimal policies for multistage adaptive optimization. Autom Control IEEE Trans 56(12):2809–2824
Bertsimas D, Gupta V, Kallus N (2013) Data-driven robust optimization. arXiv:1401.0212v1
Calafiore GC (2008) Multi-period portfolio optimization with linear control policies. Automatica 44(10):2463–2473
Calafiore GC (2009) An affine control method for optimal dynamic asset allocation with transaction costs. SIAM J Control Optim 48(4):2254–2274
DeHoratius N, Raman A (2008) Inventory record inaccuracy: an empirical analysis. Manage Sci 54(4):627–641
Goh J, Sim M (2011) Robust optimization made easy with rome. Oper Res 59(4):973–985
Guigues V, Sagastizábal C (2012) The value of rolling-horizon policies for risk-averse hydro-thermal planning. Eur J Oper Res 217(1):129–140
Gurobi Optimization Inc (2015) Gurobi optimizer reference manual. http://www.gurobi.com
Guslitzer E (2002) Uncertainty-immunized solutions in linear programming. M.Sc. thesis, Technion-Israel Institute of Technology
Haug A, Zachariassen F, van Liempd D (2011) The costs of poor data quality. J Ind Eng Manag 4(2):168–193
Iancu DA, Trichakis N (2013) Pareto efficiency in robust optimization. Manage Sci 60(1):130–147
Iancu DA, Sharma M, Sviridenko M (2013) Supermodularity and affine policies in dynamic robust optimization. Oper Res 61(4):941–956
Kök AG, Shang KH (2007) Inspection and replenishment policies for systems with inventory record inaccuracy. Manuf Serv Oper Manag 9(2):185–205
Löfberg J (2004) Yalmip-a toolbox for modeling and optimization in MATLAB. In: Proceedings of the CACSD Conference. Taipei, Taiwan
Löfberg J (2012) Automatic robust convex programming. Optim Methods Softw 27(1):115–129
Ng TS, Sy C (2014) An affine adjustable robust model for generation and transmission network planning. Int J Electr Power Energy Syst 60:141–152
Ordóñez F, Zhao J (2007) Robust capacity expansion of network flows. Networks 50(2):136–145
Redman TC (1998) The impact of poor data quality on the typical enterprise. Commun ACM 41(2):79–82
Rocha P, Kuhn D (2012) Multistage stochastic portfolio optimisation in deregulated electricity markets using linear decision rules. Eur J Oper Res 216(2):397–408
Rockafellar RT (1970) Convex Analysis. Princeton University Press, Princeton
de Ruiter FJCT, Brekelmans RCM, den Hertog D (2016) The impact of the existence of multiple adjustable robust solutions. Mathematical Programming, pp 1–15. doi:10.1007/s10107-016-0978-6 (advance online publication)
Soffer P (2010) Mirror, mirror on the wall, can I count on you at all? Exploring data inaccuracy in business processes. In: Enterprise, Business-Process and Information Systems Modeling. Springer, New York, pp 14–25
Author information
Authors and Affiliations
Corresponding author
Additional information
Frans de Ruiter was supported by the NWO Grant No. 406-14-067.
Appendices
Appendix 1: Proof of Theorem 2
Proof
We can replace the semi-infinite constraint by constraints involving maximization over the uncertainty and obtain the following constraint:
or, by using the definition of support functions,
Hence, all we need to do is to find an expression for the support function, similar as we did in the proof of Theorem 1. To do so, note that for the indicator function we have now
If we define the function \(h_t(\varvec{\zeta }, {\widehat{\varvec{\zeta }}}^{t}) = \delta \left( \left( {\widehat{\varvec{\zeta }}}^t - {\varvec{\zeta }}\right) \ |\ {\widehat{\mathcal {Z}}}_t\right) \), then by using the definition of conjugate functions we obtain
Using this conjugate function, and the fact that \(\mathcal {U}\) has nonempty relative interior, we can now find the expression for the support function in (5) using the sum relation for conjugate functions (see again Rockafellar 1997, Chapter 16):
Substituting this result into (11) yields that (6) is feasible if and only if there exist \(\varvec{z}_i\), \({\varvec{\widetilde{z}}_{i1}},\ldots ,{\varvec{\widetilde{z}}_{iT}}\), \(\varvec{w}_{i1},\ldots ,\varvec{w}_{iT}\), \({\varvec{\widetilde{w}}_{i1}},\ldots ,{\varvec{\widetilde{w}}_{iT}} \in \mathbb {R}^L\) that satisfy
The result then follows by elimination of the variables \({\varvec{\widetilde{w}}_{it}}\), \({\varvec{\widetilde{z}}_{it}}\) for all \(t=1,\ldots ,T\) and \(\varvec{z}_i\). \(\square \)
Appendix 2: The tractable robust counterpart based on inexact data
Here we present the final tractable robust counterpart for the model (P:ARCID). Note that all but the last two sets of constraints on \(V_{\text {min}}\) and \(V_{\text {max}}\) are the same as in Ben-Tal et al. (2004), since those are the only constraints involving both the true demand parameters and their inexact estimates.

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
de Ruiter, F.J.C.T., Ben-Tal, A., Brekelmans, R.C.M. et al. Robust optimization of uncertain multistage inventory systems with inexact data in decision rules. Comput Manag Sci 14, 45–66 (2017). https://doi.org/10.1007/s10287-016-0253-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10287-016-0253-6